 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How does aggregation of doxorubicin molecules affect its solvation and membrane penetration?†
Sadaf
Shirazi-Fard
 a,
Amin Reza
Zolghadr
a,
Amin Reza
Zolghadr
 *a and
Axel
Klein
*a and
Axel
Klein
 *ab
*ab
aDepartment of Chemistry, Shiraz University, Shiraz, 71946-84795, Iran. E-mail: arzolghadr@shirazu.ac.ir; Tel: +98 71 3613 7157
bUniversity of Cologne, Faculty of Mathematics and Natural Sciences, Department of Chemistry, Greinstrasse 6, D-50939 Cologne, Germany. E-mail: axel.klein@uni-koeln.de; Tel: +49-221-470-4006
First published on 14th November 2023
Abstract
Intermolecular interactions of drug molecules can lead to aggregation, which has a significant impact on their application. This problem might escape the attention when studying their solubility as small aggregates might behave almost as single molecules. We studied the aggregation behaviour of doxorubicin (DOX) molecules through density functional (DFT) methods and molecular dynamics (MD) simulations in water, dimethylformamide (DMF), ethanol (EtOH), and dimethyl sulfoxide (DMSO). We described the degree of aggregation by MD-calculated radial distribution function, combined radial/angular distribution functions, autocorrelation functions, and the number of hydrogen bonds of individual DOX and solvent atoms. MD-calculated diffusion coefficients for DOX decrease along the series water > DMF > EtOH > DMSO (0.101 × 10−9, 0.047 × 10−9, 0.025 × 10−9, and 0.007 × 10−9 m2 s−1, respectively) consistent with increasing aggregation found in the MD simulations. These aggregates have different characters, depending on the DOX⋯solvent interactions, and include hydrogen bonding and π-stacking. Even though the solvation energy of a single DOX molecule in DMSO (−24.8 kcal mol−1) is higher than in other solvents, the formation of larger aggregates in this solvent prevents proper solvation. Further, the orientation of doxorubicin molecules at octanol/water and dipalmitoylphosphatidylcholine (DPPC)/water interfaces was studied with two different orientations from the bivariate maps. In the case of the DPPC/water interface, the anthracycline part points toward the aqueous phase, while this part is oriented almost parallel to the octanol/water interface in DMSO.
1 Introduction
One of the most important limitations for the biological activity and, thus, for the administration of drugs is poor solubility. Solubility issues are one of the main reasons why drug candidates that have reached clinical trials were later discarded. For many commercial drugs, formulations had to be developed to make them usable.1–4 Solubility is influenced by many parameters, such as pressure, temperature, and pH of the medium. On the molecular level, solubility depends on the intermolecular forces between the solute and the solvent.5–8 Strong solute⋯solute interactions overruling solute⋯solvent interactions lead to nanoscale or microscale aggregation, and the structure and properties of these aggregates, as well as the dynamics of aggregate formation, and decomposition, are determined by the nature of the solvents. Therefore, the investigation of interactions between drug molecules and solvents provides important information to design suitable drug–solvent combinations and to develop new solvents or formulations.One of the most widely studied and used chemotherapy agents in recent years is doxorubicin (DOX, Scheme 1). DOX, also known as Adriamycin, is an antiproliferative drug that intercalates into the DNA, thus hampering the division of cancer cells and eventually inducing apoptosis.3,4,9–14 DOX as hydrochloride is water-soluble (∼10 mg mL−1) and is injected in patients. Recently, the use of DOX formulations, especially polyethylene glycol encapsulated (PEGlated) or liposomal encapsulated DOX instead of pure DOX has helped to reduce the side effects such as cardiotoxicity.3,4,11,13–16
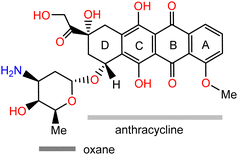 | ||
| Scheme 1 The schematic structure of doxorubicin with labelling of the anthracycline and oxane moieties. | ||
DOX is composed of a hydrophobic anthracycline unit (Scheme 1), substituted with two keto, two hydroxy, and a methoxy function at the aromatic core (rings A to C). A rather hydrophilic part of DOX is constituted from the amine and hydroxy functionalised oxane moiety with a hydroxymethyl and a β-hydroxycarbonyl group at the saturated end of the anthracycline core (ring D). DOX molecules form aggregates in various media due to their amphiphilic nature.17 A previous experimental study using permeation techniques showed that dimers or trimers are formed even at very low DOX concentrations, while aggregates of about 3.7 nm containing approximately 40 DOX molecules are detected in 1 mM aqueous solution.18 Another, more recent experimental study using different imaging techniques reported large vesicular aggregates of DOX in imidazolium-based ionic liquids (IL) promoted by hydrogen bonding, hydrophobic, and π-stacking interactions.19
Molecular dynamics (MD) simulation is a potent tool in modern molecular modelling that computes the motions and dynamics of individual molecules which are not directly observable by experiments.20 MD simulations have been previously used for studying the interaction between DOX and a dipalmitoylphosphatidylcholine (DPPC)/cholesterol lipid bilayer21 and also for investigating the interactions of DOX and hydrophobically modified chitosan oligosaccharides.22 MD simulations and first-principles density functional theory (DFT) calculations have also been used to study the partial-charge distribution and the electronic structure of DOX in three different model environments, which were solvated, isolated, and intercalated in a DNA complex, respectively.23 A recent MD simulation study was carried out to probe for the interactions of four anthracycline derivatives, including DOX, with two different lipid bilayers, the unsaturated POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) and the saturated DMPC (dimyristoylphosphatidylcholine).24 Similar MD simulations were performed to study the pH-dependent adsorption of DOX on carbon quantum dots25 and the interaction of DOX in sphingomyelin-based lipid membranes.26 A further MD simulation of DOX aggregation in water media was carried out to find applications for targeted drug delivery using DOX in immune complexes.27 MD studies have also been carried out on pH-dependent diffusion, loading, and release of DOX from graphene, graphene oxide,28 and carbon nanotubes.29,30 We have very recently contributed to this field by studying the encapsulation and release of DOX from TiO2 nanotubes experimentally and in all-atom MD simulations.31
Herein, we present a detailed MD study on the interactions of DOX with the four solvents water, N,N-dimethylformamide (DMF), ethanol (EtOH), and dimethyl sulfoxide (DMSO), and DOX aggregation in these solvents. Organic solvents like DMSO, DMF, and EtOH have been frequently used to increase the solubility and thus the applicability of lipophilic anti-cancer drugs, but some studies suggest more impact of these solvents than just solubilisation and for DMSO toxic properties were found.32–34 In view of this intrinsic toxicity, the use of DMSO is discouraged, and DMF seems to be the better choice.34–38
Further, we investigated the partitioning of DOX in an octanol/water system and its permeation through water/membrane interfaces through MD and DFT calculations. The zwitter-ionic dipalmitoylphosphatidylcholine (DPPC) lipid membrane was chosen in view of its extensive application in the modelling of membrane interactions and for its well-established force-field parameters.39 To our knowledge, this study represents the first MD investigation of DOX molecule aggregation in different solvents. Our findings complement previous studies on DOX interaction with POPC, DMPC, and sphingomyelin-based model membranes.24,26
2 Computational methods
2.1 Density functional theory calculations
DFT-optimised geometries of DOX in the gas phase and solvents environments were calculated using the Gaussian 09 program suite at B3LYP/6-311+G* level (Fig. 1 and Fig. S1 in the ESI,† for atoms labelling).40 The polarized continuum model (PCM) was used to include solvent effects.41,42 Using this model, solvation energies (the free energy differences in the solvent and the gas phase), the energy gap (ELUMO − EHOMO), and dipole moments were calculated.Molecular electrostatic potential (MEP) maps were calculated in the gas phase. The atom charges for DOX and the solvents were calculated using the natural bond orbital (NBO) method,43 results are provided in Tables S1–S5 (ESI†). In first trials, we also performed the simulations using electrostatic potential-based (ESP) charges but could not find significant differences in the structural characteristics of the aggregated DOX molecules. We thus continued the simulations using NBO charges (Fig. S2 and Table S6, ESI†).
2.2 Molecular dynamics simulations
The MD simulations were carried out using the GROMACS 4.5.4 package.44 We simulated two different systems: (I) DOX aggregation in four solvents, including water, DMF, EtOH, and DMSO. (II) DOX molecules at DPPC/water and octanol/water interfaces. The structure and topology of DOX were produced using the small molecule topology generator PRODRG.45 Well-approved force-field parameters for the DPPC lipid membrane are available.39Molecular mechanics force fields of DOX, water, DMF, EtOH, DMSO, and octanol were parameterised with the GROMOS (53A6) force field.46 The interaction parameters of dissimilar atoms were calculated from the standard force field mixing rules  . 12 DOX molecules were added to the boxes, filled with 2000 solvent molecules, and equilibrated with final box sizes of 43 × 43 × 43 Å, 53 × 57 × 57 Å, 50 × 63 × 63 Å, and 59 × 64 × 64 Å, respectively. Periodic boundary conditions in three dimensions were applied for the whole ensembles. The equations of motion were solved using the leapfrog integrator. The heating/cooling procedure was performed. Then, the temperatures were increased at intervals of 20 K up to 400 K. The simulation was conducted for 5 ns under constant number, volume, and temperature (NVT) conditions at each temperature for each system. Afterward, the temperature of the systems was decreased to 300 K at steps of 50 K. Furthermore, we conducted an additional simulation for the DOX/water system using a larger simulation box containing 10
. 12 DOX molecules were added to the boxes, filled with 2000 solvent molecules, and equilibrated with final box sizes of 43 × 43 × 43 Å, 53 × 57 × 57 Å, 50 × 63 × 63 Å, and 59 × 64 × 64 Å, respectively. Periodic boundary conditions in three dimensions were applied for the whole ensembles. The equations of motion were solved using the leapfrog integrator. The heating/cooling procedure was performed. Then, the temperatures were increased at intervals of 20 K up to 400 K. The simulation was conducted for 5 ns under constant number, volume, and temperature (NVT) conditions at each temperature for each system. Afterward, the temperature of the systems was decreased to 300 K at steps of 50 K. Furthermore, we conducted an additional simulation for the DOX/water system using a larger simulation box containing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules. Since no significant differences were observed in comparison with the small-sized simulation, we continued the simulation using the smaller one. To validate the force field, a simulation for DOX/water system was performed using the Amber force field (GAFF)47 considering the partial charges of DOX calculating through the restrained electrostatic potential (RESP) method27,48 which was carried out by RED server service (see Tables S7 and S8, ESI†).49 Also, the simple point charge extended (SPC/E) approach was applied for modeling water molecules.50 In addition, the simulation was performed for both neutral (DOX) and positive charged (DOXH+) DOX molecules.
000 water molecules. Since no significant differences were observed in comparison with the small-sized simulation, we continued the simulation using the smaller one. To validate the force field, a simulation for DOX/water system was performed using the Amber force field (GAFF)47 considering the partial charges of DOX calculating through the restrained electrostatic potential (RESP) method27,48 which was carried out by RED server service (see Tables S7 and S8, ESI†).49 Also, the simple point charge extended (SPC/E) approach was applied for modeling water molecules.50 In addition, the simulation was performed for both neutral (DOX) and positive charged (DOXH+) DOX molecules.
The equilibration of DOX in the solvents was carried out in three stages. First, initial energy minimisation applying the steepest descent algorithm was applied to remove close contacts and to find a minimum on the potential energy surface. Then, an equilibration under constant NVT conditions was performed over 5 ns. Finally, the systems were equilibrated for 5 ns under constant number, pressure, and temperature (NPT) conditions. The final configurations from these procedures were taken as the initial structures for the 30 ns production runs under NPT condition at 300 K. The first 10 ns was set aside for equilibration and discarded for analysis. 20 ns were sufficient to detect the convergence of the calculations.
The behaviour of DOX at octanol/water interface was modelled using 512 molecules of octanol in the simulation box, and the box was equilibrated for 20 ns in order to generate an octanol slab with the final thickness of 95 Å. The simulation box was extended to 180, 80, and 50 Å in the z, x, and y directions, respectively. Then, 12 DOX molecules were added on both sides of the octanol slab surfaces. Finally, the simulation box was filled with 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules. The simulation was performed under constant NVT conditions for 5 ns and then under NPT conditions for 5 ns. The final configurations from these steps were used as the initial structure for the 50 ns production runs under NPT conditions at 310 K.
000 water molecules. The simulation was performed under constant NVT conditions for 5 ns and then under NPT conditions for 5 ns. The final configurations from these steps were used as the initial structure for the 50 ns production runs under NPT conditions at 310 K.
For DOX at the DPPC/water interface, the pre-equilibrated coordinates force field parameters of the DPPC bilayer (128 lipids) were used and initial structures of DPPC membranes were taken from previous publications of the Tieleman group39,51 and their website. Simulations were performed using the GROMOS96 53A6 force field.46
The system was extended to 150 Å in z-direction (64 Å, each for x and y). Then, 12 DOX molecules were added on both sides of the DPPC surfaces, and the box was filled with 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules. An equilibration under constant NVT conditions was performed over 5 ns, and then the system was equilibrated for 5 ns under constant NPT conditions. Finally, the production runs were conducted for 50 ns under NPT conditions at 310 K.
000 water molecules. An equilibration under constant NVT conditions was performed over 5 ns, and then the system was equilibrated for 5 ns under constant NPT conditions. Finally, the production runs were conducted for 50 ns under NPT conditions at 310 K.
Under constant NVT conditions, all simulated systems were connected to the improved velocity-rescaling thermostat with a time constant of 0.1 ps. The Parrinello–Rahman barostat (with a time constant of 2 ps) algorithm was used for the simulations under constant NPT conditions.52,53 In each simulation, a short-range cut-off distance of 12 Å was applied for Lennard-Jones interactions. Additionally, to account for long-range Coulombic interactions, the particle mesh Ewald (PME) method was employed with a cut-off distance of 15 Å.54 In addition, the LINCS algorithm was implemented to allow for a 2 × 10−3 ps time step in each system.55 Explicit water molecules were modelled using the simple point charge (SPC) approach.56 The visual molecular dynamics (VMD) software57 was used to visualise the results.
2.3 Analysis
| ΔGsol = Gsol − Ggas | (1) |
| μtot = (μx2 + μy2 + μz2)1/2 | (2) |
 | (3) |
The diffusion coefficients were derived from the MSDs; the slopes of MSD curves represent the diffusion coefficients (Di). Di is calculated using the Einstein relation (eqn (4)).61
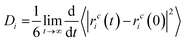 | (4) |
The average cluster size (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) n) was calculated from eqn (5)
n) was calculated from eqn (5)
 | (5) |
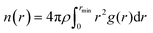 | (6) |
Combined radial/angular distribution functions (CDFs) were calculated to get more detailed information about hydrogen bonding. The standard approach for a hydrogen bond criterion is a distance less than 3 Å and an angle α between 150° and 180°. The CDF analyses were performed using combined radial and angular distribution functions using the TRAVIS (Trajectory Analyzer and Visualizer) package.67
The number of intermolecular DOX⋯DOX hydrogen bonds were calculated using the so-called gh bond utility of the GROMACS package.44
 | (7) |
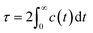 | (8) |
The density profiles of DOX, DPPC (choline, glycerol, phosphate and acyl chain), octanol, and water were obtained over a simulation time of 50 ns. Furthermore, simulations of liquid/liquid interfaces were used to estimate the bulk density of a liquid. In the octanol/DOX/water system, the average density of the octanol phase is 0.864 g cm−3 which is slightly larger than the experimental value of 0.830 g cm−3 for pure octanol. The average density of water is 0.949 g cm−3, which is close to the experimental value (0.997 g cm−3) of pure water.70 In the case of DPPC/DOX/water, the average density of water is 0.942 g cm−3, which lies close to the experimental value of 0.997 g cm−3.
Additionally, atom density profiles were studied to define averaged orientation ordering and spatial positioning of the molecules at the liquid/liquid interfaces. For each system, RDFs between DOX/water, DOX/DPPC, DOX/octanol, and DOX/DOX were calculated to obtain insight into the distribution of atoms in possible configurations of DOX at the octanol/water and DPPC/water interfaces.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2θ − 1〉 where θ is the angle between the C–H bond vectors of the DPPC tail (sn-1 and sn-2 chains) relative to the normal of the bilayer averaged over all simulation trajectories. Order parameters were determined using the GROMACS program gorder. The −SCD(n) values for lipid bilayers lie usually between 0 and 0.5. A −SCD value of 0.5 shows the perfect alignment of the lipid tail to the bilayer normal and a value close to zero represents a random orientation.
cos2θ − 1〉 where θ is the angle between the C–H bond vectors of the DPPC tail (sn-1 and sn-2 chains) relative to the normal of the bilayer averaged over all simulation trajectories. Order parameters were determined using the GROMACS program gorder. The −SCD(n) values for lipid bilayers lie usually between 0 and 0.5. A −SCD value of 0.5 shows the perfect alignment of the lipid tail to the bilayer normal and a value close to zero represents a random orientation.
3 Results and discussion
3.1 DFT calculations on the solvation of DOX
The highest occupied molecular orbital (HOMO) is focused on the dihydroxybenzene ring C and extends to the quinone ring B, while the lowest unoccupied molecular orbital (LUMO) is delocalised over all three aromatic rings of the anthracycline core (A to C) (Fig. 2A). The energy gap in the gas phase is 3.3930 eV. In solution, the energies are reduced along the series EtOH > DMF > DMSO > water which is representing increasing dielectric constants. Generally, a larger HOMO–LUMO gap of DOX in the gas phase means higher stability and resistance to charge transfer and lower polarisability compared to solutions. In turn, the DOX molecule shows higher polarisability and chemical activity in solution.The solvation energies of DOX in different solvents vary only slightly from −23.5 to −24.8 kcal mol−1 (Table 1), in line with spontaneous and exothermic solvation. The DFT-calculated dipole moments of DOX (Table 1) are the same for all solvents and larger in solution than in the gas phase, in line with the interaction of DOX with the dielectric properties of solvents. At the same time, the same values for the dipole moments in the four solvents mean that the DFT–PCM approach fails to give precise information on the DOX⋯solvent interactions. Moreover, it cannot explain the difference in the extent of DOX aggregation we found in the MD simulations (see below). The standard deviation for the energy gaps, the dipole moment, and the solvation energies as compiled in Table 1 show acceptable values for n = 8.
| Medium | Energy gap (eV) | Dipole moment (Debye) | Solvation energies (kcal mol−1) | Dielectric constantb |
|---|---|---|---|---|
| a Standard deviations in parentheses. b The dielectric constant is the input parameter in the PCM model. | ||||
| Gas phase | 3.393 | 5.77 | — | — |
| Water | 3.274 (0.0001) | 6.243 (0.0003) | −24.347 (0.301) | 80.4 |
| DMSO | 3.273 (0.0001) | 6.243 (0.0004) | −24.787 (0.195) | 47.2 |
| DMF | 3.276 (0.0002) | 6.243 (0.0003) | −24.096 (0.290) | 38.3 |
| EtOH | 3.278 (0.0002) | 6.243 (0.0005) | −23.531 (0.232) | 24.3 |
The electron density of DOX in the gas phase was calculated by using the three-dimensional electrostatic potential map (EPM) surfaces (Fig. 2B). They show markedly negatively charged keto functions C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 and C
O8 and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O9 in the quinone ring (ring B) extending a bit in the direction of the O–H⋯Oketo hydrogen bonds (ring C) located on the hydrophobic part of DOX, while positive charges were found in the hydrophilic part in the amine and hydroxy functionalised oxane moiety and to a minor extent in the hydroxymethyl and β-hydroxycarbonyl group in the saturated ring of the anthracycline (ring D). Atomic charges for several sites of DOX in the gas phase and solvents are shown in Table S9 (ESI†). We found that the charges on the O and N atoms of DOX became more negative compared to the gas phase.
O9 in the quinone ring (ring B) extending a bit in the direction of the O–H⋯Oketo hydrogen bonds (ring C) located on the hydrophobic part of DOX, while positive charges were found in the hydrophilic part in the amine and hydroxy functionalised oxane moiety and to a minor extent in the hydroxymethyl and β-hydroxycarbonyl group in the saturated ring of the anthracycline (ring D). Atomic charges for several sites of DOX in the gas phase and solvents are shown in Table S9 (ESI†). We found that the charges on the O and N atoms of DOX became more negative compared to the gas phase.
3.2 MD simulation of DOX in different solvents
Radial distribution functions (RDFs). The most dominant DOX⋯solvent interactions are found between the H and O atoms of DOX with the H or O atoms of the solvents (Fig. 3, complete data in Table S10, ESI†).
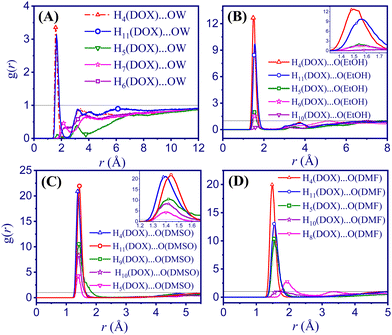 | ||
| Fig. 3 Radial distribution functions (RDFs) of DOX with various solvents. (A) DOX/water (B) DOX/EtOH (C) DOX/DMSO (D) DOX/DMF. | ||
The H4 and H11 atoms of DOX (see Fig. 1 for atom labelling) have a higher probability and short-range distance interaction with the oxygen sites of the solvents under study. The solvation shells are better organised around the hydroxyl groups of aminoglycoside and ketone side chain, than around the amine group of the oxane unit or the quinone ring (B in Scheme 1). In the DOX/water system, the shortest interactions between H4 and H11 and the O atom of water (OW) are located at 1.58 Å and 1.64 Å, respectively. However, these values are lower in the DOX/EtOH system with a H4⋯O(EtOH) distance of 1.48 Å and an H11⋯O(EtOH) distance of 1.56 Å. For the DOX/DMF system, the distances between H4⋯O(DMF) and H11⋯O(DMF) are very similar with the values in EtOH, which 1.48 Å and 1.54 Å, respectively (Table S10, ESI†). For DOX/DMSO, the H4⋯O(DMSO) (1.38 Å) and H11⋯O(DMSO) (1.44 Å) distances are the shortest in the series of solvents. These differences confirm that the interactions of H4 and H11 of DOX with DMSO molecules are stronger with higher probabilities than for the other studied solvents. The intensity of the H⋯O RDF is substantially lower in the case of water, which suggests that the hydrogen bond network between water and DOX leads to a more homogeneous system at a microscopic level. Clearly, the sharp RDFs of the other solvents resemble that of a system with low dynamics.
The RDF plots between different atom sites of DOX were calculated at different simulation times. The plots show that all systems are well equilibrated (Fig. S3, ESI†). To further assess the equilibration of the systems, total energies, density stabilisation, and RMSDs were investigated. As shown in Fig. S4A (ESI†), the total energy trajectory of the systems remained stable during the entire simulation time. Moreover, the density values are stable over the simulation time (see Fig. S4B, ESI†). Furthermore, RMSD was employed as a monitoring parameter to evaluate the equilibration of the systems, as depicted in Fig. S4C (ESI†). To ensure the equilibration of the DOX/DMF system, a simulation was conducted for an extended period of further 30 ns. The analysis of the RMSD of DOX/DMF showed a plateau after about 20 ns in line with a stable equilibrium (Fig. S4D, ESI†). The most probable DOX⋯DOX radial distribution functions (Fig. S5, ESI†) resemble intensified solid-like peaks, especially for non-aqueous solvents.
Coordination number. The coordination numbers of the H4 and H11 atoms representing the two peripheral hydroxyl functions in ring D and the oxane unit of DOX with the O atoms of the solvents were calculated up to the first minimum to probe for hydrophilic interactions of this part of DOX. As expected, the coordination number of both H4⋯(O(solvent) and H11⋯O(solvent) are higher in water than in the other solvents (Table 2).
| Solvent | Water | DMSO | DMF | EtOH |
|---|---|---|---|---|
| Contacts | n(r) | n(r) | n(r) | n(r) |
| H4(DOX)⋯O(solvent) | 0.992 | 0.910 | 0.907 | 0.833 |
| H11(DOX)⋯O(solvent) | 0.975 | 0.909 | 0.858 | 0.827 |
Combined radial/angular distribution functions (CDFs). The CDFs of DOX in water (Fig. 4) show the most intense peak in the histogram for the H4⋯OW interaction at a distance of 1.58 Å and an angle α of 165° ≤ α ≤ 180° for O4–H4–OW, representing largely electrostatic hydrogen bonds.74,75 In the case of DOX/EtOH (Fig. S6, ESI†), a H4⋯O(EtOH) hydrogen bond is found at 1.48 Å (165° ≤ ∝ ≤ 180°). The peak for H11⋯O(EtOH) is centred around 1.56 Å, with an angle of about 180° (a linear hydrogen bond) with a higher probability. Further strong interactions are O4⋯H(EtOH) (1.64 Å and 165° ≤ ∝ ≤ 180°), O11⋯H(EtOH) (1.60 Å and 170° ≤ ∝ ≤ 180°), O5⋯H(EtOH) (1.70 Å and 170° ≤ ∝ ≤ 180°), and H5⋯O(EtOH) (1.54 Å and 170° ≤ ∝ ≤ 180°).
The CDF histograms in the DOX/DMSO system (Fig. S7, ESI†) show the H4⋯O(DMSO) interaction at a distance of 1.38 Å with an angle between 170° ≤ ∝ ≤ 180°, while the peak between H11⋯O(DMSO) is located at 1.44 Å with α ∼ 180° which represents a linear hydrogen bond and exhibits high probability in comparison with other peaks. The H5⋯O(DMSO), H9⋯O(DMSO), and H10⋯O(DMSO) correlations are also strong with a distance of 1.40 Å, 1.42 Å, and 1.42 Å, respectively, and angles between 165° ≤ ∝ ≤ 180°.
In the DOX/DMF system (Fig. S8, ESI†), the H4⋯O(DMF) interaction is found at a distance of 1.48 Å and an O4–H4–O(DMF) angle of 165° ≤ ∝ ≤ 180°. The H11⋯O(DMF) hydrogen bond is found at 1.54 Å with angles between 165° ≤ ∝ ≤ 180°, while H5⋯O(DMF) has the same distance, but an angle close to 180° in line with a linear hydrogen bond. However, the H9⋯O(DMF) and the H10⋯O(DMF) interactions are reduced with angles between 140° ≤ ∝ ≤ 160°. The hydrogen bonding patterns of DOX and solvents show that the H4, H11, O4, and O11 atoms of DOX have a higher tendency to interact with solvents and have stronger hydrogen bonds.
The correlations between O4⋯HW (1.66 Å; 170° ≤ α ≤ 180°) and H11⋯OW (1.64 Å; 165° ≤ α ≤ 180°) are also intense, whereas the O11⋯HW (1.74 Å; 165 ≤ α ≤ 180°), H5⋯OW (1.68 Å; 165° ≤ α ≤ 180°) and O5⋯HW interactions (1.74 Å; 165° ≤ α ≤ 180°) are less probable.
Thus, the H4⋯O(solvent) interaction is always the shortest of all hydrogen bonds with increasing distances along the series DMSO < DMF/EtOH < water, followed by the H11⋯O(solvent) with increases along the same series. On the other hand, the H4⋯O(solvent) hydrogen bond has increasing probabilities from water < EtOH < DMF < DMSO while H11⋯O(solvent) increased along water < DMF < EtOH < DMSO. The last series do not simply correlate with the H4 or H11 coordination numbers (Table 2). It is obvious, that, simple correlations are not possible based on the CDF histograms, since it is always a multitude of H(DOX)⋯O(solvent) bonds and also O(DOX)⋯H(solvent) bonds that contribute to the overall solvation energy.
Number of DOX⋯DOX hydrogen bonds. The average number of DOX⋯DOX hydrogen bonds decreased along the series water (37.84) > EtOH (35.15) > DMF (28.92) > DMSO (24.77) (Fig. S9, ESI†) in line with the predominantly hydrophobic character of DOX. Interestingly, the hydrogen bonds in the series water > EtOH > DMF > DMSO were successively replaced by π-stacking interactions. The most probable π-stacking interactions between the anthracycline units of DOX⋯DOX was investigated using RDFs between the carbon atoms C5⋯C12 and C4⋯C9 of the DOX molecules, as shown in Fig. S10 (ESI†). These π-stacking interactions were observed in all systems and decrease along the series DMSO > DMF > EtOH > water.
Mean-square displacements (MSDs). Previous studies showed that DOX aggregates in aqueous solutions form dimers and larger oligomers.76 Aggregates containing about 40 molecules in aqueous 0.5 mg mL−1 doxorubicin solutions were observed by TEM studies.19 As the fluorescence spectrum of aggregated DOX is markedly different from that of DOX monomers, aggregation equilibria of doxorubicin hydrochloride at high drug and NaCl concentrations were previously studied by temperature scan fluorescence spectroscopy.77 Our previous simulations confirmed the aggregation of DOX molecules confined in TiO2 nanotubes.31 In this work, after 30 ns of simulations, marked DOX aggregation is observed in all four solvents (Fig. S11, ESI†). The mean-square displacements (MSDs) decrease along the series water > DMF > EtOH > DMSO with the highest values in water (Fig. 5).
The calculated diffusion coefficients for DOX are 0.101 × 10−9 (water), 0.047 × 10−9 (DMF), 0.025 × 10−9 (EtOH), and 0.007 × 10−9 m2 s−1 (DMSO). We attribute the lower diffusion of DOX molecules in DMSO to the formation of large aggregates through hydrophobic and π-stacking interactions in line with a recent MD simulation study on the structure and dynamics of DOX in ionic liquids (IL).78 Further, the MD-calculated diffusion coefficient for water is 4.345 × 10−9 m2 s−1, which is in good agreement with the experimental value of 2.299 × 10−9 m2 s−1 at room temperature.79
To better clarify this observation, we calculated the number of formed clusters as a function of time (Fig. S12, ESI†) and found cluster sizes of 4.33 (DMSO), 3.95 (EtOH), 3.56 (DMF), and 3.26 (water) molecules, with the highest value in DMSO, as expected from the diffusion. In our study, the size of the DOX aggregates in different media and the time scale of simulations were rather restricted owing to the atomistic character of the investigation and when extending the timescale to 200 ns we obtained the same cluster size in water as after 20 ns. Hence, it is needed to extend the investigation to a coarse-grained representation that can accommodate significantly larger system sizes and longer time scales. Coarse-grained simulations, as demonstrated in previous studies, offer the opportunity to study aggregation processes on a larger scale and for a longer duration.80,81 On the other hand, to determine the specific impact of changing the type of simulation models (all atomic or coarse-grained), we would need to conduct simulations with an optimised force field in our future study and evaluate its impact on the aggregation size.80,81
Time-dependent autocorrelation functions. The lifetimes of hydrogen bonds determined from hydrogen bond existence autocorrelation functions (ACFs)) between DOX and solvent molecules are shown in Fig. S13 and Table S11 (ESI†). They decrease in the order DOX/DMSO > DOX/EtOH > DOX/DMF > DOX/water. The lifetimes in DMSO (5.495 × 10−3 ps) are longer than those in other solvents, the lowest lifetime was found for water (0.970 × 10−3 ps).
Comparison between Amber and GROMOS force field for an aqueous DOX solution. To validate the force field, a simulation for the DOX/water system was performed using the Amber force field (GAFF) method and SPC/E water for 200 ns.47 The results showed no significant differences compared to the GROMOS force field method. Various parameters, including RDFs, MSDs, number of hydrogen bonds, and cluster size were investigated and showed no appreciable changes when compared to the GROMOS-based calculations (see Fig. S14 and S15, ESI†).
In our study, the pH value did not exceed pH 7.4 and we studied the aggregation of DOX molecules in both their protonated, cationic (DOXH+) and their neutral form (DOX).82 Additionally, a simulation considering the protonation state of DOX was carried out using the Amber force field (GAFF) method for 200 ns.47 To maintain the neutrality of the protonated DOXH+ system, chloride ions were added. Different parameters were calculated, revealing no significant changes between the two states (as shown in Fig. S14 and S15, ESI†). A previous study has shown that neutral DOX molecules can aggregate more readily than the protonated cations.83 In fact, the aggregation of DOX is a stepwise process, leading to the formation of aggregates of variable sizes. With an increase in drug concentration, the size of the aggregates is enhanced.18 Based on the present study, from a molecular point of view, the size of clusters for both the charged and uncharged DOX is approximately the same during the same simulation time. However, different conditions, especially variations in pH, can significantly affect the mechanism of DOX release and adsorption processes by drug carriers. For instance, the hybrid material consisting of single-walled carbon nanotube-congo red-DOX can be used as a drug carrier system capable of controlled drug release through pH change (Congo red is known to bind to some drugs through intercalation).83 The decrease in pH had an effect on the structure and stability of the examined triple systems, ultimately leading to enhanced drug release efficiency. The calculated diffusion coefficients of DOX and DOXH+ are 0.133 × 10−9 and 0.125 × 10−9, respectively. These values align well with the diffusion coefficient of the system obtained using GROMOS. To evaluate the equilibration of both species, total energies, density stabilisation and RMSD were calculated. These calculations demonstrated compatibility with the results of the previous approach using GROMOS, as shown in Fig. S16 (ESI†).
3.3 MD simulation of DOX at octanol/water and DPPC/water interfaces
Phosphatidylcholine (PC) lipids contain quaternary ammonium with three methyl groups attached. The presence of hydrogen bond acceptors in this functional group leads to the interactions between lipid membrane and hydrogen bond donors of DOX molecules, which strongly impact interfacial structure and dynamics.84,85 The effect of surfactants and polar solvents on the hydrogen bond dynamics and area per lipid of oil–water and lipid–water interfaces are investigated using ultrafast two-dimensional infrared spectroscopy and molecular dynamics simulations.86,87 Therefore, characterising interfacial structure and dynamics is the first step towards understanding the impact of DOX on biological interfaces. And indeed, structural and dynamical properties of phospholipids in water have previously been studied extensively using different force fields and experimental methods.88,89
To verify the results, the simulation time of the DOX/DPPC/water system was extended to 300 ns. Despite this, the DOX molecules continued to remain at the interface. The DOX molecules might be unable to flip–flop from one side to the other side of the membrane, thus, might not be able to cross the membranes. We conducted atomistic MD simulations for 300 ns to investigate how DOX enters bilayer membranes to see whether uptake is energy dependent. We found that DOX did not spontaneously penetrate the lipid membrane. This showed that the process of DOX entering the membrane from the water phase faces a free energy barrier that needs to be overcome.90,91 Also, no appreciable changes were observed in the analysis of RDF plots and snapshots when compared to previous results as shown in Fig. S18 and S19A (ESI†). Furthermore, an additional simulation was performed for 300 ns. The simulation conditions remained consistent with the previous one, with one notable difference: an ensemble of 256 lipid molecules was employed. Interestingly, no significant differences in the simulation results between the two ensemble sizes were observed. Considering this lack of appreciable variation, we decided to utilise the smaller ensemble size for our study as well. The snapshot of the last structure of DOX at DPPC/water is shown in Fig. S19B (ESI†).
In the octanol/DOX/water system, the DOX molecules move towards the octanol phase from the side of their O4 and O11 atoms. After 50 ns of simulation, the atom sites O6 and O9 have entered the octanol phase according to their atomic density profiles (Fig. S21A, ESI†). As the simulation proceeded for the system DPPC/DOX/water, the water molecules migrated towards the head group region of the DPPC phase and reached the interface. Moreover, DOX molecules tend to move towards the polar head groups of the DPPC phase, guided by their O11 and O4 atoms, at the end of the simulation time (Fig. S21B, ESI†). After this, the part containing the O8 and O9 atoms entered the DPPC phase. This would mean that the polar/hydrophilic part of DOX is located in the oxane ring, and the saturated ring D is guiding the molecule towards the hydrophilic part of the DPPC/octanol phase, while the non-polar/hydrophobic part (rings A to C) bind the DOX in the interface and water phase in the DPPC/water phase.
In the case of octanol/DOX/water, the RDFs show interactions between H atoms of DOX and O atoms of octanol (Fig. S24, ESI†). The H4⋯O(oct) and H11⋯O(oct) interactions have short-range distances at 1.45 Å and 1.67 Å, respectively, and high probabilities. The shortest correlation between O atoms of DOX and H atoms of octanol is found for O6⋯H(oct) at 1.67 Å. The probability of all these peaks is low. This means that the probability of finding O atoms of DOX close to octanol H atoms is generally low, including those (O9 and O10) in the hydrophobic part.
The peaks between H4⋯OW, H11⋯OW, O4⋯HW, and O11⋯HW are all located at around 1.67 Å and show high probabilities compared to other interactions (Fig. S25, ESI†). Interestingly, while the shapes of the RDFs resemble typical H⋯O g(r), the intensity of the peaks indicates that the nature of forces responsible for the hydrogen bonding is different.
The equilibration of the DOX/octanol/water and DOX/DPPC/water systems was evaluated by investigating the total energies and RMSD. We observed that both the total energies and RMSD remained stable throughout the simulation period (see Fig. S26, ESI†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0.65 and 0° < Φ < 15° (Fig. 7A). The most probable regions for the octanol/water interface are centred at −0.2 < cos
θ < 0.65 and 0° < Φ < 15° (Fig. 7A). The most probable regions for the octanol/water interface are centred at −0.2 < cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0.1 with 0° < Φ < 10°, −0.1 < cos
θ < 0.1 with 0° < Φ < 10°, −0.1 < cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0.2 with 30° < Φ < 40°, and −0.1 < cos
θ < 0.2 with 30° < Φ < 40°, and −0.1 < cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ < 0.2 with 50° < Φ < 70° (Fig. 7B).
θ < 0.2 with 50° < Φ < 70° (Fig. 7B).
 | ||
| Fig. 7 Bivariate orientation distribution map of DOX molecules at (A) DPPC/water and (B) octanol/water interfaces. | ||
This is in line with the hydrophilic aminoglycoside (oxane) part of the DOX molecule being in contact with the DPPC phase, while the anthracycline part points towards the aqueous phase (Fig. 8A). In contrast to this, the anthracycline part of the DOX molecule is oriented almost parallel to the octanol/water interface (Fig. 8B) as can be expected from the hydrophobic character of this part. Thus, the potential penetration of DOX into the interface starts with very different interactions. In future work, we will try to model such a penetration process.
When plotting the averaged −SCD values as a function of the C atoms along the lipid tails of DPPC (Fig. S27, ESI†) higher values were observed for both –CH2– chains along the lipid tails in line with a higher ordering through van der Waals interactions in the presence of DOX.
4. Conclusions
Density functional theory (DFT) calculations and molecular dynamics (MD) simulations were carried out to examine the aggregation of doxorubicin (DOX) molecules in the solvents water, dimethyl sulfoxide (DMSO), ethanol (EtOH), and N,N-dimethylformamide (DMF). DOX⋯DOX and DOX⋯solvent interactions are the fundamental interactions that drive the aggregation of this important anti-cancer drug. MD-calculated diffusion coefficients for DOX decrease along the series water > DMF > EtOH > DMSO (0.101 × 10−9, 0.047 × 10−9, 0.025 × 10−9, and 0.007 × 10−9 m2 s−1, respectively) and the dipole moment of the DOX molecule is more significant in solution (∼6.2 Debye) compared with the gas phase (5.7 Debye) corresponding to stronger intermolecular DOX⋯DOX interactions. On the other hand, the DFT–PCM approach produced almost the same values for the dipole moments and solvation energies for the different solvents and is thus unsuitable to give detailed insight. The MD simulations show an increasing degree of aggregation in water < DMF < EtOH < DMSO consistent with the diffusion coefficients. The aggregation of DOX molecules mainly occurs through the hydroxy ketone side chain in the unsaturated ring D in the anthracycline moiety, and the aminoglycoside ring (oxane) rather than through its quinone part in the unsaturated rings A to C of the anthracycline moiety. Also, the average number of hydrogen bonds between DOX molecules decreased from water (37.84) to DMSO (24.77), in line with the assumption that aggregates in water are formed mainly through hydrogen bonding, while π-stacking interactions make the predominant contribution to aggregation in DMSO and the other organic solvents as can be seen from intense DOX⋯DOX radial density functions (RDFs). The calculated diffusion coefficient of DOX in water is much higher than in the other studied solvents. As expected, with increasing size of the aggregates, their diffusion coefficients decrease. The interactions leading to the aggregates are quite complex. The most dominant RDFs have short-range peaks of narrow width, indicating that DOX⋯solvent interactions are strong and of low dynamics. While DOX⋯water interactions resemble typical solvation shell models of the liquid state, the correlations between DOX and other solvents (DMSO, EtOH, and DMF) show solid-like features. The hydrogen bonds between DOX and the solvent molecules were studied further at DPPC/water and octanol/water interfaces by correlation functions. Also, here, a rapid formation of DOX aggregates was found. The DOX molecules approach the DPPC (octanol) side of the interface as small amorphous aggregates. The simulation of the migration of DOX molecules and aggregates, together with the assessment of the orientation of single DOX molecules at the DPPC/water interface, showed that the hydrophilic hydroxy ketone site and the aminoglycoside ring of DOX bind to the outer DPPC surface where the polar end-groups of DPPC are located when equilibration is reached. In contrast, DOX aligns its hydrophobic anthracycline core parallel to the octanol/water interface and points with its hydrophilic parts into the water phase.As the lipid membrane permeability of drug molecules depends on the extent of their aggregation, the aggregation of DOX can influence its biological activity. Our very detailed description of the dynamics of DOX molecules in different solvents and at the DPPC/water and octanol/water interfaces, including the assessment of the extent of aggregation, the driving forces of the aggregation, the time-course of the aggregation and the binding to the interfaces, as well as the molecular orientation of the DOX molecules at the interfaces through the determination of bivariate orientation distributions are the first that has been published so far. It shows that both statistical MD simulations and views on single molecules are helpful in understanding the dynamics and interactions in such systems. We are confident that this methodology is also applicable to other important drug molecules. Further, from this point we can now start studying the aggregation of DOX in solvent mixtures and the penetration of DOX (or other molecules) through membranes (two interfaces). The methodology might also allow designing new drug molecules with improved solvation/aggregation/penetration properties.
Author contributions
Conceptualisation: S. S. F., A. R. Z. and A. K.; methodology: S. S. F., A. R. Z.; investigation: S. S. F.; resources: A. R. Z; data curation: S. S. F. and A. R. Z; visualisation: S. S. F. and A. K.; supervision and project administration: A. R. Z; manuscript original draft: S. S. F.; manuscript editing: A. R. Z and A. K. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors are indebted to the research council of Shiraz University for the financial supports. We also thank “Iran Science Elites Federation” for support of this work. A. K. acknowledges the German Academic Exchange Service (DAAD) KD_0001052598-2 for a short-time guest lectureship at the Shiraz University.References
- G. C. M’bitsi-Ibouily, T. Marimuthu, P. Kumar, Y. E. Choonara, L. C. du Toit, P. Pradeep, G. Modi and V. Pillay, Synthesis, Characterisation and In Vitro Permeation, Dissolution and Cytotoxic Evaluation of Ruthenium(II)-Liganded Sulpiride and Amino Alcohol, Sci. Rep., 2019, 9, 4164 (1–18) CrossRef PubMed.
- P. Tran, Y.-C. Pyo, D.-H. Kim, S.-E. Lee, J.-K. Kim and J.-S. Park, Overview of the manufacturing methods of solid dispersion technology for improving the solubility of poorly water-soluble drugs and application to anticancer drugs, Pharmaceutics, 2019, 11, 132–157 CrossRef CAS PubMed.
- S. Rivankar, An overview of doxorubicin formulations in cancer therapy, J. Cancer Res. Ther., 2014, 10, 853–858 CrossRef PubMed.
- S. Sritharan and N. Sivalingam, A comprehensive review on time-tested anticancer drug doxorubicin, Life Sci., 2021, 278, 119527 (1–10) CrossRef PubMed.
- C. A. Bergström, W. N. Charman and C. J. Porter, Computational prediction of formulation strategies for beyond-rule-of-5 compounds, Adv. Drug Delivery Rev., 2016, 101, 6–21 CrossRef PubMed.
- Q. Hou, R. Bourgeas, F. Pucci and M. Rooman, Computational analysis of the amino acid interactions that promote or decrease protein solubility, Sci. Rep., 2018, 8, 14661 (1–13) Search PubMed.
- M. F. Mabesoone, A. R. Palmans and E. W. Meijer, Solute–Solvent Interactions in Modern Physical Organic Chemistry: Supramolecular Polymers as a Muse, J. Am. Chem. Soc., 2020, 142, 19781–19798 CrossRef CAS PubMed.
- V. Alizadeh and B. Kirchner, Molecular level insight into the solvation of cellulose in deep eutectic solvents, J. Chem. Phys., 2021, 155, 084501 CrossRef CAS PubMed.
- M. B. Martins-Teixeira and I. Carvalho, Antitumour anthracyclines: progress and perspectives, ChemMedChem, 2020, 15, 933–948 CrossRef CAS PubMed.
- A. A. Moiseeva, Anthracycline Derivatives and Their Anticancer Activity, INEOS OPEN, 2019, 2, 9–18 CrossRef CAS.
- O. Tacar, P. Sriamornsak and C. R. Dass, Doxorubicin: an update on anticancer molecular action, toxicity and novel drug delivery systems, J. Pharm. Pharmacol., 2013, 65, 157–170 CrossRef CAS PubMed.
- J. Shi, P. W. Kantoff, R. Wooster and O. C. Farokhzad, Cancer nanomedicine: progress, challenges and opportunities, Nat. Rev. Cancer, 2017, 17, 20–37 CrossRef CAS PubMed.
- L. Borlle, A. Dergham, Z. Wund, B. Zumbo, T. Southard and K. R. Hume, Salinomycin decreases feline sarcoma and carcinoma cell viability when combined with doxorubicin, BMC Vet. Res., 2019, 15, 36 (1–12) Search PubMed.
- A. N. Tevyashova, E. N. Olsufyeva, M. N. Preobrazhenskaya, A. A. Klyosov, E. Zomer and D. Platt, New conjugates of antitumor antibiotic doxorubicin with water-soluble galactomannan: synthesis and biological activity, Russ. J. Bioorganic Chem., 2007, 33, 139–145 CrossRef CAS.
- L. J. C. Albuquerque, V. Sincari, A. Jäger, J. Kucka, J. Humajova, J. Pankrac, P. Paral, T. Heizer, O. Janouskova, I. Davidovich, Y. Talmon, P. Pouckova, P. Stepanek, L. Sefc, M. Hruby, F. C. Giacomelli and E. Jäger, pH-responsive polymersome-mediated delivery of doxorubicin into tumor sites enhances the therapeutic efficacy and reduces cardiotoxic effects, J. Controlled Release, 2021, 332, 529–538 CrossRef CAS PubMed.
- M. Mahdavi, A. Fattahi, E. Tajkhorshid and S. Nouranian, Molecular Insights into the Loading and Dynamics of Doxorubicin on PEGylated Graphene Oxide Nanocarriers, ACS Appl. Bio Mater., 2020, 3, 1354–1363 CrossRef CAS PubMed.
- I. Willerich and F. Gröhn, Molecular Structure Encodes Nanoscale Assemblies: Understanding Driving Forces in Electrostatic Self-Assembly, J. Am. Chem. Soc., 2011, 133, 20341–20356 CrossRef CAS PubMed.
- Z. Fülöp, R. Gref and T. Loftsson, A permeation method for detection of self-aggregation of doxorubicin in aqueous environment, Int. J. Pharm., 2013, 454, 559–561 CrossRef PubMed.
- A. Pyne, S. Kundu, P. Banerjee and N. Sarkar, Unveiling the Aggregation Behavior of Doxorubicin Hydrochloride in Aqueous Solution of 1-Octyl-3-methylimidazolium Chloride and the Effect of Bile Salt on These Aggregates: A Microscopic Study, Langmuir, 2018, 34, 3296–3306 CrossRef CAS PubMed.
- E. Lindahl, Molecular Modeling of Proteins, Springer, Humana Press, New York, NY, USA, 2015, pp. 3–26 Search PubMed.
- T. J. Yacoub, A. S. Reddy and I. Szleifer, Structural Effects and Translocation of Doxorubicin in a DPPC/Chol Bilayer: The Role of Cholesterol, Biophys. J., 2011, 101, 378–385 CrossRef CAS PubMed.
- P. Shan, J. W. Shen, D. H. Xu, L. Y. Shi, J. Gao, Y. W. Lan, Q. Wang and X. H. Wei, Molecular dynamics study on the interaction between doxorubicin and hydrophobically modified chitosan oligosaccharide, RSC Adv., 2014, 4, 23730–23739 RSC.
- L. Poudel, A. M. Wen, R. H. French, V. A. Parsegian, R. Podgornik, N. F. Steinmetz and W. Y. Ching, Electronic structure and partial charge distribution of doxorubicin in different molecular environments, ChemPhysChem, 2015, 16, 1451–1460 CrossRef CAS PubMed.
- D. Toroz and I. R. Gould, A computational study of Anthracyclines interacting with lipid bilayers: correlation of membrane insertion rates, orientation effects and localisation with cytotoxicity, Sci. Rep., 2019, 9, 2155 (1–12) Search PubMed.
- P. Wolski, Molecular Dynamics Simulations of the pH-Dependent Adsorption of Doxorubicin on Carbon Quantum Dots, Mol. Pharm., 2020, 18, 257–266 CrossRef PubMed.
- P. Siani, E. Donadoni, L. Ferraro, F. Re and C. Di Valentin, Molecular dynamics simulations of doxorubicin in sphingomyelin-based lipid membranes, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 183763 CrossRef CAS PubMed.
- A. Jagusiak and T. Pańczyk, Interaction of Congo Red, Evans Blue and Titan Yellow with doxorubicin in aqueous solutions. A molecular dynamics study, J. Mol. Liq., 2019, 279, 640–648 CrossRef CAS.
- M. Mahdavi, F. Rahmani and S. Nouranian, Molecular simulation of pH-dependent diffusion, loading, and release of doxorubicin in graphene and graphene oxide drug delivery systems, J. Mater. Chem. B, 2016, 4, 7441–7451 RSC.
- R. Maleki, H. H. Afrouzi, M. Hosseini, D. Toghraie and S. Rostami, Molecular dynamics simulation of Doxorubicin loading with N-isopropyl acrylamide carbon nanotube in a drug delivery system, Comput. Methods Programs Biomed., 2020, 184, 105303 CrossRef PubMed.
- R. Maleki, H. H. Afrouzi, M. Hosseini, D. Toghraie, A. Piranfar and S. Rostami, pH-sensitive loading/releasing of doxorubicin using single-walled carbon nanotube and multi-walled carbon nanotube: a molecular dynamics study, Comput. Methods Programs Biomed., 2020, 186, 105210 CrossRef PubMed.
- S. Shirazi-Fard, F. Mohammadpour, A. R. Zolghadr and A. Klein, Encapsulation and Release of Doxorubicin from TiO2 Nanotubes: Experiment, Density Functional Theory Calculations, and Molecular Dynamics Simulation, J. Phys. Chem. B, 2021, 125, 5549–5558 CrossRef CAS PubMed.
- Y. Ilieva, L. Dimitrova, M. Margaritova Zaharieva, M. Kaleva, P. Alov, I. Tsakovska, T. Pencheva, I. Pencheva-El Tibi, H. Najdenski and I. Pajeva, Cytotoxicity and Microbicidal Activity of Commonly Used Organic Solvents: A Comparative Study and Application to a Standardized Extract from Vaccinium macrocarpon, Toxics, 2021, 9, 92 (1–16) CrossRef PubMed.
- P. Larsson, H. Engqvist, J. Biermann, E. Werner Rönnerman, E. Forssell-Aronsson, A. Kovács, P. Karlsson, K. Helou and T. Z. Parris, Optimization of cell viability assays to improve replicability and reproducibility of cancer drug sensitivity screens, Sci. Rep., 2020, 10, 5798 CrossRef CAS PubMed.
- M. D. Hall, K. A. Telma, K.-E. Chang, T. D. Lee, J. P. Madigan, J. R. Lloyd, I. S. Goldlust, J. D. Hoeschele and M. M. Gottesman, Say No to DMSO: Dimethylsulfoxide Inactivates Cisplatin, Carboplatin and Other Platinum Complexes, Cancer Res., 2014, 74, 3919–3922 CrossRef.
- S. Garbe, M. Krause, A. Klimpel, I. Neundorf, P. Lippmann, I. Ott, D. Brünink, C. A. Strassert, N. L. Doltsinis and A. Klein, Cyclometalated Pt Complexes of CNC Pincer Ligands: Luminescence and Cytotoxic Evaluation, Organometallics, 2020, 39, 746–756 CrossRef CAS.
- H. Huang, N. Humbert, V. Bizet, M. Patra, H. Chao, C. Mazet and G. Gasser, Influence of the Dissolution Solvent on the Cytotoxicity of Octahedral Cationic Ir(III) Hydride Complexes, J. Organomet. Chem., 2017, 839, 15–18 CrossRef CAS.
- J. Schur, A. Lüning, A. Klein, R. W. Köster and I. Ott, Platinum alkynyl complexes: cellular uptake, inhibition of thioredoxin reductase and toxicity in zebrafish embryos, Inorg. Chim. Acta, 2019, 495, 118982 (1–5) CrossRef.
- V. Novohradsky, L. Markova, H. Kostrhunova, M. Svitelova, J. Kasparkova, A. Barbanente, P. Papadia, N. Margiotta, J. D. Hoeschele and V. Brabec, Pt(II) Complex Containing the 1R,2R Enantiomer of trans-1,2-diamino-4-cyclohexene Ligand Effectively and Selectively Inhibits the Viability of Aggressive Pancreatic Adenocarcinoma Cells and Alters Their Lipid Metabolism, Inorg. Chem. Front., 2022, 9, 3295–3305 RSC.
- D. P. Tieleman and H. J. C. Berendsen, Molecular dynamics simulations of a fully hydrated dipalmitoylphosphatidylcholine bilayer with different macroscopic boundary conditions and parameters, J. Chem. Phys., 1996, 105, 4871–4880 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, USA, 2016 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilization of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55, 117–129 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO, version 3.1, Gaussian. Inc., Pittsburgh, PA, USA, 2003 Search PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, GROMACS 4:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed. - A. W. Schüttelkopf and D. M. Van Aalten, PRODRG: a tool for high-throughput crystallography of protein–ligand complexes, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2004, 60, 1355–1363 CrossRef PubMed.
- J. A. Lemkul, W. J. Allen and D. R. Bevan, Practical considerations for building GROMOS-compatible small-molecule topologies, J. Chem. Inf. Model., 2010, 50, 2221–2235 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, RED Server: a web service for deriving RESP and ESP charges and building force field libraries for new molecules and molecular fragments, Nucleic Acids Res., 2011, 39, W511–W517 CrossRef CAS PubMed.
- H. Berendsen, J. Grigera and T. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. J. Marrink, O. Berger, P. Tieleman and F. Jähnig, Adhesion Forces of Lipids in a Phospholipid Membrane Studied by Molecular Dynamics Simulations, Biophys. J., 1998, 74, 931–943 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- H. J. Berendsen, J. P. Postma, W. F. van Gunsteren and J. Hermans, Interaction models for water in relation to protein hydration. In Intermolecular forces: proceedings of the fourteenth Jerusalem symposium on quantum chemistry and biochemistry held in Jerusalem, 1981.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. H. Dokoohaki, A. R. Zolghadr, M. H. Ghatee and A. Klein, Aqueous solutions of binary ionic liquids: insight into structure, dynamics, and interface properties by molecular dynamics simulations and DFT methods, Phys. Chem. Chem. Phys., 2020, 22, 27882–27895 RSC.
- N. Ngueanngam, T. Chaivisuthangkura, N. Asawutmangkul, B. Jityuti and P. Boonsri, Molecular Design of the Triphenylamine Substitution on Isoindigo-Based as Promising Hole Transport Materials for Perovskite Solar Cell, SWU Sci. J., 2022, 38, 48–61 Search PubMed.
- M. Vatanparast and Z. Shariatinia, Isoindigo derivatives as promising hole transport materials for perovskite solar cells, Sol. Energy, 2021, 230, 260–268 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, Oxford, UK, 2017 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- T. Ikeshoji, B. r Hafskjold, Y. Hashi and Y. Kawazoe, Molecular dynamics simulation for the cluster formation process of Lennard-Jones particles: magic numbers and characteristic features, J. Chem. Phys., 1996, 105, 5126–5137 CrossRef CAS.
- L. Ratke and P. W. Voorhees, Growth and coarsening: Ostwald ripening in material processing, Springer Science & Business Media, Berlin, Germany, 2002 Search PubMed.
- N. Zhang, J. Huo, B. Yang, X. Ruan, X. Zhang, J. Bao, W. Qi and G. He, Understanding of imidazolium group hydration and polymer structure for hydroxide anion conduction in hydrated imidazolium-g-PPO membrane by molecular dynamics simulations, Chem. Eng. Sci., 2018, 192, 1167–1176 CrossRef CAS.
- J. Huo, W. Qi, H. Zhu, B. Yang, G. He, J. Bao, X. Zhang, X. Yan, L. Gao and N. Zhang, Molecular dynamics simulation on the effect of water uptake on hydrogen bond network for OH− conduction in imidazolium-g-PPO membrane, Int. J. Hydrogen Energy, 2019, 44, 3760–3770 CrossRef CAS.
- M. Brehm and B. Kirchner, TRAVIS – A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- D. B. Singh, Computer-aided drug design, Springer, 2020 Search PubMed.
- A. A. Yekeen, O. A. Durojaye, M. O. Idris, H. F. Muritala and R. O. Arise, CHAPERONg: a tool for automated GROMACS-based molecular dynamics simulations and trajectory analyses, Comput. Struct. Biotechnol. J., 2023, 21, 4849–4858 CrossRef CAS PubMed.
- M. Tanaka, G. Girard, R. Davis, A. Peuto and N. Bignell, Recommended table for the density of water between 0C and 40C based on recent experimental reports, Metrologia, 2001, 38, 301–309 CrossRef CAS.
- P. Jedlovszky, A. Vincze and G. Horvai, New insight into the orientational order of water molecules at the water/1,2-dichloroethane interface: a Monte Carlo simulation study, J. Chem. Phys., 2002, 117, 2271–2280 CrossRef CAS.
- P. Jedlovszky, A. Vincze and G. Horvai, Full description of the orientational statistics of molecules near to interfaces. Water at the interface with CCl4, Phys. Chem. Chem. Phys., 2004, 6, 1874–1879 RSC.
- W. J. Allen, J. A. Lemkul and D. R. Bevan, GridMAT-MD: a grid-based membrane analysis tool for use with molecular dynamics, J. Comput. Chem., 2009, 30, 1952–1958 CrossRef CAS PubMed.
- T. Steiner, The Hydrogen Bond in the Solid State, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- R. S. Rathore, Y. Alekhya, A. K. Kondapi and K. Sathiyanarayanan, Statistical descriptors to measure the effectiveness of hydrogen bonding groups and an example of ether oxygen, CrystEngComm, 2011, 13, 5234–5238 RSC.
- R. Anand, S. Ottani, F. Manoli, I. Manet and S. Monti, A close-up on doxorubicin binding to γ-cyclodextrin: an elucidating spectroscopic, photophysical and conformational study, RSC Adv., 2012, 2, 2346–2357 RSC.
- E. Tasca, J. Alba, L. Galantini, M. D’Abramo, A. M. Giuliani, A. Amadei, G. Palazzo and M. Giustini, The self-association equilibria of doxorubicin at high concentration and ionic strength characterized by fluorescence spectroscopy and molecular dynamics simulations, Colloids Surf., A, 2019, 577, 517–522 CrossRef CAS.
- J. M. Vicent-Luna, J. M. Romero-Enrique, S. Calero and J. A. Anta, Micelle formation in aqueous solutions of room temperature ionic liquids: a molecular dynamics study, J. Phys. Chem. B, 2017, 121, 8348–8358 CrossRef CAS PubMed.
- M. Holz, S. R. Heil and A. Sacco, Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- A. Jain, C. Globisch, S. Verma and C. Peter, Coarse-grained simulations of peptide nanoparticle formation: role of local structure and nonbonded interactions, J. Chem. Theory Comput., 2019, 15, 1453–1462 CrossRef CAS PubMed.
- M. Y. Shelley, M. E. Selvan, J. Zhao, V. Babin, C. Liao, J. Li and J. C. Shelley, A new mixed all-atom/coarse-grained model: application to melittin aggregation in aqueous solution, J. Chem. Theory Comput., 2017, 13, 3881–3897 CrossRef CAS PubMed.
- Z. Hasanzade and H. Raissi, Molecular mechanism for the encapsulation of the Doxorubicin in the cucurbit[n]urils cavity and the effects of diameter, protonation on loading and releasing of the anticancer drug: mixed quantum mechanical/molecular dynamics simulations, Comput. Methods Programs Biomed., 2020, 196, 105563 CrossRef PubMed.
- A. Jagusiak, K. Chlopas, G. Zemanek, P. Wolski and T. Panczyk, Controlled release of doxorubicin from the drug delivery formulation composed of single-walled carbon nanotubes and congo red: a molecular dynamics study and dynamic light scattering analysis, Pharmaceutics, 2020, 12, 622 CrossRef CAS PubMed.
- M. L. Valentine, M. K. Waterland, A. Fathizadeh, R. Elber and C. R. Baiz, Interfacial dynamics in lipid membranes: the effects of headgroup structures, J. Phys. Chem. B, 2021, 125, 1343–1350 CrossRef CAS PubMed.
- C. P. Baryiames and C. R. Baiz, Slow Oil, Slow Water: Long-Range Dynamic Coupling across a Liquid–Liquid Interface, J. Am. Chem. Soc., 2020, 142, 8063–8067 CrossRef CAS PubMed.
- R. K. Venkatraman and C. R. Baiz, Ultrafast dynamics at the lipid–water interface: DMSO modulates H-bond lifetimes, Langmuir, 2020, 36, 6502–6511 CrossRef CAS PubMed.
- D. Maltseva, G. Gonella, J. M. Ruysschaert and M. Bonn, Phospholipid acyl tail affects lipid headgroup orientation and membrane hydration, J. Chem. Phys., 2022, 156, 234706 CrossRef CAS PubMed.
- S. Abel, F. Y. Dupradeau and M. Marchi, Molecular dynamics simulations of a characteristic DPC micelle in water, J. Chem. Theory Comput., 2012, 8, 4610–4623 CrossRef CAS PubMed.
- J. Lipfert, L. Columbus, V. B. Chu, S. A. Lesley and S. Doniach, Size and shape of detergent micelles determined by small-angle X-ray scattering, J. Phys. Chem. B, 2007, 111, 12427–12438 CrossRef CAS PubMed.
- A. R. Zolghadr and S. S. Moosavi, Interactions of neutral gold nanoparticles with DPPC and POPC lipid bilayers: simulation and experiment, RSC Adv., 2019, 9, 5197–5205 RSC.
- H. Karimi, M. H. Dokoohaki, A. R. Zolghadr and M. H. Ghatee, The interactions of an Aβ protofibril with a cholesterol-enriched membrane and involvement of neuroprotective carbazolium-based substances, Phys. Chem. Chem. Phys., 2019, 21, 11066–11078 RSC.
- A. Seelig and J. Seelig, Dynamic structure of fatty acyl chains in a phospholipid bilayer measured by deuterium magnetic resonance, Biochemistry, 1974, 13, 4839–4845 CrossRef CAS PubMed.
- H. I. Petrache, S. W. Dodd and M. F. Brown, Area per lipid and acyl length distributions in fluid phosphatidylcholines determined by 2H NMR spectroscopy, Biophys. J., 2000, 79, 3172–3192 CrossRef CAS PubMed.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Lipid bilayer structure determined by the simultaneous analysis of neutron and X-ray scattering data, Biophys. J., 2008, 95, 2356–2367 CrossRef PubMed.
- O. Berger, O. Edholm and F. Jähnig, Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature, Biophys. J., 1997, 72, 2002–2013 CrossRef CAS PubMed.
- J. F. Nagle and S. Tristram-Nagle, Structure of lipid bilayers, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS PubMed.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, Closer look at structure of fully hydrated fluid phase DPPC bilayers, Biophys. J., 2006, 90, L83–L85 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nj06221f |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2023 |






