Intervalley scattering induced significant reduction in lattice thermal conductivities for phosphorene†
Yu
Wu
 *a,
Ying
Chen
b,
Lei
Peng
b,
Hao
Zhang
*a,
Ying
Chen
b,
Lei
Peng
b,
Hao
Zhang
 *bc and
LiuJiang
Zhou
*bc and
LiuJiang
Zhou
 *ad
*ad
aYangtze Delta Region Institute (Huzhou), University of Electronic Science and Technology of China, Huzhou 313001, China. E-mail: 291320917@qq.com; ljzhou@uestc.edu.cn
bSchool of Information Science and Technology, Fudan University, Shanghai 200433, China. E-mail: zhangh@fudan.edu.cn
cYiwu Research Institute of Fudan University, Chengbei Road, Yiwu City, Zhejiang 322000, China
dSchool of Physics, University of Electronic Science and Technology of China, Chengdu 610054, China
First published on 4th May 2023
Abstract
The thermal transport properties of buckled phosphorene (β-P) and antimonene (β-Sb) are investigated using first-principles methods. The large acoustic–optical phonon gaps of 3.8 THz and 2.2 THz enable the four-phonon interaction to play an important role in phonon scattering for both β-P and β-Sb. Considering the electron–phonon coupling, the lattice thermal conductivity can further undergo 84% decrease to 4.9 W mK−1 for p-type β-P at n = 5 × 1013 cm−2. By quantitatively describing the scattering probability of electrons in different paths combined with electron–phonon coupling matrix element analysis, it is found that multi-valley features of electronic band structure and strong electron–phonon coupling strength make electrons have strong intervalley scattering behavior in β-P. The former plays an important role in the energy conservation condition of the scattering process, and the latter determines the selection rule. Our work elucidates the contribution of higher-order phonon interactions as well as electron–phonon coupling effects to lattice thermal conductivity, and provides a new idea for finding materials with low lattice thermal conductivity induced by intervalley scattering.
New conceptsThe interaction between phonons has long been considered as the dominant factor in phonon scattering in materials. However, we find that the intervalley scattering effect caused by the electron–phonon coupling dominates the phonon scattering in phosphorene with multi-valley features, and the interaction of four phonons in the material cannot be ignored due to the large acoustic–optical phonon gap. Our work provides a new idea for finding materials with low lattice thermal conductivity induced by intervalley scattering. |
1 Introduction
When the carrier concentration is not very high, the intrinsic phonon–phonon interaction usually dominates the phonon scattering.1,2 Electron–phonon coupling has long been considered to limit the electrical transport performance and has a trivial effect on phonon thermal transport in lowly doped semiconductors. The lattice thermal conductivities κL calculated by the first-principles method considering phonon–phonon interaction can be in good agreement with the experimental results in a wide variety of materials with low carrier concentration.3–6 However, with the improvement of doping technology, the carrier concentration can reach 1021 cm−3 for 3D materials and 1014 cm−2 for 2D materials,7,8 motivating researchers to reconsider the contribution of electron–phonon coupling to phonon scattering.9–11For instance, Liao et al. reported a dramatic reduction of lattice thermal conductivity by as much as 45% for bulk silicon considering the electron–phonon coupling effect with 1021 cm−3 carrier concentration at room temperature.9 Li et al. found that the indirect interaction between the ZA phonons and electrons mediated by the TA and LA phonons in graphene can result in 21% reduction of lattice thermal conductivity at room temperature.12 Liu et al. explained the abnormal suppression effect of electron–phonon interaction on lattice thermal conductivity in p-type PtSSe by analyzing the electron–phonon coupling strength and electronic band characteristics.13
The dispersion of electronic structure plays an important role in the energy conservation conditions of the electron–phonon coupling process and then further affects the phonon scattering rate. In general, the higher the density of states near the Fermi level, the more scattering channels of electrons, and the stronger the electron–phonon interaction. Group-V elemental materials (P, As, Sb, Bi) have a stable buckled honeycomb structure and have been successfully synthesized via molecular beam epitaxy (MBE) or pulsed laser deposition (PLD).14–17 They have diverse band structures and prove to own many intriguing and useful electrical transport properties.18–22 Previous calculations show that β-P has ultra-low hole mobility (0.9 cm2 V−1 s−1) due to the strong electron–phonon coupling effect induced by its extremely flat valence band structure with multi-valleys.23 We expect that this strong coupling effect can in turn efficiently increase the phonon scattering rate and limit the phonon transport properties. Here, the effect of electron–phonon coupling on the lattice thermal conductivity of β-P is systematically investigated from first principles calculations and compared with the results of β-Sb with the same structure. The four-phonon scattering effect is included due to the large acoustic–optical (a–o) gap in both β-P and β-Sb, which is considered as the inducement of strong four-phonon scattering.24,25 The results show that four-phonon scattering and the intervalley scattering effect caused by electron–phonon coupling play important roles in phonon scattering and can effectively reduce the lattice thermal conductivity.
2 Results and discussion
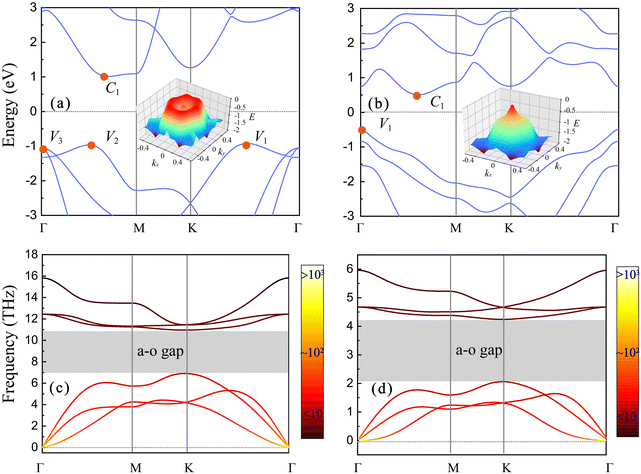
The configurations of the monolayer β-P/Sb are shown in Fig. S1 (ESI†). Different from the planar geometry of graphene, the monolayer β-P/Sb has a buckled structure with two sublayers and thus the horizontal mirror symmetry is broken. The broken mirror symmetry can lead to different phonon–phonon and electron–phonon coupling strengths from graphene. Actually, studies have shown that symmetry breaking can significantly reduce the phonon degeneracy and enhance the avoid-crossing behavior of phonon branches, which results in an increase in the phonon–phonon scattering phase space to limit lattice heat transport.26,27 The optimized lattice constants are 3.28 Å and 4.12 Å for β-P and β-Sb, respectively, which are in good agreement with the previous work.28,29 The calculated band structures are shown in Fig. 1(a and b) and the corresponding energy of the center of the band gap is set to zero. The indirect band gaps of β-P and β-Sb are 1.94 eV and 0.99 eV, respectively. The conduction band minimum (CBM) of β-P and β-Sb locates at the C1 point close to the middle of the Γ–M direction. It is noted that the band structure of β-P near the CBM is particularly flat, which will significantly enhance the electron–phonon coupling. The valence band maximum (VBM) of β-P locates at the V1 point along the Γ–K direction, while for β-Sb the VBM locates at the Γ point. There exists high band degeneracy in the Brillouin Zone for both systems, which may induce intervalley scattering channels of electrons in the electron–phonon coupling process. The band degeneracy near the CBM is Nc = 6 for both β-P and β-Sb. The valence band of β-P possesses local peaks V2 (Nv = 6) and V3 (Nv = 2) below the global VBM (Nv = 6) that will play an important role in the lattice thermal conductivity of the system under p-type doping. The energy difference between V2 and V1 (V3 and V1) is 49 meV (162 meV). The insets of Fig. 1(a and b) show the 3D band structure of the valence band for β-P and β-Sb, respectively. The valence band of β-P possesses multiple valleys and peaks which are shallow in energy and connected with each other. In contrast, only a sharp and deep peak locates at the Γ point for β-Sb and the holes can only experience intravalley scattering in the electron–phonon coupling process.The phonon dispersion curves of β-P and β-Sb are shown in Fig. 1(c and d) with the color of the curve indicating the average phonon occupancy at room temperature calculated using the Bose-Einstein distribution 1/(ehω/kBT − 1). Different from the planar graphene, the buckled structure of β-P and β-Sb results in the coupling of in-plane and flexural phonons, leading to a considerable a–o gap of 3.8 THz and 2.2 THz, respectively. The large a–o gap makes the excited phonons mainly concentrated on the acoustic branch and the phonon occupation number in the optical branch is mainly less than unity. In general, the large a–o gap is associated with significant four-phonon scattering due to the fact that the total energy of three acoustic phonons is large enough to cross the a–o gap recombining into an optical phonon.
The calculated T-dependent lattice thermal conductivity κL is shown in Fig. 2(a and b). The calculated κL of 114.1 W mK−1 and 10.7 W mK−1 at 300 K for β-P and β-Sb under the perspective of three-phonon scattering is close to the previous calculations.30,31 We find that the four-phonon and electron–phonon interaction have strong effects on the lattice heat transport properties of β-P and β-Sb. Specifically, at 300 K, the κL is 30.1 W mK−1 (74% decrease) for β-P when including the four-phonon scattering in the pristine case and further reduces to 4.9 W mK−1 (84% decrease) and 14.7 W mK−1 (51% decrease) by p-type and n-type doping, respectively. For β-Sb, the κL is 2.0 W mK−1 (81% decrease), 1.6 W mK−1 (20% decrease) and 1.3 W mK−1 (35% decrease) when considering four-phonon scattering for the pristine, p-type and n-type system, respectively. This indicates that four-phonon interaction dominates the phonon scattering in both β-P and β-Sb while the effect of electron–phonon coupling on phonon scattering is more obvious in β-P. Moreover, it can be found that the κL with four-phonon scattering exhibits stronger temperature dependence while the case is the opposite when the electron–phonon coupling is taken into account. The κL is nearly inversely proportional (∝T−1) to temperature when only considering three-phonon scatterings, which is due to the dominance of Umklapp processes among the total scatterings. At high temperature, more phonons are excited, and the four-phonon interaction is more obvious, making κL more dependent on temperature. On the contrary, the phonon scattering from electron–phonon coupling is almost T-independent. Therefore the impact of electron–phonon coupling on κL is more obvious at lower temperature. As seen in Fig. 2(c, d), considering phonon–phonon scatterings, the κL of β-P and β-Sb is mainly dominated by acoustic phonons, and the optical phonons have less contribution to thermal transport. Therefore, the contribution of electron–phonon coupling effect on phonon scattering only needs to consider the participation of acoustic phonons. The insets of Fig. 2(c and d) show the contribution of different acoustic phonon modes to κL. LA modes play a very important role in thermal transport when the effect of electron–phonon coupling is not considered. This is due to the large a–o gap in β-P and β-Sb, which suppresses the recombination of LA phonons into optical phonons. In order to clearly describe the phonon recombination process, the phase space of three phonon interaction for recombination process P3+ is calculated and shown in Fig. S2 (ESI†). For β-P, in the phonon frequency of 0–4 THz, the P3+ of the LA phonons is mainly lower than other acoustic branches. When the frequency is further increased, some of the LA phonons can be recombined into optical phonons, leading to gradual increases of P3+. For β-Sb, since the maximum frequency of LA phonons is smaller than the a–o gap, the process of LA phonon recombination into optical phonons is completely inhibited, and the P3+ of the LA phonons remains small in a wide frequency range. However, the inclusion of the electron–phonon coupling makes TA phonons become the main source of thermal transport.
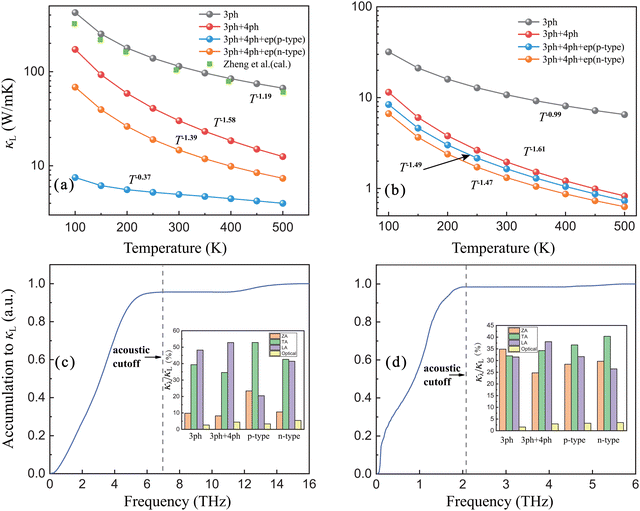 | ||
| Fig. 2 The variation of lattice thermal conductivity κL with temperature considering different sources of phonon scattering for (a) β-P and (b) β-Sb. The calculated result considering three-phonon interaction for β-P from reference is also shown with green points (ref. 30). Accumulation functions of κL considering phonon–phonon interaction at 300 K for (c) β-P and (d) β-Sb. The insets show the contribution of ZA, TA, LA and optical phonon modes to κL. | ||
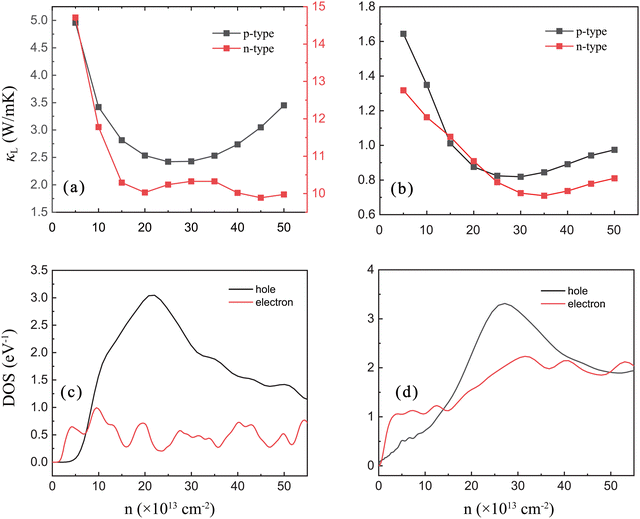
The κL for β-P and β-Sb at 300 K, varying with carrier concentration, is shown in Fig. 3(a and b). It is found that the variation of κL with carrier concentration generally presents a trend of rapid decrease first and then a slow increase. As a result, the κL reaches its minimum value near n = 2.5 × 1014 cm−2 (n = 4.5 × 1014 cm−2) and n = 2.5 × 1014 cm−2 (n = 3.5 × 1014 cm−2) for p-type (n-type) β-P and p-type (n-type) β-Sb, respectively. The electrons participating in the electron–phonon coupling are mainly concentrated near the Fermi level. Hence, when more electrons occupy the state near the Fermi level, the phonons are more strongly scattered from electron–phonon coupling. Carrier concentration is a function of the Fermi level EF, defined as32,33
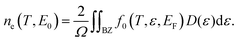 | (1) |
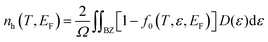 | (2) |
In addition to the lattice thermal conductivity κL, carriers can also contribute to heat transport, denoted as electronic thermal conductivity κe. The κe exhibits a similar trend with electronic conductivity σ according to the Wiedemann–Franz law,34i.e. κe = LσT, where L is the Lorenz number. Hence, increasing σ leads to the increase of κe. A stronger electronic conductivity often indicates that the carriers are less scattered by phonons, and the electron–phonon coupling is weaker, which will have less influence on the lattice thermal conductivity. According to the Boltzmann transport theory, Fig. S4(a and b) (ESI†) show the κeversus carrier concentration of β-P and β-Sb at 300 K. The κe remains small over the range of considered concentration for β-P due to the strong electron–phonon coupling induced by intervalley scattering. Compared with κL, the contribution of κe to the total thermal conductivity is almost negligible in β-P. For β-Sb, the κe is comparable to κL for the n-type system. Due to the large dispersion of the valence band in β-Sb, κe dominates the thermal transport for the p-type system. Fig S4(c and d) (ESI†) show the total thermal conductivities κtotal for β-P and β-Sb. It can be seen that the profile of κtotal for β-P has hardly changed compared with κL. However, for β-Sb, the value and trend of κtotal have changed significantly.
For more insights, Fig. 4 shows the phonon scattering rates of β-P and β-Sb contributed from phonon–phonon interaction and electron–phonon coupling at 300 K with n = 5 × 1013 cm−2. The value of the phonon–phonon scattering rate is small in the low frequency region and increases slowly with the increase of the frequency. This is because the phonon emission process is limited in the low frequency region. The phonon scattering rate coming from the electron–phonon coupling does not show obvious frequency dependence. The four-phonon scattering rate is comparable to the three-phonon scattering rate in β-P and even exceeds the three-phonon scattering rate in the high frequency region in β-Sb. This reveals the importance of four-phonon scattering in materials with large a–o gap. The LA phonons possess higher group velocity due to large phonon dispersion and smaller scattering rate under phonon–phonon interaction, making it contribute more to κL. It is clear that the electron–phonon coupling plays a dominant role in phonon scattering of β-P and covers a broad frequency range. In particular, the scattering rate of the ZA phonon reaches ∼100 ps−1, three orders of magnitude higher than the value under phonon–phonon interaction. Compared with TA phonons, the scattering rate of ZA and LA phonons from electron–phonon coupling is much higher than the three-phonon and four-phonon scattering rate, resulting in TA phonons dominating thermal transport in Fig. 2(c). For β-Sb, the LA phonons in the frequency range of 0–1 THz have an electron–phonon coupling scattering rate comparable to that of phonon–phonon interactions for both p-type and n-type systems. However, a small number of ZA and TA phonons in a narrow frequency range have an electron–phonon coupling scattering rate with a significant value.
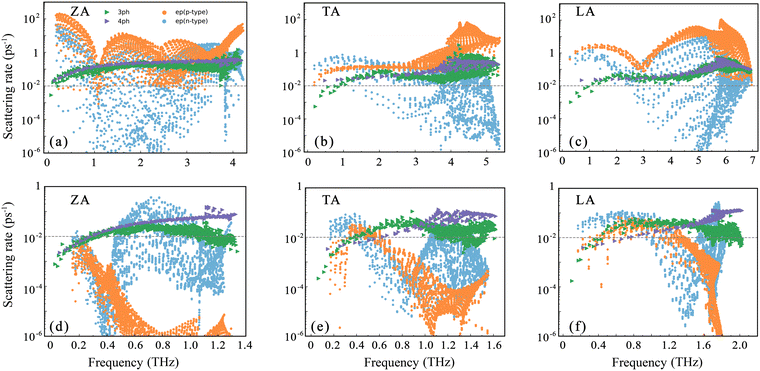 | ||
| Fig. 4 The three-phonon (3ph), four-phonon (4ph), and electron–phonon (ep) scattering rates at n = 5 × 1013 cm−2 of (a, d) ZA, (b, e) TA and (c, f) LA modes at T = 300 K for β-P and β-Sb. | ||
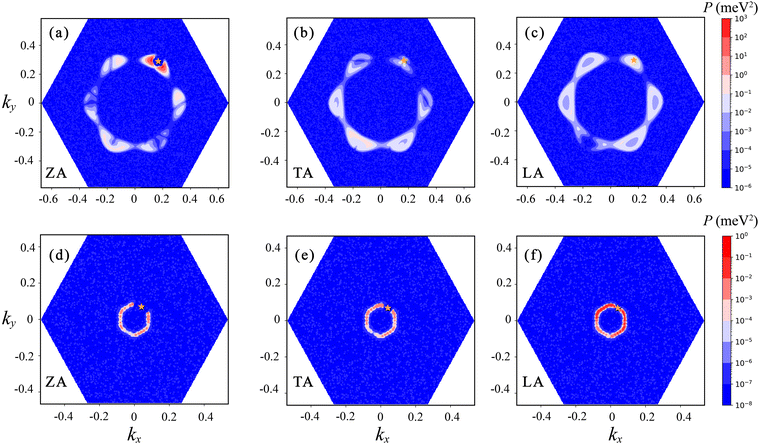
To explain the large difference in the electron–phonon coupling scattering rate, we define a physical quantity P reflecting the scattering probabilities of electrons in the electron–phonon coupling process, written as,
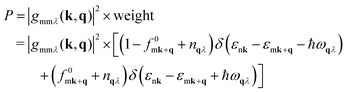 | (3) |
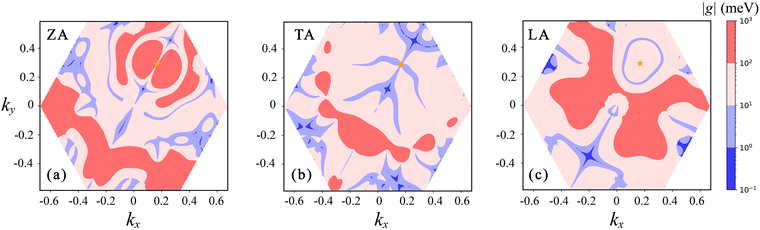 | ||
| Fig. 6 The electron–phonon coupling matrix elements |g| of the holes in β-P involving (a) ZA, (b) TA and (c) LA phonons. The orange star represents the initial states of holes. | ||
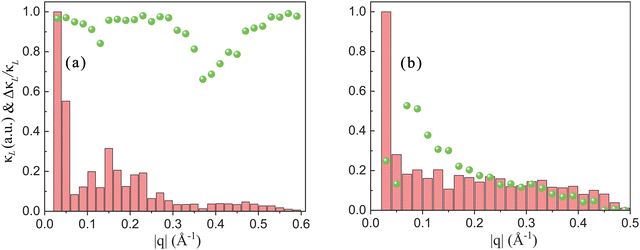
In order to further understand the influence of the electron–phonon coupling effect on the lattice thermal conductivity of these two materials, we distinguish the contribution of phonons with different momentum to κL considering three-phonon interactions. As shown in Fig. 7, when considering phonon–phonon interaction, phonons with small (0–0.1 Å−1) and medium momentum (0.1–0.3 Å−1) mainly contribute to κL for β-P. The former mainly participate in the intravalley scattering of electrons in the electron–phonon coupling process, and the latter mainly participate in the intervalley scattering. For β-Sb, except for phonons near 0.02 Å−1 contributing much to κL, phonons with other momentum have a similar contribution. Considering p-type doping with n = 5 × 1013 cm−2, the change of κL (ΔκL/κL) is depicted as a green sphere in Fig. 7. It is clear that due to the special valence band structure of β-P, the electron–phonon coupling effect obviously limits the lattice thermal conductivity over a wide range of momenta. However, since only intravalley scattering is involved in electron–phonon coupling for β-Sb, the contribution of phonons with small momentum to lattice thermal conductivity is greatly affected by electron–phonon coupling.
3 Conclusion
In conclusion, we investigate the lattice thermal transport properties of β-P and β-Sb through first-principles calculations. The large a–o gap makes the acoustic phonons dominate the thermal transport and the four-phonon interaction plays an important role in the phonon scattering. Considering the phonon–phonon interaction, LA phonons dominate the heat transport due to their large phonon dispersion and low scattering rate. A significant reduction of lattice thermal conductivity occurs when the electron–phonon coupling effect is included in phonon scattering, especially for p-type β-P with an 84% decrease at n = 5 × 1013 cm−2. The large electronic density of states often induces a large phonon scattering rate, and the minimum of lattice thermal conductivity appears near the corresponding carrier concentration. By analyzing the electron scattering probability and electron–phonon coupling matrix, we find that a strong intervalley scattering effect exists in the multi-valley degenerate system, which can cause a sharp drop in lattice thermal conductivity. Our work provides a deep understanding of higher-order phonon interactions and electron–phonon coupling effects on lattice thermal conductivity and provides theoretical guidance for finding novel materials with low lattice thermal conductivity.Numerical method and computational details
According to the Boltzmann transport equation, the lattice thermal conductivity tensor can be expressed as,35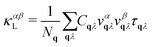 | (4) |
| 1/τqλ = 1/τPPqλ + 1/τepqλ | (5) |
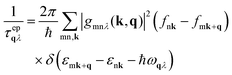 | (6) |
The density functional theory (DFT) calculations are carried out by the QUANTUM ESPRESSO code.37 During the processes of self-consistent and non self-consistent calculations, the kinetic energy cutoff is set to be 90 Ry, and the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional38 and the fully relativistic norm-conserving pseudopotentials that include the spin-orbit coupling (SOC) are employed.39 A fine final grid of 120 × 120 × 1 for both k and q is used for calculating τqλep implemented in the EPW package.40 We use BoltzTraP2 code based on the rigid band approach to calculate the electronic thermal conductivity.33 In this code, the input of electron relaxation time is treated as both band- and momentum-dependent obtained from EPW. The phonon–phonon interaction is calculated by the ShengBTE package35 with an iterative self-consistent algorithm where a 8 × 8 × 1 and 6 × 6 × 1 supercells are built for the harmonic and anharmonic interatomic force constants (IFCs), respectively. The eight and three nearest neighboring atoms are considered for third-order and forth-order interactions, respectively. We have modified the code to consider the electron–phonon coupling effect on the lattice thermal conductivity. To get converged thermal conductivities, a q-mesh of 120 × 120 × 1 and 40 × 40 × 1 is used for the calculation of the third-order and forth-order phonon relaxation time, respectively. To deal with 2D thermal conductivity, an effective thickness of 5.63 Å and 3.76 Å is adopted for β-P and β-Sb,30 respectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Shanghai Municipal Natural Science Foundation under Grant No. 19ZR1402900.References
- P. Klemens, Thermochim. Acta, 1993, 218, 247–255 CrossRef CAS
.
- J. M. Ziman and P. W. Levy, Phys. Today, 1961, 14, 64–66 CrossRef
.
- D. A. Broido, M. Malorny, G. Birner, N. Mingo and D. A. Stewart, Appl. Phys. Lett., 2007, 91, 231922 CrossRef
.
- J. Garg, N. Bonini, B. Kozinsky and N. Marzari, Phys. Rev. Lett., 2011, 106, 045901 CrossRef PubMed
.
- S. Li, Q. Zheng, Y. Lv, X. Liu, X. Wang, P. Y. Huang, D. G. Cahill and B. Lv, Science, 2018, 361, 579–581 CrossRef CAS PubMed
.
- F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou, T.-H. Liu, M. Goni, Z. Ding, J. Sun, G. A. G. U. Gamage, H. Sun, H. Ziyaee, S. Huyan, L. Deng, J. Zhou, A. J. Schmidt, S. Chen, C.-W. Chu, P. Y. Huang, D. Broido, L. Shi, G. Chen and Z. Ren, Science, 2018, 361, 582–585 CrossRef CAS PubMed
.
- D. K. Efetov and P. Kim, Phys. Rev. Lett., 2010, 105, 256805 CrossRef
.
- C.-L. Wu, H. Yuan, Y. Li, Y. Gong, H. Y. Hwang and Y. Cui, Nano Lett., 2018, 18, 2387–2392 CrossRef CAS PubMed
.
- B. Liao, B. Qiu, J. Zhou, S. Huberman, K. Esfarjani and G. Chen, Phys. Rev. Lett., 2015, 114, 115901 CrossRef
.
- J.-Y. Yang, G. Qin and M. Hu, Appl. Phys. Lett., 2016, 109, 242103 CrossRef
.
- Y. Zhang, Z. Tong, A. Pecchia, C. Yam, T. Dumitrică and T. Frauenheim, Nanoscale, 2022, 14, 13053–13058 RSC
.
- X. Yang, A. Jena, F. Meng, S. Wen, J. Ma, X. Li and W. Li, Mater. Today Phys., 2021, 18, 100315 CrossRef CAS
.
- C. Liu, M. Yao, J. Yang, J. Xi and X. Ke, Mater. Today Phys., 2020, 15, 100277 CrossRef
.
- J. L. Zhang, S. Zhao, C. Han, Z. Wang, S. Zhong, S. Sun, R. Guo, X. Zhou, C. D. Gu, K. D. Yuan, Z. Li and W. Chen, Nano Lett., 2016, 16, 4903–4908 CrossRef CAS PubMed
.
- M. Fortin-Deschênes and O. Moutanabbir, J. Phys. Chem. C, 2018, 122, 9162–9168 CrossRef
.
- Y. Shao, Z.-L. Liu, C. Cheng, X. Wu, H. Liu, C. Liu, J.-O. Wang, S.-Y. Zhu, Y.-Q. Wang, D.-X. Shi, K. Ibrahim, J.-T. Sun, Y.-L. Wang and H.-J. Gao, Nano Lett., 2018, 18, 2133–2139 CrossRef CAS PubMed
.
- Z. Yang, Z. Wu, Y. Lyu and J. Hao, InfoMat, 2019, 1, 98–107 CrossRef CAS
.
- Z. Wu and J. Hao, npj 2D Mater. Appl., 2020, 4, 4 CrossRef CAS
.
- D. Kecik, V. O. Özçelik, E. Durgun and S. Ciraci, Phys. Chem. Chem. Phys., 2019, 21, 7907–7917 RSC
.
- Y. Wang, P. Huang, M. Ye, R. Quhe, Y. Pan, H. Zhang, H. Zhong, J. Shi and J. Lu, Chem. Mater., 2017, 29, 2191–2201 CrossRef CAS
.
- Y. Wu, B. Hou, Y. Chen, J. Cao, H. Shao, Y. Zhang, C. Ma, H. Zhu, R. Zhang and H. Zhang, npj Comput. Mater., 2021, 7, 145 CrossRef CAS
.
- Y. Wu, B. Hou, C. Ma, J. Cao, Y. Chen, Z. Lu, H. Mei, H. Shao, Y. Xu, H. Zhu, Z. Fang, R. Zhang and H. Zhang, Mater. Horiz., 2021, 8, 1253–1263 RSC
.
- L. Cheng, C. Zhang and Y. Liu, J. Am. Chem. Soc., 2019, 141, 16296–16302 CrossRef CAS PubMed
.
- J. Chen, J. He, D. Pan, X. Wang, N. Yang, J. Zhu, S. A. Yang and G. Zhang, Sci. China: Phys., Mech. Astron., 2022, 65, 117002 Search PubMed
.
- X. Yang, T. Feng, J. Li and X. Ruan, Phys. Rev. B, 2019, 100, 245203 CrossRef CAS
.
- C. Liu, C. Wu, T. Song, Y. Zhao, J. Yang, P. Lu, G. Zhang and Y. Chen, ACS Appl. Energy Mater., 2022, 5, 15356–15364 CrossRef CAS
.
- C. Liu, Z. Chen, C. Wu, J. Qi, M. Hao, P. Lu and Y. Chen, ACS Appl. Mater. Interfaces, 2022, 14, 46716–46725 CrossRef CAS PubMed
.
- S. Balendhran, S. Walia, H. Nili, S. Sriram and M. Bhaskaran, Small, 2014, 11, 640–652 CrossRef PubMed
.
- D.-C. Zhang, A.-X. Zhang, S.-D. Guo and Y. F. Duan, RSC Adv., 2017, 7, 24537–24546 RSC
.
- G. Zheng, Y. Jia, S. Gao and S.-H. Ke, Phys. Rev. B, 2016, 94, 155448 CrossRef
.
- B. Peng, D. Zhang, H. Zhang, H. Shao, G. Ni, Y. Zhu and H. Zhu, Nanoscale, 2017, 9, 7397–7407 RSC
.
- J. Yang, H. Li, T. Wu, W. Zhang, L. Chen and J. Yang, Adv. Funct. Mater., 2008, 18, 2880–2888 CrossRef CAS
.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS
.
- X. Zheng, D. Cahill, P. Krasnochtchekov, R. Averback and J. Zhao, Acta Mater., 2007, 55, 5177–5185 CrossRef CAS
.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS
.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef
.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- D. R. Hamann, Phys. Rev. B, 2013, 88, 085117 CrossRef
.
- J. Noffsinger, F. Giustino, B. D. Malone, C.-H. Park, S. G. Louie and M. L. Cohen, Comput. Phys. Commun., 2010, 181, 2140–2148 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00090g |
| This journal is © The Royal Society of Chemistry 2023 |