Open Access Article
Open Access ArticleHow clathrin-coated pits control nanoparticle avidity for cells†
Oliver
Zimmer
 and
Achim
Goepferich
and
Achim
Goepferich
 *
*
Department for Pharmaceutical Technology, University of Regensburg, Regensburg, 93050, Germany. E-mail: achim.goepferich@ur.de
First published on 20th December 2022
Abstract
The paramount relevance of clathrin-coated pits (CCPs) to receptor-mediated endocytosis of nanoparticles, extracellular vesicles, and viruses has made them the focus of many studies; however, the role of CCP geometry in the ligand–receptor interactions between multivalent nanoparticles and cells has not been investigated. We hypothesized the general dependence of nanoparticle binding energy on local membrane curvature to be expandable to the specific case of ligand-functionalized nanoparticles binding cell membranes, in the sense that membrane structures whose curvature matches that of the particle (e.g., CCPs) signficantly contribute to binding avidity. We investigated this hypothesis with nanoparticles that bind multivalently to angiotensin II receptor type 1, which is subject to clathrin-mediated endocytosis. When we used cholesterol extraction to prevent the action of CCPs, we found a 67 to 100-fold loss in avidity. We created a theoretical model that predicts this decrease based on the loss of ligand–receptor interactions when CCPs, which perfectly match nanoparticle geometry, are absent. Our findings shed new light on how cells “see” nanoparticles. The presence or absence of CPPs is so influential on how cells interact with nanoparticles that the number of particles required to be visible to cells changes by two orders of magnitude depending on CCP presence.
New conceptsOur work identified the geometric alignment of ligand-functionalized nanoparticles and nano-scaled cell membrane morphology as a previously unknown parameter dictating avidity. We report here for the first time that the positive effect on receptor interaction mediated cell binding ability due to multivalent ligand functionalization of nanoparticles is completely leveled upon induced absence of membrane nano-morphology. This was experimentally demonstrated for the interaction of an angiotensin II functionalized model particle with AT1 receptor-bearing cells, where the absence of nano-scaled membrane morphology affected only the particle avidity but not the affinity of the ligand itself. This unequivocally demonstrates that the long known concept of multivalent functionalization works only when geometric nanoparticle–membrane alignment is given. We further introduce a theoretical model that describes the avidity of our investigated ligand-functionalized particle as a function of ligand affinity and geometric membrane alignment in clathrin-coated pits. To the best of our knowledge, this is the first model expressing avidity as a function of membrane morphology, which was demonstrated to accurately predict the effect of changes in membrane morphology on particle avidity. The findings have important practical implications, by identifying nanoscale membrane morphology as a crucial parameter to be considered in the development of high-avidity nanoparticles. |
Introduction
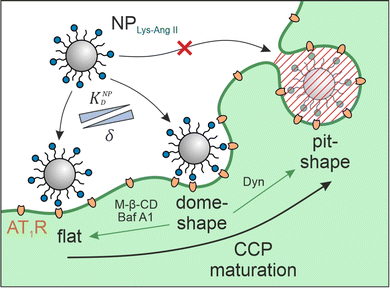
Cell–nanoparticle interactions have been extensively investigated. This is because these interactions, as a crucial step of ligand–receptor-mediated target cell recognition by nanoparticles, are of outstanding importance for the development of targeted nanotherapeutics and the understanding of phenomena such as extracellular vesicle signaling and viral infections. Numerous investigations of size,1–5 shape,1,2,4 surface charge,2,4,6 receptor–ligand density and mobility,2,7–9 linker characteristics,7,8 and hetero-multivalency10,11 have yielded a detailed picture of the avidity that nanoparticles have for cells, but surprisingly little attention has been given to the cell membrane structures that participate in particle identification and binding. A better understanding of these processes would be very beneficial to the development of novel nanotherapeutics because high binding avidity is key when designing targeted nanoparticles that are highly selective and specific.12 To date, we have only a vague understanding of the impact of clathrin-coated pit (CCP) geometry on cell-nanoparticle interactions. Studies that have attempted to close this gap using supported lipid bilayers (SLBs) as model systems13–15 were unsuccessful because the nanoscale invaginations are not maintained during SLB preparation.The problem intensifies when nanoparticles carry ligands for cell surface receptors, making it possible that they will bind multivalently through several simultaneous ligand–receptor interactions.16 When the receptor in question is subject to clathrin-mediated endocytosis it may be located on flat membrane sections or in CCPs, which are highly dynamic structures that undergo constant morphological changes.17 Bucher et al. describe three morphological states during early- and late CCP maturation.18 The flat, dome, and pit morphologies (Fig. 1) differ in surface area, membrane curvature, and clathrin lattice composition. CCP geometry has been described according to the constant area19 and the constant curvature20–22 approach. It was found that, on average, 20% CCPs have dome morphology.23 We hypothesized that these dome-shaped CCPs should have a tremendous impact on nanoparticle binding to cells because dome morphology corresponds perfectly to the size and shape of most studied nanoparticles (spherical geometry, d < 100 nm).24 Receptors located in CCPs25 with shapes complementary to nanoparticles should maximize the contact area between cell membrane and nanoparticle corona, yielding the highest possible number of receptor–ligand-interactions and significantly increasing nanoparticle avidity.26–28
In the general context of nanoparticle membrane interactions Agudo-Canalejo et al., Yu et al., Deserno and Bickel, and Bahrami et al. have provided excellent work on the process of particle membrane wrapping, including investigations of the initial attachment of nanoparticles to membranes. Considering this initial attachment, the aforementioned works found that a membrane curved towards a particle will require a lower bending energy to be overcome during binding. Consequently, a lower adhesion strength will be sufficient for a particle to bind, or assuming a constant adhesion strength, more particles will bind to a membrane curved towards them. With these findings the groups provide a main body of fundamental knowledge about particle membrane interactions acquired to date.29–33 Barbul et al. conducted simulations suggesting that multivalent nanoparticle binding can induce partial membrane wrapping.31 Our approach in the present work differs insofar as our focus is on the study of multivalent ligand-functionalized nanoparticles and thus adds a parameter not fully investigated so far. We want to point out that our focus further differs from the aforementioned works by investigating the effect of the presence or absence of CCPs as particular geometrical entities spontaneously occurring34 in the membrane.
To confirm our hypothesis, we investigated the avidity of receptor binding nanoparticles for their target cells in the presence and absence of CCPs invaginations. We depleted cell membranes of cholesterol, which increases membrane stiffness and enforces a flat CCP morphology.35,36 To investigate the impact of CCP geometry on nanoparticle avidity, we used particles carrying angiotensin II (NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II) in their corona, which enables them to multivalently bind to the CCP-associated angiotensin II receptor type 1 (AT1R).37 This receptor is present on rat mesangial cells, which were used for binding studies performed with and without several potent inhibitors of pit formation: methyl-β-cyclodextrin (M-β-CD), bafilomycin A1 (Baf A1), and dynasore (Dyn). M-β-CD extracts cholesterol from cell membranes.38,39 M-β-CD induces a strong shift in the frequency distribution of the different maturation stages of CCPs. In untreated cells, most CCPs in the membrane are present at intermediate or late maturation stages. Thus, the membrane is highly indented and dome-shaped and pit-shaped CCPs are present. Treatment with M-β-CD results in stopping almost all CCPs at early maturation stages, where the membrane has very shallow or no invaginations. The proportion of dome- and pit-shaped CCPs is significantly reduced.35,36 Baf A1 is a specific inhibitor of vacuolar-type H+ ATPase (VATPase) that inhibits pH-dependent lysosomal cholesterol transport, thus reducing intracellular cholesterol trafficking.40 Similar to M-β-CD, inhibition of VATPase by Baf A1 was shown to almost completely eliminate the population of dome-shaped CCPs after treatment. The CCPs are predominantly present at earlier maturation stages, thus showing very little invagination and a significantly increased neck width.41,42 Dyn is a potent inhibitor of dynamin GTPase that additionally hinders intracellular cholesterol trafficking and freezes CCPs late in their maturation phase. Thus, in terms of its effect on CCP morphology, Dyn has the opposite effect to M-β-CD and Baf A1. It accumulates late-stage CCPs that are about to undergo dynamin-induced pinching off from the membrane. The neck is already very narrow, and the membrane is deeply invaginated.43–45 Along with this experimental data, we developed a theoretical model to predict the avidity change in the presence and absence of pits. It describes nanoparticle avidity (KNPD) as a function of ligand affinity (KLD) and the nanoparticle wrapping fraction (δ) between the nanoparticle corona and cell membrane structure. Overall, the intention of our experimental and theoretical work was to explore the impact of CCP geometry on nanoparticle avidity for target cells. Hereby, we aim to better understand the nano-bio interactions between ligand-functionalized nanoparticles and cell receptors, which is a crucial question in the rational development of nanotherapeutics.46–50
II) in their corona, which enables them to multivalently bind to the CCP-associated angiotensin II receptor type 1 (AT1R).37 This receptor is present on rat mesangial cells, which were used for binding studies performed with and without several potent inhibitors of pit formation: methyl-β-cyclodextrin (M-β-CD), bafilomycin A1 (Baf A1), and dynasore (Dyn). M-β-CD extracts cholesterol from cell membranes.38,39 M-β-CD induces a strong shift in the frequency distribution of the different maturation stages of CCPs. In untreated cells, most CCPs in the membrane are present at intermediate or late maturation stages. Thus, the membrane is highly indented and dome-shaped and pit-shaped CCPs are present. Treatment with M-β-CD results in stopping almost all CCPs at early maturation stages, where the membrane has very shallow or no invaginations. The proportion of dome- and pit-shaped CCPs is significantly reduced.35,36 Baf A1 is a specific inhibitor of vacuolar-type H+ ATPase (VATPase) that inhibits pH-dependent lysosomal cholesterol transport, thus reducing intracellular cholesterol trafficking.40 Similar to M-β-CD, inhibition of VATPase by Baf A1 was shown to almost completely eliminate the population of dome-shaped CCPs after treatment. The CCPs are predominantly present at earlier maturation stages, thus showing very little invagination and a significantly increased neck width.41,42 Dyn is a potent inhibitor of dynamin GTPase that additionally hinders intracellular cholesterol trafficking and freezes CCPs late in their maturation phase. Thus, in terms of its effect on CCP morphology, Dyn has the opposite effect to M-β-CD and Baf A1. It accumulates late-stage CCPs that are about to undergo dynamin-induced pinching off from the membrane. The neck is already very narrow, and the membrane is deeply invaginated.43–45 Along with this experimental data, we developed a theoretical model to predict the avidity change in the presence and absence of pits. It describes nanoparticle avidity (KNPD) as a function of ligand affinity (KLD) and the nanoparticle wrapping fraction (δ) between the nanoparticle corona and cell membrane structure. Overall, the intention of our experimental and theoretical work was to explore the impact of CCP geometry on nanoparticle avidity for target cells. Hereby, we aim to better understand the nano-bio interactions between ligand-functionalized nanoparticles and cell receptors, which is a crucial question in the rational development of nanotherapeutics.46–50
Experimental
Materials
Fura-2 AM (Thermo Scientific, USA) was used as a ratio-metric Ca2+ indicator. Custom peptide Lysine-Angiotensin II (sequence: NH2-KDRVYIHPF-COOH) was synthesized to order (GenScript, Netherlands). The inhibitors used in cell binding assays were methyl-β-cyclodextrin, dynasore (both Sigma-Aldrich, USA), and bafilomycin A1 (Cayman Chemical, USA). Polymers used for synthesis of block-copolymer were carboxy-PEG5k (JenKem Technology, USA, Mn = 5000 ± 500 g mol−1, stated on certificate of analysis) and ester-terminated PLGA (Resomer® RG 502, ester-terminated, Mw 7000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich, USA). Other chemicals used in the syntheses were 3,6-dimethyl-1,4-dioxane-2,5-dione and 1,8-diazabicyclo[5.4.0]undec-7-ene (both Sigma-Aldrich, USA). Cholesterol was quantified using components of the Amplex™ Red Cholesterol Assay Kit (Thermo Scientific, USA). Lys-Ang II was quantified using Pierce™ BCA Protein Assay Kit (Thermo Scientific, USA).
000, Sigma-Aldrich, USA). Other chemicals used in the syntheses were 3,6-dimethyl-1,4-dioxane-2,5-dione and 1,8-diazabicyclo[5.4.0]undec-7-ene (both Sigma-Aldrich, USA). Cholesterol was quantified using components of the Amplex™ Red Cholesterol Assay Kit (Thermo Scientific, USA). Lys-Ang II was quantified using Pierce™ BCA Protein Assay Kit (Thermo Scientific, USA).
Syntheses and nanoparticle preparation
Carboxy-terminated poly(ethylene glycol)-b-poly(D,L-lactide) (carboxy-PEG-PLA) block-copolymer was synthesized as previously described by our group.11,49 Briefly, 3.0 g of 3,6-dimethyl-1,4-dioxane-2,5-dione was recrystallized from ethyl acetate at 85 °C and dried under vacuum at 40 °C for 12 h. Carboxy-terminated poly(ethylene glycol) (carboxy-PEG) was dried under vacuum at 45 °C for 12 h before use. For polymerization, 677.9 mg (0.13 mmol) carboxy-PEG (Mn = 5085 g mol−1) was charged into a round-bottom flask and dissolved in 10 mL anhydrous DCM. Subsequently, 1.322 g (9.17 mmol) of 3,6-dimethyl-1,4-dioxane-2,5-dione and 437 μL (0.46 mmol) of 1 M 1,8-diazabicyclo[5.4.0]undec-7-ene in THF were added.50 The round-bottom flask was fitted with a CaCl2 drying tube. The reaction mixture was stirred at room temperature for 1 h, after which the polymerization was quenched by adding 280 mg (2.29 mmol) of benzoic acid. Finally, the solution was finally added dropwise to 200 mL vigorously stirred diethyl ether to precipitate the carboxy-PEG-PLA block-copolymer. Dried co-polymer was characterized via1H-NMR. Number-average molecular weight Mn = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459 g mol−1 was derived by calculating number-average PLA molecular weight from 1H-NMR data using the following equation.
459 g mol−1 was derived by calculating number-average PLA molecular weight from 1H-NMR data using the following equation.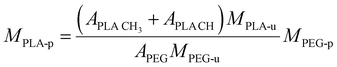 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH is the lactic acid (–CH–) integral, and APEG is the PEG (–OCH2CH2–) integral (Fig. S3, ESI†). Note that both monomer units possess the same number of protons (four each). 1H-NMR data was also analyzed to estimate monomer conversion rate. Considering the employed quantities of carboxy-PEG (0.13 mmol) and 3,6-dimethyl-1,4-dioxane-2,5-dione (9.17 mmol equivalent to 2 × 9.17 mmol PLA monomer), based on MPLA-u = 72 g mol−1 we yield a maximum number-average molecular weight of MPLA-p = 10157 g mol−1. Based on 1H-NMR data, we calculated a number-average molecular weight of MPLA-p of 9374 g mol−1 yielding an estimated monomer conversion rate of 92.3%.
CH is the lactic acid (–CH–) integral, and APEG is the PEG (–OCH2CH2–) integral (Fig. S3, ESI†). Note that both monomer units possess the same number of protons (four each). 1H-NMR data was also analyzed to estimate monomer conversion rate. Considering the employed quantities of carboxy-PEG (0.13 mmol) and 3,6-dimethyl-1,4-dioxane-2,5-dione (9.17 mmol equivalent to 2 × 9.17 mmol PLA monomer), based on MPLA-u = 72 g mol−1 we yield a maximum number-average molecular weight of MPLA-p = 10157 g mol−1. Based on 1H-NMR data, we calculated a number-average molecular weight of MPLA-p of 9374 g mol−1 yielding an estimated monomer conversion rate of 92.3%.
To conjugate the lysine-N-modified angiotensin II (Lys-Ang II) to the carboxy-PEG-PLA block copolymer, 200 mg (13.8 μmol) of carboxy-PEG-PLA, 66 mg (172.5 μmol) EDC, and 40 mg (172.5 μmol) NHS were dissolved in 1 mL of anhydrous DMF and reacted under stirring at 500 rpm for 3 h at room temperature. 120 μL (862.5 μmol) 2-mercaptoethanol was added to quench the reaction. 19.6 mg (16.7 μmol) of Lys-Ang II peptide was dissolved in 500 μL anhydrous DMF. Before adding the peptide solution, 23 μL (66.0 μmol) of N,N-diisopropylethylamine was added to the polymer solution. After adding Lys-Ang II peptide, the united solution was stirred at 500 rpm for an additional 48 h at room temperature. The mixture was diluted in 15 mL of milliQ H2O to yield a DMF content below 10% (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v). This solution was dialyzed for 24 h using a 6–8 kDa regenerated cellulose (RC) membrane. Medium was replaced after 30, 60 min, 2, 4, 6, 12, and 24 h. Finally, the solution was frozen at −80 °C and lyophilized for four days (0.005 mbar, −20 °C). Polymer micelles were prepared for characterization as follows. Lyophilized product was dissolved in acetonitrile (ACN) to yield a 40 mg mL−1 stock solution. 75 μL of this stock solution was mixed with 225 μL ACN to yield 10 mg mL−1 working solution for micelle preparation. This was added dropwise to 3 mL of milliQ H2O under stirring at 700 rpm. ACN was allowed to evaporate for 3 h. Lys-Ang II-PEG-PLA micelles were characterized regarding Lys-Ang II and PEG molarity to determine the Lys-Ang II coupling efficiency (Fig. S2C, ESI†). Lys-Ang II was quantified using a Pierce™ BCA assay kit. A standard serial dilution of free Lys-Ang II was prepared (1000, 750, 500, 250, 125, and 25 μg mL−1 + milliQ H2O as blank) to yield a calibration curve (Fig. S2B, ESI†). 25 μL of micelle sample and each standard were pipetted on a 96-well plate. 200 μL of BCA working reagent prepared according to manufactures instructions were added to each well. The plate was placed on a lab shaker for 30 s (50 rpm) and incubated for further 30 min (37 °C, 5% CO2, protected from light). After cooling down to room temperature the absorbance was recorded at 562 nm on a FLUOstar Omega plate-reader (BMG Labtech, Germany). PEG was quantified via an iodine assay. A standard serial dilution was prepared using carboxy-PEG (40, 30, 20, 10, 5 μg mL−1 + milliQ H2O as blank) to derive a calibration curve (Fig. S2A, ESI†). 40 μL 5% (m/V) BaCl2 solution in 1 M HCl and 20 μL 0.1 M iodine solution were mixed in each well of a 96-well-plate. 140 μL of a 1
v). This solution was dialyzed for 24 h using a 6–8 kDa regenerated cellulose (RC) membrane. Medium was replaced after 30, 60 min, 2, 4, 6, 12, and 24 h. Finally, the solution was frozen at −80 °C and lyophilized for four days (0.005 mbar, −20 °C). Polymer micelles were prepared for characterization as follows. Lyophilized product was dissolved in acetonitrile (ACN) to yield a 40 mg mL−1 stock solution. 75 μL of this stock solution was mixed with 225 μL ACN to yield 10 mg mL−1 working solution for micelle preparation. This was added dropwise to 3 mL of milliQ H2O under stirring at 700 rpm. ACN was allowed to evaporate for 3 h. Lys-Ang II-PEG-PLA micelles were characterized regarding Lys-Ang II and PEG molarity to determine the Lys-Ang II coupling efficiency (Fig. S2C, ESI†). Lys-Ang II was quantified using a Pierce™ BCA assay kit. A standard serial dilution of free Lys-Ang II was prepared (1000, 750, 500, 250, 125, and 25 μg mL−1 + milliQ H2O as blank) to yield a calibration curve (Fig. S2B, ESI†). 25 μL of micelle sample and each standard were pipetted on a 96-well plate. 200 μL of BCA working reagent prepared according to manufactures instructions were added to each well. The plate was placed on a lab shaker for 30 s (50 rpm) and incubated for further 30 min (37 °C, 5% CO2, protected from light). After cooling down to room temperature the absorbance was recorded at 562 nm on a FLUOstar Omega plate-reader (BMG Labtech, Germany). PEG was quantified via an iodine assay. A standard serial dilution was prepared using carboxy-PEG (40, 30, 20, 10, 5 μg mL−1 + milliQ H2O as blank) to derive a calibration curve (Fig. S2A, ESI†). 40 μL 5% (m/V) BaCl2 solution in 1 M HCl and 20 μL 0.1 M iodine solution were mixed in each well of a 96-well-plate. 140 μL of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 diluted micelle sample and undiluted standards were added. The plate was incubated for 15 min at room temperature. Absorbance was measured at 535 nm on a FLUOstar Omega plate-reader. NPLys-Ang
60 diluted micelle sample and undiluted standards were added. The plate was incubated for 15 min at room temperature. Absorbance was measured at 535 nm on a FLUOstar Omega plate-reader. NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II was analyzed as described above except that a 1
II was analyzed as described above except that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 dilution was used for the iodine assay. The molar ratio of Lys-Ang II to PEG found for the Lys-Ang II-PEG-PLA micelles gave the coupling efficiency, while the ratio found for NPLys-Ang
100 dilution was used for the iodine assay. The molar ratio of Lys-Ang II to PEG found for the Lys-Ang II-PEG-PLA micelles gave the coupling efficiency, while the ratio found for NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II characterizes the degree of particle functionalization.
II characterizes the degree of particle functionalization.
Nanoparticles were prepared using solvent evaporation technique. Lys-Ang II-modified PEG-PLA, carboxy-PEG-PLA, and poly(D,L-lactide-co-glycolide) (PLGA) were dissolved in ACN to obtain 40 mg mL−1 stock solutions. These were mixed to obtain a molar core (PLGA)/shell (Lys-Ang II-PEG-PLA and carboxy-PEG-PLA) ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and a normalized ligand density for Lys-Ang II of 0.2. The mixed polymers were diluted with ACN to obtain a total polymer concentration of 10 mg mL−1. This solution was added dropwise to 10 mL DPBS stirring at 500 rpm on a magnetic stirrer. ACN was allowed to evaporate for 3 h. Subsequently, nanoparticles were re-concentrated using Microsep® Advance 30k centrifugal filters (2.5 rcf, 20 min). Nanoparticles were characterized for ligand density using an iodine and BCA assay. Particle hydrodynamic diameters were determined by DLS on a Nano ZS zetasizer (Malvern, UK) (Fig. S2D and E, ESI†) using 633 nm He–Ne laser and 173° backscatter configuration. By measuring polymer dry weight mp after freeze drying, the number of nanoparticles per volume Vs was determined. Using a literature value of 1.25 g cm−3 for the density (ρ) of PEG-PLA,51 the hydrodynamic diameter dh as determined by DLS, and the reciprocal Avogadro's constant NA, eqn (2) yields the molar nanoparticle concentration cNP.
7 and a normalized ligand density for Lys-Ang II of 0.2. The mixed polymers were diluted with ACN to obtain a total polymer concentration of 10 mg mL−1. This solution was added dropwise to 10 mL DPBS stirring at 500 rpm on a magnetic stirrer. ACN was allowed to evaporate for 3 h. Subsequently, nanoparticles were re-concentrated using Microsep® Advance 30k centrifugal filters (2.5 rcf, 20 min). Nanoparticles were characterized for ligand density using an iodine and BCA assay. Particle hydrodynamic diameters were determined by DLS on a Nano ZS zetasizer (Malvern, UK) (Fig. S2D and E, ESI†) using 633 nm He–Ne laser and 173° backscatter configuration. By measuring polymer dry weight mp after freeze drying, the number of nanoparticles per volume Vs was determined. Using a literature value of 1.25 g cm−3 for the density (ρ) of PEG-PLA,51 the hydrodynamic diameter dh as determined by DLS, and the reciprocal Avogadro's constant NA, eqn (2) yields the molar nanoparticle concentration cNP.
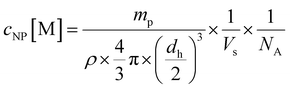 | (2) |
Cholesterol quantification assay
Cholesterol extracted by M-β-CD was quantified using an AmplexTM Red-based two-step enzymatic cholesterol quantification assay. rMCs were grown to confluency on 96-well plates and treated with 5, 10, 30, or 50 mM M-β-CD in Leibovitz's medium. M-β-CD-free medium was used as control to quantify the cholesterol content in untreated rMCs. After 45 min incubation at room temperature, the supernatant was discarded, and rMCs were washed twice using DPBS. rMCs were lysed by incubating with 0.25% trypsin for 24 h at 37 °C with 5% CO2. Complete cell lysis was confirmed by light microscopy, and the lysate was used for the cholesterol quantification assay.80 μL samples of the cell lysates were collected (N = 3), mixed with 160 μL assay reaction buffer (0.1 M potassium phosphate, 0.05 M NaCl, 5 mM cholic acid, and 0.1% Triton® X-100; pH 7.4), and pre-incubated for 2.5 h (37 °C, 5% CO2) to ensure sufficient solubilization of cholesterol for the assay. From these pre-incubated samples, 10 μL samples were collected (N = 2) and mixed with 90 μL Amplex® Red reagent buffer (300 μM AmplexTM Red reagent, 2 U mL−1 horseradish peroxidase, and 2 U mL−1 cholesterol oxidase in 1× assay reaction buffer). The reaction was incubated for 30 min (37 °C, 5% CO2) protected from light. Fluorescence intensities were measured using a FLUOstar Omega plate-reader using top-optics (ex/em: 544/590 nm, double orbital shaking at 500 rpm) (Fig. S3A, ESI†). The measured fluorescence signals were normalized against a control.
To confirm that the cholesterol quantification assay worked in our cell-based setting, we conducted preliminary experiments measuring cholesterol in 37.5, 75, 150, and 300 k cell rMC pellets. Lysates were prepared as described above. Fitting of the fluorescence signals confirmed good linearity of the signal and absence of significant background fluorescence. Assays performed on cell lysates yielded results comparable to the cholesterol standards (Fig. S3C and D, ESI†). Possible stability issues due to the enzymes used in the assay being exposed to residual trypsin during the reaction were also addressed by preliminary testing. For this, 2 U mL−1 horseradish peroxidase and 2 U mL−1 cholesterol oxidase were incubated for 45 min (37 °C, 5% CO2, protected from light) in the presence of 300 μM AmplexTM Red reagent and 4 μg mL−1 cholesterol standard in the presence or absence of 0.016% trypsin. No significant loss in activity was found (Fig. S3B, ESI†).
Fura-2 AM-based Ca2+ mobilization assay
For Fura-2 AM-based Ca2+ mobilization assays, rMCs were harvested by applying 0.25% Trypsin for 90 s (37 °C, 5% CO2). Prior to use, 50 μL DMSO was added to 50 μg of Fura-2 AM. We incubated the vial for 3 h, desiccated and protected from light to ensure complete dissolution of Fura-2 AM. For Fura-2 AM loading, rMCs were centrifuged at 0.2 rcf for 5 min using slow acceleration and deceleration mode on a 5702 R centrifuge (Eppendorf, Germany). The supernatant was discarded, and the cell pellet was carefully resuspended in Leibovitz's-based Fura-2 AM loading medium, transferred to a small culture dish, and incubated with 8.3 μM Fura-2 AM, 2.5 mM OAT-inhibitor probenecid, and 0.017% (m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V) pluronic F127 on a lab shaker at 50 rpm for 2.5 h at room temperature protected from light.
V) pluronic F127 on a lab shaker at 50 rpm for 2.5 h at room temperature protected from light.
The dye-loaded cells were centrifuged using the settings described above. The Fura-2 AM loading medium was discarded, and the cells were resuspended in Leibovitz's-based measurement buffer containing 2.5 mM OAT-inhibitor probenecid. Cell number was adjusted to 106 rMCs mL−1 using a Neubauer-improved counting chamber (Marienfeld, Germany). Cell suspensions were immediately used for measurements with M-β-CD (5, 10, 30 mM, 45 min) or Dyn (100 μM, 1 h) treatment. To investigate the effect of Baf A1, cells were pretreated with 100 nM Baf A1 for 24 h ahead of the assay. All buffers used during the assay were supplemented with 100 nM Baf A1. All treatments were carried out in the presence of 2.5 mM OAT-inhibitor probenecid. The effect of probenecid on cholesterol extraction efficiency of M-β-CD was investigated and found to be negligible for M-β-CD concentrations ≥10 mM (Fig. 4C). Baf A1 and Dyn were used at concentrations known to perturb CCP maturation.42–46
Ratio-metric fluorescence intensity read-out was performed on a FLUOstar Omega plate-reader. Plates were prepared by adding 10 μL of ten-fold over-concentrated serial dilutions of Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II per well. The assay was started by adding 90 μL of Fura-2 AM-loaded cell suspension to each sample via the FLUOstar Omega pump system set to a speed of 100 μL s−1. Each sample was alternately excited at λ 340 nm and 380 nm every 1.5 s, measuring emission at λ 510 nm. Data was collected for 30 s per sample. Three replicates were measured for each concentration of Lys-Ang II and NPLys-Ang
II per well. The assay was started by adding 90 μL of Fura-2 AM-loaded cell suspension to each sample via the FLUOstar Omega pump system set to a speed of 100 μL s−1. Each sample was alternately excited at λ 340 nm and 380 nm every 1.5 s, measuring emission at λ 510 nm. Data was collected for 30 s per sample. Three replicates were measured for each concentration of Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II. The highest measured ratio of each sample was used for the calculation of intracellular Ca2+ levels using the Grynkiewicz-equation.52 For calibration, the maximum ratio (Rmax) was obtained by measuring Fura-2 AM-loaded cells lysed with 10 μL of 1% Triton® X-100 in PBS. The minimum ratio (Rmin) was measured using 10 μL of 1% Triton® X-100 in PBS supplemented with 45 mM EGTA and 0.5 M NaOH.
II. The highest measured ratio of each sample was used for the calculation of intracellular Ca2+ levels using the Grynkiewicz-equation.52 For calibration, the maximum ratio (Rmax) was obtained by measuring Fura-2 AM-loaded cells lysed with 10 μL of 1% Triton® X-100 in PBS. The minimum ratio (Rmin) was measured using 10 μL of 1% Triton® X-100 in PBS supplemented with 45 mM EGTA and 0.5 M NaOH.
Fitting models
The binding curves obtained from the Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II Ca2+ mobilization assays were fit using a four-parameter nonlinear regression model (eqn (3)).
II Ca2+ mobilization assays were fit using a four-parameter nonlinear regression model (eqn (3)).Y = 100/(1 + 10(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50−X)·n) EC50−X)·n) | (3) |
| Y = Emax·X/(KD + X) | (4) |
Results
Cholesterol depletion of cell membranes decreases nanoparticle avidity for cells
For our binding experiments, we used a particle system well established in our group based on a core-shell design. A poly(ethylene glycol)-b-poly(D,L-lactide) (PEG-PLA)/poly(D,L-lactide-co-glycolide) (PLGA)-based particle was prepared. For this, a carboxy-terminated PEG-PLA polymer (carboxy-PEG-PLA) was synthesized via DBU catalyzed ring-opening polymerization of lactide on a carboxy-PEG starter. Ligand functionalization was performed by coupling Lys-Ang II to carboxy-PEG-PLA prior to particle preparation using EDC/NHS chemistry (Lys-Ang II-PEG-PLA). Coupling efficiency for Lys-Ang II-PEG-PLA and degree of ligand functionalization for NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II was quantified using Pierce BCA and iodine assay. Synthesized carboxy-PEG-PLA was characterized via1H-NMR. NPLys-Ang
II was quantified using Pierce BCA and iodine assay. Synthesized carboxy-PEG-PLA was characterized via1H-NMR. NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II size was determined via DLS (Fig. S2, also refer to experimental section for detailed specifications, ESI†). The size of our particle NPLys-Ang
II size was determined via DLS (Fig. S2, also refer to experimental section for detailed specifications, ESI†). The size of our particle NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II was in good agreement with the dimensions of CCPs regarding depth and neck width42 as wells as curvature53 and found to be in range with dimensions of dome-shaped CCPs.
II was in good agreement with the dimensions of CCPs regarding depth and neck width42 as wells as curvature53 and found to be in range with dimensions of dome-shaped CCPs.
To investigate the role of CCPs in the binding of ligand-functionalized nanoparticles to cells, we incubated AT1R-positive rat mesangial cells (rMCs)54 with angiotensin II-decorated nanoparticles. The binding studies consisted of four sub-experiments, in which the binding of free ligand (Lys-Ang II) and ligand-functionalized nanoparticles NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II was assessed in the absence and presence of CCP inhibitors.37,43,44
II was assessed in the absence and presence of CCP inhibitors.37,43,44
We found the Fura-2 AM based Ca2+ mobilization assay to be best suited for our binding experiments as it enables us to directly compare the binding data found for the free ligand with the data for our ligand functionalized nanoparticle due to the identical readout. The interaction of Ang II with the AT1 receptor induces the activation of phospholipase C, which in turn catalyzes the formation of diacylglycerol (DAG) and inositol trisphosphate (IP3).55 The latter induces the intracellular release of Ca2+ from the endoplasmic reticulum (ER).56
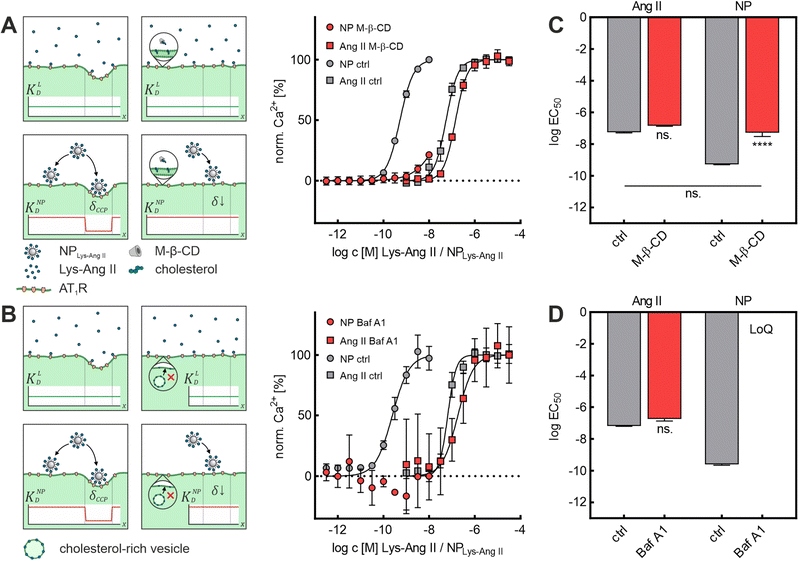
First, we investigated the effect of M-β-CD-induced cholesterol depletion on the binding intensity of Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II to cells (Fig. 2A). The EC50 values revealed no significant effect of M-β-CD treatment on Lys-Ang II affinity (ctrl: log
II to cells (Fig. 2A). The EC50 values revealed no significant effect of M-β-CD treatment on Lys-Ang II affinity (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −7.26 ± 0.02; M-β-CD: log
EC50 = −7.26 ± 0.02; M-β-CD: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −6.84 ± 0.02; mean ± sem), while the avidity of NPLys-Ang
EC50 = −6.84 ± 0.02; mean ± sem), while the avidity of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II decreased significantly compared to control (ctrl) (ctrl: log
II decreased significantly compared to control (ctrl) (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −9.28 ± 0.01; M-β-CD: log
EC50 = −9.28 ± 0.01; M-β-CD: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −7.28 ± 0.14; mean ± sem) (Fig. 2C). In the context of Ca2+ mobilization based binding assays, our control experiments consisted throughout of testing both free Lys-Ang II and NPLys-Ang
EC50 = −7.28 ± 0.14; mean ± sem) (Fig. 2C). In the context of Ca2+ mobilization based binding assays, our control experiments consisted throughout of testing both free Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II on untreated rMCs that were otherwise handled identically.
II on untreated rMCs that were otherwise handled identically.
One concern we had regarding the results of the M-β-CD experiments was the ability of M-β-CD to complex hydrophobic molecules. In the case of complexation of particle-bound ligands by M-β-CD, a significant effect on particle binding would have been expected. Thus, the observations could also have been due to such complexation.
On the one hand, the fact that hardly any effects on the interaction of the free ligand with the rMCs were observed speaks against this possibility. In addition, we wanted to test a CCP inhibitor that would affect CCP morphology in the same way as M-β-CD but would not be able to complex particle-bound ligands. To rule out this concern, we investigated the impact of Baf A1 on Lys-Ang II and NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II binding parameter log
II binding parameter log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 in binding assays on rMCs (Fig. 2B). Baf A1 inhibits CCP formation via a different mechanism of V-ATPase inhibition inducing cytosolic acidification resulting in impairment of cholesterol transport to the plasma membrane.41 The results confirmed the observations made with M-β-CD. While no significant effect was observed for the free ligand (ctrl: log
EC50 in binding assays on rMCs (Fig. 2B). Baf A1 inhibits CCP formation via a different mechanism of V-ATPase inhibition inducing cytosolic acidification resulting in impairment of cholesterol transport to the plasma membrane.41 The results confirmed the observations made with M-β-CD. While no significant effect was observed for the free ligand (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −7.18 ± 0.03; Baf A1: log
EC50 = −7.18 ± 0.03; Baf A1: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −6.74 ± 0.14; mean ± sem). NPLys-Ang
EC50 = −6.74 ± 0.14; mean ± sem). NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II binding was massively reduced. The avidity of particles in the presence of Baf A1 was poor. Not even with the highest possible nanoparticle concentration was it possible to elicit enough biological effect to obtain a binding curve that allowed for the calculation of an EC50 value (ctrl: log
II binding was massively reduced. The avidity of particles in the presence of Baf A1 was poor. Not even with the highest possible nanoparticle concentration was it possible to elicit enough biological effect to obtain a binding curve that allowed for the calculation of an EC50 value (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50: −9.61 ± 0.05; Baf A1: exceeds limit of quantification; mean ± sem) (Fig. 2D).
EC50: −9.61 ± 0.05; Baf A1: exceeds limit of quantification; mean ± sem) (Fig. 2D).
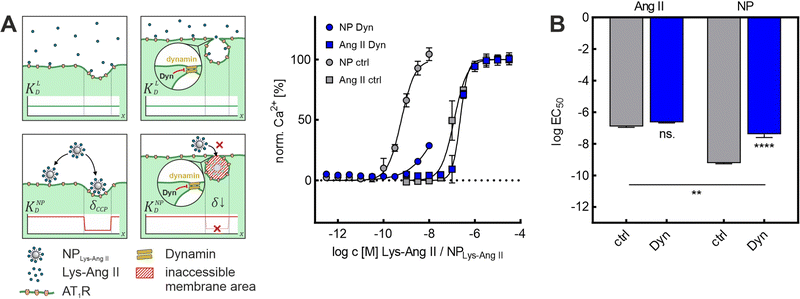
Because both inhibitors act by depleting cell membranes of cholesterol, we decided to repeat the experiments with Dyn, which operates via a different mechanism. Dyn freezes CCPs in late maturation stages. Most CCPs in the membrane exhibit a strong invagination as well as a narrow neck width after Dyn treatment. The Dyn experiments are of particular importance because of this primary mechanism of action. Since M-β-CD and Baf A1 exert their effects mainly via a change in membrane cholesterol content, a change in lateral receptor mobility57 cannot be ruled out in these cases. Due to its different mechanism of action, at least a smaller effect on receptor mobility can be assumed for Dyn treatment. The Dyn experiments supported the previous results. Again, while Lys-Ang II binding (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −6.94 ± 0.04; Dyn: log
EC50 = −6.94 ± 0.04; Dyn: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −6.64 ± 0.02; mean ± sem) was unaltered, nanoparticle avidity (ctrl: log
EC50 = −6.64 ± 0.02; mean ± sem) was unaltered, nanoparticle avidity (ctrl: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −9.22 ± 0.03; Dyn: log
EC50 = −9.22 ± 0.03; Dyn: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 = −7.39 ± 0.12; mean ± sem) was massively reduced in the Dyn-mediated absence of CCPs (Fig. 3A and B). In summary, these studies confirmed that dome-shaped CCPs are crucial for nanoparticle avidity, as their absence decreased nanoparticle binding significantly, irrespective of the type of CCP inhibitor that was used.
EC50 = −7.39 ± 0.12; mean ± sem) was massively reduced in the Dyn-mediated absence of CCPs (Fig. 3A and B). In summary, these studies confirmed that dome-shaped CCPs are crucial for nanoparticle avidity, as their absence decreased nanoparticle binding significantly, irrespective of the type of CCP inhibitor that was used.
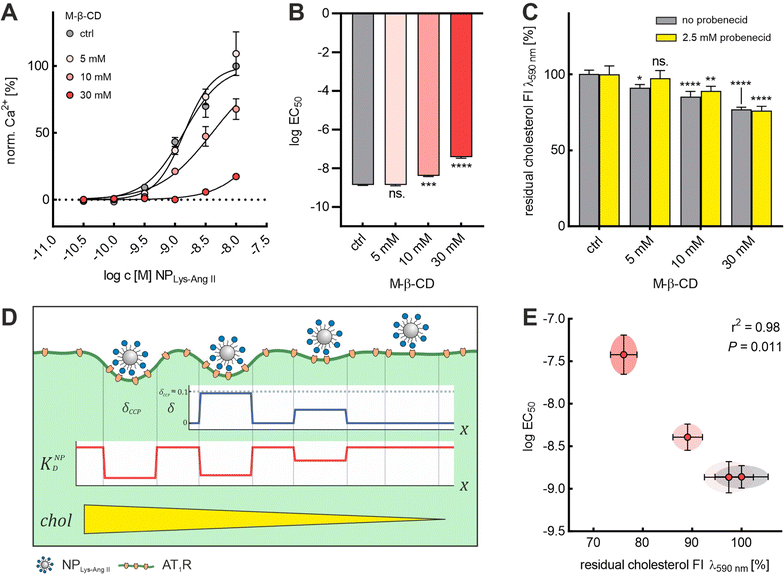
We demonstrated that it was possible to extract cholesterol from the membrane in a controlled manner using M-β-CD. With increasing concentration of M-β-CD, larger amounts of cholesterol were extracted (Fig. 4C). Also, based on the agreement of the results from the NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II binding studies with Baf A1 and M-β-CD (Fig. 2A and B), we concluded that M-β-CD does not appear to complex the ligands on the particle surface. With these given prerequisites, we decided to further investigate the effects of cholesterol depletion on nanoparticle binding. (Fig. 4A and B). To this end, we quantified the amount of cholesterol extracted from cell membranes as a function of M-β-CD concentrations (Fig. 4C and Fig. S3, ESI†). We observed that M-β-CD only induced a change of EC50 values when its concentration was sufficiently high to reduce the cell cholesterol content (Fig. 4A and B). We noticed a strong correlation (r2 = 0.98, P = 0.011) between the log
II binding studies with Baf A1 and M-β-CD (Fig. 2A and B), we concluded that M-β-CD does not appear to complex the ligands on the particle surface. With these given prerequisites, we decided to further investigate the effects of cholesterol depletion on nanoparticle binding. (Fig. 4A and B). To this end, we quantified the amount of cholesterol extracted from cell membranes as a function of M-β-CD concentrations (Fig. 4C and Fig. S3, ESI†). We observed that M-β-CD only induced a change of EC50 values when its concentration was sufficiently high to reduce the cell cholesterol content (Fig. 4A and B). We noticed a strong correlation (r2 = 0.98, P = 0.011) between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 value and the normalized cholesterol signal obtained (Fig. 4C and E). Our observation of decreasing nanoparticle binding with decreasing cholesterol content (Fig. 4D) is in line with findings that cholesterol depletion increases mechanical membrane stiffness,36,37,58 which, as Bucher et al. recently confirmed, suppresses the transition of flat clathrin-associated membrane structures to CCPs.23 This is consistent with simulations conducted by Hassinger et al. Here, the effect of increased membrane tension on the formation of membrane curvature was investigated.59
EC50 value and the normalized cholesterol signal obtained (Fig. 4C and E). Our observation of decreasing nanoparticle binding with decreasing cholesterol content (Fig. 4D) is in line with findings that cholesterol depletion increases mechanical membrane stiffness,36,37,58 which, as Bucher et al. recently confirmed, suppresses the transition of flat clathrin-associated membrane structures to CCPs.23 This is consistent with simulations conducted by Hassinger et al. Here, the effect of increased membrane tension on the formation of membrane curvature was investigated.59
Modelling nanoparticle binding to CCPs can predict nanoparticle avidity
To explore the impact of CCP presence on NP avidity, we developed a model that estimates the efficacy of nanoparticle binding to the cell membrane based on the nanoparticle wrapping fraction in CCPs. First, we defined the conditions for a perfect morphological alignment of nanoparticle and cell membrane. We assumed that this was the case when the nanoparticle curvature kNP is equal to the membrane Gaussian curvature Km (Fig. 5A, ESI†). To account for the degree of geometrical match, we employed the nanoparticle wrapping fraction δ, which is defined as the ratio of the part of the membrane surface area that is in contact with the nanoparticle Am (Km ≈ kNP) and the total nanoparticle surface area ONP (eqn (5), Fig. 5A). | (5) |
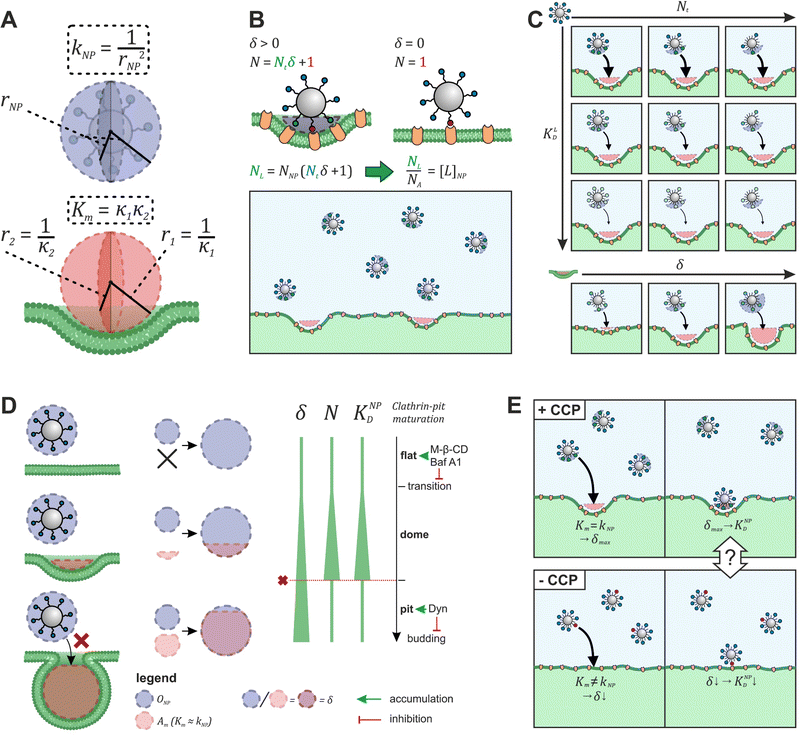 | ||
| Fig. 5 Model to predict KNPD shifts occurring upon cholesterol depletion. (A) Scheme illustrating the alignment of nanoparticle curvature kNP and Gaussian membrane curvature Km of a CCP. (B) Illustration how the effective ligand concentration [L]NP is calculated when a nanoparticle interacts with a cell membrane in the presence and absence of non-flat CCPs. (C) Illustration how the developed model (eqn (5)) can be used to derive binding curves for any combination of nanoparticle valency Nt, ligand affinity KLD and wrapping fraction δ. (D) Presentation of the preferential nanoparticle binding model assuming the constant curvature model20–22 for CCP maturation. After the initiation of membrane curvature, wrapping fraction δ increases as the maturation proceeds. Number of involved ligands N and nanoparticle avidity KNPD increase until dome-pit-transition occurs. After this, accessibility to the CCP for the nanoparticle is no longer given (red dashed line). The preferential nanoparticle binding model was also applied to a novel maturation model most recently introduced by Bucher et al.23 yielding the same conclusion of preferential binding of nanoparticles to dome-state CCPs (Fig. S1, ESI†). (E) Scheme illustrates the goal of eqn (7) to describe the effect of CCP invaginations on NP avidity KNPD. δCCP is the highest wrapping fraction for the considered membrane section. It occurs where Gaussian membrane curvature Km and nanoparticle curvature kNP align (Km = kNP). δ theoretically ranges from 0 to 1 (no vs. full wrapping of the particle). | ||
Initially, considering the case where a single nanoparticle binds to a membrane, the number of ligand–receptor bonds formed N can be estimated by correcting the valence Nt of the particle (total number of ligands on the particle) by the wrapping factor δ (ranging from 0 to 1: no to full wrapping of the particle). We consider this step justified as Wang et al. and Silpe et al. showed a clear valency dependence for nanoparticle avidity. The term +1 denotes a single ligand–receptor bond that can be formed regardless of whether a membrane structure is present (e.g., CCPs) that provides a wrapping fraction >0 to the particle.60,61
| N = δNt + 1 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NP for a given wrapping fraction δ. Assuming that the same wrapping fraction occurs for all particles, this can be easily done by multiplying the number of particles considered NNP by the number of ligands binding per particle determined according to eqn (6) (Nall
NP for a given wrapping fraction δ. Assuming that the same wrapping fraction occurs for all particles, this can be easily done by multiplying the number of particles considered NNP by the number of ligands binding per particle determined according to eqn (6) (Nall![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NP = NNP(δNt + 1)). The introduction of the Avogadro constant NA (Fig. 5B, ESI,†eqn (10) and (11)) yields [L]NP as shown in eqn (7).
NP = NNP(δNt + 1)). The introduction of the Avogadro constant NA (Fig. 5B, ESI,†eqn (10) and (11)) yields [L]NP as shown in eqn (7).| [L]NP = cNP(δNt + 1) | (7) |
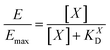 | (8) |
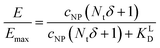 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II). For our Ca2+ mobilization assay, Emax was calculated by fitting data of NPLys-Ang
II). For our Ca2+ mobilization assay, Emax was calculated by fitting data of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II control experiment (Fig. 6B, grey symbols) using eqn (4). Eqn (9) can be used to model saturation binding curves for any given ligand-functionalized nanoparticle with a known number of ligands Nt and ligand affinity KLD for any given wrapping fraction δ (Fig. 5C). A nanoparticle's avidity KNPD can be calculated for E = Emax/2 where cNP equals KNPD. If we modify eqn (9) in this way, we obtain eqn (10), the first step of a derivation of a general relation of KNPD and KLD in dependence of the wrapping fraction δ.
II control experiment (Fig. 6B, grey symbols) using eqn (4). Eqn (9) can be used to model saturation binding curves for any given ligand-functionalized nanoparticle with a known number of ligands Nt and ligand affinity KLD for any given wrapping fraction δ (Fig. 5C). A nanoparticle's avidity KNPD can be calculated for E = Emax/2 where cNP equals KNPD. If we modify eqn (9) in this way, we obtain eqn (10), the first step of a derivation of a general relation of KNPD and KLD in dependence of the wrapping fraction δ.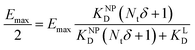 | (10) |
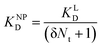 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II can be considered realistic. For the presence of exclusively flat-shaped CCPs our model would predict an avidity loss of 2.1 to 2.7 orders of magnitude, which is perfectly in line with our experimentally observed KD shifts of NPLys-Ang
II can be considered realistic. For the presence of exclusively flat-shaped CCPs our model would predict an avidity loss of 2.1 to 2.7 orders of magnitude, which is perfectly in line with our experimentally observed KD shifts of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II (Fig. 6F).
II (Fig. 6F).
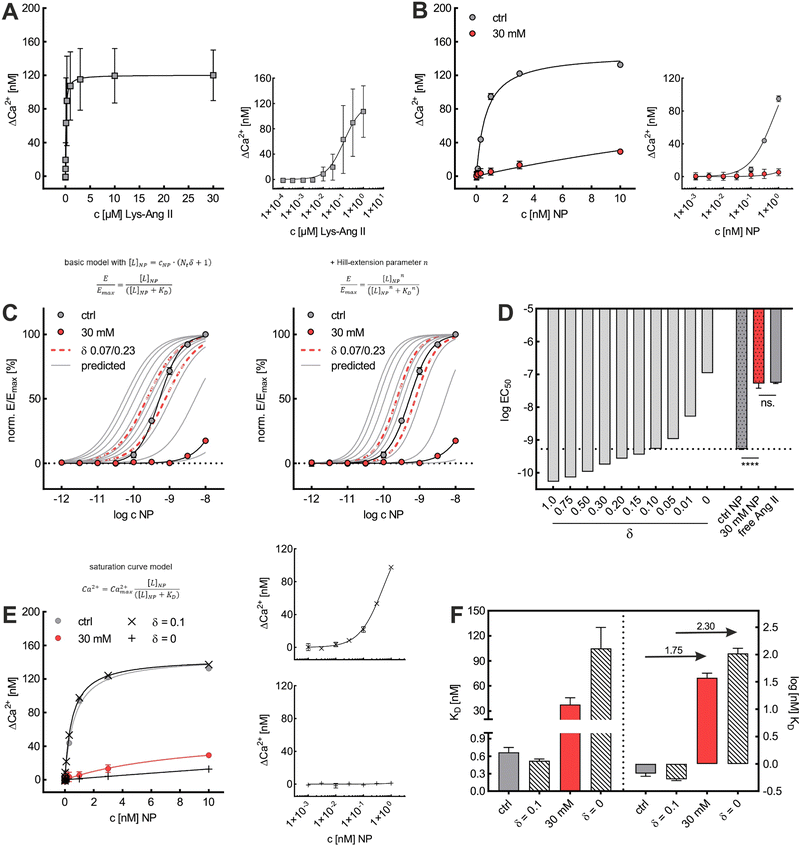 | ||
Fig. 6 Comparison of model to predicted KNPD shift with experimental data. (A) Saturation curve derived from data acquired for free Lys-Ang II in Ca2+ mobilization assay (experiment + one repeat, each N = 3). (B) Saturation curves derived for binding of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II to untreated and 30 mM M-β-CD pretreated cells (N = 3). In (A) and (B), data acquired for lower concentrations (Lys-Ang II 0.1 nM–1 μM; NPLys-Ang II to untreated and 30 mM M-β-CD pretreated cells (N = 3). In (A) and (B), data acquired for lower concentrations (Lys-Ang II 0.1 nM–1 μM; NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II 1 pM–1 nM) were also plotted against a log-scale for clarity. (C) Binding curves predicted for a series of δ-values were plotted and compared to binding curves based on data derived from Ca2+ mobilization assay. Binding curves were predicted using eqn (5) and the model further modified via Hill-extension (eqn (8)). Red dashed lines are predicted binding curves for the lower and upper limits of δ (δ = 0.07 and δ = 0.23, ESI†) (error bars in (A), (B), and (C) reflect standard deviation). (D) Comparison of log II 1 pM–1 nM) were also plotted against a log-scale for clarity. (C) Binding curves predicted for a series of δ-values were plotted and compared to binding curves based on data derived from Ca2+ mobilization assay. Binding curves were predicted using eqn (5) and the model further modified via Hill-extension (eqn (8)). Red dashed lines are predicted binding curves for the lower and upper limits of δ (δ = 0.07 and δ = 0.23, ESI†) (error bars in (A), (B), and (C) reflect standard deviation). (D) Comparison of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 values of predicted binding curves for a series of values of δ and log EC50 values of predicted binding curves for a series of values of δ and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 values determined for Ca2+ mobilization assays for NPLys-Ang EC50 values determined for Ca2+ mobilization assays for NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II in presence (ctrl NP) and absence (30 mM NP) of CCPs and for Lys-Ang II. Dashed line refers to the log II in presence (ctrl NP) and absence (30 mM NP) of CCPs and for Lys-Ang II. Dashed line refers to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50 value for the binding of NPLys-Ang EC50 value for the binding of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II in control experiments (ctrl NP). Data were compared via one-way ANOVA analysis with subsequent Tukey's multiple comparison test (ns. – not significant, **** – P < 0.0001; error bars reflect standard error of mean; α = 0.001, F = 194.1, df = 8). (E) Comparison of experimental saturation curves and model-based predictions for best-fit value δ = 0.1 and δ = 0. (F) Corresponding KD values (error-bars reflect the 95% CI). The values above the arrows indicate the decrease of KD in log-steps. II in control experiments (ctrl NP). Data were compared via one-way ANOVA analysis with subsequent Tukey's multiple comparison test (ns. – not significant, **** – P < 0.0001; error bars reflect standard error of mean; α = 0.001, F = 194.1, df = 8). (E) Comparison of experimental saturation curves and model-based predictions for best-fit value δ = 0.1 and δ = 0. (F) Corresponding KD values (error-bars reflect the 95% CI). The values above the arrows indicate the decrease of KD in log-steps. | ||
To investigate the predictive power of our theoretical model, we analyzed the impact of cholesterol-depletion via M-β-CD on the dissociation constant KD of nanoparticle binding and on their avidity. For this, we plotted data derived from Ca2+ mobilization assays investigating effects of M-β-CD to obtain saturation curves (Fig. 6A and B). In untreated cells, the nanoparticle's KD of 0.67 nM exceeded the free ligand's KD of 108 nM by approximately 160-fold. In contrast, when cells were treated with M-β-CD, nanoparticles were subject to a massive avidity loss. KD values increased to 37.7 nM, meaning that the nanoparticles had a mere 2.9-fold binding strength increase compared to the free ligand.
Based on KD values found for the free ligand Lys-Ang II, we predicted binding curves to investigate the impact of the wrapping fraction δ (eqn (9)) and the corresponding Hill-slope n modified model (eqn (12), Fig. 6C). This allowed us to find the best possible estimate of δ for our nanoparticle model system in the presence and absence of CCPs (Fig. 6D and Fig. S4, ESI†).
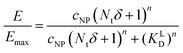 | (12) |
Discussion & conclusion
Our studies have shown that CCPs, which provide a given wrapping fraction for nanoparticles due to their perfect geometric match, are essential for receptor-mediated nanoparticle membrane interactions. We found a 1–2 order of magnitude lower avidity of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II for receptor-positive mesangial cells in the absence of CCPs. We attribute this to decreases in multivalent receptor binding and the number of interactions between nanoparticle and cell when dome- and pit-shaped CCPs are absent. We conclude that the arrangement of receptors in invaginated CCPs allows for more ligand receptor interactions leading to the observed affinity increase. In this context, reference should be made to the work of Martinez-Veracoechea et al. who demonstrated that accumulation of nanoparticles occurs in a directional manner towards cells with higher receptor concentration.64 Also, observations made by Barbul et al. indicated that smallest changes in receptor density can have significant effects on nanoparticle membrane binding.34 By analogy, our results suggest that particle accumulation could also occur on a single cell depending on the wrapping fraction. The results of Martinez-Veracoechea et al. suggest that due to the higher proximity of ligands and receptors in a membrane section with a given wrapping fraction for particles (e.g., CCPs), there might be a preferential accumulation of nanoparticles towards such sections. M-β-CD treatment decreases the EC50 of NPLys-Ang
II for receptor-positive mesangial cells in the absence of CCPs. We attribute this to decreases in multivalent receptor binding and the number of interactions between nanoparticle and cell when dome- and pit-shaped CCPs are absent. We conclude that the arrangement of receptors in invaginated CCPs allows for more ligand receptor interactions leading to the observed affinity increase. In this context, reference should be made to the work of Martinez-Veracoechea et al. who demonstrated that accumulation of nanoparticles occurs in a directional manner towards cells with higher receptor concentration.64 Also, observations made by Barbul et al. indicated that smallest changes in receptor density can have significant effects on nanoparticle membrane binding.34 By analogy, our results suggest that particle accumulation could also occur on a single cell depending on the wrapping fraction. The results of Martinez-Veracoechea et al. suggest that due to the higher proximity of ligands and receptors in a membrane section with a given wrapping fraction for particles (e.g., CCPs), there might be a preferential accumulation of nanoparticles towards such sections. M-β-CD treatment decreases the EC50 of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II to the value obtained for the free ligand Lys-Ang II on cells that were not cholesterol-depleted. From this we conclude that the avidity gain of multivalent nanoparticles is a combined effect of multivalency65,66 and the presence of membrane structures (e.g., CCPs) offering nanoparticles a certain wrapping fraction for initial membrane attachment.
II to the value obtained for the free ligand Lys-Ang II on cells that were not cholesterol-depleted. From this we conclude that the avidity gain of multivalent nanoparticles is a combined effect of multivalency65,66 and the presence of membrane structures (e.g., CCPs) offering nanoparticles a certain wrapping fraction for initial membrane attachment.
Comparison of the results presented in this work with findings of Bahrami et al.33 indicates that fundamental laws governing the interaction of particles with membranes may be transferable to the case of a multivalent ligand-functionalized particle. In the mentioned work, total energies of particles interacting with the inside of a vesicle enclosing them are described. With the radius of particle and vesicle membrane approaching each other, a steepening decrease of the internal energy with increasing wrapping fraction is reported. Considering CCPs as structures offering a particle a membrane section that already displays an area Am(Km ≈ kNP) > 0 (consequently δ > 0), it can be concluded from the results of Bahrami et al. that this interaction should be energetically favored.
This was confirmed by our simple theoretical model that accounts for the morphological match of nanoparticle and CCP geometry. An effective available ligand concentration [L]NP derived from the contact area between nanoparticle and pit allowed us to predict nanoparticle binding curves based on the free ligand's affinity. Our model suggests 10% alignment between CCPs and our model nanoparticle surfaces (δ = 0.10), which corresponds very well with our initial expectations (δ = 0.07–0.23) estimated from the geometrical fit of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II to unaltered CCPs (Fig. 6C and D).53,63 When we calculated the cholesterol depletion-induced avidity loss of NPLys-Ang
II to unaltered CCPs (Fig. 6C and D).53,63 When we calculated the cholesterol depletion-induced avidity loss of NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II, it predicted a 2.3 order of magnitude decrease, which is close to the experimental value (Fig. 6E and F). This underlines the predictive power of our model and the relevance of our theoretical considerations.
II, it predicted a 2.3 order of magnitude decrease, which is close to the experimental value (Fig. 6E and F). This underlines the predictive power of our model and the relevance of our theoretical considerations.
The implications of our findings go far beyond a more precise understanding of the role of CCPs in nanoparticle binding to cells. The relationship between the relative curvatures of the nanoparticle and cell membrane suggest how nanoparticle size and geometry can be tailored to improve their interactions with target cells. It provides researchers designing targeted nanoparticles with a solid rational for the optimization of binding avidity. A second important consideration for nanoparticle design is the target receptor; for example, nanoparticles binding to caveolae-associated receptors may be subject to similar considerations as we had for CCPs. Ultimately, these two factors need to be reconciled to yield a nanoparticle in good morphological correspondence to the membrane structure most relevant for the targeted receptor. However, morphological dependence of nanoparticle binding could be a challenging aspect to consider for biomedical applications in which nanoparticle geometry cannot be altered. An approach could be to design systems that adapt their structure according to the membrane morphology they encounter, such as flexible nanofibers.67 Moreover, our results could explain recent findings that the avidity of influenza as well as SARS-CoV-2 virions for target cells is cholesterol sensitive, but this conclusion awaits further exploration.68,69
Finally, we want to point out and discuss limitations of the present work. Regarding our theoretical model it should be noted that the procedure of correcting the valency of the nanoparticle (Nt) for its wrapping fraction (δ) (eqn (6)) determines the maximum possible number of receptor–ligand pairs that could theoretically be formed based on the particle valency. For the case of low receptor–ligand binding energy, the number of receptor–ligand pairs formed could be lower than eqn (6) would suggest due to receptor entropy loss during binding.
Regarding the NPLys-Ang![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II binding experiments, we think that based on our control experiments with the free ligand, a significant influence on the receptor activity due to cholesterol extraction (via M-β-CD and Baf A1 treatment) can be excluded as a primary cause for the presented observations. However, with respect to lateral receptor mobility, it should be noted that Dyn also influences cholesterol trafficking in addition to its primary mechanism of action (arrest of CCPs in late stages of maturation). Thus, a partial involvement of reduced lateral receptor mobility57 or abrogation of cholesterol dependent liquid-ordered lipid phases70 cannot be excluded with certainty. To estimate the involvement or the degree of involvement of this factor, methods would be required to inhibit the formation of CCPs without further side effects on the membrane. Currently, we do not see any method that perfectly fulfills this requirement.
II binding experiments, we think that based on our control experiments with the free ligand, a significant influence on the receptor activity due to cholesterol extraction (via M-β-CD and Baf A1 treatment) can be excluded as a primary cause for the presented observations. However, with respect to lateral receptor mobility, it should be noted that Dyn also influences cholesterol trafficking in addition to its primary mechanism of action (arrest of CCPs in late stages of maturation). Thus, a partial involvement of reduced lateral receptor mobility57 or abrogation of cholesterol dependent liquid-ordered lipid phases70 cannot be excluded with certainty. To estimate the involvement or the degree of involvement of this factor, methods would be required to inhibit the formation of CCPs without further side effects on the membrane. Currently, we do not see any method that perfectly fulfills this requirement.
Regarding the general applicability of the presented theoretical model, the present work provides a first insight into the role of CCPs for avidity of particle-membrane interactions. To draw clearer conclusions in this context, it would be helpful to study particles with varying size and geometry. This is difficult to do with the PEG-PLA/PLG-based particle used in this study. Other particle models that allow precise control of size and geometry (e.g. Au nanoparticles)71 would be a promising platform for this purpose. Further studies investigating different nanoparticle platforms will also have to reveal how parameters like ligand density or linker lengths effect the model's predictive power.
Author contributions
A. G., O. Z. Conceptualization, A. G., O. Z. methodology, O. Z. formal analysis, O. Z. investigation, A. G., O. Z. validation, O. Z. writing – original draft, A.G. writing – review & editing, O. Z. visualization, A. G. supervision, A. G. funding acquisition.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) grant GO 565/20-1. The authors thank Prof. Miriam Breunig, Dr Sara Maslanka Figueroa, Dr Daniel Fleischmann, Felix Baumann, Melanie Walter, Jonas Groner, and Clara Barbey for many constructive discussions on the conducted research. Also, the authors thank Renate Liebl and Viktoria Eismann for their excellent technical assistance.Notes and references
- B. D. Chithrani, A. A. Ghazani and W. C. W. Chan, Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells, Nano Lett., 2006, 6, 662–668 CrossRef CAS PubMed.
- A. Albanese, P. S. Tang and W. C. W. Chan, The effect of nanoparticle size, shape, and surface chemistry on biological systems, Annu. Rev. Biomed. Eng., 2012, 14, 1–16 CrossRef CAS PubMed.
- W. Jiang, B. Y. S. Kim, J. T. Rutka and W. C. W. Chan, Nanoparticle-mediated cellular response is size-dependent, Nat. Nanotechnol., 2008, 3, 145–150 CrossRef CAS PubMed.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Understanding biophysicochemical interactions at the nano-bio interface, Nat. Mater., 2009, 8, 543–557 CrossRef CAS PubMed.
- N. Hoshyar, S. Gray, H. Han and G. Bao, The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction, Nanomedicine, 2016, 11, 673–692 CrossRef CAS PubMed.
- Z.-G. Yue, W. Wei, P.-P. Lv, H. Yue, L.-Y. Wang, Z.-G. Su and G.-H. Ma, Surface charge affects cellular uptake and intracellular trafficking of chitosan-based nanoparticles, Biomacromolecules, 2011, 12, 2440–2446 CrossRef CAS PubMed.
- K. Abstiens, M. Gregoritza and A. M. Goepferich, Ligand Density and Linker Length are Critical Factors for Multivalent Nanoparticle-Receptor Interactions, ACS Appl. Mater. Interfaces, 2019, 11, 1311–1320 CrossRef CAS PubMed.
- C. H. Kapadia, S. Tian, J. L. Perry, J. C. Luft and J. M. DeSimone, Role of Linker Length and Antigen Density in Nanoparticle Peptide Vaccine, ACS Omega, 2019, 4, 5547–5555 CrossRef CAS PubMed.
- S. M. Figueroa, D. Fleischmann, S. Beck and A. Goepferich, The Effect of Ligand Mobility on the Cellular Interaction of Multivalent Nanoparticles, Macromol. Biosci., 2020, e1900427 CrossRef PubMed.
- C. L. Modery-Pawlowski and A. S. Gupta, Heteromultivalent ligand-decoration for actively targeted nanomedicine, Biomaterials, 2014, 35, 2568–2579 CrossRef CAS.
- S. M. Figueroa, A. Veser, K. Abstiens, D. Fleischmann, S. Beck and A. Goepferich, Influenza A virus mimetic nanoparticles trigger selective cell uptake, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9831–9836 CrossRef CAS PubMed.
- M. B. Deci, M. Liu, Q. T. Dinh and J. Nguyen, Precision engineering of targeted nanocarriers, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2018, 10, e1511 Search PubMed.
- S. Block, V. P. Zhdanov and F. Höök, Quantification of Multivalent Interactions by Tracking Single Biological Nanoparticle Mobility on a Lipid Membrane, Nano Lett., 2016, 16, 4382–4390 CrossRef CAS.
- D. Di Iorio, M. L. Verheijden, E. van der Vries, P. Jonkheijm and J. Huskens, Weak Multivalent Binding of Influenza Hemagglutinin Nanoparticles at a Sialoglycan-Functionalized Supported Lipid Bilayer, ACS Nano, 2019, 13, 3413–3423 CrossRef CAS PubMed.
- H. Jung, A. D. Robison and P. S. Cremer, Multivalent ligand–receptor binding on supported lipid bilayers, J. Struct. Biol., 2009, 168, 90–94 CrossRef CAS PubMed.
- R. S. Kane, Thermodynamics of multivalent interactions: influence of the linker, Langmuir, 2010, 26, 8636–8640 CrossRef CAS PubMed.
- M. Ehrlich, W. Boll, A. van Oijen, R. Hariharan, K. Chandran, M. L. Nibert and T. Kirchhausen, Endocytosis by random initiation and stabilization of clathrin-coated pits, Cell, 2004, 118, 591–605 CrossRef CAS PubMed.
- M. Kaksonen and A. Roux, Mechanisms of clathrin-mediated endocytosis, Nat. Rev. Mol. Cell Biol., 2018, 19, 313–326 CrossRef CAS PubMed.
- O. Avinoam, M. Schorb, C. J. Beese, J. A. G. Briggs and M. Kaksonen, ENDOCYTOSIS. Endocytic sites mature by continuous bending and remodeling of the clathrin coat, Science, 2015, 348, 1369–1372 CrossRef CAS.
- T. Kirchhausen, Coated pits and coated vesicles—sorting it all out, Curr. Opin. Struct. Biol., 1993, 3, 182–188 CrossRef CAS.
- T. Kirchhausen, Imaging endocytic clathrin structures in living cells, Trends Cell Biol., 2009, 19, 596–605 CrossRef CAS PubMed.
- M. Lampe, S. Vassilopoulos and C. Merrifield, Clathrin coated pits, plaques and adhesion, J. Struct. Biol., 2016, 196, 48–56 CrossRef CAS PubMed.
- D. Bucher, F. Frey, K. A. Sochacki, S. Kummer, J.-P. Bergeest, W. J. Godinez, H.-G. Kräusslich, K. Rohr, J. W. Taraska, U. S. Schwarz and S. Boulant, Clathrin-adaptor ratio and membrane tension regulate the flat-to-curved transition of the clathrin coat during endocytosis, Nat. Commun., 2018, 9, 1109 CrossRef PubMed.
- A. A. Yetisgin, S. Cetinel, M. Zuvin, A. Kosar and O. Kutlu, Therapeutic Nanoparticles and Their Targeted Delivery Applications, Molecules, 2020, 25, 2193 CrossRef CAS PubMed.
- T. Kirchhausen, D. Owen and S. C. Harrison, Molecular structure, function, and dynamics of clathrin-mediated membrane traffic, Cold Spring Harbor Perspect. Biol., 2014, 6, a016725 CrossRef PubMed.
- A. J. Simnick, C. A. Valencia, R. Liu and A. Chilkoti, Morphing low-affinity ligands into high-avidity nanoparticles by thermally triggered self-assembly of a genetically encoded polymer, ACS Nano, 2010, 4, 2217–2227 CrossRef CAS PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Polyvalent Interactions in Biological Systems: Implications for Design and Use of Multivalent Ligands and Inhibitors, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef PubMed.
- M. Wang, S. R. Ravindranath, M. K. Rahim, E. L. Botvinick and J. B. Haun, Evolution of Multivalent Nanoparticle Adhesion via Specific Molecular Interactions, Langmuir, 2016, 32, 13124–13136 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Adhesive Nanoparticles as Local Probes of Membrane Curvature, Nano Lett., 2015, 15, 7168–7173 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Uniform and Janus-like nanoparticles in contact with vesicles: energy landscapes and curvature-induced forces, Soft Matter, 2017, 13, 2155–2173 RSC.
- Q. Yu, S. Othman, S. Dasgupta, T. Auth and G. Gompper, Nanoparticle wrapping at small non-spherical vesicles: curvatures at play, Nanoscale, 2018, 10, 6445–6458 RSC.
- M. Deserno and T. Bickel, Wrapping of a spherical colloid by a fluid membrane, Europhys. Lett., 2003, 62, 767–774 CrossRef CAS.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, The role of membrane curvature for the wrapping of nanoparticles, Soft Matter, 2016, 12, 581–587 RSC.
- A. Barbul, K. Singh, L. Horev-Azaria, S. Dasgupta, T. Auth, R. Korenstein and G. Gompper, Nanoparticle-Decorated Erythrocytes Reveal That Particle Size Controls the Extent of Adsorption, Cell Shape, and Cell Deformability, ACS Appl. Nano Mater., 2018, 1, 3785–3799 CrossRef CAS.
- K. A. Sochacki, B. L. Heine, G. J. Haber, J. R. Jimah, B. Prasai, M. A. Alfonzo-Méndez, A. D. Roberts, A. Somasundaram, J. E. Hinshaw and J. W. Taraska, The structure and spontaneous curvature of clathrin lattices at the plasma membrane, Dev. Cell, 2021, 56, 1131–1146.e3 CrossRef CAS PubMed.
- F. J. Byfield, H. Aranda-Espinoza, V. G. Romanenko, G. H. Rothblat and I. Levitan, Cholesterol depletion increases membrane stiffness of aortic endothelial cells, Biophys. J., 2004, 87, 3336–3343 CrossRef CAS PubMed.
- S. K. Rodal, G. Skretting, O. Garred, F. Vilhardt, B. van Deurs and K. Sandvig, Extraction of cholesterol with methyl-beta-cyclodextrin perturbs formation of clathrin-coated endocytic vesicles, Mol. Biol. Cell, 1999, 10, 961–974 CrossRef CAS PubMed.
- W. G. Thomas, T. J. Thekkumkara and K. M. Baker, Molecular mechanisms of angiotensin II (AT1A) receptor endocytosis, Clin. Exp. Pharmacol. Physiol., Suppl., 1996, 3, S74–S80 CrossRef CAS PubMed.
- S. Mahammad and I. Parmryd, in Methods in Membrane Lipids, ed. D. M. Owen, Springer New York, New York, NY, 2015, pp. 91–102 Search PubMed.
- R. Zidovetzki and I. Levitan, Use of cyclodextrins to manipulate plasma membrane cholesterol content: evidence, misconceptions and control strategies, Biochem. Biophys. Acta, 2007, 1768, 1311–1324 CAS.
- A. Subtil, I. Gaidarov, K. Kobylarz, M. A. Lampson, J. H. Keen and T. E. McGraw, Acute cholesterol depletion inhibits clathrin-coated pit budding, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6775–6780 CrossRef CAS PubMed.
- T. Furuchi, K. Aikawa, H. Arai and K. Inoue, Bafilomycin A1, a specific inhibitor of vacuolar-type H(+)-ATPase, blocks lysosomal cholesterol trafficking in maceophages, J. Biol. Chem., 1993, 268, 27345–27348 CrossRef CAS.
- P. Kozik, N. A. Hodson, D. A. Sahlender, N. Simecek, C. Soromani, J. Wu, L. M. Collinson and M. S. Robinson, A human genome-wide screen for regulators of clathrin-coated vesicle formation reveals an unexpected role for the V-ATPase, Nat. Cell Biol., 2013, 15, 50–60 CrossRef CAS PubMed.
- E. Macia, M. Ehrlich, R. Massol, E. Boucrot, C. Brunner and T. Kirchhausen, Dynasore, a cell-permeable inhibitor of dynamin, Dev. Cell, 2006, 10, 839–850 CrossRef CAS PubMed.
- E. Girard, J. L. Paul, N. Fournier, P. Beaune, L. Johannes, C. Lamaze and B. Védie, The dynamin chemical inhibitor dynasore impairs cholesterol trafficking and sterol-sensitive genes transcription in human HeLa cells and macrophages, PLoS One, 2011, 6, e29042 CrossRef CAS PubMed.
- G. Preta, J. G. Cronin and I. M. Sheldon, Dynasore - not just a dynamin inhibitor, Cell Commun. Signaling, 2015, 13, 24 CrossRef.
- S. Hua, M. B. C. de Matos, J. M. Metselaar and G. Storm, Current Trends and Challenges in the Clinical Translation of Nanoparticulate Nanomedicines: Pathways for Translational Development and Commercialization, Front. Pharmacol., 2018, 9, 790 CrossRef PubMed.
- J. I. Hare, T. Lammers, M. B. Ashford, S. Puri, G. Storm and S. T. Barry, Challenges and strategies in anti-cancer nanomedicine development: An industry perspective, Adv. Drug Delivery Rev., 2017, 108, 25–38 CrossRef CAS.
- L. Sercombe, T. Veerati, F. Moheimani, S. Y. Wu, A. K. Sood and S. Hua, Advances and Challenges of Liposome Assisted Drug Delivery, Front. Pharmacol., 2015, 6, 286 Search PubMed.
- H. Nehoff, N. N. Parayath, L. Domanovitch, S. Taurin and K. Greish, Nanomedicine for drug targeting: strategies beyond the enhanced permeability and retention effect, Int. J. Nanomed., 2014, 9, 2539–2555 Search PubMed.
- J.-M. Rabanel, J. Faivre, S. F. Tehrani, A. Lalloz, P. Hildgen and X. Banquy, Effect of the Polymer Architecture on the Structural and Biophysical Properties of PEG-PLA Nanoparticles, ACS Appl. Mater. Interfaces, 2015, 7, 10374–10385 CrossRef CAS.
- G. Grynkiewicz, M. Poenie and R. Y. Tsien, A New Generation of Ca2+ Indicators with Greatly Improved Fluorescence Properties, J. Biol. Chem., 1985, 260, 3440–3450 CrossRef CAS.
- V. Ramanan, N. J. Agrawal, J. Liu, S. Engles, R. Toy and R. Radhakrishnan, Systems biology and physical biology of clathrin-mediated endocytosis, Integr. Biol., 2011, 3, 803–815 CrossRef CAS PubMed.
- R. Hennig, K. Pollinger, J. Tessmar and A. Goepferich, Multivalent targeting of AT1 receptors with angiotensin II-functionalized nanoparticles, J. Drug Targeting, 2015, 23, 681–689 CrossRef PubMed.
- K. K. Griendling, S. E. Rittenhouse, T. A. Brock, L. S. Ekstein, M. A. Gimbrone and R. W. Alexander, Sustained diacylglycerol formation from inositol phospholipids in angiotensin II-stimulated vascular smooth muscle cells, J. Biol. Chem., 1986, 261, 5901–5906 CrossRef CAS PubMed.
- S. Greco, M. Elia, A. Muscella, C. Storelli and S. Marsigliante, AT1 Angiotensin II receptor mediates intracellular calcium mobilization in normal and cancerous breast cells in primary culture, Cell Calcium, 2002, 32, 1–10 CrossRef CAS PubMed.
- J. Brejchová, J. Sýkora, P. Ostašov, L. Merta, L. Roubalová, J. Janáček, M. Hof and P. Svoboda, TRH-receptor mobility and function in intact and cholesterol-depleted plasma membrane of HEK293 cells stably expressing TRH-R-eGFP, Biochem. Biophys. Acta, 2015, 1848, 781–796 Search PubMed.
- A. Biswas, P. Kashyap, S. Datta, T. Sengupta and B. Sinha, Cholesterol Depletion by MβCD Enhances Cell Membrane Tension and Its Variations-Reducing Integrity, Biophys. J., 2019, 116, 1456–1468 CrossRef CAS PubMed.
- J. E. Hassinger, G. Oster, D. G. Drubin and P. Rangamani, Design principles for robust vesiculation in clathrin-mediated endocytosis, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1118–E1127 CrossRef CAS PubMed.
- J. Wang, J. Min, S. A. Eghtesadi, R. S. Kane and A. Chilkoti, Quantitative Study of the Interaction of Multivalent Ligand-Modified Nanoparticles with Breast Cancer Cells with Tunable Receptor Density, ACS Nano, 2020, 14, 372–383 CrossRef CAS PubMed.
- J. E. Silpe, M. Sumit, T. P. Thomas, B. Huang, A. Kotlyar, M. A. van Dongen, M. M. Banaszak Holl, B. G. Orr and S. K. Choi, Avidity modulation of folate-targeted multivalent dendrimers for evaluating biophysical models of cancer targeting nanoparticles, ACS Chem. Biol., 2013, 8, 2063–2071 CrossRef CAS PubMed.
- A. J. Clark, The reaction between acetyl choline and muscle cells, J. Physiol., 1926, 61, 530–546 CrossRef CAS PubMed.
- N. J. Agrawal, J. Nukpezah and R. Radhakrishnan, Minimal mesoscale model for protein-mediated vesiculation in clathrin-dependent endocytosis, PLoS Comput. Biol., 2010, 6, e1000926 CrossRef PubMed.
- F. J. Martinez-Veracoechea and D. Frenkel, Designing super selectivity in multivalent nano-particle binding, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10963–10968 CrossRef CAS PubMed.
- L. Woythe, N. B. Tito and L. Albertazzi, A quantitative view on multivalent nanomedicine targeting, Adv. Drug Delivery Rev., 2021, 169, 1–21 CrossRef CAS PubMed.
- P. Varilly, S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, A general theory of DNA-mediated and other valence-limited colloidal interactions, J. Chem. Phys., 2012, 137, 94108 CrossRef PubMed.
- S. Kajdič, O. Planinšek, M. Gašperlin and P. Kocbek, Electrospun nanofibers for customized drug-delivery systems, J. Drug Delivery Sci. Technol., 2019, 51, 672–681 CrossRef.
- I. N. Goronzy, R. J. Rawle, S. G. Boxer and P. M. Kasson, Cholesterol enhances influenza binding avidity by controlling nanoscale receptor clustering, Chem. Sci., 2018, 9, 2340–2347 RSC.
- D. W. Sanders, C. C. Jumper, P. J. Ackerman, D. Bracha, A. Donlic, H. Kim, D. Kenney, I. Castello-Serrano, S. Suzuki, T. Tamura, A. H. Tavares, M. Saeed, A. S. Holehouse, A. Ploss, I. Levental, F. Douam, R. F. Padera, B. D. Levy and C. P. Brangwynne, SARS-CoV-2 requires cholesterol for viral entry and pathological syncytia formation, eLife, 2021, 10, e65962 CrossRef CAS PubMed.
- D. Marsh, Liquid-ordered phases induced by cholesterol: a compendium of binary phase diagrams, Biochem. Biophys. Acta, 2010, 1798, 688–699 CAS.
- L. F. d Freitas, G. H. C. Varca, J. G. D. S. Batista and A. B. Lugão, An Overview of the Synthesis of Gold Nanoparticles Using Radiation Technologies, Nanomaterials, 2018, 8, 939 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00543c |
| This journal is © The Royal Society of Chemistry 2023 |