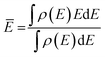Open Access Article
Open Access ArticleSolvent-induced local environment effect in plasmonic catalysis†
Tien
Le
 and
Bin
Wang
and
Bin
Wang
 *
*
School of Sustainable Chemical, Biological and Materials Engineering, University of Oklahoma, Norman, OK 73019, USA. E-mail: wang_cbme@ou.edu
First published on 2nd October 2023
Abstract
Solvents are known to affect the local surface plasmon resonance of metal nanoparticles; however, how solvents can be used to manipulate the interfacial charge and energy transfer in plasmonic catalysis remains to be explored. Here, using NH3 decomposition on a Ru-doped Cu surface as an example, we report density functional theory (DFT) and delta self-consistent field (SCF) calculations, through which we investigate the effect of different protic solvent molecules on interfacial charge transfer by calculating excitation energy of an electronic transition between the metal and the molecular reactant. We find that the H-bonds between water and NH3 can alter the direct interfacial charge transfer due to the shift of the molecular frontier orbitals with respect to the metal Fermi level. These effects are also observed when the H-bonds are formed between methanol (or phenol) and ammonia. We show that the solvent possessing stronger basicity induces a more pronounced effect on the excitation energy. This work thus provides valuable insights for tuning the excitation energy and controlling different routes to channel the photon energy into plasmonic catalysis.
Introduction
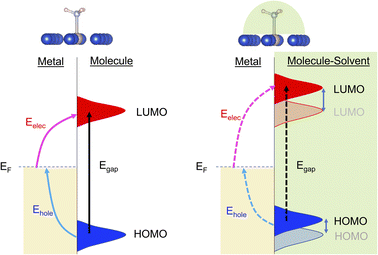
Plasmonic catalysis has received extensive interest over the last decade due to its potential to activate chemical bonds by channeling the photonic energy via non-equilibrium charge carriers instead of a traditional heat-induced vibrational population.1–6 This potential motivates researchers to design a catalyst system to achieve desirable product selectivity, which is a challenge in many thermal-driven reactions, especially for processes that are typically performed at relatively high temperatures such as dehydrogenation, ammonia synthesis, CO2 reduction, and hydrocarbon reforming.7Plasmonic catalysis is stimulated by the intensive charge polarization and the amplified near field due to local surface plasmon resonance (LSPR) of the metal nanoparticles. When LSPR dissipates the energy via non-radiative decay, non-equilibrium charge carriers (energetic electrons and holes) can be generated. If there are electron-accepting orbitals available in the proximity, such as unoccupied orbitals of adsorbed molecules, these high energy electrons with adequate energy can be transferred to the adsorbates and induce chemical reactions. Therefore, it is essential to determine the required excitation energy within a complex containing the plasmonic metal and molecular adsorbates. The plasmonic excitation and interfacial energy/charge transfer highly depends on several factors such as size and composition of the metal nanoparticles and the electronic structure of the adsorbed reactants, since these factors define the wavefunction overlap at the interface between reactants and the catalyst surface. Therefore, interfacial engineering provides a venue to modify the interaction between reactants and the catalyst surface and tune the interfacial energy and charge transfer.
This tunability can be enhanced by the presence of a liquid phase. In liquid-phase catalysis, solvents can alter the interfacial binding and even participate directly in the reactions.8,9 Such effects of solvents were also studied in plasmonic catalysis but mostly focused on the changes in the LSPR of the metal nanoparticles.10–15 For example, the presence of solvents can cause light scattering, introduce different refractive indices,15 and manipulate density of surface charges.10 The energy of LSPR can also be dissipated into the solvent bath through electron–phonon coupling, but its kinetics is normally much slower than that of electron–electron scattering and charge recombination.16 In addition, solvents, such as methanol as a hole scavenger, and solute species (e.g., OH−, O2) dissolved in the solvents may also perturb the charge transfer at the interface.17–19 Furthermore, the electrical double layer at the solid–liquid interface can also reduce the Schottky barrier to promote charge injection.20 Apart from these mentioned multiple effects of the solvents in plasmonic catalysis, the effect of solvents on the interfacial excitation energy and charge transfer between the plasmonic metal and the molecular reactants remains to be explored. This includes how the hydrogen bonds between solvents and reactants change the excitation energy and how such a change can be controlled to achieve different activities and selectivities by using different solvents.
Here, we applied DFT and the linear expansion ΔSCF calculations to investigate the effects of solvent molecules on excitation to induce the interfacial charge and energy transfer. We used NH3 decomposition on Ru-doped Cu as a probe reaction since NH3 is a promising hydrogen-carrier for H2 storage and transportation.21–23 The Ru-doped Cu was reported to be an effective photocatalyst for NH3 decomposition previously: Cu was selected as the plasmonic metal based on its abundancy, and well-dispersed Ru is incorporated into the Cu surface to provide an active center for N–H bond activation due to its suitable binding energy with NH3.22 A few prototype polar solvents, such as water, methanol and phenol, were selected to study the effect of the local environment induced by solvents around the surface-adsorbed NH3. We find that H-bonds formed between these solvents and NH3 increase the excitation energy of an electron from the Fermi level of the system to the lowest unoccupied molecular orbital (LUMO) of NH3 and reduce the excitation energy of an electron from the highest occupied molecular orbital (HOMO) of NH3 to the Fermi level. We also find that changing the basicity of solvents can alter the LUMO of NH3 to different levels, resulting in a change in the electronic excitation to the LUMO. That is, the higher the basicity of the solvent, the higher the required energy to populate the LUMO of NH3. The HOMO–LUMO excitation can also be perturbed by the presence of solvents, but this effect is less extensive than the increase in excitation energy of interfacial charge transfer. This observation that the hydrogen bonding between solvents and reactants can modify the plasmonic excitation energy (Scheme 1) provides a valuable route for controlling the selectivity of channeling the photonic energy into a targeted molecular orbital for specific reactions.
Computational methods
A single Ru atom incorporated into the Cu (111) surface was selected as the model in this study since low loading of Ru was used in previous experiments, and this model was used in the literature to explain the enhanced rates of NH3 decomposition over the Ru-doped Cu photocatalyst.21–23 We adopted this model here to investigate the effect of solvents and illustrate the concept.The DFT calculations with the PBE-GGA exchange–correlation functional were performed using VASP version 5.4.1.24,25 The van der Waals (vdW) interaction was included using the DFT-D3 dispersion model.26 A plane-wave basis set with a kinetic energy cutoff of 500 eV was used for structural optimization, in which the criteria of atomic force was set to be less than 0.02 eV Å−1. A four-layer √21 × √21 Ru-doped Cu(111) (RuCu83) slab was constructed to model the surface of the Ru-doped Cu nanoparticle. While the two top layers were fully relaxed, the two bottom layers were fixed at the Cu bulk positions. A 15 Å vacuum was added in the z-direction to separate slabs from their periodic images. The k-point grid of (4 × 4 × 1) was used to converge the total energy. The energy convergence for electronic relaxation was set to 10−4 eV. The total energy was extrapolated to 0 K. The NH3 molecule was surrounded by one, two, or three molecules of protic solvents. In this study, we focus on solvents that can serve as hydrogen bond acceptors due to their more significant enhancement of NH3 adsorption (Table S1†). Both water and methanol have weaker adsorption than NH3 over the Ru-doped Cu(111) surface (Table S2†). Phenol may compete for adsorption sites due to its very comparable adsorption energies with that of NH3, and it is included here to show the trend of the excitation energy as a function of the strength of the H-bonds between the solvent molecules and NH3. The effect of solvents on the excitation energy when the solvents are hydrogen bond donors will be investigated in a future study.
Since the GGA functionals often underestimate the HOMO–LUMO gap, the excitation energy from the HOMO to the LUMO, from the Fermi level to the LUMO, and from the HOMO to the Fermi level was calculated via the delta SCF method instead of directly using the HOMO and LUMO energy levels from GGA. The fully relaxed structures in the ground state calculated with VASP were adopted to calculate excited states via the vertical excitation using GPAW version 22.1.0.27,28 The exchange-correlation functional, plane-wave cutoff, and k-point grid in GPAW were kept the same as those applied in VASP. The linear expansion ΔSCF29 approach was used to calculate the energy of the system at excited states; we recently showed that this approach could provide excitation energy values that were in good agreement with experiments.30
The center of the molecular orbital is the mean energy calculated as follows:
It is worth noting that the nuclear quantum effect can influence the hydrogen-bonded system, either increasing the proton sharing or promoting the hydrogen-bond breaking.32 Here we focused on the NH3 adsorption and H-bond-induced change in the excitation energy; it is expected that the nuclear quantum effect is less pronounced and that its effect on the excitation energy probably cancels out when adding more solvent molecules. However, for N–H activation and proton shuttling, a further study including the nuclear quantum effect, e.g., using PIMD, is valuable to bring more insights. In addition, since GGA functionals often overestimate the strength of the hydrogen bond,33,34 instead of using the hydrogen bond length or energy, we used the hydrogen bond acceptor parameter (HBA or β) in the literature to compare the effects of solvents.
Results and discussion
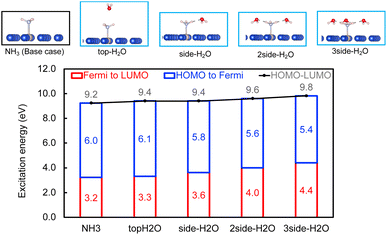
Within the mechanism of direct interfacial charge transfer in plasmonic catalysis, the charge excitation can take place from metal nanoparticles to unoccupied frontier orbitals of adsorbates, generating energetic electrons in the molecule. If the reactions are driven by holes, the excitation energy of an electron from the occupied states of the adsorbate to the Fermi level is more relevant. Instead, if the reaction follows the resonance energy transfer (RET) instead of the charge transfer mechanism, the excitation within the molecular adsorbates is important. These scenarios are schematically shown in Scheme 1, in which we illustrate the concept that the shift of the molecular frontier orbitals can lead to change in the excitation energy. In the following section we use NH3 activation over a Ru-doped Cu surface to reveal the effect of solvents.As shown in the literature,21–23 at low surface coverage, the first N–H bond dissociation in NH3 is the rate-limiting step for light-driven NH3 decomposition on a Ru-doped Cu surface. In addition, the interfacial charge transfer between the catalyst and adsorbed reactant, i.e., the injection of the hot carriers into the antibonding orbitals of the metal-adsorbate system, was found to be essential for plasmonic ammonia decomposition on a Ru-doped Cu surface.23 Therefore, we first study the interfacial charge transfer between the metal and the adsorbed reactant as the base case, in which NH3 adsorbs on a clean Ru-doped Cu surface without solvents. The optimized structure is shown in the top channel in Fig. 1. In this study, the interfacial charge transfer is analyzed via both the hole transfer process, which is represented by exciting an electron from the HOMO of NH3 to the Fermi level (denoted as Ehole), and the electron transfer process, in which an electron is excited from the Fermi level to the LUMO of NH3 (denoted as Eelec). In the absence of solvents, Ehole and Eelec are 6.0 and 3.2 eV, respectively. In a recent experiment, the plasmonic NH3 decomposition rate reaches the maximum at 2.6 eV,23 which is 0.6 eV lower compared to the calculated Eelec of the base case. This difference could result from a more complicated conformation of the real catalyst surface of Ru-dopped Cu compared to that of the single-atom dopant model used here. The adsorption energy of NH3 on the clean RuCu83 surface is about −1.4 eV, which is comparable with literature values.23
The effect of the local environment induced by solvents on the interfacial charge transfer is then studied by surrounding NH3 with H2O solvents. In this case we use NH3, rather than NH4+, to illustrate the concept. When solvents act as the hydrogen bond acceptors, it is expected that the presence of ammonium ions is not pronounced. A further study on the effect on ammonium ions in water is valuable for capturing the complete picture of this process. Nevertheless, we find that the adsorption energy of NH3 increases when there is interaction between H2O and NH3 (Table S1 and Fig. S4†); however, a more significant impact is observed when a H-bond is formed between NH3 and H2O at a side-adsorption configuration compared to the on-top adsorption of H2O on NH3 (Fig. 1). The on-top adsorption of H2O on NH3 does not alter the interaction between NH3 and the metal surface much, leading to a similar value of excitation energy to the one on a clean surface without solvents (Fig. 1). Instead, the side adsorption of H2O, through a hydrogen bond, alters the excitation energy for both the electron and the hole transfer process. The more hydrogen bonds formed between H2O and NH3 as the number of surrounding H2O molecules increases, the higher the excitation energy needed. We observed that the Eelec increases by 0.4 eV per H-bond between H2O and NH3, while the value of Ehole decreases by 0.2 eV per H-bond (Fig. 1).
This change in the excitation energy can be attributed to the strong electronegativity of the oxygen atom in water, which polarizes the molecule and upshifts the HOMO and LUMO centre as shown in Fig. 2. The more pronounced effect on Eelec than Ehole could be related to the fact that the LUMO of NH3 is mainly located on H atoms, which can be directly influenced by the H-bonds with water. Instead, the dominant part of the HOMO is located on the N atom in NH3. As shown in Fig. 2, the centre of the HOMO shifts from −4.43 eV in the absence of solvents to −4.20, −3.98, and then −3.80 eV with respect to the Fermi level of the system when one, two, and three H2O molecules are added in the proximity of NH3. The centre of the LUMO also moves to a higher energy, from 3.73 to 4.07, 4.38, and 4.68 eV with respect to the Fermi level as the number of surrounding H2O molecules increases. The local hydrogen-bonding environment around NH3 can thus modulate the excitation energy landscape for NH3 adsorbed over the Ru-doped Cu surface.
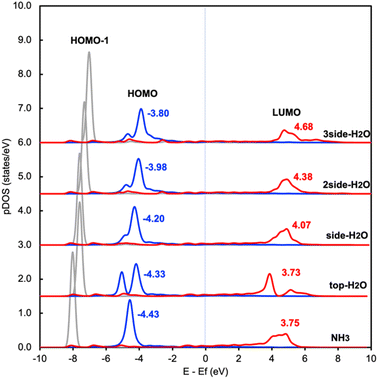 | ||
| Fig. 2 Density of states projected onto frontier orbitals of NH3 adsorbed on RuCu83 with and without water. The center of the HOMO and LUMO of NH3 are shown above the main peak. | ||
It is worth noting that another possibility of the change in the excitation energy involving the Fermi level is the modification of the work function. We have examined the change in work function of the catalyst surface with and without the surrounding H2O molecules and find that there is only a slight change in the work function of the metal surface (Fig. S1†). In addition, there is no difference between the calculated core level energy of the 1s orbital of Cu with and without H2O. These results imply that the change in Ehole and Eelec shown in Fig. 1 is related to the adjustment of the HOMO and LUMO due to the H-bond formation between NH3 and H2O rather than the change in the electronic properties of the metal substrate. In addition, we also investigated the effect of H2O on the Cu surface instead of the Ru-doped Cu surface and find a similar trend between these two catalyst surfaces (Table S1 and S3†).
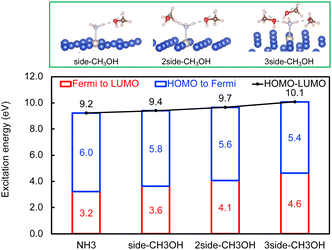
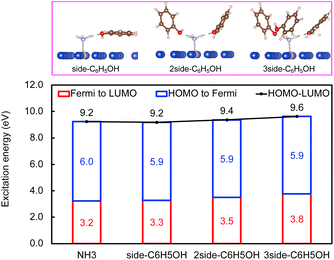
Next, the concept of solvent-induced local environment change in the interfacial charge transfer is explored with two other solvents – methanol and phenol (Fig. 3 and 4). Both molecules can form hydrogen bonds with the molecular adsorbate. Since the top adsorption configuration of water does not affect the interfacial charge transfer much, only the side adsorption of methanol and phenol is considered in the following discussion. As expected for a solvent with slightly higher basicity than that of water (Table S4†), methanol induces an increase of about 0.5 eV of Eelec per hydrogen bond formed between it and NH3, which is higher by 0.1 eV per H-bond in the presence of water.
In contrast, the H-bond between phenol and NH3 only causes an increase of less than 0.2 eV of Eelec per H-bond (Fig. 4), which is lower than the value with water. A comparison of Eelec when water or phenol is introduced near NH3 is displayed in Fig. 5. When the number of solvent molecules increases, the bond length between N and Ru decreases due to the stronger interaction between NH3 and the catalyst surface. This increased interaction results from the upshifts of frontier orbitals and reduction of occupation in the antibonding states of Ru–N bond hybridization (Fig. S4†). Despite the similar trend of the bond length and the excitation energy, the calculated values suggest that the impact of water is more significant than that of phenol. Since this effect is determined by the electron donation capability of the solvents, the difference caused by the three protic solvents could be attributed to the varied basicity of solvents, which can be represented by the β (hydrogen bond acceptor) value. The solvent with a higher β value leads to a more significant upshift of the frontier orbitals and a larger change in the excitation energy. On the other hand, there is only a negligible change in Ehole when NH3 forms a H-bond with the surrounding phenol molecules despite the upward shift of the HOMO when more phenol molecules are introduced (Fig. 4 and Fig. S2†). The changes in Ehole are similar for water and methanol (i.e., decreasing by 0.2 eV per H-bond), implying that the slight difference of basicity between water and methanol is not impactful enough to cause a difference in the generation of hot holes.
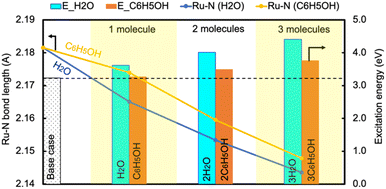 | ||
| Fig. 5 The change in the excitation energy to excite an electron from the Fermi level to the LUMO of NH3 and the Ru–N bond length as the number of H2O/C6H5OH molecules increases. | ||
In plasmonic catalysis, apart from the interfacial charge transfer mechanism between the metal and adsorbed molecules, the plasmonic RET mechanism has also been reported as a main mechanism for some reactions.21,35–37 The RET mechanism depends on the electronic excitation within the reactant's frontier orbitals, e.g., the excitation from the HOMO to the LUMO, driven by the strong interfacial dipole–dipole coupling. Therefore, the RET excitation energies can be determined by using the HOMO–LUMO excitation energy (Ehomo–lumo). We first calculated the Ehomo–lumo simply as the sum of the Eelec and Ehole. We find that the effect of solvents on the Eelec is stronger than that on the Ehomo–lumo for the three solvents. That is, a change of 0.6 eV of the Ehomo–lumo is observed compared to a change of 1.2 eV of Eelec when the number of water molecules increased from 0 to 3 (Fig. 2). In the case of methanol and phenol, the value of the Ehomo–lumovs. Eelec is 0.9 vs. 1.4 eV and 0.4 vs. 0.6 eV, respectively. Moreover, we also explicitly calculated the excitation energy from the HOMO to the LUMO using GPAW (Fig. S3†). Both approaches show the same trend for all studied solvents. The effect of the local environment induced by solvents on plasmonic catalysis thus depends on the mechanism (charge transfer vs. RET) of the chemical reaction.
Finally, we discuss the experimental implication derived from the calculated solvent effects on plasmonic excitation energy. The tunability of excitation energy achieved via hydrogen bonding of solvents with the adsorbed reactants can be used to shift the molecular frontier orbitals to match the excitation energy with the supplied photon energy, especially in the case of a fixed photon energy source such as light-emitting diodes (LEDs). The solid–liquid interface also provides an opportunity for optimizing the selectivity/efficiency of plasmonic catalysis based on the uneven shift of the frontier orbitals (as demonstrated by the difference of LUMO and HOMO excitation). That is, these orbitals compete for hot carriers' population in the absence of solvents can in principle be lifted beyond the range of the photon energy by introducing a solvent so that the photon energy can be more selectively channeled into targeted orbitals. The solvents also provide dielectric screening that helps reduce the recombination of the hot carriers, increasing the lifetime of these carriers and thus the efficiency of plasmonic catalysis.
Conclusions
By calculating the excitation energy of the direct interfacial charge transfer and resonance energy transfer in plasmonic catalysis at the solid–liquid interfaces, we show that the hydrogen bond formed between reactants and protic solvents can affect the excitation energy by adjusting the molecular frontier orbitals. Water, methanol, and phenol surrounding the adsorbed ammonia can increase the energy required for exciting an electron from the Fermi level to the LUMO and decrease that for HOMO-to-Fermi excitation. We find that the higher the basicity of the solvents, the stronger the impact on the electron transfer process. The solvents can also alter the HOMO–LUMO intramolecular excitation within the adsorbates, but to a lower extent than the Fermi-to-LUMO excitation. Therefore, the solvents may have effects on plasmonic excitation at varying extents depending on the plasmonic catalysis mechanism. Our results provide insights for understanding how solvents impact plasmonic catalysis and how to tune the reaction environment to enhance the efficiency of a photocatalyst. It is expected that this concept can be validated experimentally by measuring rates of a prototype reaction as a function of photon energy in different solvents.Author contributions
Tien Le performed the calculations and prepared the manuscript, and Bin Wang conceptualized the research, supervised the student to conduct this research, and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Condensed Phase and Interfacial Molecular Science (Grant DE-SC0020300). The computations were performed at the OU Supercomputing Center for Education & Research and the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility. Some calculations were performed with the Texas Advanced Computing Center (TACC) at The University of Texas at Austin supported by the NSF ACCESS/XSEDE.References
- S. Ezendam, M. Herran, L. Nan, C. Gruber, Y. Kang, F. Gröbmeyer, R. Lin, J. Gargiulo, A. Sousa-Castillo and E. Cortés, ACS Energy Lett., 2022, 7, 778–815 CrossRef CAS PubMed.
- Y. Zhang, S. He, W. Guo, Y. Hu, J. Huang, J. R. Mulcahy and W. D. Wei, Chem. Rev., 2017, 118, 2927–2954 CrossRef PubMed.
- M. L. Brongersma, N. J. Halas and P. Nordlander, Nat. Nanotechnol., 2015, 10, 25–34 CrossRef CAS PubMed.
- M. Sayed, J. Yu, G. Liu and M. Jaroniec, Chem. Rev., 2022, 122, 10484–10537 CrossRef CAS PubMed.
- S. B. Ramakrishnan, F. Mohammadparast, A. P. Dadgar, T. Mou, T. Le, B. Wang, P. K. Jain and M. Andiappan, Adv. Opt. Mater., 2021, 9, 2101128 CrossRef CAS.
- U. Aslam, V. G. Rao, S. Chavez and S. Linic, Nat. Catal., 2018, 1, 656–665 CrossRef.
- E. Cortés and P. H. Camargo, Plasmonic Catalysis: from Fundamentals to Applications, John Wiley & Sons, 2021 Search PubMed.
- G. Li, B. Wang and D. E. Resasco, ACS Catal., 2019, 10, 1294–1309 CrossRef.
- G. Li, B. Wang and D. E. Resasco, Surf. Sci. Rep., 2021, 76, 100541 CrossRef CAS.
- K. P. Rice, E. J. Walker Jr, M. P. Stoykovich and A. E. Saunders, J. Phys. Chem. C, 2011, 115, 1793–1799 CrossRef CAS.
- A. Sanchez-Gonzalez, S. Corni and B. Mennucci, J. Phys. Chem. C, 2011, 115, 5450–5460 CrossRef CAS.
- V. N. Nemykin, R. G. Hadt, R. V. Belosludov, H. Mizuseki and Y. Kawazoe, J. Phys. Chem. A, 2007, 111, 12901–12913 CrossRef CAS PubMed.
- J. Neugebauer, C. Curutchet, A. Munoz-Losa and B. Mennucci, J. Chem. Theory Comput., 2010, 6, 1843–1851 CrossRef CAS PubMed.
- J. Moskowitz, R. Sindi and C. D. Geddes, J. Phys. Chem. C, 2020, 124, 5780–5788 CrossRef CAS.
- S. K. Ghosh, S. Nath, S. Kundu, K. Esumi and T. Pal, J. Phys. Chem. B, 2004, 108, 13963–13971 CrossRef CAS.
- K. O. Aruda, M. Tagliazucchi, C. M. Sweeney, D. C. Hannah, G. C. Schatz and E. A. Weiss, Proc. Natl. Acad. Sci., 2013, 110, 4212–4217 CrossRef CAS PubMed.
- A. Y. Bykov, D. J. Roth, G. Sartorello, J. U. Salmón-Gamboa and A. V. Zayats, Nanophotonics, 2021, 10, 2929–2938 CrossRef CAS.
- L. R. Baker, C.-M. Jiang, S. T. Kelly, J. M. Lucas, J. Vura-Weis, M. K. Gilles, A. P. Alivisatos and S. R. Leone, Nano Lett., 2014, 14, 5883–5890 CrossRef CAS PubMed.
- V. G. Rao, U. Aslam and S. Linic, J. Am. Chem. Soc., 2018, 141, 643–647 CrossRef PubMed.
- S. W. Lee, H. Kim and J. Y. Park, Nano Lett., 2023, 23, 5373–5380 CrossRef CAS PubMed.
- J. L. Bao and E. A. Carter, J. Am. Chem. Soc., 2019, 141, 13320–13323 CrossRef CAS PubMed.
- L. Zhou, D. F. Swearer, C. Zhang, H. Robatjazi, H. Zhao, L. Henderson, L. Dong, P. Christopher, E. A. Carter and P. Nordlander, Science, 2018, 362, 69–72 CrossRef CAS PubMed.
- Y. Yuan, L. Zhou, H. Robatjazi, J. L. Bao, J. Zhou, A. Bayles, L. Yuan, M. Lou, M. Lou and S. Khatiwada, Science, 2022, 378, 889–893 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. Hansen, J. Phys.: Condens.Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. Gavnholt, T. Olsen, M. Engelund and J. Schiøtz, Phys. Rev. B, 2008, 78, 075441 CrossRef.
- T. Salavati-fard and B. Wang, ACS Catal., 2022, 12, 12869–12878 CrossRef CAS.
- T. Le, T. Salavati-fard and B. Wang, ACS Catal., 2023, 13, 6328–6337 CrossRef CAS.
- T. E. Markland and M. Ceriotti, Nat. Rev. Chem, 2018, 2, 0109 CrossRef CAS.
- B. Civalleri, E. Garrone and P. Ugliengo, J. Mol. Struct.: THEOCHEM, 1997, 419, 227–238 CrossRef CAS.
- A. D. Boese, ChemPhysChem, 2015, 16, 978–985 CrossRef CAS PubMed.
- J. L. Bao and E. A. Carter, ACS Nano, 2019, 13, 9944–9957 CrossRef CAS PubMed.
- J. M. P. Martirez and E. A. Carter, J. Am. Chem. Soc., 2017, 139, 4390–4398 CrossRef CAS PubMed.
- V. A. Spata and E. A. Carter, ACS Nano, 2018, 12, 3512–3522 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The change in the work function and core level, the DOS of the phenol case, the comparison of the direct and indirect calculation of the HOMO–LUMO gap, and the results of a pristine Cu surface. See DOI: https://doi.org/10.1039/d3na00835e |
| This journal is © The Royal Society of Chemistry 2023 |