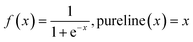DOI:
10.1039/D3NA00816A
(Paper)
Nanoscale Adv., 2023,
5, 6647-6658
Numerical study of thermal and solutal advancements in ZnO–SAE50 nanolubricant flow past a convergent/divergent channel with the effects of thermophoretic particle deposition
Received
24th September 2023
, Accepted 31st October 2023
First published on 7th November 2023
Abstract
The present research focuses on the significance of thermophoretic particle deposition on a ZnO–SAE50 nanolubricant flow in a stretchable/shrinkable convergent/divergent channel in the presence of an applied magnetic field and nonlinear heat radiation. A parameter in the governing differential equations and wall boundary conditions defines the physical mechanism of the model. The Galerkin finite element method, combined with similarity transformation, is adopted to solve the governing equations. The Levenberg–Marquardt backpropagating algorithm of an artificial neural network model forecasts heat and mass transfer properties. The results reveal that by stretching/shrinking the walls enough, the classical flow and heat properties are significantly affected. The stretching of the convergent or divergent channel is observed to increase the velocity profiles, whilst shrinking results in backflow regions. In terms of the temperature field, stretching causes more heat to be produced in the flow; nevertheless, the thermal layer is decreased and cooling is attained by channel shrinkage, which may have important technical implications.
1. Introduction
Fluid flow may often occur in various technical and natural systems and in both convergent and divergent channels (CDCs). These channels include alterations in the cross-sectional area along the flow direction, which substantially influences the behaviour of the fluid moving through the channel. CDCs play essential roles in various technical applications, including nozzles and diffusers in water jets, jet engines and hydraulic systems. To build effective and secure systems, it is necessary to have a solid understanding of the factors that control the flow of fluids via these channels. Analyzing and predicting fluid flow behaviour in CDCs represent a common task for engineers, who often utilize various mathematical models to do so. The significance of physical factors on the thermal attributes of nanofluid (NF) flow in CDCs was evaluated by Hamedani et al.1 Utilizing the novel hybrid model, Khan et al.2 studied the heat transmission attributes of the NF flow past a CDC. The consequence of heat production on the flow of NF past a permeable CDC was explained by Mishra et al.3 The flow of magnetic NFs via a stretchy CDC was elaborated by Hashim and Chu.4 The heat transmission analysis of a non-Newtonian NF flow past CDCs was examined by Rehman et al.5 using numerical modelling. Turkyilmazoglu6 has analyzed the extended Jeffery–Hamel flow in the stretching/shrinking of a CDC.
Nanoparticles significantly enhance heat transmission in nanoliquids, which are nanoparticle suspensions in a base liquid such as water or oil. This growing topic of study has attracted substantial interest because of its potential to boost the efficiency of many heat transport applications. Recently, Razaq et al.7 explored a flow with three nanoparticle suspensions. Khan et al.8 explored the heat transmission features in nanoliquid flow past the Homann stagnation region with heat radiation. Sarfraj et al.9 explored the flow of fluid with two different nanoparticle suspensions. Recently, Sarfraz and Khan10–13 explored the thermal and mass transmission features in different nanoliquids with various nanoparticle suspensions past different surfaces with varied physical characteristics. Qureshi et al.14 examined the morphological nanolayer effect on the flow of hybrid nanoliquids generated by the dispersion of a polymer/CNT nanocomposite material. The heat transfer in hybrid micropolar ferrofluid flow across a non-linearly stretched sheet was investigated by Rauf et al.15
Nanolubricants are a subcategory of advanced lubricants that make use of nanoparticles as a means of improving the lubricating qualities of the product. The ZnO (zinc oxide)–SAE50 nanolubricant is a particular form of nanolubricant intended to fulfil the SAE50 viscosity grade and includes zinc oxide nanoparticles. This viscosity grade is often used in engine oils for various industrial and automotive applications. Recently, Nayak et al.16 investigated the flow of ZnO–SAE50 nanolubricant (NL) via a moving Riga surface in the presence of heat radiation. Muhammad and Ahmed17 debriefed an unsteady ZnO–SAE50 NL flow in a permeable channel using the subdomain method. Utilizing the Cattaneo–Christov model, Riaz et al.18 explored variable attributes of the ZnO–SAE50 NL flow via a Riga plate. Riaz et al.19 inspected the behaviour of ZnO–SAE50 NL flow across a Riga plate. Utilizing the Buongiorno model, Nagapavani et al.20 explored variable attributes of the ZnO–SAE50 NL flow via a heated disk.
A complicated and significant phenomenon in fluid mechanics with respect to heat transfer is fluid flow with thermal radiation. The interaction of fluid flow and thermal radiation is an essential component of heat transport in a number of different technical and natural systems. To improve energy efficiency, develop better systems, and solve difficulties associated with climate change, it is vital to understand this coupled phenomenon and optimize it as much as possible. The complexity of the flow of fluids with heat radiation is being addressed in a wide variety of applications, and researchers and engineers are continuing to investigate novel methods for doing so. The influence of radiation on the Maxwell liquid flow past an SS was elaborated by Khan et al.21 utilizing a numerical scheme. The flow of Casson fluid past an SS with the effect of thermal radiation was inspected by Eswaramoorthi et al.22 Srilatha et al.23 debriefed the flow of non-Newtonian fluid via an SS with the impact of radiation. The flow of nanoliquid across an SS with the consequence of thermal radiation was probed by Khan et al.24 The flow of Reiner–Rivlin fluid past an SS with heat radiation was analyzed by Khan et al.25
The movement of suspended particles in a fluid (liquid or gas) and their deposition onto surfaces due to thermophoresis are described as a complicated process known as fluid flow with thermophoretic particle deposition. This method is essential in various applications, including the management of air pollution, the field of nanotechnology, and the deposition of aerosols. This is a process in which temperature gradients cause particles to be guided toward surfaces and deposited there. It is crucial to understand and be able to regulate this process in distinct scientific and technical domains since it has numerous applications, from the regulation of air pollution to the development of nanotechnology. The flow of Oldroyd-B fluid past a spinning disk subjected to thermophoretic particle deposition (TPD) was analyzed by Hafeez et al.26 The consequence of TPD on the flow of fluid via a revolving disk was scrutinized by Prasannakumara and Gowda.27 Bashir et al.28 analyzed the effect of TPD on the flow of Oldroyd-B liquid via an SS. Kumar et al.29 investigated the effect of TPD on Maxwell liquid flow through an SS. Ramesh et al.30 examined TPD's impact on fluid flow through a stretchable surface to determine its relevance.
In several areas of artificial intelligence and machine learning, artificial neural networks (ANNs), have shown success. One of the main challenges is optimizing ANN parameters to reduce loss function. There may be issues with gradient descent and other traditional optimization strategies, such as sluggish convergence or convergence to local minima. The Levenberg–Marquardt (LM) methodology is a widely used method for ANN optimization. This approach was developed to solve the problems mentioned above. The LM algorithm combines Gauss–Newton and the steepest descent techniques. It is now used to train ANNs. However, it was first developed to handle nonlinear least-squares issues. Mishra and Chaudhuri31 examined the flow of third-grade fluid on heated plates using an ANN approach to explore their results. Shafiq et al.32 used the ANN technique to examine the Williamson fluid flow via a radiative surface. The analysis of entropy generation in the fluid flow past the rotating disk was evaluated by Zhao et al.33 using the ANN scheme. Srinivasacharya and Kumar34 examined Casson fluid flow past a radial SS using the ANN approach. The heat transport attributes of the fluid flow using the ANN scheme were studied by Sedani et al.35 Recently,36–40 have utilized the LM backpropagating algorithm to analyze the thermal and mass transmission characteristics in vertical geometries such as a vertical channel, vertical annulus and inclined annulus under significant effects such as heat generation/absorption, heat sources/sinks, chemical reactions and thermal non-equilibrium conditions.
To improve the functionality of modern lubricants like ZnO–SAE50 NL, researchers are delving into the complexities of stretching/shrinking of CDCs. This novel technology uses radiation's ability to generate changes at the nanoscale, which are then used to fine-tune the characteristics of the lubricant. Scientists are at the forefront of creating nanoscale lubrication solutions that have the potential to revolutionize industries dependent on environmentally friendly and efficient machinery. They are doing this by utilizing advanced techniques such as thermophoretic particle deposition and utilizing the power of ANNs and finite element modelling (FEM). The advancement of lubrication science is being driven toward new levels of efficiency and sustainability by the synergy of various professions that are complementary to one another.
2. Mathematical formulation
The steady two-dimensional flow of an incompressible, laminar transmitting viscous ZnO–SAE50 NL from a source or sink of two walls that can expand or contract at an angle of 2α at channel walls that intersects on the z-axis and lies in planes is considered in a system of cylindrical polar coordinates (r, θ, z). Fig. 1 depicts the problem's schematic diagram.
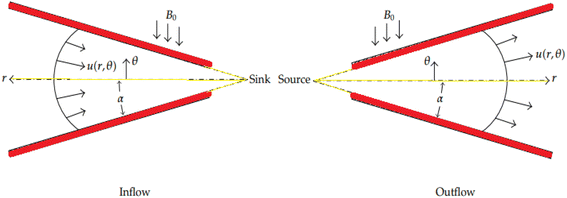 |
| | Fig. 1 Geometrical configuration. | |
The vector form of the equations is given by
| | | ρnf[vjvi,j] = −∇pi + μnf∇2vi + J × B, | (2) |
| | 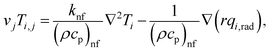 | (3) |
| | | vjCi,j = DB∇2Ci − ∇(CVT)j. | (4) |
We assumed that uθ = 0, it indicates that there have been no modifications to the z-direction, and thus, the flow is exclusively in the radial direction and solely depends on r and θ. Along the z-axis, there is a negligible magnetic field. A uniform magnetic field is exerted perpendicular to the direction of flow. The mass, linear momentum, thermal, and solutal balance laws are the foundation of the governing equations for this issue. They have been adjusted to consider the existence of the magnetic field and the effects of nonlinear heat radiation in this convergent/divergent channel. The governing equations are (see ref. 3–6 and 18)
| | 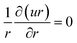 | (5) |
| | 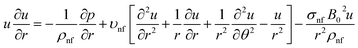 | (6) |
| | 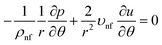 | (7) |
| | 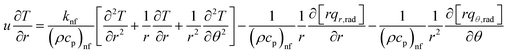 | (8) |
| | 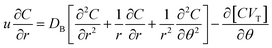 | (9) |
Using Roseland approximation for radiation (see ref. 3–6 and 18)
| | 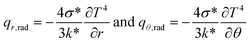 | (10) |
The thermophoretic deposition velocity in the θ – direction is of the form
| | 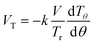 | (11) |
Because of the presumption of symmetry at the channel midline
| | 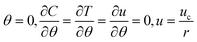 | (12) |
Because of the plate stretching/shrinking convergent/divergent wall conditions,
| | 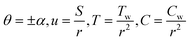 | (13) |
The radial velocity can be expressed as
| | 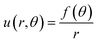 | (14) |
On integration of the azimuthal velocity expression the stretching pressure can be written as
| | 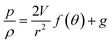 | (15) |
Similarity variables (see ref. 3–6 and 18)
| | 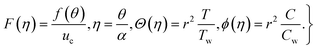 | (16) |
Invoking ref. 41–45, the ZnO–SAE50 nanolubricant effective dynamic viscosity, effective density, heat capacitance, and effective thermal conductivity are determined by using
| | | μnf = μZnO–SAE50 = μSAE50(−0.002407T + 1.035 + 0.04336ϕ), | (17) |
| | μSAE50 = 2.174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.06062T, e−0.06062T, | (18) |
| | | ρnf = ρSAE50(1 − ϕ) + ρZnOϕ = ρZnO–SAE50, | (19) |
| | | (ρCp)nf = (1 − ϕ)(ρCp)SAE50 + (ρCp)ZnOϕ = (ρCp)ZnO–SAE50, | (20) |
| | 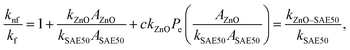 | (21) |
| | 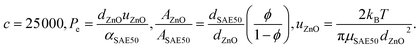 | (22) |
The governing equations are:
| | 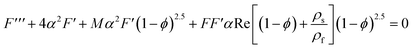 | (23) |
| | | (A2 + N)Θ′′ + 4α2(A2 + N)Θ + 2FPrα2Θ[1 + A1ϕ − ϕ] = 0 | (24) |
| | 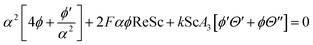 | (25) |
The boundary conditions are
| | | F(0) = 1, F′(0) = 0, F(1) = λ, Θ′(0) = 0, Θ(1) = 1, ϕ′(0) = 0, ϕ(1) = 1. | (26) |
where
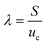
is the stretching (
λ > 0) or shrinking (
λ < 0) parameter and
| | 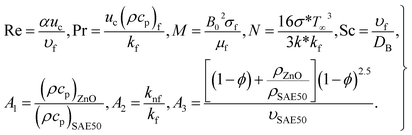 | (27) |
Using the heat flux 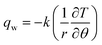 the Nusselt number is given by
the Nusselt number is given by
| | 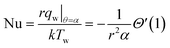 | (28) |
3. Numerical method
The governing coupled nonlinear PDEs, eqn (5)–(9), are transformed into coupled nonlinear ODEs, eqn (23)–(25), by adopting apt similarity transformation eqn (16) and the relative boundary conditions provided in eqn (26). These equations are solved by adopting Galerkin FEM. The system of equations is transformed into a matrix form using GFEM, and the matrix elements are then merged to give the global matrix for the whole area. This global matrix is then iteratively solved to provide fluid flow, thermal and mass transmission fields. The computed solution error level is set at 0.00001 to ensure high precision in the results. When the disparity between the original state and the current state for the elements at all nodes reaches the aforementioned error level, the iterative process comes to an end.
Quadratic elements with three nodal points are used to determine the velocities, temperatures, concentrations, and heat and mass transport coefficients. The quadratic trail and shape functions are given below:
| | | F(η) = N1(η)F1 + N2(η)F2 + N3(η)F3 | (29) |
| | | Θ(η) = N1(η)Θ1 + N2(η)Θ2 + N3(η)Θ3 | (30) |
| | | ϕ(η) = N1(η)ϕ1 + N2(η)ϕ2 + N3(η)ϕ3 | (31) |
The shape functions are
| | 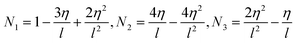 | (32) |
The element stiffness matrix at one node can be written as ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) = [K1K2K3K4].
= [K1K2K3K4].
The stretching of the divergent channel on the velocity profile for the specific values α = 5, Re = 50, M = 0, ϕ = 0, N = 0, and A1 = A2 = 1 are compared with the existing Mustafa Turkyilmazoglu6 results and a good concurrence is noticed between these two results (Fig. 2).
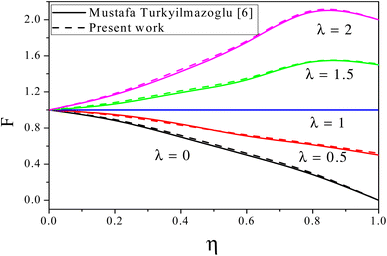 |
| | Fig. 2 Comparison of the present work with Turkyilmazoglu.6 | |
4. Results and discussion
In this part, the effects of expanding or shrinking of CDCs via the factor are researched on the flow model being investigated to analyze the flow and heat transport features. This section aims to describe the graphical and numerical results of different critical factors of relevance on the pertinent characteristics of the ZnO–SAE50 NL. The modified system of ODEs and BCs is numerically addressed using GFEM. The data have been plotted to examine the behaviors of relevant profiles in response to variations in a wide range of factors of interest. The thermophysical properties of base fluid and nanoparticle are given in Table 1.
Table 1 The SAE50 (base fluid) and ZnO (nanoparticles) features (see ref. 41–45)
| Sl. No. |
|
ZnO |
SAE50 |
| 1 |
ρ (kg m−3) |
5.606 |
0.906 |
| 2 |
C
p (J kg−1 K−1) |
544 |
1900 |
| 3 |
k (W m−1 K−1) |
19 |
0.15 |
| 4 |
μ
f (N s m−2) |
— |
0.192543 |
| 5 |
df/ds (nm) |
60 |
40 |
| 6 |
σ
|
0.01 |
— |
Fig. 3 and 4 explain the impact of N on the Θ(η) for the stretching/shrinking of the CDC. It has been discovered that the NL temperature rises when greater values of N are applied to any of the two scenarios. When the radiation phenomenon is used, the NL absorbs radiation, and as a result, the thermal energy of the nanolubricant increases. Therefore, the Θ(η) experiences a tremendous increment for increased N. Fig. 5 and 6 represent the effect of Sc on ϕ(η) for the stretching/shrinking of the CDC, respectively. The rise in the Sc increases the momentum diffusion of nanoparticles inside the base fluid and, as a result, reduces the nanoparticle volume fraction of the fluid in the divergent channel. In a convergent channel, higher values of Sc negligible increment can be observed in the concentration profile.
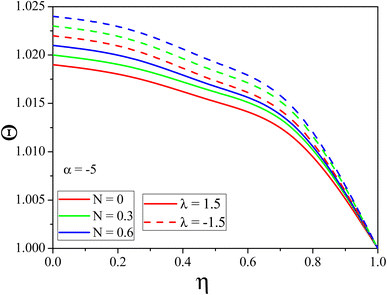 |
| | Fig. 3
Θ(η) variation with distinct values of N for the convergent channel. | |
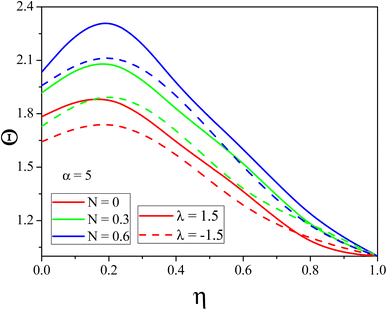 |
| | Fig. 4
Θ(η) variation with distinct values of N for the divergent channel. | |
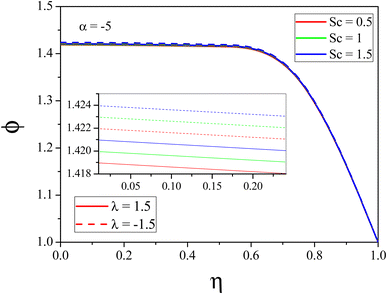 |
| | Fig. 5
ϕ(η) variation with distinct values of Sc for the convergent channel. | |
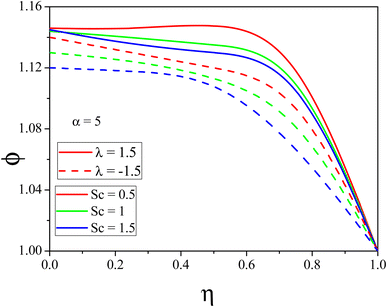 |
| | Fig. 6
ϕ(η) variation with distinct values of Sc for the divergent channel. | |
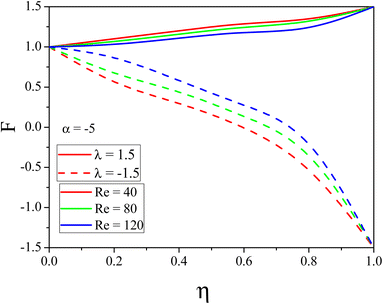
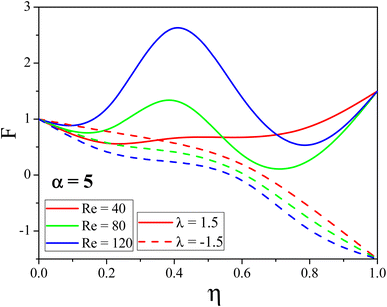
The influence of k on mass transport is shown in Fig. 7 and 8. In the convergent channel, an augment in k rises the concentration profile. Meanwhile in the stretching divergent channel the concentration profile decreases with k since when there is a significant thermal difference, the thermophoretic force attracts more particles to the surface, which lowers the concentration. The upshots of M on F(η) for both the cases are depicted in Fig. 9 and 10 respectively. As M increases the fluid velocity decreases in both CDCs. The Lorentz force is generated when a magnetic field is applied to conducting liquid. This force exerts its influence in the opposite direction of the flow, resulting in a slowing of the flow and, therefore, a reduction in the velocity of the fluid. This decrease in the flow speed, is accompanied by an increase in the temperature state of the fluid. This phenomenon is made abundantly obvious by the observable decrease in fluid velocity as well as the accompanying increase in fluid temperature. Fig. 11 and 12 represent the Reynolds number influence on F(η). In Fig. 11 and 12, the momentum boundary layer exhibits a mixed pattern of expansion and decline. This can be seen in both figures. When either the α or the Re is increased, the thickness of the thermal boundary layer is shown to be significantly increased in Fig. 11 and 12. This occurs regardless of whether the boundary layer is being stretched or shrunk.
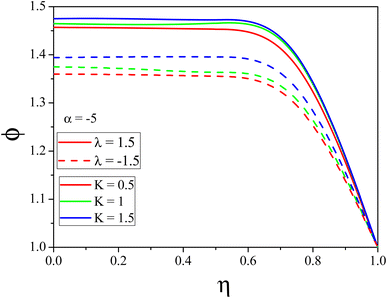 |
| | Fig. 7
ϕ(η) variation with distinct values of K for the convergent channel. | |
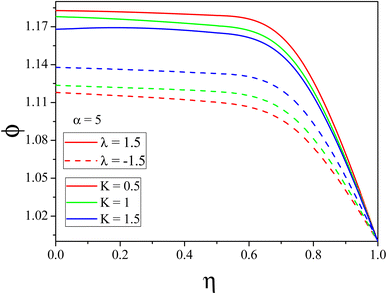 |
| | Fig. 8
ϕ(η) variation with distinct values of K for the divergent channel. | |
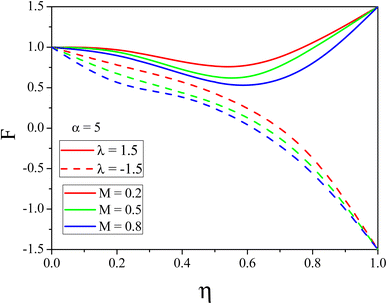 |
| | Fig. 9
F(η) variation with distinct values of M for the divergent channel. | |
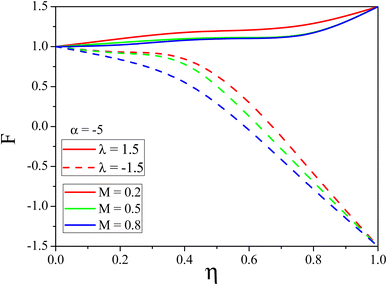 |
| | Fig. 10
F(η) variation with distinct values of M for the convergent channel. | |
 |
| | Fig. 11
F(η) variation with distinct values of Re for the convergent channel. | |
 |
| | Fig. 12
F(η) variation with distinct values of Re for the divergent channel. | |
5. ANN model
An artificial intelligence method was used to investigate the thermal and mass transport in the channel. This method was developed to serve as an alternative to the more traditional mathematical approaches. The ANN model is used as the analytical technique that is being taken here. With their complex logic, ANN models are an optimal tool that works well in simulations of intricate structures even when there is no functional relationship between them. This is because ANN models have sophisticated logic. The multi-layer perceptron (MLP) network model is used in the ANN model, which is designed to estimate the Nu and Sh values. Due to the MLP network model's robust construction, it has a reliable estimating capability. Each layer in MLP networks has a direct association with the one above it, since the design of these networks is layered. An MLP network's first layer, known as the input layer, is the point at which new information is introduced into the system and in any MLP network, there is always a hidden layer. The very last layer of the MLPNN and the layer that is directly subsequent to the hidden layer is the output layer, where the results of simulations are collected. The underlying physical structure of this method is shown in Fig. 13(a) and (b).
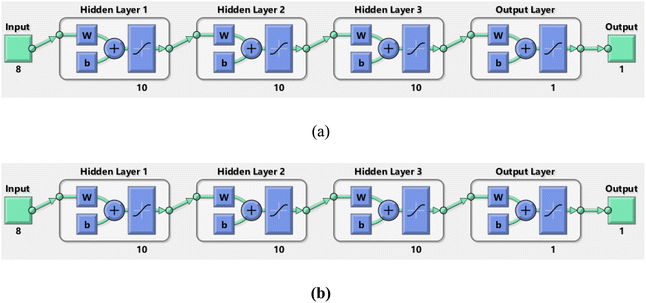 |
| | Fig. 13 Neural network for (a) heat transfer and (b) mass transfer. | |
The artificial neural network model is employed to analyze the thermal and mass transport features in the channel. The significant parameters such as M, Re, N, Pr, Sc, K, α and λ are considered as input parameters for the neural network. Nu and Sh are taken as output parameters. Fig. 13(a) and (b) show the neural network architecture for the considered ANN model. In this model four hidden layers are considered and in each hidden layer ten neurons are considered to forecast the heat and mass transport features. The input data are categorized into three parts, first part 70% is utilized for training, the second part 15% used for testing and 15% used for validation.
For the MLP network model, the Levenberg–Marquardt training (LMT) method was selected as the optimal option. The LMT approach is the one that is most often used in MLPNNs because of its excellent learning capabilities. The MLP network's hidden and output layers employ the tan-sig and purelin transport functions, respectively, as transfer functions. The transfer function models that were used are outlined below.
Fig. 14(a)–(e) and 15(a)–(e) represent the ANN model to forecast the heat and mass transport properties. Fig. 14(a) and 15(a) show the regression plot for the thermal and mass transport and it is clear that the root mean square and mean squared error values for heat and mass transfer are R = 9.99999 × 10−1 and R = 9.99999 × 10−1, MSE = 5.8874 × 10−9 and MSE = 3.4265 × 10−6 respectively. After training a feed forward neural network, an error histogram is created by creating a histogram of the discrepancies between the goal values and the forecast values. It is possible for these error figures to be in the negative since they indicate the amount by which expected values differ from goal values. Bins are used to denote the number of vertical bars that are present in the graph. The whole error range is divided up into thirty distinct buckets for easier analysis. The number of samples from the dataset that are included inside a certain bin is shown along the Y-axis. Fig. 14(b) illustrates a bin in the center of the plot, which corresponds to an error of −1.7 × 10−5, and the maximum height of that bin for the training dataset is less than but close to 3, but the maximum height of that bin for the validation dataset and the test dataset is between 3 and 5. It denotes that a number of samples taken from a variety of datasets include an error that is located somewhere within the following range. The zero-error line illustrates the point at which the error axis (sometimes known as the X-axis) has a value of zero. In this particular illustration, the zero error point may be found within the bin that has a center value of −1.7 × 10−6. In Fig. 15(d) the zero error line lies at 6.82 × 10−7 and also the validation and test dataset is between 12 and 18. Fig. 14(c) represents the performance plot of the training state in which the gradient is 7.6791 × 10−6 at epoch 59. The training continues until 6 at epoch 59. Similarly in Fig. 15(b) the gradient is 1.1233 × 10−5 at epoch 1000. Fig. 14(d)–(e) and 15(c) and (e) represent the best fit and function fit for the heat and mass transfer, respectively.
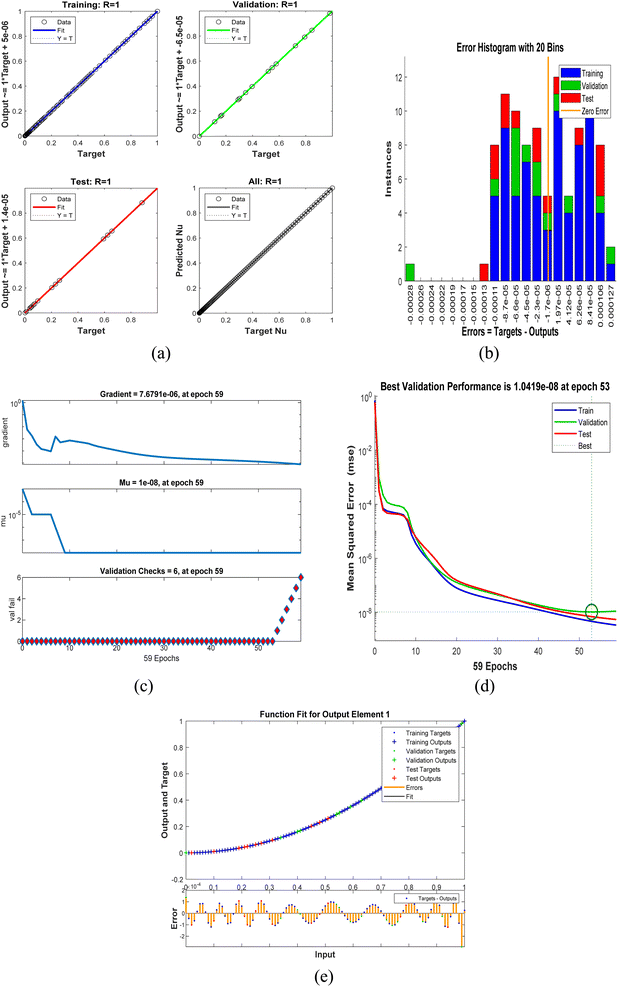 |
| | Fig. 14 ANN model for heat transfer analysis: (a) regression plot, (b) error histogram, (c) training state performance, (d) performance validation and (e) function fit plot. | |
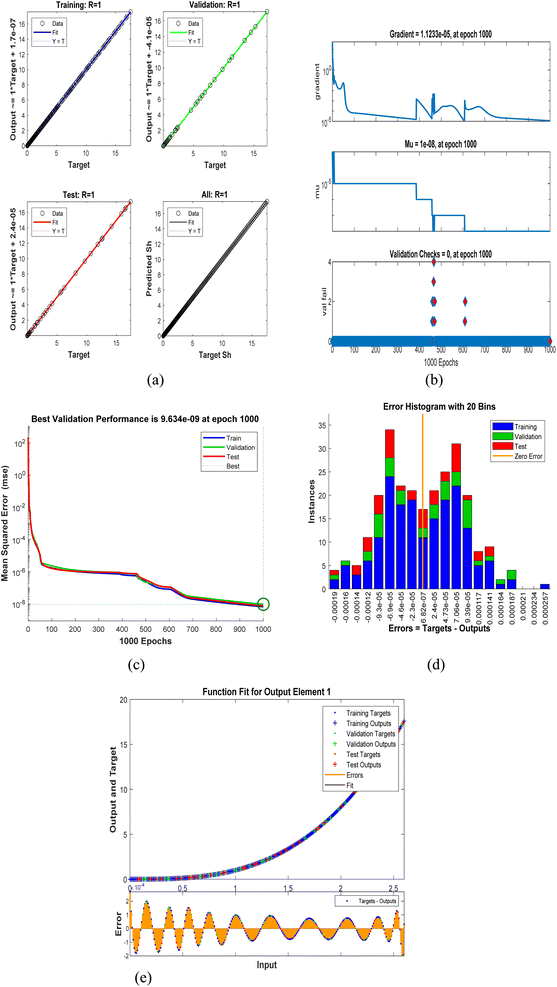 |
| | Fig. 15 ANN model for mass transfer analysis: (a) regression plot, (b) training state performance, (c) performance validation, (d) error histogram and (e) function fit plot. | |
6. Conclusions
The current work analyses the significance of thermophoretic particle deposition on ZnO–SAE50 nanolubricant flow with magnetic field and nonlinear thermal radiations in a stretchable/shrinkable divergent/convergent channel. After converting the governing PDEs into nonlinear ODEs, the Galerkin finite element technique is used to solve these equations. The attained results are compared with the existing results and a good agreement is noticed. Also, the LM backpropagating ANN model is utilized to forecast the thermal and mass transport characteristics.
The following are conclusions drawn from the present work:
❖ The temperature of the nanolubricant increases in both convergent/divergent channels for increased N.
❖ As the Schmidt number goes up, the mass transfer rate goes up, and as a result, the mass transport goes down.
❖ In the convergent channel an increase in the thermophoretic coefficient enhances the concentration profile. Meanwhile in the stretching divergent channel the concentration profile decreases with k since when there is a substantial thermal difference, the thermophoretic force attracts more particles to the surface, which lowers the concentration.
❖ The liquid velocity in both the channel cases decreases as the Hartmann number rises. The Lorentz force is produced when a magnetic field is applied to an electrically conducting fluid. This force exerts its influence in the opposite direction of the flow, resulting in flow deceleration and, as a direct consequence of this, a reduction in the velocity of the fluid.
❖ The consequence of the Reynolds number on the liquid's speed of the stretching and shrinking of both the channels indicates a mixed characteristic of growth or decrease in the momentum boundary layer, depending on whether shrinking or stretching is applied to the channel.
Due to the many uses of flow through CDCs in engineering and industry, it is essential to understand how to construct relationships between flow, mass, and heat transport properties for various nanoliquids. Consequently, potential future research may centre on entropy production in addition to the influence of Stefan blowing, convective heat conditions, Newtonian heating, and non-uniform heat sources/sinks on various models of nanoliquid streams. This would allow researchers to construct well-targeted numerical models and simulate distinct hydrodynamic and thermal interface constraints under different conditions, ultimately developing a mathematical model for non-Newtonian nanofluid flow.
Abbreviations
|
B
0
| Transverse magnetic field |
|
u
| Velocity component (m s−1) |
|
k
T
| Thermal diffusion ratio |
|
r
| Radial direction |
|
z
| Axial direction |
|
p
| Pressure (Pa) |
|
f
| A function of θ |
|
k
| Thermophoretic coefficient |
|
c
p
| Specific heat (J kg−1 K−1) |
|
T
| Temperature (K) |
|
q
| Radiative heat flux |
|
D
B
| Brownian motion coefficient |
|
C
| Concentration |
|
V
T
| Non-dimensional thermophoretic velocity |
|
u
c
| Rate of movement in the radial direction (m2 s−1) |
|
S
| Stretching/shrinking rate |
|
T
w
| Surface temperature of the channel (K) |
|
C
w
| Concentration at the surface |
|
g
| A function of r |
|
V
| Thermophoretic deposition velocity |
|
F
| Dimensionless radial velocity |
|
M
| Hartmann number |
| Re | Reynolds number |
|
N
| Radiation parameter |
| Pr | Prandtl number |
| Sc | Schmidt number |
|
k
| Thermal conductivity |
|
q
w
| Heat flux (W m−2) |
| Nu | Nusselt number |
Greek letters
|
θ
| Azimuthal direction |
|
α
| Elevation angle of convergent/divergent channels |
|
ρ
| Density |
|
υ
| Kinematic viscosity |
|
σ
| Electrical conductivity |
|
η
| Similarity variable |
|
Θ
| Temperature in non-dimensional form |
|
ϕ
| Volumetric expansion coefficient in dimensionless form |
|
μ
| Dynamic viscosity |
|
λ
| Stretching/shrinking parameter |
Subscripts
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the large group Research Project under grant number RGP2/3/44.
References
- F. A. Hamedani, S. S. M. Ajarostaghi and S. A. Hosseini, Numerical evaluation of the effect of geometrical and operational parameters on thermal performance of nanofluid flow in convergent–divergent tube, J. Therm. Anal. Calorim., 2020, 140(3), 1483–1505, DOI:10.1007/s10973-019-08765-w.
- U. Khan,
et al., A Novel Hybrid Model for Cu–Al2O3/H2O Nanofluid Flow and Heat Transfer in Convergent/Divergent Channels, Energies, 2020, 13(7), 7, DOI:10.3390/en13071686.
- A. Mishra, A. K. Pandey, A. J. Chamkha and M. Kumar, Roles of nanoparticles and heat generation/absorption on MHD flow of Ag–H2O nanofluid via porous stretching/shrinking convergent/divergent channel, J. Egypt. Math. Soc., 2020, 28(1), 17, DOI:10.1186/s42787-020-00079-3.
- M. H. Hashim and Y. M. Chu, Numerical simulation for heat and mass transport analysis for magnetic-nanofluids flow through stretchable convergent/divergent channels, Int. J. Mod. Phys. B, 2021, 35(19), 2150198, DOI:10.1142/S0217979221501988.
- S. Rehman, Hashim and S. I. Ali Shah, Numerical simulation for heat and mass transport of non-Newtonian Carreau rheological nanofluids through convergent/divergent channels, Proc. Inst. Mech. Eng., Part C, 2022, 236(11), 6025–6039, DOI:10.1177/09544062211065688.
- M. Turkyilmazoglu, Extending the traditional Jeffery-Hamel flow to stretchable convergent/divergent channels, Comput. Fluids, 2014, 100, 196–203 CrossRef.
- A. Razaq, T. Hayat, S. A. Khan and S. Momani, ATSS model based upon applications of Cattaneo-Christov thermal analysis for entropy optimized ternary nanomaterial flow with homogeneous-heterogeneous chemical reactions, Alexandria Eng. J., 2023, 79, 390–401, DOI:10.1016/j.aej.2023.08.013.
- M. Khan, M. Sarfraz, J. Ahmed, L. Ahmad and A. Ahmed, Viscoelastic nanofluid motion for Homann stagnation-region with thermal radiation characteristics, Proc. Inst. Mech. Eng., Part C, 2021, 235(21), 5324–5336, DOI:10.1177/0954406220987266.
- M. Sarfraz, M. Khan and M. Yasir, Dynamics of water conveying iron oxide and graphene nanoparticles subject to stretching/spiraling surface: An asymptotic approach, Ain Shams Eng. J., 2023, 14(8), 102021, DOI:10.1016/j.asej.2022.102021.
- M. Sarfraz and M. Khan, Thermodynamic irreversibility analysis of water conveying argentum and titania nanoparticles subject to inclined stretching surface, Phys. Scr., 2023, 98(2), 025205, DOI:10.1088/1402-4896/acab92.
- M. Sarfraz and M. Khan, Heat transfer efficiency in planar and axisymmetric ternary hybrid nanofluid flows, Case Stud. Therm. Eng., 2023, 44, 102857, DOI:10.1016/j.csite.2023.102857.
- M. Sarfraz and M. Khan, Cattaneo-Christov double diffusion-based heat transport analysis for nanofluid flows induced by a moving plate, Numer. Heat Transfer, Part A, 2023, 1–13, DOI:10.1080/10407782.2023.2186551.
- M. Sarfraz and M. Khan, Magnetized homann flow comprising GO and Co3O4 nanoparticles past a biaxially stretching surface, Phys. Scr., 2023, 98(3), 035218, DOI:10.1088/1402-4896/acba61.
- M. Z. A. Qureshi,
et al., Morphological nanolayer impact on hybrid nanofluids flow due to dispersion of polymer/CNT matrix nanocomposite material, AIMS Math., 2023, 8(1), 633–656 Search PubMed.
- A. Rauf, N. A. Shah, A. Mushtaq and T. Botmart, Heat transport and magnetohydrodynamic hybrid micropolar ferrofluid flow over a non-linearly stretching sheet, AIMS Math., 2023, 8(1), 164–193 Search PubMed.
- M. K. Nayak, R. Mehmood, T. Muhammad, A. U. Khan and H. Waqas, Entropy minimization in mixed convective Falkner-Skan flow of ZnO-SAE50 nanolubricant over stationary/moving Riga plate, Case Stud. Therm. Eng., 2021, 26, 101176, DOI:10.1016/j.csite.2021.101176.
- N. Muhammad and N. Ahmed, Subdomain method for unsteady flow of ZnO − SAE50 nano-lubricant through expanding/contracting walls in an asymmetric porous horizontal channel, Int. Commun. Heat Mass Transfer, 2022, 138, 106410, DOI:10.1016/j.icheatmasstransfer.2022.106410.
- M. Riaz, N. Khan, M. S. Hashmi and J. Younis, Heat and mass transfer analysis for magnetized flow of ZnO-SAE50 nanolubricant with variable properties: an application of Cattaneo–Christov model, Sci. Rep., 2023, 13(1), 1, DOI:10.1038/s41598-023-35988-7.
- M. Riaz, N. Khan and S. A. Shehzad, Rheological behavior of magnetized ZnO – SAE50 nanolubricant over Riga plate: A theoretical study, Adv. Mech. Eng., 2023, 15(3), 16878132231162304, DOI:10.1177/16878132231162305.
- M. Nagapavani, G. Venkata Ramana Reddy and M. D. Alsulami, Cubic auto-catalysis chemical reaction in non-Newtonian nanolubricant flow over a convectively heated rotating porous disk, Int. J. Mod. Phys. B, 2023, 37(26), 2350301, DOI:10.1142/S0217979223503010.
- I. Khan, N. A. Shah and L. C. C. Dennis, A scientific report on heat transfer analysis in mixed convection flow of Maxwell fluid over an oscillating vertical plate, Sci. Rep., 2017, 7(1), 1, DOI:10.1038/srep40147.
- S. Eswaramoorthi, K. Loganathan, M. Faisal, T. Botmart and N. A. Shah, Analytical and numerical investigation of Darcy-Forchheimer flow of a nonlinear-radiative non-Newtonian fluid over a Riga plate with entropy optimization, Ain Shams Eng. J., 2023, 14(3), 101887, DOI:10.1016/j.asej.2022.101887.
- P. Srilatha,
et al., Effect of Nanoparticle Diameter in Maxwell Nanofluid Flow with Thermophoretic Particle Deposition, Mathematics, 2023, 11(16), 16, DOI:10.3390/math11163501.
- S. A. Khan, A. Razaq, A. Alsaedi and T. Hayat, Modified thermal and solutal fluxes through convective flow of Reiner-Rivlin material, Energy, 2023, 283, 128516, DOI:10.1016/j.energy.2023.128516.
- S. A. Khan, T. Hayat and A. Alsaedi, Bioconvection entropy optimized flow of Reiner-Rivlin nanoliquid with motile microorganisms, Alexandria Eng. J., 2023, 79, 81–92, DOI:10.1016/j.aej.2023.07.069.
- A. Hafeez, M. Khan and J. Ahmed, Oldroyd-B fluid flow over a rotating disk subject to Soret–Dufour effects and thermophoresis particle deposition, Proc. Inst. Mech. Eng., Part C, 2021, 235(13), 2408–2415, DOI:10.1177/0954406220946075.
- B. C. Prasannakumara and R. J. P. Gowda, Heat and mass transfer analysis of radiative fluid flow under the influence of uniform horizontal magnetic field and thermophoretic particle deposition, Waves Random Complex Media, 2022, 1–12, DOI:10.1080/17455030.2022.2096943.
- S. Bashir, M. Ramzan, H. A. S. Ghazwani, K. S. Nisar, C. A. Saleel and A. Abdelrahman, Magnetic Dipole and Thermophoretic Particle Deposition Impact on Bioconvective Oldroyd-B Fluid Flow over a Stretching Surface with Cattaneo–Christov Heat Flux, Nanomaterials, 2022, 12(13), 13, DOI:10.3390/nano12132181.
- R. Naveen Kumar,
et al., Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet, J. Mol. Liq., 2021, 334, 116494, DOI:10.1016/j.molliq.2021.116494.
- G. K. Ramesh, J. K. Madhukesh, N. Ali Shah and S.-J. Yook, Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition, Alexandria Eng. J., 2023, 64, 969–979, DOI:10.1016/j.aej.2022.09.026.
- V. K. Mishra and S. Chaudhuri, Genetic algorithm-assisted artificial neural network for retrieval of a parameter in a third grade fluid flow through two parallel and heated plates, Heat Transfer, 2021, 50(3), 2090–2128, DOI:10.1002/htj.21970.
- A. Shafiq, A. B. Çolak, T. N. Sindhu, Q. M. Al-Mdallal and T. Abdeljawad, Estimation of unsteady hydromagnetic Williamson fluid flow in a radiative surface through numerical and artificial neural network modeling, Sci. Rep., 2021, 11(1), 1, DOI:10.1038/s41598-021-93790-9.
- T.-H. Zhao, M. I. Khan and Y.-M. Chu, Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks, Math. Methods Appl. Sci., 2023, 46(3), 3012–3030, DOI:10.1002/mma.7310.
- D. Srinivasacharya and R. S. Kumar, Artificial neural network modeling of the Casson fluid flow over unsteady radially stretching sheet with Soret and Dufour effects, J. Therm. Anal. Calorim., 2022, 147(24), 14891–14903, DOI:10.1007/s10973-022-11694-w.
- C. Sedani, P. Chaudhuri and M. Kumar Gupta, Heat transfer and fluid flow analysis of pebble bed and its verification with artificial neural network, Nucl. Mater. Energy, 2023, 35, 101439, DOI:10.1016/j.nme.2023.101439.
- B. Shilpa, V. Leela and H. P. Rani, Stability analysis of MHD radiative mixed convective flow in vertical cylindrical annulus: thermal nonequilibrium approach, Heat Transfer, 2023, 52, 707–733 CrossRef.
- B. Shilpa and V. Leela, An artificial intelligence model for heat and mass transfer in an inclined cylindrical annulus with heat generation/absorption and chemical reaction, Int. Commun. Heat Mass Transfer, 2023, 147, 106956 CrossRef CAS.
- B. Shilpa, V. Leela, B. C. Prasannakumara and P. Nagabhushana, Soret and Dufour effects on MHD double-diffusive mixed convective heat and mass transfer of couple stress fluid in a channel formed by electrically conducting and non-conducting walls, Waves Random Complex Media, 2022 DOI:10.1080/17455030.2022.2119491.
- B. Shilpa and V. Leela, Galerkin finite element analysis of heat and mass transfer of Jeffrey, Maxwell and Oldroyd-B nanofluids in a vertical annulus with an induced magnetic field and a non–uniform heat source/sink, Int. J. Ambient Energy, 2023, 44(1), 1887–1903 CrossRef CAS.
- H. P. Rani, V. Leela, B. Shilpa and P. Nagabhushana, Numerical analysis of hydromagnetic mixed convective flow in an internally heated vertical porous layer using thermal nonequilibrium model, Heat Transfer, 2022, 51(7), 6249–6273 CrossRef.
- K. Sepyani, M. Afrand and M. Hemmat Esfe, An experimental evaluation of the effect of ZnO nanoparticles on the rheological behavior of engine oil, J. Mol. Liq., 2017, 236, 198–204, DOI:10.1016/j.molliq.2017.04.016.
- M. K. Nayak, J. Prakash, D. Tripathi and V. S. Pandey, 3D radiative convective flow of ZnO-SAE50nano-lubricant in presence of varying magnetic field and heterogeneous reactions, Propuls. Power Res., 2019, 8(4), 339–350, DOI:10.1016/j.jppr.2019.10.002.
- O. Pourmehran, M. Rahimi-Gorji and D. D. Ganji, Heat transfer and flow analysis of nanofluid flow induced by a stretching sheet in the presence of an external magnetic field, J. Taiwan Inst. Chem. Eng., 2016, 65, 162–171, DOI:10.1016/j.jtice.2016.04.035.
-
H. E. Patel, K. B. Anoop, T. Sundararajan, and S. K. Das, A micro-convection model for thermal conductivity of nanofluids, presented at the International Heat Transfer Conference, 2006, vol. 13, DOI:10.1615/IHTC13.p8.240.
- M. K. Nayak, R. Mehmood, O. D. Makinde, O. Mahian and A. J. Chamkha, Magnetohydrodynamic flow and heat transfer impact on ZnO-SAE50 nanolubricant flow over an inclined rotating disk, J. Cent. South Univ., 2019, 26(5), 1146–1160, DOI:10.1007/s11771-019-4077-8.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *c,
Naveen Kumar
R.
d,
Samia
Ben Ahmed
e and
Raman
Kumar
f
*c,
Naveen Kumar
R.
d,
Samia
Ben Ahmed
e and
Raman
Kumar
f
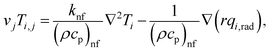
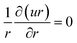
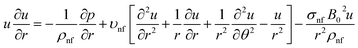
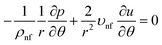
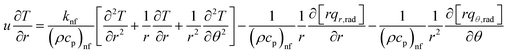
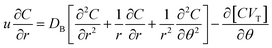
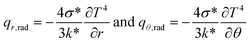
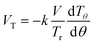
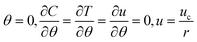
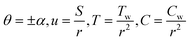
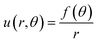
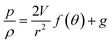
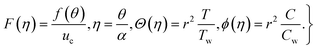
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.06062T,
e−0.06062T,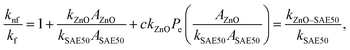
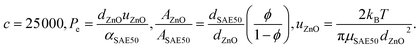
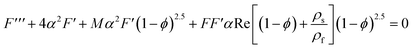
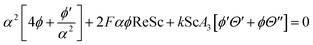
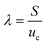 is the stretching (λ > 0) or shrinking (λ < 0) parameter and
is the stretching (λ > 0) or shrinking (λ < 0) parameter and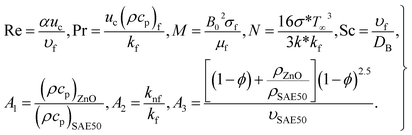
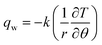 the Nusselt number is given by
the Nusselt number is given by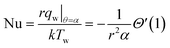
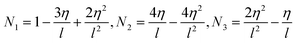
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) = [K1K2K3K4].
= [K1K2K3K4].