Morphology-dependent adsorption energetics of Ru nanoparticles on hcp-boron nitride (001) surface – a first-principles study

Abstract

Active B₅-sites on Ru catalysts can be exploited for various catalytic applications; in particular, the epitaxial formation of Ru nanoparticles with hexagonal planar morphologies on hexagonal boron nitride sheets increases the number of active B₅-sites along the nanoparticle edges. The energetics of adsorption of Ru nanoparticles on hexagonal boron nitride were investigated using density functional theory calculations. Then, to understand the fundamental reason for this morphology control, adsorption studies and charge density analysis were performed on fcc and hcp Ru nanoparticles heteroepitaxially formed on a hexagonal boron nitride support. Among the explored morphologies, hcp Ru(0001) nanoparticles exhibited the highest adsorption strength of −31.656 eV. To verify the hexagonal planar morphologies of the hcp-Ru nanoparticles, three different hcp-Ru(0001) nanoparticles—Ru60, Ru53, and Ru 41—were adsorbed onto the BN substrate. In agreement with the experimental studies, the hcp-Ru60 nanoparticles exhibited the highest adsorption energy owing to their long-range and perfect hexagonal match with the interacting hcp-BN(001) substrate.

---

Introduction

Ruthenium nanoparticles (Ru NPs) containing B₅-type active sites have been reported to be excellent and versatile catalysts for many applications, particularly ammonia decomposition, methane decomposition, and carbon monoxide oxidation.^1–5 However, the population of B₅-sites is dependent on the morphology of the Ru NPs, with more-hexagonal Ru NPs having a higher number of B₅-sites. Furthermore, the catalytic activity of the sites can be enhanced by adding a suitable support material. Two-dimensional materials with structures similar to that of graphene, such as hexagonal boron nitride (h-BN), have recently emerged as promising support materials for various applications. In particular, h-BN sheets are chemically robust and free-standing, and can therefore act as a support for metal clusters and nanoparticles, enabling the fabrication of versatile and functional heterostructures.⁶ In addition, h-BN is thermodynamically stable under all possible operating conditions, and is therefore a suitable alternative for graphene as a support material. Jacobsen studied the stability of Ru/BN catalysts at high temperatures for catalytic ammonia synthesis.⁷ Similarly, a few computational studies involving the embedding of different metal atoms, such as Co, Fe, Ru, and Au, onto an h-BN layer have been conducted to investigate their effect on CO oxidation performance.^8–10 Zhou et al. studied the intriguing electronic and magnetic properties of noble metal (Pd, Pt, Ag, and Au) doped on h-BN layer.¹¹ Thupsuri et al. designed transition metal (TM = V, Cr, Mn, Nb, Mo, Tc, Ta, W, or Re) doped on boron nitride nanosheets for hydrogen and formaldehyde adsorptions.¹² Recently, Fan et al. reported the synthesis of Ru atoms onto porous h-BN via B–Ru and N–Ru coordination through vacuum filtration for the purpose of CO₂ methanation.¹³ Our experimental group also reported a novel synthesis method in which Ru NPs with abundant B₅-sites were successfully grown on a h-BN support using selective morphology-control driven by nanoscale heteroepitaxy for low-temperature ammonia dehydrogenation.¹⁴ Notably, the synthesized catalyst exhibited better activity for ammonia dehydrogenation compared to previously reported catalysts. Herein, to gain fundamental insight into this novel synthesis method, we investigated different facets and morphologies of Ru NPs adsorbed onto h-BN supports using density functional theory (DFT) calculations. We performed adsorption studies on Ru NPs of various shapes, namely truncated octahedral FCC (Ru55-O) with (111) and (001) facets, hexagonal close packing (Ru63-H) with (0001), (11−20), and (10−10) facets, icosahedral FCC (Ru55-I) NPs with the (111) facet, and decahedral FCC (Ru54-D) NPs with the (111) facet, on h-BN(001) surfaces.

Computational methodology

Periodic DFT calculations were performed using the Vienna ab initio Simulation Package (VASP)^15–18 with the projected augmented wave (PAW)^19,20 pseudopotentials and the generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof exchange-correlation functional to describe the core–valence interactions.²¹ The plane-wave cutoff energy was set to 550 eV for hcp-boron nitride and 400 eV for Ru NPs. All relaxed atom structures were fully optimized until the total energy change between the self-consistent (SCF) steps was less than 10⁻⁴ eV. The Brillouin zone in reciprocal space was sampled using a Γ-centered Monkhorst–Pack scheme with 16 × 16 × 16 and 2 × 2 × 1 k-point grids for hcp-boron nitride bulk and surface calculations and 1 × 1 × 1 k-point grids for Ru NPs.²² Accounting for long-range dispersion forces, we used the DFT-D2 approach described by Grimme,²³ which is essential for accurate description of the hcp-BN interlayer interactions and the interactions between the Ru NPs and hcp-BN(001) surface. Ab initio molecular dynamics (AIMD) simulation were performed for understanding the thermal and kinetic stability of the system.

Results and discussion

Herein, we modeled stable Ru NPs of various shapes, such as truncated octahedral FCC (Ru55-O) with (111) and (001) facets, hexagonal close packing (Ru63-H) with (0001), (11−20), and (10−10) facets, icosahedral FCC (Ru55-I) with the (111) facet, and decahedral FCC (Ru54-D) NPs with the (111) facet, as shown in Fig. 1.²⁴

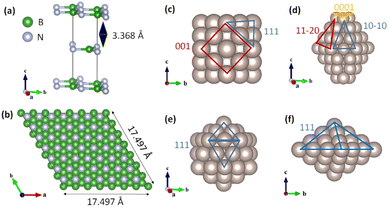Fig. 1 Optimized structures of (a) bulk and (b) (7 × 7) h-BN(001) surface. (c) Ru55-O (truncated octahedral FCC) nanoparticles, (d) Ru63-hcp nanoparticles, (e) Ru55-I (icosahedral FCC), and (f) Ru54-D (decahedral FCC) nanoparticles.

Different binding orientations of the Ru NPs were considered to obtain the adsorption complexes with the lowest energy. The adsorption energy of the adsorbate on the (7 × 7) h-BN(001) surface was calculated using the following equation.

E_ads = E_{7×7 h-BN(001)+Ru Nps} − (E_{7×7 h-BN(001)} + E_{Ru Nps})

here, E_{7×7 h-BN(001)+Ru Nps} represents the total energy of the Ru NP-adsorbed h-BN(001) surface, E_{7×7 h-BN(001)} represents the total energy of the h-BN(001) surface, and E_{Ru Nps} is the energy of the Ru NPs. The differences in adsorption energies reflect the trends in surface reactivity; therefore, E_ads is useful for characterizing activity trends and relative energetics. In case 1, Ru-O, Ru-H, Ru-I NPs and Ru-D NPs were adsorbed onto the 7 × 7 h-BN(001) surface (Fig. 2(a)–(d)); the corresponding adsorption energy correlations are shown in Fig. 2(e). At sites 1 and 2 on the 7 × 7 h-BN(001) surface, the adsorption energies were −28.548 and −27.518 eV for Ru-O NPs, −31.656 and −30.189 eV for Ru-H NPs, −28.896 and −29.844 eV for Ru-I NPs, and −28.648 and −28.906 eV for Ru-D NPs, respectively. It was concluded that Ru-H NPs at site 1, with an adsorption energy of −31.656 eV, exhibited the best stability. The larger number of adsorption energies were attributed to the more number of atoms in the nanoparticles.

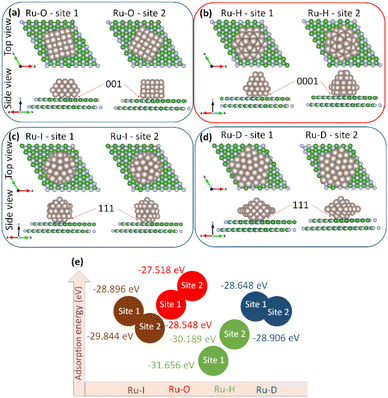Fig. 2 Adsorption of Ru nanoparticles ((a) Ru-O, (b) Ru-H, (c) Ru-I, and (d) Ru-D) on 7 × 7 h-BN(001) surface. (e) Adsorption energy correlation of the systems.

In case 2, different Ru-H(0001) NPs, such as Ru60 (bottom layer removed from Ru63H), Ru53 (two bottom layers removed from Ru63H), and Ru41 (three bottom layers removed from Ru63H), were modeled to adsorb onto the 7 × 7 h-BN(001) surface at two different sites, as shown in Fig. 3. The hcp-Ru60 NPs, which contain seven interfacial Ru atoms at the bottom, exhibited strong interaction with the h-BN(001) surface, with adsorption energies of −32.374 eV (site 1) and −32.091 eV (site 2). Similarly, hcp-Ru41 NPs (19 interfacial Ru atoms at the bottom) had adsorption energies of −25.129 eV (site 1) and −23.656 eV (site 2), and hcp-Ru53 NPs (12 interfacial Ru atoms at the bottom) had adsorption energies of −31.656 eV (site 1) and −30.189 eV (site 2). In addition, variation in bond length between Ru–Ru, Ru–B, Ru–N, and B–N were observed for the three Ru-H(0001) NPs on h-BN(001) system. Adsorption energies and structural properties of Ru-H(0001) NPs on h-BN(001) system were listed in Tables 1 and 2. Thus, hcp-Ru60 NPs had the strongest adsorption energy among the hcp-Ru(0001) NPs, which can be attributed to its perfect hexagonal matching with the h-BN(001) surface.

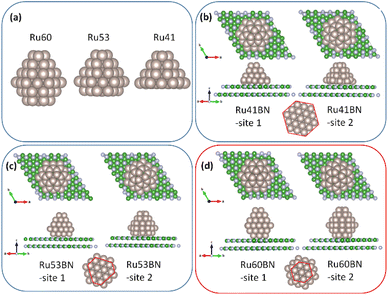Fig. 3 (a) Ru60, R53, and Ru41 nanoparticles. Adsorption of (b) Ru41, (c) R53, and (d) Ru60 nanoparticles on 7 × 7 h-BN(001) surface.

Table 1 Adsorption energies of Ru-H(0001) NPs on h-BN(001) system

System	Site 1 (eV)	Site 2 (eV)
Ru41BN (19 interfacial Ru atoms at the bottom)	−25.129	−23.656
Ru53BN (12 interfacial Ru atoms at the bottom)	−31.656	−30.189
Ru60BN (7 interfacial Ru atoms at the bottom)	−32.374	−32.091

---

Table 2 Structural properties of Ru-H(0001) NPs on h-BN(001) system

System	Ru–Ru (Å)	Ru–B (Å)	Ru–N (Å)	B–N (Å)
Ru41BN	2.366–2.957	2.505–2.984	2.339–2.428	1.423–1.469
Ru53BN	2.671–2.782	2.480–2.716	2.272–2.368	1.436–1.494
Ru60BN	2.619–2.749	2.546–2.841	2.267–2.355	1.457–1.479

---

Recently, our experimental group observed the formation of Ru NPs on the hexagonal lattices of the h-BN(001) zone axis using high-resolution transmission electron microscopy (TEM) (Fig. 4(a)); long-range hexagonal Moiré patterns were clearly visible.^25,26 The regions enclosed by orange boxes in Fig. 4(a) were highlighted using fast Fourier-transform (FET) patterns in Fig. 4(b), which confirmed the orientation of Ru NPs on the h-BN surface, using atomistic models of the well-reproduced hexagonal Moiré pattern in Fig. 4(c). Thus, both experimental and computational studies clearly indicated the epitaxial growth of Ru NPs on the h-BN(001) surface owing to its long-range hexagonal patterns and the perfect matching between the Ru atoms adsorbed and the h-BN(001) surface.

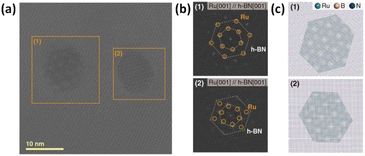Fig. 4 (a) High-resolution TEM image of Ru nanoparticles supported on h-BN (b) fast Fourier-transforms of boxed regions shown in (a). The hexagonal patterns from Ru(001) and h-BN(001) lattices are marked with circles and dotted lines, respectively. (c) Atomistic models of Ru/h-BN observed in (a). Reproduced with permission from Kang et al. (2023).¹⁴ Copyright 2023, Wiley, Wiley-VCH.

To understand the thermal and kinetic stability of the system, we performed ab initio molecular dynamics simulation at targeted temperature T = 400 K at 0.5 fs using canonical (Nose–Hoover) thermostat for the Ru41, Ru53, and Ru60 NPs adsorbed on h-BN(001) surface and temperature–energy profiles were exhibited in Fig. 5. The average total energy and simulation average temperature of 200 MD steps reveals the systems were highly stable.

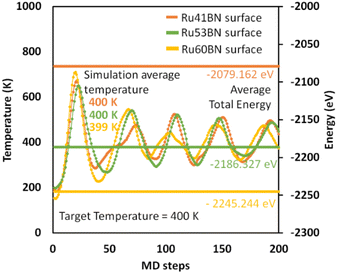Fig. 5 Temperature–energy profiles of Ru41, Ru53, and Ru60 nanoparticles on 7 × 7 h-BN(001) surface.

Excess Bader charge was calculated to identify the electron rearrangement that occurred between the h-BN(001) surface and the Ru NPs.^27,28 Charge density redistribution on the Ru-adsorbed h-BN(001) surface was determined from the isosurface plots of the charge density difference (CDD), and calculated as follows

Δρ = ρ(BN_sur + Ru_np) − (ρ(BN_sur) + ρ(Ru_np))

where ρ(BN_sur + Ru_np), ρ(BN_sur), and ρ(Ru_np) are the electron densities of the Ru-adsorbed h-BN(001) surface, h-BN(001) surface, and Ru NP, respectively.

The hcp-Ru hexagonal NPs composed of 60, 53, 41 Ru atoms (Ru60_h-BN(001)) exhibited a perfect hexagonal match with the h-BN(001) surface, as shown in Fig. 6. The results of excess Bader charge analysis of the Ru60, Ru53, and Ru41 NP on h-BN(001) system are presented in Table 3. The analysis showed that the overall excess Bader charge on the Ru60, Ru53, Ru41 NP was −0.390e, −0.680e, −1.039e (charge loss) and h-BN(001) surfaces was +0.390e, +0.680e, +1.039e (charge gain), respectively, which indicates that charge transfer occurs from the Ru NPs to the h-BN(001) surface. Notably, the bottom Ru NP layer contributed the most Ru60 (−0.953e), Ru53 (−1.195e), and Ru41 (−1.426e) to the charge transfer to the top layer of the h-BN(001) surface. The charge density difference (CDD) isosurface plot (Fig. 6) shows electron-density redistribution between the h-BN(001) surface and Ru (Ru60, Ru53, and Ru41) NPs. In particular, significant electron-density redistribution was observed between the h-BN(001) surface and the adsorbed Ru60 NPs owing to the perfect hexagonal matching between them.

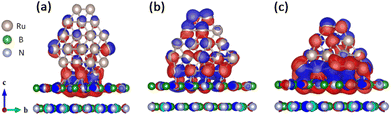Fig. 6 Isosurface of charge density difference (CDD) contours upon (a) Ru60, (b) Ru53, and (c) Ru41 nanoparticle adsorption on the h-BN(001) surface. The red and blue regions denote electron density accumulation and depletion by 0.05 e Å⁻³, respectively.

Table 3 Results of excess Bader charge analysis of Ru60, Ru53, and Ru41 NP on_h-BN(001) system

Excess Bader charge	Ru60_h-BN(001)	Ru53_h-BN(001)	Ru41_h-BN(001)
h-BN(001) surface: overall
Overall excess charge on BN layer	0.390	0.680	1.039
Overall excess charge on B	0.915	1.291	1.593
Overall excess charge on N	−0.524	−0.611	−0.554
h-BN(001) surface: top layer
Excess charge on BN (top layer)	0.439	0.715	1.063
Excess charge on B (top layer)	0.850	1.201	1.542
Excess charge on N (top layer)	−0.411	−0.486	−0.479
h-BN(001) surface: bottom layer
Excess charge on BN (bottom layer)	−0.049	−0.035	−0.024
Excess charge on B (bottom layer)	0.065	0.090	0.051
Excess charge on N (bottom layer)	−0.114	−0.125	−0.075

---

RuNanoparticle	Ru60 NP	Ru53 NP	Ru41 NP
Overall excess charge on Ru	−0.390	−0.680	−1.039
Excess charge on Ru (bottom layer)	−0.953	−1.195	−1.426

---

Conclusions

In this study, the adsorption strength of Ru NPs on h-BN(001) surfaces was investigated using DFT calculations. To support our recent experimental findings and to gain fundamental insight into the heteroepitaxial growth of B5-sites on Ru NPs enhanced on h-BN supports, we performed adsorption studies for fcc and hcp Ru NPs on h-BN(001) surfaces. We found that the hcp Ru63(0001) NPs had better adsorption energy (−31.656 eV) than fcc Ru NPs. Moreover, to investigate the hexagonal planar morphology on 0001 facets, hcp-Ru63(0001) NPs were studied by removing a few layers from the NPs to form three different hcp-Ru(0001) NPs—Ru60, Ru53, and Ru 41—which were adsorbed onto the h-BN(001) surface. Among them, hcp-Ru60(0001) NPs had the best adsorption energy of −32.374 eV owing to their perfect hexagonal match with the interacting h-BN(001) surface. Thus, the observed results support the recent experimental findings, and also prove that a strong support such as h-BN(001) can increase the heteroepitaxial growth of B₅-sites on Ru NPs.

Author contributions

Thillai Govindaraja Senthamaraikannan: data curation, formal analysis, investigation, validation, writing of original draft, review and editing. Chang Won Yoon: conceptualization, formal analysis, validation, review and editing. Dong-Hee Lim: conceptualization, formal analysis, funding acquisition, supervision, validation, writing, review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was financially supported by the National Research Foundation (NRF) of Korea, funded by the Korean government (NRF-2021R1I1A3059884 and NRF-2022M3I3A1082499). This work was also supported by Chungbuk National University BK21 program (2021).

References

1. C. A. Casey-Stevens, S. G. Lambie, C. Ruffman, E. Skúlason and A. L. Garden, J. Phys. Chem. C, 2019, 123, 30458–30466.
2. S. Dahl, A. Logadottir, R. Egeberg, J. Larsen, I. Chorkendorff, E. Törnqvist and J. K. Nørskov, Phys. Rev. Lett., 1999, 83, 1814.
3. F. García-García, A. Guerrero-Ruiz and I. Rodríguez-Ramos, Top. Catal., 2009, 52, 758–764.
4. R. L. Arevalo, S. M. Aspera, M. C. S. Escaño, H. Nakanishi and H. Kasai, J. Phys.: Condens. Matter, 2017, 29, 184001.
5. C. Strebel, S. Murphy, R. M. Nielsen, J. H. Nielsen and I. Chorkendorff, Phys. Chem. Chem. Phys., 2012, 14, 8005–8012.
6. R. Koitz, J. K. Nørskov and F. Studt, Phys. Chem. Chem. Phys., 2015, 17, 12722–12727.
7. C. J. Jacobsen, J. Catal., 2001, 200, 1–3.
8. S. Lin, X. Ye, R. S. Johnson and H. Guo, J. Phys. Chem. C, 2013, 117, 17319–17326.
9. C. Huang, X. Ye, C. Chen, S. Lin and D. Xie, Comput. Theor. Chem., 2013, 1011, 5–10.
10. M. Gao, A. Lyalin and T. Taketsugu, J. Chem. Phys., 2013, 138, 034701.
11. Y. G. Zhou, P. Yang, X. Sun, Z. G. Wang, X. T. Zu and F. Gao, J. Appl. Phys., 2011, 109, 084308.
12. S. Thupsuri, C. Tabtimsai, V. Ruangpornvisuti and B. Wanno, Phys. E, 2021, 134, 114859.
13. M. Fan, J. D. Jimenez, S. N. Shirodkar, J. Wu, S. Chen, L. Song, M. M. Royko, J. Zhang, H. Guo and J. Cui, ACS Catal., 2019, 9, 10077–10086.
14. S. Kang, J. Cha, Y. S. Jo, Y.-J. Lee, H. Sohn, Y. Kim, C. K. Song, Y. Kim, D.-H. Lim, J. Park and C. W. Yoon, Adv. Mater., 2023, 35, 2203364.
15. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
16. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
17. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
18. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
19. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
20. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
22. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
23. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
24. Y. Nanba, T. Ishimoto and M. Koyama, J. Phys. Chem. C, 2017, 121, 27445–27452.
25. K. Reidy, G. Varnavides, J. D. Thomsen, A. Kumar, T. Pham, A. M. Blackburn, P. Anikeeva, P. Narang, J. M. LeBeau and F. M. Ross, Nat. Commun., 2021, 12, 1–9.
26. H. Lim, S. I. Yoon, G. Kim, A.-R. Jang and H. S. Shin, Chem. Mater., 2014, 26, 4891–4903.
27. R. F. Bader, Chem. Rev., 1991, 91, 893–928.
28. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00037k

‡ Equally contributed corresponding authors.

---