 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature-modulated solution-based synthesis of copper oxide nanostructures for glucose sensing†
Yujiang
Zhu
a,
Carolina
Vigil-Hernandez
 a,
Curran
Kalha
a,
Nathalie Kanchena
Fernando
a,
Curran
Kalha
a,
Nathalie Kanchena
Fernando
 a,
Steve
Firth
a,
Gemma-Louise
Davies
a,
Katarzyna
Bialas
b,
Despina
Moschou
a,
Steve
Firth
a,
Gemma-Louise
Davies
a,
Katarzyna
Bialas
b,
Despina
Moschou
 b and
Anna
Regoutz
b and
Anna
Regoutz
 *a
*a
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: a.regoutz@ucl.ac.uk
bCentre for Biosensors, Bioelectronics and Biodevices (C3Bio), Department of Electronic and Electrical Engineering, University of Bath, Claverton Down, Bath BA2 7AY, UK
First published on 17th July 2023
Abstract
Glucose sensors are widely applied in society as an effective way to diagnose and control diabetes by monitoring the blood glucose level. With advantages in stability and efficiency in glucose detection, non-enzymatic glucose sensors are gradually replacing their enzymatic counterparts and copper(II) oxide (CuO) is a leading material. However, previous work extensively shows that even if the synthesis of CuO nanostructures is performed under nominally similar conditions, entirely different nanostructured products are obtained, resulting in varying physical and chemical properties of the final product, thereby leading to a differing performance in glucose detection. This work investigates the temperature dependence of a wet chemical precipitation synthesis for CuO nanostructures with the resulting samples showing selectivity for glucose in electrochemical tests. X-ray diffraction (XRD), Raman spectroscopy, and X-ray photoelectron spectroscopy (XPS) demonstrate that all products are predominantly CuO, with some contribution from Cu(OH)2 and other surface species varying across synthesis temperatures. The most important change with increasing synthesis temperature is that the overall nanostructure size changes and the morphology shifts from nanoneedles to nanoparticles between 65 and 70 °C. This work helps to understand the critical relationship between synthesis temperature and final nanostructure and can explain the seemingly random nanostructures observed in the literature. The variations are key to controlling sensor performance and ultimately offering further development in copper oxide-based glucose sensors.
1 Introduction
Diabetes mellitus, commonly known as diabetes, is a group of metabolic disorders characterised by elevated levels of blood glucose, in which the body's immune system attacks and destroys the cells that produce insulin (type 1 diabetes), or in which the body does not produce enough insulin or the body's cells do not react to insulin (type 2 diabetes).1 Diabetes can trigger many additional complications, such as retinopathy, heart attack, neuropathy, tinnitus, and nephropathy.2–4 Unfortunately, recent years have witnessed a steady increase in the number of cases and no effective method to cure diabetes exists. It is important to control diabetes and to keep diabetic patients from further deterioration, such as serious secondary symptoms or even death. The increase of glucose levels in the bloodstream can indicate the onset of diabetes. Therefore, monitoring the blood sugar level precisely is essential for early diabetes diagnosis and further treatment.Traditionally, diabetic tests have relied on enzymatic sensors based on glucose oxidase (GOD) or glucose dehydrogenase (GDH) immobilised on a screen-printed electrode, which is an electrochemical or colorimetric readout system.5–7 Although enzymatic glucose sensors are still dominating the market, their environmental sensitivity limits their use.5,8–11 Non-enzymatic glucose sensors not only eliminate the environmental restrictions associated with the use of enzymes, but also make the reaction more efficient with the help of modified electrodes.12,13 Therefore, they are gradually replacing their enzymatic counterparts. Generally, non-enzymatic glucose sensors rely on the direct redox reaction of glucose on the surface of a metal (Au, Pt), metal oxide (Co3O4, CuO, ZnO, RuO2), or alloy (PtPb, PtRu) electrode.6,14–16 Copper(II) oxide (CuO), also known as cupric oxide, has been widely explored for non-enzymatic glucose sensors with a large body of published work since the 1990s.17–21 Its high electrochemical activity, relatively low cost, and non-toxicity, as well as the possibility to readily modify it into different nanostructures have led to its status as a promising material in this area.21–24 Besides the material itself, the structure also impacts the glucose sensing properties of final products. Nanostructures are widely synthesised because they greatly improve the efficiency of non-enzymatic sensors. This is due to their higher surface area to volume ratio compared to structures on the micrometer length scale, which consequently results in a greater number of active sites for the electron transfer process across the electrode, leading to a higher turnover reaction.25
Since You et al. first enhanced glucose sensor sensitivity and stability with CuO/Cu(OH)2 in 2002,19 there has been a large drive in CuO-based non-enzymatic glucose sensor research. In the past two decades, various synthesis methods for copper oxide nanostructures have been proposed and consistently optimised to fabricate sensors. Among them, wet chemical precipitation synthesis is widely applied as it is simple and controllable.26–28 A notable fact is that although syntheses are performed under similar conditions in the literature, even nominally identical protocols create entirely different product nanostructures, from zero-dimensional (nanoparticles) to three-dimensional (nanoflowers or spherical structures), which induces different final properties.29–31 Synthesis temperature has been identified as having a strong influence on the final nanostructures and a small number of previous studies has reported that a synthesis temperature increase leads to the growth of nanoparticles, which become more crystalline and have a narrower band gap (Eg).32–34
This work investigates how synthesis temperature impacts the growth of nanostructures and aims to establish a connection between nanostructure type and glucose sensing properties. CuO nanostructures are synthesised by a facile wet chemical precipitation method and cyclic voltammetry is used to test their glucose sensing behaviour. An extensive range of materials characterisation techniques, including scanning electron microscopy (SEM), transmission electron microscopy (TEM), X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), Raman spectroscopy, and ultraviolet-visible (UV-vis) spectroscopy, is applied to explore the morphology, structure, surface chemistry, and electronic structure of the nanostructures. Clear differences are observed following the change in synthesis temperature, including a change in morphology from nanoneedles to nanoparticles and a variation of their surface chemistry.
2 Experimental
2.1 CuO nanostructure synthesis
A wet chemical precipitation synthesis method derived from the work by Ahmad et al. was applied to synthesise copper oxide nanostructures.35 Copper (2) acetate (≥98%, Sigma-Aldrich), sodium hydroxide (≥97%, Fisons Scientific Equipment), acetic acid (≥99%, Honeywell), and deionised (DI) water were used. A copper (2) acetate solution (0.02 M, 200 mL) was placed in a three-neck round-bottom flask connected to a reflux condenser. The solution was heated, and stirred continuously at 400 rpm until it reached the target synthesis temperature, which was varied between 45 and 85 °C in 10 °C increments. An additional synthesis was performed at 70 °C based on initial electron microscopy results. Temperature control was achieved using an Al DrySyn single position block on a ceramic stirring hotplate (Thermo Fisher Scientific, UK), which was temperature calibrated before the experiment and the temperature deviation was controlled within ±1 °C. 0.02 mol (0.8 g) of sodium hydroxide (NaOH) powder was added in the flask once the required temperature was reached, followed by 0.5 mL of concentrated acetic acid. This solution was mixed and heated for 15 min. Thereafter, it was left to cool down to room temperature and the nanostructures were separated by centrifugation (Sigma 2-16KL) at 7000 rpm for 5 min. After removing the supernatant and resuspending the nanostructures using an ultrasonic bath, the samples were washed twice in deionised (DI) water and twice in ethanol (≥99.8%, Fisher Chemical), and centrifuged after each washing step at the same speed and duration as the initial centrifugation. Finally, they were placed in a vacuum desiccator to dry completely.2.2 Glucose sensing behaviour
Cyclic voltammetry (CV) was employed to test the glucose-sensing behaviour of the nanostructures. An AUTOLAB PGSTAT302 potentiostat (Metrohm Electrochemistry Instrumentation, UK) was used for all CV measurements. The gold working electrodes (ϕ = 2 mm, CHI101), counter electrode (Pt wire), reference electrode (Ag/AgCl with saturated NaCl solution), and SVC-3 glass cell (20 mL) with Teflon cap were purchased from IJ Cambria Scientific Ltd. In the cleaning process, the working electrode was incubated in 50 mM KOH/30% H2O2 for 15 min and then rinsed using DI water. It was then polished using a 1 μm Al2O3 slurry for 3 min followed by 6 min sonication (3 min in ethanol and 3 min in DI water). The polishing process was then repeated using a 0.3 μm Al2O3 slurry and same sonication procedures. The electrolyte for the electrochemical cleaning was an acidic aqueous solution containing 500 mM H2SO4 and the CVs were performed at a scan rate of 0.2 V s−1 from 0 to 1.5 V for 50 cycles. The CuO nanostructures were then drop-cast onto the clean working electrode as follows. 2 mg of the CuO nanostructures were dispersed in 1 mL DI water and sonicated for at least one hour to ensure that the suspension was uniform before drop casting. Five times 5 μL of the suspension were drop cast onto the active area of the working electrode (one by one, waiting for each layer to dry completely before drop-casting another). The glucose detection was performed in a 0.1 M NaOH solution with 1 mM glucose from −0.5 V to 1 V (100 cycles) with a 0.05 V s−1 scan rate. The control experiment including fructose interference was performed in the same concentration of fructose alkaline solution under the same CV conditions.2.3 Materials characterisation
A STOE STADI P X-ray diffractometer with a Cu Kα source (λ = 1.54 Å) in transmission geometry was used to examine the crystal structure and phase composition of the as-synthesised samples and TOPAS Academic v7 was applied for data analysis.36 Samples were ground in an agate mortar and mounted in XRD capillary tubes (ϕ = 0.3 mm, wall thickness = 0.01 mm, borosilicate glass) supplied by Capillary Tube Supplies Ltd. A beam voltage of 40 kV and current of 30 mA were used. The data were collected across a 2θ range of 2–90° with a scanning rate of 0.5° per step and 5 s per step. The peak profile, Chebychev polynomial background parameters, and instrument factors parameters were refined. A pseudo-Voigt function was used.The morphologies of all samples were investigated using a field emission SEM (JEOL JSM-6701F) with 10 kV accelerating voltage and 10 μA emission current, and a TEM (JEM-2100) fitted with a tungsten filament thermionic gun, 200 kV analytical electron microscope. Electron microscopy images were processed using the ImageJ software package.37
XPS measurements were conducted on a Thermo Scientific K-Alpha spectrometer, which employs a monochromated Al Kα X-ray source (hv = 1486.7 eV), a 180° double focusing hemispherical analyser, and a 128 channel position sensitive detector. The energy resolution was 0.6 eV at 20 eV pass energy, determined by extracting the Fermi edge width from the measurement of a polycrystalline gold foil (≥99.95%, Alfa Aesar) using the 16/84% method.38 A 400 μm elliptical spot size was used with the X-ray gun operating with a 12 kV cathode voltage and 6 mA current, and a flood gun operating at 100 μA emission current. Samples were mounted on the holder plate using conductive carbon tape. Survey, core level and valence band spectra were collected using pass energies of 200, 20 and 15 eV, respectively. CuO (≥99.9995%, Alfa Aesar) and Cu2O (≥99.99%, sealed ampoule, Sigma-Aldrich) powders were measured as reference points. All data were analysed using the Thermo Avantage (V5.9925) software package. Spectra were aligned with respect to the binding energy (BE) of the adventitious C 1s peak at 284.8 eV, and normalised to the Cu 2p3/2 area.
A Renishaw inVia Raman Microscope with a 633 nm He:Ne laser setting at three iterations with 30 s accumulation time each was applied for Raman spectroscopy. A UV-2600 UV-vis spectrophotometer with an integrating sphere (Shimadzu, Japan) was employed to investigate electronic and optical properties. CuO samples and BaSO4 (Fisher Scientific, ≥98%) were mixed in an agate mortar in a weight ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and then mounted on the sample plate. Absorbance spectra were collected from 200 to 1000 nm with medium scan speed. The sampling interval was 1 nm and the accumulation time 0.1 s. The light source wavelength change occurred at 370 nm. Before each measurement, the baseline was corrected using a white board filled with BaSO4 only.
4 and then mounted on the sample plate. Absorbance spectra were collected from 200 to 1000 nm with medium scan speed. The sampling interval was 1 nm and the accumulation time 0.1 s. The light source wavelength change occurred at 370 nm. Before each measurement, the baseline was corrected using a white board filled with BaSO4 only.
3 Results and discussion
Fig. 1 displays the CV characteristics of as-prepared CuO nanostructures in glucose and fructose NaOH solution. The different plot colours used represent the colour change of the solution as the temperature is increased and before adding NaOH. Redox peaks at 0.45 V and 0.70 V, marked with red arrows in the solid curves, indicate an efficient reaction occurred within the specified potential region between glucose and the as-prepared copper oxide nanostructures. No peaks were observed in the fructose control group (see dashed lines in the figure), which demonstrates that the CuO samples exhibit selectivity towards glucose. The corresponding reactions are presumed as follows:39,40| CuO + OH− → CuO(OH) + e−, | (1) |
| 2CuO(OH) + glucose → 2CuO + 2H2O + gluconolactone. | (2) |
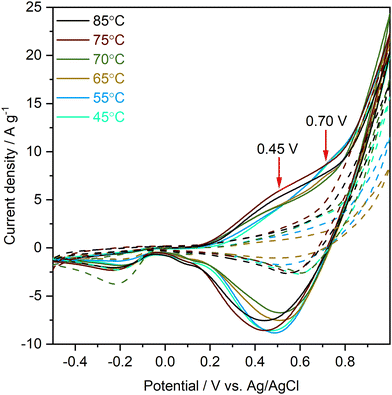 | ||
| Fig. 1 Cyclic voltammograms collected at 0.05 V s−1 in 0.1 M NaOH solution with 1 mM glucose (solid lines) and with 1 mM fructose (dashed lines). All curves shown are taken from the 30th cycle of each CV run, which is representative of the stable behaviour of the nanostructures during electrochemical testing (the full data set across 100 cycles can be found in the ESI†). The main redox peaks are marked with red arrows. | ||
The redox peak position for 45, 55, and 65 °C synthesis temperature occurs at 0.70 V, and with an increase in temperature (70, 75, and 85 °C), this oxidation peak shifts to 0.45 V. As the conditions of CV collection are kept consistent for all samples, the shift observed is attributed to the changes in physico-chemical characteristics of the samples, including morphology, crystallinity, and surface chemical state. The CV data can also be used to determine the surface area of porous materials.41,42 Shown in Table 1 are the electroactive surface area (ESA) values calculated from the observed CV peak currents.42 An overall trend of a decrease in ESA with increasing synthesis temperature is observed. However, values are not entirely systematic, which can be partly explained by the intrinsic limitations of this method, as it only measures the area of the outer contour of the diffusion layer, i.e. it measures the surface area of large pores rather than small voids.43,44
| T/°C | ESA/cm2 | |
|---|---|---|
| 30th cycle | 100th cycle | |
| 45 | 2.01 | 1.71 |
| 55 | 1.22 | 1.24 |
| 65 | 2.23 | 2.06 |
| 70 | 1.18 | 1.12 |
| 75 | 1.58 | 1.52 |
| 85 | 1.06 | 1.04 |
Both nanoneedle and nanoparticle samples show a high level of stability during repeat CV cycles with the redox peak position remaining stable over 100 repeat CV cycles for all samples, with minimal variations of ± 0.01 V. Except for the sample synthesised at 45 °C, the peak current density and therefore the ESA show only small variations. Table 1 compares the ESA values for the 30th and 100th CV cycles and the redox peak positions and peak current densities can be found in the ESI.† The observed level of stability is promising for repeat and real-time applications. To further understand this difference in electrochemical sensing performance, and in particular the clear outlier behaviour of the sample synthesised at 70 °C, a range of materials characterisation techniques was employed.
Electron microscopy was used to study the effect of synthesis temperature variation on the morphology and size of the nanostructures. From the SEM and TEM images shown in Fig. 2, it is clear that nanoneedles gradually convert into nanoparticles with an increase in synthesis temperature. The temperature range between 65 and 75 °C represents a transition region from nanoneedles to nanoparticles. Therefore, another batch of nanostructures was synthesised at 70 °C in order to follow the change of morphology more closely. The SEM and TEM images of the 70 °C sample in Fig. 2(d) show that the morphology change is not sudden and it proceeds through a mixture of morphologies explaining the behaviour observed in the ESA results. In addition to the overall change in morphology, the size of the nanostructures changed. The diameter of the nanoneedles was determined via SEM imaging while the nanoparticle dimensions were determined from TEM images. Values for the nanoneedle length are not reported due to the high level of uncertainty in quantifying this value due to the entangelement of individual needles. The size measurements performed using the ImageJ software package from the images of the CuO nanostructures are summarised in Table 2. With increasing temperature the nanostructures decrease in length with a clear difference in width observed between nanoneedles and nanoparticles. At the crucial transition temperature of 70 °C, nanoparticles appear. When the temperature exceeds 70 °C, the primary CuO nanoparticles agglomerate into nanospheres (Fig. 2(d) and (e)), a common occurrence in small particles which is driven by a need to minimise surface energy.45,46
| Nanoneedles | ||
|---|---|---|
| T/°C | l/nm | w/nm |
| 45 | — | 35 ± 8 |
| 55 | — | 23 ± 5 |
| 65 | 104 ± 23 | 24 ± 7 |
| Nanoparticles | ||
| 70 | 42 ± 21 | 10 ± 3 |
| 75 | 21 ± 9 | 10 ± 2 |
| 85 | 17 ± 7 | 9 ± 2 |
Table 3 summarises the size of these agglomerated nanospheres. With the increase in synthesis temperature, a clear increase in the number as well as the size of observed agglomerated nanospheres occurs, which can be understood as follows. The specific surface area of a sphere is less than that of any other shape so that the lowest possible surface area to volume ratio requires the least energy to maintain its shape. Temperature plays an important role in the formation of CuO spherical nanoparticles by reducing the size of coalesced particles through providing more energy, stimulating the particle movement, as well as increasing collisions among particles. This causes higher nucleation rates of CuO particles which leads to the preferential formation of spherical nanoparticles.32 As discussed, individual nanoparticles tend to agglomerate to reduce the overall surface energy and therefore, nanospheres dominate the morphology at relatively high temperatures. From the TEM images in Fig. 2(d)–(f), the clear boundary of the primary nanoparticles in spheres indicates oriented attachment as a plausible growth mechanism.47–49 The morphology transformation with synthesis temperature observed in electron microscopy can explain the redox peak shift observed in the CV curves. When nanoneedles dominate, the redox peak is around 0.75 V, while when nanoparticles/nanospheres dominate, the peak shifts to 0.45 V.
| T/°C | d SEM/nm | N | d TEM/nm | N |
|---|---|---|---|---|
| 70 | 348 ± 65 | 50 | 337 ± 76 | 50 |
| 75 | 289 ± 90 | 100 | 262 ± 80 | 100 |
| 85 | 385 ± 87 | 100 | 389 ± 75 | 100 |
Following from the clear observation of changes to the morphology of the nanostructures, XRD was carried out to characterise the crystallinity and phase composition of the CuO nanostructures. XRD patterns are shown in Fig. 3(a). All observed diffraction peaks could be indexed to match CuO (ICSD Collection Code: 67850),50 confirming that the bulk of all samples is in the monoclinic CuO phase (space group C2/c (15)). No additional phase or impurity peaks are detected, indicating the formation of a single crystalline phase. Le Bail refinement was performed to further characterise all samples and a representative Le Bail refinement of the 45 °C sample is shown in Fig. 3(b). All other refinements can be found in Fig. S1 in the ESI.† The minimal difference between experiment and fit (Yobs − Ycalc) shows that there is very good agreement between experimental data (Yobs) and fit (Ycalc) across all samples. The experimental lattice parameters determined from the Le Bail refinements are summarised in Table S1 in the ESI.† The lattice parameters match CuO and only minimal changes are observed between samples.50–52
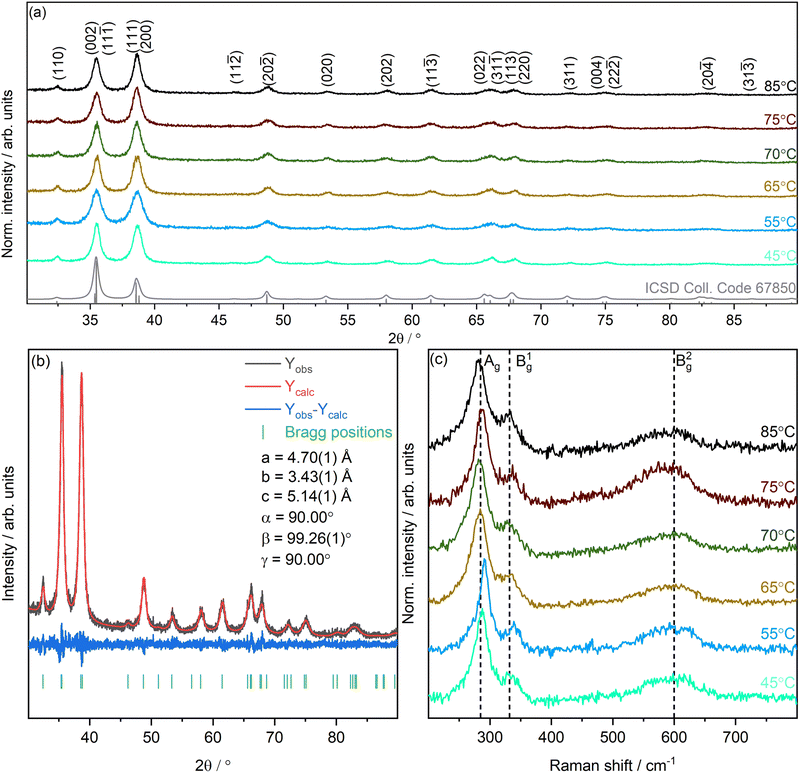 | ||
| Fig. 3 Structural characterisation of the nanostructures using XRD and Raman. (a) Diffraction patterns for CuO nanostructures synthesised at 45–85 °C including a simulated reference pattern for CuO (ICSD Coll. Code: 67850).50 (b) Representative Le Bail refinement of the XRD pattern of CuO nanostructures synthesised at 45 °C. Yobs is the raw data from XRD and Ycalc is the Le Bail refinement. (c) Raman spectra of as-prepared CuO nanostructures. | ||
The crystallite size (CS) of the nanostructures can be determined from XRD and compared with observations from electron microscopy. Two approaches are compared in Table 4 using (i) the Scherrer equation,53 and the full width at half maximum (FWHM) of the main peaks at 35.5° and 38.7° determined from Le Bail refinement, and (ii) direct analysis implemented in the TOPAS software package. As expected a deviation between the two methods is observed as the Scherrer equation simply uses the FWHM of the peaks, whereas the size/strain method using the TOPAS Macro uses a full peak profile. The size/strain method implemented here assumes spherical crystallites.54–56 Comparing these values with the nanostructure sizes obtained from electron microscopy, the crystallite sizes are consistently smaller than the observed particle sizes. This suggests that the nanostructures are polycrystalline.
| T/°C | CSScherrer/nm | CSTOPAS/nm |
|---|---|---|
| 45 | 11.2 | 11.6 |
| 55 | 7.3 | 5.5 |
| 65 | 10.5 | 9.0 |
| 70 | 8.8 | 14.8 |
| 75 | 9.8 | 14.3 |
| 85 | 11.3 | 15.4 |
Complementary structural information of the CuO nanostructures was obtained by Raman spectroscopy. Fig. 3(c) shows the corresponding spectra. Previous studies have demonstrated that the zone centre Raman active modes ΓRA of CuO crystals can be described as 4Au + 5Bu + Ag + 2Bg.57–59 There are three acoustic modes (Au + 2Bu), six infrared active modes (3Au + 3Bg), and three Raman active modes (Ag + 2Bg).59 The main modes observed at 294, 341, and 618 cm−1 are attributed to Ag, Bg1 and Bg2 modes, respectively.60 Clear variations in the positions across the samples are observed, with the Ag mode varying from 281 to 291 cm−1, the Bg1 mode varying from 328 to 340 cm−1, and the Bg2 mode varying from 594 to 605 cm−1. These differences originate from the observed changes in nanostructure size and morphology,61–64 and further confirm the observations from electron microscopy and XRD that the CuO nanostructures synthesised are crystalline and exhibit the monoclinic CuO phase, but significantly vary in their morphology. Overall the morphological and structural bulk characteristics of the nanostructures suggest that the difference in glucose sensing properties can be attributed to the changes in size and shape observed, with a clear difference between nanoneedles and nanoparticle regimes.
In order to probe beyond the bulk and structural properties of the nanostructures, X-ray photoelectron spectroscopy (XPS) and UV-Vis spectroscopy were used. XPS was employed to monitor changes in the surface chemistry of the as-prepared samples. The XPS survey spectra collected for all samples show the expected elements – Cu and O, as well as a small amount of C (see Fig. S2 in the ESI†). The main XPS core level spectra of interest are shown in Fig. 4. In Fig. 4(a), the Cu 2p3/2 peak for the majority of the as-prepared samples is slightly shifted towards lower binding energies (BEs) relative to a CuO reference. In addition, subtle differences in the spectral width are noted. These differences are particularly obvious for the lower synthesis temperatures. One might suggest that this is due to the presence of Cu2O, which occurs at a lower BE compared to CuO (932.8 eV and 933.6 eV), respectively.65–68 However, the BE shift is not large enough for this to be the case and the difference in spectra in fact originates from a mixture of CuO and Cu(OH)2 being present. The presence of hydroxide can be explained by the reactions occurring when the solution reaches the required temperature and NaOH is added:
| Cu2++ 2OH− →Cu(OH)2, | (3) |
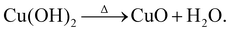 | (4) |
Depending on the synthesis temperature the conversion of Cu(OH)2 to CuO may not be complete and therefore hydroxide remains within the nanostructures. Aside from the main photoemission peak in the Cu 2p3/2 spectra, a noticeable satellite feature is observed on the higher BE side between 940–945 eV, a typical fingerprint for Cu2+ which is not observed for Cu1+. Such satellites occur due to the change in effective nuclear charge after the emission of an electron, which then leads to a reduction in the shielding of electrons. When Cu2+ is present, e.g. in CuO, satellite peaks can be observed in the spectra because of the open 3d9 configuration of Cu2+.69–73
For a full exploration of the oxidation and chemical state of Cu in the samples, Cu Auger lines were also collected with XPS (see Fig. 4(b)). The main Auger line of interest for Cu compounds is L3M4,5M4,5,74,75 occurring due to transitions between the 2p3/2 (L3) and 3d5/2 and 3d3/2 (M4,5) levels. The spectral line shape and kinetic energy position of the Auger peaks are near identical for all samples and are in good agreement with the CuO reference. The main peak is at a kinetic energy of 917.7 eV and the modified Auger parameter for all samples is 1851.0 ± 0.2 eV. The Auger spectra further confirm that the samples are predominantly CuO, as the reference spectrum for Cu2O appears at much lower kinetic energy.
The O 1s spectrum shown Fig. 4(c) exhibits three identifiable contributions at BEs of 529.7, 531.2, and 533.7 eV, respectively. The dominant peak at 529.7 eV is attributed to lattice oxygen in a metal oxide, such as CuO, the peak at 531.2 eV is assigned predominantly to hydroxyl groups (although undercoordinated oxygen sites in metal oxides as well as adsorbed surface species also contribute), and the peak at 533.7 eV indicates the existence of COO environments, most likely from trace amounts of acetate species remaining from the synthesis.76,77 The C 1s spectra shown in Fig. 4(d) confirm this assignment. They show small amounts of carbon present in the samples, with the main low BE peak assigned to adventitious C0 and smaller, higher BE features arising from C–O and COO environments.
The O 1s spectra show the largest differences across the samples, with a strong variation in the intensity of oxide observed in comparison to other species. The atomic ratio between Cu and O in the features assigned to metal oxide environments is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 within the associated errors (see Table S2 in the ESI†). The ratio does not change with the increase of temperature, confirming that CuO was formed for all samples. The ratio between OOxide and OOther is around 2
1 within the associated errors (see Table S2 in the ESI†). The ratio does not change with the increase of temperature, confirming that CuO was formed for all samples. The ratio between OOxide and OOther is around 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the low synthesis temperatures and drops when the temperature increases, representing an increase in hydroxyl groups in particular. This can be explained by the change in the morphology of the nanostructures and therefore a change in how much of the nanostructures is probed due to the surface sensitivity of XPS. To summarise, XPS confirms the formation of CuO in all samples in agreement with the structural characterisation presented. In addition, varying amounts of Cu(OH)2 depending on the nanostructure morphology are observed with nanoneedles synthesised at lower temperatures exhibiting a higher proportion of CuO compared to nanoparticle samples synthesised at higher temperatures.
1 for the low synthesis temperatures and drops when the temperature increases, representing an increase in hydroxyl groups in particular. This can be explained by the change in the morphology of the nanostructures and therefore a change in how much of the nanostructures is probed due to the surface sensitivity of XPS. To summarise, XPS confirms the formation of CuO in all samples in agreement with the structural characterisation presented. In addition, varying amounts of Cu(OH)2 depending on the nanostructure morphology are observed with nanoneedles synthesised at lower temperatures exhibiting a higher proportion of CuO compared to nanoparticle samples synthesised at higher temperatures.
Finally, UV-Vis spectroscopy and XPS were used to explore the electronic structure of the nanostructures. The optical absorption spectra from UV-Vis spectroscopy are shown in Fig. 5(a). All samples show three main absorption features typical for copper nanostructures marked with dashed lines in the figure. The peak around 225 nm is due to interband transitions of electrons near the Cu Fermi level.78,79 The broad absorption feature between 300–400 nm is typical for the formation of CuO nanostructures.80 The weak peak at 620 nm is attributed to the plasma resonance absorption of the copper particles.80,81 It is clear that the synthesis temperature affects the optical absorption peaks as well as the overall absorption, which increases gradually with the temperature. The size of the formed nanostructures influences the UV-Vis absorption, which is particularly noticeable for the feature between 300–400 nm. The overall shape, width, and position are distinctly different between the low synthesis temperature nanoneedles and the higher synthesis temperature nanoparticles.
Beyond the qualitative changes observed in the UV-Vis spectra, the optical band gap (Eg) can be determined from the data based on Tauc analysis (see Fig. S3 in the ESI† for the Tauc plots of all samples), following equation:82
| (αhν)1/n = A(hν − Eg), | (5) |
XPS valence band spectra provide further information on the electronic structure of the nanostructures formed and are shown in Fig. 5(b). Five principal features are identified and labelled with Roman numerals 1 to 5, located at 1.4, 3.6, 10.3, 12.2, and 17.1 eV, respectively. The dominant feature 2 as well as feature 1 originate from Cu 3d states,87 and features 3–5 are predominantly due to O 2p states. The overall shape of the nanostructure VB spectra is in good agreement with a CuO reference powder spectrum as well as the existing literature.72,88 The position of the valence band maximum (VBM) was determined from linear fits to the final drop in intensity close to the Fermi energy (EF) at 0 eV (the VBM-EF separation values can be found in the ESI†). The observed values relative to the optical band gap from UV-Vis are typical for a p-type semiconductor with the VBM located close to EF. For the nanoneedle samples, the value is around 0.3 eV, which then decreases once nanoparticles start to form. With increasing agglomeration and the formation of nanospheres it increases again, showing a clear correlation of nanostructure morphology and size with the electronic structure in line with the observation of the optical band gap.
4 Conclusions
This work clearly demonstrates the influence of the synthesis temperature T on the physico-chemical properties of CuO nanostructures, including morphology, structure, chemistry, and electronic structure, and explains the seemingly random results presented in the existing literature. All prepared nanostructures show selectivity towards glucose with excellent stability over repeat sensing cycles. A clear difference is found in the position of the main redox peak with synthesis temperature, which decreases from 0.70 eV at lower T to 0.5 eV at higher T in line with the change from nanoneedles to nanospheres being formed during synthesis. This change in morphology goes hand-in-hand with a change in surface chemistry and electronic structure and the interplay between the different material characteristics results in the changes in electrochemical sensing behaviour observed. The collected data also illustrates the influence of agglomeration on the characteristics of the nanostructures, with the formation of nanospheres driving e.g. changes in electronic structure. Overall, the presented results highlight the importance of a high level of synthetic control to target specific nanostructures and sensing performance. Furthermore, this study motivates future investigations into the structure and surface chemistry sensitivity of metal-oxide-based glucose sensors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
YZ, CVH and CK acknowledge the support from the Department of Chemistry, UCL. AR acknowledges the support from the Analytical Chemistry Trust Fund for her CAMS-UK Fellowship. NKF acknowledges support from the Engineering and Physical Sciences Research Council (EP/L015277/1).References
- K. G. M. M. Alberti and P. Z. Zimmet, Diabetic Med., 1998, 15, 539–553 CrossRef CAS PubMed.
- Y. Zheng, S. H. Ley and F. B. Hu, Nat. Rev. Endocrinol., 2018, 14, 88–98 CrossRef PubMed.
- S. H. G. Mousavi, B. Sajadinejad, S. Khorsandi and A. Farhadi, Maedica, 2021, 16, 580 Search PubMed.
- A. V. A. Mariadoss, A. S. Sivakumar, C.-H. Lee and S. J. Kim, Biomed. Pharmacother., 2022, 151, 113134 CrossRef CAS PubMed.
- K. Tian, M. Prestgard and A. Tiwari, Mater. Sci. Eng., C, 2014, 41, 100–118 CrossRef CAS PubMed.
- Q. Dong, H. Ryu and Y. Lei, Electrochim. Acta, 2021, 370, 137744 CrossRef CAS.
- G. A. Naikoo, T. Awan, H. Salim, F. Arshad, I. U. Hassan, M. Z. Pedram, W. Ahmed, H. L. Faruck, A. A. Aljabali and V. Mishra, et al. , Bioeng. Transl. Med., 2022, 7, 1–17 Search PubMed.
- M. K. Weibel and H. Brights, J. Biol. Chem., 1971, 246, 2734–2744 CrossRef CAS PubMed.
- J. Wang, Chem. Rev., 2008, 108, 814–825 CrossRef CAS PubMed.
- D. W. Hwang, S. Lee, M. Seo and T. D. Chung, Anal. Chim. Acta, 2018, 1033, 1–34 CrossRef CAS PubMed.
- Q. Mao, W. Jing, F. Zhou, S. Liu, W. Gao, Z. Wei and Z. Jiang, Mater. Sci. Semicond. Process., 2021, 121, 105391 CrossRef CAS.
- M. Wei, Y. Qiao, H. Zhao, J. Liang, T. Li, Y. Luo, S. Lu, X. Shi, W. Lu and X. Sun, Chem. Commun., 2020, 56, 14553–14569 RSC.
- M. H. Hassan, C. Vyas, B. Grieve and P. Bartolo, Sensors, 2021, 21, 4672 CrossRef CAS PubMed.
- J. M. George, A. Antony and B. Mathew, Microchim. Acta, 2018, 185, 1–26 CrossRef CAS PubMed.
- X. Jin and M. A. Alam, IEEE Trans. Biomed. Eng., 2020, 67, 679–687 Search PubMed.
- G. A. Naikoo, H. Salim, I. U. Hassan, T. Awan, F. Arshad, M. Z. Pedram, W. Ahmed and A. Qurashi, Front. Chem., 2021, 9, 1–20 Search PubMed.
- Y. Xie and C. O. Huber, J. Electroanal. Chem. Interfacial Electrochem., 1991, 63, 1714–1719 CAS.
- K. Kano, M. Torimura, Y. Esaka, M. Goto and T. Ueda, J. Electroanal. Chem., 1994, 372, 137–143 CrossRef CAS.
- T. You, O. Niwa, M. Tomita, H. Ando, M. Suzuki and S. Hirono, Electrochem. Commun., 2002, 4, 468–471 CrossRef CAS.
- X. Kang, Z. Mai, X. Zou, P. Cai and J. Mo, Anal. Biochem., 2007, 369, 71–79 CrossRef CAS PubMed.
- T. T. Aun, N. M. Salleh, U. F. M. Ali and N. S. A. Manan, Crit. Rev. Anal. Chem., 2021, 1–57 Search PubMed.
- J. Ghijsen, L. H. Tjeng, J. Van Elp, H. Eskes, J. Westerink, G. A. Sawatzky and M. T. Czyzyk, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 11322–11330 CrossRef CAS PubMed.
- F. Cao and J. Gong, Anal. Chim. Acta, 2012, 723, 39–44 CrossRef CAS PubMed.
- Z. H. Ibupoto, K. Khun, V. Beni, X. Liu and M. Willander, Sensors, 2013, 13, 7926–7938 CrossRef CAS PubMed.
- K. J. Cash and H. A. Clark, Trends Mol. Med., 2010, 16, 584–593 CrossRef CAS PubMed.
- A. Sedighi, M. Montazer and S. Mazinani, Biosens. Bioelectron., 2019, 135, 192–199 CrossRef CAS PubMed.
- M. Jagadeesan, K. Movlaee, T. Krishnakumar, S. Leonardi and G. Neri, J. Electroanal. Chem., 2019, 835, 161–168 CrossRef CAS.
- C. Muiva, L. M. Lepodise, R. Bosigo and A. Juma, Mater. Charact., 2020, 170, 110707 CrossRef CAS.
- T. Jiang, Y. Wang, D. Meng, X. Wu, J. Wang and J. Chen, Appl. Surf. Sci., 2014, 311, 602–608 CrossRef CAS.
- D. M. Ye, G. Z. Li, G. G. Wang, Z. Q. Lin, H. L. Zhou, M. Han, Y. L. Liu and J. C. Han, Appl. Surf. Sci., 2019, 467–468, 158–167 CrossRef CAS.
- Y. Li, Y. L. Lu, K. D. Wu, D. Z. Zhang, M. Debliquy and C. Zhang, Rare Met., 2021, 40, 1477–1493 CrossRef CAS.
- A. Rahnama and M. Gharagozlou, Opt. Quantum Electron., 2012, 44, 313–322 CrossRef CAS.
- M. Jyoti, D. Vijay and S. Radha, Int. J. Sci. Res. Publ., 2013, 3, 1–5 Search PubMed.
- J. Koshy and K. C. George, Int. J. Nanosci. Nanotechnol., 2015, 6, 1–8 Search PubMed.
- R. Ahmad, M. Vaseem, N. Tripathy and Y. B. Hahn, Anal. Chem., 2013, 85, 10448–10454 CrossRef CAS PubMed.
- A. Coelho, TOPAS: general profile and structure analysis software for powder diffraction data, Bruker AXS GmbH, Karlsruhe, Germany, 2003 Search PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- W. E. Unger, M. Senoner, J. M. Stockmann, V. Fernandez, N. Fairley, C. Passiu, N. D. Spencer and A. Rossi, Surf. Interface Anal., 2022, 54, 320–327 CrossRef CAS.
- V. Vinoth, T. D. Shergilin, A. M. Asiri, J. J. Wu and S. Anandan, Mater. Sci. Semicond. Process., 2018, 82, 31–38 CrossRef CAS.
- T. Sridara, J. Upan, G. Saianand, A. Tuantranont, C. Karuwan and J. Jakmunee, Sensors, 2020, 20, 808 CrossRef CAS PubMed.
- A. G. M. Ferrari, C. W. Foster, P. J. Kelly, D. A. Brownson and C. E. Banks, Biosensors, 2018, 8, 1–10 Search PubMed.
- P. Zhu and Y. Zhao, Mater. Chem. Phys., 2019, 233, 60–67 CrossRef CAS.
- E. O. Barnes, X. Chen, P. Li and R. G. Compton, J. Electroanal. Chem., 2014, 720, 92–100 CrossRef.
- P. Zhu and Y. Zhao, RSC Adv., 2017, 7, 26392–26400 RSC.
- Y. Zare, Composites, Part A, 2016, 84, 158–164 CrossRef CAS.
- S. C. Endres, L. C. Ciacchi and L. Mädler, J. Aerosol Sci., 2021, 153, 105719 CrossRef CAS.
- X. Xue, R. L. Penn, E. R. Leite, F. Huang and Z. Lin, CrystEngComm, 2014, 16, 1419–1429 RSC.
- B. Ni and X. Wang, CrystEngComm, 2015, 17, 6796–6808 RSC.
- L. Xiang, J. Guo, C. Wu, M. Cai, X. Zhou and N. Zhang, J. Mater. Res., 2018, 33, 2264–2280 CrossRef CAS.
- O. Garcia-Martinez, R. Rojas, E. Vila and J. M. De Vidales, Solid State Ionics, 1993, 63, 442–449 CrossRef.
- J. Forsyth and S. Hull, J. Phys.: Condens. Matter, 1991, 3, 5257 CrossRef CAS.
- V. Massarotti, D. Capsoni, M. Bini, A. Altomare and A. Moliterni, Z. Kristallogr. – Cryst. Mater., 1998, 213, 259–265 CrossRef CAS.
- P. Scherrer, J. Math. Phys., 1918, 2, 98–100 Search PubMed.
- D. Balzar, N. Audebrand, M. R. Daymond, A. Fitch, A. Hewat, J. I. Langford, A. Le Bail, D. Louër, O. Masson, C. N. McCowan, N. C. Popa, P. W. Stephens and B. H. Toby, J. Appl. Crystallogr., 2004, 37, 911–924 CrossRef CAS.
- N. V. Scarlett and I. C. Madsen, Powder Diffr., 2006, 21, 278–284 CrossRef CAS.
- M. A. Miranda and J. M. Sasaki, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 54–65 CrossRef CAS PubMed.
- J. Chrzanowski and J. Irwin, Solid State Commun., 1989, 70, 11–14 CrossRef CAS.
- J. Irwin, J. Chrzanowski, T. Wei, D. Lockwood and A. Wold, Phys. C, 1990, 166, 456–464 CrossRef CAS.
- J. F. Xu, W. Ji, Z. X. Shen, W. S. Li, S. H. Tang, X. R. Ye, D. Z. Jia and X. Q. Xin, J. Raman Spectrosc., 1999, 30, 413–415 CrossRef CAS.
- D. P. Volanti, M. O. Orlandi, J. Andrés and E. Longo, CrystEngComm, 2010, 12, 1696–1699 RSC.
- W. Wang, Y. Zhuang and L. Li, Mater. Lett., 2008, 62, 1724–1726 CrossRef CAS.
- K. Khoo, A. Zayak, H. Kwak and J. R. Chelikowsky, Phys. Rev. Lett., 2010, 105, 1–4 CrossRef PubMed.
- M. Rashad, M. Rüsing, G. Berth, K. Lischka and A. Pawlis, J. Nanomater., 2013, 2013, 1–6 CrossRef.
- Y. Gao, X. Zhao, P. Yin and F. Gao, Sci. Rep., 2016, 6, 1–5 CrossRef PubMed.
- S. Gaarenstroom and N. Winograd, J. Chem. Phys., 1977, 67, 3500–3506 CrossRef CAS.
- J. P. Tobin, W. Hirschwald and J. Cunningham, Appl. Surf. Sci., 1983, 16, 441–452 CrossRef CAS.
- J. Ghijsen, L.-H. Tjeng, J. van Elp, H. Eskes, J. Westerink, G. A. Sawatzky and M. T. Czyzyk, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 11322 CrossRef CAS PubMed.
- G. Deroubaix and P. Marcus, Surf. Interface Anal., 1992, 18, 39–46 CrossRef CAS.
- G. Schön, Surf. Sci., 1973, 35, 96–108 CrossRef.
- S. K. Chawla, N. Sankarraman and J. H. Payer, J. Electron Spectrosc. Relat. Phenom., 1992, 61, 1–18 CrossRef CAS.
- T. Ghodselahi, M. Vesaghi, A. Shafiekhani, A. Baghizadeh and M. Lameii, Appl. Surf. Sci., 2008, 255, 2730–2734 CrossRef CAS.
- A. Stadnichenko, A. Sorokin and A. Boronin, J. Struct. Chem., 2008, 49, 341–347 CrossRef CAS.
- T. Ivanova, K. Maslakov, A. Sidorov, M. Kiskin, R. Linko, S. Savilov, V. Lunin and I. Eremenko, J. Electron Spectrosc. Relat. Phenom., 2020, 238, 146878 CrossRef CAS.
- M. Cini, Solid State Commun., 1977, 24, 681–684 CrossRef CAS.
- G. Sawatzky and A. Lenselink, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 1790 CrossRef CAS.
- N. McIntyre and M. Cook, Anal. Chem., 1975, 47, 2208–2213 CrossRef CAS.
- N. McIntyre, S. Sunder, D. Shoesmith and F. Stanchell, J. Vac. Sci. Technol., 1981, 18, 714–721 CrossRef CAS.
- A. Oliver, J. C. Cheang-Wong, J. Roiz, J. M. Hern Andez, L. Rodr Õguez Fern Andez and A. Crespos, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 175–177, 495–499 CrossRef CAS.
- H. Ehrenreich and H. R. Philipp, Phys. Rev., 1962, 128, 1622–1629 CrossRef CAS.
- Y. Zhao, J. J. Zhu, J. M. Hong, N. Bian and H. Y. Chen, Eur. J. Inorg. Chem., 2004, 4072–4080 CrossRef CAS.
- K. B. Manjunatha, R. S. Bhat, A. Shashidhara, H. S. Kumar and S. Nagashree, J. Electron. Mater., 2021, 50, 3415–3421 CrossRef CAS.
- B. D. Viezbicke, S. Patel, B. E. Davis and D. P. Birnie, Phys. Status Solidi B, 2015, 252, 1700–1710 CrossRef CAS.
- F. Koffyberg and F. Benko, J. Appl. Phys., 1982, 53, 1173–1177 CrossRef CAS.
- F. Marabelli, G. Parravicini and F. Salghetti-Drioli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1433 CrossRef CAS PubMed.
- D. Wu, Q. Zhang and M. Tao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235206 CrossRef.
- P. Chen, X. Xu, C. Koenigsmann, A. C. Santulli, S. S. Wong and J. L. Musfeldt, Nano Lett., 2010, 10, 4526–4532 CrossRef CAS PubMed.
- J. Folmer and F. Jellinek, J. Less-Common Met., 1980, 76, 153–162 CrossRef CAS.
- Z.-X. Shen, R. List, D. Dessau, F. Parmigiani, A. Arko, R. Bartlett, B. Wells, I. Lindau and W. Spicer, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 8081 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00149k |
| This journal is © The Royal Society of Chemistry 2023 |



