Open Access Article
Open Access ArticleA microfluidic chip for geoelectrical monitoring of critical zone processes†
Flore
Rembert
 *ab,
Arnaud
Stolz
*ab,
Arnaud
Stolz
 b,
Cyprien
Soulaine
b,
Cyprien
Soulaine
 a and
Sophie
Roman
a and
Sophie
Roman
 a
a
aUniv. Orléans, CNRS, BRGM, ISTO, UMR 7327, Orléans, F-45071, France. E-mail: flore.rembert@univ-orleans.fr; Tel: +33 238 492 573
bUniv. Orléans, CNRS, GREMI, UMR 7344, Orléans, F-45067, France
First published on 7th July 2023
Abstract
We miniaturize geoelectrical acquisition using advanced microfabrication technologies to investigate coupled processes in the critical zone. We focus on the development of the complex electrical conductivity acquisition with the spectral induced polarization (SIP) method on a microfluidic chip equipped with electrodes. SIP is an innovative detection method that has the potential to monitor biogeochemical processes. However, due to the lack of microscale visualization of the processes, the interpretation of the SIP response remains under debate. This approach at the micrometer scale allows working in well-controlled conditions, with real-time monitoring by high-speed and high-resolution microscopy. It enables direct observation of microscopic reactive transport processes in the critical zone. We monitor the dissolution of pure calcite, a common geochemical reaction studied as an analog of the water–mineral interactions. We highlight the strong correlation between SIP response and dissolution through image processing. These results demonstrate that the proposed technological advancement will provide a further understanding of the critical zone processes through SIP observation.
1 Introduction
The critical zone (CZ) refers to the near-surface environment extending from the canopy to the non-altered rocks. It was named as such because of human activities, which degrade this natural environment, while most of the drinking water resources and continental life are hosted there.1 Detailed understanding of the water–rock interactions in the CZ is of great importance in many areas of applied science and engineering,2 including contaminant transfers and mineral reactivity.3,4 Calcite is one major mineral of the CZ whose reactive transport study is significant for applications ranging from risk management with the survey of dissolution-driven karstification,5,6 to subsurface bioremediation by precipitation.7 Furthermore, the characterization of calcite reactivity is relevant across scales, from understanding the underlying microscopic mechanisms to predicting its impact on catchment behavior. Therefore, the CZ study requires an interdisciplinary and multi-scale approach based on the characterization of the mechanisms involved between air, water, soil, living organisms, and the rock matrix.8,9Hydrogeophysical methods are based on the acquisition of physical properties (density, electrical conductivity, elastic wave propagation velocity, and magnetic susceptibility) of the sub-surface, and propose the development of appropriate techniques (gravimetry, electric, electromagnetic, and seismic) for the monitoring of hydrological and biogeochemical processes in a non-intrusive and low-cost manner10 compared to, e.g., time-consuming isotope or saline tracer techniques.11 Among the existing techniques, geoelectrical methods have already proven their ability to monitor such processes.12 They are now a standard hydrogeophysical tool for environmental studies related to CZ characterization.13,14
Spectral induced polarization (SIP) is a geoelectrical method measuring the complex electrical conductivity, a property directly influenced by lithology, rock structure, water content and chemistry, and mineral surface state.15,16 All of these are of interest for reactive transport modeling.17–20 SIP measures both electrical conduction and interfacial polarization in a porous medium.21,22 SIP instruments dedicated to geoscientific applications were developed decades ago (see the reviews of Collett23 and Seigel et al.24 and references therein). For studies on sedimentary rocks, new high-precision instruments have been recently produced.25–27 They are now standard and ready-to-use equipment for SIP investigations of hydrological and environmental issues. A four-electrode array is used to investigate mineral–water interface polarization for an alternating injected current at low frequencies, typically from mHz to kHz. Over this frequency range, the polarization comes from the transitory reorganization of an excess of charges in the vicinity of the surface of the mineral, which is called the electrical double layer (EDL). The structure of the EDL comprises the thin Stern layer coated by the wider diffuse layer.28 Similarly, bubbles have a surface charge and generate EDL polarization.29 In the frequency range of EDL polarization, the frequency-dependent behavior of the complex electrical conductivity is related to relaxation times, associated with characteristic lengths in the porous medium (e.g., pore length, pore aperture, grain size, roughness).16,30–32 Pore water composition and surface complexation reactions, driven by mineral dissolution and precipitation processes, influence the SIP response.33–35
The interpretation of the SIP signal is based on the development of petrophysical models that relate the complex electrical conductivity to structural, hydrodynamical, and geochemical properties or distributions. State-of-the-art petrophysical models, however, have a limited range of validity and lump too many microscopic mechanisms into macroscale parameters. For example, the study of calcite precipitation in columns monitored with SIP has shown variations of the electrical signature33 that later have been related to the grain size distribution.32,36 Later experimental investigations have shown that reaction conditions, such as pH, reagent concentrations, and flow rate, play a role in the amplitude of the signal34,35 and that linking SIP measurements to grain size distribution only is a questionable interpretation.37,38 Calcite dissolution is considered in the literature to not create conditions of measurable polarization39 and is, thus, not much investigated with SIP, while it is an important process abundantly studied by geochemists.40–45 Direct observations of the underlying processes coupled with geoelectrical monitoring are key to deconvolve the bio-chemo–physical mechanisms responsible for the measured polarization at the mineral–water interface and, then, to develop more reliable models.
Microfluidic experiments enable direct visualization of flows, reactions, and transport at the pore-scale thanks to transparent microfluidic chips coupled with optical microscopy and high-resolution imaging techniques.46 Micromodels are a two-dimensional representation of the porous medium, ranging in complexity from single channels to replicas of natural rocks.47,48 Cutting-edge micromodels use reactive minerals to investigate the water–mineral interactions involved in the CZ.49,50 For example, microfluidic studies investigate the dissolution of calcite51–53 and two-phase flow.54,55
Impedance spectroscopy characterization at the microscale started to be developed in the late 1990s in the field of biological sciences.56 Several types of electrodes have been developed in this field.57 They are based on a two-electrode array designed for high-frequency measurements from radio to microwaves (10 kHz to 10 GHz). They investigate static systems as pure liquids in small volumes58 or estimate the concentration of cells.59 Some studies have applied this technology to investigate the dielectric properties of soils and determine their water content.60,61 Today, however, geoelectrical measurements with a four-electrode array located in a flow-through microfluidic channel, for geoscience applications, including reactive transport and two-phase flow, are still missing.
In this paper, we propose a new kind of micromodel equipped with electrodes designed for SIP acquisition. Our aim is to assess the use of geoelectrical methods during microfluidic experiments to investigate reactive transport processes representative of the CZ.
2 Materials and methods
This section gives a summary of the theory of the SIP geoelectrical method, then introduces the design of the micromodel equipped with electrodes, and finally presents the experimental protocol for microfluidics with geoelectrical acquisition applied to calcite dissolution monitoring.2.1 SIP measurement technique
The SIP method is based on the injection of a sinusoidal electric current I(t) (Å) typically in the mHz to kHz frequency range by a pair of electrodes| I(t) = |I|sin(ωt), | (1) |
| U(t) = |U|sin(ωt + φ), | (2) |
As commonly used in electricity to address the system as linear equations, the current and the voltage are written as complex numbers I* = |I|eiωt and U* = |U|ei(ωt+φ), where 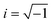 is the imaginary unit. From the ratio of the voltage over the electric current, one obtains the electric impedance Z* (Ω)
is the imaginary unit. From the ratio of the voltage over the electric current, one obtains the electric impedance Z* (Ω)
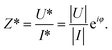 | (3) |
The value of the measured voltage, and thus, of the resulting impedance, is related to the volume that is investigated between the electrodes. To overcome the effect of the acquisition geometry, a geometric coefficient kG (m) is determined. For field acquisition, the subsurface is approximated as an infinite half-space for which kG can be related analytically to the distance between the electrodes.16 For laboratory investigations, the geometry of the studied system cannot be simplified in this manner. Thus, the geometric coefficient kG is determined using numerical simulation accounting for the acquisition geometry and the shape of the electrodes.62 In this study, we used EIDORS (Electrical Impedance and Diffuse Optical tomography Reconstruction Software) to estimate kG.
The physical property determined from the complex impedance and the geometric coefficient is named the complex electrical conductivity σ* (S m−1) defined as
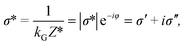 | (4) |
The acquisition of the electrical conductivity is performed using the PSIP instrument from Ontash & Ermac,26 designed for high-precision voltage acquisition over a frequency range from mHz to 10 kHz. Over this frequency range, the complex electrical conductivity depends on conduction and polarization mechanisms linked to the porous medium microstructure,18 the presence of interfaces (e.g., EDL and between different phases), and the mineral surface state.15,16
For carbonate rocks and in the absence of metallic particles (e.g., pyrite), the increase of σ′ can be related, e.g., to an increase in the electrolyte conductivity, the water content, the connected porosity, or the permeability of the rock matrix. Note that when studying clay-bearing rocks, the increase in σ′ may be interpreted differently since clays are highly conductive and low-permeable materials. Over the investigated frequency range, polarization mainly comes from the EDL polarization mechanism described in the introduction. At frequencies over 102 Hz,16 the coexistence of solid, liquid, and gas phases creates interfaces where charges accumulate between phases presenting different electrical properties. This type of interfacial polarization is called the Maxwell–Wagner polarization.64,65 The presence of local maxima of σ′′ at various frequencies comes from specific mechanisms related to, e.g., the grain size22,32 or surface roughness30 (both due to EDL polarization).
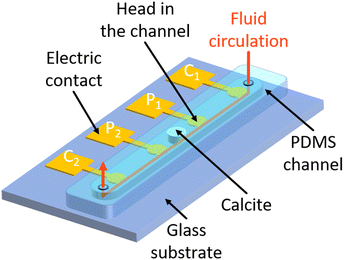
2.2 Design of micromodels equipped with electrodes
The microfluidic chip design is represented in Fig. 1, and its dimensions are given in Table 1. The microfluidic chip follows the geometry of a straight channel molded in polydimethylsiloxane (PDMS) and bonded on a glass substrate on which four electrodes are deposited. Each electrode consists of a round head and a square shape electrical contact. The round head is inside the channel, to be in contact with the electrolyte, and the electrical contact is outside. The round head is connected to the electrical contact by a thin track that runs under the wall of the channel.| Channel | Material | PDMS |
| Length (mm) | 40 | |
| Width (mm) | 1.5 | |
| Thickness (mm) | 0.15 | |
| Electrodes | Material | Cr–Au |
| Thickness (nm) | 400 | |
| Head's shape | Disk | |
| Head's size (mm) | 0.9 | |
| Trace's width (mm) | 0.4 | |
| Pad's shape | Square | |
| Pad's size (mm) | 5 × 5 | |
| Spacing (mm) | 10 | |
| Geometric coefficient (m) | 19 × 10−5 |
2.3 Microfabrication of micromodels including electrodes
For the realization of the electrodes, the glass substrate is first cleaned with a Decon Neutracon solution to avoid any organic contamination. We start by depositing two photoresists (1.5 μm Shipley 1813 on 2 μm LOR20B) on the substrate previously treated with hexamethyldisilazane (HMDS) for better adhesion. The photoresist thickness is chosen to get a cap profile for a better lift-off process after metalization. Then, we realize the exposure at 90 mJ cm−2 at 365 nm wavelength to weaken the exposed parts through the photomask. This exposure patterns the outline of the electrodes in the photoresists after a bath in the MF319 developer. For the metal deposition, we use the plasma magnetron sputtering technique to deposit successively a 40 nm chromium (Cr) layer and a 360 nm gold (Au) layer. The lift-off process is done with the SVC14 stripper. Cr is used to ensure better adhesion of Au onto the glass substrate. Au has the advantage of not being affected by corrosion. The literature about the test of different kinds of electrodes for SIP acquisition25,66 shows good results for Au electrodes compared to unpolarizable electrodes (e.g., Ag–AgCl, Cu–CuSO4). Note that the electrodes are deposited onto the glass surface. This means that they form a thicker layer than the channel walls. Nevertheless, the total thickness of the electrodes is small compared to the channel (0.4 ≪ 150 μm, see Table 1).To manufacture the channel, we start by depositing on a cleaned silicon wafer a 150 μm thickness of a negative high-viscosity photoresist (SU-8 2075). After the first soft-bake at 65 °C for 7 min and 95 °C for 45 min, we realize the exposure at 400 mJ cm−2 at 365 nm wavelength. The exposed parts consolidate by using a photomask revealing the shape of the channels. After the second bake at 65 °C for 5 min and 95 °C for 20 min, the development is done with SU-8 developer. A final hard bake at 180 °C is done to relax the strains into the photoresist. The casting of the PDMS is done by mixing Dow Corning Sylgard 184 (50 g) with its activator (5 g). Once dried, we remove the PDMS from the mold, cut it, and drill it to connect the tubing. The last step consists in the O2 plasma bonding treatment between the glass substrate and the PDMS channel.
2.4 Validation of the SIP acquisition
To examine the compatibility of the microfluidic chip with SIP acquisition, we performed measurements on the channel saturated with two sodium chloride (NaCl) solutions of different concentrations (10−3 and 10−1 mol L−1). The channel saturated with NaCl brine is a non-polarizable medium in the frequency range of the SIP measurements. Thus, one expects a flat spectrum at a value corresponding to the brine conductivity σw for the in-phase conductivity σ′ and a spectrum at zero over the frequency range for the quadrature conductivity σ′′. The results presented in the ESI† show that the microscale electrode array enables SIP acquisition with accurate measurements of the in-phase conductivity and low polarization effects. These results also reveal the accuracy of the geometric coefficient determination from EIDORS simulation, whose value is kG = 1.9 × 10−5 m.2.5 Experimental protocol for SIP monitoring of calcite dissolution: a key reactive transport process of the CZ
The dissolution of calcite is a common geochemical reaction of the carbonate CZ generating reactive transport. Working at atmospheric pressure, a two-phase flow is generated with the production of carbon dioxide (CO2) bubbles. Our setup is an analogous system that captures the dissolution process and the two-phase flow. It is presented in Fig. 2.The micromodel is mounted on the translation stage of the microscope and connected to the PSIP unit using the Wenner-α configuration described above. The electrical contacts on the chip are connected to the PSIP unit via wires bundled in a sheath and attached to a 3D-printed clamp. The clamp is equipped with a system of screws and nuts to connect the electrical wires, which are terminated with eyelets. A groove running through the clamp allows the wires to be routed. Banana female connectors are installed at the end of the wires to connect them to the PSIP unit. The Bayonet Neill–Concelman (BNC) sockets of the PSIP unit are fitted with adapters from the BNC male to single banana plugs. A piece of calcite of 150 μm thickness and 1 mm diameter is inserted in the middle of the microfluidic channel, between the two electrodes P1 and P2, and is sandwiched between the glass substrate and the top of the channel (Fig. 1 and 2). In this configuration, the flow is channeled around the cylinder, not over or under. Fig. 3 shows the calcite sample in the channel. The shape of the sample is more complex than a cylinder. The contour does not follow a circle but is driven by sharp cuts. The sample is conical because of the rounding of the tip of the burr that was used to drill the cylinder on a thin calcite sheet. The irregularities observed on the surface of the cylinder are oriented on the side of the PDMS. Because of its elastic properties, the latter keeps good contact with the surface of the mineral and prevents the acid from infiltrating. The other surface facing the glass is smooth thanks to polishing prior to carving the cylinder.
The channel is initially saturated with a solution of water balanced with calcite, named S0, which has a conductivity σS0 = 0.013 S m−1. Under atmospheric pressure and temperature conditions, a solution composed of 0.05%m chloride acid (HCl) is injected in the microfluidic channel with a constant flow rate of 1.25 mL h−1. We track the dissolution simultaneously with optical images at ×5 magnification captured every 30 s in transmission mode and SIP monitoring. SIP spectra are acquired every 7 min over a frequency range of 100 to 103 Hz, with 10 points per decade and a swipe going from the highest frequencies toward the lowest ones. Data acquired at 50 Hz and 100 Hz have been removed due to the noise from the electrical grid. The reference resistor (Fig. 2) used to compute the stimulus current is set to 1 MΩ to fit in the range of 20–100% of the resistance of the channel, as recommended. The amplitude of the stimulus voltage is set to ±1 V to ensure a high signal-to-noise ratio.25 The other used acquisition settings are the ones recommended by the manufacturer.
3 Results and discussion
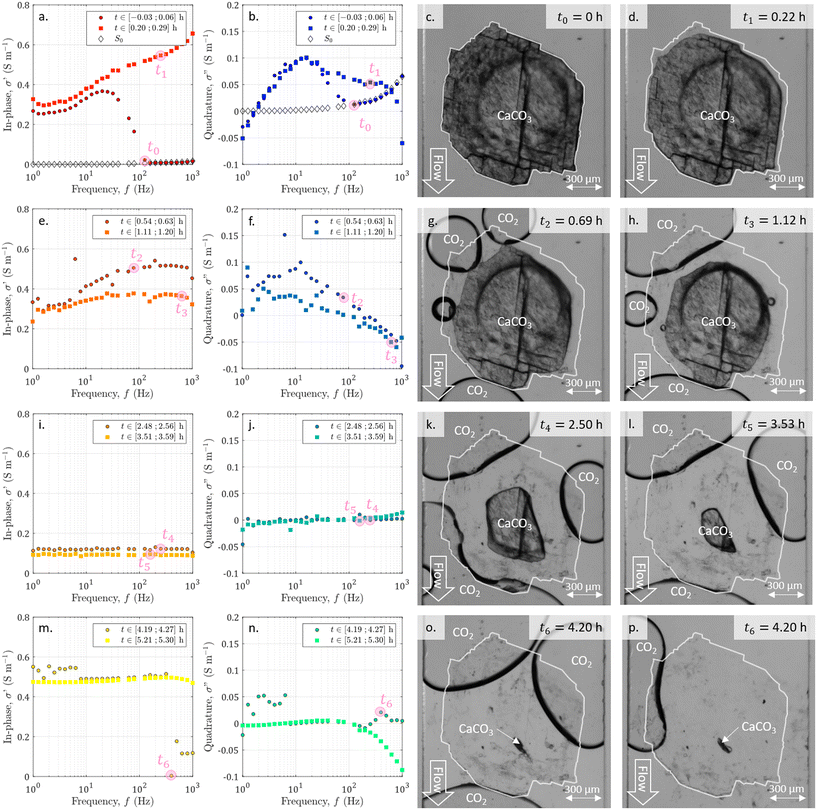
During the entire experiment, we recorded 600 images and 50 SIP spectra. A video of the dissolution and the entire SIP dataset are available in the ESI.† Selected data are represented in Fig. 4. From the whole sequence of images, we extract 8 of them at seven specific times of interest t0 = 0 h, t1 = 0.22 h, t2 = 0.69 h, t3 = 1.12 h, t4 = 2.50 h, t5 = 3.53 h, and t6 = 4.20 h. The colors of the spectra ranging from dark red to yellow for the in-phase conductivity and from dark blue to green for the quadrature conductivity give an indication of the acquisition times. In addition, we present the spectra of in-phase and quadrature conductivity obtained for the channel saturated with the initial solution S0 with empty diamonds with black edges.From the displayed spectra in Fig. 4, it is clear that the complex electrical conductivity response evolves through time and is frequency dependent, especially for the quadrature component. Fig. 5 represents the time variations of the in-phase component at the frequency f1 = 2.5 Hz and the time variations of the quadrature conductivity at three frequencies covering all the decades of the investigated frequency range (f1 = 2.5 Hz, f2 = 13 Hz, and f3 = 250 Hz). The time evolution of all the reported frequencies presents smooth variations. The low frequency f1 is chosen to present the in-phase component σ′ analogous to direct current (DC) conductivity.
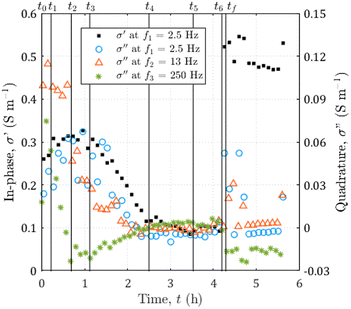 | ||
| Fig. 5 Time evolution of the complex electrical conductivity during the dissolution of calcite. The in-phase component at f1 = 2.5 Hz on the left axis and the quadrature component for three frequencies going from f1 = 2.5 to f3 = 250 Hz on the right axis. The vertical black lines correspond to the seven times of interest of the experiment reported in Fig. 4 and the additional time tf = 4.29 h, corresponding to the end of the dissolution. | ||
The seven times of interest in Fig. 4 and the additional time tf = 4.29 h corresponding to the end of the dissolution are displayed in Fig. 5.
3.1 Direct visualization of calcite dissolution
During the dissolution, the series of images (Fig. 4) shows the calcite sample size reduction and the surface becoming less and less rough. As already observed,52,67 the dissolved grain takes on an elongated shape in the direction of flow, with more dissolution on the side exposed to the acid influx (particularly visible in Fig. 4h). In addition, carbon dioxide (CO2) bubbles are generated by calcite dissolution. Their behavior is comparable to the observations made by Soulaine et al.53 First, there is the nucleation of small bubbles, which grow (Fig. 4g). Then, neighboring bubbles coalesce, forming large, evenly spaced bubbles that are fed by smaller ones (Fig. 4d–l). Once very close and hindering the circulation of the acid (Fig. 4o), the large bubbles suddenly detach (Fig. 4p). Overall the calcite sample of about 0.3 mm3 volume is fully dissolved in 4.2 h.3.2 Visualization of the acid arrival with SIP monitoring
Simultaneously with the initiation of dissolution and image acquisition, we launched the SIP acquisition. In Fig. 4a and b, we plot the first measured spectra of the temporal series. The comparison with the spectra obtained for the channel saturated with the initial solution S0 shows that for the highest frequencies, corresponding to the earliest times, these spectra overlap. For frequencies below 126 Hz the first measured spectra of the temporal series have a strongly changing behavior. This break in trend is due to the arrival of the acid between the electrodes. It is assumed to correspond to the beginning of the dissolution and is referred to as time zero. This time lag is also taken into account for the images in Fig. 4.3.3 Time evolution of the SIP signature during dissolution
From the temporal variations of the spectra from t0 to t4 in Fig. 5, we observe progressive time evolution for the first two-and-a-half hours, with the reduction of the in-phase component and the convergence towards zero for the quadrature conductivity at the three frequencies f1, f2, and f3. Then, for the following hour and forty minutes (from t4 to t6), the in-phase and quadrature conductivity values stagnate around 0.1 and 0 S m−1, respectively. Then, at time t6, there is an abrupt change in the amplitude of the in-phase conductivity. After the final time tf, the values are noisy (t ∈ [4.25; 4.73] h) but then stabilize around 0.5 S m−1 for the in-phase component, close to zero for the quadrature conductivity at f1, f2, and f3.About the frequency dependence of the in-phase conductivity, first, for the spectrum overlapping t1 (red squares in Fig. 4a), the different frequencies present various amplitudes with higher values towards higher frequencies. This trend is a sign of non-negligible surface conduction, which is reported for saturating electrolytes presenting low conductivity (lower or of the same order of magnitude as 10−1 S m−1).68 Then, comparing the spectra overlapping t1, t2, and t3 (Fig. 4a and b), the spectra tend to flatten around 0.3 and 0.4 S m−1, with the major decrease for frequencies above 7 Hz. For the spectra acquired for the subsequent times, there is no remarkable frequency dependence of the in-phase conductivity.
These results indicate that the optically observed acid dissolution steps are well captured by SIP monitoring.
3.4 Mineral–water interface polarization interpretation based on direct observation
The quadrature component of the complex electrical conductivity measures the reversible energy storage related to polarization mechanisms.69 The frequency dependence of the quadrature conductivity reflects a distribution of relaxation times that are related to a distribution of polarization length scales.30,31 For the frequencies f1, f2, and f3, there are initial non-zero quadrature conductivities that plunge for the frequency f3, moderately drop for the frequency f2, and slightly increase before slowly decreasing for the frequency f1. Over the investigated frequency range, non-zero quadrature conductivities are related to the polarization of the mineral–water interface coating the surface of the calcite crystal.32 Due to chemical disequilibrium, calcite possesses a non-zero surface charge which is compensated for by the accumulation of counterions at the surface of the crystal.70 The quadrature conductivity spectrum, represented with blue squares in Fig. 4b, overlaps with time t1 and corresponds to the first SIP acquisition during the dissolution of calcite without CO2 degassing. We observe two local maxima at f2 = 13 Hz and f3 = 250 Hz. The quadrature conductivity values measured at these frequencies are large (σ′′(f2) = 0.1 S m−1 and σ′′(f3) = 0.05 S m−1) and as presented in the ESI,† the electrodes are not the source of polarization at these frequencies. Yet the surface charge of calcite is known to be low at equilibrium. During dissolution with the strong acid HCl (pH = 2), the conditions are far from equilibrium and are responsible for the measured values. In addition, SIP measurements in the case of calcite precipitation have shown very different values from one experiment to another.33–35 The main parameters proposed to explain these variations are the concentrations of the reagents, the pH, and the hydrodynamic regime. Moreover, a millifluidic experiment38 reveals higher values of quadrature conductivity compared to other studies of reactive percolation in columns.36,37From the image sequence, dissolution occurs exclusively at the surface of the calcite crystal and not within the crystal, leading to, first, the disappearance of the surface roughness, then to crystal shrinking. In the literature about source mechanisms for EDL polarization, the roughness of the grains is evoked for a critical frequency fc around 102 Hz.30 From the comparison of the image sequence and the quadrature conductivity time evolution at frequency f3 (Fig. 5), it appears, however, that the surface roughness vanishes as fast as the quadrature conductivity as frequency f3 decreases towards zero. Thus, since the frequency f3 has a value close to fc, it is reasonable to relate the initial quadrature conductivity local maximum at frequency f3 to the roughness of the calcite surface.
For frequencies below 50 Hz, the initial local maximum at frequency f2 slowly decreases and shifts with time towards the lowest frequencies. This leads to an increase in the quadrature conductivity at the frequency f1 with time between t0 and t3 in Fig. 5. Compared with the image series, the trend of the quadrature conductivity at low frequencies appears linked to the decrease of the available reactive surface of the calcite crystal.
3.5 Impact of the bubbles on the SIP acquisition
Calcite dissolution is expected to increase the in-phase conductivity4 as observed between t0 and t2 in Fig. 5. The subsequent decrease followed by stagnation of the in-phase conductivity close to 0.1 S m−1 from t3 to t6 is simultaneous with the growth of CO2 bubbles, which progressively invade the channel and reduce the volume available for the electrolyte to conduct electric current (Fig. 4e, i, m, g, h, k, l, and o). Quadrature conductivities decrease to zero as bubbles grow. Regardless of the size of the bubbles, they do not appear to contribute to EDL polarization.At t6, the bubbles detach (Fig. 4o and p) and the in-phase conductivity jumps close to 0.5 S m−1 for the frequencies below 400 Hz, acquired for latter times than for the highest frequencies (Fig. 4m). The reached value around 0.5 S m−1 is higher than at the beginning of the dissolution because the calcite sample has been extremely reduced in size and the volume is more occupied by the electrolyte. This abrupt leap is not remarkable on the quadrature conductivities (Fig. 4n). We interpret this as evidence that bubbles add noise and that the initial quadrature signal is related to calcite dissolution. For frequencies below 7 Hz, corresponding to times comprised between 4.25 and 4.27, the spectra with black-bordered discs displayed in Fig. 4m and n get noisy. From the temporal variations of Fig. 5 this lasts at 4.73 h. This may result from bubbles displaced on electrodes downstream of the microscope observation window.
These results indicate that the growth and transport of optically tracked bubbles create two-phase flow conditions that are well captured by SIP monitoring.
4 Conclusions
This study is the first attempt of developing electrical characterization of the critical zone geochemical reactivity on a microfluidic chip, while geophysical methods are essential monitoring tools in the geosciences community. Miniaturization is a real technological challenge, and we have succeeded in developing a device that works well at this scale. The very unique experimental results obtained from the comparison of the optical image acquisition with the SIP survey of calcite dissolution bring a deeper understanding of the physical interpretation of the complex electrical conductivity of dissolved calcite. Major advances in understanding natural processes are expected from this small-scale approach using geophysical detection methods. Future work will be addressed to enhance the acquisition device for 2D SIP acquisition to introduce spatial discretization, which is of interest for the description of the CZ processes. More largely, this new technology will certainly help in the study of a large panel of research fields, since SIP is a promising investigation technique giving insights into structure properties and surface states.Author contributions
Conceptualization, F. R., A. S., C. S., and S. R.; data curation, F. R.; formal analysis, F. R., funding acquisition, C. S., and S. R.; investigation, F. R.; methodology, F. R., A. S., S. R.; project administration, C. S. and S. R.; resources, A. S. and S. R.; software, F. R. and S. R.; supervision, A. S., C. S., and S. R.; validation, F. R.; visualization, F. R.; writing – original draft, F. R.; writing – review & editing, F. R., A. S., C. S., and S. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the French national research agency (ANR) on the LabEx VOLTAIRE (grant number ANR-10-LABX-100-01) and the research project IMAGE (grant agreement ANR-21-CE04-0013-02), the research project CNRS MITI “défi Changement Climatique” CaraMBar, and the European Union (ERC, TRACE-it, grant agreement n°101039854). The authors thank Damien Jougnot for loaning the PSIP device and acknowledge the technical support of Ontash & Ermac company. The authors gratefully acknowledge the guidance of Philippe Leroy in discussing the SIP measurements. The authors would like to thank the Renatech network and the CERTeM 2020 Program for supporting the cleanroom facilities. The authors thank the students of Polytech Orleans who helped with microfluidic chip manufacturing and testing: Pierre-Philippe Horville, Nadine Mahfouf, Xiaosen Chen, Tahina Ralala, and Aubine Tsemo. The authors acknowledge the technical support of Hugues Raimbourg, Julien Lemaire, and Remi Champallier.References
- J. R. Giardino and C. Houser, Developments in Earth Surface Processes, Elsevier, 2015, vol. 19, pp. 1–13 Search PubMed.
- F. Osselin, C. Soulaine, C. Fauguerolles, E. C. Gaucher, B. Scaillet and M. Pichavant, Nat. Geosci., 2022, 15, 765–769 CrossRef CAS.
- Y. Fan, G. Grant and S. P. Anderson, Hydrol. Processes, 2019, 33, 3146–3151 CrossRef.
- F. Rembert, M. Leger, D. Jougnot and L. Luquot, Hydrol. Earth Syst. Sci., 2023, 27, 417–430 CrossRef CAS.
- D. Ford and P. D. Williams, Karst hydrogeology and geomorphology, John Wiley & Sons, 2013 Search PubMed.
- D. Drew, P. E. Lamoreaux, C. Coxon, J. W. Wess, L. D. Slattery, A. P. Bosch and H. Hötzl, Karst hydrogeology and human activities: impacts, consequences and implications, ed. D. Drew and H. Hötzl, 5th edn, 2017 Search PubMed.
- S. Saneiyan, D. Ntarlagiannis, J. Ohan, J. Lee, F. Colwell and S. Burns, Ecol. Eng., 2019, 127, 36–47 CrossRef.
- S. L. Brantley, M. B. Goldhaber and K. V. Ragnarsdottir, Elements, 2007, 3, 307–314 CrossRef CAS.
- J. Chorover, R. Kretzschmar, F. Garcia-Pichel and D. L. Sparks, Elements, 2007, 3, 321–326 CrossRef CAS.
- H. Vereecken, A. Binley, G. Cassiani, A. Revil and K. Titov, Applied Hydrogeophysics, Dordrecht, 2006, pp. 1–8 Search PubMed.
- N. Goldscheider, J. Meiman, M. Pronk and C. Smart, Int. J. Speleol., 2008, 37, 27–40 CrossRef.
- W. Daily, A. Ramirez, D. LaBrecque and J. Nitao, Water Resour. Res., 1992, 28, 1429–1442 CrossRef.
- S. S. Hubbard and N. Linde, Treatise on Water Science, Elsevier, Oxford, 2011, pp. 401–434 Search PubMed.
- A. Binley, A. S. Hubbard, J. A. Huisman, A. Revil, D. A. Robinson, K. Singha and L. D. Slater, Water Resour. Res., 2015, 51, 3837–3866 CrossRef PubMed.
- A. Kemna, A. Binley, G. Cassiani, E. Niederleithinger, A. Revil, L. Slater, K. Williams, A. F. Orozco, F. Haegel, A. Hordt, S. Kruschwitz, V. Leroux, K. Titov and E. Zimmermann, Near Surf. Geophys., 2012, 10, 453–468 CrossRef.
- A. Revil, M. Karaoulis, T. Johnson and A. Kemna, Hydrogeol. J., 2012, 20, 617–658 CrossRef.
- Q. Niu and C. Zhang, Water Resour. Res., 2019, 55, 3107–3121 CrossRef.
- F. Rembert, D. Jougnot and L. Guarracino, Adv. Water Resour., 2020, 145, 103742 CrossRef.
- S. B. Moshe, P. Kessouri, D. Erlich and A. Furman, Hydrol. Earth Syst. Sci., 2021, 25, 3041–3052 CrossRef CAS.
- F. Rembert, D. Jougnot, L. Luquot and R. Guerin, Water, 2022, 14, 1632 CrossRef CAS.
- A. Binley and A. Kemna, in DC Resistivity and Induced Polarization Methods, ed. Y. Rubin and S. S. Hubbard, Springer Netherlands, Dordrecht, 2005, pp. 129–156 Search PubMed.
- A. Revil, M. Schmutz, F. Abdulsamad, A. Balde, C. Beck, A. Ghorbani and S. Hubbard, Geoderma, 2021, 403, 115380 CrossRef CAS.
- L. S. Collett, in History of induced polarization method, ed. J. B. Fink, B. K. Sternberg, W. G. Widuwilt and S. H. Ward, 1990, ch. 1, pp. 5–22 Search PubMed.
- H. Seigel, M. Nabighian, D. S. Parasnis and K. Vozoff, The Leading Edge, 2007, vol. 26, pp. 312–321 Search PubMed.
- E. Zimmermann, A. Kemna, J. Berwix, W. Glaas, H. M. Munch and J. A. Huisman, Meas. Sci. Technol., 2008, 19, 105603 CrossRef.
- Ontash and Ermac, Portable Field/Lab Spectral Induced Polarization (SIP) Unit (PSIP), https://www.ontash.com/products.htm#PSIP, 2015.
- RadicResearch, Instruments, http://radic-research.de/Instruments.htm, 2021.
- F. Heberling, T. P. Trainor, J. Lutzenkirchen, P. Eng, M. A. Denecke and D. Bosbach, J. Colloid Interface Sci., 2011, 354, 843–857 CrossRef CAS PubMed.
- P. Leroy, D. Jougnot, A. Revil, A. Lassin and M. Azaroual, J. Colloid Interface Sci., 2012, 388, 243–256 CrossRef CAS PubMed.
- P. Leroy, A. Revil, A. Kemna, P. Cosenza and A. Ghorbani, J. Colloid Interface Sci., 2008, 321, 103–117 CrossRef CAS PubMed.
- A. Revil, K. Koch and K. Holliger, Water Resour. Res., 2012, 48(5), W05602 CrossRef.
- P. Leroy, S. Li, A. Revil and Y. Wu, Geophys. J. Int., 2017, 209, 123–140 CAS.
- Y. Wu, S. Hubbard, K. H. Williams and J. Ajo-Franklin, J. Geophys. Res.: Space Phys., 2010, 115, G00G04 Search PubMed.
- C. Zhang, L. Slater, G. Redden, Y. Fujita, T. Johnson and D. Fox, Environ. Sci. Technol., 2012, 46, 4357–4364 CrossRef CAS PubMed.
- S. Izumoto, J. A. Huisman, Y. Wu and H. Vereecken, Geophys. J. Int., 2020, 220, 1187–1196 CrossRef CAS.
- B. Bate, J. Cao, C. Zhang and N. Hao, Acta Geotech., 2021, 16, 841–857 CrossRef.
- S. Saneiyan, D. Ntarlagiannis and F. Colwell, Geophys. J. Int., 2021, 224, 1811–1824 CrossRef CAS.
- S. Izumoto, J. A. Huisman, E. Zimmermann, E. Heyman, J. Heyman, F. Gomez, H. Tabuteau, R. Laniel, H. Vereecken, Y. Meheust and T. Le Borgne, Environ. Sci. Technol., 2022, 56, 4998–5008 CrossRef CAS PubMed.
- M. Halisch, S. Hupfer, A. Weller, R. Dlugosch and H.-P. Plumhoff, Proceedings of the international symposium of the society of core analysts, 2018, pp. 27–31 Search PubMed.
- F. Golfier, C. Zarcone, B. Bazin, R. Lenormand, D. Lasseux and M. Quintard, J. Fluid Mech., 2002, 457, 213–254 CrossRef CAS.
- C. Noiriel, P. Gouze and D. Bernard, Geophys. Res. Lett., 2004, 31, L24603 CrossRef.
- C. Noiriel, D. Bernard, P. Gouze and X. Thibault, Oil Gas Sci. Technol., 2005, 60, 177–192 CrossRef.
- T. Rotting, L. Luquot, J. Carrera and D. J. Casalinuovo, Chem. Geol., 2015, 403, 86–98 CrossRef CAS.
- M. Leger, D. Roubinet, M. Jamet and L. Luquot, Chem. Geol., 2022, 594, 120763 CrossRef CAS.
- M. Leger, L. Luquot and D. Roubinet, Chem. Geol., 2022, 121008 CrossRef CAS.
- S. Roman, C. Soulaine, M. A. Al Saud, A. Kovscek and H. Tchelepi, Adv. Water Resour., 2016, 95, 199–211 CrossRef.
- W. Yun, C. Ross, S. Roman and A. Kovscek, Lab Chip, 2017, 17, 1462–1474 RSC.
- C. Soulaine and S. Roman, Pour la Science, 2022, vol. 535, pp. 50–58 Search PubMed.
- F. Osselin, P. Kondratiuk, A. Budek, O. Cybulski, P. Garstecki and P. Szymczak, Geophys. Res. Lett., 2016, 43, 6907–6915 CrossRef.
- J. Poonoosamy, C. Soulaine, A. Burmeister, G. Deissmann, D. Bosbach and S. Roman, Lab Chip, 2020, 20, 2562–2571 RSC.
- W. Song, T. W. de Haas, H. Fadaei and D. Sinton, Lab Chip, 2014, 14, 4382–4390 RSC.
- C. Soulaine, S. Roman, A. Kovscek and H. A. Tchelepi, J. Fluid Mech., 2017, 827, 457–483 CrossRef CAS.
- C. Soulaine, S. Roman, A. Kovscek and H. A. Tchelepi, J. Fluid Mech., 2018, 855, 616–645 CrossRef CAS.
- S. Roman, C. Soulaine and A. R. Kovscek, J. Colloid Interface Sci., 2020, 558, 269–279 CrossRef PubMed.
- M. Mansouri-Boroujeni, C. Soulaine, M. Azaroual and S. Roman, Adv. Water Resour., 2023, 171, 104353 CrossRef.
- R. Gomez, R. Bashir, A. Sarikaya, M. Ladisch, J. Sturgis, J. Robinson, T. Geng, A. Bhunia, H. Apple and S. Wereley, Biomed. Microdevices, 2001, 3, 201–209 CrossRef CAS.
- X. Cheng, Y.-S. Liu, D. Irimia, U. Demirci, L. Yang, L. Zamir, W. R. Rodriguez, M. Toner and R. Bashir, Lab Chip, 2007, 7, 746–755 RSC.
- H. Mariam, P. Poulichet, H. Takhedmit, F. Deshours, E. Richalot and O. Francais, IEEE Sens. J., 2022, 22, 3553–3564 CAS.
- Q. Chen, D. Wang, G. Cai, Y. Xiong, Y. Li, M. Wang, H. Huo and J. Lin, Biosens. Bioelectron., 2016, 86, 770–776 CrossRef CAS PubMed.
- N. Wagner, M. Schwing and A. Scheuermann, IEEE Trans. Geosci. Remote Sens., 2014, 52, 880–893 Search PubMed.
- J. G. D. Oliveira, E. N. M. G. Pinto, V. P. S. Neto and A. G. D'Assuncao, Sensors, 2020, 20, 255 CrossRef PubMed.
- D. Jougnot, A. Ghorbani, A. Revil, P. Leroy and P. Cosenza, Geophys. J. Int., 2010, 180, 210–224 CrossRef.
- H. J. Vinegar and M. H. Waxman, Geophysics, 1984, 49, 1267–1287 CrossRef.
- Y. Chen and D. Or, Water Resour. Res., 2006, 42, W06424 Search PubMed.
- P. Leroy, A. Hordt, S. Gaboreau, E. Zimmermann, F. Claret, M. Bucker, H. Stebner and J. A. Huisman, Cem. Concr. Compos., 2019, 104, 103397 CrossRef CAS.
- F. Abdulsamad, N. Florsch, M. Schmutz and C. Camerlynck, J. Appl. Geophy., 2016, 135, 449–455 CrossRef.
- A. J. C. Ladd, L. Yu and P. Szymczak, J. Fluid Mech., 2020, 903, A46 CrossRef CAS.
- A. Mendieta, D. Jougnot, P. Leroy and A. Maineult, J. Geophys. Res.: Solid Earth, 2021, 126, e2020JB021125 Search PubMed.
- A. Revil and N. Florsch, Geophys. J. Int., 2010, 181, 1480–1498 Search PubMed.
- S. Li, P. Leroy, F. Heberling, N. Devau, D. Jougnot and C. Chiaberge, J. Colloid Interface Sci., 2016, 468, 262–275 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00377a |
| This journal is © The Royal Society of Chemistry 2023 |