Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the charging of supercapacitors by electrochemical quartz crystal microbalance
Liang
Niu
 a,
Long
Yang
a,
Jingjing
Yang
a,
Ming
Chen
a,
Long
Yang
a,
Jingjing
Yang
a,
Ming
Chen
 a,
Liang
Zeng
a,
Pan
Duan
a,
Taizheng
Wu
a,
Emmanuel
Pameté
a,
Liang
Zeng
a,
Pan
Duan
a,
Taizheng
Wu
a,
Emmanuel
Pameté
 b,
Volker
Presser
b,
Volker
Presser
 bcd and
Guang
Feng
bcd and
Guang
Feng
 *a
*a
aState Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology (HUST), 430074 Wuhan, China. E-mail: gfeng@hust.edu.cn
bINM – Leibniz Institute for New Materials, Campus D2 2, 66123, Saarbrücken, Germany
cSaarland University, Campus D2 2, 66123, Saarbrücken, Germany
dSaarene – Saarland Center for Energy Materials and Sustainability, Campus C4 2, 66123, Saarbrücken, Germany
First published on 19th December 2022
Abstract
Supercapacitors are highly valued energy storage devices with high power density, fast charging ability, and exceptional cycling stability. A profound understanding of their charging mechanisms is crucial for continuous performance enhancement. Electrochemical quartz crystal microbalance (EQCM), a detection means that provides in situ mass change information during charging–discharging processes at the nanogram level, has received greatly significant attention during the past decade due to its high sensitivity, non-destructiveness and low cost. Since being used to track ionic fluxes in porous carbons in 2009, EQCM has played a pivotal role in understanding the charging mechanisms of supercapacitors. Herein, we review the critical progress of EQCM hitherto, including theory fundamentals and applications in supercapacitors. Finally, we discuss the fundamental effects of ion desolvation and transport on the performance of supercapacitors. The advantages and defects of applying EQCM in supercapacitors are thoroughly examined, and future directions are proposed.
Keywords: EQCM; Supercapacitors; Charging mechanisms; Quantitative characterization.
1 Introduction
Electrochemical energy storage (EES) systems, serving as a key technology in modern society, are widely used in portable electronic devices, renewable energy sources, and electric vehicles.1–3 Supercapacitors have gathered great attention among various EES technologies because of their high power density, fast charging ability and excellent cycling stability.4 They are utilized in grid peaking, energy recovery, backup power, and vehicle starting.5,6 Through remarkable progress, commercial supercapacitors could provide a high specific power of 30 kW kg−1.7 However, their energy density is lower than lead-acid and lithium-ion batteries, impeding their further application.7,8 Numerous studies focus on the way to get high power density and energy density simultaneously. It is widely accepted that supercapacitors' power and energy density are strongly impacted by the charging process, including ion desolvation and ion transport.9–11 Hence, a deep comprehension of these phenomena can help redesign supercapacitors with improved performance.Owing to the development of evaluation theory, various inspection methods, including electrochemical quartz crystal microbalance (EQCM), nuclear magnetic resonance (NMR) spectroscopy, infrared spectroscopy, scattering methods and theoretical simulations, allow a detailed examination of ion adsorption, pore-selection effect, charging rate and chemical changes under polarization, thus significantly enhancing our understanding of the charging mechanisms in supercapacitors.11–14 Among them, the EQCM method, characterized by non-destructive, economical, low demand, and high sensitivity, provides in situ mass change and viscosity response information during the charging–discharging process.15–17 As shown in Fig. 1, since investigating ion flux in porous carbon in 2009, EQCM has been considered a crucial tool for studying the charging mechanisms in supercapacitors.17–20 Moreover, combining EQCM and other in situ characterization techniques and simulation methods has achieved quantitative ion transport detection, providing a molecular-level picture of supercapacitors.21,22
Several reviews have focused on the theory and typical applications of EQCM in supercapacitors.13,20,23,24 Levi et al.20,23 introduced the in situ gravimetric and deformations monitoring of electrodes during their charging. Shpigel et al.25 reviewed the application of EQCM in capacitive deionization. Recently, Ji et al.26 summarized the application of EQCM in batteries for mechanistic studies. These reviews provide insightful information on the recent advance in the application of EQCM in capacitive and battery technologies. However, it remains essential to distill and analyze these studies to establish a comprehensive understanding of ion transport and desolvation. In addition, the combination of EQCM with other experimental or computation methods has not yet been discussed systematically. Herein, we provide an overview of the theory and development progress of EQCM, especially the preparation techniques for coating electrode film on the quartz crystal surface.23 Moreover, we summarize the application of EQCM in supercapacitors concerning ion transport, ion desolvation, and quantitative characterization. Finally, the future research direction of EQCM is explored to inspire new ideas for developing EQCM in supercapacitors.
2 Fundamentals of the EQCM
2.1 Theory and history of EQCM
The EQCM system is shown in Fig. 2, comprising a test module, a quartz crystal microbalance (QCM), a potentiostat, and a computer. The theoretical basis of EQCM can be traced 140 years back. In 1880, Jacques and Pierre Curie discovered that some crystals appear to have a voltage proportional to the applied pressure.27,28 When an alternating current voltage is applied to these crystals, they undergo a period of mechanical distortion, called vibrate.27,28 In 1959, Sauerbrey29 observed a linear relationship between the change of vibration frequency and mass variation of the load on the quartz crystal surface, which was proposed as the Sauerbrey formula:29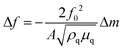 | (1) |
In addition to the mass response, viscoelastic changes of coatings on the quartz crystal have also been studied. Then, the EQCM technology route has developed in two directions. On the one hand, Rodahl et al.33 proposed in 1995 the theory of EQCM-D to simultaneous evaluation the change of mass and the viscous properties, where the dissipation factor D was defined as:
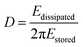 | (2) |
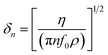 | (3) |
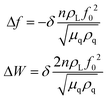 | (4) |
With these breakthroughs, EQCM is now widely used in electrochemical energy storage, biology, crystallization and electroplating, sensors, and other fields.28,37–39 The representative application of EQCM in supercapacitors is listed in Fig. 3. In 2009, Levi et al.18 used the EQCM to detect ion flux within porous carbon materials, introducing this advanced in situ mean in the analysis of the charging mechanism of supercapacitors. Further, EQCM was utilized to investigate the ion transport and desolvation of supercapacitors by comparing the theoretical mass change with measured experimental mass variation.19,20,40 The application of EQCM in supercapacitors has gained rapid development in the past few years. In 2020, EQCM was used to research the various behavior in two-dimensional graphene channels with different spacings.22 In 2021, EQCM helped understand the role of anionic species during the energy stored process in Mxenes.41 In 2022, Zhang et al.42 demonstrated at a molecular level that N-doping strongly influences the charging mechanism in porous carbon with the aid of EQCM.42 These applications demonstrate the key role of EQCM in the study of the charging mechanism of supercapacitors.
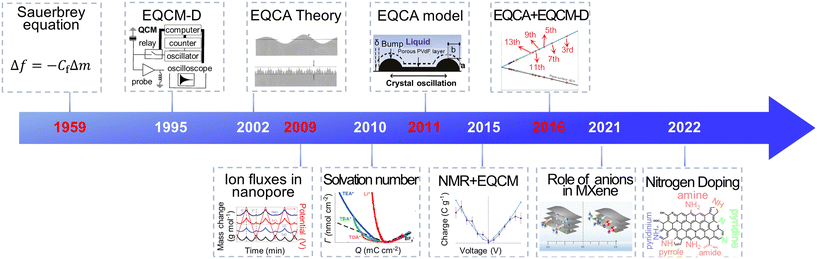 | ||
| Fig. 3 The history of EQCM application in supercapacitors (Copyright 1995 AIP Publishing, Copyright 2002 American Chemical Society, Copyright 2009 Springer Nature, Copyright 2010 American Chemical Society, Copyright 2011 American Chemical Society, Copyright 2015 Springer Nature, Copyright 2016 Springer Nature, Copyright 2021 American Chemical Society, Copyright 2022 American Chemical Society).18,19,21,29,33–36,41–43 | ||
2.2 Film coating method
The application of EQCM in supercapacitors is based on the Sauerbrey formula.18,29 This formula is derived by assuming the film and quartz crystal as a unit and no slip occurs during the measurement. Therefore, the Sauerbrey formula is only suitable for rigid films, suggesting that the prepared films must remain rigid without changes in volume or porosity in solution and polarization conditions.23 In practical testing, a low-frequency change and a small dissipation/resistance value is required.44,45 Due to these strict demands, a high-quality film is essential for EQCM measurement, which significantly relies on the film preparation method.The film preparation commonly includes spray-assisted coating, spin coating, pyrolysis, direct pyrolysis, electrochemical deposition, physical/chemical deposition and vacuum filtration transfer (VFT).44,46 The spray-assisted coating is the most used method owing to its easy operation, low price, and reasonable uniformity, but it still suffers from problems of poor reproducibility and discontinuity.46 The spin coating method can be applied continuously; however, the mass loading is low. The direct pyrolysis method is suitable for some materials (such as LiMn2O4).36 Nevertheless, the temperature is limited to 400 °C and the experiment parameter needs to be optimized. The electrochemical deposition method can be used for in situ mass monitoring but is commonly applicable for metallic substances. Vapor deposition has the advantage of high uniformity and precise thickness control but usually requires high-temperature annealing.46 In 2019, the VFT method proposed by Zhang et al.,44 significantly improved the uniformity of porous carbon, manganese dioxide nanoparticles, carbon nanotubes, MXenes, manganese dioxide nanorods and manganese oxide nanosheet films, which is advantageous for more reliable charging mechanism exploration of various electrode materials by EQCM. In the future, this approach may play an important role in the application of EQCM.
3 Applications of EQCM in supercapacitors
EQCM, owing to the ability to detect ionic behaviors by monitoring the mass changes during charging–discharging progress, has become a key tool for investigating the charging mechanisms of supercapacitors.17 EQCM results show that the pore size, topological structures, surface functional groups of the electrode, and the ionic size and charge number of the electrolytes, have a crucial effect on charging mechanisms.19,40,47 In addition, the combination of EQCM with other in situ characterization techniques has provided a quantitative molecular-level picture of the charge storage process in supercapacitors, significantly elevating our knowledge of the supercapacitor charging mechanisms.213.1 Ion transport in supercapacitors
The crucial role of understanding the charging mechanisms for improving the performance of supercapacitors has been widely accepted.11,17 Ion transport plays a vital role in the charging mechanisms. In 2009, Levi et al.18 first indicated the feasibility of EQCM to probe ion flux in nanopores, finding that porous carbon represents a more noticeable frequency change during charge–discharge progress than non-porous carbon black (Fig. 4a). Based on this landmark work, Levi et al.47 proposed to detect the charging mechanisms by comparing the experimental slope with the theoretical slope calculated from the Faraday law (assuming that only bare counter-ion adsorption occurs)| ke/kt = ΔΓ/Q | (5) |
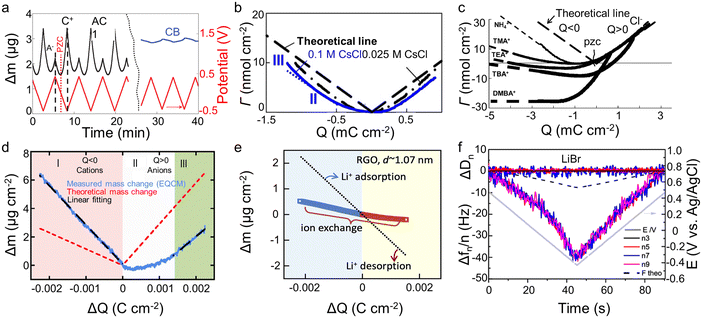 | ||
| Fig. 4 (a) Potential–time dependencies (red line) and the related mass changes (Δm) of activated carbon (black line) and carbon black (blue line) electrodes. The dashed straight lines mark the mass change peaks of the cation and the anion. The position of the point of zero charges (PZC) is shown by the dotted red line (Copyright 2009 Springer Nature);18 (b) related molar amounts of ions (Γ) during charge–discharge vs. electrode charge (Q) (Copyright 2010 Elsevier B.V.);40 (c) the amounts of adsorbed ions (Γ) as a function of the electrode charge density (Copyright 2011 Wiley-VCH);47 (d) electrode mass change (Δm) versus charge (ΔQ) during the polarization of CDC-1 nm in 2 M EMIM-TFSI + acetonitrile (ACN) (Copyright 2014 American Chemical Society);50 (e) the simultaneous mass change (Δm) of reduced graphene oxide (RGO) film during the cyclic voltammetry (CV) cycle. The blue and yellow backgrounds refer to the electrodes under negative and positive polarizations, respectively. The dotted line represents the theoretical mass change of pure solvated Li+ adsorption and desorption (Copyright 2020 Elsevier B.V.);22 (f) frequency (Δf) and dissipation changes (ΔD) as a function of time for third through ninth overtone orders. The theoretical frequency changes are denoted as black dashed lines (Copyright 2021 American Chemical Society).41 | ||
| Electrode materials | Electrolyte | Low charge density | High charge density (negative) | High charge density (positive) | Solvation number | Ref. | |
|---|---|---|---|---|---|---|---|
| Cation | Anion | ||||||
| YP-17 | 0.1 M LiCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 2.2 | 0.6 | 60 |
| 0.1 M NaCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 1.3 | 0.6 | 60 | |
| 0.1 M KCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0.5 | 0.6 | 60 | |
| 0.1 M CsCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 5.8 | 0.6 | 60 | |
| 0.1 M MgCl2 | Counter-ion adsorption | Counter-ion adsorption | Counter-ion adsorption | 3.7 | 0.6 | 60 | |
| 0.1 M CaCl2 | Counter-ion adsorption | Counter-ion adsorption | Counter-ion adsorption | 2.8 | 0.6 | 60 | |
| 0.1 M BaCl2 | Counter-ion adsorption | Counter-ion adsorption | Counter-ion adsorption | 0.5 | 1.4 | 60 | |
| 0.025 M KF | Counter-ion adsorption | Counter-ion adsorption | 0.5 | 0.6 | 60 | ||
| 0.025 M KCl | Counter-ion adsorption | Counter-ion adsorption | 0.5 | 0.05 | 60 | ||
| 0.025 M KBr | Counter-ion adsorption | Counter-ion adsorption/ion exchange | 0.5 | 0 | 60 | ||
| 0.025 M KI | 60 | ||||||
| 0.025 M CsCl | Ion exchange | Counter-ion adsorption | 40 | ||||
| 0.1 M CsCl | Ion exchange | Counter-ion adsorption | 40 | ||||
| 0.05 M NH4Cl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 47 | |||
| 0.025 M NH4Cl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 47 | |||
| 0.025 M TMACl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 47 | |||
| 0.025 M TEACl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 47 | |||
| 0.025 M TBACl | Ion exchange | Counter-ion adsorption | 47 | ||||
| 0.025 M DMBACl | Ion exchange | Ion exchange | 47 | ||||
| 0.2 M CsCl + 0.005 M HCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 20 | |||
| BP-880 | 0.025 M CsCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 20 | ||
| 0.1 M CsCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 20 | |||
| 0.025 M LiCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 2 | 0.1 | 20 | |
| 0.025 M NaCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0.8 | 0.1 | 20 | |
| 0.025 M KCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0.1 | 0.1 | 20 | |
| 0.025 M CsCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0 | 0.1 | 20 | |
| 0.025 M KF | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0.1 | 1.2 | 20 | |
| 0.025 M KCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 0.1 | 0.1 | 20 | |
| 0.025 M KBr | Ion exchange | Counter-ion adsorption | Counter-ion adsorption/ion exchange | 0.1 | 0 | 20 | |
| 0.025 M KI | Ion exchange | Counter-ion adsorption | Counter-ion adsorption/ion exchange | 0.1 | 0 | 20 | |
| BP-2000 | 0.025 M LiCl | Ion exchange | Ion exchange | Ion exchange | 2.3 | 0.3 | 20 |
| 0.025 M NaCl | Counter-ion adsorption | Ion exchange | Ion exchange | 1.8 | 0.3 | 20 | |
| 0.025 M KCl | Counter-ion adsorption | Ion exchange | Ion exchange | 0.7 | 0.3 | 20 | |
| 0.025 M CsCl | Counter-ion adsorption | Ion exchange | Ion exchange | 0.3 | 0.3 | 20 | |
| 0.025 M KF | Counter-ion adsorption | Ion exchange | Ion exchange | 0.7 | 1.5 | 20 | |
| 0.025 M KCl | Counter-ion adsorption | Ion exchange | Ion exchange | 0.7 | 0.3 | 20 | |
| 0.025 M KBr | Counter-ion adsorption | Ion exchange | Ion exchange | 0.7 | 0 | 20 | |
| 0.025 M KI | Counter-ion adsorption | Ion exchange | Ion exchange | 0.7 | 0 | 20 | |
| 0.05 M CsCl | Counter-ion adsorption | Counter-ion adsorption | 20 | ||||
| 0.1 M CsCl | Ion exchange | Counter-ion adsorption | 20 | ||||
| TiC-CDC-800 | 2 M EMIMTFSI + ACN | Counter-ion adsorption | Counter-ion adsorption | 57 | |||
| TiC-CDC-1100 | 2 M EMIMTFSI + ACN | Ion exchange | 2.6 | 0.6 | 57 | ||
| CDC-1 nm | EMIMTFSI | Ion exchange | Counter-ion adsorption | Ion exchange | 50 | ||
| CDC-1 nm | 2 M EMIMTFSI + ACN | Counter-ion adsorption | Ion exchange | 1.6 | 50 | ||
| CDC-0.65 nm | 2 M EMIMTFSI + ACN | Counter-ion adsorption | 3.7 | 50 | |||
| TiC-CDC | 0.025 M KCl | Ion exchange | Ion exchange | Ion exchange | 20 | ||
| TiC-CDC | 0.2 M CsCl + 0.005 M HCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 20 | ||
| Activated carbon | 0.25 M BMIMNTf2 + PC | Ion exchange | Counter-ion adsorption | Ion exchange | 62 | ||
| Activated carbon | 0.025 M TEABF4 + PC | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 19 | ||
| 0.1 M TEABF4 + PC | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 19 | |||
| Activated carbon | 0.5 M CsCl | Ion exchange | Counter-ion adsorption | Counter-ion adsorption | 18 | ||
| Na0.55Mn2O4·1.5H2O | Na2SO4 | Ion exchange | Ion exchange | 49 | |||
| RGO film | 1 M Li2SO4 | Ion exchange | Ion exchange | Ion exchange | 22 | ||
| RGO film | 0.5 M K2SO4 | Ion exchange | Ion exchange | Ion exchange | 22 | ||
| RGO film | 1 M KCl | Ion exchange | Ion exchange | Ion exchange | 22 | ||
| RGO film | 1 M LiCl | Ion exchange | Ion exchange | Ion exchange | 22 | ||
| RGO film | 1 M CaCl2 | Ion exchange | Ion exchange | Ion exchange | 22 | ||
Besides electric double-layer capacitors, EQCM is also essential for investigating pseudocapacitors. Combining EQCM with in situ Raman spectroscopy, Zhang et al.49 discovered that 2D cation-intercalated manganese oxide Na0.55Mn2O4·1.5H2O (NMO) mainly displayed surface-controlled pseudocapacitance at low charge densities and intercalation pseudocapacitance under high charge density. Similar to these efforts, the key role of charge density in the charging mechanisms was broadly identified.11,43,50
The concentration and ion size of the electrolyte significantly affect the ion transport behavior. As shown in Table 1, in microporous activated carbon (Kuraray, type YP-17), while the concentration of the CsCl aqueous solution increases from 0.025 M to 0.1 M, the increasing ion number enhances co-ion and counter-ion exchange effects, thus leading to an ion exchange over a wider voltage range (Fig. 4b).40 Similarly, the effect of electrolyte concentration on the charging mechanism has been concluded in the same electrode with organic electrolyte.19 In addition to the electrolyte concentration, ion sizes are also thought to affect the performance of supercapacitors. Based on conventional electrochemical tests, it has been widely agreed that the capacitance of supercapacitors decreases significantly when the ion size is larger than the pore size, exhibiting an apparent ion-sieving effect.51,52 However, these methods failed to obtain the detail of the charging mechanism of supercapacitors. The advent of EQCM makes it possible to understand ion sieving at a molecular scale. Compared to NH4+ ions, the ion-exchange region of symmetrical quaternary tetraalkyl ammonium cations [tetramethylammonium (TMA+), tetraethylammonium (TEA+), tetrabutylammonium (TBA+)], or the unsymmetrical surfactant cation (tetradecyl)dimethylbenzylammonium (DMBA+) with a larger size expands to higher charge density in microporous carbon YP-17 (Fig. 4c).47 This effect is ascribed to the larger ion size decreasing desolvation energy, favoring ion exchange.47
Ionic liquids have been widely used as supercapacitor electrolytes due to their wide electrochemical window, excellent thermal stability, non-volatility, and non-flammability.53 In ionic liquids, the unique property of strong interaction between anions and cations may result in different charging mechanisms. Tsai et al.50 found that in pure 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide (EMIM-TFSI) electrolyte, the charge stored in the pores of CDC-1 nm is dominated by counterion (EMIM+) adsorption at a negative voltage, similar to the permeation selectivity (charging by permselective cation) introduced by Levi et al.19,20 The charge storage depended on the electrode charge density under a positive voltage. Specifically, ion exchange dominates at low charge densities, implying a failure of permeation selectivity; while recovering as the charge density increase further.50 The above phenomenon indicates that the ionic migration of EMIM+ is easier than TFSI− anion. Moreover, the effect of solvent on charging mechanisms in the ionic liquid is investigated.50,54 The difference in charging behavior between the 2 M EMIM-TFSI acetonitrile solution and pure EMIM-TFSI appears under the positive polarization, where permeation selectivity failed even at high charge density (Fig. 4d). This consequence suggests that the cation exchange dominates the charging of CDC-1 nm in the presence of acetonitrile, differing from the behavior of the microporous activated carbon in the propylene carbonate solution.19
The pore size also impacts the charging mechanisms significantly. The charging mechanisms in microporous/mesoporous carbon have been analyzed, including activated carbons (such as YP-17, YP-50), carbon black, and carbide-derived carbons (including TiC-CDC).19,20,40,50 For instance, Tsai et al.50 investigated the effect of electrode pore size by CDC-1 nm and CDC-0.65 nm in 2 M EMIM-TFSI acetonitrile solution. The CDC-0.65 nm electrode displayed negligible mass change under a positive voltage, indicating the inaccessibility of pores for the larger TFSI− anion and the increased mass caused by adsorbed anions outside the pore is balanced by the expelled acetonitrile molecules. Instead, the CDC-1 nm electrode shows an obvious mass change during positive polarization, and the charge is stored by anions and cations exchange.
Two-dimensional materials, especially graphene and MXenes, have become a very active direction for supercapacitor electrodes by their high specific surface area, excellent electrical conductivity, good mechanical stability, and flexibility.55,56 Bo et al.22 used EQCM to study ion transport behaviors of Li2SO4 aqueous electrolytes in disordered porous carbon and graphene films containing adjustable two-dimensional channels. The porous carbon only showed permeation selectivity at high charge density and stored charge by ion exchange at low charge density, similar to previous results.19,20,40,50 In contrast, the mass of the graphene films changes approximately linearly to the stored charge, and the electrode mass decreases under negative voltage, exhibiting a Li+-dominated charging process (Fig. 4e). This difference is linked to the enhanced ions pre-filling caused by the ordered two-dimensional structure, negative surface charge, and better wettability of graphene films.22 As another 2D material, MXenes also store charge through ion intercalation. Therefore, understanding the charging mechanism is vital for applying MXenes as supercapacitors electrode materials. However, the role of anions in charge storage and their influence on electrochemical behavior remained unknown until 2021.41 Shpigel et al.41 found that the mass of MXene electrodes increased when the voltage changed from positive to negative potential (−0.4 V). In comparison, the opposite trend was identified at positive polarization (from −0.4 to 0.5 V) (Fig. 4f). Furthermore, although the masses of Cl− and Br− varied considerably, the mass change during the above processes was similar. These results indicate that the anions are not involved in the electrochemical process. In addition to anions, cations exhibit unique behavior in water-in-salt electrolytes. Wang et al.15 noticed that MXenes show a pair of clearly separated battery-type redox peaks in a 19.8 mol kg−1 LiCl electrolyte. The EQCM results demonstrated that the peaks are related to the desolvation-free Li+ insertion progress. This anomalous behavior increased in the layer spacing, thus enhancing the charge storage.15
Compared with two-dimensional materials, single-layer graphene (SLG) provides a platform for understanding the ionic adsorption interaction of graphene under polarization.43,54 In EMIM-TFSI ionic liquid, the mass of the SLG electrode shows barely change under negative polarization and linearly decreases with a stored charge under positive polarization. Considering the capacitance still presents under negative polarization, the above EQCM results suggest that the charge storage process is dominated by ion rearrangement under a negative voltage and relies on cation desorption under a positive voltage. This behavior is believed to be related to the strong π–π interactions between EMIM+ and the graphene surface.54 The work showed the significant effects of electrode–electrolyte interaction. Yin et al.57 further test carbon material with a more complex three-dimensional porous structure, demonstrating that the local structure of carbon has an important influence on the charging mechanism.57
3.2 Ions desolvation in supercapacitors
In electrolytes with solvent, the ions are surrounded by solvent molecules, called solvated ions. Previous reports have shown that ions can enter nanopores with a size smaller than the solvated ion by desolvating their solvent molecules, leading to influencing the capacitance.58,59 Further studies reported that an anomalous increase in capacitance occurs when the ion size is close to the pore size, showing the significant effect of ion desolvation on the supercapacitor performance.58Since the desolvation process is accompanied by mass change, EQCM plays a crucial role in the study of ion desolvation. The solvation number mainly characterizes the desolvation of ions. Levi et al.20,60 calculated the average solvation number of ions by comparing the theoretical slope calculated from Faraday's law with the experimental slope (Fig. 5a), which is given by:20,60
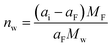 | (6) |
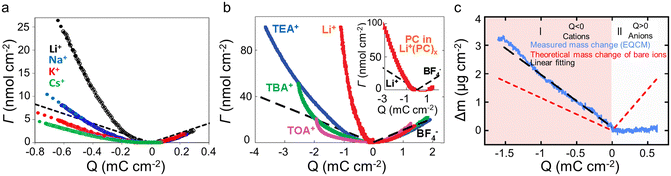 | ||
| Fig. 5 (a) ΔΓ vs electrode charge (Q) obtained with BP-880 carbon in 0.025 M solutions of alkaline metal chlorides (Copyright 2013 American Chemical Society);20 (b) amount of cations and anions (ΔΓ) as a function of the charge density (Q) for the different salts dissolved in propylene carbonate (PC). The inset compares the number of solvent molecules (the solid red curve) (Copyright 2010 American Chemical Society);19 (c) electrode mass change (Δm) vs. charge (Q) (solid blue lines) during the polarization of CDC-0.65 nm in 2 M EMIM-TFSI + ACN. The red dashed lines are the theoretical mass change of neat ions calculated from Faraday's law. The black dashed line shows the linear fitting of measured mass change (Copyright 2014 American Chemical Society).50 | ||
In addition to the electrolyte, the electrode structure also has a crucial effect on ion desolvation. Tsai et al.50 claimed that in 2 M EMIM-TFSI acetonitrile solution, the solvation number of EMIM+ decreased from 3.7 to 1.6 when the pore size of the CDC reduced from 1 nm to 0.65 nm (Fig. 4d and 5c).50 Similar to the CDC porous electrode, Bo et al.22 found that the solvation number decreased under a smaller layer spacing, and the solvation number of Li+ in 1 M Li2SO4 aqueous solution at a layer spacing of ∼0.4 nm is 1.4. These results indicated that solvated ions are partially desolvated when entering narrow pores; meanwhile, the narrower pores lead to a higher degree of desolvation. However, other reports gave a different view: Levi et al.20 showed that in both alkali metal cations and halide anions, BP-880 (containing 16 nm interstitial pores) had a smaller solvation number than the microporous carbon YP-17 (with an average pore size of approximately 1 nm), as summarized in Table 1. This phenomenon is ascribed to the easier replacement of water in BP-880 without confinement conditions.20 Additionally, Srimuk et al.61 provided a work of sodium desolvation in different materials. Among these, Mo11/3C-MXene showed a nearly ideal pseudocapacitor behavior, and only 10% of the initial number of solvent molecules was maintained after cation insertion between the MXene nanolayers. This may be because of the presence of nanoconfined water between the MXene sheets. Moreover, in pseudocapacitive Na0.44MnO2 with a different structure, sodium would lose all water molecules during the insertion process.61
The electrode–electrolyte correlation also needs to be taken into consideration. Recent EQCM measurements demonstrate that the solvation number of EMIM+ on the SLG surface in a 2 M EMIMTFSI acetonitrile solution is only 1, much smaller than that (3–4) in porous carbon with a pore size of 1 nm.54 This result is surprising, as there is no confinement effect on the SLG. The phenomenon is related to the strong specificity interaction of the CH–π and π–π between EMIM+ and SLG.54
3.3 Combination of EQCM with other experimental/computational methods
In EQCM experiments, the change of charge and mass can be detected simultaneously. Nevertheless, it is difficult to distinguish the contribution of each electrolyte component since many electrolytes typically contain cations, anions, and solvent molecules. Undeniably, the qualitative results reported to date have significantly promoted our knowledge of the energy storage mechanism within supercapacitors. However, more precise quantitative characterization is necessary for further elucidation. The attempts hitherto to achieve this objective can be divided into two directions: (1) optimizing the analyte itself, such as using ionic liquids containing only two species or selecting the electrode/electrolyte so that only cation or anion is involved during the charging process (2) combining various experimental or simulation analysis methods, such as the incorporation of EQCM, in situ NMR, and molecular dynamic (MD)/density-functional theory (DFT).Adopting ionic liquid containing only two species is auspicious and convenient for quantitative characterization. However, ionic liquids are not a predominant choice in EQCM reported hitherto,43,50 which may be related to the technical problems associated with the high viscosity of ionic liquids.15 In addition to the usage of ionic liquids, Dou et al.62 grafted anion or cation on silica nanoparticles that is significantly larger than the pore size (Fig. 6a). As a result, only ungrafted anion/cation or solvent molecule can enter the pore.62 Regarding the electrode, some materials, like MXenes may only allow cations and solvent molecules to enter the interlayer, thus enabling quantitative characterization of ion transport (Fig. 6b).41,63 Although quantitative characterizations are achievable without reforming the detection equipment, these methods greatly limit our research region, which is harmful to studying energy storage mechanisms in supercapacitors.
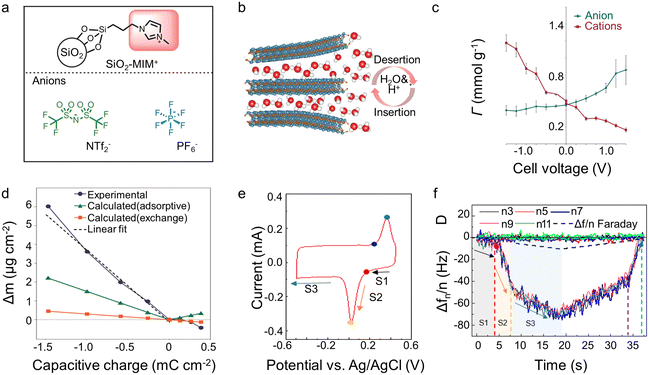 | ||
| Fig. 6 (a) Structure of anions, and silica nanoparticle-grafted cation (Copyright 2017 Springer Nature);62 (b) scheme of MXene electrode interaction with 1 M H2SO4 aqueous electrode (Copyright 2022 Wiley-VCH);63 (c) in-pore ion populations (Γ) for YP-50F in the range −1.5 V to +1.5 V, deconvoluted from the resonance intensities of NMR (Copyright 2015 Springer Nature);21 (d) experimental and calculated electrode mass changes (Δm) for a YP-50F electrode (Copyright 2015 Springer Nature);21 (e) CV recorded of Ti3C2Tx in water-in-salt electrolytes during EQCM measurements (Copyright 2021 American Chemical Society);15 (f) frequency (Δf) and dissipation (D) changes as a function of time obtained in saturated LiBr for MXene electrode (Copyright 2021 American Chemical Society).15 | ||
A landmark work about the combination of various characterization modalities appeared in 2015. Griffin et al.21 quantitatively characterized the charge storage process of porous carbon at the molecular level by combining in situ NMR and EQCM (Fig. 6c and d). The in situ NMR provides the precise amounts of anions and cations separately that are not available in EQCM measurements. EQCM allows the characterization of solvent molecules which is difficult to measure accurately in in situ NMR due to their fast mobility.21 Afterward, more and more work has focused on combining EQCM with other detection tools.15,21,41 The combination of in situ Raman and EQCM provides an accurate characterization of NMO, showing that the energy storage mechanism is related to the pH of the electrolyte and the degree of polarization.49 In Na2SO4 electrolytes, NMO displays surface pseudocapacitance at low charge density but intercalation pseudocapacitance at high charge density. In contrast, it exhibits a distinct battery-like behavior during the whole operating voltage window in NaOH solutions.49 Furthermore, the combination of EQCM and electrochemical dilatometry links the microscopic energy storage mechanism with the macroscopic electrode swelling behavior, showing that charge storage dominated by counter-ion adsorption at high charge density leads to a significant increase in electrode deformation.48
Additionally, the combination of experiments and simulations synergetically provides added value and enhanced understanding. In this respect, the combination of DFT and MD simulation with EQCM has shown great potential. Wang et al.15 obtained the solvation number of Li+ in the interlayer of MXenes by DFT calculations, which strongly supported the EQCM results (Fig. 6e and f). Using MD simulation, Bo et al.22 discovered that the effective diffusion coefficients of Li+ in the graphene channel were significantly higher than that of SO42− when the interlayer spacing was ∼0.4 nm. The apparent difference in diffusion coefficients resulted in a Li+-dominated charge/discharge mechanism, confirmed by the results of EQCM. Furthermore, the results of the MD simulation show that the addition of solvent to the ionic liquid could promote the counter-ion adsorption mechanism on the electrode surface under polarization, which is also in line with the results of the EQCM.54
The above two attempts provide a novel perspective for understanding the energy storage mechanism of supercapacitors. We believe that the combination of EQCM and simulation methods has great potential. Nevertheless, developing a full combination and quantitative comparison of simulation results and experimental EQCM data is required.
4 Conclusion and outlook
Through monitoring the mass and viscosity variation of electrodes under polarization, EQCM, as one of the advanced in situ inspection techniques, greatly help understand the energy storage mechanism of supercapacitors. Here, we first introduce the development of EQCM and the film coating techniques that have a crucial impact on the measurement results. Then, we summarize the achievements hitherto of the supercapacitor energy storage mechanism study based on EQCM from three aspects: ion transport, ion desolvation, and quantitative characterization.Although the EQCM technique has acquired immense success, its application in supercapacitors is still limited. The flaws and perspectives are listed as follows:
(1) For systems containing three or more species, since only two types of data, mass and charge, are available, the information obtained from EQCM data using the current analysis methods is still qualitative, thus impeding the research of supercapacitors. The current EQCM testing and data analysis methodologies require further innovation to gather additional information. For instance, Zheng et al.63 used matrix calculations to deconvolute the real-time fluxes and ion currents of various ions from EQCM data, which provides a new idea for the analysis of EQCM data. In addition, the advanced electrogravimetric analysis method, which combines electrochemical impedance spectroscopy (EIS) and EQCM, is considered as a powerful tool for evaluating the chemical structure and dynamics of the electrical double layer.64
(2) The combination of EQCM with other simulation approaches could deliver more molecular-level information. For instance, the ion orientation43,54 and diffusion coefficients22 obtained from simulation enable an accurate interpretation of EQCM data. However, a more comprehensive and quantitative combination between experiments and simulations is desired. Among the different simulation methods, MD simulation can capture detailed information on the mass change, ion exchange, and distribution. In-depth integration of EQCM with MD simulation could improve our understanding of the supercapacitor energy storage process considerably. Thus, combining EQCM and MD simulation is an essential development direction.
(3) Although the combination of EQCM with different experimental techniques has obtained remarkable achievements, the various test methods cannot perform in the same system, which may affect the quality of the obtained data. In the future, simultaneous measurements of EQCM with other experimental techniques in the same system will greatly improve the accuracy of experiments.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the funding support from the National Natural Science Foundation of China (52161135104 and 52106090) and Hubei Provincial Natural Science Foundation of China (2020CFA093) as well as the Program for HUST Academic Frontier Youth Team. M. C. also thanks to the Postdoctoral Creative Research Funding of Hubei Province. The INM authors thank Eduard Arzt (INM) for his continued support.References
- P. Simon and Y. Gogotsi, Materials for electrochemical capacitors, Nat. Mater., 2008, 7, 845–854 CrossRef CAS.
- H. Shao, Y. C. Wu, Z. Lin, P. L. Taberna and P. Simon, Nanoporous carbon for electrochemical capacitive energy storage, Chem. Soc. Rev., 2020, 49, 3005–3039 RSC.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Carbons and electrolytes for advanced supercapacitors, Adv. Mater., 2014, 26, 2283–2283 CrossRef.
- P. Simon and Y. Gogotsi, Perspectives for electrochemical capacitors and related devices, Nat. Mater., 2020, 19, 1151–1163 CrossRef CAS.
- N. Choudhary, C. Li, J. Moore, N. Nagaiah, L. Zhai, Y. Jung and J. Thomas, Asymmetric supercapacitor electrodes and devices, Adv. Mater., 2017, 29, 1605336 CrossRef PubMed.
- F. Wang, X. Wu, X. Yuan, Z. Liu, Y. Zhang, L. Fu, Y. Zhu, Q. Zhou, Y. Wu and W. Huang, Latest advances in supercapacitors: from new electrode materials to novel device designs, Chem. Soc. Rev., 2017, 46, 6816–6854 RSC.
- L. Y. Liu, P. L. Taberna, B. Dunn and P. Simon, Future directions for electrochemical capacitors, ACS Energy Lett., 2021, 6, 4311–4316 CrossRef CAS.
- Z. P. Cano, D. Banham, S. Y. Ye, A. Hintennach, J. Lu, M. Fowler and Z. W. Chen, Batteries and fuel cells for emerging electric vehicle markets, Nat. Energy, 2018, 3, 279–289 CrossRef.
- P. Simon and Y. Gogotsi, Confined water controls capacitance, Nat. Mater., 2021, 20, 1597–1598 CrossRef CAS PubMed.
- S. Fleischmann, Y. Zhang, X. P. Wang, P. T. Cummings, J. Z. Wu, P. Simon, Y. Gogotsi, V. Presser and V. Augustyn, Continuous transition from double-layer to faradaic charge storage in confined electrolytes, Nat. Energy, 2022, 7, 222–228 CrossRef CAS.
- A. C. Forse, C. Merlet, J. M. Griffin and C. P. Grey, New perspectives on the charging mechanisms of supercapacitors, J. Am. Chem. Soc., 2016, 138, 5731–5744 CrossRef CAS.
- B. Pal, A. Yasin, R. Kaur, M. Tebyetekerwa, F. Zabihi, S. Y. Yang, C. C. Yang, Z. Sofer and R. Jose, Understanding electrochemical capacitors with in-situ techniques, Renewable Sustainable Energy Rev., 2021, 149, 111418 CrossRef CAS.
- A. Patra, K. Namsheer, J. R. Jose, S. Sahoo, B. Chakraborty and C. S. Rout, Understanding the charge storage mechanism of supercapacitors: in situ/operando spectroscopic approaches and theoretical investigations, J. Mater. Chem. A, 2021, 9, 25852–25891 RSC.
- H. Wang, T. K. Koster, N. M. Trease, J. Segalini, P. L. Taberna, P. Simon, Y. Gogotsi and C. P. Grey, Real-time NMR studies of electrochemical double-layer capacitors, J. Am. Chem. Soc., 2011, 133, 19270–19273 CrossRef CAS PubMed.
- X. Wang, T. S. Mathis, Y. Sun, W. Y. Tsai, N. Shpigel, H. Shao, D. Zhang, K. Hantanasirisakul, F. Malchik, N. Balke, D. E. Jiang, P. Simon and Y. Gogotsi, Titanium carbide Mxene shows an electrochemical anomaly in water-in-salt electrolytes, ACS Nano, 2021, 15, 15274–15284 CrossRef CAS.
- H. Varela, M. Malta and R. M. Torresi, Low cost in situ techniques in electrochemistry: the quartz crystal microbalance, Quim. Nova, 2000, 23, 664–679 CrossRef CAS.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P. L. Taberna, C. P. Grey, B. Dunn and P. Simon, Efficient storage mechanisms for building better supercapacitors, Nat. Energy, 2016, 1, 1–10 Search PubMed.
- M. D. Levi, G. Salitra, N. Levy, D. Aurbach and J. Maier, Application of a quartz-crystal microbalance to measure ionic fluxes in microporous carbons for energy storage, Nat. Mater., 2009, 8, 872–875 CrossRef CAS.
- M. D. Levi, N. Levy, S. Sigalov, G. Salitra, D. Aurbach and J. Maier, Electrochemical quartz crystal microbalance (EQCM) studies of ions and solvents insertion into highly porous activated carbons, J. Am. Chem. Soc., 2010, 132, 13220–13222 CrossRef CAS.
- M. D. Levi, S. Sigalov, D. Aurbach and L. Daikhin, In situ electrochemical quartz crystal admittance methodology for tracking compositional and mechanical changes in porous carbon electrodes, J. Phys. Chem. C, 2013, 117, 14876–14889 CrossRef CAS.
- J. M. Griffin, A. C. Forse, W. Y. Tsai, P. L. Taberna, P. Simon and C. P. Grey, In situ NMR and electrochemical quartz crystal microbalance techniques reveal the structure of the electrical double layer in supercapacitors, Nat. Mater., 2015, 14, 812–819 CrossRef CAS PubMed.
- Z. Bo, J. Y. Yang, H. L. Qi, J. H. Yan, K. F. Cen and Z. J. Han, Revealing ion transport in supercapacitors with sub-2 nm two-dimensional graphene channels, Energy Storage Mater., 2020, 31, 64–71 CrossRef.
- M. D. Levi, L. Daikhin, D. Aurbach and V. Presser, Quartz crystal microbalance with dissipation monitoring (EQCM-D) for in-situ studies of electrodes for supercapacitors and batteries: a mini-review, Electrochem. Commun., 2016, 67, 16–21 CrossRef CAS.
- M. D. Levi, N. Shpigel, S. Sigalov, V. Dargel, L. Daikhin and D. Aurbach, In situ porous structure characterization of electrodes for energy storage and conversion by EQCM-D: a review, Electrochim. Acta, 2017, 232, 271–284 CrossRef CAS.
- N. Shpigel, M. D. Levi, S. Sigalov, D. Aurbach, L. Daikhin and V. Presser, Novel in situ multiharmonic EQCM-D approach to characterize complex carbon pore architectures for capacitive deionization of brackish water, J. Phys.: Condens. Matter, 2016, 28, 114001 CrossRef.
- Y. Ji, Z. W. Yin, Z. Yang, Y. P. Deng, H. Chen, C. Lin, L. Yang, K. Yang, M. Zhang, Q. Xiao, J. T. Li, Z. Chen, S. G. Sun and F. Pan, From bulk to interface: electrochemical phenomena and mechanism studies in batteries via electrochemical quartz crystal microbalance, Chem. Soc. Rev., 2021, 50, 10743–10763 RSC.
- J. Curie and P. Curie, Développement par compression de l'électricité polaire dans les cristaux hémièdres à faces inclinées, Bull. Mineral., 1880, 3, 90–93 Search PubMed.
- D. A. Buttry and M. D. Ward, Measurement of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance, Chem. Rev., 1992, 92, 1355–1379 CrossRef CAS.
- G. Sauerbrey, Verwendung von schwingquarzen zur wägung dünner schichten und zur mikrowägung, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- T. Nomura and M. Okuhara, Frequency shifts of piezoelectric quartz crystals immersed in organic liquids, Anal. Chim. Acta, 1982, 142, 281–284 CrossRef CAS.
- R. Schumacher, G. Borges and K. K. Kanazawa, The quartz microbalance: a sensitive tool to probe surface reconstructions on gold electrodes in liquid, Surf. Sci. Lett., 1985, 163, L621–L626 CrossRef CAS.
- S. J. Martin, V. E. Granstaff and G. C. Frye, Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading, Anal. Chem., 1991, 63, 2272–2281 CrossRef CAS.
- M. Rodahl, F. Höök, A. Krozer, P. Brzezinski and B. Kasemo, Quartz crystal microbalance setup for frequency and Q-factor measurements in gaseous and liquid environments, Rev. Sci. Instrum., 1995, 66, 3924–3930 CrossRef CAS.
- L. Daikhin, E. Gileadi, G. Katz, V. Tsionsky, M. Urbakh and D. Zagidulin, Influence of roughness on the admittance of the quartz crystal microbalance immersed in liquids, Anal. Chem., 2002, 74, 554–561 CrossRef CAS PubMed.
- L. Daikhin, S. Sigalov, M. D. Levi, G. Salitra and D. Aurbach, Quartz crystal impedance response of nonhomogenous composite electrodes in contact with liquids, Anal. Chem., 2011, 83, 9614–9621 CrossRef CAS PubMed.
- N. Shpigel, M. D. Levi, S. Sigalov, O. Girshevitz, D. Aurbach, L. Daikhin, P. Pikma, M. Marandi, A. Janes, E. Lust, N. Jackel and V. Presser, In situ hydrodynamic spectroscopy for structure characterization of porous energy storage electrodes, Nat. Mater., 2016, 15, 570–575 CrossRef CAS PubMed.
- J. G. Hu, X. H. Huang and A. Knoll, Measurement of QCM mass sensitivity using electrodeposition method, IEEE Trans. Appl. Supercond., 2021, 31, 1–4 Search PubMed.
- X. Zhao, H. Gao, Y. Hou, L. Gbologah, X. Zeng and Y. Wang, Analysis of crystallization and deposition process using electrochemical-quartz crystal microbalance: a review, J. Electroanal. Chem., 2022, 904, 115936 CrossRef CAS.
- O. Shekhah, J. Liu, R. A. Fischer and C. Woll, MOF thin films: existing and future applications, Chem. Soc. Rev., 2011, 40, 1081–1106 RSC.
- S. Sigalov, M. D. Levi, G. Salitra, D. Aurbach and J. Maier, EQCM as a unique tool for determination of ionic fluxes in microporous carbons as a function of surface charge distribution, Electrochem. Commun., 2010, 12, 1718–1721 CrossRef CAS.
- N. Shpigel, A. Chakraborty, F. Malchik, G. Bergman, A. Nimkar, B. Gavriel, M. Turgeman, C. N. Hong, M. R. Lukatskaya, M. D. Levi, Y. Gogotsi, D. T. Major and D. Aurbach, Can anions be inserted into Mxene?, J. Am. Chem. Soc., 2021, 143, 12552–12559 CrossRef CAS.
- E. Zhang, Y. C. Wu, H. Shao, V. Klimavicius, H. Zhang, P. L. Taberna, J. Grothe, G. Buntkowsky, F. Xu, P. Simon and S. Kaskel, Unraveling the capacitive charge storage mechanism of nitrogen-doped porous carbons by EQCM and ssNMR, J. Am. Chem. Soc., 2022, 144, 14217–14225 CrossRef CAS PubMed.
- J. Ye, Y. C. Wu, K. Xu, K. Ni, N. Shu, P. L. Taberna, Y. Zhu and P. Simon, Charge storage mechanisms of single-layer graphene in ionic liquid, J. Am. Chem. Soc., 2019, 141, 16559–16563 CrossRef CAS PubMed.
- Q. N. Zhang, M. D. Levi, Y. G. Chai, X. Zhang, D. W. Xiao, Q. Y. Dou, P. J. Ma, H. X. Ji and X. B. Yan, Vacuum filtration-and-transfer technique helps electrochemical quartz crystal microbalance to reveal accurate charge storage in supercapacitors, Small Methods, 2019, 3, 1900246 CrossRef CAS.
- D. Johannsmann, The quartz crystal microbalance in soft matter research, Springer, Switzerland, 2015 Search PubMed.
- N. Shpigel, M. D. Levi and D. Aurbach, EQCM-D technique for complex mechanical characterization of energy storage electrodes: background and practical guide, Energy Storage Mater., 2019, 21, 399–413 CrossRef.
- M. D. Levi, S. Sigalov, G. Salitra, D. Aurbach and J. Maier, The effect of specific adsorption of cations and their size on the charge-compensation mechanism in carbon micropores: the role of anion desorption, ChemPhysChem, 2011, 12, 854–862 CrossRef CAS.
- N. Jäckel, S. Patrick Emge, B. Krüner, B. Roling and V. Presser, Quantitative information about electrosorption of ionic liquids in carbon nanopores from electrochemical dilatometry and quartz crystal microbalance measurements, J. Phys. Chem. C, 2017, 121, 19120–19128 CrossRef.
- Q. N. Zhang, M. D. Levi, Q. Y. Dou, Y. L. Lu, Y. G. Chai, S. L. Lei, H. X. Ji, B. Liu, X. D. Bu, P. J. Ma and X. B. Yan, The charge storage mechanisms of 2D cation-intercalated manganese oxide in different electrolytes, Adv. Energy Mater., 2019, 9, 1802707 CrossRef.
- W. Y. Tsai, P. L. Taberna and P. Simon, Electrochemical quartz crystal microbalance (EQCM) study of ion dynamics in nanoporous carbons, J. Am. Chem. Soc., 2014, 136, 8722–8728 CrossRef CAS PubMed.
- M. Lazzari, M. Mastragostino, A. G. Pandolfo, V. Ruiz and F. Soavi, Role of carbon porosity and ion size in the development of ionic liquid based supercapacitors, J. Electrochem. Soc., 2011, 158, A22–A25 CrossRef CAS.
- R. Lin, P. L. Taberna, J. Chmiola, D. Guay, Y. Gogotsi and P. Simon, Microelectrode study of pore size, ion size, and solvent effects on the charge/discharge behavior of microporous carbons for electrical double-layer capacitors, J. Electrochem. Soc., 2009, 156, A7 CrossRef CAS.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, A review of electrolyte materials and compositions for electrochemical supercapacitors, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- Y. C. Wu, J. Ye, G. Jiang, K. Ni, N. Shu, P. L. Taberna, Y. Zhu and P. Simon, Electrochemical characterization of single layer graphene/electrolyte interface: effect of solvent on the interfacial capacitance, Angew. Chem., Int. Ed., 2021, 60, 13317–13322 CrossRef CAS PubMed.
- X. L. Li, Z. D. Huang, C. E. Shuck, G. J. Liang, Y. Gogotsi and C. Y. Zhi, Mxene chemistry, electrochemistry and energy storage applications, Nat. Rev. Chem., 2022, 6, 389–404 CrossRef.
- Z. N. Yu, L. Tetard, L. Zhai and J. Thomas, Supercapacitor electrode materials: nanostructures from 0 to 3 dimensions, Energy Environ. Sci., 2015, 8, 702–730 RSC.
- H. Yin, H. Shao, B. Daffos, P. L. Taberna and P. Simon, The effects of local graphitization on the charging mechanisms of microporous carbon supercapacitor electrodes, Electrochem. Commun., 2022, 137, 107258 CrossRef CAS.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer, Science, 2006, 313, 1760–1763 CrossRef CAS.
- J. Chmiola, C. Largeot, P. L. Taberna, P. Simon and Y. Gogotsi, Desolvation of ions in subnanometer pores and its effect on capacitance and double-layer theory, Angew. Chem., Int. Ed., 2008, 47, 3392–3395 CrossRef CAS PubMed.
- M. D. Levi, S. Sigalov, G. Salitra, R. Elazari and D. Aurbach, Assessing the solvation numbers of electrolytic ions confined in carbon nanopores under dynamic charging conditions, J. Phys. Chem. Lett., 2011, 2, 120–124 CrossRef CAS PubMed.
- P. Srimuk, J. Lee, Ö. Budak, J. Choi, M. Chen, G. Feng, C. Prehal and V. Presser, In situ tracking of partial sodium desolvation of materials with capacitive, pseudocapacitive, and battery-like charge/discharge behavior in aqueous electrolytes, Langmuir, 2018, 34, 13132–13143 CrossRef CAS.
- Q. Dou, L. Liu, B. Yang, J. Lang and X. Yan, Silica-grafted ionic liquids for revealing the respective charging behaviors of cations and anions in supercapacitors, Nat. Commun., 2017, 8, 1–9 CrossRef CAS.
- K. Zheng, Y. Q. Xian and Z. F. Lin, A method for deconvoluting and quantifying the real-time species fluxes and ionic currents using in situ electrochemical quartz crystal microbalance, Adv. Mater. Interfaces, 2022, 9, 2200112 CrossRef CAS.
- E. Bendadesse, A. V. Morozov, A. M. Abakumov, H. Perrot, J.-M. Tarascon and O. Sel, Deciphering the double-layer structure and dynamics on a model LixMoO3 interface by advanced electrogravimetric analysis, ACS Nano, 2022, 16, 14907–14917 CrossRef CAS PubMed.
| This journal is © Institute of Process Engineering of CAS 2023 |