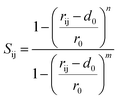Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxidation and de-alloying of PtMn particle models: a computational investigation†
Thantip
Roongcharoen
ab,
Xin
Yang
c,
Shuang
Han
c,
Luca
Sementa
a,
Tejs
Vegge
 c,
Heine Anton
Hansen
c,
Heine Anton
Hansen
 *c and
Alessandro
Fortunelli
*c and
Alessandro
Fortunelli
 *a
*a
aCNR-ICCOM & IPCF, Consiglio Nazionale delle Ricerche, via G. Moruzzi 1, Pisa, 56124, Italy. E-mail: alessandro.fortunelli@cnr.it
bDepartment of Chemistry and Industrial Chemistry, DCCI, University of Pisa, Via G. Moruzzi 13, Pisa, Italy
cDepartment of Energy Conversion and Storage, Technical University of Denmark, Fysikvej, 2800 Kgs. Lyngby, Denmark. E-mail: heih@dtu.dk
First published on 5th October 2022
Abstract
We present a computational study of the energetics and mechanisms of oxidation of Pt–Mn systems. We use slab models and simulate the oxidation process over the most stable (111) facet at a given Pt2Mn composition to make the problem computationally affordable, and combine Density-Functional Theory (DFT) with neural network potentials and metadynamics simulations to accelerate the mechanistic search. We find, first, that Mn has a strong tendency to alloy with Pt. This tendency is optimally realized when Pt and Mn are mixed in the bulk, but, at a composition in which the Mn content is high enough such as for Pt2Mn, Mn atoms will also be found in the surface outmost layer. These surface Mn atoms can dissociate O2 and generate MnOx species, transforming the surface-alloyed Mn atoms into MnOx surface oxide structures supported on a metallic framework in which one or more vacancy sites are simultaneously created. The thus-formed vacancies promote the successive steps of the oxidation process: the vacancy sites can be filled by surface oxygen atoms, which can then interact with Mn atoms in deeper layers, or subsurface Mn atoms can intercalate into interstitial sites. Both these steps facilitate the extraction of further bulk Mn atoms into MnOx oxide surface structures, and thus the progress of the oxidation process, with typical rate-determining energy barriers in the range 0.9–1.0 eV.
1. Introduction
The chemical state of catalyst nanoparticles (NPs) under reaction conditions, and in particular the chemical state of their catalytically active surfaces, is a topic of great interest and active current research due to its implications in the chemical activity and selectivity of the catalysts1 as well as in a wealth of other phenomena, including corrosion, surface treatment, etc.2–4 In heterogeneous catalysis, in particular, the presence and role of strongly interacting oxygen species, ubiquitous in all oxidation processes, in affecting structural and chemical dynamics at the NP surfaces has been long debated. Pure NPs5–20 have been thus investigated, at both experimental and theoretical levels and in both surface-science model set-ups and under progressively more and more realistic (in situ) reaction conditions. The importance of surface oxidation in modulating the system work function, surface faceting and restructuring, and corrugation (insertion of oxygen atoms into subsurfaces) has been demonstrated and quantitatively discussed. Oxidation mechanisms of monometallic surfaces and particles have also been investigated for monometallic NPs of, e.g., Pt20 and Pd,19,20 suggesting a possible role of amorphization at high temperatures. Fewer studies have dealt with the more challenging topic of nanoalloy oxidation,21–27 where the additional phenomenon of surface segregation induced by ligand adsorption offers a further complication.28 Metal nanoalloys in fact undergo dynamic processes under reaction conditions, especially upon adsorption of strongly interacting species such as oxygen atoms. Less accumulated knowledge is however available on NP oxidation and oxidation-induced segregation of nanoalloys, due to the complexity of the phenomena involved and despite the critical role that rigorous information on these effects could have in understanding and eventually controlling surface structure, composition, and catalytic activity. To take an example, in the aqueous phase reforming (APR) reaction for hydrogen production,29,30 Pt catalysts show a good catalytic performance, but the rate of hydrogen yield strongly depends on the amount of Pt loading.31 Thus, in an effort to reduce the percent loading of the expensive Pt element, Pt-based bimetallic nanoalloy catalysts such as Pt–Mn have been proposed and demonstrated to be efficient catalysts and potentially superior in catalytic performance for hydrogen production compared to Pt catalysts. However, the Pt–Mn systems suffer from dealloying/oxidation of the electropositive element and leaching into the aqueous solution.32 Oxidation-induced dealloying of the more electropositive element in a bimetallic system is thus an important concern, that a deeper understanding of its atomistic mechanisms could help avoid or at least minimize. Previous theoretical work has shed some light in this field, especially considering the kinetics of atomic inter-diffusion in metal clusters and particles. Both first-principles sampling of selected kinetic paths to atomic exchange and rearrangement and more systematic stochastic approaches using force-fields have been utilized,33–35 pointing to a critical role of vacancy formation and surface diffusion/displacements in these phenomena. Despite this pioneering work, to the best of our knowledge no systematic investigation of the surface oxidation and mechanisms of multi-metallic systems has been conducted so far.To make progress in this direction, here we investigate via computational simulations the energetics and atomistic mechanisms of the oxidation (and the resulting dynamics of chemical ordering, with special attention to Mn leaching) of Pt–Mn systems. To reduce the computational effort to manageable levels, we use slabs modeling the fcc (111) extended facets of alloy nanoparticles, and we limit our study to the Pt2Mn composition. We use Density-Functional Theory (DFT) as a first-principles basis of energetics, and accelerate the sampling of the Potential Energy Surface (PES) and associated reactive mechanisms by mapping DFT onto Neural Network Potentials (NNPs). We do this in an incremental protocol which uses standard Molecular Dynamics (MD) and accelerated MD in the form of meta-Dynamics (m-Dyn) to generate candidate configurations whose DFT energy and forces are used as a database to interpolate the potential energy surface (PES) via the NNPs. We find that oxidation of the Pt–Mn system goes through successive steps, in which surface Mn atoms dissociate O2 and generate MnOx supported surface-oxide species (with x the degree of oxidation), simultaneously creating vacancy sites in the metallic framework. These vacancies favor the intercalation of oxygen or bulk Mn atoms into sub-surface interstitial sites, thus allowing the surface diffusion (segregation) of Mn atoms in deeper layers.
2. Computational approach
First-principles energetics was obtained via Density Functional Theory (DFT) calculations using the Quantum Espresso (QE) code.36,37 Perdew–Burke–Ernzerhof (PBE)38 functionals with GBRV’s ultra-soft pseudopotential39 were used to calculate an exchange–correlation energy. A plane-wave cutoff of 200 Ry and a kinetic cutoff of 40 Ry were employed. The Grimme-D3 (ref. 40) scheme as implemented in the QE package was adopted to account for the van der Waals dispersion.We create slab models of size (3 × 3 × 6) and we focus on the composition Pt2Mn which is of interest because it is around the composition investigated in several catalytic applications32,41 and also because it seems that in the bulk phase diagram there is a competition between different chemical orderings: L12, L10 and a layered phase in which 2 Pt (111) planes alternate with 1 Mn (111) plane. The lattice parameters were DFT-relaxed for a bulk structure built as a mixture of L12 and L10 chemical ordering as shown in Fig. S2 of the ESI.† Working with 6-layer Pt2Mn (111) slabs, we used a 6 × 6 × 3 k-point to sample the Brillouin zone for the bulk structure. After relaxation of the bulk, a vacuum space of 15 Å in the Z-direction was added to avoid the interaction between periodic images. In all m-Dyn and DFT simulations, we keep the atoms in the three bottom layers frozen, while allowing the first three layers to fully relax. The convergence energy threshold for the self-consistent-field (SCF) was set to 1 × 10−6 Ry and 3 × 3 × 1 k-point grids were applied to sample the Brillouin zone.
In order to obtain transition states (TS) and energy barriers (Ea) for the PtMn oxidation, we performed two steps of transition state search. The nudged elastic band (NEB) method42 was used in an initial TS calculation to find an approximate minimum energy path and TS. Then, a NEB climbing-image (CI-NEB)43 simulation was further performed to locate an accurate TS structure and energy. All NEB and CI-NEB calculations were performed using 6 intermediate images and the convergence on the force was set to 0.1 eV Å−1.
The Ea was calculated as:
| Ea = ETS − EIS |
The Neural Network Potential (NNP) is a versatile tool which can be used in several technologies especially in materials science.44,45 The generation of the NNPs, also named machine-learning potentials or machine-learning force-fields, was realized via the Behler–Parrinello method44 as applied to a database of DFT configurations with associated energy and forces. In this study, we use the NNPs as the potentials to investigate reliably possible mechanisms for the oxidation of bimetallic Pt–Mn catalysts. We name the successive NNP generations as NNP1, NNP2, etc. in sequential order, also of increasing accuracy. We use the Behler–Parrinello formalism as implemented in n2p2.46,47 For the architecture of the NNP, neural networks with 30 nodes in two hidden layers for each element were employed to fit the Potential Energy Surface (PES), which is decomposed into the sum of atomic energies that depend on the local environments of atoms. In this work we apply a cutoff radius of 6 Å to include all relevant interactions. All parameters of the NNP run are listed in Section S1 of the ESI.† The construction of the NNPs is heavily data-driven and relies on the accurate description of the atomic environment, which is realized via symmetry functions in the Behler–Parrinello method. Both the collection of DFT reference configurations and the choice of symmetry functions are essential for accurately reproducing the DFT PES. As described below, we extract DFT reference configurations from Molecular Dynamics (MD) or meta-Dynamics (m-Dyn) runs using an NNP. In particular, for the m-Dyn simulations that sample a vast reaction configurational space, the importance of collecting reference structures has been further leveraged. Here we used the active learning scheme underpinned by the CUR matrix decomposition method48,49 that can incrementally and iteratively select new representative configurations from MD and m-Dyn simulations driven by each NNP/CV combination. The CUR decomposition method enables us to evaluate the importance of rows and columns that correspond to atoms and symmetry functions in our case. Therefore, the representative structures and the symmetry functions that best describe the atomic environment can be selected. The source codes for choosing symmetry functions are listed in Section S2 in the ESI.†
In this work, the meta-Dynamics (m-Dyn)50 method as implemented in PLUMED software51 is employed. m-Dyn is an efficient method for enhancing sampling in molecular dynamics simulation and determining the potential energy surface that provides the information of chemical reaction mechanisms. The details of the m-Dyn technique and its application in various catalytic fields were described by A. Barducci, M. Parrinello, et al.52 In detail, the system can be defined as a function of a finite number of collective variables (CVs) Sα(x), α = 1,2,…d where d means the dimension of the CV space. The obtained potential energy surface and reaction mechanisms from the metadynamics run depend on the choice of the CVs. In this study, we use the coordination number (Sij) between atom i and atom j as the CV. The expression to calculate the number of contacts between two sets of elements can be defined as  According to this equation, Sij is equal to 1 if the contact between atom i and j is fully formed. If there is no interaction between i and j, the value of Sij is zero. The actual value of Sij is calculated as a switching function, whose equation is given by:
According to this equation, Sij is equal to 1 if the contact between atom i and j is fully formed. If there is no interaction between i and j, the value of Sij is zero. The actual value of Sij is calculated as a switching function, whose equation is given by:
We applied the well-tempered metadynamics53 to generate the database for the construction of the NNPs and to explore oxidation mechanisms in Pt–Mn systems. The meta-Dynamics (m-Dyn)/NNP simulations were run using the following collective variables (CVs): CV-PtMn, CV-MnO, and CV-SurfMnO. CV-PtMn and CV-MnO refer to Pt–Mn coordination numbers and Mn–O coordination numbers, respectively. These two CVs were mainly used as global collective variables (global-CVs) to generate the training set for NNP constructions and start investigating the oxidation mechanism on various Pt2Mn slabs. In a successive stage, we use the coordination number of an individual surface Mn and 4O (CV-SurfMnO) as a local CV to further investigate other relevant oxidation mechanisms. The Gaussian width and height in the m-Dyn approach were 0.05 Å and 0.1 eV, respectively. The Gaussian was added to the system every 500 steps of simulation time. The m-Dyn were run at two different temperatures: 300 K and 500 K (simulations at 500 K were used to accelerate the reactions of interest to within 100 ps for computational convenience).
The starting database of configurations for bare and oxidized systems was produced using the ACAT code.54 We generate 200 structures for the bare system and 200 structures for the oxidized system via a stochastic generation. The details of the structure generation by this ACAT code can be found in ref. 54. The energy and forces of the training structures were evaluated via DFT single point calculations using the chosen DFT approach and the QE code. To investigate (oxidation) dynamics, we employed a variant of current protocols55–58 engineered to incrementally explore the reactive space of the system. We used the starting database of configurations, energies, and forces to generate a first NNP1 via the Behler–Parrinello method (see above). We then perform short runs of MD simulations in the canonical ensemble (NVT) using the NNP at a temperature T = 300 K and for a typical time initially very short: t = 1–5 ps, from which a set of single point configurations with associated energy and forces were extracted via the CUR decomposition approach to sample the neighborhood of the initial local minima. This procedure was repeated 5 times. The last NNP (NNP5) was then used to run m-Dyn simulations starting from a set of about 1000 structures with different chemical orderings and 4 oxygen atoms on the surface as initial points. In the m-Dyn runs, we used CV-PtMn and CV-MnO at temperature T = 300 K and for a time initially in the range t = 10–30 ps (in the successive m-Dyn runs, we progressively increased the simulation time up to 600 ps). DFT single-point calculations were then performed on configurations extracted from the m-Dyn runs via the CUR decomposition approach, and added to the DFT database to generate the next NNP version. The idea underlying this strategy is to sample configurations progressively further from the local minima and closer to the saddle points55,58 as pictorially illustrated in a schematic way in Fig. S1 of the ESI.† In particular, in the initial NNP generations we extracted from the m-Dyn runs the first “extrapolation warning” configurations, i.e., the firstly appeared m-Dyn configurations for which these structures were estimated to be outside the validity range of NNP prediction (implying that the NNPs are not able to predict the forces and energy errors of these warning structures accurately). Increasing the training set with the “extrapolation warning” structures has been reported as a convenient technique to extend the range of validity of NNP potentials since only missing structures will be further calculated at the DFT level and added to the training set.46,59,60 As the NNP improved along the various generations, the number of “extrapolation warning” configurations decreased, so that we were able to progressively run the m-Dyn for longer times and include all of the fewer “warning” structures along the entire m-Dyn run in the DFT database. We repeated the above procedure iteratively several times, arriving at NNP12. We then switched to a local CV in the m-Dyn, i.e., CV-SurfMnO, ran m-Dyn simulations at 500 K for 100 ps, and extracted significant configurations via the CUR decomposition approach to generate an NNP able to describe the reaction PES accurately. We repeated the above procedure iteratively a few times, generating a final NNP19, with a final database containing ≈12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures. The energy and force root mean square errors (RMSEs) on the training set are less than 5 meV per atom and 0.18 eV Å−1, respectively. In general, we found that all NNPs starting from NNP12 produce m-Dyn runs with reasonably few warning structures. The low values of RSME imply that NNP19 is capable of describing the potential energy surface of the oxidation process accurately enough to provide paths and mechanisms to be finally double-checked with DFT/NEB. Indeed, the final step of our protocol (whose results are reported in Fig. 2–5 below) consists of extracting a candidate reaction path, with initial and final states and intermediate configurations, from each m-Dyn local-CV run, DFT-relaxing the initial and final states, and finally performing a DFT/NEB starting with the initial and final relaxed states and NEB images taken from the intermediate m-Dyn configurations.
000 structures. The energy and force root mean square errors (RMSEs) on the training set are less than 5 meV per atom and 0.18 eV Å−1, respectively. In general, we found that all NNPs starting from NNP12 produce m-Dyn runs with reasonably few warning structures. The low values of RSME imply that NNP19 is capable of describing the potential energy surface of the oxidation process accurately enough to provide paths and mechanisms to be finally double-checked with DFT/NEB. Indeed, the final step of our protocol (whose results are reported in Fig. 2–5 below) consists of extracting a candidate reaction path, with initial and final states and intermediate configurations, from each m-Dyn local-CV run, DFT-relaxing the initial and final states, and finally performing a DFT/NEB starting with the initial and final relaxed states and NEB images taken from the intermediate m-Dyn configurations.
3. Results and discussion
The logical stages of our study are as follows. In Section 3.1 we start from an analysis of the energetics of the bare systems, then we add oxygen adatoms and re-assess the energetics, and finally we use global CVs to start exploring the oxidation process. In Section 3.2 we extend the previous results by employing local CVs to trigger further steps in the oxidation process and we analyze them in detail.3.1 Energetics and first oxidation steps
As anticipated in Section 2, the first step of our study consisted of generating an initial database of slab configurations for bare Pt–Mn and oxidized Pt–Mn–O systems. On these configurations we calculated energy and forces using the chosen DFT approach and the QE code. We restricted ourselves to fcc (111) slab models and the composition with Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio = 2
Mn ratio = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
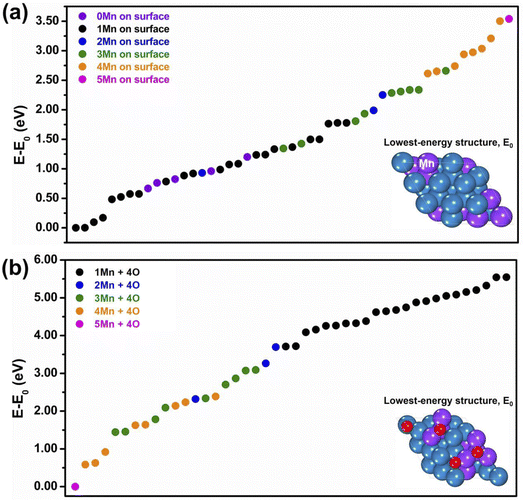
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, however varying the distribution of the Mn atoms over the slab framework to explore a wide set of “homotops” (i.e., isomers sharing the same structural framework but differing in chemical ordering). To this purpose we used the ACAT code,54 and generated stochastically around 200 bare-system configurations. In Fig. 1(a) we report the so-derived relative energies of the homotops with the lowest energies, i.e., the energy difference (E–E0) between the total energy of each model and the total energy of the lowest-energy structure, coloring the data points differently according to the number of Mn atoms present in the top-most surface layer. Without going into a detailed analysis of the results, which would go beyond the scope of the present work, we mention that, around the chosen Pt2Mn composition, (i) ordered phases exist in the experimentally-derived bulk Pt–Mn phase diagram, and in particular the L10 phase at Pt
1, however varying the distribution of the Mn atoms over the slab framework to explore a wide set of “homotops” (i.e., isomers sharing the same structural framework but differing in chemical ordering). To this purpose we used the ACAT code,54 and generated stochastically around 200 bare-system configurations. In Fig. 1(a) we report the so-derived relative energies of the homotops with the lowest energies, i.e., the energy difference (E–E0) between the total energy of each model and the total energy of the lowest-energy structure, coloring the data points differently according to the number of Mn atoms present in the top-most surface layer. Without going into a detailed analysis of the results, which would go beyond the scope of the present work, we mention that, around the chosen Pt2Mn composition, (i) ordered phases exist in the experimentally-derived bulk Pt–Mn phase diagram, and in particular the L10 phase at Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn = 1
Mn = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the L12 phase at Pt
1 and the L12 phase at Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn = 3
Mn = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, in addition to a layered phase in which 2 Pt (111) planes alternate with 1 Mn (111) plane, and (ii) our DFT energetics are consistent with these indications. In particular, we built a bulk structure at the chosen Pt2Mn composition as a hybrid mixture of L10 and L12 phases, as schematically illustrated in Fig. S2 of the ESI,† and we relaxed its lattice parameters, which were then used in the slab simulations after freezing the unit cell in the directions parallel to the surface and the coordinates of the lower-most 3 layers. From both bulk and slab DFT simulations, we found that Mn has a strong tendency to alloy with Pt: configurations with aggregated Mn clusters were typically found at much higher energies than the ones in which Mn was well-distributed and intermixed with Pt. We also noticed a tendency of Mn to avoid outmost surface positions, but at the selected composition some minimal Mn surface segregation is needed to avoid Mn aggregation. Indeed in Fig. 1(a) the lowest-energy configurations of our slab models exhibit 1 Mn atom at the surface (the lowest-energy pure Pt surface model lies >0.7 eV higher than the global minimum homotop). For the convenience of the reader, the ten lowest-energy configurations in Fig. 1(a) are schematically depicted in Fig. S3 of the ESI.† The situation changes drastically when surface oxygen adatoms are added to the system. We again use the ACAT code to generate initial structures in which 4 O atoms are added randomly to hollow fcc sites of the low-energy models of Fig. 1(a), to produce 200 oxidized structures. The corresponding energetics are shown in Fig. 1(b), where it can be clearly observed that structures with surface Mn are now strongly favored. For the convenience of the reader, the ten lowest-energy configurations in Fig. 1(b) are also schematically depicted in Fig. S4 of the ESI.† Assuming that reduced (non-oxidized) Pt–Mn nanoparticles are produced by the experimental synthetic procedure as is typically the case, these well-alloyed, mostly few-surface-Mn configurations will therefore correspond to meta-stable states after interaction with an oxidizing environment, and there will be a thermodynamic driving force to transform them into oxidation-induced Mn-surface-segregated and de-alloyed structures. To give an idea, we quote that the reaction energy of the process in which the 1-surface-Mn bare-system global minimum of Fig. 1(a) reacts with 2 O2 molecules to give the lowest-energy 1-surface-Mn oxidized 4O-model of Fig. 1(b) amounts to −6.96 eV. This thermodynamic preference continues to hold when the free-energy of O2 molecules is included: the oxidation process is energetically favorable under a wide set of thermodynamic conditions (oxygen dissociation on the surface can be energetically favorable even on the bare Pt surface).15
1, in addition to a layered phase in which 2 Pt (111) planes alternate with 1 Mn (111) plane, and (ii) our DFT energetics are consistent with these indications. In particular, we built a bulk structure at the chosen Pt2Mn composition as a hybrid mixture of L10 and L12 phases, as schematically illustrated in Fig. S2 of the ESI,† and we relaxed its lattice parameters, which were then used in the slab simulations after freezing the unit cell in the directions parallel to the surface and the coordinates of the lower-most 3 layers. From both bulk and slab DFT simulations, we found that Mn has a strong tendency to alloy with Pt: configurations with aggregated Mn clusters were typically found at much higher energies than the ones in which Mn was well-distributed and intermixed with Pt. We also noticed a tendency of Mn to avoid outmost surface positions, but at the selected composition some minimal Mn surface segregation is needed to avoid Mn aggregation. Indeed in Fig. 1(a) the lowest-energy configurations of our slab models exhibit 1 Mn atom at the surface (the lowest-energy pure Pt surface model lies >0.7 eV higher than the global minimum homotop). For the convenience of the reader, the ten lowest-energy configurations in Fig. 1(a) are schematically depicted in Fig. S3 of the ESI.† The situation changes drastically when surface oxygen adatoms are added to the system. We again use the ACAT code to generate initial structures in which 4 O atoms are added randomly to hollow fcc sites of the low-energy models of Fig. 1(a), to produce 200 oxidized structures. The corresponding energetics are shown in Fig. 1(b), where it can be clearly observed that structures with surface Mn are now strongly favored. For the convenience of the reader, the ten lowest-energy configurations in Fig. 1(b) are also schematically depicted in Fig. S4 of the ESI.† Assuming that reduced (non-oxidized) Pt–Mn nanoparticles are produced by the experimental synthetic procedure as is typically the case, these well-alloyed, mostly few-surface-Mn configurations will therefore correspond to meta-stable states after interaction with an oxidizing environment, and there will be a thermodynamic driving force to transform them into oxidation-induced Mn-surface-segregated and de-alloyed structures. To give an idea, we quote that the reaction energy of the process in which the 1-surface-Mn bare-system global minimum of Fig. 1(a) reacts with 2 O2 molecules to give the lowest-energy 1-surface-Mn oxidized 4O-model of Fig. 1(b) amounts to −6.96 eV. This thermodynamic preference continues to hold when the free-energy of O2 molecules is included: the oxidation process is energetically favorable under a wide set of thermodynamic conditions (oxygen dissociation on the surface can be energetically favorable even on the bare Pt surface).15
After having clarified the energetics of the initial and final states of the oxidation process, we started exploring the reaction paths connecting the initial alloyed configurations to the final oxidation products. To this end, we used meta-dynamics (m-Dyn) runs and two different collective variables to drive the system’s dynamics: CV-PtMn and CV-MnO as defined in Section 2. These are global collective variables (CVs) in which we force the Pt–Mn or Mn–O coordination of all atoms in the system. We expect that these global variables are capable of sampling configurations away from the local minima and progressively closer to the reaction saddle points, as illustrated in Fig. S1 of the ESI.†
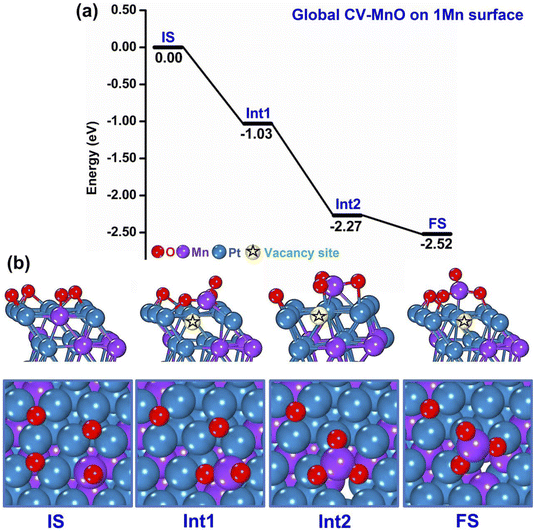
A representative example of these initial m-Dyn simulations starting from the global minimum of the bare systems (only 1 Mn atom at the surface) to which 4 O atoms are added is provided in Fig. 2(a and b), whose results were obtained using NNP19 in an m-Dyn based on CV-MnO lasting 100 ps at a temperature of 500 K. In Fig. 2(a and b) we report for simplicity only the energy and the geometry of the local minimum states (after DFT structure relaxation) as extracted from an analysis of the m-Dyn run, although the m-Dyn naturally provides also candidate saddle-point structures and energetics, because we intend to focus attention on the major results of these initial simulations. As apparent in Fig. 2(a), there exists a strong thermodynamic driving force in going from the Initial State (IS) to the first (Int1) and second (Int2) intermediate states, with drops of more than 1 eV in the DFT energy. This drop in energy is associated with the extraction of the surface Mn atom from the metallic framework into a surface oxide configuration, as apparent in Fig. 2(b). In particular, Int1 corresponds to a MnO2 surface oxide structure, which then transforms in Int2 into a MnO3 oxide, that finally rearranges into a slightly more stable Final State (FS) structural isomer with a more modest energy drop of −0.25 eV. Notably, the extraction process leaves a vacancy site in the framework, to illustrate which we have tried to pictorially highlight the so-formed vacancy with a star symbol in the images of Fig. 2(b). As we will see later, the formation of a vacancy is a critical step to give way to successive steps in the oxidation process.
A second representative example of the initial m-Dyn simulations, now starting from a higher-energy state of the bare systems (2 Mn atoms are initially at the surface, to which 4 O atoms are added) is provided in Fig. 3(a and b), whose results were obtained using NNP19 in an m-Dyn based on CV-MnO lasting 100 ps at a temperature of 500 K. In Fig. 3(a and b) we report again for simplicity only the energy and the geometry of the local minimum states after DFT structure relaxation. Once more, a strong thermodynamic force with steps of 0.65–1.13 eV in the DFT energy drives the system from the Initial State (IS) into the first (Int1) intermediate state, corresponding to a MnO2 surface oxide structure, and then to a MnO3 surface oxide second (Int2) intermediate state, which then rearranges into Int3 and Int4 lower-energy intermediate isomers before extracting the second surface Mn atom into the over-layer in the Int5 and then the FS configurations. For the convenience of the reader, we have pictorially highlighted the vacancy site in the metallic framework with a star symbol in the images of Fig. 3(b). We underline that we are still considering 4 oxygen atoms on the surface: considering that we are now investigating structures with 2 Mn atoms on the top-most layer initially, this corresponds to a situation in which O is “under-stoichiometric”, i.e., the system would thermodynamically favor the adsorption of a larger number of oxygen atoms, enough to create a MnO3 surface oxide structure for both the surface Mn atoms. This is the reason why the drops in energy are generally smaller than in the previous case, and the vacancy sites are in some instances partially filled by the under-stoichiometric Mn2O4 species (e.g., in the FS configuration). Despite this “lean-oxygen” situation, the thermodynamics of the process is still strongly exothermic (and also the NNP barriers suggest viable mechanisms, see below). We do not report examples of m-Dyn runs based on CV-PtMn, but we mention that the picture is qualitatively the same as that obtained using CV-MnO.
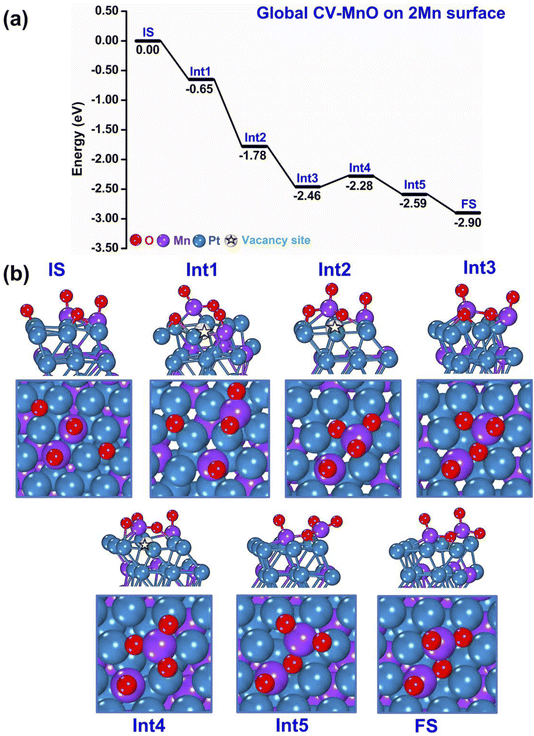 | ||
| Fig. 3 Sequence of steps leading to oxidation of the PtMn system starting from a configuration with 2 Mn in the surface layer. (a) Reaction (oxidation) energy diagram, punctuated by local minima (IS = initial state, IntN = N-th intermediate, FS = final state). (b) Atomistic depiction of the stable configurations involved in the oxidation path, from a side-view (top row) or top-view (bottom row). Color coding as in Fig. 2. | ||
We can conclude from these results that the global CVs thus far employed are useful to give a first exploration of the reaction steps of the system. We can observe the diffusion of oxygen atoms on the surface toward the Mn species, and the extraction of Mn atoms from the top-most surface layer to form MnyOx surface oxides. However, CV-PtMn and CV-MnO are global CVs that do not capture locality phenomena in the oxidation process. In the next subsection we then switched to a local CV, CV-SurfMnO, and used this local CV to trigger further, more localized oxidation mechanisms so as to achieve a qualitatively complete picture.
3.2 Later oxidation steps
As discussed in the previous section, the oxidation mechanisms obtained from m-Dyn runs using global-CVs mainly involve Mn and oxygen atoms on the surface: both 1 Mn- and 2 Mn-surface systems tend to form MnxOy species and leave a vacancy site on the surface of the metallic framework as illustrated in Fig. 2 and 3. However, we observed that the later stages of the m-Dyn runs tended to produce high-energy configurations with dubious physical significance. To investigate further possible oxidation mechanisms, we then used the local CV-SurfMnO (see Section 2 for the definition of CV-SurfMnO).First, we ran m-Dyn starting from the global minimum of the bare systems (only 1 Mn atom at the surface, to which 4 O atoms are added) using the local CV-SurfMnO and NNP19 for a total of 100 ps simulation time at a temperature of 500 K. From this m-Dyn simulation we extracted the important structures, confirmed their stability via DFT relaxation, and calculated the DFT saddle points via NEB simulations. As an initial side observation, we note that when we switch from global CVs to a local CV, there is an obvious structure transformation as a function of the change of 1 Mn–O coordination numbers as depicted in Fig. S5.† In Fig. 4(a and b) we plot the DFT energy and geometry profiles along the oxidation path in this 1 Mn-surface system. The reaction starts with a configuration in which the surface Mn atom is coordinated to only 1 oxygen adatom (a Mn–O species) as the Initial State (IS) and then forms MnO2 and MnO3 surface oxide species at the Int2 and Int3 states with downhill reaction energy changes of −0.83/−1.00 eV at each step. As discussed in the previous subsection using m-Dyn runs using global-CVs and here confirmed by m-Dyn runs using a local-CV, the formation of the MnO2 and MnO3 surface oxides leaves a vacancy site in the metallic framework (the vacancy site in the metallic framework is pictorially highlighted with a star symbol in the pictures). The NEB and CI-NEB calculations allow us to locate the transition states and determine the kinetic barriers at each elementary step of the reaction. The results show that O migrations and surface Mn extraction to form MnO2 at TS1 and MnO3 at TS2 require a low kinetic barrier of 0.17 eV for MnO2 creation and 0.43 eV for the MnO3 formation (Fig. 4(a)). After a vacancy site is created at Int1–Int2, in Int3 a further step (not seen in the simulations of Section 3.1) brings a Mn atom from subsurface into an interstitial site between the topmost first and second layers next to the vacancy, a position stabilized by the interaction with the Mn atom of the MnO3 species. This process is nearly isoenergetic, and the barrier at TS3 is 0.45 eV. In the successive step (Int4), the MnO3 species is pushed back away from the metal framework, and the subsurface Mn overcomes an energy barrier of 0.90 eV to occupy stably the empty vacancy site interacting with one of the surface oxygen atoms, with this latter interaction strongly stabilizing the system with an associated energy drop of 2.04 eV (the total energy drop is −3.82 eV). The reaction then continues with a final step in which the O atom lifts up the subsurface Mn and helps it to migrate into a Mn2O4 surface oxide structure as a final FS state. The energy barrier of this final step at TS5 is 0.81 eV while the reaction energy of the entire process is −3.77 eV. Overall, the oxidation of the bimetallic PtMn system is therefore a strongly exothermic process. The rate-determining step corresponds to extracting the subsurface Mn from the vacancy site to the adlayer (thus re-creating a vacancy that can give rise to further processes) and has the highest energy barrier of 0.90 eV.
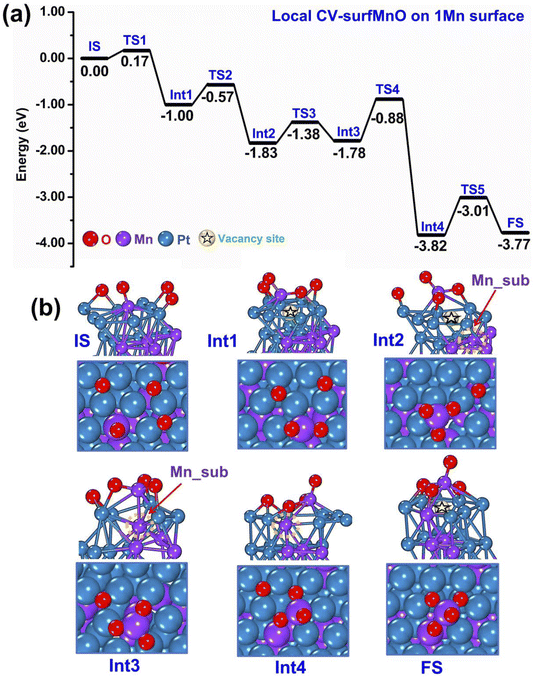 | ||
| Fig. 4 Sequence of steps leading to oxidation of the PtMn system starting from a configuration with 1 Mn in the surface layer. (a) Reaction (oxidation) energy diagram, punctuated by local minima (IS = initial state, IntN = N-th intermediate, FS = final state) and saddle points (TSN = N-th transition state). (b) Atomistic depiction of the configurations involved in the oxidation path, from a side-view (top row) or top-view (bottom row). Color coding as in Fig. 2. | ||
Second, we ran m-Dyn starting from a configuration of the bare system with 2 Mn atoms and 4 added O atoms at the surface using the local CV-SurfMnO and NNP19 for a total of 100 ps simulation time at a temperature of 500 K. As before, from this m-Dyn simulation we extracted the important structures, confirmed their stability via DFT relaxation, and calculated the DFT saddle points via NEB simulations. In Fig. 5(a and b) we plot the DFT energy and geometry profiles along the oxidation path. The reaction starts with a configuration in which the two surface Mn atoms are coordinated to 2 oxygen adatoms in Mn–O species as the Initial State (IS). The first steps then correspond to progressively extracting both Mn atoms from the framework and forming MnO2 and MnO3 surface oxide species via Int2–Int3 intermediates to get the Int4 state, with a downhill reaction energy change of ≈−1.8 eV. It is interesting to note that three steps of formation of MnxOy surface oxide species are thermodynamically favorable with very low kinetic barriers around 0.3/0.5 eV (see TS1–TS3). As discussed before, vacancy sites are so created in the metallic framework, and are pictorially highlighted with a star symbol in the pictures. The next oxidation steps are unique to this local-CV m-Dyn simulation: one of the oxygen atoms from the surface fills one of the vacancy sites thus coming to interact with a subsurface Mn atom, that is highlighted with an arrow in the Int5–Int6–Int7 configurations of Fig. 5(b). Naturally, this process even “worsens” the under-stoichiometric oxygen coordination of the surface Mn species, so that this raises the total energy by 0.26 eV. The reaction continues with the migration of the subsurface Mn into the interstitial layer in Int6. The O atom helps take the subsurface Mn to migrate into the interstitial layer, however the metal bonds of Mn–Pt and Mn–Mn in the second layer are elongated and constrained, so that this mechanism corresponds to the rate-determining step and requires a barrier of around 1 eV at TS6. In Int7 the subsurface Mn atom is finally brought to the topmost surface layer, through an essentially isoenergetic process. In the conclusive two steps (Int8 and FS), the under-stoichiometric Mn3O4 species migrate to fill the vacancy sites to reform Mn–O motifs and the Pt atom on the surface replaces the subsurface vacancy to stabilize the structure, corresponding to an overall energy drop of −1.14 eV. As in Section 3.1, we underline that, despite the “lean-oxygen” situation of this 2-surface-Mn case (the system would thermodynamically favor the adsorption of a larger number of oxygen atoms, enough to create a MnO3 surface oxide structure for all the surface Mn atoms), the thermodynamics of the process is exothermic and the barriers indicate viable mechanisms, with a rate-determining barrier of 1.00 eV.
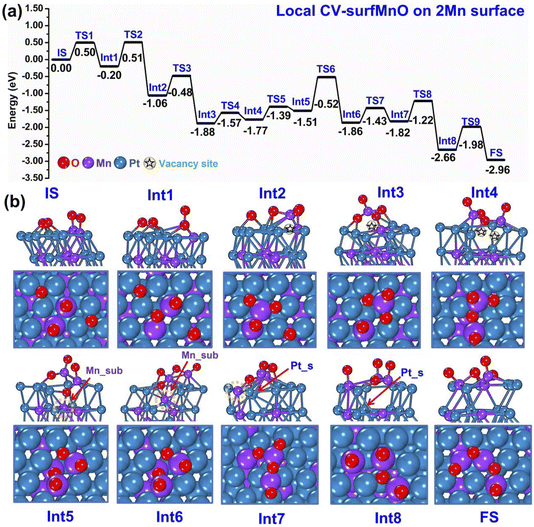 | ||
| Fig. 5 Sequence of steps leading to oxidation of the PtMn system starting from a configuration with 2 Mn in the surface layer. (a) Reaction (oxidation) energy diagram, punctuated by local minima (IS = initial state, IntN = N-th intermediate, FS = final state) and saddle points (TSN = N-th transition state). (b) Atomistic depiction of the various stable configurations involved in the oxidation path, from a side-view (top row) or top-view (bottom row). Color coding as in Fig. 2. | ||
4. Conclusions
The oxidation process of metallic surfaces is technologically important in a variety of fields, ranging from catalysis to corrosion, surface treatment, etc.1–28 In heterogeneous catalytic processes in which oxygen species can appear, in particular, such as partial oxidation or hydrogen generation reactions, the importance of such oxygen species in determining static and dynamic structural properties such as surface faceting and restructuring, and corrugation, as well as electronic properties such as the system work function and the optical response, has long been researched. This has accumulated a wealth of information, especially at the fundamental model-system level, whereas the picture under realistic (in situ) reaction conditions is much less clear, due to the complexity of the phenomena involved and the difficulty in monitoring reaction intermediates and paths with atomistic precision. The situation is further complicated in the nanoalloy field. In bimetallic nanosystems, oxidation plays a critical role in determining the surface composition and structure, and thus all connected quantities, including chemical, optical and electronic properties, especially when the two elements have very different oxygen propensity, or electronegativity. Metal nanoalloys can then undergo dynamic processes under reaction conditions, especially upon adsorption of strongly interacting species such as oxygen atoms, such as leaching and de-alloying. Due to the difficulty in correctly interpreting experiments in this complicated scenario so as to derive rigorous information, theory and simulations can play a crucial role in this topic, by clarifying thermodynamics and unveiling kinetics of oxygen adsorption on and restructuring of metal NPs and nanoalloys, including atomistic mechanisms of oxidation and the associated dynamics of chemical ordering.Here we aim at shedding light on this topic by investigating via computational simulations one such case: the oxidation of Pt–Mn alloyed systems and the resulting surface migration and segregation into oxidized species of the electropositive Mn element. To reduce our study to a manageable computational effort, we use slabs modeling extended facets of Pt–Mn alloy nanoparticles at a fixed Pt2Mn composition. We then combine DFT local geometry relaxations and single-point calculations of energy and forces with a recursive generation of machine learning force fields (Neural Network Potentials, NNPs) which are then used to explore increasingly larger basins of the Potential Energy Surface (PES) so as to feedback onto and enlarge the DFT database to generate increasingly more accurate NNPs. This protocol can be seen as the extension to reactive, dynamic processes (saddle points) of the procedures for deriving NNPs targeted to thermodynamic quantities (local minima), as in current active research.58 The latest-generation NNPs are so accurate that they can be used in MD or accelerated MD in the form of meta-Dynamics (m-Dyn) simulations to produce reaction paths that can then be validated by DFT/NEB saddle point searches, whose outcome is then fed back onto the DFT database and used for a final NNP refinement.
The picture resulting from the adopted computational protocol offers a comprehensive and apparently reasonable view of the oxidation and de-alloying process in Pt–Mn systems. The presence of Mn atoms in the topmost surface layer, which is thermodynamically favored at the Pt2Mn composition, provides the initial weak points for system dynamics. These atoms in fact not only easily dissociate incoming O2 molecules and attract existing oxygen adatom species, but their strong interaction with these species drives the systems from surface-alloyed Mn toward MnOx surface oxide structures supported on the metallic framework (with x the degree of oxidation). This simultaneously leads to creating one or more vacancy sites in the metallic slab, which then favor atomistic exchange and rearrangement mechanisms, in which an exohedral surface oxygen can migrate into the framework filling up a vacancy site, or a subsurface Mn atom can diffuse to interstitial sites next to the vacancy. The configurations resulting from both these mechanisms are then prone to further evolution, in which the migrated or a surface oxygen picks up a subsurface or the interstitial Mn atom and draws it to the surface. The DFT estimate of the rate-determining barriers along such reaction paths ranges around 0.9–1.0 eV, thus suggesting a kinetics from a few tens of minutes to a few tens of hours at room temperature, in reasonable agreement with available experimental data.30
Finally, we note that the present study offers several possibilities of development, among which we highlight two. First, now that an accurate NNP for the Pt–Mn–O system has been derived, this is available for tackling more complex phenomena occurring on realistic Pt–Mn NPs under a wide set of reaction conditions. Second, the database of structures and energetics derived for the Pt–Mn system could be used in a similar study to accelerate the derivation of NNPs for other ternary (bimetallic + oxygen) systems, thus possibly allowing one to derive general trends in the complex phenomenon of the oxidation of bimetallic NPs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the BIKE project for the financial support. The BIKE project has received funding from the European Union’s Horizon 2020 Research and Innovation Program under the Marie Skłodowska-Curie grant agreement no. 813478.References
- H. K. G. Ertl, F. Schuth and J. Weitkamp, Handbook of Heterogeneous Catalysis, Wiley, New York, 2nd edn, 2008 Search PubMed.
- N. Le Bozec, C. Compère, M. L’Her, A. Laouenan, D. Costa and P. Marcus, Corros. Sci., 2001, 43, 765–786 CrossRef CAS.
- F. Shi, W. Gao, H. Shan, F. Li, Y. Xiong, J. Peng, Q. Xiang, W. Chen, P. Tao, C. Song, W. Shang, T. Deng, H. Zhu, H. Zhang, D. Yang, X. Pan and J. Wu, Chem, 2020, 6, 2257–2271 CAS.
- J. Gong and C. B. Mullins, Acc. Chem. Res., 2009, 42, 1063–1073 CrossRef CAS PubMed.
- M. Todorova, W. X. Li, M. V. Ganduglia-Pirovano, C. Stampfl, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2002, 89, 096103 CrossRef CAS.
- E. Lundgren, J. Gustafson, A. Mikkelsen, J. N. Andersen, A. Stierle, H. Dosch, M. Todorova, J. Rogal, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2004, 92, 046101 CrossRef CAS.
- G. E. Ramirez-Caballero and P. B. Balbuena, Chem. Phys. Lett., 2008, 456, 64–67 CrossRef CAS.
- L. O. Paz-Borbon, R. L. Johnston, G. Barcaro and A. Fortunelli, Eur. Phys. J. D, 2009, 52, 131–134 CrossRef CAS.
- N. Seriani, J. Harl, F. Mittendorfer and G. Kresse, J. Chem. Phys., 2009, 131, 054701 CrossRef.
- M. Hatanaka, N. Takahashi, N. Takahashi, T. Tanabe, Y. Nagai, A. Suda and H. Shinjoh, J. Catal., 2009, 266, 182–190 CrossRef CAS.
- L. K. Ono, B. Yuan, H. Heinrich and B. R. Cuenya, J. Phys. Chem. C, 2010, 114, 22119–22133 CrossRef CAS.
- L. M. Molina, S. Lee, K. Sell, G. Barcaro, A. Fortunelli, B. Lee, S. Seifert, R. E. Winans, J. W. Elam, M. J. Pellin, I. Barke, V. von Oeynhausen, Y. Lei, R. J. Meyer, J. A. Alonso, A. Fraile Rodríguez, A. Kleibert, S. Giorgio, C. R. Henry, K.-H. Meiwes-Broer and S. Vajda, Catal. Today, 2011, 160, 116–130 CrossRef CAS.
- D. J. Miller, H. Öberg, S. Kaya, H. Sanchez Casalongue, D. Friebel, T. Anniyev, H. Ogasawara, H. Bluhm, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2011, 107, 195502 CrossRef CAS.
- R. K. Nomiyama, M. J. Piotrowski and J. L. F. Da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 100101 CrossRef.
- D. Fantauzzi, J. Bandlow, L. Sabo, J. E. Mueller, A. C. T. van Duin and T. Jacob, Phys. Chem. Chem. Phys., 2014, 16, 23118–23133 RSC.
- Y. Lykhach, S. M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2016, 15, 284–288 CrossRef CAS PubMed.
- M. A. van Spronsen, J. W. M. Frenken and I. M. N. Groot, Nat. Commun., 2017, 8, 429 CrossRef.
- R. Mom, L. Frevel, J.-J. Velasco-Vélez, M. Plodinec, A. Knop-Gericke and R. Schlögl, J. Am. Chem. Soc., 2019, 141, 6537–6544 CrossRef CAS PubMed.
- B. Kirchhoff, L. Braunwarth, C. Jung, H. Jónsson, D. Fantauzzi and T. Jacob, Small, 2020, 16, 1905159 CrossRef CAS PubMed.
- L. Gai, Y. K. Shin, M. Raju, A. C. T. van Duin and S. Raman, J. Phys. Chem. C, 2016, 120, 9780–9793 CrossRef CAS.
- P. Landon, P. J. Collier, A. F. Carley, D. Chadwick, A. J. Papworth, A. Burrows, C. J. Kiely and G. J. Hutchings, Phys. Chem. Chem. Phys., 2003, 5, 1917–1923 RSC.
- F. Tao, M. E. Grass, Y. Zhang, D. R. Butcher, J. R. Renzas, Z. Liu, J. Y. Chung, B. S. Mun, M. Salmeron and G. A. Somorjai, Science, 2008, 322, 932–934 CrossRef CAS.
- F. Gao, Y. Wang and D. W. Goodman, J. Am. Chem. Soc., 2009, 131, 5734–5735 CrossRef CAS.
- P. S. West, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Phys. Chem. C, 2010, 114, 19678–19686 CrossRef CAS.
- F. Tao, M. E. Grass, Y. Zhang, D. R. Butcher, F. Aksoy, S. Aloni, V. Altoe, S. Alayoglu, J. R. Renzas, C.-K. Tsung, Z. Zhu, Z. Liu, M. Salmeron and G. A. Somorjai, J. Am. Chem. Soc., 2010, 132, 8697–8703 CrossRef CAS PubMed.
- K. Paredis, L. K. Ono, F. Behafarid, Z. Zhang, J. C. Yang, A. I. Frenkel and B. R. Cuenya, J. Am. Chem. Soc., 2011, 133, 13455–13464 CrossRef CAS.
- B. Zhu, G. Thrimurthulu, L. Delannoy, C. Louis, C. Mottet, J. Creuze, B. Legrand and H. Guesmi, J. Catal., 2013, 308, 272–281 CrossRef CAS.
- F. Negreiros, L. Sementa, G. Barcaro, I. Fechete, L. Piccolo and A. Fortunelli, in Nanoalloys, ed. F. Calvo, Elsevier, Oxford, 2nd edn, 2020, pp. 267–345 Search PubMed.
- H.-D. Kim, H. J. Park, T.-W. Kim, K.-E. Jeong, H.-J. Chae, S.-Y. Jeong, C.-H. Lee and C.-U. Kim, Int. J. Hydrogen Energy, 2012, 37, 8310–8317 CrossRef CAS.
- G. W. Huber, J. W. Shabaker, S. T. Evans and J. A. Dumesic, Appl. Catal., B, 2006, 62, 226–235 CrossRef CAS.
- T.-W. Kim, H.-D. Kim, K.-E. Jeong, H.-J. Chae, S.-Y. Jeong, C.-H. Lee and C.-U. Kim, Green Chem., 2011, 13, 1718–1728 RSC.
- F. Bossola, X. I. Pereira-Hernández, C. Evangelisti, Y. Wang and V. Dal Santo, J. Catal., 2017, 349, 75–83 CrossRef CAS.
- F. R. Negreiros, F. Taherkhani, G. Parsafar, A. Caro and A. Fortunelli, J. Chem. Phys., 2012, 137, 194302 CrossRef CAS PubMed.
- F. Calvo, A. Fortunelli, F. Negreiros and D. J. Wales, J. Chem. Phys., 2013, 139, 111102 CrossRef CAS PubMed.
- M. Asgari, F. R. Negreiros, L. Sementa, G. Barcaro, H. Behnejad and A. Fortunelli, J. Chem. Phys., 2014, 141, 041108 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. L. Ayastuy, M. P. González-Marcos, J. R. González-Velasco and M. A. Gutiérrez-Ortiz, Appl. Catal., B, 2007, 70, 532–541 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef.
- A. Singraber, T. Morawietz, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 3075–3092 CrossRef CAS.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and M. Ceriotti, J. Chem. Phys., 2018, 148, 241730 CrossRef PubMed.
- C. Li, X. Wang, W. Dong, J. Yan, Q. Liu and H. Zha, IEEE Trans. Pattern Anal. Mach. Intell., 2019, 41, 1382–1396 Search PubMed.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 1, 826–843 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- S. Han, ACAT: Alloy Catalysis Automated Toolkit, 2021. https://gitlab.com/asm-dtu/acat Search PubMed.
- M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, Chem. Rev., 2021, 121, 9719–9721 CrossRef CAS PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- M. Yang, L. Bonati, D. Polino and M. Parrinello, Catal. Today, 2022, 387, 143–149 CrossRef CAS.
- N. Artrith and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045439 CrossRef.
- N. Artrith, B. Hiller and J. Behler, Phys. Status Solidi B, 2013, 250, 1191–1203 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2fd00107a |
| This journal is © The Royal Society of Chemistry 2023 |