 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating machine learning models to predict microbial activity during ozonation–biofiltration†
Mahshid S. Z.
Farzanehsa
 a,
Guido
Carvajal
a,
Guido
Carvajal
 b,
John
Mieog
c and
Stuart J.
Khan
b,
John
Mieog
c and
Stuart J.
Khan
 *a
*a
aSchool of Civil and Environmental Engineering, University of New South Wales, Sydney, NSW, Australia. E-mail: s.khan@unsw.edu.au
bFacultad de Ingeniería, Universidad Andrés Bello, Antonio Varas 880, Providencia, Santiago, Chile
cMelbourne Water, 990 La Trobe St, Docklands, Victoria 3008, Australia
First published on 9th December 2022
Abstract
Continuous online monitoring of water treatment process performance is an essential step in ensuring reliable water quality outcomes. In particular, it is important to ensure effective removal of microbial substances during advanced wastewater treatment processes. However, most microbial indicators cannot be continuously monitored by online processes. Therefore, it is necessary to monitor treatment process performance based on surrogate measures which can be reliably and continuously monitored. For example, water quality data such as colour, turbidity and chemical oxygen demand (COD) can be measured quickly and easily. In this study, a combined ozonation–biological media filtration process (O3/BMF), was used to reduce microbial indicator concentration. After gathering water quality data and corresponding microbial indicator concentrations, we applied machine learning to develop models for predicting the amount of change in microbial indicator concentration following O3/BMF treatment. Three microbial indicators were studied, namely Clostridium perfringens, E. coli, and somatic coliphage. The most effective physico-chemical predictors for the removal of these microbial indicators were determined by means of mutual information. Associations between changes in the predictors' concentration during O3/BMF and the reduction of the microbial indicators were identified using a range of supervised learning algorithms including Naïve Bayes, random forest, support vector machines and generalised linear model. The impact of the type of prediction algorithm on prediction accuracy was investigated and the superior classifier was determined. Performance measures for microbial removal prediction were found to be superior for the support vector machines (SVM) classifier. Using SVM with a Gaussian kernel classifier, prediction accuracy for all microbial removal was above 75%. Moreover, other performance measures such as area under curve (AUC) and kappa statistics (KS) were higher in SVM compared to the other applied classifiers (AUC ≥ 0.80; KS ≥ 0.34). From this study, we have identified an objective and efficient method that can predict the effectiveness of the O3/BMF process in removing the three microbial indicators in water from a short list of commonly measured physico-chemical parameters.
Water impactTo ensure water quality, online monitoring of pathogen removal is very important which is not possible with current technologies. Therefore, it is essential to find surrogate measures that can be easily monitored online. In this study, we have investigated machine learning techniques to predict microbial removal through surrogates such as water quality data in ozonation and biofiltration processes. |
Introduction
Previous studies have shown that ozonation can effectively reduce microbial concentrations, organic content, colour and trace chemicals in wastewater.1–4 It has been observed that ozone increases the oxygen concentration and the biodegradability of organic material, facilitating more rapid biodegradation during subsequent biological filtration.Current international guidelines for water recycling promote a risk management approach for the control of hazards with a primary emphasis on pathogens because of their potential acute, severe and widespread impacts.5–7 These guidelines draw principles from Hazard Analysis Critical Control Point (HACCP) standards for the monitoring and control of hazards across a multi-barrier system. The performance of treatment barriers is evaluated through validation, which is the process of ensuring that the system can effectively control the hazards. For pathogens, this performance is measured by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 reduction values (LRV). Log removal value (LRV) is the percentage that a pathogen will be inactivated by a disinfection method. In mathematical form,
10 reduction values (LRV). Log removal value (LRV) is the percentage that a pathogen will be inactivated by a disinfection method. In mathematical form,  .
.
A LRV equal to 1 means that the pathogen is reduced by 90% from its initial value. The monitoring of critical control points requires online parameters indicative of the hazard removal performance of the process. For ozonation and biological media filtration (BMF), however the water matrix characteristics play a crucial role in the disinfection effectiveness which has limited the use of indicators such as ozone dose and CT, applied elsewhere in water treatment.8–10 This limitation has impeded the formal attribution of LRV credits to ozonation and BMF for wastewater in many jurisdictions. LRV credits have been awarded to post-ozonation at Melbourne Water's Eastern Treatment Plant (ETP) (the subject of this study) on the basis of CT disinfection. Post-ozonation CT disinfection is only possible due to the pre-treatment provided by pre-ozone and BMF primarily through satisfying ozone demand. There are, however reported studies on the use of alternative indicators for monitoring of microbial performance removal including bromate formation, O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOC ratio, and UVA reduction.11–13 These studies have focussed on ozonation under ideal conditions, for example by removing suspended solids and using benchtop reactors.11 The ability to obtain LRV credits for ozonation/BMF could translate into major cost savings for wastewater recycling projects by reducing the need for additional treatment processes such as high-energy photochemical processes, or by reducing chemical consumption for downstream disinfection processes. Alternatively, obtaining additional LRV credits for a treatment system can increase the resilience of recycled water production in the event of sub-optimal performance of one or more pathogen reduction barriers.
TOC ratio, and UVA reduction.11–13 These studies have focussed on ozonation under ideal conditions, for example by removing suspended solids and using benchtop reactors.11 The ability to obtain LRV credits for ozonation/BMF could translate into major cost savings for wastewater recycling projects by reducing the need for additional treatment processes such as high-energy photochemical processes, or by reducing chemical consumption for downstream disinfection processes. Alternatively, obtaining additional LRV credits for a treatment system can increase the resilience of recycled water production in the event of sub-optimal performance of one or more pathogen reduction barriers.
Some previous studies have reported efforts to develop models for the prediction of microbial concentration based on some water quality data and operational parameters. Using an on-line UV absorbance analyser, Gerrity (2012)11 developed a model to predict microbial inactivation during ozonation. Gamage (2013)14 used O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TOC ratio, ΔUV254 and ΔTF to predict the inactivation of three surrogate microbes. Using a linear correlation for the prediction of microbial removal, Gamage reported that ΔUV254 and ΔTF were able to most effectively predict microbial inactivation in ozone/H2O2 systems. Gamage reported high variability in the prediction of E. coli concentration under different dosing conditions. However, traditional regression models might not be the optimum prediction tools for the complex relationships between microbial removal and operational or water quality data. Recently, multivariant predictive models based on Naïve Bayes have been developed to predict disinfection by-products (DBPs) concentration in drinking water streams.15 Although a few studies have investigated the prediction capacity of Naïve Bayes in the LRV performance of pathogens from wastewater streams,16 there are still limited studies on the use of prediction tools for on-line monitoring of water treatment process performance.
TOC ratio, ΔUV254 and ΔTF to predict the inactivation of three surrogate microbes. Using a linear correlation for the prediction of microbial removal, Gamage reported that ΔUV254 and ΔTF were able to most effectively predict microbial inactivation in ozone/H2O2 systems. Gamage reported high variability in the prediction of E. coli concentration under different dosing conditions. However, traditional regression models might not be the optimum prediction tools for the complex relationships between microbial removal and operational or water quality data. Recently, multivariant predictive models based on Naïve Bayes have been developed to predict disinfection by-products (DBPs) concentration in drinking water streams.15 Although a few studies have investigated the prediction capacity of Naïve Bayes in the LRV performance of pathogens from wastewater streams,16 there are still limited studies on the use of prediction tools for on-line monitoring of water treatment process performance.
The aim of this paper was to evaluate the use of several water quality and operational parameters as surrogates for the removal efficiency of microbial indicators during full-scale ozonation and biological media filtration of secondary treated wastewater. This research assessed previous reported indicators including colour and UVA. The key outcome is the presentation of a method for evaluating useful predictive variables through mutual information and calculating microbial LRVs using these predictors. This outcome is significant because it allows us to perform on-line monitoring to indicate the likely presence or removal of microbial substances in water samples without requiring cumbersome or time-consuming microbial measurements.
Methodology
Full scale wastewater treatment plant
Melbourne Water's Eastern Treatment Plant (ETP) is located 30 km south east of Melbourne, Australia, and treats around 40% of Melbourne's sewage. The ETP is a tertiary wastewater treatment plant which produces around 400 ML per day of high-quality treated water which meets the requirements of both safe discharge to the receiving marine environment and “Class A” recycled water. The ETP process uses ozonation and biological media filtration as an advanced treatment train for secondary treated wastewater. A simplified process diagram of the O3/BMF configuration at the ETP is depicted in Fig. 1. A dataset with 105 records of grab sample water quality from secondary effluent and BMF effluent was provided by Melbourne Water and used in developing prediction models.LRV observations from the data shows that the reduction of microbial indicators i.e., Clostridium perfringens, E. coli, and somatic coliphage was evidently successful through pre-ozonation and biological media filtration. Fig. 2 shows the average reduction of each microbial indicator after pre-ozonation and biological media filtration (sample point 2).
 | ||
| Fig. 2 log removal reduction of three microbial indicator after pre-ozonation and biological media filtration. | ||
Water quality data from sample points 1 and 2 were also measured for a range of parameters, including microbial indicators, suspended solids (SS), alkalinity, nitrite, nitrate, ammonia, ultraviolet transmittance (UVT), and colour.
Analytical methods
A portable Hach HQ30d meter was used to measure pH and temperature, and a portable Hach 2100Q IS meter was used to measure the turbidity of samples. Hach colourimetric methods with a Hach DR1900 meter were used for the measurement of nitrite, nitrate, COD, and colour. UVT, UVA and total suspended solids (TSS) were analysed by Australian Laboratory Services (ALS), Environmental Division, Melbourne, Australia. TOC was measured by Australian Water Quality Centre, South Australia. Bromate and Bromide were measured by National Measurement Institute (NMI), North Ryde, New South Wales, Australia. Microbial concentration of C. perfringens spores, E. coli and somatic coliphage was measured by Australian Water Quality Centre, South Australia.Prediction model development
The development of the prediction model was undertaken through a supervised learning scheme, as presented in Fig. 3. First, the predictive features and outcome of interest were pre-processed and went through discretisation steps. Then, in the feature selection step, the most useful (predictive) features were identified. The selected features along with the corresponding outcome labels were then used for the classification stage. This process was cross-validated 10-fold, and in each iteration of this validation, 80% of data were used for feature selection and training, while the remaining 20% of data were used for testing the classifier.The modelling processes applied here incorporates a range of statistical methods. These are summarised, indicating common terminology, acronyms and abbreviations in Table 1.
| Abbreviation | Meaning | Explanation |
|---|---|---|
| PA | Prediction accuracy | Quantifies the number of correctly predicted values divided by the total number of cases |
| PE | Prediction error | Quantifies the number of incorrectly predicted values divided by the total number of cases |
| KS | Kappa statistic | Measures the agreement between model predictions and actual values as a metric in the range [−1, 1]. KS = 1 means perfect agreement, KS = 0 means that agreement is equal to chance, and KS = −1 means “perfect” disagreement |
| AUC | Area under the curve for the receiver operating characteristic curve (ROC) | AUC ranges between 0 and 1, where 1 represents perfect matching, 0.5 reflects totally random models, and <0.5 indicates models generating predominantly inaccurate predictions |
| TPR | True positive rate | Rate of correct positive predictions (high reductions) |
| FPR | False positive rate | Failure to detect low reductions when they occurred |
| TNR | True negative rate | Rate of correct negative predictions (low reductions) |
| FNR | False negative rate | Failure to detect high reductions when they occurred |
| NB | Naïve Bayes | Probabilistic classifier based on Bayes theorem |
| GLM | Generalised linear model | Conventional linear regression models for a continuous response variable given continuous and/or categorical predictors |
| RF | Random forest | |
| SVM/bn | Support vector machine/binary | SVM algorithm can find a hyperplane in an N-dimensional space that distinctly classifies the data points using binary kernel function |
| SVM/GK | Support vector machine/Gaussian kernel | SVM algorithm that uses Gaussian kernel |
| SVM/PK | Support vector machine/polynomial kernel | SVM algorithm that uses polynomial kernel |
| SVM/rbf | Support vector machine/radial basis function | SVM algorithm that uses radial basis function as the kernel function |
In the following sections, “features” denote the system parameters which can be easily and continuously monitored (e.g., operational parameters and physico-chemical parameters with online detection). The features included: amount of change (pre O3/BMF − post O3/BMF) in total organic carbon (TOC), UV absorbance, UV transmittance, suspended solids, pH, alkalinity, colour, ammonia, nitrate and nitrite concentrations. “Outcome” denotes the amount of change (pre O3/BMF − post O3/BMF) in microbial indicators, which are more difficult and laborious to continuously measure. The features are used to make a prediction model, which can predict the outcomes through a supervised learning process.
Pre-processing
In the pre-processing step, features with too many missing values were excluded. For a feature to be assessed as useful, at least 25% of the feature values had to be non-missing. For the remaining features, missing values were replaced with mean values from the non-missing values of that attribute.Feature selection
The broad objective of feature selection is to identify the features with greatest predictive value. Finding the most characterising features is a crucial step in many pattern recognition applications.21,22 Feature selection shows the importance of features for prediction, and how these features are related, and thus minimizes the number of predictors in the final machine learning model and improves the performance of model.23 The central assumption when using a feature selection technique is that the data contain redundant or irrelevant features. Redundant features are those, which provide no more information than the currently selected features, and irrelevant features provide no useful information in any context.24,25 The specific purpose of feature selection is to minimize the number of redundant and irrelevant parameters in the final machine learning model to improve performance and generalizability.26 In this study, most predictive features were selected from the following water quality parameters: suspended solids (SS), alkalinity, nitrite, nitrate, ammonia, ultraviolet transmittance (UVT), and colour. By doing so, a reasonable ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15) between the number of features7 and the number of data samples (105) was attained.
15) between the number of features7 and the number of data samples (105) was attained.
In this study we used the minimal-redundancy-maximal-relevance algorithm (mRMR) developed by Peng (2005)23 because of its advantages in terms of both feature selection complexity and feature classification accuracy. The focus of this method is on mutual-information-based feature selection. The mutual information between two random variables X and Y is defined based on their entropies and their probabilistic density functions, as shown in (eqn 1(a)) to (1(c)):
| I(X, Y) = H(X) − H(X|Y) | (1(a)) |
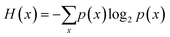 | (1(b)) |
And thus from (eqn 1(a)) and (1(b)):
 | (1(c)) |
The mRMR method seeks to maximise the relevance of a feature set for a specific class and minimise the redundancy of all features in the feature set. Relevance is defined by the average value of all mutual information (MI) values between the individual feature (xj) and the specific class (c). This is shown in formula (2), where (Sm−1) is a feature set with m − 1 features. The task is to select the mth feature from the set {X − Sm−1}. This is done through an incremental search method by selecting the feature that maximizes the condition inside the square brackets. Redundancy is the average value of all MI values (denoted with I in formula (1)) between the individual feature and every other feature in the set (xi).
 | (2) |
Using the mRMR method, for each outcome variable (i.e., microbial indicator concentration), the top features were determined from a random 80% of the data and used for training the prediction model in the next step. Assessment of the number of features' effect on prediction accuracy showed that selection of the top four features resulted in the best performance (ESI† A).
Discretisation
The outcome variables (i.e., microbial indicator concentrations) had continuous values. In order to perform multiclass classification, they needed to be discretised. Values of each outcome variable were divided into four quantiles, such that each quantile contained the same fraction of the total population. This approach was taken to ensure a balanced number of elements in each of the four classes.27For an n-element vector X, quantiles were computed by using a sorting-based algorithm as follows:
1. The sorted elements in X are taken as the (0.5/n), (1.5/n), …, ([n − 0.5]/n) quantiles. For example:
• For a data vector of five elements such as {6, 3, 2, 10, 1}, the sorted elements {1, 2, 3, 6, 10} respectively correspond to the 0.1, 0.3, 0.5, 0.7, 0.9 quantiles.
• For a data vector of six elements such as {6, 3, 2, 10, 8, 1}, the sorted elements {1, 2, 3, 6, 8, 10} respectively correspond to the (0.5/6), (1.5/6), (2.5/6), (3.5/6), (4.5/6), (5.5/6) quantiles.
2. Linear interpolation was used to compute quantiles for probabilities between (0.5/n) and ([n − 0.5]/n).
3. For the quantiles corresponding to the probabilities outside that range, the minimum or maximum values of the elements in X was assigned.
As a visual example, Fig. 4 shows the histogram of data values for log removal of variable E. coli. The bin edges were set such that it resulted in four quantiles, as explained above. The data that fell in the first quantile (first histogram bin) were labelled class 1, data in the second quantile were labelled class 2 and so on for classes 3 and 4.
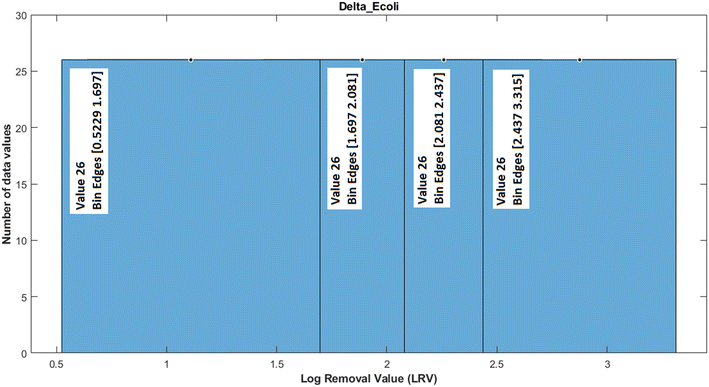 | ||
| Fig. 4 Histogram of log removal values for the outcome variable E. coli. Bin edges denote the boundaries of the four quantiles for discretisation. | ||
For consistency, all the classification algorithms compared in this study used discretised data values.
Classifiers
After completing pre-processing, feature selection and discretisation steps, prediction was carried out through several widely used supervised learning classifiers, namely Naïve Bayes (NB), support vector machines (SVM) with binary, Gaussian, radial basis function, and polynomial kernels, generalized linear model (GLM), and random forest (bootstrap-aggregated) decision trees. The definition for each of these classifiers are described below.The premise is to train a computer model by giving it features along with their corresponding outcomes, such that the model can later predict an outcome based on input features only. The algorithms to train and test the computer model were developed in MATLAB Version (R2019b). The computer algorithms find patterns between features that are exclusively associated with the outcomes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 split draws its justification from the well-known Pareto principle.31 This procedure was repeated 10 times with the training and testing partitions selected randomly each time.17 The model performance was assessed with several performance parameters. These parameters included prediction accuracy, prediction error, kappa statistic, area under the receiver operating characteristic curve (AUC), true positive rate (TPR), false positive rate (FPR), true negative rate (TNR) and false negative rate (FNR). Average ± standard deviation of performance measures over the 10 iterations of cross-validation was calculated.
20 split draws its justification from the well-known Pareto principle.31 This procedure was repeated 10 times with the training and testing partitions selected randomly each time.17 The model performance was assessed with several performance parameters. These parameters included prediction accuracy, prediction error, kappa statistic, area under the receiver operating characteristic curve (AUC), true positive rate (TPR), false positive rate (FPR), true negative rate (TNR) and false negative rate (FNR). Average ± standard deviation of performance measures over the 10 iterations of cross-validation was calculated.
Results and discussions
This study yielded a model that learned the multivariate associations between physico-chemical predictors and microbial indicators from a training dataset sampled from Melbourne Eastern Treatment Plant (Melbourne Water). Three specific findings resulting from this study were: 1) identifying the most predictive features; 2) discerning the predictor-outcome associations; and 3) assessing the impact of alternative prediction algorithms.Identifying the most predictive features
Following the feature selection process, the top four features for each microbial indicator were determined as shown in Table 2. These features were the most frequently selected in the 10-fold cross validation. The frequency of each top feature after the cross-validation is also shown in Table 2. UVT, nitrite, nitrate, and colour were the most predictive features for all of the studied microbial indicators. The reader is reminded that all features were Δ values (pre O3/BMF − post O3/BMF).Predictor-outcome association
The results from our model showed that an increase in Δ nitrite (from <0.1 mg L−1 to >0.4 mg L−1) with ΔUVT greater than 24% was found to be associated with an increase of Clostridium perfringens LRV from 0.5 to 1.3. This is consistent with the fact that high levels of nitrite can stimulate the growth of bacteria, and therefore the effectiveness of the water treatment process in decreasing nitrite concentration is correlated with reduction in microbial concentration of water. An increase in ΔUVT (from <19% to >33%), and colour reduction of 53 Pt–Co or more, with Δ nitrate >0.34 mg L−1 was found to be associated with increased E. coli LRV from 1.5 to 3.1. An increase in Δ colour (from <75% to >87%), and Δ nitrite of greater than 0.2 mg L−1 was found to be associated with increase of coliphage LRV from 1.2 to 3.6.While these findings are noteworthy and useful as a guideline to the influence of changes in physico-chemical predictors on changes in microbial indicator concentration, it should be noted that the predictors are surrogate measures of the treatment performance and that there is not necessarily a direct relationship between the measurement and the presence of the microbial indicator.
Many more hidden and intricate associations may exist between these variables that cannot be detected from simple assessment of data. Pattern recognition and sophisticated machine learning algorithms were used to detect those associations and be able to predict the amount of microbial LRV due to O3/BMF solely based on measurement of the four predictors before and after the water treatment process.
Effect of prediction algorithm
The prediction model, developed in the form of a MATLAB script, took the difference between four physico-chemical measurements (namely UVT, colour, nitrite and nitrate) before and after the O3/BMF process as inputs and predicted the microbial removal value range associated with those inputs. Classification was performed using a range of prediction algorithms, which were described in the classifiers section. The performance measures for each of these classifiers are presented in Table 3. Eight performance matrices were compared in Table 3 (abbreviations are described in Table 1). These values were calculated based on 10-fold cross validation for each of the seven prediction algorithms. The calculation method for the reported performance measures is explained in ESI† B.| Pathogen | Performance measure | NB | GLM | RF | SVM/bn | SVM/GK | SVM/PK | SVM/rbf |
|---|---|---|---|---|---|---|---|---|
| NB: Naïve Bayes, GLM: generalized linear model, RF: random forests, SVM/bn: support vector machines with binary kernel, SVM/GK: support vector machines with Gaussian kernel, SVM/PK: support vector machines with polynomial kernel, SVM/rbf: support vector machines with radial basis function kernel, LRV: log removal, PA: prediction accuracy, PE: prediction error, KS: kappa statistic, AUC: area under curve, TPR: true positive rate, FPR: false positive rate, TNR: true negative rate, FNR: false negative rate. | ||||||||
| Clostridium perfringens LRV | PA | 0.73 ± 0.03 | 0.92 ± 0.00 | 0.77 ± 0.03 | 0.76 ± 0.03 | 0.78 ± 0.02 | 0.75 ± 0.02 | 0.77 ± 0.03 |
| PE | 0.27 ± 0.03 | 0.08 ± 0.00 | 0.23 ± 0.03 | 0.24 ± 0.03 | 0.22 ± 0.02 | 0.25 ± 0.02 | 0.23 ± 0.03 | |
| KS | 0.26 ± 0.10 | 0.00 ± 0.00 | 0.34 ± 0.09 | 0.32 ± 0.07 | 0.37 ± 0.06 | 0.31 ± 0.05 | 0.33 ± 0.09 | |
| AUC | 0.81 ± 0.01 | 0.79 ± 0.01 | 0.71 ± 0.04 | 0.80 ± 0.11 | 0.90 ± 0.01 | 0.76 ± 0.08 | ||
| TPR | 0.47 ± 0.07 | 0.00 ± 0.00 | 0.56 ± 0.07 | 0.54 ± 0.06 | 0.61 ± 0.05 | 0.49 ± 0.05 | 0.60 ± 0.08 | |
| FPR | 0.18 ± 0.02 | 0.02 ± 0.00 | 0.14 ± 0.02 | 0.14 ± 0.02 | 0.13 ± 0.01 | 0.16 ± 0.02 | 0.13 ± 0.02 | |
| TNR | 0.82 ± 0.02 | 0.98 ± 0.00 | 0.86 ± 0.02 | 0.86 ± 0.02 | 0.87 ± 0.01 | 0.84 ± 0.02 | 0.87 ± 0.02 | |
| FNR | 0.53 ± 0.07 | 1.00 ± 0.00 | 0.44 ± 0.07 | 0.46 ± 0.06 | 0.39 ± 0.05 | 0.51 ± 0.05 | 0.40 ± 0.08 | |
| E. coli LRV | PA | 0.74 ± 0.02 | 0.93 ± 0.00 | 0.74 ± 0.03 | 0.75 ± 0.03 | 0.75 ± 0.02 | 0.75 ± 0.03 | 0.73 ± 0.03 |
| PE | 0.26 ± 0.02 | 0.07 ± 0.00 | 0.26 ± 0.03 | 0.25 ± 0.03 | 0.25 ± 0.02 | 0.25 ± 0.03 | 0.27 ± 0.03 | |
| KS | 0.29 ± 0.07 | 0.00 ± 0.00 | 0.31 ± 0.07 | 0.34 ± 0.07 | 0.34 ± 0.06 | 0.32 ± 0.09 | 0.28 ± 0.08 | |
| AUC | 0.79 ± 0.01 | 0.82 ± 0.01 | 0.73 ± 0.06 | 0.88 ± 0.01 | 0.70 ± 0.11 | 0.88 ± 0.01 | ||
| TPR | 0.49 ± 0.05 | 0.00 ± 0.00 | 0.49 ± 0.05 | 0.50 ± 0.05 | 0.52 ± 0.05 | 0.50 ± 0.06 | 0.47 ± 0.06 | |
| FPR | 0.17 ± 0.02 | 0.02 ± 0.00 | 0.17 ± 0.02 | 0.17 ± 0.02 | 0.16 ± 0.02 | 0.17 ± 0.02 | 0.18 ± 0.02 | |
| TNR | 0.83 ± 0.02 | 0.98 ± 0.00 | 0.83 ± 0.02 | 0.83 ± 0.02 | 0.84 ± 0.02 | 0.83 ± 0.02 | 0.82 ± 0.02 | |
| FNR | 0.51 ± 0.05 | 1.00 ± 0.00 | 0.51 ± 0.05 | 0.50 ± 0.05 | 0.48 ± 0.05 | 0.50 ± 0.06 | 0.53 ± 0.06 | |
| Coliphage | PA | 0.75 ± 0.02 | 0.92 ± 0.00 | 0.75 ± 0.04 | 0.76 ± 0.02 | 0.78 ± 0.02 | 0.76 ± 0.02 | 0.76 ± 0.03 |
| PE | 0.25 ± 0.02 | 0.08 ± 0.00 | 0.25 ± 0.04 | 0.24 ± 0.02 | 0.22 ± 0.02 | 0.24 ± 0.02 | 0.24 ± 0.03 | |
| KS | 0.33 ± 0.07 | 0.00 ± 0.00 | 0.34 ± 0.09 | 0.35 ± 0.06 | 0.41 ± 0.05 | 0.37 ± 0.06 | 0.37 ± 0.08 | |
| AUC | 0.83 ± 0.01 | 0.85 ± 0.01 | 0.82 ± 0.04 | 0.91 ± 0.01 | 0.75 ± 0.14 | 0.92 ± 0.01 | ||
| TPR | 0.49 ± 0.04 | 0.00 ± 0.00 | 0.51 ± 0.07 | 0.51 ± 0.04 | 0.56 ± 0.04 | 0.53 ± 0.05 | 0.53 ± 0.06 | |
| FPR | 0.17 ± 0.02 | 0.02 ± 0.00 | 0.16 ± 0.02 | 0.16 ± 0.01 | 0.15 ± 0.01 | 0.16 ± 0.01 | 0.16 ± 0.02 | |
| TNR | 0.83 ± 0.02 | 0.98 ± 0.00 | 0.84 ± 0.02 | 0.84 ± 0.01 | 0.85 ± 0.01 | 0.84 ± 0.01 | 0.84 ± 0.02 | |
| FNR | 0.51 ± 0.04 | 1.00 ± 0.00 | 0.49 ± 0.07 | 0.49 ± 0.04 | 0.44 ± 0.04 | 0.47 ± 0.05 | 0.47 ± 0.06 | |
The AUC score varies from 0–1, with 0.5 indicating a totally random model and 1 no error in prediction. AUC < 0.5 denotes models predicting erroneously most of the time. Values of 0.5–0.7 indicate poor classification performance; values of 0.7–0.9 indicate fair classification performance, and values higher than 0.9 indicate excellent classification performance. Prediction accuracy is calculated as the total number of correct predictions divided by the total number of cases. This metric ranges between 0 and 100% with higher values indicating better prediction. Cohen's kappa statistic measures the agreement between model predictions and actual values as a metric in the range [−1, 1] considering adjustment due to chance effects.32 Kappa = 1 means perfect agreement, kappa = 0 means that agreement is equal to chance, and kappa = −1 means “perfect” disagreement.32 Distinct levels of agreement in the range between 0 and 1 have been defined for kappa coefficient:33 <0.2 = slight; 0.2–0.4 = fair; 0.4–0.6 = moderate; 0.6–0.8 = substantial; and >0.8 = almost perfect.
Assessing the prediction performance for three microbial communities showed that with the exception of the GLM classifier, the prediction accuracy for other classifiers (including NB, RF and all types of SVM) is around 75%, which is very promising. However, in order to evaluate the performance of a classifier, all performance measures should be considered simultaneously. Performance of a classifier is reliable when the value of both the true positive rate (TPR) and true negative rate (TNR) are greater than 50%. The higher KS and AUC is also representative of a better prediction performance.
Although prediction accuracy of the GLM classifier was above 90%, TPR was around zero and TNR is around 1 which means that relying on prediction accuracy was not sufficient and GLM was not an effective classifier for prediction of microbial removal during these water treatment processes.
With the TPR of less than 50% (47%, 49% and 47% for clostridium perfringens, E. coli and coliphage LRV, respectively), the Naïve Bayes model was also not a good classifier for any of the microbial communities. On the other hand, support vector machine with Gaussian kernel had above 50% TPR for all three microbial indicators. FPR was also very promising. Moreover, AUC and KS were the highest compared to the values of other classifiers.
For coliphage LRV, although the value of PA, TPR and TNR were almost similar in RF and all types of SVM, however, the AUC and KS was higher in SVM/GK. Therefore, SVM/GK was considered the most suitable classifier among all other classifiers.
The significance of results lies in the capacity of the SVM/GK model to predict the microbial indicator log removal value of a sample with unknown microbial concentration based on its previously learned knowledge and four simple measurements (i.e., UVT, colour, nitrite and nitrate) before and after the O3/BMF process. As shown in ESI† A, optimal prediction accuracy resulted with these four predictors. This has great implications for faster and more cost-effective assessment of the efficacy of O3/BMF water treatment process for microbial activity removal. The prediction model, developed in the form of a MATLAB script, takes the four physico-chemical measurements as inputs and calculates the microbial removal value range associated with those inputs.
Conclusions
Using mutual information and support vector machines, we showed that several surrogate measures can efficiently predict the level of microbial indicator removal during ozonation–biofiltration (O3/BMF).Key findings from this study are:
• Three microbial indicators; Clostridium perfringens, E. coli, and somatic coliphage have been efficiently removed by the combination of ozonation and biological media filtration.
• Removal of three microbial indicators Clostridium perfringens, E. coli, and somatic coliphage can be predicted based on physico-chemical measurements.
• Feature selection based on mutual information showed that the top four physico-chemical predictors of microbial indicator removal were UVT, colour, nitrite and nitrate concentrations.
• The best prediction algorithm was found to be support vector machines with Gaussian kernel (SVM/GK), followed by SVM with radial basis function, and random forests.
• Using the SVM/GK classifier, prediction accuracy for all microbial removals was above 75%, AUC ≥ 0.80, and kappa statistic (KS) ≥ 0.34.
• This prediction model, developed in the form of a MATLAB script, takes the four physico-chemical measurements as inputs, and calculates the microbial removal value range associated with those inputs. Therefore, this model can be used to assess the performance of other systems based on changes in the surrogate measures from pre- to post-water treatment process.
While removal of most microbial indicators during O3/BMF cannot be continuously monitored by online processes, the methodology discussed in this study provides a fast and cost-effective alternative based on surrogate measures. This is important because continuous online monitoring of water treatment process performance is an essential step in ensuring reliable water quality outcomes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was supported by funding provided by the Australian Research Council (ARC) Future Fellowships Program, FT170100371. The authors gratefully acknowledge Melbourne Water for access to water treatment processes and samples and John Mieog from Melbourne Water for his assistance.References
- M. M. Huber, A. Göbel, A. Joss, N. Hermann, D. Löffler and C. S. McArdell, et al., Oxidation of pharmaceuticals during ozonation of municipal wastewater effluents: A pilot study, Environ. Sci. Technol., 2005, 39(11), 4290–4299 CrossRef CAS PubMed.
- M. C. Dodd, M. O. Buffle and U. Von Gunten, Oxidation of antibacterial molecules by aqueous ozone: Moiety-specific reaction kinetics and application to ozone-based wastewater treatment, Environ. Sci. Technol., 2006, 40(6), 1969–1977 CrossRef CAS PubMed.
- M. C. Dodd, H. P. E. Kohler and U. Gunten, Oxidation of antibacterial compounds by ozone and hydroxyl radical: Elimination of biological activity during aqueous ozonation processes, Environ. Sci. Technol., 2009, 43(7), 2498–2504 CrossRef CAS PubMed.
- C. Sigmon, G. A. Shin, J. Mieog and K. G. Linden, Establishing Surrogate - Virus Relationships for Ozone Disinfection of Wastewater, Environ. Eng. Sci., 2015, 32(6), 451–460 CrossRef CAS.
- US Environmental Protection Agency, Guidelines for Water Reuse, Development, 2012, 26, 252 Search PubMed.
- Natural Resources Management Ministerial Council, Australia Guidelines for Water Recycling: Managing Health and Environmental Risks (Phase 1), Natl Water Qual Manag Strateg, 2006, 415 Search PubMed.
- World Health Organisation, Guidance for Producing Safe Drinking-Water, 2017, p. 152 Search PubMed.
- M. A. Sari, J. Oppenheimer, K. Robinson, J. E. Drewes, A. N. Pisarenko and V. Sundaram, et al., Persistent contaminants of emerging concern in ozone-biofiltration systems: Analysis from multiple studies, AWWA Water Sci., 2020, 2(5), 1–19 Search PubMed.
- M. Arnold, J. Batista, E. Dickenson and D. Gerrity, Use of ozone-biofiltration for bulk organic removal and disinfection byproduct mitigation in potable reuse applications, Chemosphere, 2018, 202, 228–237 CrossRef CAS PubMed.
- D. Gerrity, M. Arnold, E. Dickenson, D. Moser, J. D. Sackett and E. C. Wert, Microbial community characterization of ozone-biofiltration systems in drinking water and potable reuse applications, Water Res., 2018, 135, 207–219 CrossRef CAS PubMed.
- D. Gerrity, S. Gamage, D. Jones, G. V. Korshin, Y. Lee and A. Pisarenko, et al., Development of surrogate correlation models to predict trace organic contaminant oxidation and microbial inactivation during ozonation, Water Res., 2012, 46(19), 6257–6272 CrossRef CAS PubMed.
- V. Nanaboina and G. V. Korshin, Evolution of absorbance spectra of ozonated wastewater and its relationship with the degradation of trace-level organic species, Environ. Sci. Technol., 2010, 44(16), 6130–6137 CrossRef CAS PubMed.
- A. N. Pisarenko, B. D. Stanford, D. Yan, D. Gerrity and S. A. Snyder, Effects of ozone and ozone/peroxide on trace organic contaminants and NDMA in drinking water and water reuse applications, Water Res., 2012, 46(2), 316–326 CrossRef CAS PubMed.
- S. Gamage, D. Gerrity, A. N. Pisarenko, E. C. Wert and S. A. Snyder, Evaluation of Process Control Alternatives for the Inactivation of Escherichia coli, MS2 Bacteriophage, and Bacillus subtilis Spores during Wastewater Ozonation, Ozone: Sci. Eng., 2013, 35(6), 501–513 CrossRef CAS.
- R. A. Li, J. A. McDonald, A. Sathasivan and S. J. Khan, A multivariate Bayesian network analysis of water quality factors influencing trihalomethanes formation in drinking water distribution systems, Water Res., 2021, 190, 116712 CrossRef CAS PubMed.
- G. Carvajal, D. J. Roser, S. A. Sisson, A. Keegan and S. J. Khan, Modelling pathogen log10 reduction values achieved by activated sludge treatment using naïve and semi naïve Bayes network models, Water Res., 2015, 85, 304–315 CrossRef CAS PubMed.
- D. Koller and N. Friedman, Probabilistic graphical models: principles and techniques, MIT Press, Massachusetts, 2009 Search PubMed.
- U. B. Kjræulff and A. L. Madsen, Bayesian Networks and Influence Diagrams: a Guide to Construction and Analysis, Springer Science+Business Media, New York, 2009, pp. 63–131 Search PubMed.
- B. G. Marcot, Metrics for evaluating performance and uncertainty of Bayesian network models, Ecol. Modell., 2012, 230, 50–62 CrossRef.
- I. H. Witten and E. Frank, The Morgan Kaufmann Series in Data Management Systems, Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations, 1999, vol. 31, p. 371 Search PubMed.
- F. J. Iannarilli and P. A. Rubin, Feature selection for multiclass discrimination via mixed-integer linear programming, IEEE Trans. Pattern Anal. Mach. Intell., 2003, 25(6), 779–783 CrossRef.
- A. Jain and D. Zongker, Feature selection: evaluation, application, and small sample performance, IEEE Trans. Pattern Anal. Mach. Intell., 1997, 19(2), 153–158 CrossRef.
- H. Peng, F. Long and C. Ding, Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy, Lect Notes Comput Sci (including Subser Lect Notes Artif Intell Lect Notes Bioinformatics), 2005, vol. 278, pp. 1226–1238 Search PubMed.
- N. Memarian, S. Kim, S. Dewar, J. Engle Jr. and R. J. Staba, Multimodal data and machine learning for surgery outcome prediction in complicated cases of mesial temporal lobe epilepsy, Physiol. Behav., 2017, 176(3), 139–148 Search PubMed.
- A. L. Blum and P. Langley, Artificial Intelligence Selection of relevant features and examples in machine, Artif. Intell., 1997, 97(1–2), 245–271 CrossRef.
- W. T. Kerr, P. K. Douglas, A. Anderson and M. S. Cohen, The utility of data-driven feature selection: Re: Chu et al., 2012, Neuroimage, 2014, 84, 1107–1110 CrossRef PubMed.
- E. Langford, Quartiles in elementary statistics, J. Stat. Educ., 2006, 14(3), 1–20 Search PubMed.
- B. E. Boser, V. N. Vapnik and I. M. Guyon, Training Algorithm Margin for Optimal Classifiers, Perception, 1992, 144–152 Search PubMed.
- P. McCullagh and J. A. Nelder, Generalized Linear Models, Chapman and Hall, London, 2nd edn, 1989 Search PubMed.
- L. Breiman, Random forests, in Machine learning, Kluwer Academic Publishers, Boston, 2001, pp. 5–32 Search PubMed.
- V. R. Joseph and H. M. Stewart, Optimal ratio for data splitting, Statistical Analysis and Data Mining, 2022, vol. 15(3), pp. 531–538 Search PubMed.
- G. H. Rosenfield and K. Fitzpatrick-Lins, A coefficient of agreement as a measure of thematic classification accuracy, Photogramm. Eng. Remote Sens., 1986, 52(2), 223–227 Search PubMed.
- J. R. Landis and G. G. Koch, The measurement of observer agreement for categorical data, Biometrics, 1977, 33(1), 159–174 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ew00747a |
| This journal is © The Royal Society of Chemistry 2023 |


