Understanding the impact of catholyte flow compartment design on the efficiency of CO₂ electrolyzers

Abstract

This work explores and provides new understanding how catholyte flow compartment design and catholyte bubble flow characteristics of a gas diffusion electrode inside a CO₂ flow cell electrolyzer affect its electrocatalytic reactivity and product selectivity. Focusing on Cu-based GDEs for CO₂ electroreduction to hydrocarbons at high current densities (50–700 mA cm⁻²), four basic compartment designs were selected, 3D printed and investigated. Experiments were coupled to computational fluid dynamics simulation of catholyte flow and bubble dynamics. The findings from this work suggest a homogenous fluid velocity distribution combined with fluid velocity in the range between 0.1–0.01 m s⁻¹ to be optimal for high yields in C₂₊ products at high current densities. Special focus was placed on the role and relation between gas bubble dynamics and local pH, both strongly affected by the design architecture. From our experimental observations and simulations, we propose a hydrodynamic “volcano” model addressing the competition between bubble release rate and local pH, both controlled by catholyte flow velocity. The balance between fast bubble release and high enough local pH across the electrode surface puts the electrolyzer operation at the top of the performance volcano.

---

Broader context

Electrochemical CO₂ reduction is a promising way to use renewable electricity combined with concentrated CO₂ from point sources or atmospheric CO₂ from direct air capture as a sustainable source for value-added chemicals, energy storage molecules or liquid fuels. For the industrial application of CO₂ electrolyzers, devices must be developed to operate at high current densities and product selectivity. To realize such high-performing CO₂RR electrolyzers, cell design and its complicated effects on mass transport need to be understood. This study focused on Cu-based GDEs for CO₂ electroreduction to hydrocarbons at high current densities (50–700 mA cm⁻²). We designed, simulated and experimentally tested several fluid compartments to understand how fluid flow affects copper-based GDEs selectivity. Particular focus was placed on the role and relation between gas bubble dynamics and local pH, both strongly influenced by the design architecture. From our experimental observations and simulations, we propose a hydrodynamic “volcano” model addressing the competition between bubble release rate and local pH, both controlled by catholyte flow velocity.

Introduction

The continuous rise of atmospheric CO₂ concentration drives the increase of global temperatures, demanding strategies to reduce anthropogenic CO₂ emissions.^1,2 Accordingly, there is international understanding on the urgent need to set emission goals on an avenue leading towards a “net zero” emission future.³ To achieve that, the transition from fossil energy carriers to renewables is crucial, and at the same time, carbon capture and utilization strategies will be necessary to reduce global CO₂ emissions further.⁴ The electrochemical CO₂ reduction is a promising way to use renewable electricity combined with concentrated CO₂ from point sources or atmospheric CO₂ from direct air capture as a sustainable source for value-added chemicals, energy storage molecules or liquid fuels.⁵

Early research in electrochemical CO₂ reduction utilized H-cells that relied on CO₂ saturation by bubbling in the bulk electrolyte for supply of reactant and fully submerged electrodes.^6–8 This method allowed screening catalysts and performing fundamental studies; however, this cell type is limited by CO₂ transport, allowing only very low current density (∼35 mA cm⁻²) making it unsuitable for industrialization and scale-up.⁹ To increase the current density of CO₂ electrolyzers, gas diffusion electrodes (GDEs) were proposed, which ensure a more direct catalyst/electrode interface to gaseous CO₂. This enabled current densities exceeding 1 A cm⁻².^10,11 This vast difference in available CO₂RR currents between GDE-based cells and H-type cells lies in the improved delivery of CO₂ in GDEs towards the catalytically active centers.¹² GDEs have become an integral part of a number of different CO₂ electrolyzer cell configurations, such as MEAs,^13,14 dual electrolyte flow cells,^15,16 zero-gap and finite-gap architectures¹⁷ and microfluidic cells.¹⁸ While impressive electrolyzer performances resulted from studies of such cells, only few works set out to understand the impact of CO₂ electrolyzer cell component design, in particular the catholyte flow compartment design, on selectivity, activity and stability. Corral et al. optimized electrochemical cells via 3D printing and showed the significant advantage of such techniques for rapid development of electrochemical cells.¹⁹ Xing et al. investigated the effects of CO₂ reactant delivery, where the CO₂ delivery into the GDE-based catalyst layer could be enhanced by changing from a serpentine towards an interdigitated flow field.²⁰ Then, Subramanian et al. reported, contrary to the findings of Xing et al., that the serpentine flow field was superior in terms of long-term stable CO production due to reduced issues correlated to salt precipitation.²¹ Recently, Blake et al. developed a 2D computational model for a CO₂RR flow electrolyzer and showed that the scale-up from a 5 cm² to a 1 m² sized system is accompanied with inhomogeneities in the flow channel that resulted in the decrease of several performance metrics.²² Overall, a small number of key electrolyte flow compartment designs for CO₂RR flow cells were put forward and utilized to date in the literature, among them the linear,^23,24 serpentine,²⁵ shifted^26,27 or designs with a stagnant electrolyte.²⁸ However, to date, no rationale design principles were ever put forward for the choice of a particular electrolyte flow architecture or the choice of specific flow operation conditions. This made the previous design choices appear somewhat arbitrary. More specifically, there is only a very small body of work on CO₂RR electrolyzers that critically analyzed and discussed the appearance and impact of gas bubbles in the catholyte compartment.^29,30 There is much to be learned from the water electrolysis community, where discussions of bubble-induced effects on catalyst stability, energy efficiency and mass transport have greatly progressed in recent years and hence are more prevalent.^31,32 This contribution addresses this unmet need.

The present work explores and provides deeper understanding of the effects of electrolyte flow compartment geometry (sometimes referred to as electrolyte channel or electrolyte flow field) and of the effect of flow conditions (local velocities and bubble density) on the performance of liquid-fed CO₂RR cells at high current densities (50–700 mA cm⁻²). We selected a set of archetypical flow compartment architectures (linear, serpentine and shifted) and 3D print manufactured a range of specific design implementations. The flow compartments were combined with Cu based GDEs into single CO₂RR flow electrolyzers. In parallel to experiments, we carried out CFD simulations to predict and understand how the electrolyte flow compartment design affects the fluid velocity distribution. Correlating our experiments with our simulations, we found that the electrolyte fluid velocity distribution is critical to achieve high C₂₊ product selectivity at high rates. Our study suggests a homogenous fluid velocity distribution combined with fluid velocities in the range between 0.1–0.01 m s⁻¹ as optimal for high yields in C₂₊ products at high current densities. Additionally, we analyze and discuss the role and relation of gas bubble formation and detachment during electrolysis and the resulting local pH, which are both strongly affected by the choice of flow design. We propose a simple hydrodynamic volcano model that can rationalize the experimental observation in line with computations.

CO₂ electrolyzer test setup and design workflow

Fig. 1 details the CO₂ electrolyzer setup, cell design and catholyte compartment design workflow. Fig. 1a shows a flow diagram with all relevant fluid flows and components (an image of the setup is shown in Fig. S1, ESI†). We note that two separate CO₂ feeds were employed, one directly entering the electrolysis cell and the other purging the gas headspace of the catholyte gas–liquid separation vessel. The purge line proved vital for the discovery of unusual, previously overlooked patterns of product gas distribution between gas and liquid compartments discussed below. Importantly, a nitrogen-“bleed” was included as an internal standard for accurate evaluation of exit flows and subsequent faraday efficiencies (FE).^13,33 Pressure levels at various points along the electrolyzer system were measured and controlled using sensors and regulators, which is key to establish a reproducible and stable pressure drop across the cell. Fig. 1b shows an exploded view of our single (cathode)-gap flow electrolyzer. The gas diffusion layer (GDL) used for all experiments was PTFE-based and covered by a catalyst layer composed of a copper oxide catalyst and Nafion binder. Top-view SEM images of the prepared electrodes and after reaction can be seen in Fig. S2 and S3 (ESI†). Our focus, however, lies on the design of the catholyte compartment. Further details on the cell assembly are given in Fig. S4 (ESI†). Images and configurations of the four individual fluid compartments explored here are shown in Fig. S5–S7 (ESI†). Fig. 1c illustrates our research workflow. First, the individual electrolyte compartment configurations were designed using a CAD software, then computational fluid dynamics (CFD) modelling was performed to study fluid velocity distribution inside the electrolyte chamber. After that, specific designs were selected and 3D printed. Finally, the newly prepared fluid compartments were subjected to our CO₂ electrolyzer test protocol, data analyzed and evaluated.

Fig. 1 Illustration of the main components of this work. (a) Process flow diagram of the setup used for electrochemical cell testing. (b) Exploded view of our cell deployed for catalytic tests. (c) Schematic representation of the workflow starting from the initial CAD design of fluid compartments to the final electrochemical experiments.

Geometric choice and CFD Study of flow compartments

The catholyte compartment comprises the electrolyte-filled space between the membrane and cathode surface. To investigate the impact of fluid dynamics in catholyte compartments of CO₂ flow electrolyzers, we selected and designed three distinct types of flow compartment geometries and studied a total of four different designs. Fig. 2 displays the selected catholyte compartment designs and the associated CFD simulation results. All experimental measurements and computational CFD simulations were performed using an electrolyte flow rate of 50 mL min⁻¹. Other simulations parameters are provided in Table S1 (ESI†) and an exemplary mesh structure is shown in Fig. S8 (ESI†). All fluid compartments had a 0.2 mm gap between the endplate and cathode surface dictated by experimental compression of employed gaskets. This small space enables, even in the case of the Serpentine flow compartment, that the electrode surface below the Serpentine ribs (land) remains wetted with electrolyte, which is vital for a fair electrochemical performance comparison.

Fig. 2 CFD simulation results of studied flow compartment geometries. Shown here are contour and vector representations of the CFD results for the studied flow compartments. CFD simulation results shown for: (a) Linear flow arrangement, “Linear-wide”; (b) Shifted flow arrangement, “Shifted”; (c) Serpentine flow arrangement, “Serpentine” and (d) Linear flow arrangement, “Linear”. Inlet and outlet diameters leading to the central flow compartment are 2 × 1 mm² in all cases, except for “Linear-wide” that is 3.45 × 2 mm².

(Co)linear flow designs

We chose two distinct linear geometries shown in Fig. 2a and d. While in both cases the electrolyte inlet and outlet flow channel directions are arranged colinear and diagonally, their diameter differs. The design referred to as “Linear wide”, Fig. 2a, has inlet and outlet apertures of 3.45 × 2 mm², wider than the 2.0 × 1.0 mm² of that referred to as “Linear”, Fig. 2d. The fluid velocity distribution of “Linear wide” was quite inhomogeneous, which can be seen in both contour and vector representation of Fig. 2a. The reason for this rather inhomogeneous flow is the large inlet and outlet apertures leading to a diagonally directed flow across the center of the flow chamber and relatively weak recirculation and, therefore, stagnant zones in the edges of the flow chamber. By contrast, the “Linear” design, Fig. 2d, showed a more pronounced recirculation, originating from the smaller size of inlet and outlet apertures. This creates a considerable barrier for the fluid flow, causing higher turbulence and mixing inside the fluid chamber.

Shifted flow design

Another commonly used flow compartment design is what we here call “Shifted”. In the Shifted geometry, shown in Fig. 2b, the fluid is forced to flow against the wall of the fluid compartment and then redistribute before flowing into the outlet. This causes a more homogenous fluid velocity distribution compared to the linear arrangement. Importantly, the Shifted arrangement eliminates the high fluid flow stream condition that is observed for either “Linear” design in the center of the fluid chamber.

Serpentine flow design

Finally, a fourth fluid compartment design referred to as “Serpentine” is shown in Fig. 2c. It differs fundamentally from the other open fluid compartment designs due to the addition of ribs (often referred to as “land” in the fuel cell and water electrolyzer literature) that form a serpentine path for a guided flow of the electrolyte. This fluid compartment design can be perceived as an open fluid chamber design with an additional turbulence promoter, which is a commonly employed feature in electrochemical flow cells. The Serpentine geometry results in the most homogenous fluid flow distribution inside the chamber out of all investigated flow compartment geometries, as seen in the contour representation of the flow velocity in Fig. 2c.

Electrochemical performance comparison of fluid compartment designs

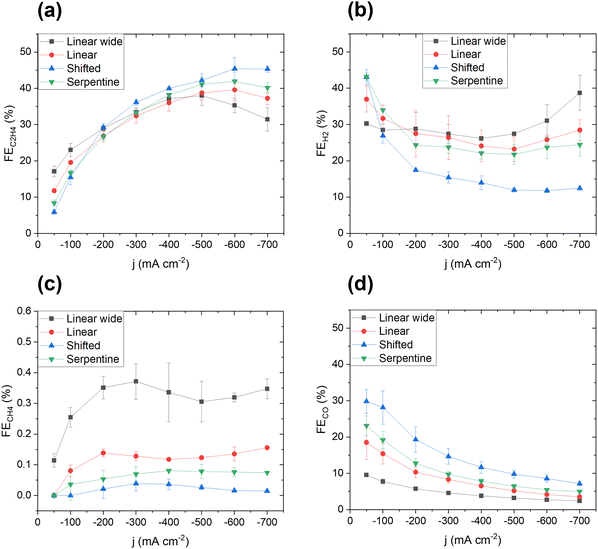
In Fig. 3, the faradaic efficiencies, FE, of the four major gas products are shown versus the applied cathodic current density. The ethylene faradaic efficiency correlated exceptionally strong with current density, (Fig. 3a) for all designs. In the low current density regime (50–200 mA cm⁻²), the Linear wide compartment showed the most favorable faradaic ethylene efficiency, FE_C2H4, followed by the Linear, Serpentine and Shifted fluid compartment designs. At 200 mA cm⁻², the FE_C2H4 values almost coincide for all flow designs, before they show an opposite trend at higher current densities (200–700 mA cm⁻²). A similar trend is evident for FE_H2 (Fig. 3b), when comparing the high and low current density regimes. In the low current density regime, the Linear wide produced the least amount of hydrogen, followed by Linear, Serpentine and Shifted. Beyond 100 mA cm⁻², the Shifted started to reveal a favorably low hydrogen production, a trend that was sustained up to 700 mA cm⁻². Again, 200 mA cm⁻² appeared to be a critical current density point for the system, which will be further discussed below. Interestingly, neither the methane faradaic efficiency, FE_CH4, (Fig. 3c), nor the carbon monoxide faradaic efficiency, FE_CO, (Fig. 3d) exhibited efficiency crossover points. Trends were maintained at all currents, and their trends were perfectly opposite to each other. This analysis reveals that the hydrodynamics of the Shifted flow compartment design represents the most desirable cell configuration for superior operation over a wide load range.

Fig. 3 Electrochemical performance comparison for all tested flow compartment designs. Faradaic efficiency (y-axis) as a function of applied geometric current density (x-axis) was plotted for (a) ethylene, (b) hydrogen, (c) methane and (d) CO.

The corresponding cathode polarization curves of each design are shown Fig. S9 (ESI†). A comparison remained meaningful up to approximately 200 mA cm⁻² beyond which gas bubbles induced a high noise level. Linear wide exhibited the highest cathode potential, followed by Linear, while Serpentine and Shifted were comparable.

Fluid dynamics – cell performance relationship and mechanisms

To arrive at a deeper understanding of the observed electrolyzer cell performance trends, we correlate the fluid velocity distributions of each design. Our analyses reveals that a homogenous fluid velocity distribution in the cathode flow compartment invariably resulted in an enhancement of ethylene production. Therefore, we propose that the catholyte fluid velocity distribution serves as an important controlling factor for high ethylene production with suppressed competing hydrogen production at relevant large current density. We hypothesize that the impact of the fluid dynamics inside the cathode flow compartment originates from two basic mechanisms: (i) the variations in the local chemical reaction environment, e.g. pH, and (ii) the local rate of removal of gaseous products from the cathode surface, e.g. via a hydrodynamic “bubble management”. We will discuss the two mechanisms now in more detail.

As to the effects of local pH, there is consensus that high local pH suppresses the production of methane and hydrogen due to the proton dependence of their rate laws, thereby favoring the CO dimerization reaction.^10,15 Accordingly, a more stagnant electrolyte layer will lead to a thicker Nernst diffusion layer due to reduced convection. This leads to an increase in local pH, especially at higher current densities. The Linear wide flow compartment has more stagnant zones than the other flow chamber designs, leading to areas with high local pH. This consistently explains why the Linear wide flow compartment design outperforms the other fluid compartments in terms of FE_H2 and FE_C2H4 in the low current density regime. However, the two Linear designs also show central regions of high fluid velocity that promote hydrogen and methane production. This effect of local pH change due to variations in fluid velocity was studied further using the Linear fluid compartment (Fig. S10, ESI†). Indeed, by increasing the average fluid velocity in the electrolyte flow chamber, FE_CH4 and FE_H2 increased. As a result, our analysis is able to provide guidelines for fluid compartment designs and reveals fluid velocities in the range of 0.01 to 0.1 m s⁻¹ as optimal to remove gas bubbles efficiently and establish an optimal local pH to suppress HER and the formation of methane. We elaborate on this guideline further in the Supplementary discussion I and Fig. S11 (ESI†).

As to the gas bubble formation and dynamics, we observed characteristic discolorations on the electrode surfaces after disassembly, especially when we used the Serpentine and Linear wide flow compartments. Images of the electrodes after disassembly are shown in Fig. S12 (ESI†). SEM (Fig. S13, ESI†) revealed that these differently colored spots are areas where the electrode morphology changed from an initial needle-like morphology into a more dendritic structure. We hypothesize that this characteristic surface transformation resulted from high and highly dynamic bubble coverage, which induced a mechanical-morphological rearrangement of surface atoms at large local overpotentials and current densities. To corroborate these conclusions, we conducted a bubble study in addition to the CFD results (see Fig. S14 and S15, ESI†) and observed that both Serpentine and Linear wide designs exhibit regions of low and slow bubble transport. On the other hand, both Shifted and Linear compartments showed enhanced bubble release and detachment, which was evident by the increased visible gas bubble densities in the flow compartment chambers (see Simulations in Fig. S15, ESI†). Longer bubble surface residence times consistently correlated with the observed morphological changes and discolored spots on the electrode surface. To further support our conclusions on bubble dynamics, and to provide a better understanding of bubble transport dynamics and its impact on the interfacial reactions, we also generated computational animated video files that detail the complex bubble dynamics (bubble density, bubble velocity) for each compartment design, see Videos S1–S4 (ESI†). The local bubble residence time and dynamics explain the inferior performance of the Serpentine flow chamber design compared to the Shifted design: Due to accumulation of gas bubbles below the ribs, the effective catalytically active surface area is reduced, which leads to more pronounced mass transport limitations and therefore a higher production of hydrogen in the high current density regime.

Unusual selectivity-zone driven product gas distribution

An unexpected discovery was made when we studied the destination of catalytically formed product gas. Generally, largely based on diffusional transport and solubility inside the Gas diffusion electrode (GDE), the generated product gas distributes between the cathodic CO₂ gas compartment and the catholyte liquid flow compartment in form of gas bubbles, Fig. 4. For the Shifted compartment design, an analysis of the product gas composition in the catholyte revealed an unusual and surprising correlation between the applied current and the chemical identity of the product gas bubbles in the catholyte, Fig. 4a. Between 50–100 mA cm⁻², there is essentially no gas crossover at all into the electrolyte channel, reflected by the very low FE values (≤ 1%) for ethylene and hydrogen. At 200 mA cm⁻², there is a sharp increase in gas species detected in the catholyte channel, which coincides with the efficiency crossover and inversion point of ethylene and hydrogen selectivity observed earlier. From 200 mA cm⁻² to 400 mA cm⁻² both ethylene and hydrogen cross over into the catholyte. However, beyond 400 mA cm⁻², there is a reproducible, steep rise in hydrogen gas transport into the liquid electrolyte coupled to a corresponding decrease in ethylene crossover. Accordingly, at current densities beyond 400 mA cm⁻², all gas bubbles exiting the GDE towards the catholyte are essentially pure hydrogen. We also note that we do not see any carbon monoxide or methane in the catholyte. For clarity we also provided a complete product spectrum in Fig. 4c, to compare the amounts of gas phase products detected in the liquid phase against the total production of electrolysis products in the liquid and gas phase. Fig. 4b quantifies our unexpected finding for “H₂ liquid” (bubbles in catholyte) and “H₂ gas” (gas compartment). To characterize our findings further, we distinguish three distinct current regimes: At j < 200 mA cm⁻², the majority of H₂ is exiting through the gas compartment and almost no H₂ is detected in the catholyte. For 200 mA cm⁻² < j < 500 mA cm⁻², near equal amounts of H₂ exit through gas and liquid compartment. For j > 500 mA cm⁻², H₂ crossover and bubble formation in the catholyte becomes dominant. To rationalize our observations, we recall our earlier concept of spatial “selectivity and reactivity zones” inside the GDE.¹⁵ Hydrogen is produced at the catalyst's outer layers, closest to the liquid catholyte. This zone is followed by the C₁ zone and, closer to the CO₂ gas compartment, by the C₂₊ zone. The selectivity zones are characterized by OH⁻ and CO₂ mass transport. The hydrogen zone, therefore, is associated with a low local pH and CO₂ concentration, while the C₂₊ zone is characterized by high local pH and CO₂ concentration. We provide further details and discussions on the topic of selectivity zones in the ESI† Supplementary discussion II along with Fig. S16 (ESI†). It follows that by variation of the fluid velocity based on flow compartment design, we were varying the Nernst diffusion layer, the local pH, and the extent of product selectivity zones.

Fig. 4 Identification of gas bubble species and its effects. (a) Quantification of gas phase products crossing over from the catalyst layer into the liquid electrolyte studied exemplary for the Shifted flow compartment. On the y-axis, the faradaic efficiency for ethylene and hydrogen are plotted against the applied cathodic current density. Note that carbon monoxide and methane could not be detected. (b) Faradaic efficiency distribution for hydrogen crossing into the liquid electrolyte compartment and hydrogen diffusing back into the gas compartment is plotted on the y-axis. On the x-axis we plot the applied current density (c) Complete product distribution for the Shifted compartment, including liquid products. On the y-axis, the faradaic efficiency for various products is plotted against the applied cathodic current density on the x-axis. (d) A bubble transport model according to Schmidt et al., including the following layers: I catalyst layer/electrode, II adherence layer, III bubble diffusion layer, IV bulk electrolyte. (e) Qualitative schematic based on the bubble transport model displaying the product gas concentration in the electrolyte on the y-axis as a function of the distance from the electrode. Note that a distance of zero in this schematic represents the catalyst layer denoted as I. Blue and green dashed lines mark the thickness of the bubble diffusion layer III. (f) Qualitative schematic of the proposed correlation of the C₂₊ FE against the fluid velocity in the catholyte chamber. A volcano-type relation is suggested, indicating that systems with low average fluid velocity are bubble transport limited and systems with high average fluid velocity are pH limited. Therefore, a system exists that shows an optimal fluid velocity distribution across the electrode and would therefore be placed at the top of the hypothetical volcano curve.

A fluid dynamic volcano relationship

To illustrate our current understanding of the effect of catholyte velocity distribution at the electrode surface on the selectivity and activity of electrodes, we propose a bubble transport model shown in Fig. 4d–f.³⁴ The bubble model includes the catalyst surface, denoted I, an adjacent bubble adherence layer II (10s of μm), Nernst diffusion layer III (100s of μm) and finally, the convection layer of the bulk electrolyte IV. Variations in catholyte fluid velocity (“stagnant” vs. “well-mixed” in Fig. 4e) impact the size of III and, with it, control the product gas concentration gradient and thus its transport from II across III into IV. Bubble transport away from the surface benefits the catalytically active surface area. Variations in the Nernst diffusion layer III, in turn, impact local pH and thus the CO₂RR selectivity. We propose that there is an optimum value for the catholyte fluid velocity u, which should enable an optimal bubble removal rate from the surface at an optimal local surface pH to maximize C₂₊ product formation. Such a “hydrodynamic volcano”-type relation is illustrated in Fig. 4f. The top of the volcano occurs at a value of u where gas bubble transport and local surface pH balance out. We discuss the volcano relation using two limiting scenarios:

Scenario 1: low catholyte velocity. Low values of u (stagnant bulk catholyte) lead to higher product gas bubble coverage at the electrode surface. This decreases the catalytically active surface area and renders the galvanostatic current density distribution inhomogeneous, as local current densities and corresponding electrode overpotentials must rise. This, in turn, raises the local pH in these current hot spots due to the faster generation of OH⁻ coupled to a larger Nernst diffusion layer thickness. This local bubble coverage-current–potential scenario is directly evidenced from the experimental polarization curves of Linear wide compared to Shifted compartment designs in Fig. S9 (ESI†). So, a particular bubble coverage on the surface or in the porous structure of the electrode modulates the local pH along with applied local overvoltage, which affects the resulting selectivity for CO₂RR.

Scenario 2: high catholyte velocity. High values of u (well-mixed bulk catholyte) decrease the size of the Nernst diffusion layer, enabling fast OH⁻ transport away from the reactive interface. This lowers the local pH favoring the competing HER. A higher 2-electron HER activity raises the stoichiometric gas evolution and, with it, the bubble formation rate. This scenario was reported in CO₂RR measurements, where an enhancement in HER resulted from increase in the rotation speed of an Au RDE electrode.^35,36 High values of u therefore correspond to conditions of higher buffer capacity. Under such conditions, we previously reported preferred HER and C1 product formation.¹⁵ So, increasing u beyond the optimal value, u_opt, for a given set of operation conditions increases HER rate without additional benefit of enhanced bubble transport.

Conclusion

This study addresses the importance and impact of cell component design for efficient CO₂RR electrolyzer operation at industrial current densities. It provided new insight in the inherent correlation between catholyte fluid dynamics and catalytic selectivity of an electrolyzer cell. More specifically, this study has explored how catholyte compartment design affects the electrochemical CO₂RR activity and selectivity inside a Gas Diffusion Electrode (GDE). The results suggest that a balanced fluid velocity distribution along the entire electrode surface is key to effectively remove gaseous products from the cathodes surface while establishing a balanced local pH for C₂₊ product generation. The combination of CFD simulations and experimental CO₂RR electrolyzer tests revealed that an open-flow compartment design employing the Shifted geometry, out of all compartment designs studied, achieved these very balanced superior fluid velocity distribution conditions, resulting in favorable cell performance in the industrially-relevant high current density regime. We have further derived a volcano-shaped performance characteristic for CO₂ electrolyzers with the local catholyte fluid velocity acting as the control parameter. High catholyte fluid velocity operation is limited by local pH, while low catholyte fluid velocity operation is bubble-transport limited. Based on our simulations and experiments, we suggest an average fluid velocity in the range of 0.01–0.1 m s⁻¹ as optimal for C₂₊ production given a homogenous velocity distribution. A self-regulated gas separation mechanism was discovered, which we attributed to the presence of characteristic local selectivity zones inside the GDE. We suggest future directions on CO₂RR/CORR, including cell design, parameter design and GDE optimization and also encourage further research in fluid flow effects, especially in scaled-up catholyte-fed cells.

Author contributions

M. F. and. T. M. designed the electrochemical experiments, analysed the results, and wrote the manuscript. L. L. conducted SEM measurements. P. S. co-designed and co-wrote the manuscript. All authors participated in the discussion and evaluation of results.

Conflicts of interest

There is no conflict to declare.

Acknowledgements

The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement no. 101006701, ECOFUEL. The work leading to this publication was supported by the PRIME program of the German Academic Exchange Service (DAAD) with funds from the German Federal Ministry of Education and Research (BMBF). We also thank Toby Hodges and Elena C. Corbos from Johnson Matthey for supplying the copper catalyst powder.

References

1. B. Obama, Science, 2017, 355, 126–129.
2. K. O. Yoro and M. O. Daramola, Adv. Carbon Capture, 2020, 3–28,  DOI:10.1016/b978-0-12-819657-1.00001-3.
3. J. Deutch, Joule, 2020, 4, 2237–2240.
4. A. I. Osman, M. Hefny, M. I. A. Abdel Maksoud, A. M. Elgarahy and D. W. Rooney, Environ. Chem. Lett., 2021, 19, 797–849.
5. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
6. K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5.
7. H. Yoshio, K. Katsuhei and S. Shin, Chem. Lett., 1985, 1695–1698.
8. Y. Hori, A. Murata and R. Takahashi, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2309–2326.
9. T. Burdyny and W. A. Smith, Energy Environ. Sci., 2019, 12, 1442–1453.
10. C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. G. D. Arquer, A. Kiani, J. P. Edwards, P. D. Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787.
11. F. P. G. d Arquer, C.-T. Dinh, A. Ozden, J. Wicks, C. McCallum, A. R. Kirmani, D.-H. Nam, C. Gabardo, A. Seifitokaldani, X. Wang, Y. C. Li, F. Li, J. Edwards, L. J. Richter, S. J. Thorpe, D. Sinton and E. H. Sargent, Science, 2020, 367, 661–666.
12. N. T. Nesbitt, T. Burdyny, H. Simonson, D. Salvatore, D. Bohra, R. Kas and W. A. Smith, ACS Catal., 2020, 10, 14093–14106.
13. S. Brückner, Q. Feng, W. Ju, D. Galliani, A. Testolin, M. Klingenhof, S. Ott and P. Strasser, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-z6v6m.
14. A. Ozden, Y. Wang, F. Li, M. Luo, J. Sisler, A. Thevenon, A. Rosas-Hernández, T. Burdyny, Y. Lum, H. Yadegari, T. Agapie, J. C. Peters, E. H. Sargent and D. Sinton, Joule, 2021, 5, 706–719.
15. T. Möller, T. Ngo Thanh, X. Wang, W. Ju, Z. Jovanov and P. Strasser, Energy Environ. Sci., 2021, 14, 5995–6006.
16. N. S. Romero Cuellar, C. Scherer, B. Kaçkar, W. Eisenreich, C. Huber, K. Wiesner-Fleischer, M. Fleischer and O. Hinrichsen, J. CO2 Util., 2020, 36, 263–275.
17. G. Lee, A. S. Rasouli, B.-H. Lee, J. Zhang, D. H. Won, Y. C. Xiao, J. P. Edwards, M. G. Lee, E. D. Jung, F. Arabyarmohammadi, H. Liu, I. Grigioni, J. Abed, T. Alkayyali, S. Liu, K. Xie, R. K. Miao, S. Park, R. Dorakhan, Y. Zhao, C. P. O’Brien, Z. Chen, D. Sinton and E. Sargent, Joule, 2023, 7, 1277–1288.
18. D. T. Whipple, E. C. Finke and P. J. A. Kenis, Electrochem. Solid-State Lett., 2010, 13, B109.
19. D. Corral, J. T. Feaster, S. Sobhani, J. R. DeOtte, D. U. Lee, A. A. Wong, J. Hamilton, V. A. Beck, A. Sarkar, C. Hahn, T. F. Jaramillo, S. E. Baker and E. B. Duoss, Energy Environ. Sci., 2021, 14, 3064–3074.
20. Z. Xing, L. Hu, D. S. Ripatti, X. Hu and X. Feng, Nat. Commun., 2021, 12, 136.
21. S. Subramanian, K. Yang, M. Li, M. Sassenburg, M. Abdinejad, E. Irtem, J. Middelkoop and T. Burdyny, ACS Energy Lett., 2023, 8, 222–229.
22. J. W. Blake, V. Konderla, L. M. Baumgartner, D. A. Vermaas, J. T. Padding and J. W. Haverkort, ACS Sustainable Chem. Eng., 2023, 11, 2840–2852.
23. D. Ren, J. Gao, S. M. Zakeeruddin and M. Gratzel, J. Phys. Chem. Lett., 2021, 12, 7583–7589.
24. U. O. Nwabara, A. D. Hernandez, D. A. Henckel, X. Chen, E. R. Cofell, M. P. De-Heer, S. Verma, A. A. Gewirth and P. J. A. Kenis, ACS Appl. Energy Mater., 2021, 4, 5175–5186.
25. X. Fu, J. B. Pedersen, Y. Zhou, M. Saccoccio, S. Li, R. Sažinas, K. Li, S. Z. Andersen, A. Xu, N. H. Deissler, J. B. V. Mygind, C. Wei, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Science, 2023, 379, 707–712.
26. Q. Gong, P. Ding, M. Xu, X. Zhu, M. Wang, J. Deng, Q. Ma, N. Han, Y. Zhu, J. Lu, Z. Feng, Y. Li, W. Zhou and Y. Li, Nat. Commun., 2019, 10, 2807.
27. K. Liu, W. A. Smith and T. Burdyny, ACS Energy Lett., 2019, 4, 639–643.
28. Y. Song, J. R. C. Junqueira, N. Sikdar, D. Ohl, S. Dieckhofer, T. Quast, S. Seisel, J. Masa, C. Andronescu and W. Schuhmann, Angew. Chem., Int. Ed., 2021, 60, 9135–9141.
29. C. Lee, B. Zhao, J. K. Lee, K. F. Fahy, K. Krause and A. Bazylak, iScience, 2020, 23, 101094.
30. Z.-Z. Niu, L.-P. Chi, R. Liu, Z. Chen and M.-R. Gao, Energy Environ. Sci., 2021, 14, 4169–4176.
31. J. K. Lee and A. Bazylak, Joule, 2021, 5, 19–21.
32. A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Joule, 2020, 4, 555–579.
33. M. Ma, E. L. Clark, K. T. Therkildsen, S. Dalsgaard, I. Chorkendorff and B. Seger, Energy Environ. Sci., 2020, 13, 977–985.
34. V. M. Schmidt, Elektrochemische Verfahrenstechnik, 2003, pp. 135–229.
35. G. Marcandalli, K. Boterman and M. T. M. Koper, J. Catal., 2022, 405, 346–354.
36. G. Marcandalli, M. C. O. Monteiro, A. Goyal and M. T. M. Koper, Acc. Chem. Res., 2022, 55, 1900–1911.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee02243a

‡ These authors contributed equally to this work.

---