 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heteroelements in polyoxometalates: a study on the influence of different group 15 elements on polyoxometalate formation†
Jan-Christian
Raabe
 a,
Froze
Jameel
b,
Matthias
Stein
a,
Froze
Jameel
b,
Matthias
Stein
 b,
Jakob
Albert
b,
Jakob
Albert
 a and
Maximilian J.
Poller
a and
Maximilian J.
Poller
 *a
*a
aInstitute for Technical and Macromolecular Chemistry, Universität Hamburg, Bundesstraße 45, 20146 Hamburg, Germany. E-mail: maximilian.poller@uni-hamburg.de
bMax Planck Institute for Dynamics of Complex Technical Systems, Molecular Simulations and Design Group, Sandtorstrasse 1, 39106, Magdeburg, Germany
First published on 4th December 2023
Abstract
In the field of polyoxometalate (POM) chemistry, different heteroelements are integrated into the cage-like structures, to obtain different structural types of so-called heteropolyanions (HPAs). While it is generally accepted, that some elements favor certain types of structure, a systematic study is still missing. In this article, we present a systematic investigation of the influence of the group 15 elements nitrogen, phosphorous, arsenic, and antimony on the formation of different POM structure types. Our study is comprised of DFT calculations and corresponding experimental structural analysis. In this context, the DFT study establishes the thermodynamics of formation of different coordination geometries with various heteroelements on two POM structure types, the Keggin and the Anderson–Evans structures. Our POM synthesis experiments were performed at two different pH values (1 and 5) and resulted in a variety of heteropolytungstates, which were identified and characterized by elemental analysis as well as single crystal X-ray diffraction and vibrational spectroscopy. With these methods, we were able to establish a clear trend, showing that heavier elements lead to formation of different structure types than lighter elements. These results signify a large step towards a better understanding of POM formation specifically with respect to the choice of heteroelement.
1. Introduction
Polyoxometalates (POMs) are a class of inorganic polyanionic clusters, consisting of different transition metals (often Mo or W in their highest oxidation states), which are connected via oxo ligands.1 A subclass of POMs are the so-called heteropolyanions (HPAs), which contain an additional heteroelement in the center of their structure.2–6 Most of the HPA structures are formed with group 15 elements, but structures with group 14 and 16 elements are also known.7–10 However, some of those HPAs tend to be less stable than others, making a detailed study of those POMs difficult.11 The most common structures are formed with a tetrahedrally coordinated phosphorus(V) atom such as the Keggin type [PM12O40]n− or the Wells–Dawson type [P2M18O62]n− anions.3,6,12–18In a typical Keggin-type structure the heteroelement X is tetrahedrally coordinated by four oxygen atoms. Each of these oxygen atoms is part of a M3O13 unit. All twelve octahedrally coordinated metal atoms are bridged via oxo ligands resulting in M–O–M motifs. On each metal atom is one terminally coordinated oxo ligand with partial double bond character as indicated by a shortened bond length.5,12,19–21 The stabilizing effect caused by P(V) in the Keggin-type POMs goes so far that a substitution of the addenda framework metal with other elements such as vanadium(V), niobium(V), iron(III), manganese(II), cobalt(II) etc. is possible without compromising the structural integrity of the cluster.12–15,21,22
On the other hand, in the Anderson–Evans HPA structures, the heteroelement is in an octahedral coordination geometry of six oxo ligands. It is surrounded by six octahedrally coordinated framework metal atoms with two terminally coordinated oxo ligands on each metal atom. The oxo ligands of the central XO6 octahedron are connected to all six metal atoms.23 The resulting Anderson–Evans structure is planar (α isomer), with a disk-like appearance.23 A schematic representation of the both structure types is given in Fig. 1.
 | ||
| Fig. 1 Schematic representation of a Keggin (left) and a planar Anderson–Evans-type structure (right). | ||
The difference in the preferred coordination number of the heteroelements correlates with their atomic radii.24–30 There are two main coordination motifs found in POM chemistry: the tetrahedral (CN 4) and the octahedral geometry (CN 6), whereby heavier elements (larger radii) prefer the octahedral configuration and lighter elements (smaller radii) prefer the tetrahedral configuration.1 This can be exemplarily seen when comparing the oxides of phosphorus (P4O10) and antimony (Sb2O5). The pnictogen is coordinated tetrahedrally in the former but octahedrally in the latter.31,32 In our here presented study, we systematically investigated the influence of the group 15 elements nitrogen, phosphorus, arsenic, and antimony on the formation of POM structures. To this end, we combined suitable precursors of the group 15 elements with sodium tungstate under conditions that lead to the formation of POMs via polycondensation of the tungstate. Afterwards, we structurally characterized the resulting products using single crystal X-ray diffraction and vibrational spectroscopy. The results of these heteroatom substitutions are complemented by Density Functional Theory (DFT) calculations of the structural changes and relative free energies of the Keggin and the Anderson–Evans structures containing different elements of group 15.
2. Results and discussion
2.1. Thermodynamics of formation and structural parameters upon inclusion of heteroatoms
DFT calculations were performed to probe the structural and thermodynamic differences by exchanging the central group 15 atom of Keggin and Anderson–Evans type complexes (see Fig. 2 and 3). The structural changes in POM (Keggin and Anderson–Evans) structure upon exchanging the central heteroatoms were characterized based on: (i) non-metal heteroatom–oxygen distance (X–Oa), (ii) distance of oxygen coordinated to the central non-metal atom and the neighboring tungsten atoms (Oa–W) and the molecular volume of the complexes with optimized Keggin and Anderson–Evans type complexes containing different non-metal heteroelements.In the DFT optimized Keggin complex with nitrogen as heteroatom, the X–Oa bond distance is reduced by 0.14 Å when compared to the Keggin complex with phosphorous as central non-metal heteroatom due to the smaller atomic radius of nitrogen compared to phosphorous. This reduction in the atomic radii also weakens the tungsten–oxygen coordination as the Oa–W distance increases by 0.17 Å in [NW12O40]3− compared to an Oa–W distance in [PW12O40]3− Keggin complex. The molecular volume expansion by 22 Å3 for the Keggin complex, when phosphorous is substituted by nitrogen, shows that non-metallic heteroatom exchange with an atom having small atomic radius such as nitrogen, significantly affects the shape of the Keggin complex (see Fig. 2). The expansion of molecular volume by introducing smaller atoms seems to be counterintuitive. The Gibbs energies of formation were calculated from isodesmic reactions of the Keggin and Anderson–Evans complexes with their respective acids (hybrid DFT functional, thermodynamic corrections plus solvation are included; see ESI†). From DFT calculations, however, it can be shown that the relative thermodynamics, here the Gibbs energy for the formation, of a Keggin-type complex with nitrogen as heteroatom is significantly higher (ΔG = 332 kJ mol−1) compared to the Keggin complex with phosphorous as central non-metal atom. This shows that the formation of a Keggin complex with nitrogen as central heteroatom is structurally and thermodynamically inaccessible.
However, when phosphorous is exchanged with the heavier elements within group 15 such as arsenic (As) and antimony (Sb), there is a very small change of a mere 2 and 4 Å3 in molecular volume compared to the [PW12O40]3− complex. For both As and Sb exchange, the elongation in X–Oa bond distances due to larger atomic radii is partially compensated by the reduction in the Oa–W distances, thus conserving the molecular volume of the resulting [AsW12O40]3− and [SbW12O40]3− complexes. Since the Gibbs energy of formation for the Keggin complexes containing arsenic and antimony as non-metal central heteroatoms is higher compared to the [PW12O40]3−, the formation of Keggin complexes with As and Sb as heteroatoms is thermodynamically less favorable (see Fig. 2).
Despite several efforts, the optimization of an Anderson–Evans type complex with nitrogen as the central non-metal heteroatom, was not successful due to the small atomic radius of the nitrogen atom. However, for atoms of group 15 with larger atomic radii such as phosphorous, arsenic and antimony, DFT calculations show that the formation of Anderson–Evans complex with antimony as heteroatom is energetically favored compared to the complexes with arsenic and phosphorous as heteroatoms. With the increase in the atomic radius going down the group, the molecular volume increases by only 7 and 9 Å3 for the substitution of phosphorus with arsenic and antimony, respectively. Similarly, the X–Oa distance increases however, the Oa–W remains almost the same (see Fig. 3).
Our DFT calculations show that the formation of a Keggin-type POM structure appears to be only favorable for elements with small atomic radii and unfavorable for elements with larger radii. In contrast, heteroatom substitutions for Anderson–Evans type structures are favored for elements with larger atomic radii and less so for those with small radii. This observation is in full agreement with inorganic structure concepts and thus explained by the different coordination geometries of the heteroelement in both structural motifs.33,34 In the Keggin structure, the coordination geometry for the heteroelement is a tetrahedron (CN 4) and for the Anderson–Evans structure an octahedron (CN 6).19,23 The coordination geometry correlates with the atomic radius of the element of interest. Ligands coordinating a central element tend to maximize the distance between them due to the repulsion of their electron shells. Therefore, for CN 4 the tetrahedral and for CN 6 the octahedral coordination geometry is the most thermodynamically favorable arrangement. The higher the atomic radius of the element, the more ligands can be coordinated by an element and the more the octahedral geometry is preferred. Elements with a small atomic radius can coordinate fewer ligands, resulting in a preference for the tetrahedral geometry.33,34 Likewise, the Anderson–Evans structure with large elements as heteroelements could be stabilized by adopting planarity. The planarity results in an opening for the introduction of a heteroelement perpendicular to the plane upwards and downwards, giving the heteroelement more space.
These trends are also confirmed by our experimental observations: using different group 15 elements together with sodium tungstate, we performed typical POM synthesis procedures at pH values 1 and 5, which are typical for the synthesis of Keggin- and Anderson-type POMs repectively.35,36 Nitric acid was used as precursor for N(V), phosphoric acid for P(V), arsenic(III) oxide for As(V) and potassium hexahydroxoantimonate for Sb(V). Arsenic(III) oxide was oxidized in situ with hydrogen peroxide to the required As(V) species. The obtained products were desalinated using our previously reported nanofiltration technique21,37 and the powder samples were then recrystallized to identify the resulting structure by single-crystal X-ray diffraction (scXRD). Detailed experimental procedures are provided in our ESI.†
2.2. Experimental synthesis and characterization of heteroelement incoproration
 | ||
Fig. 4 Solid-state structure of the anion [W12O40]8− determined by scXRD. Polyhedra representation above and atom model bottom. The compound was crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2). R1: 4.74%, wR2: 9.47%, Rint: 4.76%, GooF: 1.078. Color code: blue: metal atoms (W), red: oxygen atoms. The .cif file is available in the CCDC database. Deposition number: 2293850.† (2). R1: 4.74%, wR2: 9.47%, Rint: 4.76%, GooF: 1.078. Color code: blue: metal atoms (W), red: oxygen atoms. The .cif file is available in the CCDC database. Deposition number: 2293850.† | ||
It is composed of four corner-linked WO6 triads, with the linking of the triads resulting in a large cavity inside the structure. Important bond lengths of our investigated structural motifs are summarized in Table 1. In order to confirm the structure of the bulk product, the material was characterized by vibrational spectroscopy (Fig. 5 and 6). Typical vibrational bands of POM structures include the terminal oxygen–metal vibrational bands W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in the range of 800–1000 cm−1, and different types of W–O–W vibrational modes below 900 cm−1.42–45 From comparison of the experimental and calculated spectra for the above described structure, the following vibrational assignments can be made: in the IR spectrum of Na8[W12O40] the peaks appearing at 944 and 930 cm−1 agree well with the small peaks at 912 and 903 cm−1 in the DFT calculated IR spectrum that corresponds to the asymmetric W
O in the range of 800–1000 cm−1, and different types of W–O–W vibrational modes below 900 cm−1.42–45 From comparison of the experimental and calculated spectra for the above described structure, the following vibrational assignments can be made: in the IR spectrum of Na8[W12O40] the peaks appearing at 944 and 930 cm−1 agree well with the small peaks at 912 and 903 cm−1 in the DFT calculated IR spectrum that corresponds to the asymmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot stretches. The peak at 955, 882 and 878 cm−1 in the experimental spectrum differs by only 13, 9 and 7 cm−1 (968, 891 and 871 cm−1) from the calculated spectrum and belongs to symmetric W
Ot stretches. The peak at 955, 882 and 878 cm−1 in the experimental spectrum differs by only 13, 9 and 7 cm−1 (968, 891 and 871 cm−1) from the calculated spectrum and belongs to symmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot bond stretches. Similarly, the broad peak at 847 cm−1 in the experimental spectrum can be assigned to the peaks appearing at 853 and 829 cm−1 in the calculated spectrum of Na8[W12O40], where both peaks corresponds to a symmetric W–O–W distortion along the vertex. A peak 740 cm−1 in the experimental spectrum appears at 732 cm−1 in the calculated spectrum and corresponds to the asymmetric W–O–W bond stretch. Finally, peaks at 638 cm−1 in the experimental spectrum and 652 cm−1 (calculated) refer to asymmetric W–O–W stretches. Overall, the comparison of the calculated and experimental vibrational spectra leads to the conclusion that the isolated paradodecatungstate is the main product of this reaction. Critical spectral peak positions from IR and Raman are summarized in Table 1.
Ot bond stretches. Similarly, the broad peak at 847 cm−1 in the experimental spectrum can be assigned to the peaks appearing at 853 and 829 cm−1 in the calculated spectrum of Na8[W12O40], where both peaks corresponds to a symmetric W–O–W distortion along the vertex. A peak 740 cm−1 in the experimental spectrum appears at 732 cm−1 in the calculated spectrum and corresponds to the asymmetric W–O–W bond stretch. Finally, peaks at 638 cm−1 in the experimental spectrum and 652 cm−1 (calculated) refer to asymmetric W–O–W stretches. Overall, the comparison of the calculated and experimental vibrational spectra leads to the conclusion that the isolated paradodecatungstate is the main product of this reaction. Critical spectral peak positions from IR and Raman are summarized in Table 1.
 | ||
| Fig. 5 IR spectra of the [W12O40]8− anion determined in the solid-state (bottom) and DFT calculated (middle). Spectrum of WO3 (top). | ||
 | ||
| Fig. 6 Raman spectra of the [W12O40]8− anion determined in the solid-state (bottom) and DFT calculated (top). | ||
| Peak position/cm−1 | Assignmentc |
|---|---|
| a FTIR. b Raman. c Based on computations. | |
| 96b | Ot–W–O (out-of-plane) |
| 109b | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O wagging (out-of-plane) O wagging (out-of-plane) |
| 133b | O–W–O twist (out of plane) |
| 161b | Ot–W–O (in-plane) |
| 217b | W–O–W bend along vertex (out-of-plane) |
| 238b | W–O–W bend along vertex (in-plane) |
| 311b | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O scissoring (in-plane) O scissoring (in-plane) |
| 360b | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bend (out-of-plane) O bend (out-of-plane) |
| 638a | W–O–W stretch (asymmetric) |
| 656b | |
| 740a | W–O–W stretch along vertex (symmetric) |
| 847a | |
| 878a | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot stretch (symmetric) Ot stretch (symmetric) |
| 892a,b | |
| 912b | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot stretch (asymmetric) Ot stretch (asymmetric) |
| 930a | |
| 944a | |
| 955a | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch (symmetric) O stretch (symmetric) |
| 965b | |
Performing the same reaction at a pH of 1, which should usually lead to the formation of a Keggin-type structure, resulted in the formation of tungsten oxide, which was identified by powder X-ray diffraction (Fig. 7). The oxides formed were identified as a mixture of different phases of the tungsten oxides WO3 and W18O49 using comparative data from measurements of commercial WO3 and from the ICSD database, with only two WO3 and one W18O49 phase being used for visualization.
 | ||
| Fig. 7 Powder XRD of the different tungsten oxide samples obtained from the reaction mixtures in comparison with different solid-state phases of WO3, W18O49, Sb2O5 and commercially available WO3. | ||
The fact that the N(V) atom is not part of the POM structure shows that nitrogen is not a suitable heteroelement for the formation of heteropolyanions. This result is consistent with the particularly high relative energy of the hypothetical [NW12O40]3− anion in our DFT calculations and the absence of a convergence in DFT calculations for the hypothetical [NW6O24]7−. NO3− is known for its trigonal-planar geometry34 and a NO43− analogous to the phosphate anion PO43− does not exist. To the best of our knowledge there is no structural motif known in which N(V) is coordinated octahedrally.33 Therefore, the formation of a Keggin- or Anderson–Evans-structure is excluded for geometrical reasons. From our previous work on Keggin structures, we know that the diameter of the PO43− tetrahedron in the center of the Keggin structure is approximately 3.074 Å.12 To estimate the size of a hypothesized NO43− anion, we measured the dimensions of a tetramethylammonium cation (CCDC database deposition number: 1916596), since the carbon atom is similar in size to the oxygen atom. This would give an approximate size of 2.984 Å for a hypothetical NO43− tetrahedron, which is smaller than the PO43− tetrahedron and presumably too small to act as the center of a Keggin-type structure.
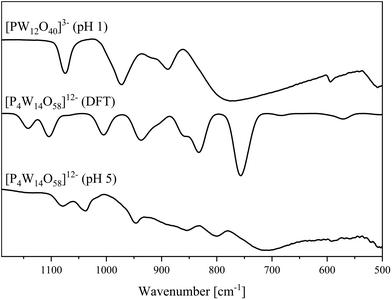 | ||
| Fig. 8 IR spectra of the [P4W14O58]12− anion determined in the solid-state (bottom) and DFT calculated (middle). Spectrum of [PW12O40]3− (top). | ||
In agreement with our previous published study, the 31P NMR peak for Na3[PW12O40] was found at −15.3 ppm.22 The big peak at ∼0 ppm is a result of the excess H3PO4 used during the experimental procedure.
At a pH value of 5, we unexpectedly obtained a polyoxoanion with the composition [P4W14O58]12− (Fig. 9).49 For this structure type, we were not able to find a .cif file in the CCDC/ICSD database.
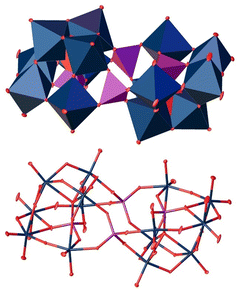 | ||
Fig. 9 Solid-state structure of the anion [P4W14O58]12− determined by scXRD. Polyhedra representation above and atom model bottom. The compound was crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2). R1: 2.83%, wR2: 7.19%, Rint: 7.53%, GooF: 1.076. Color code: blue: metal atoms (W), red: oxygen atoms, purple: phosphorous. The .cif file is available in the CCDC database. Deposition number: 2293849.† (2). R1: 2.83%, wR2: 7.19%, Rint: 7.53%, GooF: 1.076. Color code: blue: metal atoms (W), red: oxygen atoms, purple: phosphorous. The .cif file is available in the CCDC database. Deposition number: 2293849.† | ||
The structure is composed of two oppositely oriented hemispheres connected by two central tetrahedrally coordinated P(V) atoms. Both are composed of seven WO6 octahedra, which are held together by a central PO43− tetrahedron. In total, this structure motif consists of 14 WO6 octahedra and four PO43− tetrahedra, resulting in the final 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 P
14 P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W ratio.50
W ratio.50
The IR and Raman spectra of the bulk material (Fig. 8 and 10) show the typical vibrational bands of the [P4W14O58]12− anion. In addition to the different types of W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and W–O–W vibrational bands, the P–O band is found as a split band in the IR spectrum at 1080 and 1037 cm−1. This can be explained by considering the solid-state structure in Fig. 9 which has two different types of P–O tetrahedra: two PO4 tetrahedra in the center of each hemisphere and two PO4 tetrahedra connecting the hemispheres. The agreement between calculated and experimental IR spectra is excellent and allows a spectral assignment of peaks which correspond to symmetric and antisymmetric P–O bond stretches for all four phosphates groups, respectively (1005 and 1071 cm−1). The peaks at 1104 and 1142 cm−1 belong to the P–O bond stretches in the phosphates connecting two hemispheres and the central PO43− tetrahedra, respectively. The peak corresponding to vibration of the terminal W
O and W–O–W vibrational bands, the P–O band is found as a split band in the IR spectrum at 1080 and 1037 cm−1. This can be explained by considering the solid-state structure in Fig. 9 which has two different types of P–O tetrahedra: two PO4 tetrahedra in the center of each hemisphere and two PO4 tetrahedra connecting the hemispheres. The agreement between calculated and experimental IR spectra is excellent and allows a spectral assignment of peaks which correspond to symmetric and antisymmetric P–O bond stretches for all four phosphates groups, respectively (1005 and 1071 cm−1). The peaks at 1104 and 1142 cm−1 belong to the P–O bond stretches in the phosphates connecting two hemispheres and the central PO43− tetrahedra, respectively. The peak corresponding to vibration of the terminal W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot bonds appears at 941 and 862 cm−1 in the calculated spectrum and can be found at 950 and 856 cm−1 respectively, in the experimental spectrum. The peak at 800 cm−1 in the experimental spectrum match well with calculated peaks at 851, 835 and 827 cm−1 and refer to the W–O–W bond stretches along the vertex. The broad peak at 713 in the calculated spectrum appears at 760 cm−1 in the calculated IR spectrum and corresponds the W–O–W bond vibrations along the edge.
Ot bonds appears at 941 and 862 cm−1 in the calculated spectrum and can be found at 950 and 856 cm−1 respectively, in the experimental spectrum. The peak at 800 cm−1 in the experimental spectrum match well with calculated peaks at 851, 835 and 827 cm−1 and refer to the W–O–W bond stretches along the vertex. The broad peak at 713 in the calculated spectrum appears at 760 cm−1 in the calculated IR spectrum and corresponds the W–O–W bond vibrations along the edge.
 | ||
| Fig. 10 Raman spectra of the [W12O40]8− anion determined in the solid-state (bottom) and DFT calculated (middle). Spectrum of [PW12O40]3− (top). | ||
In summary, the calculated and experimental spectra match the structure of the isolated single crystal, confirming the structure of the bulk material. Important IR and Raman peak positions are summarized in Table 2.
| Peak position/cm−1 | Assignmentc |
|---|---|
| a FTIR. b Raman. c From calculations. | |
| 100b | Ot![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot rock (symmetric) Ot rock (symmetric) |
| 145b | Ot![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot rock (asymmetric) Ot rock (asymmetric) |
| 216b | P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W twist (out-of-plane) W twist (out-of-plane) |
| 373b | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O scissoring (in-plane) O scissoring (in-plane) |
| 507b | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W bend (in-plane) W bend (in-plane) |
| 713a | W–O–W (edge) |
| 800a | W–O–W (vertex) |
| 856a | W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot stretch (symmetric) Ot stretch (symmetric) |
| 950a | |
| 964b | P–O stretch (symmetric) |
| 983b | |
| 1037a | |
| 1080a | |
 | ||
Fig. 11 Solid-state structure of the anion [AsW9O34]9− determined by scXRD resulting from the experiment with As(V). Two [AsW9O34]9− anions are bridged by coordinating via six sodium cations. Polyhedral representation left and atom model right. The compound was crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2). R1: 4.23%, wR2: 10.71%, Rint: 6.65%, GooF: 1.115. Color code: brown: arsenic (As), blue: metal atoms (W), red: oxygen atoms and turquoise: sodium cations. The .cif file is available in the CCDC database. Deposition number: 2293851.† (2). R1: 4.23%, wR2: 10.71%, Rint: 6.65%, GooF: 1.115. Color code: brown: arsenic (As), blue: metal atoms (W), red: oxygen atoms and turquoise: sodium cations. The .cif file is available in the CCDC database. Deposition number: 2293851.† | ||
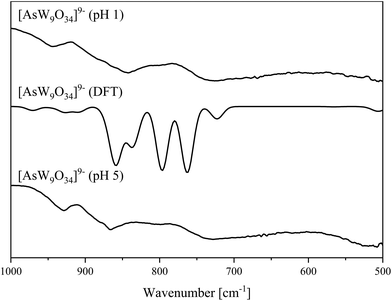 | ||
| Fig. 12 IR spectra of the [AsW9O34]9− anion (pH 5 and 1) determined in the solid-state (bottom/top) and DFT calculated (middle). | ||
In the solid-state structure, two [AsW9O34]9− units are joined by six sodium cations. Here, the terminal oxo ligands of the vacancy positions are coordinating to the sodium cations.
The crystallographic dataset shows that the diameter of a tetrahedrally coordinated AsO43− is 3.377 Å (literature: 3.295 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54), which is significantly larger than the PO43− tetrahedron (3.085 Å, CCDC deposition number 2177881).12 These observations are in agreement with our DFT calculations in which the Keggin-type structure [AsW12O40]3− also has a significantly higher relative energy of formation than the classical Keggin-type structure [PW12O40]3−. A Keggin anion [AsW12O40]3− has been reported previously but has been characterized as unstable.55–57 Presumably, the larger AsO43− tetrahedron is too bulky to comfortably fit in the Keggin structure, leading to the formation of the tri-lacunary Keggin units which provide more space. This can specifically be observed when comparing the O–O distances of the O atoms coordinating to Na+ in the [AsW9O34]9− dimer (4.121 Å) with the corresponding distances of bridging O atoms in the [PW12O40]3− Keggin ion (2.753 Å).48 The Na+ ions saturate the open coordination sites on the lacunary O atoms, leading to the observed coordination dimer. The bond length between the lacunar O and Na+ ions is 2.830 Å which exceeds the sum of the respective covalent radii (Na: 1.55 Å and O: 0.63 Å = 2.18 Å). This suggests a weak bonding interaction. The distance is comparable to the O–Na distance between a Keggin-type anion and its Na+ counterions (2.986 Å), which we observed in a recently published crystal structure of Na6[PV3Mo9O40] (deposition number 2205007).21
54), which is significantly larger than the PO43− tetrahedron (3.085 Å, CCDC deposition number 2177881).12 These observations are in agreement with our DFT calculations in which the Keggin-type structure [AsW12O40]3− also has a significantly higher relative energy of formation than the classical Keggin-type structure [PW12O40]3−. A Keggin anion [AsW12O40]3− has been reported previously but has been characterized as unstable.55–57 Presumably, the larger AsO43− tetrahedron is too bulky to comfortably fit in the Keggin structure, leading to the formation of the tri-lacunary Keggin units which provide more space. This can specifically be observed when comparing the O–O distances of the O atoms coordinating to Na+ in the [AsW9O34]9− dimer (4.121 Å) with the corresponding distances of bridging O atoms in the [PW12O40]3− Keggin ion (2.753 Å).48 The Na+ ions saturate the open coordination sites on the lacunary O atoms, leading to the observed coordination dimer. The bond length between the lacunar O and Na+ ions is 2.830 Å which exceeds the sum of the respective covalent radii (Na: 1.55 Å and O: 0.63 Å = 2.18 Å). This suggests a weak bonding interaction. The distance is comparable to the O–Na distance between a Keggin-type anion and its Na+ counterions (2.986 Å), which we observed in a recently published crystal structure of Na6[PV3Mo9O40] (deposition number 2205007).21
Vibrational spectroscopy of the products obtained at pH 1 and pH 5 confirm that they are identical. Additionally, the vibrational spectra were simulated based on the above-described structure (Fig. 12 and 13). The spectra exhibit peaks at 928 cm−1 (929 cm−1 in the calculated spectrum) that correspond to symmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot bond stretch. The experimental IR peaks at 855 and 866 cm−1 appears at 859 and 869 cm−1 in the calculated spectrum belonging to the asymmetric W
Ot bond stretch. The experimental IR peaks at 855 and 866 cm−1 appears at 859 and 869 cm−1 in the calculated spectrum belonging to the asymmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot bond stretch and asymmetric As
Ot bond stretch and asymmetric As![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond vibration, respectively. The peak at 803 cm−1 (797 cm−1 in the calculated spectrum) can be assigned to the As–O–W and (W–O–W)vertex bond vibrations, and the peak at 729 cm−1 (calculated 723 cm−1) corresponding to W–O–W bond vibrations along the edge of the octahedra. The peak at 763 cm−1 in the calculated spectrum corresponds to the (W–O–W)bridging bond vibrations. Additionally, a small shoulder peak appears at 837 cm−1 in the calculated spectrum, which belongs to an asymmetric W–O–As bond stretching vibration. Critical IR and Raman spectral peak positions and their assignments are summarized in Table 3.
O bond vibration, respectively. The peak at 803 cm−1 (797 cm−1 in the calculated spectrum) can be assigned to the As–O–W and (W–O–W)vertex bond vibrations, and the peak at 729 cm−1 (calculated 723 cm−1) corresponding to W–O–W bond vibrations along the edge of the octahedra. The peak at 763 cm−1 in the calculated spectrum corresponds to the (W–O–W)bridging bond vibrations. Additionally, a small shoulder peak appears at 837 cm−1 in the calculated spectrum, which belongs to an asymmetric W–O–As bond stretching vibration. Critical IR and Raman spectral peak positions and their assignments are summarized in Table 3.
 | ||
| Fig. 13 Raman spectra of the [AsW9O34]9− anion (pH 5 and 1) determined in the solid-state (bottom and top) and DFT calculated (middle). | ||
At the pH value of 5, we observed the formation of the Anderson–Evans-type anion [SbW6O24]7−, which was first identified by singly crystal XRD (Fig. 14).
 | ||
Fig. 14 Solid-state structure of the anion [SbW6O24]7− determined by scXRD. Polyhedra representation above and atom model bottom. The compound was crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2). R1: 2.54%, wR2: 6.89%, Rint: 5.45%, GooF: 1.136. Color code: blue: metal atoms (W), red: oxygen atoms. The .cif file is available in the CCDC database. Deposition number: 2293848.† (2). R1: 2.54%, wR2: 6.89%, Rint: 5.45%, GooF: 1.136. Color code: blue: metal atoms (W), red: oxygen atoms. The .cif file is available in the CCDC database. Deposition number: 2293848.† | ||
This structure type consists of six WO6 octahedra surrounding one central SbO6 octahedron. The bond length between Sb and O (Sb–Oa), was measured as 1.984 Å, slightly longer than the distance between the W and the bridging O atoms (W–Ob) of 1.941 Å. This is the longest heteroatom–oxygen distance reported in this work, which is consistent with the increasing radii of the heteroatoms58 that consequently leads to a larger coordination number. These observations are also in agreement with our above presented quantum chemical calculations, indicating that the formation of the Anderson–Evans structure is energetically favored for Sb(V).
Again, the bulk material was characterized by vibrational spectroscopy (Fig. 15 and 16). Few peaks can be assigned to the Anderson–Evans structure based on previous literature.45 To fully assign the vibrational bands, the IR and Raman spectra of [SbW6O24]7− were calculated on the basis of the above described structure using computational methods.
 | ||
| Fig. 15 IR spectra of the [SbW6O24]7− anion determined in the solid-state (bottom) and DFT calculated (middle). Spectrum of WO3 (top). | ||
 | ||
| Fig. 16 Raman spectra of the [SbW6O24]7− anion determined in the solid-state (bottom) and DFT calculated (top). | ||
Going from lower to higher wavenumbers, the peaks appearing at 435 and 470 cm−1 in the calculated spectrum (experimental 419 cm−1) correspond to anti-symmetric degenerate bending and anti-symmetric degenerate stretching Sb–O bonds. The peak at 523 cm−1 in the experimental spectrum shifts by 13 cm−1 and thus appears at 510 cm−1 in the calculated spectrum and shows symmetric degenerate stretching of Sb–O bonds. The small peak at 590 cm−1 in the calculated spectrum correlates with the experimental peak at 585 cm−1 and refers to asymmetric of Sb–O bonds stretch. The large peak at 674 cm−1 in the calculated spectrum (experimental 727 cm−1) shows the O–W–O bond stretch along the vertex. The peaks at 865 and 945 cm−1 in the experimental spectrum appear at 869 and 914 cm−1 in the calculated spectrum and belong to the anti-symmetric and symmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot bond stretches, respectively. In summary, the vibrational spectra confirm the Anderson–Evans structure for the bulk material. The assignment of IR and Raman spectral peaks is summarized in Table 4.
Ot bond stretches, respectively. In summary, the vibrational spectra confirm the Anderson–Evans structure for the bulk material. The assignment of IR and Raman spectral peaks is summarized in Table 4.
The same experiment was also performed at a pH value of 1, which however yielded a mixture of tungsten oxide (WO3) and antimony(V) oxide Sb2O5, which were identified by powder X-ray diffraction (Fig. 7).
| Bond length [Å] | |||||
|---|---|---|---|---|---|
| [W12O40]8− | [P4W14O58]12− | [AsW9O34]9− | [SbW6O24]7− | Sum of covalent radii58 | |
| n.a.: not applicable. | |||||
| P–Oa | n.a. | 1.537 (1.524) | n.a. | n.a. | 1.74 |
| As–Oa | n.a. | n.a. | 1.683 (1.678) | n.a. | 1.84 |
| Sb–Oa | n.a. | n.a. | n.a. | 1.984 (2.01) | 2.03 |
| Oa–W | n.a. | 2.262 (2.33) | 2.370 (2.373) | 2.224 (2.243) | 2.00 |
| W–Ob | 1.935 (1.971) | 1.879 (1.869) | 1.943 (1.939) | 1.941 (1.951) | 2.00 |
| W–Oc | 2.236 (2.172) | 2.131 (2.195) | 2.00 | ||
W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot Ot |
1.742 (1.743) | 1.738 (1.737) | 1.742 (1.754) | 1.748 (1.765) | 2.00 |
| Ot–Na | 2.410 | 2.370 | 2.878 (2.491) | n.a. | 2.18 |
| Na–OW | 2.419 | 2.395 | 2.583 | 2.406 | 2.18 |
The experimental results are summarized in Fig. 17. From these results in combination with our computational studies, we conclude that the formation of the different structure types depends not only on the pH value, but is also highly dependent of the atomic radius of the heteroelement involved.
In agreement with our computational and experimental results, N(V) is too small (0.16 Å)33 for both coordination motifs, furthermore it forms the planar NO3− ion instead of a tetrahedral NO43− ion. Therefore, the thermodynamically preferred structure type of tungstate at pH 5 is formed without a heteroatom. In the strongly acidic medium (pH 1), decomposition of the paradodecatungstate B anion to the tungsten oxide was observed, which can be explained by an instability caused by the absence of a heteroatom. P(V) (0.38 Å)33 forms a tetrahedral PO43− structural motif, which in agreement with the DFT calculations leads to the formation of a Keggin anion in highly acidic media (pH 1). At higher pH values (5) the Keggin structure of [PW12O40]3− becomes unstable and the [P4W14O58]12− anion is formed instead, which still contains tetrahedrally coordinated P atoms. Mechanistically, the latter structure is probably formed via the former structure via a Keggin-lacunary intermediate, which is known to form in more basic media, as the lower proton concentration leads to dissociation of individual metal–oxygen polyhedra from the POM cluster.59 As(V) (atomic radius of 0.46 Å)33 is known to prefer the tetrahedral coordination geometry (e.g. in H3AsO4),34 but the Keggin formation seems to be more difficult due to the, compared to P(V), high atomic radius and subsequent larger heteroatom polyhedron. Thus, the formation of the open lacunary Keggin structure seems to be thermodynamically preferred. This structure is further stabilized by the formation of a coordination dimer, in which two [AsW9O34]9− units are held together by six alkali ions. The stability of this structure is sufficiently high, that its formation is unaffected by the different pH values. In contrast, Sb(V) (0.60 Å) preferentially forms octahedral motifs (coordination number 6).33 As predicted by DFT calculations, the addition of Sb(V) leads to the formation of an Anderson–Evans type POM at pH 5 in which all metal atoms, including the central heteroatom, are coordinated octahedrally. Outside of the pH range in which Anderson–Evans structures are stable, the respective oxides (WO3, Sb2O5) are formed.
3. Experimental procedures
Detailed synthetic procedures can be found in the ESI.†The arsenic(V) solution was prepared by dissolving arsenic(III) oxide in a mixture of a 30% solution of hydrogen peroxide (30 mL) and water (30 mL) under reflux for two hours.
The antimony(V) solution was prepared by refluxing potassium hexahydroxoantimonate(V) in water (100 mL) for one hour.
In a general procedure sodium tungstate dihydrate was dissolved in water or added to the respective As(V)/Sb(V) solution. The start volume of the reaction mixture was always 100 mL of an aqueous solution. For the experiments with the heteroelements N(V) and P(V) a 4 M solution of nitric acid or 25 wt% phosphoric acid solution in water was added to the aqueous sodium tungstate solution. The pH value was adjusted to 5 or 1 using a 37% solution of hydrochloric acid in water and the solution was concentrated under reduced pressure (85 °C, 200 to 0 mbar). All compounds were purified according to our previous published dialysis approach.21,37
Further characterization of all POMs by compositional analysis (ICP-OES) and thermogravimetric analysis, (TGA) is shown in the ESI, Table S3.†31P-NMR spectroscopy was done for Na12[P4W14O58] and Na3[PW12O40] and is presented in Fig. S1 and S2.† UV-Vis measurements were performed for all POMs and the data were analyzed according to the Lambert–Beer's law as shown in Tables S5, S6 and Fig. S3–S8 (ESI†). Precise analytical characterization of the anion [PW12O40]3− was done in our previously published study,22 therefore we do not present further characterization of this compound here.
Computational details can be found in the ESI.†
4. Conclusion
In this work, we present a combined computational and experimental study on the influence of different group 15 elements on the formation of various POM structures. Our DFT calculations suggest that the formation of a Keggin-type structure is preferred for elements with small atomic radii (such as P) and unlikely for elements with large radii (such as Sb). The trend is reversed for the formation of the Anderson–Evans structure. Our crystallographic and spectroscopic data are in agreement with the computational results. For P(V), the Keggin anion [PW12O40]3− was formed in strongly acidic (pH 1) media vs. the formation of [P4W14O58]12− at pH 5. Here, P(V) was found to be tetrahedrally coordinated in both structural motifs. As(V) also prefers tetrahedral coordination motifs, but the larger As(V) atom radius causes stress on the confined Keggin structure, resulting in the formation of lacunary structures such as the [AsW9O34]9− anion. In agreement with the calculations, the formation of the Anderson–Evans anion [SbW6O24]7− was observed at pH 5 using Sb(V). In contrast, decomposition of the anion to oxidic materials was observed at pH 1. In agreement with the computational data, the small N(V) atom is an outlier due to its small atomic radius, and the anomaly of forming a tri-coordinate oxoanion (NO3−). As a result, it is not involved in the formation of POM structures. This can be seen in the relative thermodynamics of formation, which gave the highest relative energy (compared to [PW12O40]3−) for the hypothetical [NW12O40]3− anion, while structural optimization for the [NW6O24]7− anion was not successful.All compounds were characterized by additional spectroscopic methods in the solid-state and in aqueous solution. An assignment of the different vibrational bands to the vibrational modes was possible using DFT calculated peak positions. The data obtained are of particular interest for the less common structure types such as the lacunar-based motifs [AsW9O34]9−, [P4W14O58]12−, and even the Anderson–Evans structure [SbW6O24]7−. In contrast to the Keggin structure, where the P–O vibrational band is observed in the range 1000 to 1100 cm−1, the various As–O–W vibrational bands in the lacunar-based structural motifs are found at 837 and 797 cm−1. For the Anderson–Evans structure, the different types of Sb–O vibrational bands were found at 435, 470, 510 and 590 cm−1.
The results presented here contribute to the understanding and control of POM formation, in particular, the formation of different structure types as a function of heteroelement and pH. From the results presented here, a clear trend can be observed for the group 15 elements P(V), As(V) and Sb(V), whereas N(V) is incompatible for POM chemistry.
Author contributions
Jan-Christian Raabe: conceptualization, investigation, visualization, writing the original draft. Froze Jameel: investigation, visualization, writing – review and editing. Matthias Stein: funding acquisition, resources, supervision, investigation, writing – review and editing. Jakob Albert: funding acquisition, resources, writing – review and editing. Maximilian J. Poller: project administration, supervision, conceptualization, writing – review and editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank the central elemental analysis team of Dr Dirk Eifler for measuring numerous ICP-OES samples for different elements. We thank Ute Gralla for measuring the Raman spectra, and the X-ray service team of Dr Frank Hoffmann and especially Isabelle Nevoigt for measuring numerous single-crystal XRD samples. Prof. Dr Matthias Stein and Froze Jameel are grateful to the Max Planck Society of the Advancement of Science for financial support and the Research Initiative “SmartProSys: Intelligent Process Systems for the Sustainable Production of Chemicals” funded by the Ministry for Science, Energy, Climate Protection and the Environment of the State of Saxony-Anhalt.References
- R. Dehghani, S. Aber and F. Mahdizadeh, Polyoxometalates and Their Composites as Photocatalysts for Organic Pollutants Degradation in Aqueous Media—A Review, Clean: Soil, Air, Water, 2018, 46 DOI:10.1002/clen.201800413.
- M. T. Pope and A. Müller, Chemie der Polyoxometallate: Aktuelle Variationen über ein altes Thema mit interdisziplinären Bezügen, Angew. Chem., 1991, 103, 56–70 CrossRef CAS.
- J. Albert, D. Lüders, A. Bösmann, D. M. Guldi and P. Wasserscheid, Spectroscopic and electrochemical characterization of heteropoly acids for their optimized application in selective biomass oxidation to formic acid, Green Chem., 2014, 16, 226–237 RSC.
- M. T. Pope and A. Müller, Polyoxometalate Chemistry: An Old Field with New Dimensions in Several Disciplines, Angew. Chem., Int. Ed. Engl., 1991, 30, 34–48 CrossRef.
- J.-C. Raabe, M. J. Poller, D. Voß and J. Albert, H8[PV5Mo7O40] – A Unique Polyoxometalate for Acid and RedOx Catalysis: Synthesis, Characterization, and Modern Applications in Green Chemical Processes, ChemSusChem, 2023, 16, 2013–2015 CrossRef.
- A. Modvig, C. Kumpidet, A. Riisager and J. Albert, Ru-Doped Wells–Dawson Polyoxometalate as Efficient Catalyst for Glycerol Hydrogenolysis to Propanediols, Materials, 2019, 12, 2175 CrossRef.
- I. A. Weinstock, J. J. Cowan, E. M. G. Barbuzzi, H. Zeng and C. L. Hill, Equilibria between α and β Isomers of Keggin Heteropolytungstates, J. Am. Chem. Soc., 1999, 121, 4608–4617 CrossRef.
- D. Lockey, C. Mathis, H. N. Miras and L. Cronin, Investigating the autocatalytically driven formation of Keggin-based polyoxometalate clusters, Matter, 2022, 5, 302–313 CrossRef.
- L. E. Briand, H. J. Thomas and G. T. Baronetti, Thermal stability and catalytic activity of Wells-Dawson tungsten heteropoly salts, Appl. Catal., A, 2000, 201, 191–202 CrossRef CAS.
- J. D. H. Strickland, The Preparation and Properties of Silicomolybdic Acid. I. The Properties of Alpha Silicomolybdic Acid, J. Am. Chem. Soc., 1952, 74, 862–867 CrossRef CAS.
- J. Canny, R. Thouvenot, A. Teze, G. Herve, M. Leparulo-Loftus and M. T. Pope, Disubstituted tungstosilicates. 2. .gamma.- and .beta.-isomers of tungstovanadosilicate, [SiV2W10O40]6−: syntheses and structure determinations by tungsten-183, vanadium-51 and silicon-29 NMR spectroscopy, Inorg. Chem., 1991, 30, 976–981 CrossRef CAS.
- J.-C. Raabe, J. Albert and M. J. Poller, Spectroscopic, Crystallographic, and Electrochemical Study of Different Manganese(II)-Substituted Keggin-Type Phosphomolybdates, Chem. – Eur. J., 2022, 28, 1–12 CrossRef.
- V. F. Odyakov and E. G. Zhizhina, A novel method of the synthesis of molybdovanadophosphoric heteropoly acid solutions, React. Kinet. Catal. Lett., 2008, 95, 21–28 CrossRef CAS.
- V. F. Odyakov, E. G. Zhizhina and R. I. Maksimovskaya, Synthesis of molybdovanadophosphoric heteropoly acid solutions having modified composition, Appl. Catal., A, 2008, 342, 126–130 CrossRef CAS.
- V. F. Odyakov and E. G. Zhizhina, New process for preparing aqueous solutions of Mo-V-phosphoric heteropoly acids, Russ. J. Inorg. Chem., 2009, 54, 361–367 CrossRef.
- E. G. Zhizhina and V. F. Odyakov, Alteration of the physicochemical properties of catalysts based on aqueous solutions of Mo-V-P heteropoly acids in redox processes, React. Kinet. Catal. Lett., 2008, 95, 301–312 CrossRef CAS.
- I.-M. Mbomekalle, Y. W. Lu, B. Keita and L. Nadjo, Simple, high yield and reagent-saving synthesis of pure α-K6P2W18O62·14H2O, Inorg. Chem. Commun., 2004, 7, 86–90 CrossRef CAS.
- D. R. Park, H. Kim, J. C. Jung, S. H. Lee and I. K. Song, Reduction potentials of H3+xPMo12−xVxO40 and H6+xP2Mo18−xVxO62 heteropolyacid (HPA) catalysts and their catalytic activity for the vapor-phase oxidative dehydrogenation of isobutyric acid, Catal. Commun., 2008, 9, 293–298 CrossRef CAS.
- M.-X. Xu, S. Lin, L.-M. Xu and S.-L. Zhen, Crystal structure and properties of H3[PMo12O40]·3C2H6O, Transition Met. Chem., 2004, 29, 332–335 CrossRef CAS.
- M. J. Poller, S. Bönisch, B. Bertleff, J.-C. Raabe, A. Görling and J. Albert, Elucidating activating and deactivating effects of carboxylic acids on polyoxometalate-catalysed three-phase liquid–liquid-gas reactions, Chem. Eng. Sci., 2022, 264, 118143 CrossRef CAS.
- J.-C. Raabe, T. Esser, F. Jameel, M. Stein, J. Albert and M. J. Poller, Study on the incorporation of various elements into the Keggin lacunary-type phosphomolybdate [PMo9O34]9− and subsequent purification of the polyoxometalates by nanofiltration, Inorg. Chem. Front., 2023, 10, 4854–4868 RSC.
- J.-C. Raabe, J. Aceituno Cruz, J. Albert and M. J. Poller, Comparative Spectroscopic and Electrochemical Study of V(V)-Substituted Keggin-Type Phosphomolybdates and -Tungstates, Inorganics, 2023, 11, 138 CrossRef CAS.
- K. J. Schmidt, G. J. Schrobilgen and J. F. Sawyer, Hexasodium Hexatungstotellurate(VI) 22-Hydrate, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 1115–1118 CrossRef.
- D. Ghosh and R. Biswas, Theoretical Calculation of Absolute Radii of Atoms and Ions. Part 1. The Atomic Radii, Int. J. Mol. Sci., 2002, 3, 87–113 CrossRef CAS.
- J. C. Slater, Atomic Radii in Crystals, J. Chem. Phys., 1964, 41, 3199–3204 CrossRef CAS.
- R. D. Shannon and C. T. Prewitt, Effective ionic radii and crystal chemistry, J. Inorg. Nucl. Chem., 1970, 32, 1427–1441 CrossRef.
- Y. Q. Jia, Crystal radii and effective ionic radii of the rare earth ions, J. Solid State Chem., 1991, 95, 184–187 CrossRef.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- R. D. Shannon and C. T. Prewitt, Revised values of effective ionic radii, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1046–1048 CrossRef.
- M. Rahm, R. Hoffmann and N. W. Ashcroft, Atomic and Ionic Radii of Elements 1–96, Chem. – Eur. J., 2016, 22, 14625–14632 CrossRef PubMed.
- D. W. J. Cruickshank, Refinements of structures containing bonds between Si, P, S or Cl and O or N. V. P4O10, Acta Crystallogr., 1964, 17, 677–679 CrossRef.
- M. Jansen, Die Kristallstruktur von Antimon(V)-oxid, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 539–542 CrossRef.
- U. Müller, Anorganische Strukturchemie, Vieweg+Teubner, Wiesbaden, 6th edn, 2008 Search PubMed.
- A. F. Holleman, E. Wiberg, N. Wiberg and G. Fischer, Lehrbuch der Anorganischen Chemie, Berlin, New York, 2009 Search PubMed.
- D. Drewes, E. M. Limanski and B. Krebs, The Anderson-Type Anion (TeMo6O24)6− – A Multidentate Ligand for Trivalent Rare Earth Cations, Eur. J. Inorg. Chem., 2004, 4849–4853 CrossRef.
- S. Himeno, M. Hashimoto and T. Ueda, Formation and conversion of molybdophosphate and -arsenate complexes in aqueous solution, Inorg. Chim. Acta, 1999, 284, 237–245 CrossRef.
- T. Esser, M. Huber, D. Voß and J. Albert, Development of an efficient downstream process for product separation and catalyst recycling of a homogeneous polyoxometalate catalyst by means of nanofiltration membranes and design of experiments, Chem. Eng. Res. Des., 2022, 185, 37–50 CrossRef.
- K. Sifaki, N. I. Gumerova, G. Giester and A. Rompel, Crystal structure of hexasodium tetraserinolium paratungstate B decahydrate, [Na6{(CH2OH)2CHNH3}4][W12O40(OH)2]·10H2O, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2022, 78, 207–210 CrossRef PubMed.
- X. Qu, Y. Yang, F. Zhang and X. Yu, Synthesis and characterization of a three-dimensional framework built up of paradodecatungstate-B clusters and transition metals as linkers, Struct. Chem., 2012, 23, 1867–1872 CrossRef CAS.
- C.-J. Zhang, H.-J. Pang and Y.-G. Chen, Highest Connectivity in a Purely Inorganic 3D Compound Based on Paradodecatungstate-B Clusters: Synthesis and Magnetic Properties, Z. Naturforsch. B, 2009, 64, 809–814 CrossRef CAS.
- X. Qu, Y. Yang, X. Yu, Z. Lv, M. Ji and S. Y. Feng, A novel paradodecatungstate-B compound decorated by transition metal copper, Na2Cu5(H2O)24(OH)2[H2W12O42]·10H2O: Synthesis, structure and antitumor activities, Inorg. Chem. Commun., 2015, 60, 126–130 CrossRef CAS.
- B. Courcot and A. J. Bridgeman, Structural and Vibrational Study of [Mo7O24]6− and [W7O24]6−, J. Phys. Chem. A, 2009, 113, 10540–10548 CrossRef CAS.
- A. J. Bridgeman, Computational Study of Solvent Effects and the Vibrational Spectra of Anderson Polyoxometalates, Chem. – Eur. J., 2006, 12, 2094–2102 CrossRef CAS.
- A. J. Bridgeman and G. Cavigliasso, A Comparative Investigation of Structure and Bonding in Mo and W [TeM6O24]6− and [PM12O40]3− Heteropolyanions, J. Phys. Chem. A, 2003, 107, 6613–6621 CrossRef CAS.
- K. Sifaki, N. I. Gumerova, G. Giester and A. Rompel, Synthesis and characterization of the Anderson–Evans tungstoantimonate [Na5(H2O)18{(HOCH2)2CHNH3}2][SbW6O24], Acta Crystallogr., Sect. C: Struct. Chem., 2021, 77, 420–425 CrossRef CAS PubMed.
- J. K. Lee, J. Melsheimer, S. Berndt, G. Mestl, R. Schlögl and K. Köhler, Transient responses of the local electronic and geometric structures of vanado-molybdo-phoshate catalysts H3+nPVnMo12−nO40 in selective oxidation, Appl. Catal., A, 2001, 214, 125–148 CrossRef CAS.
- S. Himeno, M. Takamoto and T. Ueda, Formation of α- and β-Keggin-Type [PW12O40]3− Complexes in Aqueous Media, Bull. Chem. Soc. Jpn., 2005, 78, 1463–1468 CrossRef CAS.
- J. F. Keggin, The structure and formula of 12-phosphotungstic acid, Proc. R. Soc. London, Ser. A, 1934, 144, 75–100 CAS.
- P. Pérez-Romo, C. Potvin, J.-M. Manoli and G. Djéga-Mariadassou, Phosphorus-Doped Tungsten Oxynitrides: Synthesis, Characterization, and Catalytic Behavior in Propene Hydrogenation and n-Heptane Isomerization, J. Catal., 2002, 205, 191–198 CrossRef.
- R. Thouvenot, A. Teze, R. Contant and G. Herve, Synthesis, structure, and phosphorus-31 and tungsten-183 NMR spectra of tungstophosphate, P4W14O5812−, Inorg. Chem., 1988, 27, 524–529 CrossRef CAS.
- L. H. Bi, E. B. Wang, J. Peng, R. D. Huang, L. Xu and C. W. Hu, Crystal structure and replacement reaction of coordinated water molecules of the heteropoly compounds of sandwich-type tungstoarsenates, Inorg. Chem., 2000, 39, 671–679 CrossRef CAS PubMed.
- N. I. Gumerova, E. Al-Sayed, L. Krivosudský, H. Ĉipĉić-Paljetak, D. Verbanac and A. Rompel, Antibacterial activity of polyoxometalates against Moraxella catarrhalis, Front. Chem., 2018, 6, 1–9 CrossRef.
- L. Berţa Grama, F. Boda, G. Borodi, A. Rusu, H. Kelemen, A. Man, A. Mare and Ş. A. Gâz-Florea, Two new sandwich-type compounds based on {AsW9} with Pd2+ and Pt4+ cations – synthesis, characterization and antibacterial activity, Farmacia, 2017, 65, 63–68 Search PubMed.
- J. R. Rea, J. B. Anderson and E. Kostiner, The crystal structures of copper chloroarsenate and cobalt chloroarsenate, Cu2(AsO4)Cl and Co2(AsO4)Cl, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 975–979 CrossRef.
- S. Himeno, M. Takamoto, R. Santo and A. Ichimura, Redox Properties and Basicity of Keggin-Type Polyoxometalate Complexes, Bull. Chem. Soc. Jpn., 2005, 78, 95–100 CrossRef.
- C. Rocchiccioli-Deltcheff, M. Fournier, R. Franck and R. Thouvenot, Vibrational investigations of polyoxometalates. 2. Evidence for anion-anion interactions in molybdenum(VI) and tungsten(VI) compounds related to the Keggin structure, Inorg. Chem., 1983, 22, 207–216 CrossRef.
- J. Piquemal, L. Salles, G. Chottard, P. Herson, C. Ahcine and J. Brégeault, Another Example of the Instability of a Keggin-Type Heteropolyanion in the Presence of Aqueous Hydrogen Peroxide: From [AsW12O40]3− to Low-Nuclearity Oxoperoxotungstates – Crystal Structure of [(nHex)4N]3[AsO4{W2O2(μ-O2)2(O2)2}2], Eur. J. Inorg. Chem., 2006, 939–947 CrossRef.
- P. Pyykkö and M. Atsumi, Molecular Single-Bond Covalent Radii for Elements 1–118, Chem. – Eur. J., 2009, 15, 186–197 CrossRef.
- D. Gabb, C. P. Pradeep, H. N. Miras, S. G. Mitchell, D.-L. Long and L. Cronin, Organic-soluble lacunary {M2(P2W15)2} polyoxometalate sandwiches showing a previously unseen αββα isomerism, Dalton Trans., 2012, 41, 10000–10005 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2293848–2293851. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt03883a |
| This journal is © The Royal Society of Chemistry 2024 |



