Unveiling the electronic and structural consequences of removing two electrons from B₁₂H₁₂²⁻

Abstract

The notion that a regular icosahedron is unattainable in neutral B₁₂H₁₂ has persisted for nearly 70 years. This is because 24 valence electrons are used for B–H bonds, while another 24 electrons are necessary to maintain the deltahedron, unlike the 26 used in the dianion. According to Wade–Mingos rules, the neutral system should be a deltahedron with a capped face. Nevertheless, our exploration of the potential energy surface of B₁₂H₁₂ reveals that the global minimum is a closed-shell form with an H₂ unit attached to a boron vertex of B₁₂H₁₀, preserving the deltahedral boron skeleton.

---

Introduction

In 1955, Longuet-Higgins and Roberts predicted that the B₁₂H₁₂²⁻ ion would have a regular icosahedron structure based on molecular orbital analysis.¹ Their goal was to determine the existence of B₁₂H₁₂. They hypothesized that a boron icosahedron would require thirteen bonding orbitals to hold it together and twelve outward-facing orbitals to connect with hydrogens, concluding that “B₁₂H₁₂, if it existed, would have forty-eight valence electrons. Twenty-four of these would be required to form the BH bonds, leaving twenty-four for the icosahedral bonding orbitals. However, these orbitals are thirteen in number, the top four being degenerate, so that the molecule would definitely not have a closed-shell electronic structure. At present all the hydrides of boron whose nuclear configurations are known appear to have closed-shell structures, so we may conclude with reasonable certainty that B₁₂H₁₂would be unstable. It is, however, not unlikely that a stable ion, B₁₂H₁₂²⁻, might exist”.¹ Five years later, Pitochelli and Hawthorne isolated this dianion,² while Wunderlich and Lipscomb performed an X-ray diffraction study of K₂B₁₂H₁₂, confirming the perfect Platonic solid structure of B₁₂H₁₂²⁻ in the crystal.³ Nevertheless, the form of the neutral B₁₂H₁₂ remains uncertain.

Schleyer and co-workers proposed an arrangement for B₁₂H₁₂ (Fig. 1) in which all twelve B–H bonds are present, but distortions occur due to the Jahn–Teller effect.⁴ The authors optimized and characterized the radical anion B₁₂H₁₂⁻ by constraining it to the I_h point group at the AM1 level. The structure was then displaced along the vector with the most negative eigenvalue and re-minimized to serve as the initial guess for a full optimization at the B3LYP/6-31G(d) level. This procedure yielded a T_h arrangement with three imaginary frequencies. Eliminating these imaginary frequencies resulted in a C_2v minimum (Fig. 1, right). In 2021, Bhattacharyya et al. partially explored the B₁₂H₁₂ potential energy surface (PES) at the CCSD/cc-pVDZ level of theory (only six forms). They found a distorted deltahedron (C_i) with five imaginary frequencies as the lowest energy structure. Their only conclusion was that this cage is unstable, and they did not explore any further.⁵

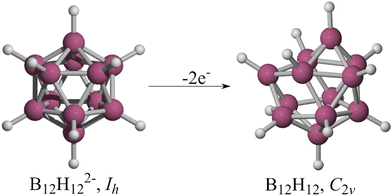Fig. 1 B₁₂H₁₂²⁻ structure and the one proposed by Schleyer as the most stable for the neutral system.

It is well-known that the global minimum of B₁₂H₁₂²⁻ is an icosahedron,⁶ so we have used it as a benchmark to validate our genetic algorithms for exploring PESs. During one of the tests, instead of achieving the icosahedron, we obtained a structure with a three-center-two-electron (3c–2e) B–H₂ bond, which was unexpected. Because of a human error, the system was submitted as neutral! Interestingly, the obtained structure differs from the one reported by Schleyer and co-workers for B₁₂H₁₂,⁴ deviating from the icosahedron with twelve B–H bonds and any other structure proposed in the past seven decades. In this paper, we show that the most stable form of B₁₂H₁₂ is a boron deltahedron with ten B–H bonds instead of twelve, along with a 3c–2e B–H₂ interaction. This structure is lower in energy by over 23.5 kcal mol⁻¹ compared to the proposal by Schleyer and co-workers.

Computational details

The PES of B₁₂H₁₂ was systematically explored using a modified genetic algorithm implemented in GLOMOS.⁷ Further details about GLOMOS are described elsewhere.⁸ The initial screening, in both singlet and triplet states, was performed at the PBE0/def2-SVP level.^9,10 The lowest-lying energy isomers within a 60 kcal mol⁻¹ range were further re-minimized at the TPSS-D3/def2-TZVP level.^10,11 Approximately 2000 initial structures were used to thoroughly explore the chemical space, and our algorithm successfully identified over 181 singlet and 200 triplets local minima at the TPSS/def2-SVP level. Stationary points were characterized by harmonic vibrational frequency analysis at the same level. Relative Gibbs free energies were computed at the CCSD(T)¹²/def2-TZVP//TPSS-D3/def2-TZVP level, including entropic contributions and thermal corrections at the DFT level at 298.15 K. The interconversion pathway of lower energy minima was also determined. Intrinsic reaction coordinate (IRC)¹³ computations were carried out to ensure that the transition states (TS) connected to the correct local minima. All of these calculations were conducted using Gaussian 16.¹⁴ The bonding analysis in these boron hydrides was carried out using Wiberg Bond Indices (WBI) and Natural Population Analysis (NPA).¹⁵ This was achieved by utilizing the wave functions generated in Gaussian and subsequently inputting them into the NBO6.0 program.

To understand the electronic distribution of the molecule in terms of n-center two-electron (nc-2e) bonds, recovering Lewis' bonding concepts and delocalized bonding elements, the Adaptive Natural Density Partitioning (AdNDP) method¹⁶ developed by Zubarev and Boldyrev and implemented in Multiwfn¹⁷ was employed.

Additionally, the nature of the interaction between B₁₂H₁₀ and H₂ was analyzed by the Energy Decomposition Analysis (EDA)^18,19 at the TPSS-D3/TZ2P//TPSS-D3/def2-TZVP level using the ADF 2016 package.^20,21 The EDA decomposes the instantaneous interaction energy, ΔE_int, into four terms: a quasi-classical electrostatic interaction (ΔV_elstat), a Pauli exchange repulsion term (ΔE_Pauli) caused by repulsion between same spin electrons, an orbital interaction term (ΔE_orb) as a result of the stabilizing orbital interaction, and a dispersion corrections (ΔE_disp) added via Grimme's D3 version approximation. Hence, ΔE_int is defined as ΔE_int = ΔE_Pauli + ΔV_elstat + ΔE_orb + ΔE_disp. The reader is referred to some comprehensive reviews for a more detailed description of EDA.^22,23 To provide quantitative insights, we carried out an isomerization energy decomposition analysis (IEDA).²⁴ This analysis allows us to decompose the isomerization energy (ΔE_iso) into the distortion energy (ΔE_dist) and the changes in interaction energies between the fragments of each isomer (ΔΔE_int). The latter term can be further decomposed into the variations in orbital (ΔΔE_orb) and electrostatic (ΔΔV_elstat) interactions, Pauli repulsion (ΔΔE_Pauli), and dispersion energy (ΔΔE_disp).

To investigate the dynamic behavior of B₁₂H₁₂, Born-Oppenheimer Molecular Dynamics (BO-MD)²⁵ computations were performed at 600 K for a period of 10 ps using a time step of 1 fs. A Nose–Hoover chain thermostat was used during the simulations to maintain a constant temperature.^26–28 Note that the selected temperature is not a real temperature in the macroscopic sense but rather a parameter to regulate the total kinetic energy of the atoms, ensuring they possess enough energy to overcome energy barriers. This allows reasonable simulation times for the interconversion between isomers to take place. These computations were done using the deMon-2k program²⁹ at the PBE0/DZVP³⁰ level.

Results

During the exploration of the B₁₂H₁₂ PES, we identified lower-energy forms that differ from that reported by Schleyer and co-workers (see Fig. 2).⁴ The global minimum (1) has C_s symmetry, with an deltahedral boron skeleton bearing ten B–H bonds only. One of the remaining boron atoms is bonded solely to B atoms, while the other is bonded to an H₂ framework, both at opposing vertices. Our computations reveal forms where one hydrogen is tricoordinate, namely, 3, 5, 6, and 9, with relative Gibbs free energies to 1 of 5.7, 8.4, 8.5, and 21.3 kcal mol⁻¹, respectively (at the CCSD(T)/def2-TZVP//TPSS-D3/def2-TZVP level). Additionally, there are two structures (4 and 8) with a hydrogen atom located at one of the edges of the deltahedron, which are 7.3 and 20.4 kcal mol⁻¹ higher in free energy than 1, respectively. In fact, 8 is identical to the one proposed by Jena and co-workers.³¹ There are two other isomers 2, (ΔG_1–2 = 3.2 kcal mol⁻¹) and 7 (ΔG_1–7 = 13.9 kcal mol⁻¹) that contain a hydrogen molecule (these forms will be discussed in further detail below). Structure 10, with C_2v symmetry, is the one reported by Schleyer⁴ as the most stable arrangement of B₁₂H₁₂ (Fig. 1, right); however, it is 23.5 kcal mol⁻¹ less stable than 1. In 10, a B–B bond forming one of the faces of the deltahedron is elongated (from 1.850 to 2.796 Å). The most stable triplet is 11, with a ΔG_1–11 of 40.3 kcal mol⁻¹. ESI† includes higher-energy isomers (Fig. S1 and S2†). So, within the energy range of 60 kcal mol⁻¹ above the global minimum, the deltahedral boron skeleton is dominant.

Fig. 2 Low-lying structures of B₁₂H₁₂. Relative Gibbs free energies (in kcal mol⁻¹) computed at the CCSD(T)/def2-TZVP//TPSS-D3/def2-TZVP level.

Let us examine the structure and bonding of the global minimum of B₁₂H₁₂, 1. The H₂ fragment has an H–H bond length of 0.838 Å, which is 0.1 Å longer than the bond distance in free H₂ (Fig. 3). These hydrogen atoms are 1.342 Å away from the neighboring boron. Notably, the boron cage of the neutral system is more compact than the dianionic one, i.e., the distance between two boron atoms at opposite vertices is reduced from 3.408 to 2.934 Å, considering the boron atom bonded to H₂ and that at the opposite vertex. On the other hand, the B–H bond lengths in the neutral system are slightly longer (1.186 Å) than in the dianion (1.137 Å).

Fig. 3 TPSS-D3/def2-TZVP structural comparison between B₁₂H₁₂²⁻ and B₁₂H₁₂ (1). All distances are given in Å.

One question that arises is whether the dianion can remain stable with the same arrangement that includes an H₂ fragment. Starting with the C_s structure of 1, two electrons were added and then optimized. During the optimization process, H₂ was reoriented, resulting in an interaction of the boron backbone and only one hydrogen atom, resulting in a complex with C_5v symmetry (1²⁻, Fig. S3†). The B⋯H distance is 2.664 Å, while the H–H bond length is 0.764 Å. The energy difference between the dianion's icosahedral structure and 1²⁻ is 89.0 kcal mol⁻¹. So, this system can be described as a complex between B₁₂H₁₀²⁻ and H₂, but it is not energetically viable at all.

Removing two electrons has interesting consequences on the geometry beyond the formation of the H₂ fragment. The B–H and B–B bond lengths in B₁₂H₁₂²⁻ are 1.137 and 1.792 Å, respectively, with corresponding WBI values of 0.96 and 0.54. In comparison, the B–H bond lengths in 1 are longer (1.186 Å), indicating weaker B–H bonds in the neutral system. This is supported by a reduction of the WBI_B–H value from 0.96 in the dianion to 0.82 in the neutral molecule.

There are also subtle changes in the boron skeleton. Let us divide the deltahedron into two hemispheres to describe these modifications. An axis of rotation crosses the system from one pole to the other. At the northern pole, the boron attached to the H₂ fragment is located, while the bare boron is at the other pole. The boron atom attached to H₂ has a B–B distance of 1.747 Å to its five neighboring boron atoms, which is slightly shorter than the B–B distance in the dianion, and a WBI value of 0.56. The B–B bond lengths connecting the northern and southern hemispheres are also slightly shorter (1.783 Å with WBI = 0.53) than those in the dianion. The B–B bond lengths of the hydrogen-free boron are much shorter (1.696 Å and WBI = 0.58). In other words, the bonds along the axis are compressed. Conversely, the B–B bonds forming the five-membered rings perpendicular to the axis lengthen to 1.832 (WBI = 0.47) and 1.844 Å (WBI = 0.50). That is, the B–B bond lengths perpendicular to the axis are expanded.

Our findings hold importance when dealing with electron-deficient B₁₂ polyhedra, especially in the context of many B₁₂-based borides. The oxidation of deltahedral B₁₂ units has long drawn the interest and curiosity of chemists, with some of the initial studies originating from the solid-state community.³² From this perspective, exploring the structures of all isomers becomes valuable in the quest to identify oxidized B₁₂ frameworks. Fig. 4 compiles all B–H and B–B distances in the eleven isomers depicted in Fig. 2. Notably, there is a distinct and well-defined peak at 1.19 Å corresponding to the 2c–2e B–H distances, which are a little longer than the B–H bond distance in the dianion (1.137 Å). Note three additional peaks with lengths ranging from 1.30 to 1.45 Å. The first of these peaks corresponds to the 3c–2e bonds involved in forming the H₂ molecule, while the other two peaks are associated with distances where the hydrogen atom is di- or tricoordinate.

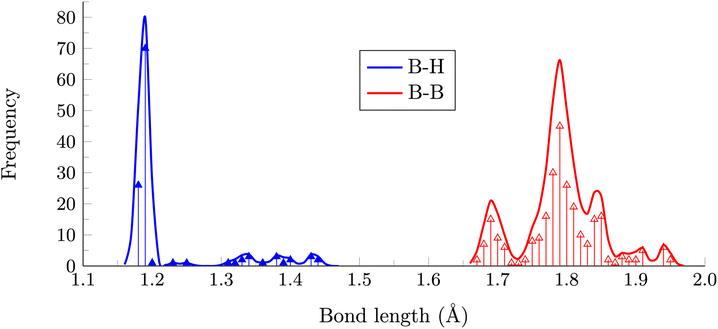Fig. 4 Distribution of B–H and B–B bond distances in the most stable isomers of B₁₂H₁₂ (γ = 0.01 Å).

In contrast, the distribution of B–B distances is considerably more intricate. There are five discernible peaks centered at 1.69, 1.79, 1.85, 1.88, and 1.94 Å, with the first three being the most prominent. The first peak is connected to B–B bonds involving bare boron, signifying that electron deficiency of this boron atom is compensated by forming more localized B–B bonds around. The other two peaks, as in 1, correspond to the B–B distances within the hemispheres, where the hemispheres are defined concerning the axis created by the bare boron atom and the opposing boron atom, regardless of the presence of an H₂ framework. The longer-distance peaks are linked to multicentric bonds where the hydrogen is tricoordinate. In such structures, both B–H and B–B distances are expanded, as two electrons must bind four atoms.

So, removing two electrons and subsequently generating a hydrogen molecule to offset this process facilitates the preservation of the deltahedral cage. This, in turn, results in the cluster containing a Lewis acidic bare boron atom, leading to a low-lying LUMO (situated on this exposed boron atom, as depicted in Fig. 5), which impacts the HOMO–LUMO gap (Table S1†). The computed gap for the dianion is 5.63 eV (at the TPSS/def2-TZVP level), while for 1, the respective value is 3.75 eV. The reduction in the gap may affect the stability of the wave function. Nevertheless, we conducted a T1 diagnostic using the CCSD/cc-pVTZ level of theory, serving as a tool to assess the quality of single-reference electron correlation methods. The T1 diagnostic values for all systems were below 0.02 (see Table S1†), confirming the suitability of our single-reference electron correlation methods.

Fig. 5 Lowest unoccupied molecular orbital (LUMO) of B₁₂H₁₂.

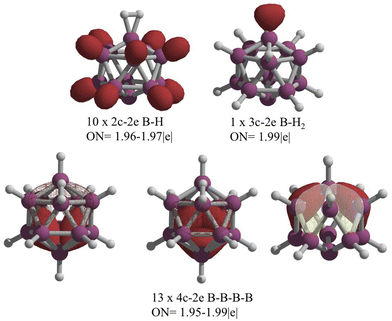
Let us analyze the chemical bonding in 1. According to AdNDP, there are ten 2c–2e B–H bonds and one 3c–2e bond involving a boron atom and the H₂ fragment, as shown in Fig. 6. The remaining electrons in the boron backbone are distributed among 4c–2e bonds. This distribution of 26 electrons throughout the skeleton is the main reason the cage retains its deltahedral form. The Wade–Mingos rules predict that removing two electrons in the closo B₁₂H₁₂²⁻ icosahedron would result in a deltahedral structure with a capped face, like the structure proposed by Schleyer and co-workers.⁴ But that is not the case. The global minimum for B₁₂H₁₂ uses the number of electrons necessary to preserve a closed-shell deltahedral cage (26 electrons). It compensates for the loss of two electrons from B₁₂H₁₂²⁻ by forming an H₂ unit that bonds to a boron atom via a 3c–2e bond. This mechanism is even distinct from the one observed in hypercloso derivatives of B₁₂H₁₂, such as hypercloso-B₁₂(OR)₁₂ (systems used as photoredox reagents, and in particular as photoinitiators for cationic polymerization), where the oxidation prevents open-shell configurations and only leads to a reduction of the I_h symmetry to D_3d.^33–36

Fig. 6 AdNDP analysis of 1. Occupation numbers (ONs) are given in |e|.

To quantitatively understand the 3c–2e B–H₂ bond in B₁₂H₁₂, we performed an EDA, choosing H₂ and B₁₂H₁₀ as fragments. The EDA shows a strong interaction between the two fragments (ΔE_int = −32.3 kcal mol⁻¹). Interestingly, the orbital contribution (ΔE_orb = −87.0 kcal mol⁻¹) is nearly twice as large as the electrostatic contribution (ΔV_elstat = −41.8 kcal mol⁻¹), contributing about two-thirds (66.4%) of the total attractive interaction. This indicates that the 3c–2e B–H₂ bond is primarily a covalent bond.

Since the dianion has a degenerate HOMO, removing the electron pair leads to an electronic state that tends toward a Jahn–Teller distortion, as suggested by Longuet-Higgins and Roberts.¹ Optimization of the neutral system within the dianion point group (I_h) yields a C_2h structure (F, Fig. S4†) with five imaginary frequencies, which is 52.7 kcal mol⁻¹ higher in energy than 1. Following the vector with the most negative eigenvalue (−656 cm⁻¹) and re-minimizing produces the local minimum 8, which is 20.4 kcal mol⁻¹ less energetically stable than 1. Note that all twelve B–H bonds are still present in 8, but one is shared with an adjacent boron atom. This raises two questions: Is 8 kinetically stable, and what is the mechanism for converting 8 to 1?

The hydrogen migration from one hemisphere to another begins with the displacement of a hydrogen atom from the B1–B2 bond (see Fig. 7) to the boron triangular face 2–3–4 (structure 6) viaTS_8–6. The barrier is negligible, only 1.0 kcal mol⁻¹. Note that 6 is more stable than 8 by 11.9 kcal mol⁻¹. The next step involves the migration of the hydrogen atom toward the 3–4–5 face (Isomer 5) viaTS_6–5, where the hydrogen bridges B3 and B4, with a barrier of only 3.6 kcal mol⁻¹. Moving from the equator to the 4–5–6 face of the northern hemisphere involves a barrier of only 2.2 kcal mol⁻¹ (TS_5–3), leading to 3, which is more stable than 5 by 2.7 kcal mol⁻¹. The final step is the formation of the H₂ molecule to produce 1, with a barrier of 3.2 kcal mol⁻¹ (TS_3–1). 1 is more stable than 3 by 5.7 kcal mol⁻¹. It is worth mentioning that all hydrogen migrations occur across edges, not vertices. So, the formation of 1 from 8 is exergonic (ΔG = 20.4 kcal mol⁻¹) with low barriers. Consequently, 8 is kinetically unstable. In other words, once the two electrons are removed, the minimum that still holds the twelve B–H bonds is kinetically unstable, and the transformation to 1 is kinetically and thermodynamically favorable. Upon the formation of 1, there exists a possibility that the B–H₂ interaction might not be strong enough and could dissociate, resulting in the formation of B₁₂H₁₀ + H₂. This dissociation process would require a Gibbs free energy of 15.8 kcal mol⁻¹ in the gas phase (with full optimization of each species). It is important to note that the value obtained may not be directly applicable to experimental conditions. This is because 1 and the resulting B₁₂H₁₀ are likely to exist in the solid state at room temperature, while H₂ will remain as a gas. However, this value is a reasonable starting point for understanding the interaction between B₁₂H₁₀ and H₂. Note that the HOMO–LUMO gap for 8 is 2.48 eV. However, when a hydrogen atom is transferred to create structures involving a bare boron atom (6, 5, 3, or 1), the gap increases, ranging from 3.51 to 3.75 eV, with 1 showing the largest gap (3.75 eV).

Fig. 7 Mechanism for the conversion of 8 to 1. Relative Gibbs free energies are in kcal mol⁻¹.

To gain further insight into the transformation process from 8 to 1, we performed a Born-Oppenheimer molecular dynamics simulation at 600 K for 10 ps, using structure 8 as the starting point. A movie depicting this BO-MD simulation is provided in the ESI,† where two hydrogen atoms have been colored differently for better visualization. At the beginning of the simulation, there is a rapid interconversion from 8 to 6, then to 5, and finally to 3 in less than 1 ps. This stage can be described as a displacement of the bridged hydrogen in 8 (in blue in the BO-MD movie) above the center of the triangular faces in 6, 5, and 3. This matches perfectly with the mechanistic pathway. At this point, the simulation shows a series of interconversions between structures 3, 5, and 6 during the first 4 ps, eventually reaching the global minimum 1. During the final step, which occurs between 4.0 and 4.3 ps, isomer 2 briefly emerges. In this isomer, the hydrogen atoms marked in blue and green combine to form an H₂ unit that becomes bonded to a boron atom on one of the upper triangular faces. Afterward, one of these hydrogen atoms (specifically the green one in this instance) quickly moves to form 1. This last migration occurs in less than 0.3 ps, hinting at a very low energy barrier for this process. Once the global minimum is attained, it maintains its structural integrity without significant distortion, confirming its kinetic stability.

Finally, Hoffmann and co-workers proposed three structures of B₁₂H₁₀, all of them retaining the deltahedral boron skeleton.³⁷ These arrangements correspond to three potential isomers resulting from the removal of two hydrogen atoms, namely ortho, meta, and para (as benzene), with the meta isomer being the most stable. Initially, adding an H₂ molecule to the para, meta, and ortho B₁₂H₁₀ isomers would yield structures 1, 2, and 7, respectively. This raises the question of how to explain the stabilization of the para isomer instead of the meta form.

To elucidate the relative stability of the ortho, meta, and para isomers of the B₁₂H₁₀⋯H₂ complexes, we carried out an EDA (Table 1). The interaction energy values for the para isomer (−32.3 kcal mol⁻¹) were found to be higher compared to those of the ortho (−27.8 kcal mol⁻¹) and meta (−26.2 kcal mol⁻¹) isomers. In all three cases, the orbital contribution was approximately double the electrostatic contribution. Despite the higher electrostatic and comparable or even higher orbital interaction values computed for the ortho and meta isomers compared to the para one, the Pauli repulsion significantly outweighs these factors. Therefore, the Pauli repulsion plays a critical role in determining the relative stability of the three systems.

Table 1 Energy decomposition analysis considering the interaction between B₁₂H₁₀ and the capping H₂ molecule at the all-electron TPSS-D3/TZ2P//TPSS-D3/def2-TZVP level. The percentage values in parentheses indicate the contribution of the total attractive interaction. Energy values are given in kcal mol⁻¹

ΔEint	−27.8	−26.2	−32.3
ΔEPauli	118.4	104.5	98.7
ΔEorb	−96.0 (65.7)	−85.5 (65.4)	−87.0 (66.4)
ΔVelstat	−48.2 (33.0)	−43.1 (33.0)	−41.8 (31.9)
ΔEdisp	−2.0 (1.4)	−2.2 (1.7)	−2.2 (1.7)

---

Let us now compare the different contributions using an isomerization energy decomposition analysis (IEDA). To conduct this analysis, we consider a hypothetical thermodynamic cycle, as depicted in Fig. S5,† where positive values favor the para isomer (Table 2). In the case of para–ortho isomerization, although both the orbital and electrostatic contributions favor the ortho structure, the Pauli repulsion in the ortho isomer tips the balance in favor of the para isomer. Therefore, both the distortion and interaction energies support the preference for the para isomer. Conversely, in the case of para–meta isomerization, although the distortion energy favors the meta structure, it is not sufficient to counterbalance the Pauli repulsion. Thus, as mentioned earlier, the para isomer is strongly favored due to the Pauli repulsion. So, even among the three neutral B₁₂H₁₂ isomers that include an H₂ unit, determining the most stable configuration is a complex task.

Table 2 Isomerization energy decomposition analysis at the TPSS-D3/TZ2P//TPSS-D3/def2-TZVP level for para–ortho and para–meta isomerizations of B₁₂H₁₂. Energy values are given in kcal mol⁻¹

	para–ortho	para–meta
ΔEiso	12.3	2.1
ΔEdist (B12H10)	7.3	−3.4
ΔEdist (H2)	0.5	−0.6
ΔΔEint	4.5	6.1
ΔΔEorb	−9.0	1.5
ΔΔVelstat	−6.3	−1.2
ΔΔEPauli	19.7	5.8
ΔΔEdisp	0.1	0.0

---

Conclusions

After conducting an exhaustive search on the potential energy surface, we found a novel structure for the global minimum of B₁₂H₁₂ that is 23.5 kcal mol⁻¹ more stable than the previously reported structure. The main difference from the dianion is the presence of a 3c–2e bond between a boron atom and an H₂ unit. Nearly 70 years ago, it was suggested that B₁₂H₁₂ has 24 valence electrons for B–H bonds and lacks electrons to maintain its deltahedral form. According to the Wade–Mingos rules, removing two electrons from the closo B₁₂H₁₂²⁻ icosahedron would result in a deltahedral structure with a capped face, similar to the Schleyer structure proposed earlier. However, our bonding analysis shows that the system prioritizes the integrity of the boron framework rather than focusing on electrons for B–H bonds (at least in this case). The formation of a multicenter bonding between a boron vertex and an H₂ unit resolves this electron deficiency. In fact, EDA indicates that this 3c–2e bond is predominantly covalent. Our mechanistic studies indicate that removing two electrons from the dianion results in a local minimum where the twelve B–H bonds are still present but evolve to the global minimum due to relatively low interconversion barriers. Clearly, predicting boron structures remains a challenge. Despite significant progress since the pioneering work of Longuet-Higgins and Roberts in 1955, accurately predicting the structure of boron clusters remains a complex task. By serendipity, we have successfully predicted the structure of a neutral system, specifically B₁₂H₁₂, which could be considered one of the most representative. This achievement would contribute to our understanding of the structure, reactivity, and potential applications of other neutral borohydrides.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work in Mexico was partially done using the supercomputing infrastructure (Kukulcán and Ixchel) at Cinvestav Mérida. GHJ and AQ thank Conacyt for their PhD fellowships. FM thank Conacyt for his postdoctoral fellowship. AVE thanks the support of the National Agency for Research and Development (ANID) through FONDECYT project 1221019. This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

References

1. H. C. Longuet-Higgins and M. de V. Roberts, The Electronic Structure of an Icosahedron of Boron Atoms, Proc. R. Soc. London, 1955, 230(1180), 110–119.
2. A. R. Pitochelli and F. M. Hawthorne, The Isolation of the Icosahedral B₁₂H₁₂⁻² Ion, J. Am. Chem. Soc., 1960, 82(12), 3228–3229.
3. J. A. Wunderlich and W. N. Lipscomb, Structure of B₁₂H₁₂⁻² Ion, J. Am. Chem. Soc., 1960, 82(16), 4427–4428.
4. M. L. McKee, Z.-X. Wang and P. v. R. Schleyer, Ab Initio Study of the Hypercloso Boron Hydrides B_nH_n and B_nH_n⁻. Exceptional Stability of Neutral B₁₃H₁₃, J. Am. Chem. Soc., 2000, 122(19), 4781–4793.
5. P. Bhattacharyya, I. Boustani and A. Shukla, Why Does a BH Icosahedron Need Two Electrons to Be Stable: A First-Principles Electron-Correlated Investigation of B_nH_n (= 6, 12) Clusters, J. Phys. Chem. A, 2021, 125(51), 10734–10741.
6. A. Goursot, E. Pénigault, H. Chermette and J. G. Fripiat, Structure électronique Des Dianions B₁₂H₁₂²⁻ et B₉C₂H_n²⁻, Can. J. Chem., 1986, 64(9), 1752–1757.
7. F. Ortiz-Chi and G. Merino, GLOMOS, Mérida, México, 2020.
8. R. Grande-Aztatzi, P. R. Martínez-Alanis, J. L. Cabellos, E. Osorio, A. Martínez and G. Merino, Structural Evolution of Small Gold Clusters Doped by One and Two Boron Atoms, J. Comput. Chem., 2014, 35(32), 2288–2296.
9. C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170.
10. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
11. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401.
12. J. D. Watts, J. Gauss and R. J. Bartlett, Coupled–cluster Methods with Noniterative Triple Excitations for Restricted Open–shell Hartree–Fock and Other General Single Determinant Reference Functions. Energies and Analytical Gradients, J. Chem. Phys., 1993, 98(11), 8718–8733.
13. K. Fukui, The Path of Chemical Reactions - the IRC Approach, Acc. Chem. Res., 1981, 14(12), 363–368.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
15. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural Bond Orbital Analysis Program, J. Comput. Chem., 2013, 34(16), 1429–1437.
16. D. Y. Zubarev and A. I. Boldyrev, Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217.
17. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592.
18. K. Morokuma, Why Do Molecules Interact? The Origin of Electron Donor-Acceptor Complexes, Hydrogen Bonding and Proton Affinity, Acc. Chem. Res., 1977, 10(8), 294–300.
19. T. Ziegler and A. Rauk, On the Calculation of Bonding Energies by the Hartree Fock Slater Method, Theor. Chim. Acta, 1977, 46(1), 1–10.
20. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967.
21. ADF2022, SCM, Theoretical chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com.
22. F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, in Reviews in Computational Chemistry, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2007, pp. 1–86.
23. G. Frenking, Towards a Rigorously Defined Quantum Chemical Analysis of the Chemical Bond in Donor–acceptor Complexes, Coord. Chem. Rev., 2003, 238–239, 55–82.
24. M. Contreras, E. Osorio, F. Ferraro, G. Puga, K. J. Donald, J. G. Harrison, G. Merino and Prof. W. Tiznado, Isomerization Energy Decomposition Analysis for Highly Ionic Systems: Case Study of Starlike E5Li⁷⁺ Clusters, Chem. Eur. J., 2013, 19, 2305–2310.
25. J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, Ab Initio Classical Trajectories on the Born–Oppenheimer Surface: Hessian-Based Integrators Using Fifth-Order Polynomial and Rational Function Fits, J. Chem. Phys., 1999, 111(9), 3800–3805.
26. S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81(1), 511–519.
27. G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover Chains: The Canonical Ensemble via Continuous Dynamics, J. Chem. Phys., 1992, 97(4), 2635–2643.
28. W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31(3), 1695.
29. A. M. Koster, G. Geudtner, A. Alvarez-Ibarra, P. Calaminici, M. E. Casida, J. Carmona-Espindola, V. D. Dominguez, R. Flores-Moreno, G. U. Gamboa, A. Goursot, T. Heine, A. Ipatov, A. de la Lande, F. Janetzko, J. M. del Campo, D. Mejia-Rodriguez, J. U. Reveles, J. Vasquez-Perez, A. Vela, B. Zuniga-Gutierrez and D. R. Salahub, deMon2k, Version 5, The deMon Developers, Cinvestav, Mexico City, 2018.
30. S. Chiodo, N. Russo and E. Sicilia, Newly Developed Basis Sets for Density Functional Calculations, J. Comput. Chem., 2005, 26(2), 175–184.
31. B. Pathak, D. Samanta, R. Ahuja and P. Jena, Borane Derivatives: A New Class of Super- and Hyperhalogens, ChemPhysChem, 2011, 12(13), 2423–2428.
32. R. Franz and H. Werheit, Jahn-Teller Effect of the B₁₂ Icosahedron and Its General Influence on the Valence Band Structures of Boron-Rich Solids, EPL, 1989, 9(2), 145–150.
33. T. Peymann, C. B. Knobler, S. I. Khan and M. F. Hawthorne, Dodeca(benzyloxy)dodecaborane, B₁₂(OCH₂Ph)₁₂: A Stable Derivative of Hypercloso-B₁₂H₁₂, Angew. Chem., Int. Ed., 2001, 40(9), 1664–1667.
34. M. L. McKee, Density Functional Theory Study of Anionic and Neutral per-Substituted 12-Vertex Boron Cage Systems, B₁₂X₁₂ⁿ⁻ (n = 2, 1, 0), Inorg. Chem., 2002, 41(5), 1299–1305.
35. O. K. Farha, R. L. Julius, M. W. Lee, R. E. Huertas, C. B. Knobler and M. F. Hawthorne, Synthesis of Stable Dodecaalkoxy Derivatives of Hypercloso-B₁₂H₁₂, J. Am. Chem. Soc., 2005, 127(51), 18243–18251.
36. L. N. Goswami, Z. H. Houston, S. J. Sarma, H. Li, S. S. Jalisatgi and M. F. Hawthorne, Synthesis of Vertex-Differentiated Icosahedral Closo-Boranes: Polyfunctional Scaffolds for Targeted Drug Delivery, J. Org. Chem., 2012, 77(24), 11333–11338.
37. P. D. Pancharatna, M. M. Balakrishnarajan, E. D. Jemmis and R. Hoffmann, Polyhedral Borane Analogues of the Benzynes and beyond: Bonding in Variously Charged B₁₂H₁₀ Isomers, J. Am. Chem. Soc., 2012, 134(13), 5916–5920.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt02652c

---