 Open Access Article
Open Access ArticleA Raman spectroscopic and ab initio investigation of aqueous boron speciation under alkaline hydrothermal conditions: evidence for the structure and thermodynamic stability of the diborate ion†
Swaroop
Sasidharanpillai
 a,
Jenny S.
Cox
a,
Jenny S.
Cox
 a,
Cory C.
Pye
a,
Cory C.
Pye
 b and
Peter R.
Tremaine
b and
Peter R.
Tremaine
 *a
*a
aDepartment of Chemistry, University of Guelph, Guelph, ON, Canada N1G 2W1. E-mail: tremaine@uoguelph.ca
bDepartment of Chemistry, Saint Mary's University, Halifax, NS, Canada B3H 3C3
First published on 27th November 2023
Abstract
Raman spectra of aqueous sodium borate solutions, with and without excess NaOH, NaCl, and LiCl, have been obtained from perpendicular and parallel polarization measurements acquired using a custom-built sapphire flow cell over the temperature range 25 to 300 °C at 20 MPa. The solvent-corrected reduced isotropic spectra include a large well-defined band at 865 cm−1 which overlaps with the boric acid B(OH)3 band at 879 cm−1, and becomes increasingly intense at elevated temperatures. This band does not correspond to the spectrum of any other previously reported aqueous polyborate ions, all of which have symmetric stretching bands at frequencies below that of borate, [B(OH)4]−, at 745 cm−1. Based on the classic high-temperature potentiometric titration study by R. E. Mesmer, C. F. Baes and F. H. Sweeton, Acidity measurements at elevated temperatures. VI. Boric acid equilibriums, Inorg. Chem., 1972, 11, 537–543, the new band was postulated to arise from a diborate ion, [B2(OH)7]− or [B2O(OH)5]−. Ab initio density functional theory (DFT), together with chemical modelling studies, suggest that it is most likely [B2(OH)7]−. Thermodynamic formation quotients derived from the peak areas showed variations with ionic strength as well as charge-balance discrepancies, which suggest one or more unidentified minor equilibrium species may also be present. The most likely candidate is the divalent diborate species [B2O2(OH)4]2− which is also predicted to have a band near 865 cm−1 and is postulated to be present as a sodium ion pair. These are the first quantitative Raman spectra ever reported for borate-rich solutions under such conditions and provide the first spectroscopic evidence of a diborate species at PWR reactor coolant temperatures.
1. Introduction
An understanding of boric acid chemistry is essential to the nuclear industry, as boron containing compounds are added to the primary coolant in order to control the neutron flux in high-temperature pressurized water reactors (PWRs). Aqueous boric acid solutions can be highly complex; at least 10 different polyborate species are known to exist in solution depending on the specific conditions. Various spectroscopic techniques such as UV-visible spectroscopy,1 infrared spectroscopy,2 Raman spectroscopy,3–10 X-ray diffraction,5,11 dielectric relaxation spectroscopy12 and NMR13 have previously been used to study aqueous boron species in order to identify different species and deduce their structures. The two principal challenges in studying boron species are the diversity of polyborate species that can co-exist at equilibrium under a wide range of conditions, and the experimental challenges associated with the quantification of these species under hydrothermal conditions.The classical high-temperature potentiometric titration study of polyborate formation constants by Mesmer et al.14 showed that, at temperatures up to 200 °C, the principal reactions are the ionization of boric acid,
 | (1) |
| xB(OH)3 + yOH− ⇌ [Bx(OH)3x+y]y− | (2) |
Although no spectra for diborate or metaborate species have been previously reported in aqueous solutions under ambient conditions, these species may be important under the high-temperature, high-pressure conditions encountered in nuclear reactor coolant. The potentiometric titration experiments reported by Mesmer and others14–16 are able to determine the boron stoichiometry and charge, but not the degree of hydration or structure, of the aqueous species in their speciation models. The diborate species inferred from potentiometric measurements, which is postulated to be either [B2(OH)7]− or [B2O(OH)5]−, forms through the reactions:
 | (3) |
 | (4) |
Although neutral and divalent diborates may form through condensation reactions, such as:
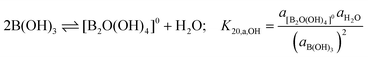 | (5) |
 | (6) |
The present study reports the reduced isotropic Raman spectra for sodium borate solutions under alkaline conditions at temperatures up to 300 °C at 20 MPa, using a newly designed titanium-alloy flow cell with sapphire windows.8 The characteristic vibrational frequencies and relative scattering coefficients reported by Applegarth et al.9 were used to calculate the equilibrium concentrations of the polyborate species from the reduced isotropic Raman spectra. The assignment of bands to the diborate species, and the relative intensities of the major peaks in the spectrum of each species, was based on density functional theory (DFT) calculations using Gaussian 03 software at several levels of theory with, and without, the polarizable continuum model solvation shell. These experimental results are not consistent with speciation calculations from the two different chemical equilibrium models of interest to the nuclear industry under these conditions, the OLI Analyzer Studio 9.2.1 software17 and the EPRI MULTEQ software (ChemWorks 4.0, MULTEQ database v. 7.0).18,19 The speciation results from the Raman measurements were used to calculate new values for the thermodynamic formation quotients of the diborate ion. These are the first quantitative Raman spectra ever reported for borate-rich solutions under hydrothermal conditions and provide the first spectroscopic evidence of a diborate species at PWR reactor coolant temperatures.
2. Experimental
2.1. Chemical and solution preparation
Boric acid, B(OH)3, (Alfa Aesar, 99.9995%), NaCl (Sigma, 99.5%), LiCl (Sigma-Aldrich, 99+%), and potassium hydrogen phthalate (KHP) (Fisher Scientific, 99.95%), were dried in an oven to constant mass before use. Sodium perchlorate (Alfa Aesar, ACS anhydrous grade, 98–102%) was used without further treatment. Carbonate-free stock solutions of 0.998 mol kg−1 and 1.023 mol kg−1 NaOH were prepared by mass from 50% w/w aqueous solution (Alfa Aesar) and standardized by triplicate titrations against KHP.All borate solutions were prepared by adding a calculated mass of B(OH)3 to a 0.998 mol kg−1 or 1.023 mol kg−1 NaOH solution to obtain the desired B(OH)3 molality in the final solution. Sodium perchlorate (0.1 mol kg−1) was added to all solutions as an internal reference standard. All solutions were prepared by mass to an estimated standard uncertainty of ±0.5%, using 18.2 MΩ cm ultrapure water from a Millipore Direct-Q 5 water purification system, and stored in sealed Nalgene bottles until used. For the solutions requiring higher NaOH molalities (buffer ratios >1), additional 50% w/w NaOH, whose composition had been quantified during the preparation of the 0.998 mol kg−1 and 1.023 mol kg−1 NaOH solutions, was added by mass. These were estimated to have a larger standard uncertainty, ±2%.
The stoichiometric buffer ratios of these solutions,
 | (7) |
 . Thus, (RBuffer = 0, mB = 0.80 mol kg−1) refers to a pure B(OH)3 solution with
. Thus, (RBuffer = 0, mB = 0.80 mol kg−1) refers to a pure B(OH)3 solution with 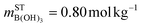 and mSTNaOH = 0.00 mol kg−1, and (RBuffer = 1.0, mB = 1.0 mol kg−1) refers to an aqueous solution of sodium borate with
and mSTNaOH = 0.00 mol kg−1, and (RBuffer = 1.0, mB = 1.0 mol kg−1) refers to an aqueous solution of sodium borate with  and mSTNaOH = 1.00 mol kg−1.
and mSTNaOH = 1.00 mol kg−1.
In order to determine the effects of ion-pair formation and ionic strength, solutions of NaB(OH)4 (RBuffer = 0.980, mB = 0.320 mol kg−1) and LiB(OH)4 (RBuffer = 1.000, mB = and 0.310 mol kg−1) were prepared using the procedures described above, to which an approximately equimolal excess of NaCl or LiCl was added by mass.
2.2. Raman spectroscopy and titanium sapphire flow cell
The reduced isotropic spectra of the borate solutions described above were measured from 25 to 300 °C at 20 MPa using a novel custom-made sapphire flow cell described previously in detail by Sasidharanpillai et al.8 The whole assembly was fitted into a Teflon cell holder in a fixed position on the translation stage of the Raman microscope. Experiments were carried out in constant flow mode at a flow rate of 0.5 ml min−1, with temperature controlled to within ±1 °C over the several hours required to make each set of measurements. Constant pressure in the line was maintained using a syringe pump (Teledyne ISCO Inc.) filled with ultrapure water and a backpressure regulator (TESCOM 26-1722-24) located at the end of the flow line. The solutions to be studied were pumped through the cell using a 24 mL sample injection loop on a Rheodyne injector.Raman spectra were obtained from polarized back-scattering measurements at constant temperature using a custom-made Horiba Jobin Yvon HR800 LabRAM system constructed with a fiber-optic coupled OLYMPUS confocal microprobe, using a 532 nm laser exciting line and a super-long-working-distance achromatic 20× objective lens (SLMPlan, OLYMPUS). Spectra were collected with polarizers set parallel and perpendicular to the polarization of exciting beam such that a baseline-corrected reduced isotropic spectra could be obtained, following the experimental protocol from Sasidharanpillai et al.8
The solvent-subtracted baseline-corrected spectra for quantitative equilibrium constants were obtained by recording the spectra of the water blanks and solutions, using both polarizations as a series on the same day, with the flow cell in a fixed position under the confocal microscope at constant temperature and pressure. Each Raman spectrum for the parallel (||) and perpendicular (⊥) polarizations was the average of eight runs in order to reduce the background noise. A perchlorate standard solution was injected at the beginning and end of the day's runs, and these spectra varied by <5% during the course of the day, indicating the laser power remained constant during the full set of runs. The temperature thermostatting over the course of each day was constant to ±2 °C or better.
Isotropic Raman spectra, IIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ), were obtained from the parallel (||) and perpendicular (⊥) polarized spectra using previously described methods.8,9,20 The isotropic water spectrum was subtracted to obtain each solvent-corrected isotropic spectrum IIso(
), were obtained from the parallel (||) and perpendicular (⊥) polarized spectra using previously described methods.8,9,20 The isotropic water spectrum was subtracted to obtain each solvent-corrected isotropic spectrum IIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ).8,9,20 The reduced isotropic spectra, RIso(
).8,9,20 The reduced isotropic spectra, RIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) was obtained by correcting for the frequency dependence and the Boltzmann distribution.8,20 An example of the experimental Raman spectra for both solution and water at parallel and perpendicular polarizations, the isotropic spectra of the solution and solvent, and the resulting solvent-corrected isotropic spectrum is shown in ESI (Fig. S1†).
) was obtained by correcting for the frequency dependence and the Boltzmann distribution.8,20 An example of the experimental Raman spectra for both solution and water at parallel and perpendicular polarizations, the isotropic spectra of the solution and solvent, and the resulting solvent-corrected isotropic spectrum is shown in ESI (Fig. S1†).
2.3. Ab initio and DFT calculations
Calculations were performed using Gaussian 03 software, with MP2 calculations carried out using the frozen core approximation. The geometries were optimized using a stepping stone approach, in which the geometries at the levels HF/6-31G*, HF/6-31+G*, HF/6-311+G*, B3LYP/6-31G*, B3LYP/6-31+G*, B3LYP/6-311+G*, MP2/6-31G*, MP2/6-31+G*, and MP2/6-311+G* were sequentially optimized, and the geometry and molecular orbital reused as an initial guess for the subsequent level. Default optimization specifications were generally used. After each optimization, a frequency calculation was performed at the same level and the resulting Hessian was used in the subsequent optimization. Symmetry-constrained Z-matrix coordinates were used to speed up the optimizations. If imaginary frequencies were found, then the symmetry was lowered along the appropriate irreducible representation and the process was repeated. The Hessian was evaluated at the first geometry (Opt = CalcFC) for the first level in a series in order to aid geometry convergence. Full details of the computational methods are reported elsewhere.21 The Raman intensities and depolarization ratios were calculated by default for Hartree–Fock calculations; for B3LYP and MP2 calculations, these were done by specifying Freq = Raman. For selected structures, the process was repeated with the conductor-like polarizable-continuum solvation model (SCRF = CPCM). Calculations for the divalent diborate species and the triborate species were done with Gaussian 16.3. Raman spectroscopic results
3.1. Reduced isotropic Raman spectra
Fig. 1 displays a plot of the reduced isotropic Raman spectra of an aqueous solution prepared with equal ratios of NaOH and boric acid (Solution 1, RBuffer = 0.980, mB = 1.019 mol kg−1) for temperatures from 25 °C to 300 °C at 20 MPa. At 25 °C, there are two peaks at 745 cm−1 and 936 cm−1, which correspond to [B(OH)4]− and the [ClO4]− internal standard, respectively. At temperatures above 75 °C, two overlapping peaks appear, with maxima at ∼865 and ∼875 cm−1, whose intensities increase as the temperature is increased. The band at ∼875 cm−1 is clearly the B(OH)3 symmetric stretch, however, the lower frequency shoulder at ∼865 cm−1 does not correspond to any previously reported aqueous borate or polyborate species. The B(OH)3 peak and the unknown peak (marked as “Species X”) were not well resolved at lower temperatures, but became better resolved above 150 °C. At higher temperatures, the borate peak intensity decreased, while the intensities of the B(OH)3 band and the unknown peak both increased. All peaks shifted to lower energies with increasing temperature.To confirm that the new species is an equilibrium species at high temperature, reduced isotropic Raman spectra for a solution of (RBuffer = 0.980, mB = 1.019 mol kg−1, with 0.0902 mol kg−1 sodium perchlorate) were recorded at 22 °C, then again after heating to 200 °C, and a final time after cooling it back to 22 °C (ESI, Fig. S2†). Both spectra at 22 °C were identical and showed the presence of only the borate and perchlorate peaks, while the spectrum at 200 °C clearly indicated three peaks (borate, unknown species X, and boric acid). This showed that the new species at 865 cm−1 was formed only at high temperatures, and that the reaction is reversible.
The Raman spectra for Solution 1 (RBuffer = 0.980, mB = 1.019 mol kg−1, and perchlorate standard) were run in duplicate on a separate day, at 20 MPa and temperatures from 25 to 250 °C, and a second solution with similar composition (Solution 2, Table 1) was also run under the same conditions. Peak fitting to integrate the area under each band was done with a Voigt function using the curve fitting function in Origin Pro 2016 software. The fitting parameters for the position and the Lorentzian and Gaussian widths of the boric acid peak at each temperature were constrained to be same as those reported by Sasidharanpillai et al.,8 for the boric acid peak in a 0.780 molal boric acid solution acquired with the same instrument under similar experimental conditions. As an example, the deconvoluted spectrum of Solution 1 at 250 °C is shown in Fig. 2. The areas were determined as the areas of peaks for species i relative to the perchlorate internal standard, Ai/AIS. Following established practice,8 the sum of the areas of the two peaks at ∼935 cm−1 and ∼920 cm−1 was used in the calculation of the total area of the perchlorate band. The standard errors in the relative areas for the boron bands were 10% or less. The solutions and initial concentrations run in this study, together with the frequencies and relative peak areas corresponding to each of the deconvoluted Raman bands, are tabulated in Table 1.
 | ||
Fig. 2 Reduced isotropic Raman spectra of NaB(OH)4 (aq.), RIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ), at 250 °C and 20 MPa, showing the fitted Voight functions used to determine peak positions and peak areas relative to the perchlorate internal standard for Solution 1, Run 1 (RBuffer = 0.980, mB = 1.019 mol kg−1, 0.0902 mol kg−1 sodium perchlorate). Where “X” is diborate, Fig. 6 is believed to be a more accurate representation of the individual species bands. ), at 250 °C and 20 MPa, showing the fitted Voight functions used to determine peak positions and peak areas relative to the perchlorate internal standard for Solution 1, Run 1 (RBuffer = 0.980, mB = 1.019 mol kg−1, 0.0902 mol kg−1 sodium perchlorate). Where “X” is diborate, Fig. 6 is believed to be a more accurate representation of the individual species bands. | ||
| t/°C | 745 cm−1 band | 865 cm−1 band | 875 cm−1 band | |||
|---|---|---|---|---|---|---|
| [NaB(OH)4]0 + [B(OH)4]− + “Unknown(s)” | “Unknown X” | B(OH)3 | ||||
| ν/cm−1 | Area | ν/cm−1 | Area | ν/cm−1 | Area | |
| a Standard uncertainties, ±, were taken to be equal to the relative standard errors of the Voight function fits to the perchlorate and species bands. b LiB(OH)4 solution. | ||||||
| Solution 1 (Run 1), RBuffer = 0.980, mB = 1.0188 mol kg−1, mNaClO4 = 0.0902 mol kg−1 | ||||||
| 150 | 745 | 1.126 ± 0.066 | 866 | 0.128 ± 0.009 | 875 | 0.046 ± 0.003 |
| 200 | 742 | 1.084 ± 0.082 | 863 | 0.225 ± 0.018 | 873 | 0.108 ± 0.009 |
| 250 | 741 | 0.895 ± 0.034 | 862 | 0.361 ± 0.015 | 872 | 0.170 ± 0.010 |
| 275 | 740 | 0.787 ± 0.041 | 861 | 0.450 ± 0.024 | 872 | 0.181 ± 0.010 |
| 300 | 740 | 0.894 ± 0.028 | 858 | 0.469 ± 0.016 | 872 | 0.211 ± 0.007 |
| Solution 1 (Run 2), RBuffer = 0.980, mB = 1.0188 mol kg−1, mNaClO4 = 0.0902 mol kg−1 | ||||||
| 150 | 742 | 1.147 ± 0.073 | 866 | 0.146 ± 0.010 | 874 | 0.054 ± 0.005 |
| 200 | 741 | 1.038 ± 0.075 | 863 | 0.252 ± 0.020 | 873 | 0.082 ± 0.008 |
| 250 | 740 | 0.894 ± 0.090 | 859 | 0.382 ± 0.039 | 872 | 0.158 ± 0.016 |
| Solution 2, RBuffer = 0.984, mB = 1.0391 mol kg−1, mNaClO4 = 0.0955 mol kg−1 | ||||||
| 150 | 741 | 1.112 ± 0.037 | 866 | 0.132 ± 0.009 | 873 | 0.043 ± 0.008 |
| 200 | 740 | 0.958 ± 0.046 | 862 | 0.227 ± 0.013 | 872 | 0.099 ± 0.006 |
| 250 | 739 | 0.809 ± 0.053 | 859 | 0.342 ± 0.024 | 870 | 0.155 ± 0.011 |
| Solution 3, RBuffer = 1.716, mB = 0.96404 mol kg−1, mNaClO4 = 0.0945 mol kg−1 | ||||||
| 150 | 744 | 1.161 ± 0.033 | 864 | 0.192 ± 0.007 | NA | NA |
| 200 | 743 | 1.044 ± 0.081 | 863 | 0.260 ± 0.021 | NA | NA |
| 250 | 741 | 0.930 ± 0.057 | 858 | 0.405 ± 0.026 | NA | NA |
| Solution 4, RBuffer = 3.542, mB = 0.90062 mol kg−1, mNaClO4 = 0.0883 mol kg−1 | ||||||
| 150 | 744 | 1.237 ± 0.043 | 865 | 0.132 ± 0.010 | NA | NA |
| 200 | 743 | 0.983 ± 0.041 | 864 | 0.246 ± 0.012 | NA | NA |
| 250 | 741 | 0.901 ± 0.040 | 859 | 0.302 ± 0.017 | NA | NA |
| Solution 5a, RBuffer = 0.980, mB = 0.32012 mol kg−1, mNaClO4 = 0.0283 mol kg−1 | ||||||
| 250 | 740 | 0.818 ± 0.043 | 859 | 0.434 ± 0.026 | 872 | 0.286 ± 0.016 |
| Solution 5b, RBuffer = 0.980, mB = 0.32012 mol kg−1 + 0.301 mol kg−1 NaCl, mNaClO4 = 0.0283 mol kg−1 | ||||||
| 250 | 740 | 0.864 ± 0.061 | 859 | 0.462 ± 0.036 | 872 | 0.252 ± 0.019 |
| Solution 6ab, RBuffer = 1.000, mB = 0.30980 mol kg−1, mNaClO4 = 0.0330 mol kg−1 | ||||||
| 250 | 740 | 0.535 ± 0.029 | 859 | 0.297 ± 0.019 | 872 | 0.229 ± 0.013 |
| Solution 6bb, RBuffer = 0.980, mB = 0.30980 mol kg−1 + 0.302 mol kg−1 LiCl, mNaClO4 = 0.0330 mol kg−1 | ||||||
| 250 | 740 | 0.658 ± 0.041 | 740 | 0.384 ± 0.029 | 740 | 0.269 ± 0.019 |
We measured Raman spectra at 250 °C using sodium borate solutions in D2O with isotopically pure B(OD)3 and NaOD, similar in composition to Solutions 1, 3 and 4, in an attempt to confirm the identification of diborate species. This single set of runs using isotopically pure B(OD)3 and NaOD consumed about 1000 mL D2O. Complications arising from the Fermi resonance effects in the spectra for B(OD)3 and the shifts in speciation associated with the deuterium isotope effect on its ionization constant proved too difficult to resolve.22,23 Details are reported in ESI section S2.†
3.2. The effect of excess Na+ and Li+ cations and possible ion pairing
Previous Raman experiments on boric acid/borate confirmed that Raman spectroscopy cannot distinguish between free borate [B(OH)4]− and the ion pair [NaB(OH)4]0, possibly because [NaB(OH)4]0 exists as solvent-separated ion pairs.9 Reduced isotropic Raman spectra for NaB(OH)4 and LiB(OH)4 solutions (Solution 5: RBuffer = 0.980, mB = 0.320; and Solution 6: RBuffer = 0.980, mB = 0.310 mol kg−1; respectively), and the spectra of the same solutions to which an approximately equimolal excess of NaCl or LiCl had been added, were recorded at 250 °C and 20 MPa. Fig. 3 shows the isotropic spectra and corresponding deconvolution of peaks for Solution 5a (RBuffer = 0.980, mB = 0.320) and Solution 5b (RBuffer = 0.980, mB = 0.320, mNaCl = 0.301) at 250 °C and 20 MPa. The similarity in the spectra and corresponding deconvolution for solutions with and without excess NaCl/LiCl indicates that the presence and identity of the cation does not affect the concentration of the unknown species, and confirms either that the new band does not result from ion-pair formation, or that there is extensive ion pairing in even the dilute NaB(OH)4 and LiB(OH)4 solutions. The frequencies and relative peak areas are reported in Table 1.3.3. The effect of excess hydroxide
The Raman spectra of solutions of different RBuffer values ≥1 were recorded at 150, 200 and 250 °C and 20 MPa in order to understand the effect of hydroxide ion on the equilibrium reactions responsible for the newly observed species. The reduced isotropic Raman spectra and peak deconvolution of Solutions 3 (RBuffer = 1.716) and 4 (RBuffer = 3.542) at 250 °C and 20 MPa, are shown in Fig. 4. When the concentration of hydroxide ion was increased, the boric acid peak became negligible, and only the bands associated with the borate ion and the new species could be observed. The frequencies and peak areas of each band are listed in Table 1. The ratio of the peak areas for the bands at 865 cm−1 and 745 cm−1, A865/A745, increased with temperature, and did not depend strongly on the hydroxide concentration.4. Ab initio and DFT computational results
4.1. Borates, diborates, and higher polyborates
In a previous study on polyborates by Applegarth et al.9 at 25 and 80 °C, the predicted isotropic Raman spectra of boric acid, B(OH)3; borate ion, [B(OH)4]−; the oxo-bridged diborates [B2O(OH)6]2− and [B2O(OH)5]−; the cyclic triborate ion, [B3O3(OH)4]−; metaboric acid, B3O3(OH)3; tetraborate, [B4O5(OH)4]2−; and the pentaborates [B5O6(OH)4]− and [B5O6(OH)6]3−, were discussed and compared with experimental results. The frequencies for boric acid, borate, and the higher polyborates were reported by Applegarth et al.9 It was shown that the frequencies of unscaled MP2 and B3LYP low-temperature Raman spectra compared very favorably with experimental results for B(OH)3, [B(OH)4]−, [B3O3(OH)4]−, [B4O5(OH)4]2−, and [B5O6(OH)4]−, suggesting that these were the observed species. There was no experimental evidence from the Raman spectra for the presence of either [B2O(OH)6]2− or [B2O(OH)5]− at these temperatures, consistent with the recently completed detailed NEA/OECD literature review by the Thermodynamic Database Project.24 Generally speaking, the MP2 and B3LYP results were found to underestimate the experimental frequencies by up to 35 cm−1 because the effect of the solvent was not explicitly included in these calculations, and this effect increased with the overall charge of the species. Hartree Fock calculations, which were also carried out, were found to overestimate the frequencies by a larger, less predictable amount.The high-temperature Raman results obtained in this study were used to direct our calculations. These suggest that there is an additional species in equilibrium with B(OH)3 and [B(OH)4]−, which gives rise to a characteristic Raman band at 865 cm−1, concomitant with dissociation of borate into boric acid. Based on the known spectra of the boric acid/borate solutions at 25 °C,9 the most likely candidates are the metaborate ion, [BO(OH)2]−; one of four diborate species, [B2O(OH)5]−, [B2O3(OH)4]2−, [B2O(OH)6]2− or [B2(OH)7]−; or a higher polyborate species (possibly [B3O3(OH)5]2−) that is not a significant species at 25 °C. Less likely neutral species that might result from the condensation reactions of boric acid, driven by higher ionic strength or temperature, are [B2(OH)6]0 and [B2O(OH)4]0.
Ab initio computational studies on these species were carried out at several levels of theory, with and without solvation, as discussed in the following section. Selected gas-phase structures were taken from previous studies of Pye et al.21,25 The structures of the diborate species derived from these calculations in this study are shown in Fig. 5. Gas-phase Raman frequency calculations were done for a broader number of potential di/triborate species initially, with results listed in ESI (Table S1†). The Raman frequencies and the corresponding isotropic Raman activities for the ionic di/triborate species in solution phase are tabulated in Table 2.
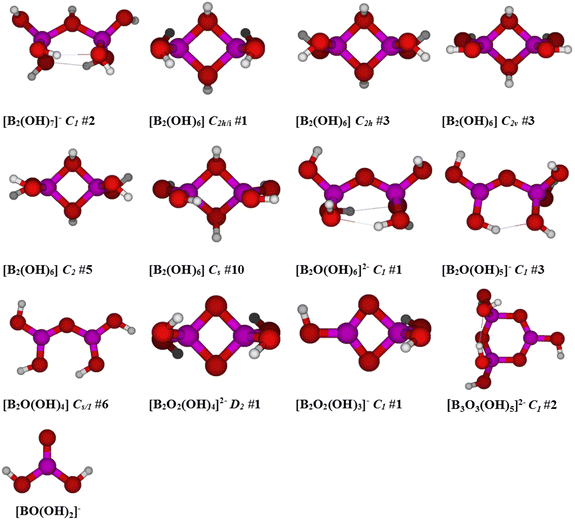 | ||
| Fig. 5 Calculated structures (using Gaussian 03) of the postulated diborate species considered for the unknown Raman peak at 865 cm−1, along with their symmetry. | ||
| Species | Basis set | HF | B3LYP | MP2 | |||
|---|---|---|---|---|---|---|---|
| ν/cm−1 | Raman activity | ν/cm−1 | Raman activity | ν/cm−1 | Raman activity | ||
| ClO4− | 6-31G* | 987 | 37.8 | 864 | 56.4 | 994 | 50.2 |
| 6-31+G* | 970 | 62.5 | 831 | 116 | 973 | 106 | |
| 6-311+G* | 959 | 58.8 | 816 | 112 | 950 | 98.4 | |
| [B2O(OH)5]− | 6-31G* | 759 | 4.77 | 713 | 7.82 | 731 | 8.29 |
| 983 | 1.82 | 925 | 4.41 | 932 | 4.12 | ||
| 6-31+G* | 748 | 5.09 | 572 | 1.11 | 581 | 1.18 | |
| 771 | 2.74 | 707 | 11.2 | 722 | 13.9 | ||
| 975 | 3.35 | 913 | 8.76 | 922 | 8.55 | ||
| 6-311+G* | 749 | 5.35 | 574 | 1.09 | 587 | 1.23 | |
| 773 | 1.57 | 703 | 9.78 | 728 | 13.1 | ||
| 853 | 0.57 | 792 | 1.05 | 813 | 0.23 | ||
| 972 | 3.02 | 911 | 8.75 | 925 | 8.44 | ||
| [B2O(OH)6]2− | 6-31G* | 749 | 7.24 | 703 | 10.6 | 692 | 1.06 |
| 719 | 10.2 | ||||||
| 6-31+G* | 743 | 11.1 | 692 | 2.44 | 700 | 2.14 | |
| 698 | 13.3 | 714 | 17.6 | ||||
| 6-311+G* | 626 | 1.30 | 695 | 6.03 | 711 | 3.09 | |
| 742 | 10.5 | 696 | 11.1 | 725 | 17.5 | ||
| [B2(OH)7]− | 6-31G* | 730 | 4.85 | 616 | 1.64 | 631 | 2.03 |
| 897 | 2.59 | 679 | 5.36 | 682 | 3.42 | ||
| 752 | 2.99 | 696 | 2.06 | ||||
| 836 | 5.09 | 742 | 4.01 | ||||
| 857 | 3.84 | ||||||
| 6-31+G* | 623 | 1.13 | 566 | 1.01 | 590 | 2.58 | |
| 727 | 5.67 | 619 | 1.53 | 621 | 1.30 | ||
| 890 | 6.16 | 689 | 8.29 | 691 | 5.66 | ||
| 829 | 8.62 | 845 | 9.88 | ||||
| 6-311+G* | 729 | 5.10 | 626 | 1.56 | 681 | 1.91 | |
| 885 | 5.97 | 690 | 7.55 | 719 | 8.66 | ||
| 824 | 8.38 | 848 | 9.11 | ||||
| [BO(OH)2]− | 6-31G* | 884 | 5.46 | 826 | 8.10 | 837 | 9.71 |
| 1144 | 3.11 | 1061 | 5.33 | 1067 | 5.97 | ||
| 1555 | 1.60 | 1568 | 1.60 | ||||
| 6-31+G* | 886 | 7.38 | 827 | 11.9 | 835 | 15.5 | |
| 1117 | 3.31 | 1031 | 4.86 | 1030 | 6.18 | ||
| 1554 | 4.61 | 1457 | 17.3 | 1446 | 16.6 | ||
| 6-311+G* | 881 | 6.49 | 824 | 10.7 | 835 | 14.0 | |
| 1136 | 3.39 | 1048 | 4.76 | 1049 | 6.31 | ||
| 1544 | 4.23 | 1449 | 17.3 | 1451 | 18.1 | ||
| [B2O2(OH)4]2− | 6-31G* | 634 | 2.47 | 588 | 3.19 | 591 | 3.37 |
| 922 | 8.58 | 845 | 10.93 | 846 | 13.06 | ||
| 6-31+G* | 636 | 4.72 | 593 | 6.35 | 591 | 7.35 | |
| 915 | 6.59 | 839 | 8.43 | 830 | 13.74 | ||
| 6-311+G* | 635 | 4.49 | 591 | 6.15 | 599 | 7.58 | |
| 910 | 6.49 | 834 | 8.30 | 836 | 12.55 | ||
| [B3O3(OH)5]2− | 6-31G* | 581 | 2.66 | 551 | 2.75 | 553 | 2.76 |
| 655 | 3.54 | 601 | 6.21 | 606 | 6.77 | ||
| 792 | 3.59 | 731 | 5.91 | 733 | 7.58 | ||
| 6-31+G* | 576 | 2.86 | 533 | 3.79 | 536 | 4.50 | |
| 651 | 6.70 | 553 | 1.38 | 590 | 8.19 | ||
| 790 | 4.01 | 587 | 5.20 | 622 | 5.45 | ||
| 615 | 6.28 | 727 | 8.26 | ||||
| 727 | 4.96 | ||||||
| 6-311+G* | 575 | 3.00 | 532 | 3.31 | 540 | 4.29 | |
| 651 | 5.99 | 551 | 2.60 | 562 | 1.66 | ||
| 789 | 3.42 | 584 | 4.53 | 594 | 8.15 | ||
| 612 | 5.78 | 632 | 3.77 | ||||
| 725 | 3.98 | 734 | 7.38 | ||||
4.2. Neutral diborate species
4.3. Ionic diborate species
The oxo-bridged diborates [B2O(OH)6]2− and [B2O(OH)5]− were previously considered9 as candidates for the band at 773 cm−1, observed as a shoulder on the borate peak at 745 cm−1. [B2O(OH)6]2− may exist as an oxo-bridged dimer with one of two C2 and three C1 structures lying within 15 kJ mol−1 of each other, having weak bands at 812–870 cm−1 which appear in the correct region for matching with the experimental band at 865 cm−1. [B2O(OH)5]− may exist as an oxo/hydroxo doubly bridged dimer, but these forms were not stable and resulted in cleavage of one of the B–μOH bonds upon relaxation of symmetry constraints, giving rise to one of nine possible oxo-bridged C1 structures. [B2O(OH)5]− is calculated to have weak bands at 890–940 cm−1 which would be too high in frequency. Additionally, both of these species have an intense band predicted at lower frequencies (680–720 cm−1), which is not experimentally observed.
Species containing two oxo bridges were also considered. [B2O2(OH)4]2− may exist as one of two possible D2h structures, neither of which was found to be stable. Desymmetrization can give rise to two D2, four C2h, and one C2v structures. The D2 #1 structure is the most stable at all levels, and the C2h #1 and D2 #2 structures are stable at some levels. For unstable structures, further desymmetrization give stable structures with C2, Ci, and Cs symmetry. The two most intense bands of roughly equal intensity in the isotropic Raman spectrum are predicted at 570–580 cm−1 and 830–850 cm−1, and these are expected to be systematically too low by about 20 cm−1. The latter band, therefore, is a viable candidate for the experimentally observed band at 865 cm−1, however, no evidence for the predicted weak band at around 600 cm−1 was observed in the experimental spectrum (RBuffer = 0.980, mB = 1.019 mol kg−1). It is possible that these peaks would be obscured if [B3O3(OH)4]− was present, but this does not appear to be the case for solutions of this composition.
The second possible species with two oxo bridges is [B2O2(OH)3]−, which could exist as one of two C2v structures, neither of which is a minimum. Desymmetrization to one of two possible C2 or four possible Cs structures also did not result in minima. Two C1 structures exist, the first of which is the most stable, however, the calculations predict the existence of several intense bands in the 500–1000 cm−1 range and none of these are a satisfactory match to experiment. In addition, of the two bands that bracket the experimental value, it is the remaining two which would have the greatest intensity.
4.4. Ionic triborate species
4.5. Solvent effects: CPCM calculations
Candidates for the unknown species were therefore reduced to [B2(OH)7]−, [B2O(OH)5]−, [B2O2(OH)4]2−, [B2O(OH)6]2− and [BO(OH)2]− based on the frequencies from different levels of gas phase calculations together with polarizable continuum model calculations. The reduced Raman isotropic frequencies and their corresponding Raman activities for the three diborate species and metaboric acid, using HF/6-31G*, HF/6-31+G*, HF/6-311+G*, B3LYP/6-31G*, B3LYP/6-31+G*, B3LYP/6-311+G*, MP2/6-31G*, MP2/6-31+G*, and MP2/6-311+G* with a polarizable continuum model, are summarized in Table 2. The Raman activities (intensities) correspond to the unpolarised spectra. Only those expected to give significant intensity in the isotropic spectra (depolarization ratio significantly less than 0.75) are listed. In the discussions below, computational frequencies for comparison with experiment were taken from the MP2/6-311+G* results in Table 2.The [B2O(OH)5]− species is calculated to have two bands, one in the range 700–750 cm−1 and the other in the range 910–975 cm−1, depending upon the level of theory and basis set (Table 2). The [B2(OH)7]− species also was also calculated to have two strong bands, with a peak in the range 690–740 cm−1 and another in the range 830–890 cm−1. The divalent species [B2O2(OH)4]2− is predicted to have a very strong band in the region 830 to 850 cm−1, which may correspond to the experimental band at 865 cm−1, but the absence of a weak band near 600 cm−1 appears to rule it out. The other divalent species, [B2O(OH)6]2−, was found to have only one strong calculated band centered in the region 700–740 cm−1, and therefore cannot be the source of the experimental band at 865 cm−1. Although the computational results for mononuclear metaborate [BO(OH)2]− do yield a very strong band at 888 cm−1, the very strong bands predicted to be at ∼1050 cm−1 and 1450 cm−1 are completely absent in the experimental spectra.
5. Chemical equilibrium modelling
5.1. Modelling considerations
The classic potentiometric study by Mesmer et al.14 identified a singly-charged diborate ion as a statistically significant species from 50 to 200 °C. As a result, it seems likely that the new species is one or both of the diborates [B2(OH)7]− and [B2O(OH)5]−, with [B2O2(OH)4]2− possibly also present as an equilibrium species at temperatures above 200 °C. Thus, the relevant diborate reactions to be considered in developing a chemical equilibrium model are:
 | (8) |
 | (9) |
and, possibly,
 | (10) |
Here, the asterisk notation,  , indicates cumulative formation of the diborate from B(OH)4− rather than B(OH)3. Eqn (8) to (10) are expressed as formation reactions from borate rather than boric acid because the equilibrium molalities of B(OH)3 are negligible at the hydroxide concentrations used in Solutions 4 and 5.
, indicates cumulative formation of the diborate from B(OH)4− rather than B(OH)3. Eqn (8) to (10) are expressed as formation reactions from borate rather than boric acid because the equilibrium molalities of B(OH)3 are negligible at the hydroxide concentrations used in Solutions 4 and 5.
The modelling approach adopted here was based on boron mass balance. Speciation calculations were carried out using the experimental peak areas of the three bands, the boron mass balance, and the known scattering coefficients of B(OH)3 and [B(OH)4]−,8,9 from the expression:
 | (11) |
Here, mi and mIS are the molalities of the species i and the perchlorate internal standard, IS, respectively; Si/SIS is the relative scattering coefficient for species i with respect to the internal standard; Ai and AIS are the peak areas of species i, and the internal standard, respectively. The values for the relative scattering coefficients Si/SIS for B(OH)3 and [B(OH)4]− were taken from Applegarth et al.9 and Sasidharanpillai et al.8 Although both monovalent species [B2(OH)7]− and [B2O(OH)5]− are predicted to have two strong bands in the frequency range relevant to this study, [B2(OH)7]− was selected because Gaussian calculations typically under-predict, rather than over-predict the experimental vibrational frequency.23 The divalent species with [B2O2(OH)4]2− was also included in the chemical equilibrium modelling as a less likely candidate species.
 | (12) |
| ABorate,745 = Atotal,745 − AB2,745 | (13) |
where AB2,745, ABorate,745 and Atotal,745 are the areas corresponding to diborate at 745 cm−1, borate at 745 cm−1 and total area of the peak at 745 cm−1, respectively. Three choices for the scattering coefficient of the diborate band at 745 cm−1, relative to the band at 865 cm−1 were considered: SB2,745/SB2,865 = 0 (Model 1); SB2,745/SB2,865 = 0.95 (Model 2); and SB2,745/SB2,865 = 1.5 (Model 3). Model 1 is applicable to diborate species postulated to have no band at 745 cm−1, corresponding exclusively to band “X” in Fig. 2. Models 2 and 3 were based on the MP2/6-311+G* computational values of SB2,745/SB2,865 for [B2(OH)7]− and [B2O(OH)5]−, respectively, in Table 2. Although computational Raman scattering intensities are known to be quite unreliable,21,25 the calculated relative Raman intensities of two bands within the same molecule are expected to be more accurate.
Models 1 and 3 proved to be not consistent with the physico–chemical constraints. For Model 1, the experimental scattering coefficient of the 865 cm−1 band relative to that of the perchlorate internal standard SB2,865/SIS was found to increase by about 300% from 150 °C to 300 °C, and had significant discrepancies in the charge balance of Solutions 1 and 2 of +10% at 150 °C, rising to +20% at 300 °C. Model 3 had an almost constant scattering coefficient, but a negligible concentration of [B(OH)4]− at 300 °C, which contradicts the results of previous studies by Mesmer et al.,14 Wang et al.17 and Palmer et al.26
Model 2 yielded scattering coefficients that were independent of concentration and temperature above 150 °C, SB2,865/SIS = 0.107 ± 0.015. The charge balances had small systematic discrepancies. For Solutions 1 and 2 it was too positive (∼15% at 150 °C rising to ∼30% above 200 °C), and for Solutions 5 and 6 at 250 °C it was similarly elevated (∼+12% after the effect of the excess NaCl and LiCl was subtracted) (ESI, Table S2†). Varying the relative scattering coefficient of the diborate bands by ±10% did not significantly change the internal consistency of the treatment. Representative fits for the reduced isotropic Raman spectra using Model 2 for Na(BOH)4(aq.), RIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ), at 250 °C and 20 MPa are shown in Fig. 6. The calculated equilibrium molalities and diborate scattering coefficients using Model 2 are tabulated in Table 3.
), at 250 °C and 20 MPa are shown in Fig. 6. The calculated equilibrium molalities and diborate scattering coefficients using Model 2 are tabulated in Table 3.
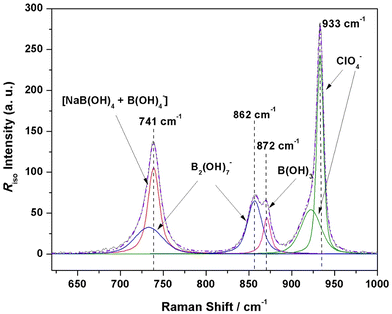 | ||
Fig. 6 Reduced isotropic Raman spectra of NaB(OH)4(aq.), RIso(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ), at 250 °C and 20 MPa from Fig. 2, indicating the calculated hypothetical contributions to the 745 cm−1 band from [B(OH)4]− and [B2(OH)7]− corresponding to a relative scattering factor for the diborate ion bands of SB2,745/SB2,865 = 0.95, as predicted by the DFT calculations. ), at 250 °C and 20 MPa from Fig. 2, indicating the calculated hypothetical contributions to the 745 cm−1 band from [B(OH)4]− and [B2(OH)7]− corresponding to a relative scattering factor for the diborate ion bands of SB2,745/SB2,865 = 0.95, as predicted by the DFT calculations. | ||
 and the resulting formation constants
and the resulting formation constants 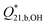 for diborate at p = 20 MPa. The relative scattering coefficients for the diborate bands 745 and 865 cm−1 where taken to be SB2,745/SB2,865 = 0.95 ± 0.10 (Model 2)a
for diborate at p = 20 MPa. The relative scattering coefficients for the diborate bands 745 and 865 cm−1 where taken to be SB2,745/SB2,865 = 0.95 ± 0.10 (Model 2)a
| t/°C | ρ w/kg m−3 | m B(OH)3 | m [B(OH)4]− | m [B2(OH)7]− | m (OH)− | I/mol kg−1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| × 103/mol kg−1 | Exp. | Wang et al.17 | Palmer24 | |||||||
a Uncertainties are propagated standard errors from the fitted Voight functions. Values in parentheses have scattering coefficients beyond the 90% confidence limit of the mean, SrB2,865 = 0.107 ± 0.015, and were considered to have systematic errors.  , from Wang et al.17 were calculated for similar Rbuffer using OLI Studio but for the formation of B2O(OH)5−. , from Wang et al.17 were calculated for similar Rbuffer using OLI Studio but for the formation of B2O(OH)5−.  , from Palmer were calculated from log K11 and log K12 expressions in Ref. 24.
b LiB(OH)4 solution. , from Palmer were calculated from log K11 and log K12 expressions in Ref. 24.
b LiB(OH)4 solution.
|
||||||||||
| Solution 1 (Run 1), RBuffer = 0.980, mB = 1.0188 mol kg−1 | ||||||||||
| 150 | 927.69 | 18.6 ± 1.4 | 616 ± 43 | 192 ± 21 | 47.65 | (0.060 ± 0.008) | 1.017 | −1.618 | −3.233 | −2.512 |
| 200 | 877.97 | 44.0 ± 3.7 | 534 ± 53 | 220 ± 26 | 49.56 | 0.092 ± 0.013 | 0.991 | −1.416 | −3.002 | −2.107 |
| 250 | 816.09 | 69.1 ± 4.0 | 339 ± 24 | 305 ± 12 | 41.04 | 0.106 ± 0.006 | 0.932 | −0.962 | −2.880 | −1.878 |
| 275 | 778.71 | 73.4 ± 4.1 | 220 ± 29 | 363 ± 15 | 32.50 | 0.112 ± 0.007 | 0.897 | −0.615 | −2.860 | −1.791 |
| 300 | 734.71 | 85.9 ± 3.2 | 275 ± 20 | 329 ± 10 | 42.25 | 0.129 ± 0.006 | 0.912 | −0.736 | −2.866 | −1.691 |
| Solution 1 (Run 2), RBuffer = 0.980, mB = 1.0188 mol kg−1 | ||||||||||
| 150 | 927.69 | 22.1 ± 1.9 | 619 ± 47 | 189 ± 23 | 40.33 | (0.070 ± 0.010) | 1.013 | −1.700 | −3.233 | −2.512 |
| 200 | 877.97 | 33.2 ± 3.3 | 490 ± 49 | 248 ± 24 | 60.27 | 0.092 ± 0.011 | 0.988 | −1.206 | −3.002 | −2.107 |
| 250 | 816.09 | 64.3 ± 6.7 | 326 ± 61 | 314 ± 31 | 42.47 | 0.109 ± 0.016 | 0.930 | −0.900 | −2.880 | −1.878 |
| Solution 2, RBuffer = 0.984, mB = 1.0391 mol kg−1 | ||||||||||
| 150 | 927.69 | 18.5 ± 3.5 | 648 ± 28 | 186 ± 14 | 50.20 | (0.067 ± 0.007) | 1.049 | −1.652 | −3.243 | −2.512 |
| 200 | 877.97 | 42.4 ± 2.8 | 482 ± 32 | 257 ± 16 | 46.32 | 0.084 ± 0.007 | 1.000 | −1.290 | −3.014 | −2.107 |
| 250 | 816.09 | 66.9 ± 4.8 | 315 ± 38 | 329 ± 19 | 39.40 | 0.099 ± 0.009 | 0.949 | −0.883 | −2.891 | −1.878 |
| Solution 3, RBuffer = 1.716, mB = 0.96404 mol kg−1 | ||||||||||
| 150 | 927.69 | 0.95 ± 0.15 | 629 ± 25 | 167 ± 13 | 857.6 | (0.109 ± 0.009) | 1.832 | −0.440 | −3.426 | −2.512 |
| 200 | 877.97 | 2.23 ± 0.64 | 513 ± 55 | 225 ± 27 | 915.8 | 0.109 ± 0.016 | 1.862 | −0.104 | −3.237 | −2.107 |
| 250 | 816.09 | 3.20 ± 0.68 | 350 ± 41 | 305 ± 20 | 996.9 | 0.126 ± 0.012 | 1.902 | 0.397 | −3.111 | −1.878 |
| Solution 4, RBuffer = 3.542, mB = 0.90062 mol kg−1 | ||||||||||
| 150 | 927.69 | 0.35 ± 0.09 | 668 ± 30 | 116 ± 15 | 2406 | (0.100 ± 0.015) | 3.336 | −0.377 | −3.767 | −2.512 |
| 200 | 877.97 | 0.95 ± 0.14 | 450 ± 27 | 225 ± 14 | 2515 | 0.097 ± 0.007 | 3.391 | 0.461 | −3.606 | −2.107 |
| 250 | 816.09 | 2.64 ± 0.39 | 368 ± 27 | 265 ± 14 | 2555 | 0.101 ± 0.008 | 3.411 | 0.964 | −3.431 | −1.878 |
| Solution 5a, RBuffer = 0.980, mB = 0.32012 mol kg−1 | ||||||||||
| 250 | 816.09 | 36.5 ± 2.0 | 78.1 ± 9.7 | 103 ± 5.0 | 19.51 | 120 ± 0.009 | 0.285 | −0.483 | −2.152 | −1.878 |
| Solution 5b, RBuffer = 0.980, mB = 0.32012 mol kg−1 + 0.301 mol kg−1 NaCl | ||||||||||
| 250 | 816.09 | 32.1 ± 2.5 | 82.0 ± 13.7 | 103 ± 7.0 | 21.97 | 0.127 ± 0.013 | 0.590 | −0.472 | −2.681 | −1.878 |
| Solution 6a,bRBuffer = 0.980, mB = 0.30980 mol kg−1 | ||||||||||
| 250 | 816.09 | 34.1 ± 2.0 | 56.8 ± 7.9 | 109 ± 4.1 | 15.22 | 0.090 ± 0.007 | 0.279 | −0.287 | −2.520 | −1.878 |
| Solution 6b,bRBuffer = 0.980, mB = 0.30980 mol kg−1 + 0.302 mol kg−1 LiCl | ||||||||||
| 250 | 816.09 | 40.1 ± 2.8 | 66.0 ± 11.3 | 102 ± 5.8 | 14.18 | 0.124 ± 0.012 | 0.581 | −0.479 | −3.024 | −1.878 |
These results provide strong evidence for the presence of a new species that is a diborate ion, with bands in the 745 region and at 865 cm−1, SB2,745/SB2,865 = 0.95 ± 0.10. The analysis above suggests that the new species is very probably [B2(OH)7]−. A factor analysis of the Raman spectra at 250 °C was performed, using the singular value decomposition ‘svds’ function on Matlab R2021b. Although the data set was limited and mathematically underdetermined, there were four statistically significant factors. In addition to the peaks at 739.4 cm−1 (borate) and 874.0 cm−1 (boric acid), there were also major peaks identified at 737.5 cm−1 and 863.7 cm−1, and minor peaks at 746.9 cm−1, 754.5 cm−1, 853.3 cm−1, and 866.0 cm−1, at 250 °C, supporting the model with a new species having a Raman peak around ∼750 and 865 cm−1.
The charge-balance discrepancy and the factor analysis of the high temperature Raman data, suggest that another anionic boron species may be present as a minor equilibrium species, possibly [B2O2(OH)4]2−. Adding a contribution from the minor divalent species to the band at 865 cm−1 did not lead to an improved model. The possibility that [B2O(OH)6]2− might have been present was addressed by adding a divalent anionic species to the 745 cm−1 band in the models noted above and varying the relative scattering coefficients of both diborate species. However, it was not possible to achieve fully temperature-independent scattering coefficients and charge balance.
Additional evidence that the 865 cm−1 band is not due to [B2O(OH)6]2− or [BO(OH)2]− is provided by the effect of hydroxide on the reduced isotropic Raman spectra at 250 °C. As can be seen in Reactions 8 and 9, hydroxide participates directly in the formation of these two diborate ions from borate. However, the divalent diborate species [B2O(OH)6]2− and metaborate form by condensation reactions which are not pH dependent, as described in Reaction 14 and by:
| [B(OH)4]− ⇌ [BO(OH)2]− + H2O | (14) |
It is clear from the stoichiometry of these reactions that the equilibria to form monovalent [B2(OH)7]− and/or its condensed product [B2O(OH)5]− are affected by changes in the concentration of OH−, whereas the formation of [B2O(OH)6]2− and/or [BO(OH)2]− are not. The constant values for the relative scattering factors in Table 3, calculated from the relative peak areas of the 745 cm−1 and 865 cm−1 bands for Solutions 3 and 4 using Model 2, support the conclusion that [B2(OH)7]− and/or [B2O(OH)5]− are the equilibrium diborate species. This is consistent with the potentiometric studies reported by Mesmer et al.14 who identified the presence of a singly charged diborate species in sodium borate solutions at higher temperature, and postulated the existence of the [B2(OH)7]− species. The consistent value obtained for the scattering factors at other temperatures over the range 200 to 300 °C, 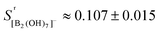 , despite changes in pH associated with changes in the boric acid ionization constant further supports this conclusion.
, despite changes in pH associated with changes in the boric acid ionization constant further supports this conclusion.
Based on the evidence presented above, our analysis was based on the premise that [B2(OH)7]− is the major equilibrium diborate species, and that polyborate formation quotients could be determined using the concentrations from Model 2.
5.2. Equilibrium chemical speciation and diborate formation quotients
The equilibrium quotient for [B2(OH)7]− diborate formation from the borate ion, according to reaction (8), was calculated from the expression: | (15) |
using the experimental molalities of the species calculated from Model 2. Here, the asterisk notation, 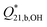 , indicates cumulative formation of the diborate from B(OH)4− rather than B(OH)3.
, indicates cumulative formation of the diborate from B(OH)4− rather than B(OH)3.
The experimental molalities of each species and resulting formation quotients for B2(OH)7− are tabulated in Table 3. For Solutions 3 and 4, the molalities of the hydroxide ions required for these calculations were calculated from charge and mass balance. For all other solutions, which had buffer ratios RBuffer ≈ 1, the hydroxide molalities were derived from the experimental borate and boric acid molalities, and the expression for the ionization constant of boric acid reported by Palmer et al.,26 as described in our previous study.8
The diborate formation quotients from Table 3 for Solutions 1 and 2 (NaBOH4(aq.), RBuffer = 1, m = 1 mol kg−1) are plotted as a function of temperature in Fig. 7, where they are compared to the equilibrium constants reported by Ferguson et al.27 and Palmer et al.26 Van't Hoff fits to the experimental formation quotients at ionic strength I = 1 mol kg−1 from this work (Solutions 1 and 2) and from Mesmer et al.14 yield the expressions:
 | (16) |
 | ||
Fig. 7 Plot of log 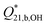 as a function of temperature (1/T) at p = 20 MPa from this work and at psat from Mesmer's experimental data.14 The filled black squares (■) and filled red circles ( as a function of temperature (1/T) at p = 20 MPa from this work and at psat from Mesmer's experimental data.14 The filled black squares (■) and filled red circles ( ) represent the experimental log ) represent the experimental log  for Solutions 1 and 2, respectively. The pink triangles ( for Solutions 1 and 2, respectively. The pink triangles ( ) are Mesmer's experimental data14 at 50, 100, and 200 °C. The blue triangle ( ) are Mesmer's experimental data14 at 50, 100, and 200 °C. The blue triangle ( ) is the extrapolated value at 250 °C from Mesmer's data by Palmer et al.26 The red lines are the van't Hoff fits to the experimental data from this work and from Mesmer et al. at I = 1 mol kg−1, eqn (16) and (17). The purple diamonds ( ) is the extrapolated value at 250 °C from Mesmer's data by Palmer et al.26 The red lines are the van't Hoff fits to the experimental data from this work and from Mesmer et al. at I = 1 mol kg−1, eqn (16) and (17). The purple diamonds ( ) represent the formation constants from conductivity experiments.26 ) represent the formation constants from conductivity experiments.26 | ||
and
 | (17) |
 from this study are systematically higher than Mesmer's potentiometric values at the same ionic strength. The difference decreases with increasing temperature.
from this study are systematically higher than Mesmer's potentiometric values at the same ionic strength. The difference decreases with increasing temperature.
The formation quotients from this Raman study are in very good agreement with those from the conductivity measurements by Ferguson et al.,27 despite the fact that these are very different methods with different assumptions and approximations. We note that these Raman and conductivity measurements were all carried out on NaB(OH)4 solutions at molalities from 0.2 mol kg−1 to 1 mol kg−1, with or without excess NaOH, in which diborate is a major species. The potentiometric measurements by Mesmer et al. were carried in 1 mol kg−1 KCl solutions with boron concentrations from 0.03 to 0.5 mol kg−1, at equilibrium hydroxide concentrations below 0.01 mol kg−1, in which diborate was a minor species. This raises the possibility that a second species, possibly a sodium ion pair, is contributing to the formation constants reported as  in Table 3 and Fig. 7.
in Table 3 and Fig. 7.
5.3. Diborate formation constants
The equilibrium constant for diborate formation, , is given by the expression:
, is given by the expression: | (18) |
 | (19) |
 | (20) |
 | ||
Fig. 8 Plot of log 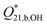 as a function of ionic strength at 250 °C at p = 20 MPa. The black squares (■) are the experimental values from this work. The blue triangle ( as a function of ionic strength at 250 °C at p = 20 MPa. The black squares (■) are the experimental values from this work. The blue triangle ( ) represents the value from conductivity experiments by Ferguson et al.27 The red triangle ( ) represents the value from conductivity experiments by Ferguson et al.27 The red triangle ( ) and circle ( ) and circle ( ) are Mesmer's value of log ) are Mesmer's value of log  at I = 1 mol kg−1 and I = 0, extrapolated to 250 °C by Palmer et al.26 The red line is the weighted linear fit to the Raman data, given by eqn (20), The 90% confidence limits for the linear model are shown by the dashed black curves. at I = 1 mol kg−1 and I = 0, extrapolated to 250 °C by Palmer et al.26 The red line is the weighted linear fit to the Raman data, given by eqn (20), The 90% confidence limits for the linear model are shown by the dashed black curves. | ||
Where  and a = 0.639 ± 0.134. The uncertainties are standard errors.
and a = 0.639 ± 0.134. The uncertainties are standard errors.
For consistency with our previous Raman study on the formation constants of triborate,8 an attempt was made to model the activity coefficient quotient using the same treatment, which is based on the expressions developed by Palmer et al.26 A simple treatment was also used in which the activity coefficients were assumed to depend only on ionic charge, so that:
| γ[B2(OH)7]− = γ[B(OH)4]− = γOH− | (21) |
 | (22) |
Neither model predicted the steep ionic-strength dependence of  shown in Fig. 8.
shown in Fig. 8.
6. Discussion
6.1. Composition dependence of  and evidence for a second diborate species
and evidence for a second diborate species
As noted in section 5.2, the formation quotients from this Raman study are in very good agreement with those from the conductivity measurements by Ferguson et al.,27 yet are systematically larger than the potentiometric results reported by Mesmer et al., which were measured in KCl solutions at lower pH. The composition-dependent equilibrium constants plotted in Fig. 8 are consistent with these trends and since the magnitude of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K increases with the molalities of Na+ and OH−. Noting that the effect of hydroxide on the equilibrium between [B2(OH)7]− and [B2O2(OH)4]2− is governed by a reaction that directly involves hydroxide,
K increases with the molalities of Na+ and OH−. Noting that the effect of hydroxide on the equilibrium between [B2(OH)7]− and [B2O2(OH)4]2− is governed by a reaction that directly involves hydroxide,| [B2(OH)7]− + OH− ⇌ [B2O2(OH)42−] + 2H2O | (23a) |
| [B2(OH)7]− + OH− + Na+ ⇌ Na[B2O2(OH)4]− + 2H2O | (23b) |
The band assignments used to derive the formation quotients reported in Table 3 are based on the computationally predicted vibrational frequencies listed in Table 2 and the assumption that no polyborate species other than [B2(OH)7]− and/or [B2O(OH)5]− contributes to the intensity of the 865 cm−1 band. While the computational spectrum of [B2O2(OH)4]2− also showed an intense band near 865 cm−1, it was rejected on the grounds that no weak band near 600 cm−1 was observed in the experimental spectra. This objection may not be valid in the case of the [B2O2(OH)4]2− contact ion pair. With reference to the structure in Fig. 5, the predicted band near 865 cm−1 is essentially the symmetric B–O(H) stretch, while the band near 600 cm−1 primarily due to the in-plane B2O2 deformation, with some coupling to the BOH bending mode. The formation of a contact ion-pair with Na+ at the ring site would be expected to shift the 600 cm−1 band to higher frequencies and to reduce its intensity.
6.2. Uncertainties in the diborate formation quotients
The formation quotients for [B2(OH)7]− from this work, plotted in Fig. 7 and 8, show a much larger experimental scatter than has been observed in similar studies using the same methods.8,9 The uncertainties arise, in part, from the possible contribution of Na[B2O2(OH)4]− to the 865 cm−1 band, and in the need to resolve the relative contributions of the diborate species and [B(OH)4]− to the band at 745 cm−1. The interpretation is complicated further by the inability of Raman spectroscopy to distinguish between the free borate ion, [B(OH)4]− and the sodium borate ion-pair, [NaB(OH)4]0.9,12 Calculations based on the ion-pair formation constants reported by Arcis et al.28 suggest that the majority of the aqueous borate species at these concentrations may in fact be solvent-separated ion pairs. As a result, the bands at 745 and 865 cm−1 may also include contributions from sodium ion pairs with diborate, [NaB2(OH)7]0, which presents a similar hydroxyl-rich surface to the surrounding hydration shell. Accurate measurements over a much wider range of solution compositions and the full temperature range would be needed to resolve these issues.6.3. Impact on chemical speciation models for aqueous boron
The complex aqueous speciation chemistry of boron is of critical interest to the nuclear industry, and is relevant to a number of other sectors including geology/geochemistry, natural waters, and various chemical and industrial processes. In the nuclear industry, two major software packages are used for modeling chemical speciation in reactor coolant. These are based on different chemical equilibrium models and independent critically evaluated thermodynamic data.26,29 The Electric Power Research Institute's (EPRI) chemical modelling software, MULTEQ, which is distributed as part of ChemWorks Tools (v.7.0), makes use of a “model species” activity coefficient treatment, the Meissner equation,30 and is most accurate at ionic strengths below 1 mol kg−1. The OLI Analyzer Studio 9.2.1 software (OLI Systems Inc.), is based on standard-state properties from the Helgeson–Kirkham–Flowers (HKF) equation31,32 and the mixed-solvent electrolyte (MSE) model for excess properties from Anderko et al.33 MULTEQ and OLI have adopted different chemical formulations for the diborate ion. MULTEQ defines the diborate ion as [B2(OH)7]−, while OLI Studio defines diborate as the condensed species [B2O(OH)5]−. It is also important to note that MULTEQ uses the equation reported by Marshall and Franck34 for the ionization constant of water, Kw, while OLI uses the expression derived for the HKF model.31,32 The critically-evaluated values for speciation, phase equilibria, and other thermodynamic properties of boron-containing systems in the OLI Analyzer Studio 9.2.1 have been reported by Wang et al.17A revision to the databases of both MULTEQ and OLI Studio to include the new diborate formation quotients from this study, should include the results from our earlier work on the formation constants for the triborate ion.8 The spectra reported for the more acidic boric acid/borate solutions in the triborate study, impose an upper limit on the formation constant of [B2(OH)7]− because the presence of diborate as an equilibrium species at concentrations above the detection limit of 0.1 mol kg−1 would have been observable as a weak band at 865 cm−1 when, in fact, no such bands were seen. This upper limit is more consistent with the formation constant reported by Palmer, than with the results in Table 3 and Fig. 7, consistent with presence of a second diborate species as discussed above.
The implication of these results for model database development are twofold. First, the experimental results demonstrate that the [B2(OH)7]− ion is a significant species that may form under ‘hideout’-type conditions in nuclear power reactors, and in hydroxide-rich borate solutions at elevated temperatures in other chemical and industrial processes. Second, the divalent ion [B2O2(OH)4]2− may also be present as an ion pair with alkali metal ions and may also affect boron hideout chemistry. Finally, as noted above, the Raman spectra of borate solutions in our recent triborate publication show that these diborate species are not expected to present at high enough concentrations to significantly affect the bulk primary coolant chemistry in PWR nuclear reactors.
7. Conclusions
The presence of a previously unreported equilibrium aqueous boron species has been identified by Raman spectroscopy in ∼1 mol kg−1 NaB(OH)4 solutions at temperatures from 150 to 300 °C and 20 MPa. The most plausible polyborate species structures were examined computationally, as well as by observing the effects of excess Li+, Na+, and OH− ions on the experimental Raman spectra. The experimental results, together with the computational frequency predictions, indicate that the most likely candidate for the boron species are [B2(OH)7]− and/or [B2O(OH)5]−, which is consistent with Mesmer's potentiometric studies.14 The DFT-predicted frequencies suggest that [B2(OH)7]− is the more likely candidate for the major species. The Raman scattering coefficients, equilibrium concentrations, and formation constants were calculated from three different modelling approaches based on peak area and mass balance. The models had charge-balance discrepancies for solutions in which hydroxide concentrations were calculated using the boric acid ionization constants and activity coefficient model reported by Palmer et al.,26 however, Model 2 yielded constant scattering coefficients within the experimental uncertainties, while other models did not. As a result of this finding and of the DFT-predicted vibrational spectra, the formation quotients for [B2(OH)7]−, , calculated from the equilibrium concentrations determined using Model 2 are most consistent with the computational and Raman results.
, calculated from the equilibrium concentrations determined using Model 2 are most consistent with the computational and Raman results.
The formation quotients for [B2(OH)7]−,  from both models showed inconsistencies that varied with temperature and composition. These may be due to the presence of another equilibrium species at temperatures above ∼150 °C, and/or a strong activity coefficient effect that is not well represented by the models used in this study. If present, the most likely candidate for a second unknown species is the divalent diborate ion pair, Na[B2O2(OH)4]−. The detection limits observed for the Raman spectra of boric-acid rich solutions at these temperatures8,9 place an upper limit on the standard-state formation constants of [B2(OH)7]− at all the temperatures studied.
from both models showed inconsistencies that varied with temperature and composition. These may be due to the presence of another equilibrium species at temperatures above ∼150 °C, and/or a strong activity coefficient effect that is not well represented by the models used in this study. If present, the most likely candidate for a second unknown species is the divalent diborate ion pair, Na[B2O2(OH)4]−. The detection limits observed for the Raman spectra of boric-acid rich solutions at these temperatures8,9 place an upper limit on the standard-state formation constants of [B2(OH)7]− at all the temperatures studied.
Author contributions
Swaroop Sasidharanpillai: data curation, formal analysis, investigation, methodology, validation, writing – original draft, writing – review & editing. Jenny S. Cox: data curation, investigation, methodology, formal analysis, validation, writing – original draft, writing – review & editing. Cory C. Pye: investigation, formal analysis, methodology, writing – original draft. Peter R. Tremaine: conceptualization, formal analysis, methodology, project administration, supervision, validation, visualization, funding acquisition, writing – original draft, writing – review & editing, resources.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was supported by the Electric Power Research Institute (EPRI Project 10006135) and by the Natural Science and Engineering Research Council of Canada (NSERC) Discovery Grant RGPIN-2017-05894. The authors thank OLI Systems Inc. (Edison, N.Y.) for donating their software package OLI Analyzer Studio 9.2.1 to the Hydrothermal Chemistry Laboratory at the University of Guelph. Dr Peiming Wang and Dr Andrzej Anderko (OLI) provided help and advice with the database and software, and insightful input to the diborate ion-pair discussions. We are grateful to Mr Case Gielen (Chemistry and Physics Machine Shop) who constructed the titanium flow cell, and Mr Ian Renaud (Chemistry Electronics Shop) who constructed the temperature controller. The authors also express their gratitude to Dr Daniel Wells (EPRI) for providing technical advice, many fruitful discussions, and steadfast support on this project. We are also grateful to Dr Shirley Dickinson and Dr Hugues Arcis (National Nuclear Laboratory, UK) and Dr Jane Ferguson (St Mary's University, NS) for many suggestions and technical discussions related to polyborate thermodynamics. Dr Matt Wolf provided input on earlier versions of the manuscript. The authors thank ACEnet for computational resources. We also thank the reviewers for insightful comments on the original manuscript and for suggesting the D2O experiments, both of which led to worthwhile improvements in the final paper.References
- L. M. Rowe, L. B. Tran and G. Atkinson, The effect of pressure on the dissociation of boric acid and sodium borate ion pairs at 25 °C, J. Solution Chem., 1989, 18(7), 675–689 CrossRef CAS.
- J. Yongzhong, G. Shiyang, X. Shuping and L. Jun, FT-IR, spectroscopy of supersaturated aqueous solutions of magnesium borate, Spectrochim. Acta, Part A, 2000, 56(7), 1291–1297 CrossRef PubMed.
- L. Jun, X. Shuping and G. Shiyang, FT-IR and, Raman spectroscopic study of hydrated borates, Spectrochim. Acta, Part A, 1995, 51(4), 519–532 CrossRef.
- R. E. Weston, Raman Spectra of Electrolyte Solutions in Light and Heavy Water, Spectrochim. Acta, 1962, 18(9), 1257–1277 CrossRef CAS.
- C. Schmidt, R. Thomas and W. Heinrich, Boron speciation in aqueous fluids at 22 to 600 °C and 0.1 MPa to 2 GPa, Geochim. Cosmochim. Acta, 2005, 69(2), 275–281 CrossRef CAS.
- Y. Q. Zhou, C. H. Fang, Y. Fang and F. Y. Zhu, Polyborates in aqueous borate solution: A Raman and DFT theory investigation, Spectrochim. Acta, Part A, 2011, 83(1), 82–87 CrossRef CAS PubMed.
- F. Y. Zhu, C. H. Fang, Y. Fang, Y. Q. Zhou, H. W. Ge and H. Y. Liu, Structure of aqueous potassium pentaborate solution, J. Mol. Struct., 2015, 1083, 471–479 CrossRef CAS.
- S. Sasidharanpillai, H. Arcis, L. Trevani and P. R. Tremaine, Triborate Formation Constants and Polyborate Speciation under Hydrothermal Conditions by Raman Spectroscopy using a Titanium/Sapphire Flow Cell, J. Phys. Chem. B, 2019, 123(24), 5147–5159 CrossRef CAS PubMed.
- L. M. S. G. A. Applegarth, C. C. Pye, J. S. Cox and P. R. Tremaine, Raman Spectroscopic and ab Initio Investigation of Aqueous Boric Acid, Borate, and Polyborate Speciation from 25 to 80 °C, Ind. Eng. Chem. Res., 2017, 56(47), 13983–13996 CrossRef CAS.
- F. Y. Zhu, C. H. Fang, Y. Fang, Y. Q. Zhou, H. W. Ge and H. Y. Liu, Structure of aqueous potassium metaborate solution, J. Mol. Struct., 2014, 1070, 80–85 CrossRef CAS.
- C. H. Fang, F. Y. Zhu, Y. Fang, Y. Q. Zhou, S. Tao and S. Xu, Structure of aqueous potassium tetraborate solutions by X-ray scattering, Phys. Chem. Liq., 2013, 51(2), 218–232 CrossRef CAS.
- R. Buchner, G. Hefter, P. M. May and P. Sipos, Dielectric relaxation of dilute aqueous NaOH, NaAl(OH)4, and NaB(OH)4, J. Phys. Chem. B, 1999, 103(50), 11186–11190 CrossRef CAS.
- K. Ishihara, A. Nagasawa, K. Umemoto, H. Ito and K. Saito, Kinetic Study of Boric Acid-Borate Interchange in Aqueous Solution by 11B NMR Spectroscopy, Inorg. Chem., 1994, 33(17), 3811–3816 CrossRef CAS.
- R. E. Mesmer, C. F. Baes and F. H. Sweeton, Acidity measurements at elevated temperatures. VI. Boric acid equilibriums, Inorg. Chem., 1972, 11(3), 537–543 CrossRef CAS.
- C. F. Baes and R. E. Mesmer, The Hydrolysis of Cations, John Wiley & Sons, New York, 1976 Search PubMed.
- N. Ingri, G. Lagerström, M. Frydman and L. G. Sillén, Equilibrium Studies of Polyanions. II. Polyborates in NaClO4 Medium, Acta Chem. Scand., 1957, 11, 1034–1058 CrossRef CAS.
- P. Wang, J. Kosinski Jerzy, M. Lencka Malgorzata, A. Anderko and D. Springer Ronald, Thermodynamic modeling of boric acid and selected metal borate systems, Pure Appl. Chem., 2013, 85(11), 2117–2144 CrossRef CAS.
- W. T. Lindsay, Jr., in Chemistry of Steam Cycle solutions: Principles, in The ASME Handbook on Water Technology for Thermal Power Systems, ed. P. Cohen, Amer. Soc. Mech. Eng., New York, 1989, pp. 341–544 Search PubMed.
- W. T. Lindsay Jr., MULTEQ: What it is and what it can do, in Control of Corrosion on the Secondary side of Steam Generators, ed. R. W. Staehle, J. A. Gorman and A. R. Mcllree, Nat. Assoc. Corrosion Eng. (NACE), Houston, TX, United States, 1996 Search PubMed.
- M. H. Brooker, O. F. Neilsen and E. Praestgaard, Assessment of Correction Procedures for Reduction of Raman Spectra, J. Raman Spectrosc., 1988, 19(2), 71–78 CrossRef CAS.
- C. C. Pye, A Crystallographic Review of Alkali Borate Salts and Ab Initio Study of Borate Ions/Molecules, in Concepts, Methods and Applications of Quantum Systems in Chemistry and Physics, ed. Y. A. Wang, M. Thachuk, R. Krems and J. Maruani, Springer International Publishing, Springer, 2018, pp. 107–142 Search PubMed.
- M. H. Brooker and P. R. Tremaine, Raman Studies of Hydration of Hydroxy Complexes and the Effect on Standard Partial Molar Heat Capacities, Geochim. Cosmochim. Acta, 1992, 56(6), 2573–2577 CrossRef CAS.
- E. Bulemela and P. R. Tremaine, D2O Isotope Effects on the Ionization of β-Naphthol and Boric Acid at Temperatures from 225 to 300 °C using UV-Visible Spectroscopy, J. Solution Chem., 2009, 38(7), 805–826 CrossRef CAS.
- D. A. Palmer, Aqueous Boron Species, in Chemical Thermodynamics: Ancillary Data. Thermochemical Database Project, ed. M. Rand, OECD Nuclear Energy Agency, Paris, France, In press Search PubMed.
- C. C. Pye, An Ab Initio Study of Boric Acid, Borate, and their Interconversion, in Concepts, Methods and Applications of Quantum Systems in Chemistry and Physics, ed. Y. A. Wang, M. Thachuk, R. Krems and J. Maruani, Springer International Publishing, SpringerCham, 2018, pp. 143–177 Search PubMed.
- D. A. Palmer, P. Benezeth and D. Wesolowski, Boric acid hydrolysis: A new look at the available data, Power Plant Chem., 2000, 2(5), 261–264 CAS.
- J. P. Ferguson, Aqueous Boric Acid Chemistry under Pressurized Water Reactor Coolant Conditions by AC Conductivity, PhD Thesis, University of Guelph, Guelph, Canada, 2018 Search PubMed.
- H. Arcis, J. P. Ferguson, G. H. Zimmerman and P. R. Tremaine, The limiting conductivity of the borate ion and its ion-pair formation constants with sodium and potassium under hydrothermal conditions, Phys. Chem. Chem. Phys., 2016, 18(34), 24081–24094 RSC.
- P. Wang, A. Anderko and R. D. Young, A speciation-based model for mixed-solvent electrolyte systems, Fluid Phase Equilib., 2002, 203(1–2), 141–176 CrossRef CAS.
- H. P. Meissner and J. W. Tester, Activity Coefficients of Strong Electrolytes in Aqueous Solutions, Ind. Eng. Chem. Process Des. Dev., 1972, 11(1), 128–133 CrossRef CAS.
- J. C. Tanger IV and H. C. Helgeson, Calculation of the Thermodynamic and Transport Properties of Aqueous Species at High Pressures and Temperatures: Revised Equations of State for the Standard Partial Molal Properties of Ions and Electrolytes, Am. J. Sci., 1988, 288, 19–98 CrossRef.
- E. L. Shock and H. C. Helgeson, Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Correlation algorithms for ionic species and equation of state predictions to 5 kb and 1000 °C, Geochim. Cosmochim. Acta, 1988, 52(8), 2009–2036 CrossRef CAS.
- A. Anderko, P. Wang and M. Rafal, Electrolyte Solutions: From Thermodynamic and Transport Property Models to the Simulation of Industrial Processes, Fluid Phase Equilib., 2002, 123–142 CrossRef CAS.
- W. L. Marshall and E. U. Franck, Ion Product of Water Substance, 0–1000 °C, 1–10,000 Bars: New International Formulation and Its Background, J. Phys. Chem. Ref. Data, 1981, 10, 295–304 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt02514d |
| This journal is © The Royal Society of Chemistry 2023 |







