IR spectra and structures of saturated ruthenium cluster carbonyl cations Ru_n(CO)_m⁺ (n = 1–6)

Abstract

A series of saturated ruthenium cluster carbonyls (Ru(CO)₅⁺, Ru₂(CO)₉⁺, Ru₃(CO)₁₂⁺, Ru₄(CO)₁₄⁺, Ru₅(CO)₁₆⁺ and Ru₆(CO)₁₈⁺) have been synthesized in the gas phase and subsequently characterized by infrared spectroscopy. Their size-specific IR spectra in the region of the carbonyl stretch vibration (1900–2150 cm⁻¹) and in the region of the Ru–C–O bending modes (420–620 cm⁻¹) are obtained by infrared multiple photon dissociation spectroscopy. The structures of these cluster carbonyls are assigned by comparison with results from density functional calculations. A multitude of differently activated CO ligands are identified in these cationic cluster carbonyls, reaching from terminal, over non-symmetrically bridging (semi-bridging) ligands with varying degrees of interaction to additional Ru atoms towards symmetrically bridging CO ligands.

---

Introduction

Metal cluster carbonyls have been an important class of substances for developing a profound understanding of the binding in polynuclear coordination compounds.^1–5 Much of the knowledge on their structures is based on the characterization of compounds that are stable and synthesizable often in bulk quantities, e.g. via X-ray crystallography. Other approaches that can also be applied to less stable metal carbonyls rely on their synthesis in (cryogenic) inert matrices^6–9 or molecular beams,^10,11 where they are typically characterized by infrared spectroscopy. The latter makes use of the often very strong absorptions related to C–O stretch vibrations and the pronounced sensitivity of its vibrational frequency, ν(CO), towards the binding environment.^12,13

Gas-phase studies that can provide – via combination with mass spectrometry – direct information on the size and stoichiometry of a cluster carbonyl are usually limited to charged carbonyls, as the susceptibility to fragmentation during the ionization process can add severe complications to the studies of neutral metal cluster carbonyls.¹⁴ Only very recently the combination of IR excitation with ‘soft’ ionization using a tunable vacuum UV free electron laser (FEL) opened up new possibilities for gas-phase experiments on neutral metal carbonyls.^15–17 So far, the majority of such studies in the gas phase, however, have focussed on charged mono and binuclear carbonyls. Recently, also the synthesis and characterization of certain polynuclear metal carbonyl cations (and dications) have been reported in the condensed phase, which become accessible, inter alia, in the presence of weakly coordinating anions.^18–20 A pertinent example is the formation of dications M₃(CO)₁₄²⁺ (M = Ru, Os) with a linear-chain arrangement of the metal skeleton.²¹

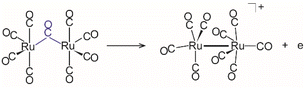
Solution studies of metal cluster carbonyls, and in particular also of ruthenium carbonyls, have intensively utilized IR spectroscopy in the range of ν(CO) to study the dynamics of such cluster compounds. Particular interest is, e.g., on their photochemical or thermal disintegration, vibrational interactions within the cluster complex or with the solvent, and the reorganization of their ligand shells.^22,23 In these solution phase experiments, intermediates may be detected based on their spectral signature; however, their identification has not always been straightforward.²⁴ Furthermore, in contrast to their fixed structure in the solid state, polynuclear carbonyls in solution show often a pronounced fluxional behaviour due to intramolecular CO exchange.^25,26 For example, Ru₃(CO)₁₂ is well known to exhibit rapid scrambling between axial and equatorial CO ligands with a low barrier of about 20 kJ mol⁻¹.²⁷ The exact reorganization mechanism and whether it involves bridging CO ligands that have been found as structural units in the ground state structure of the lighter homologue Fe₃(CO)₁₂ are still under discussion. However, intermediates containing bridging CO ligands have been experimentally detected during the photoinduced dissociation of Ru₃(CO)₁₂,^22,28,29 and their possible role in the scrambling process has been postulated based on quantum chemical calculations.^30,31 As we will show later in this article, semi-bridging CO ligands are present in cationic Ru₃(CO)₁₂⁺ and other cationic Ru carbonyls isolated in the gas phase.

Ionic carbonyls in the gas phase have the advantage that their composition can be precisely determined by means of mass spectrometry. By applying infrared multiple photon dissociation (IR-MPD) spectroscopy, size-selective structural characterization becomes possible without the interference through possible fragmentation products.^10,32–34 Already in the late 1980s, cationic polynuclear transition metal cluster carbonyls were synthesized in the gas phase via reactions of transition metal clusters with CO and their compositions were analysed by means of mass spectrometry.³⁵ At comparably high CO partial pressure and sufficient reaction time, i.e. many reactive collisions between cluster and CO molecules, characteristic abundance patterns of metal cluster carbonyls are observed, relating the nuclearity of the metal cluster core, n, to a particularly stable stoichiometry of the corresponding carbonyl. In this way, cationic cluster carbonyls have also been synthesized, and they do not have known neutral complexes as stable counterparts. The experimentally observed stoichiometries of these gas-phase carbonyl clusters are well understood in the context of the Wade–Mingos rules,^36,37 an extension of the 18 electron rule for transition metal complexes to polynuclear compounds. Within this polyhedral skeletal electron pair theory (PSEPT), the cluster's nuclearity, composition, and electronic structure are related to predict the geometry of the clusters.

The Wade–Mingos rules aim to describe the bonding and topology of the metal skeleton in polynuclear, usually closed-shell, complexes. They treat the ligand as a source of a given number of electrons shared over all the valence orbitals of the cluster complex and, therefore, cannot provide detailed structural information on the ligand arrangement in the complex. Instead, usually space-filling arguments are used to rationalize the arrangement of the ligand sphere. Infrared spectroscopy offers additional information as it is sensitive to structural details of a carbonyl complex, e.g., via the symmetry selection rule for IR activity. Furthermore, as ν(CO) is a measure of the activation of C–O through the metal–CO interaction, or more specifically through the π back-bonding, it is particularly useful to discern CO ligands in different metal coordination sites and, in particular, to differentiate between terminal and bridging CO ligands.

Cationic Rh cluster carbonyls, for instance, have been investigated by IR-MPD spectroscopy, which then allowed for a comparison between structures of the cations and those of the known stable neutral Rh carbonyls. As a result it was concluded that ionization leads to a destabilization of the μ₂ bridging CO ligands in Rh₂(CO)₈ (2 μ₂-CO) and Rh₄(CO)₁₂ (3 μ₂-CO) such that the cations only contain terminal CO ligands, while the structure of Rh₆(CO)₁₆⁺ fully resembles that of the neutral octahedral species and contains 4 μ₃ face-capping CO ligands.³⁴

Gas-phase synthesis of cationic Ru carbonyls has been reported before for the tetra to hexanuclear carbonyls of Ru and their structures as derived via application of the Wade–Mingos rules have been compared to those predicted by means of density functional theory calculations.³⁸ Here, we substantiate these structural assignments by comparing gas-phase IR-MPD spectra observed for the full series of saturated cationic Ru carbonyls Ru(CO)₅⁺, Ru₂(CO)₉⁺, Ru₃(CO)₁₂⁺, Ru₄(CO)₁₄⁺, Ru₅(CO)₁₆⁺ and Ru₆(CO)₁₈ with IR spectra calculated using DFT for the putative ground-state isomers of these carbonyls.³⁹

Experimental and theoretical methods

Experimental methods

Ruthenium carbonyl cluster cations are produced in the gas phase via laser vaporization of metallic Ru in the presence of He and CO. The initially formed ruthenium cluster cations react with CO gas at ∼30 °C in the high pressure region of the cluster source before the mixture expands into a vacuum forming a molecular beam. The distribution of cationic species embedded in the cluster beam is analysed by reflectron time-of-flight mass spectrometry. The clusters are produced at 10 Hz; on alternate shots, the beam is exposed to the focussed infrared beam of the FHI-FEL⁴⁰ that acts as an intense and tunable IR source. Upon resonant excitation and absorption of multiple IR photons, a carbonyl complex can fragment, leading to a reduction of its detected ion intensity. This intensity change, normalized by the intensity in the ion pulses that are not exposed to IR, is converted to relative IR cross sections. Thereby, also the variation of IR fluence over the tuning range of the FEL is taken into account. Typical IR pulse energies in these experiments were 3 mJ in the region of ν(CO) and 8–16 mJ at longer wavelengths (here generally called far-IR) at a pulse duration of 5–8 μs. The accuracy of the evaluated band positions in the IR spectra is limited by the step-size of IR frequencies at which separate mass spectra have been recorded that is in the ν(CO) region 5 cm⁻¹ and in the far-IR region 2 cm⁻¹. Further details on the experiment and data evaluation have been reported elsewhere.^41,42

Theoretical methods

Structures of the Ru cluster carbonyls, their relative energies, and IR spectra were calculated using density functional theory (DFT) within TURBOMOLE V6.4.⁴³ Initial guess structures were taken from the known structures of a variety of stable neutral carbonyl compounds and from structures generated via a modified basin hopping algorithm⁴⁴ that treats CO as a pseudo-atom. Basin hopping was performed using RI-DFT with the PBE functional and def-SV(P) basis sets as well as the def-ecp effective core potential for Ru as implemented in TURBOMOLE. Further optimizations and frequency calculations made use of the PBE0 hybrid functional and the larger def2-TZVP/def2-ecp combination.^45–48 Calculated harmonic vibrational frequencies were scaled by factors of 0.955 and 0.933 in the region of ν(CO) and in lower frequency modes, respectively, which have been optimized for the herein discussed carbonyls. This scaling also shows excellent agreement between calculated and experimental values⁸ for the most intense ν(CO) band in Ru₃(CO)₁₂ (ESI, Fig. S1†). For a better visual comparison between experimental and calculated spectra, the latter were folded with a Gaussian line shape function with a full-width at half maximum of 1% of the centre frequency.

Initial structural optimizations were performed without any symmetry constraints; however, the optimized structures were carefully checked for the presence of any point group symmetry and, if appropriate, re-optimized within the resulting symmetry. All of the structures reported below are true minima, and only for the lowest here reported state of Ru₆(CO)₁₈⁺ (C₂, ²B) a small imaginary frequency (8.1i cm⁻¹) remained; due to the size of the system we refrained from further optimizations.

Results and discussion

Structure of Ru carbonyls

Neutral Ru carbonyls. Before discussing the insights for the saturated cationic Ru cluster carbonyls obtained from their saturation compositions, IR-MPD spectra, and comparison with the results of DFT calculations, we summarize the knowledge available for the known neutral carbonyls of Ru. Mononuclear carbonyl Ru(CO)₅ has a trigonal bipyramidal structure of D_3h symmetry, similar to its lighter homologue, the well-known iron pentacarbonyl.⁴⁹ Ru nonacarbonyl Ru₂(CO)₉ exists only as a comparably unstable intermediate that can be produced, e.g., by irradiation of Ru(CO)₅ in solution, and it contains a single bridging CO ligand.^50,51 More recent computational studies find for the C₂ symmetric ground state a Wiberg bond order for Ru–Ru of only 0.1 suggesting the absence of significant metal–metal bonding in Ru₂(CO)₉.⁵² The most stable neutral Ru carbonyl, triruthenium–dodecacarbonyl Ru₃(CO)₁₂, is usually reported to have a D_3h structure (Fig. 1) with only terminal CO ligands which is in the solid, however, slightly distorted by intermolecular interactions. Nevertheless, quantum chemical calculations (including ours) identify a distorted propeller-shaped version of D₃ symmetry lying 0.05–0.12 eV lower in energy depending on the method.^31,53,54 Comparing the calculated bond lengths using the DFT:PBE0/def2-TZVP combination for the D₃ and D_3h structures and those resulting from the crystal structure of Ru₃(CO)₁₂ ⁵⁵ shows good agreement for both. Only the axial d(C–O) is slightly overestimated in the calculated results by ∼1% and the corresponding d(Ru–C) is too small by the same value, while the deviations for the other atomic distances are smaller (see the ESI, Table S1†).

Fig. 1 Ball and stick representations of the putative global minimum structures for cationic ruthenium carbonyls and for neutral Ru₃(CO)₁₂ with point group symmetries and electronic states given. For Ru(CO)₅⁺ and Ru₆(CO)₁₈⁺ also a higher energy isomer is shown. The colour scheme is as follows: Ru – teal, C – grey, O – red (terminal CO), C – light grey, O – orange (semi-bridging CO), C – lightgrey, and O – yellow (symmetrically bridging CO). For better clarity, some of the longer Ru–C bonds for semi-bridging ligands are depicted as dashed lines only.

Cationic Ru carbonyls. The putative global minima structures as obtained by our global optimization approach are shown in Fig. 1. The detailed structural information, calculated harmonic vibrational frequencies, and IR intensities can be found in the ESI.† All these cations possess a doublet electronic state. For the smallest sizes, for which neutral counterparts exist, these calculated structures clearly differ from those of the neutral ones, while the structures of the tetra to hexanuclear carbonyls agree very well with the predictions from Lang et al.³⁸ Minor differences relate to details of the ligand arrangement, in particular to the assignment of semi-bridging CO ligands. The metal skeleton of all putative global minima conforms to the predictions according to PSEPT (Table 1). Lang et al. reported the calculated average CO binding energies for Ru₄(CO)₁₄⁺, Ru₅(CO)₁₆⁺ and Ru₆(CO)₁₈⁺ of 1.89, 1.83 and 1.79 eV, respectively.³⁸ We refrain here from a more detailed analysis of the energetics as the actual gas-phase structures, spin states, and related energetics of the corresponding bare Ru cluster cations are experimentally unknown and the difficulties of DFT based methods in describing small Ru clusters have been addressed before.^56,57 It shall be noted, however, that small ligand-free Ru clusters are found to exhibit rather unusual structures based on cubic motifs.^58,59

Table 1 Composition of stable cationic ruthenium cluster carbonyls, number of valence electrons in the corresponding neutral (VE), counting rule and assignment to structural class, and structural assignment for the metal skeleton according to PSEPT

	VE	Rule	Structure class	Skeleton structure
Ru(CO)5^+	18	—		Atom
Ru2(CO)9^+	34	—		Dimer
Ru3(CO)12^+	48	16n	Ring	Triangle
Ru4(CO)14^+	60	15n	Three-connected	Tetrahedron
Ru5(CO)16^+	72	14n + 2	Closo deltahedral	Trigonal bipyramid
Ru6(CO)18^+	84	14n	Hypercloso deltahedral	Capped trigonal bipyramid

---

The structural representations in Fig. 1 distinguish between terminal, symmetrically μ₂-bridging, and non-symmetrically bridging or semi-bridging CO ligands. This differentiation between binding modes is based on the bridge asymmetry parameter α as introduced by Curtis.⁶⁰

In this scheme, d₁ is the shortest Ru–CO bond length for a given carbonyl ligand, while d₂ is the distance to the next-nearest Ru atom in the cluster complex, irrespective of the actual bonding interactions. Naturally, α is not defined for mononuclear complexes. According to Curtis, a value of α below 0.1 represents a (close-to) symmetric CO bridge, while up to a value of 0.6 the ligands can be characterized as semi-bridging.⁶¹ The somewhat arbitrary and certainly system-specific transition from semi-bridging to terminal CO-ligands for α > 0.6 has been recently questioned and re-analysed based on a large number of crystallographic structures. Based on these studies, a somewhat larger value of α = 0.7 has been suggested for the semi-bridging/terminal transition.⁶² In the following, however, we use the original values of Curtis.

Clearly, this still remains an arbitrary definition and in fact there is a rather smooth structural transition from ‘true’ terminal to bridging CO ligands which goes along with a lowering of the Ru–C–O bond angle, a lengthening of the C–O bond, and a red-shift of the corresponding ν(CO), as discussed below.

Saturation composition and implications from PSEPT

The reaction of gas-phase Ru cluster cations with CO molecules in the cluster source leads, at sufficiently high CO partial pressures and under stabilizing multiple collision conditions with background He gas, to a distribution of cationic carbonyl complexes (Fig. 2). The relevant partial pressures of He and CO in the source are difficult to quantify as they are both introduced by separate pulsed valves, but by comparison with the conditions in similar cluster sources a total pressure of a few tens of mbar can be deduced, consisting mostly of He carrier gas.^63–65 The reaction time can be approximated by the time the complexes spend in the cluster source, which is on the order of 100 μs. Under such conditions, for a given nuclearity of the metal cluster, a carbonyl with a specific stoichiometry (marked as n,m in Fig. 2) is formed as the major product. The mass spectrometric signals appear rather broad which is due to the natural isotopic distribution of Ru, but their position and overall width agree well with the distributions expected for the given carbonyl compositions. Furthermore, the resolution of the mass spectrometer of m/Δm ≈ 1000 is sufficient to resolve all mass signals for the lighter carbonyls showing no obvious additional signals other than those from the isotopes of Ru and C.

Fig. 2 Mass spectrum of saturated Ru cluster carbonyls Ru_n(CO)_m⁺. Compositions of particularly intense, i.e. stable, Ru carbonyls are indicated as (n,m). Additional minor signals are from less stable CO complexes.

Similar mass spectrometric results have been reported before for mass selected Ru₄⁺, Ru₅⁺ and Ru₆⁺ reacted with CO in a gas-filled radio frequency ion trap, leading to the same complex compositions.³⁸ These experiments showed that complex formation proceeds via fast successive addition of CO molecules with the saturated complex being the only observable product. While Fig. 2 includes complexes up to Ru₈(CO)₂₁⁺, the following discussion will be limited to mono to hexanuclear carbonyls as for the larger complexes no insightful IR spectra have been obtained.

The composition of saturated cluster carbonyls as derived from the mass spectrum is listed in Table 1 together with the structural predictions according to PSEPT.^1,2,5,36,66 As discussed by Lang et al., the saturated cationic carbonyls observed in their study follow the PSEPT concept as applied to the neutral species, i.e. a half-filled valence orbital can be treated as fully occupied.³⁸ In this scheme, ruthenium with its [Kr]4d⁷5s¹ configuration of the neutral atom is assumed to contribute 8 valence electrons to the total valence electron counts, while a single CO ligand acts here as a 2 electron donor. We note that this may not be a general rule as shown for the bridging CO ligands in a recent, very detailed comparative bonding analysis for M₂(CO)₉ (M = Fe, Ru, Os).⁵² The total number of valence electrons for the respective neutral cluster carbonyls and the deduced assignments are shown in Table 1. The last column of this table contains the structure derived for the metal cluster skeletons of these carbonyl clusters.

IR-MPD spectra and structural assignments

Experimental IR spectra. The IR-MPD spectra obtained for the cationic Ru carbonyls are shown in Fig. 3. Upon IR multiple photon excitation, successive loss of CO molecules is seen as a dominant fragmentation channel for all the carbonyls. For Ru₂(CO)₉⁺, Ru(CO)₅⁺ is observed as a fragment also. This indicates a comparably weak Ru–Ru bond in the binuclear carbonyl, which is in agreement with earlier theoretical findings for the neutral species.⁶⁷ The direct fragmentation of Ru₂(CO)₉⁺ into Ru(CO)₅⁺ causes an apparent negative absorption in the IR-MPD spectrum of Ru(CO)₅⁺ at around 2040–2010 cm⁻¹. Evidently only a small fraction of Ru₂(CO)₉⁺ fragments into Ru(CO)₅⁺, however, so that the changes in the intensity in the Ru(CO)₅⁺ mass channel can be neglected.

Fig. 3 Overview of IR-MPD spectra of Ru_n(CO)_m⁺. The coloured areas highlight typical ranges for terminal (blue), symmetrically bridging (orange) and non-symmetric semi-bridging CO ligands. Bands observed at longer wavelengths are assigned to delocalized Ru–C–O bending modes. In the gap between 640 and 1900 cm⁻¹ no vibrational fundamentals are expected for these complexes. The intensities in the high frequency range above 1900 cm⁻¹ are multiplied by a factor of 0.1 for a better visualization on a common intensity scale. For penta and hexanuclear carbonyls IR-MPD spectra obtained with twice the IR intensity are included in the far-IR range (grey lines) which shows additional minor features below 500 cm⁻¹.

The IR spectra show clear signals in two ranges. The bands experimentally detected in the upper far-IR (460–570 cm⁻¹) all can be assigned, by comparison with the results of DFT calculations, to strongly delocalized Ru–C–O bending modes, δ(Ru–C–O), each involving many or even all carbonyl groups. Other modes at longer wavelengths have much lower IR intensities and are not experimentally observed as they do not lead to enough energy absorption to induce CO losses. Calculations locate the Ru–CO stretch vibrations in the 370–450 cm⁻¹ range. They are highly coupled with bending and other deformation modes of the carbonyl network. Vibrations involving the Ru cluster are found below 180 cm⁻¹, which is also well below the region of skeleton vibrations of bare Ru clusters which reach up to ∼290 cm⁻¹ for cationic Ru_n⁺ (n = 7–9) clusters.⁵⁹ For further comparison, ν(Ru–Ru) of the isolated dimer has been measured at 347 cm⁻¹via Raman spectroscopy in a cryogenic argon matrix.⁶⁸ The intense bands seen between 1920 and 2130 cm⁻¹ correspond to ν(CO) modes. Note that in the region of ν(CO) the intensity in the IR spectra is scaled by a factor of 0.1. The average position of the ν(CO) bands shifts with increasing nuclearity to lower frequencies which reflects an increase of C–O bond activation in the carbonyls. This can be related to a more effective π back-donation in the larger cluster complexes due to the decreasing CO/Ru ratio (5 in Ru(CO)₅⁺vs. 3 in Ru₆(CO)₁₈⁺) together with a better delocalization of the charge in the larger clusters.⁶⁹ More detailed assignments can be based on a comparison with the results of DFT calculations. In short, bands above 2040 cm⁻¹ are seen for all of these cationic carbonyls and can be related to terminal (μ₁) CO ligands. The range between 1980 and 2040 cm⁻¹ is characteristic for non-symmetrically bridging (semi-bridging) CO with clear signals present, e.g., for Ru₃(CO)₁₂⁺ and Ru₆(CO)₁₈⁺. At even lower frequencies (∼1920–1960 cm⁻¹), bands related to symmetrically μ₂-bridging CO are found, with Ru₄(CO)₁₄⁺ showing the most prominent signal. Ru₅(CO)₁₆⁺ shows weak signals for both symmetrical and non-symmetrically bridging CO ligands. No bands are observed at a lower frequency and therefore the presence of higher coordinated, i.e. μ₃-face capping, CO ligands can be excluded for the carbonyls studied here. The range between 640 and 1900 cm⁻¹ is not shown, but has been measured partially: the far-IR measurements extend up to 750 cm⁻¹ and the higher frequency range has been studied from 1800 cm⁻¹ upwards, but no additional signals are seen in these regions.

Ru(CO)₅⁺. The smallest Ru cluster carbonyl is found to have a square-pyramidal (C_4v) geometry, in contrast to the D_3h symmetric neutral complex. A cation of D_3h symmetry is found to be significantly (1.48 eV) higher in energy than the C_4v structure. In the experimental IR spectrum, bands are observed at 535 and 2130 cm⁻¹. As can be seen in Fig. 4, the latter agrees very well with the (unresolved) predicted IR-active ν(CO) bands at 2122.7 (a₁) and 2124.4 cm⁻¹ (e) of the C_4v ground state, while the lower frequency band appears to relate to two δ(Ru–C–O) bands at 540.6 (e) and 556.3 cm⁻¹ (a₁). Although the experimental spectrum does not show a splitting of the δ(Ru–C–O) bands, the overall position fits to the prediction for the C_4v structure, while the higher energy isomer shows two bands significantly shifted from the observed value. In addition, the predicted shape of the bands in the ν(CO) region does not fit for the D_3h isomer. The structural transitions upon ionization of Ru(CO)₅ thus involve a change from a trigonal bipyramidal to a square pyramidal structure.

Fig. 4 Experimental IR-MPD spectra (black) of saturated cationic Ru cluster carbonyls compared to the predicted harmonic IR spectra (green) of the putative global minima as obtained using DFT. For Ru(CO)₅⁺ and Ru₆(CO)₁₈⁺, calculated spectra of higher energy isomers (orange) are included for comparison. The experimental and calculated intensities in the frequency range above 1900 cm⁻¹ are multiplied by a factor of 0.1 for a better visualization on a common intensity scale. For penta and hexanuclear carbonyls IR-MPD spectra obtained with twice the IR intensity are included in the far-IR range (grey lines).

For comparison, salts containing an octahedral Ru(CO)₆²⁺ have been characterized before. The IR active (T_1u) vibrational modes of this species in [Ru(CO)₆][SbF₆]₂ are measured at 2198 cm⁻¹ (ν(CO)), 556 cm⁻¹ (δ(Ru–C–O)), and 335 cm⁻¹ (ν(Ru–CO)).⁷⁰

Ru₂(CO)₉⁺. For the dimer the ν(CO) region contains three partially overlapping bands with maxima at 2061, 2094 and 2127 cm⁻¹, which fit well to the predicted pattern of the non-bridged C_s symmetric structure with 4 and 5 terminal CO ligands bound to the Ru atoms, respectively. There is no sign of bands related to bridging CO ligands that have been seen for its neutral counterpart.^50,51 In the lower frequency range, two bands are observed at 561 and 585 cm⁻¹. Their position and intensities fit nicely to the predictions for the delocalized δ(Ru–C–O) vibrations. The calculated Ru–Ru distance is 291.2 pm which is slightly longer than 287.6 pm calculated for the neutral, CO-bridged dimer of C_s symmetry by Pan et al.⁵² The similarity in Ru–Ru bond length is surprising, as the neutral dimer is suggested to be held together essentially via the single bridging CO ligand, as the Wiberg bond order for Ru–Ru is only 0.1. The cation does not contain a bridging CO, and thus it should be bound merely by Ru–Ru interaction.

The weaker Ru–Ru bonding in Ru₂(CO)₉⁺ compared to the larger Ru carbonyls gets reflected in the appearance of Ru(CO)₅⁺ as a fragment during IR-MPD.

Ru₃(CO)₁₂⁺. According to PSEPT the trimer is ring-shaped, which agrees with the identified putative ground state structure. Compared to the carbonyls discussed before, it comprises a more red-shifted band at ∼2000 cm⁻¹ that can be assigned to ν(CO) of non-symmetrically bridging CO ligands. More intense peaks centred at 2077 and 2110 cm⁻¹ relate to terminally bound CO ligands. The multitude of predicted bands in the far-IR region is not resolved in the experimental spectrum that shows a single broad band at 544 cm⁻¹ with a shoulder towards higher frequencies (∼570 cm⁻¹), but it fits in position and shape to the predictions. The two semi-bridging CO ligands spanning a Ru–Ru unit form a compensating pair of CO ligands⁷¹ and have slightly longer C–O bond lengths (113.5 and 113.9 pm) compared to the average of the terminal CO ligands (113.0 pm) in this carbonyl. This clearly reflects a stronger activation of the semi-bridging CO ligands due to an enhanced π back-bonding caused by the interaction with a second Ru atom. These interactions are also seen in the Ru–C–O bonds deviating significantly from linearity with bond angles of 171.5° and 163.7° within the compensating pair, respectively. A third semi-bridging CO ligand, pointing along a Ru–Ru edge, also appears to be slightly activated with d(C–O) = 113.4 pm and ∠(Ru–C–O) = 171.3°. Notably, semi-bridging CO-ligands have not been identified in neutral Ru₃(CO)₁₂ but only during its decomposition.^22,51,72 The calculated average Ru–Ru bond length is 285.9 pm which is similar to that of the neutral one (see the ESI, Table S1†), but whereas in the neutral the three Ru–Ru bonds are (nearly) equivalent, there are stronger deviations in the cation. Here the longest Ru–Ru distance is found to be 287.9 pm for the Ru pair spanned by two semi-bridging CO ligands, followed by the Ru pair spanned by the semi-bridging CO-ligand discussed last (287.7 pm). The third edge has a significantly shorter Ru–Ru distance of 282.1 pm. Overall, the principal change of the CO coordination upon ionization of neutral Ru₃(CO)₁₂ can be illustrated by:

showing the semi-bridging CO ligands in the cationic structure in red.

Ru₄(CO)₁₄⁺. The ground state structure of Ru₄(CO)₁₄⁺ is based on a nearly tetrahedral metal skeleton which is covered by two symmetrically μ₂-bridging CO ligands. Furthermore, each face of the metal tetrahedron is covered by a close-to face-capping ligand which just fulfils Curtis's criterion for semi-bridging ligands (α = 0.59); however, it interacts not with one additional Ru atom, but with two equally. It is somewhat unusual to refer to those as bridging ligands, and this displays the limitation of Curtis's approach which is originally applied to binuclear complexes only.^60,61 The remaining CO ligands are equally distributed such that each Ru atom is bound to two terminal and one symmetrically bridging ligand and forms a short bond with one of the close-to face-capping ligands. This results in the cluster carbonyl having perfect D_2d symmetry. The presence of bridging CO ligands is indicated in the IR-MPD spectrum by a band at the low-frequency side of the ν(CO) region at 1949 cm⁻¹. The calculations predict the IR active antisymmetric stretch of the two μ₂-CO ligands at 1945.5 cm⁻¹ (b₂). Due to the D_2d symmetry of the complex there are three types of symmetry-equivalent CO ligands, two symmetrically bridging ones, which have a calculated C–O bond length of 114.5 pm, eight terminal ones with d(Ru–C) of 113.0 pm and four more with an intermediate bond length of 113.7 pm. The latter also shows a Ru–C–O arrangement that deviates significantly from linearity with ∠(Ru–C–O) = 172.2°. While their Ru–C bond length is 189.9 pm which is similar to the other terminal CO ligands (d(Ru–C) = 190.9 pm) in this carbonyl, each of them clearly points towards one face of the Ru tetrahedron suggesting further interactions with two more Ru atoms. The band experimentally seen at 2029 cm⁻¹ contains the IR active modes of these slightly more activated CO ligands at 2029.5 cm⁻¹ (e) and 2036.4 cm⁻¹ (b₂). The two higher frequency bands experimentally detected at 2075 and 2100 cm⁻¹ can be related to three ν(CO) modes of the terminal ligands at 2073.3 (e), 2096.6 (b₂) and 2098.0 cm⁻¹ (e). The two bands seen at lower frequencies, at 518 and 550 cm⁻¹, coincide nicely with the location of the predicted IR-active δ(Ru–C–O) bands that are each actually composed of unresolved close-spaced e and b₂ symmetric modes.

Ru₅(CO)₁₆⁺. Its structure consists of a trigonal bipyramidal Ru skeleton covered by CO ligands. As indicated in Fig. 1, we identify one μ₂-symmetrically bridging CO-ligand spanning one edge of the base of the bipyramid, while a semi-bridging CO ligand (α = 0.25) is seen on the opposite side of the cluster spanning a Ru–Ru edge towards a vertex. Three more ligands can be characterized as semi-bridging according to the Curtis criterion with α ≈ 0.5. The remaining CO ligands are in a terminal configuration and distributed such that – when ignoring the symmetrically bridging CO – each Ru atom is bound to three CO ligands. This structure is very similar to the one reported by Lang et al. who report also two more closely related structural isomers within 0.36 eV.³⁸ The IR-MPD spectrum of Ru₅(CO)₁₆⁺ is less resolved and shows fewer clear features compared to the other cluster carbonyls discussed here, although it has been measured in parallel to those. A comparably broad band centred at 2090 cm⁻¹ is followed towards lower frequencies by a number of overlapping features with maxima at ∼1984 and ∼1933 cm⁻¹. The latter band is at a position close to the ν(CO) value of the predicted symmetrically bridging CO ligand at 1928.3 cm⁻¹. The next higher feature is related to the semi-bridging CO ligand with a predicted ν(CO) at 1972.6 cm⁻¹. These symmetrically and non-symmetrically bridging CO ligands have predicted bond lengths of 114.8 and 114.4 pm, respectively. In Ru₅(CO)₁₆⁺, two more semi-bridging ligands with elongated d(C–O) of 114.1 and 113.9 pm, respectively, can be identified (the average d(C–O) of the remaining CO ligands is 113.3 pm). Each of these points along an edge of the bipyramid's base, similar to the symmetrically bridging CO ligand, and they also show clear deviations of the Ru–C–O angle from 180° to 168.6° and 168.4°, respectively. These ligands have their ν(CO) at 2003.8 and 2012.9 cm⁻¹, respectively. Similarly, also the CO ligands pointing directly along the edges connecting the base and vertex show slightly elongated d(C–O) of 113.4–113.6 pm and Ru–C–O angles in the range of 172–177°. Combined stretches of the CO ligands least disturbed by additional Ru interactions, i.e. the true terminal ligands, contribute to the highest frequency peak, with the most intense mode being predicted at 2084.3 cm⁻¹. The far-IR spectrum of Ru₅(CO)₁₆⁺ shows an intense peak at 554 cm⁻¹ and, only at a higher IR fluence (grey lines in Fig. 4), a weaker feature around 479 cm⁻¹, which reasonably agrees with the spectrum predicted in that spectral range.

Ru₆(CO)₁₈⁺. The putative global minimum structure is based on a single-capped trigonal bipyramid as predicted by PSEPT. Structures based on different metal cluster arrangements are found to be comparably low in energy, e.g. the D_4h symmetric structure with an octahedral metal core (+0.54 eV) included in Fig. 1 or one with a trigonal prismatic core 0.53 eV above the ground state isomer as reported by Lang et al.³⁸ It is noteworthy that the dianion, Ru₆(CO)₁₈²⁻, has a structure similar to that of the predicted (higher-energy) D_4h isomer of the cation with an octahedral metal core, two μ₂-symmetrically bridging and two μ₃-face-capping CO-ligands, respectively.⁷³ The IR-MPD spectrum of Ru₆(CO)₁₈⁺ in the ν(CO) region does not show evidence for the presence of symmetrically bridging CO ligands; therefore the D_4h symmetric structure can be excluded. Instead, the band pattern in the ν(CO) region fits well to the predicted spectrum of the putative global minimum. The most red-shifted band seen at 2000 cm⁻¹ is due to ν(CO) of semi-bridging CO ligands and corresponds to several overlapping bands in the predicted spectrum. The double-peak structure with maxima at 2071 and 2096 cm⁻¹ can be assigned to the overlapping ν(CO) modes of terminal CO ligands. At a longer wavelength, i.e. in the region of the Ru–C–O bending modes, a peak at 555 cm⁻¹ is seen and some features of low intensity that extend to about 450 cm⁻¹ are also observed. In the predicted IR spectrum the most intense band in that region is observed at 577.1 cm⁻¹, and is slightly blue-shifted compared to the experimental band, but overall there is reasonable agreement between measured and predicted data. As for the other cluster carbonyls mentioned before there are clear differences in the predicted C–O bond length and Ru–C–O angles for the terminal and semi-bridging CO ligands. The semi-bridging CO ligands shown in Fig. 1 have d(C–O) of 114.0 and 114.0–114.1 pm with ∠(Ru–C–O) of 164.4–171.7°, respectively. The remaining ‘true’ terminal CO ligands have an average d(C–O) of 113.3 pm and an average ∠(Ru–C–O) of 177.9°.

Terminal, semi-bridging and symmetrically bridging carbonyl ligands

The presented assignments of the IR spectra based on DFT calculations reveal that the cationic ruthenium cluster carbonyls provide diverse examples of coordinated CO ligands reaching from terminal, over semi-bridging to symmetrically μ₂-bridging CO and, thereby, allow for a comparison of these structural elements with chemically very similar compounds. They are all homoleptic Ru carbonyls, while the former comparisons usually invoke complexes containing different transition metals and also other types of ligands which may account for additional steric and electronic constraints affecting the CO coordination. At this point, we do not intend to analyse the electronic structure of the cluster carbonyls further but rather discuss the resulting Ru–C–O binding geometries that can be related to the IR spectroscopic data. However, due to the open shell structure of the here discussed carbonyl cations, one may expect Jahn–Teller type distortions leading to overall symmetry reductions. This may provide the basis for a larger variation of CO coordination in the cations compared to closed shell structures of higher symmetry.

More detailed discussions of the structural parameters of differently coordinated CO ligands and the consequences for their electronic structures, in particular the M–M interactions, have been given elsewhere.^71,74–76 According to Crabtree et al.⁷⁴ one can distinguish four coordination types for CO interacting with a pair of metal atoms, (i) terminal ligands which essentially interact only with one of the metal atoms in a nearly linear M–C–O arrangement and (ii) symmetrically bridging ligands with two equivalent M–C bonds and the CO axis standing (close to) perpendicular to the bridged M–M pair. Bent semi-bridging (iii) ligands with one short and one long M–C distance and an M–C–O angle significantly deviating from linearity are formed by π back-bonding into the CO's 2π* orbital from the more distant metal atom via interaction with an M–M antibonding orbital. They are seen as intermediates between the terminal and symmetrical-bridging CO ligands. A linear semi-bridging CO (iv) indicates, however, according to Hall^76,77 π back-bonding from a filled π orbital along the M–M entity, i.e., it stabilizes the M–M bonding orbital, while the bent semi-bridging carbonyl stabilizes an antibonding orbital. In both cases the C–O bond is more weakened compared to the terminal CO ligands due to back-bonding from two metal centres which increases the electron density in the CO's 2π* orbital. Similar binding schemes can be discussed for CO interaction, e.g., with the three metal atoms of a triangular face, with the limiting cases of terminal CO binding and central face-capping (μ₃-bridging).⁷⁶ The structural difference between linear and bent semi-bridging CO ligands can be visualized according to Curtis by plotting ∠(Ru–C–O) vs. the bridge asymmetry parameter. In the case of the here studied Ru cluster carbonyls (see Fig. 5a), however, the consistent decrease of ∠(Ru–C–O) for α < 0.6 indicates that only bent semi-bridging ligands are present.

Fig. 5 (a) Curtis plot of the Ru–C–O angle vs. the bridge asymmetry parameter α. (b) Distribution of C–O bond lengths in cationic saturated Ru cluster carbonyls, Ru_n(CO)_m⁺ (n = 1–6), as a function of the Ru–C–O angle calculated using DFT. In both plots, the values for the calculated D₃ structure of neutral Ru₃(CO)₁₂ are given for comparison (black crosses).

Fig. 5b displays the gradual change in the CO coordination geometries for the cationic Ru cluster carbonyls by plotting the calculated C–O bond length as a function of the Ru–C–O bond angle. As discussed before in the assignments for the specific carbonyls, the presence of these ligands with different d(C–O) has been verified based on their characteristic absorptions in the ν(CO) region. Terminal CO, where the π system extending over the Ru–C–O unit stabilises a linear arrangement (∠(Ru–C–O) = 175.5–180°), has the shortest d(C–O) ranging from 112.6–113.7 pm. The closest to linear Ru–C–O units are found in Ru(CO)₅⁺, where no interaction with further metal atoms can occur. In the carbonyls of higher nuclearity, however, such interactions can provide additional π back-donation leading to a further increase of d(C–O). Accordingly, the longest C–O bonds are found for the symmetrically μ₂-bridging ligands in Ru₄(CO)₁₄⁺ and Ru₅(CO)₁₆⁺ with d(C–O) of 114.5 and 114.8 pm and ∠(Ru–C–O) of 139.7 and 141.0°, respectively. In between those are the bent semi-bridging ligands with d(C–O) ranging from 113.4 to 114.4 pm and ∠(Ru–C–O) = 172.5–156.4°.

Both plots in Fig. 5 also include the CO ligands in the predicted D₃ ground state of neutral Ru₃(CO)₁₂ (black crosses). Structurally, the (close to) equatorial CO ligands (α = 0.96) clearly fall into the class of terminal CO ligands, while the axial ones are very similar to semi-bridging ligands, in particular to the ones identified in the structure of the corresponding cation Ru₃(CO)₁₂⁺. This is illustrated also by the values of their bridge asymmetry parameter of α = 0.63, which is slightly above the cut-off of 0.6 for semi-bridging carbonyls according to Curtis et al.,⁶¹ but still in the range suggested later by Parmelee and Mankad which reaches up to α = 0.7.⁶² In the cation, three semi-bridging CO ligands have a bridge asymmetry parameter α between 0.34 and 0.51, and two more ligands fall into the range of α between 0.6 and 0.7 (see Fig. 5a). The strong structural similarities of the D₃ structure of Ru₃(CO)₁₂ and that of Ru₃(CO)₁₂⁺ can be realized from Fig. 1, despite the lower symmetry of the cation.

Conclusions

The IR spectra of saturated cationic ruthenium cluster carbonyls containing 1–6 Ru atoms have been obtained via infrared multiple photon dissociation spectroscopy and assigned by comparison with the spectra calculated using DFT for the putative global minima as obtained by a basin hopping global optimization algorithm. The metal skeletal arrangements of the assigned structures follow the predictions according to the polyhedral skeleton electron pair theory for the corresponding closed-shell neutral species. This supports the conclusions already drawn by Lang et al.³⁸ that, at least for the Ru carbonyls under study, within PSEPT counting schemes a half-filled valence orbital (in the cation) can be treated as fully occupied.

The smallest carbonyls, Ru(CO)₅⁺ and Ru₂(CO)₉⁺, only contain terminal CO ligands. The larger ones contain a variety of differently coordinated carbonyl ligands including terminal CO ligands, semi-bridging CO ligands, and symmetrically bridging CO units. The corresponding C–O stretch vibrations follow the well-known trend of ν(CO) showing the highest values for terminal CO ligands and gradually decreasing with increasing interaction of the CO ligand with additional Ru atoms. This gradual change goes along with a lengthening of the C–O bonds and a bending of the Ru–C–O units which is in-line with the effect of the Ru → CO π back-donation mechanism for classical transition metal carbonyls.

The large variety of differently coordinated CO ligands in the Ru carbonyl clusters analysed in this study allows for a more systematic structural comparison of the ligand environment in these carbonyls including also the most stable structure of neutral Ru₃(CO)₁₂. As a result, we notice a strong similarity between the predicted D₃ symmetric ground state of neutral Ru₃(CO)₁₂ and its cation in terms of the coordination geometry of the ‘axial’ CO ligands. One may speculate if the weakly semi-bridging character of these ligands is related to the dynamical properties of Ru₃(CO)₁₂.

More direct information on the binding interactions between transition metal atoms and CO ligands and the transition between terminal, semi- and symmetrically bridging configurations can be obtained by analysing the electron density distributions in related compounds, although the major focus of these studies often is on the metal–metal interaction. However, these experimental studies are typically performed via X-ray diffraction on crystalline samples, where, taking the example of neutral Ru₃(CO)₁₂, the molecular structure and dynamical behaviour may significantly differ from that of the isolated molecule due to substantial intermolecular interactions in the crystal. Similarly, the binding interactions may be further analysed theoretically, i.e. using the atoms-in-molecules approach,⁷⁸ but such analysis would go well beyond the scope of this study.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Gert von Helden for fruitful discussions and Dan J. Harding for help with implementing the modified basin hopping routine. We gratefully acknowledge support by the Deutsche Forschungsgemeinschaft (FI 893/3 and FI 893/5). D. Y. V. thanks the International Max Planck Research School "Functional Interfaces in Physics and Chemistry" for support. Open Access funding provided by the Max Planck Society is acknowledged.

References

1. J. W. Lauher, J. Am. Chem. Soc., 1978, 100, 5305–5314.
2. D. M. P. Mingos and D. J. Wales, Introduction to Cluster Chemistry, Prentice-Hall, London, 1990.
3. P. J. Dyson and J. S. McIndoe, Transition Metal Carbonyl Cluster Chemistry, Gordon and Breach Science Publishers, Amsterdam, 2000.
4. B. K. Teo, G. Longoni and F. R. K. Chung, Inorg. Chem., 1984, 23, 1257–1266.
5. K. Wade, J. Chem. Soc., Dalton Trans., 1971, 792–793.
6. M. Zhou, L. Andrews and C. W. Bauschlicher Jr., Chem. Rev., 2001, 101, 1931–1961.
7. H.-J. Himmel and O. Hübner, Mol. Catal., 2014, 25–52.
8. J. G. Bentsen and M. S. Wrighton, J. Am. Chem. Soc., 1987, 109, 4530–4544.
9. S. Fedrigo, T. L. Haslett and M. Moskovits, Chem. Phys. Lett., 1999, 307, 333–338.
10. A. M. Ricks, Z. E. Reed and M. A. Duncan, J. Mol. Spectrosc., 2011, 266, 63–74.
11. G.-J. Wang and M.-F. Zhou, Chin. J. Chem. Phys., 2018, 31, 1–11.
12. N. Sheppard and T. T. Nguyen, in Advances in Infrared and Raman Spectroscopy, ed. R. E. Hester and R. J. H. Clark, Heyden, London, 1978, vol. 5, pp. 67–148.
13. A. Fielicke, P. Gruene, G. Meijer and D. M. Rayner, Surf. Sci., 2009, 603, 1427–1433.
14. O. Schalk, I. Josefsson, R. Richter, K. C. Prince, M. Odelius and M. Mucke, J. Chem. Phys., 2015, 143, 154305.
15. C. Wang, Q. Li, X. Kong, H. Zheng, T. Wang, Y. Zhao, G. Li, H. Xie, J. Yang, G. Wu, W. Zhang, D. Dai, M. Zhou, X. Yang and L. Jiang, J. Phys. Chem. Lett., 2021, 12, 1012–1017.
16. G. Li, C. Wang, H.-J. Zheng, T.-T. Wang, H. Xie, X.-M. Yang and L. Jiang, Chin. J. Chem. Phys., 2021, 34, 51–60.
17. C. Wang, C.-Y. Tian, Y. Zhao, S. Jiang, T. Wang, H. Zheng, W. Yan, G. Li, H. Xie, J. Li, H.-S. Hu, X. Yang and L. Jiang, Angew. Chem., Int. Ed., 2023, e202305490.
18. M. Bodenbinder, G. Balzer-Jöllenbeck, H. Willner, R. J. Batchelor, F. W. B. Einstein, C. Wang and F. Aubke, Inorg. Chem., 1996, 35, 82–92.
19. Q. Xu, B. T. Heaton, C. Jacob, K. Mogi, Y. Ichihashi, Y. Souma, K. Kanamori and T. Eguchi, J. Am. Chem. Soc., 2000, 122, 6862–6870.
20. P. J. Malinowski and I. Krossing, Angew. Chem., Int. Ed., 2014, 53, 13460–13462.
21. M. Sellin, C. Friedmann, M. Mayländer, S. Richert and I. Krossing, Chem. Sci., 2022, 13, 9147–9158.
22. M. R. Harpham, A. B. Stickrath, X. Zhang, J. Huang, M. W. Mara, L. X. Chen and D.-J. Liu, J. Phys. Chem. A, 2013, 117, 9807–9813.
23. X. Dong, F. Yang, J. Zhao and J. Wang, J. Phys. Chem. B, 2018, 122, 1296–1305.
24. Q. Kong, J. H. Lee, A. Plech, M. Wulff, H. Ihee and M. H. J. Koch, Angew. Chem., Int. Ed., 2008, 47, 5550–5553.
25. E. Band and E. L. Muetterties, Chem. Rev., 1978, 78, 639–658.
26. L. J. Farrugia, J. Chem. Soc., Dalton Trans., 1997, 1783–1792.
27. S. Aime, W. Dastru, R. Gobetto, J. Krause and L. Milone, Organometallics, 1995, 14, 4435–4438.
28. Q. Y. Kong, M. G. Laursen, K. Haldrup, K. S. Kjær, D. Khakhulin, E. Biasin, T. B. van Driel, M. Wulff, V. Kabanova, R. Vuilleumier, S. Bratos, M. M. Nielsen, K. J. Gaffney, T. C. Weng and M. H. J. Koch, Photochem. Photobiol. Sci., 2019, 18, 319–327.
29. F. W. Vergeer, F. Hartl, P. Matousek, D. J. Stufkens and M. Towrie, Chem. Commun., 2002, 1220–1221.
30. X. Feng, J. Gu, Y. Xie, R. B. King and H. F. Schaefer, J. Chem. Theory Comput., 2007, 3, 1580–1587.
31. B. Peng, Q.-S. Li, Y. Xie, R. B. King and H. F. Schaefer III, Dalton Trans., 2008, 6977–6986.
32. D. T. Moore, J. Oomens, J. R. Eyler, G. Meijer, G. von Helden and D. P. Ridge, J. Am. Chem. Soc., 2004, 126, 14726–14727.
33. A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Am. Chem. Soc., 2005, 127, 8416–8423.
34. I. Swart, F. M. F. de Groot, B. M. Weckhuysen, D. M. Rayner, G. Meijer and A. Fielicke, J. Am. Chem. Soc., 2008, 130, 2126–2127.
35. P. Fayet, M. J. McGlinchey and L. H. Wöste, J. Am. Chem. Soc., 1987, 109, 1733–1738.
36. D. M. P. Mingos, T. Slee and L. Zhenyang, Chem. Rev., 1990, 90, 383–402.
37. D. M. P. Mingos and D. J. Wales, J. Am. Chem. Soc., 1990, 112, 930–932.
38. S. M. Lang, S. U. Fortig, T. M. Bernhardt, M. Krstic and V. Bonacic-Koutecky, J. Phys. Chem. A, 2014, 118, 8356–8359.
39. D. Yubero Valdivielso, PhD thesis, Technische Universität Berlin, 2022.
40. W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. Bluem and A. M. Todd, in Proc. SPIE 9512, Advances in X-ray Free-Electron Lasers Instrumentation III, SPIE, 2015, p. 95121L.
41. A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Phys. Chem. B, 2004, 108, 14591–14598.
42. A. Fielicke, G. von Helden and G. Meijer, Eur. Phys. J. D, 2005, 34, 83–88.
43. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
44. D. J. Harding, C. Kerpal, G. Meijer and A. Fielicke, J. Phys. Chem. Lett., 2013, 4, 892–896.
45. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
46. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
47. D. Andrae, U. Haeusermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141.
48. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
49. P. Rushman, G. N. Van Buuren, M. Shiralian and R. K. Pomeroy, Organometallics, 1983, 2, 693–694.
50. J. R. Moss and W. A. G. Graham, J. Chem. Soc., Dalton Trans., 1977, 95–99.
51. F.-W. Grevels, W. E. Klotzbuecher, J. Schrickel and K. Schaffner, J. Am. Chem. Soc., 1994, 116, 6229–6237.
52. S. Pan, L. Zhao, H. V. R. Dias and G. Frenking, Inorg. Chem., 2018, 57, 7780–7791.
53. T. Bennett, R. H. Adnan, J. F. Alvino, V. Golovko, G. G. Andersson and G. F. Metha, Inorg. Chem., 2014, 53, 4340–4349.
54. R. White, T. Bennett, V. Golovko, G. G. Andersson and G. F. Metha, ChemistrySelect, 2016, 1, 1163–1167.
55. M. R. Churchill, F. J. Hollander and J. P. Hutchinson, Inorg. Chem., 1977, 16, 2655–2659.
56. L. L. Wang and D. D. Johnson, J. Phys. Chem. B, 2005, 109, 23113–23117.
57. J. Kim and J. Kim, Chem. Phys. Lett., 2014, 592, 24–29.
58. E. Waldt, A.-S. Hehn, R. Ahlrichs, M. M. Kappes and D. Schooss, J. Chem. Phys., 2015, 142, 024319.
59. C. Kerpal, D. J. Harding, D. M. Rayner, J. T. Lyon and A. Fielicke, J. Phys. Chem. C, 2015, 119, 10869–10875.
60. R. J. Klingler, W. M. Butler and M. D. Curtis, J. Am. Chem. Soc., 1978, 100, 5034–5039.
61. M. D. Curtis, K. R. Han and W. M. Butler, Inorg. Chem., 1980, 19, 2096–2101.
62. S. R. Parmelee and N. P. Mankad, Dalton Trans., 2015, 44, 17007–17014.
63. S. C. Richtsmeier, E. K. Parks, K. Liu, L. G. Pobo and S. J. Riley, J. Chem. Phys., 1985, 82, 3659–3665.
64. J. Woenckhaus and J. A. Becker, Rev. Sci. Instrum., 1994, 65, 2019–2022.
65. A. Fielicke and K. Rademann, J. Phys. Chem. A, 2000, 104, 6979–6982.
66. D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311–319.
67. B. Peng, F. Gu, X. Zhang, Q. Luo and Q. Li, Sci. China, Ser. B: Chem., 2009, 52, 1938–1944.
68. H. M. Wang, Y. F. Liu, H. Haouari, R. Craig, J. R. Lombardi and D. M. Lindsay, J. Chem. Phys., 1997, 106, 6534–6537.
69. A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Chem. Phys., 2006, 124, 194305.
70. E. Bernhardt, C. Bach, B. Bley, R. Wartchow, U. Westphal, I. H. T. Sham, B. von Ahsen, C. Wang, H. Willner, R. C. Thompson and F. Aubke, Inorg. Chem., 2005, 44, 4189–4205.
71. F. A. Cotton, in Prog. Inorg. Chem., 1976, pp. 1–28.
72. Q. Kong, J. H. Lee, K. H. Kim, J. Kim, M. Wulff, H. Ihee and M. H. J. Koch, J. Am. Chem. Soc., 2010, 132, 2600–2607.
73. P. F. Jackson, B. F. G. Johnson, J. Lewis, M. McPartlin and W. J. H. Nelson, J. Chem. Soc., Chem. Commun., 1979, 735–736.
74. R. H. Crabtree and M. Lavin, Inorg. Chem., 1986, 25, 805–812.
75. P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238, 383–412.
76. S. Ding and M. B. Hall, in The Chemical Bond I: 100 Years Old and Getting Stronger, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2016, pp. 199–248.
77. B. J. Morris-Sherwood, C. B. Powell and M. B. Hall, J. Am. Chem. Soc., 1984, 106, 5079–5083.
78. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.

---

Footnotes

† Electronic supplementary information (ESI) available: Comparison of calculated and experimental IR spectra for neutral Ru₃(CO)₁₂. Experimental and calculated bond lengths in Ru₃(CO)₁₂. Cartesian atomic coordinates for the optimized structures, vibrational frequencies and IR intensities. See DOI: https://doi.org/10.1039/d3dt01129a

‡ Present address: Department of Physics and Astronomy, University of North Carolina at Asheville, One University Heights, Asheville, NC 28804, USA.

---