Correlation between the structural features and intrinsic activity trend of Fe surfaces for ammonia synthesis

Abstract

The Haber–Bosch process, which was developed more than a century ago, remains the primary method for nitrogen fixation on a large scale and Fe is typically the main catalyst used in the process. Despite having been extensively studied, some anomalies regarding the activity trend across various Fe surfaces still exist. To understand the intrinsic activity trend of Fe catalysts, we utilize density functional theory (DFT) to calculate the reaction energetics on various Fe surfaces in conjunction with microkinetic analyses to examine the activity of the Fe surfaces. The catalytic activity order obtained is Fe(111) > Fe(211) > Fe(210) > Fe(100) > Fe(110). We find that the activity trend is correlated to the barrier of the rate-determining step, N₂ dissociative adsorption barrier, and perhaps more importantly to the surface energies. It is also noted that the association barriers of flat surfaces are generally larger than those of stepped surfaces, for which a clear explanation is provided.

---

1. Introduction

Ammonia (NH₃) is indispensable to the global economy in both industrial and agricultural production,¹ as well as being considered as an energy carrier^2–5 to play a potential role in the storage/conversion of renewable energy. The significance of ammonia motivates extensive studies in innovating and optimizing ammonia synthesis, involving thermocatalysis, electrocatalysis, photocatalysis, biocatalysis and plasma-catalytic synthesis.^6–11 Nevertheless, the primary industrial approach to fix nitrogen to produce NH₃ is still the Haber–Bosch process (HBP), even though it is energy and capital-intensive (350–550 °C, 150–350 atm)^12,13 due to the stability of N≡N,¹⁴ consuming 2% of the total energy supply in the world and releasing more than 400 Mt of CO₂, which accounts for 3% of total global CO₂ emissions.¹⁵

Although ammonia synthesis has been industrialized for more than 100 years, designing good catalysts to moderate the reaction conditions is the eternal pursuit of researchers.^16–21 There are mainly three types of catalysts that activate nitrogen molecules: (i) homogeneous catalysts;^22,23 (ii) natural biocatalysts;^24,25 and (iii) heterogeneous catalysts.^26–30 All the existing research findings suggest that the most energy-intensive step in ammonia synthesis is either the activation of N₂ or the hydrogenation of the surface intermediate species NH_x to ammonia.²⁷ It can be inferred that an ideal catalyst for ammonia synthesis should possess both a low N₂ activation energy and a low NH_x hydrogenation barrier, which are difficult to realize simultaneously due to the scaling relationship on the transition metal (TM) surface. In any case, the active sites for these steps play significant and crucial roles in catalysis. Gaining an understanding of these active sites is probably one of the most essential problems in ammonia synthesis.

Somorjai and co-workers³¹ showed clearly that ammonia synthesis was a structure-sensitive reaction by using various single crystal surfaces of Fe and reckoned that C₇ sites were the active sites that exist only on Fe(111) and Fe(211), exhibiting reaction activity: Fe(111) > Fe(211) > Fe(100) > Fe(210) > Fe(110). Meanwhile, it is difficult to measure microscopic reaction pathways experimentally. Theoretically, the ammonia synthesis mechanism and kinetics on the Fe(111) and reconstructed Fe(211) surfaces were studied by Qian et al. and Fuller et al., respectively.^32,33 At variance with common thinking, Fuller et al. suggested that the reconstructed Fe(211) surface is the active phase under the HBP conditions.³³ To further explore the active site of the Fe catalyst, Zhang et al.³⁴ investigated the intrinsic rate of the nitrogen reduction reaction (NNR) on each surface site exposed over bcc Fe particles, addressing the effects of intrinsic activity, the density of active sites and the particle size. Theoretical results showed that the activity of Fe surfaces varied, being consistent with the experiment³¹ except Fe(100).³⁴ It is clear that these Fe surfaces deserve further investigations.

Fundamentally, the active site is generally an important concept in heterogeneous catalysis, which should lay a foundation for understanding any catalytic system. Liu and Hu³⁵ studied some typical reactions occurring on flat, stepped, and kinked metal surfaces, obtaining several rules to predict where the reaction should occur. It would be interesting to apply similar approaches to systematically study the active sites of Fe catalysts for ammonia synthesis (Fig. 1).

Fig. 1 Nitrogen reduction reaction activity. (a) Activity of single Fe crystal surfaces from the experimental work of Somorjai and co-workers.³¹ Adapted with permission from ref. 31 copyright (1994) Topics in Catalysis. (b) Calculated reaction rates from the theoretical work of Li and co-workers.³⁴ Adapted with permission from ref. 34 copyright (2019) ChemCatChem. Both figures are redrawn here according to the original figures. To a large extent, both trends are similar with some differences.

Thus far, there has been a lack of a correlation between the surface structure of Fe catalysts and activity of ammonia synthesis, and some puzzles regarding the different activity on various Fe surfaces have not been rationalized. In particular, the following questions remain unanswered: (i) Fe(210) and Fe(211) are structurally similar. However, why does the large difference exist in activity? (ii) Experimentally, Fe(100) was found to be more active than Fe(210) even though Fe(100) is the most inactive surface from theoretical calculations.^31,34 How can one rationalise these results? (iii) What are the controlling factors that influence the activity trend of Fe catalysts for ammonia synthesis?

To answer these questions, in this work we carried out a detailed density functional theory (DFT) study of ammonia synthesis on various Fe surfaces and developed a kinetic model to determine the activity trend across them. We found that the order of activity is Fe(111) > Fe(211) > Fe(210) > Fe(100) > Fe(110), which is linearly correlated with the surface energy and N₂ dissociative adsorption barrier. Furthermore, we examined the electronic and geometric effects and discussed our findings.

2. Computational methods

2.1 Surface model

A p(3 × 3) supercell was constructed to calculate the elementary reactions of ammonia synthesis on various Fe surfaces. The layer number varies; there are 6 layers for Fe(100), 5 layers for Fe(110), and 4 layers for Fe(111), Fe(210) and Fe(211), respectively. When optimizing the structure for each elementary reaction, the top 2–3 layers with the surface species were fully relaxed while the rest of the bottom layers of the surface model were fixed (see Fig. S1 in the ESI†). The thickness of the vacuum layer in the Z direction was set as 15 Å. The parameter k-point grid involved in the calculation could be determined according to the lattice parameters through the Monkhorst–Pack scheme,³⁶ typically 2 × 2 × 1 k-point meshes in this case, and has been confirmed by k-point sampling tests (see Fig. S2 in the ESI†).

2.2 Computational details

In this work, all the calculations were performed with spin-polarized density functional theory with the Vienna ab initio simulation package (VASP),³⁷ using the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).³⁸ The core–valence electron interaction was described by the project-augmented wave (PAW) method,³⁹ and the valence electronic states were expanded in the plane wave basis sets with an energy cutoff of 450 eV. The constraint optimization method^40,41 is adopted to search the transition state (TS) and the force convergence standard during structural optimization which is set at 0.05 eV Å⁻¹. All the transition states were checked by vibrational frequency analysis.

2.3 Microkinetic modelling with/without coverage effects

According to the current consensus,¹⁸ the reaction mechanism of N₂ and H₂ converting to ammonia on the surface of the Fe-based catalyst consists of the following elementary steps listed in Table 1 (* represents the free site). r_i is the rate of reaction for reaction step i (i = 1, 2…, 7). k_i and k_−i are the forward rate constant and reverse rate constant, respectively. The microkinetic modelling and analyses were performed using CATKINAS.^42–44 While there are still some challenges associated with microkinetics, such as the incompatibility of non-random distribution models,⁴⁵ our group has developed a novel method that integrates surface coverage effects with microkinetics, which offers a valuable means to achieve the consistency between theory and experimental results.⁴⁶

Table 1 Elementary steps and the rate equations of ammonia synthesis used in the microkinetic modelling (* represents the free site on the surface). Details of the microkinetic software can be found in ref. 41–43

	Surface reactions	Rate equations
1	H2(g) + 2* ↔ 2H*
2
3		r 3 = k3θN2θ* − k−3θ^2N
4	N* + H* ↔ NH* + *	r 4 = k4θNθH − k−4θNHθ*
5		r 5 = k5θNHθH − k−5θNH2θ*
6		r 6 = k6θNH2θH − k−6θNH3θ*
7		r 7 = k7θNH3 − k−7PNH3θ*

---

With coverage effects. The two-line model was used to quantify the dominance of the coverage effects over chemisorption energies and reaction barriers.^46–49 The entire coverage is determined by the sum of all the adsorbate coverages. The two-line model describes mainly how the energy of chemisorption varies at low and high coverages:where θ, θ_j, i and j represent the total coverage, the coverage of species j, the target adsorbate i, and environmental species j, respectively. a and b are the slope and intercept of the two-line model. θ_c is the critical point separating the low coverage from the high coverage.

The definition of the differential chemisorption energy of all species under various coverage conditions is:

where E_ads,N and E_env,N−1 are the total energy after adsorption of N adsorbates and the N − 1 environmental species, respectively, and E_gas is the energy of the adsorbate in the gas phase.

The definition of the N₂ dissociative adsorption barrier under various coverage conditions is:

E^dis_a(θ_N) = E_TS,N − E_env,N−2 − E_N2 (3)

The turnover frequency (TOF) was calculated using a self-consistent microkinetic model shown in the scheme in Fig. S17 in the ESI† which was performed under experimental conditions with a temperature of 673 K and pressure of 20 bar.³¹ The converged TOF and coverages for different species at the steady-state were achieved when the convergence of coverages reaches a sufficiently low level.

Without coverage effects. On Fe(111) and Fe(110), the adsorption energies with a coverage of 0.04 ML were used in the coverage-independent model, whereas a coverage of 0.17 ML was employed for the dissociative adsorption barrier. They are 0.03 ML and 0.13 ML for Fe(100) and Fe(211), and 0.06 ML and 0.25 ML for Fe(210), repectively.

3. Results and discussion

3.1 Structures and energies of reaction intermediates

In order to obtain a comprehensive understanding of activity on various Fe surfaces, in this section we focus on the structures and energies of the reaction intermediates. Firstly, the surface energy⁵⁰ as an important property of the catalyst surface, which is difficult to quantify experimentally, was calculated in this work. The surface energy is defined as follows:where E is the total energy; E_bulk is the bulk energy; n is the multiple of the number of surface atoms to the number of atoms in the bulk phase; S is the surface area. The α-Fe bulk phase energy was calculated to be −8.31 eV.

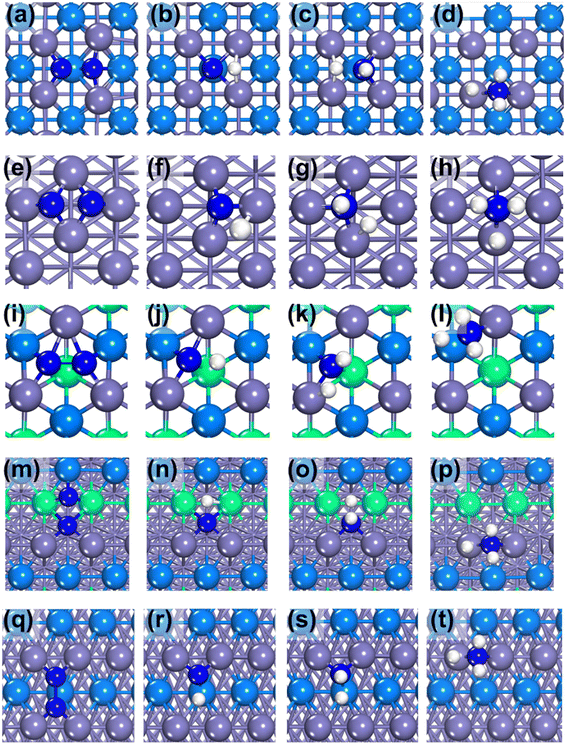
Our calculation results display that the surface energy order is Fe(111) > Fe(211) > Fe(210) > Fe(100) > Fe(110) (see Table 2), which is consistent with the trend of the literature value.¹⁶ The most active surface of Fe, i.e., Fe(111), has the highest surface energy, 0.166 eV, which is similar to the literature value (only 0.004 eV lower).¹⁸ Not surprisingly, Fe(110) as the most inactive surface has the lowest surface energy. The structure of each Fe surface is shown in Fig. 2. As can be seen, both Fe(100) and Fe(110) are flat surfaces, while Fe(111), Fe(210) and Fe(211) possess stepped surface features.

Table 2 Surface energies of various Fe surfaces calculated versus the values in the literature. It can be seen that the agreement is good

Fe surface	γ (eV Å^−2)	The literature value^16
Fe(100)	0.155	0.156
Fe(110)	0.151	0.153
Fe(111)	0.166	0.170
Fe(210)	0.156	—
Fe(211)	0.160	0.163

---

Fig. 2 Top (a–e) and side (f–j) views of the optimized surface structures of Fe(100), Fe(110), Fe(111), Fe(210) and Fe(211). The Fe atoms on the top layer are grey; the second Fe atoms are blue, and the next layer is green. Grey, blue and green balls indicate the top layer, the second layer and the third layer of Fe, respectively.

Then the N₂ adsorption was calculated. In this work, three adsorption sites of N₂ were considered: top, bridge and hollow sites. After optimizations, the N₂ bond length is found to be elongated from 1.115 Å to 1.277 Å, when adsorbing on the hollow site of Fe(110). It is observed that the longer the N–N bond length on the surface, the stronger the adsorption of N₂. For N, the adsorption energies on the top, bridge and hollow sites are −0.74 eV, −0.54 eV and −0.85 eV, respectively. Because the adsorption energy on the hollow site (Fig. 3(c)) is the strongest, the hollow adsorption state was selected to be calculated for the N₂ dissociation (Table 3).

Fig. 3 Optimized structures of N₂ adsorption on Fe(110). Dark blue represents the N atom. (a) Top site, (b) bridge site, and (c) hollow site. The distances between N atoms are illustrated in the figure.

Table 3 Reaction barrier (E_a) and enthalpy change (ΔH) of each elementary step in ammonia synthesis on the Fe surfaces

Fe surface	H2 + 2* ⇌ 2H*						N* + H* ⇌ NH* + *
	E a	ΔH	E a	ΔH	E a	ΔH	E a	ΔH	E a	ΔH	E a	ΔH	E a	ΔH
Fe(100)		−0.80		−0.95	1.15	−2.15	1.25	0.36	1.25	0.28	1.31	0.34		0.88
Fe(110)		−1.37		−1.02	1.34	−1.72	1.51	0.23	1.32	0.96	1.50	0.47		0.89
Fe(111)		−0.86		−0.77	0.35	−1.43	0.96	0.40	0.90	−0.03	1.04	0.09		1.05
Fe(210)		−1.35		−0.91	0.81	−1.90	1.23	0.72	1.19	0.15	1.61	0.63		1.04
Fe(211)		−1.15		−1.08	0.69	−1.22	1.20	0.47	0.88	−0.21	1.37	0.71		1.02

---

Hydrogenation reactions from N to NH, NH₂ and NH₃ were also calculated. By a comparison of each elementary reaction among various Fe surfaces, it is found that almost all the reaction barriers follow the order: Fe(111) < Fe(211) < Fe(210) < Fe(100) < Fe(110), except the step of . Surprisingly, in the last step of the hydrogenation process the activity order changes markedly, following this order: Fe(111) < Fe(100) < Fe(211) < Fe(110) < Fe(210). As shown in Fig. 4, the bond length of nitrogen initially starts at 1.115 Å, which is lengthened after adsorption, leading to easier N₂ dissociation. For the more reactive Fe(111) and Fe(211) surfaces, the N–N bond length is longer than 1.3 Å while for the less reactive Fe(100), Fe(110) and Fe(210) surfaces, the N–N bond length is less than 1.3 Å.

Fig. 4 Optimized structures of N₂ adsorption on (a) Fe(100), (b) Fe(110), (c) Fe(111), (d) Fe(210), and (e) Fe(211). The distances between N atoms are illustrated in the figure.

It can be seen from Fig. 5 that Fe(111) with the highest catalytic activity has a relatively uniform arrangement of C₇. The transition state structures of the last hydrogenation step are similar except that on Fe(111), on the which nitrogen atom is only coordinated with one Fe atom, lowering the hydrogenation reaction barrier. It is worth noting that the longer the bond between the Fe atom and N atom, the easier it is for the Fe–N bond to break. Based on this observation, we can explain why the reaction barrier order is Fe(111) < Fe(100) < Fe(211) < Fe(110) < Fe(210) using the Fe–N bond length.

Fig. 5 Structures of the nitrogen dissociation transition states and step-wise hydrogenation on each Fe surface. (a–d) The structures on Fe(100), (e–h) on Fe(110), (i–l) on Fe(111), (m–p) on Fe(210), and (q–t) on Fe(211). White balls represent the H atoms.

3.2 Kinetic analyses without coverage effects

Based on the DFT calculated energy barriers above, we carried out microkinetic simulations for ammonia synthesis in a wide range of conditions (273–873 K, 10⁻²–10³ bar, N₂ : H₂ : NH₃ = 1 : 3 : 0.01), which is similar to the work of Nørskov and co-workers.¹⁸ Using the DFT energetics at low coverages (0.04 ML) from Fe(111), we created a 2D activity heatmap depicting the TOF as a function of temperature and pressure from the microkinetic modelling, considering that the two variables can be varied independently of each other. This trend is similar on each surface; as the temperature and pressure increase, the activity is increased (Fig. 6).

Fig. 6 2D activity (lg(TOF)) heatmap of Fe(111) calculated at 273–873 K, 10⁻²–10³ bar, N₂ : H₂ : NH₃ = 1 : 3 : 0.01. The line illustrates the boundary between the NH₃ formation and NH₃ decomposition.

To compare the relative activity of various Fe surfaces, the typical ammonia synthesis conditions (673 K, 100 bar) were chosen as an example. Under these conditions, the activity order of ammonia synthesis reaction from our simulations is

Fe(111) > Fe(211) > Fe(210) > Fe(100) > Fe(110),

while the order from the experiment work³¹ is

Fe(111) > Fe(211) > Fe(100) > Fe(210) > Fe(110).

It can be seen that they are the same except the relative positions of Fe(210) vs. Fe(100): the experimental work showed that Fe(100) is more active than Fe(210) while our simulations demonstrate that this is not the case. How can we understand the discrepancy between the experimental work³¹ and our calculations for Fe(210) and Fe(100)? At first glance, our result appears to be more reasonable: Fe(210) is a stepped-like surface while Fe(100) is a flat surface; it is expected that the stepped surface is more active than the flat surface. More analyses can confirm this (see below).

In order to understand the activity trend, we studied the rate-determining step of each Fe surface, finding that regardless of the Fe surface, R3 (dissociation of ) is always the rate-determining step under the typical conditions (673 K, 100 bar). However, for the most active Fe(111) surface, the situation changes in the range of 600–700 K at 100 bar, which is shown in Fig. 7: R2 (adsorption of N₂) begins to dominate the overall reaction, while R5 (hydrogenation of NH*) and R6 (hydrogenation of ) also play some considerable roles. This is reasonable; on active catalysts the rate-determining step is typically accelerated to prevent any single step from becoming too dominant.

Fig. 7 Degree of rate control from microkinetic simulations on Fe(111) under the condition of 100 bar. Reactions R2, R3, R5 and R6 are listed in Table 1.

As shown in Fig. 8(a) and (b), for the less reactive surfaces Fe(100), Fe(110) and Fe(210), dissociation (R3) maintains the role of being the rate-determining step. However, for Fe(111) and Fe(211), only in a narrower temperature range, the rate-determining step is the dissociation. Fig. 8(c) shows that the adsorption of N₂ and the N₂ dissociation cancel each other largely on the reaction control degree. The result that the rate-determining step is the N₂ dissociation is consistent with the fact that the overall activity order is similar to that of the N₂ dissociation (Fig. 8(d)).

Fig. 8 Degree of rate control as a function of temperature under industrial reaction conditions (P = 100 bar); (a) N₂ adsorption (R2); (b) dissociation (R3); (c) N₂ dissociative adsorption (R2 + R3). (d) TOF against temperature.

The relationship between the N₂ dissociation barrier and TOF value of each surface is shown in Fig. 9(a). Comparing the calculated results and the experimental ones or other relevant theoretical calculations, interestingly, several differences can be found. Firstly, the activity on Fe(210) surpasses that on Fe(100), which disagrees with experiment work, as mentioned before,³¹ but it is consistent with the work of Li and co-workers.³⁴ Secondly, the result that Fe(100) substitutes Fe(110) as the least activity surface³⁴ is contrary to our results and also experimental one.

Fig. 9 Coverage-independent kinetic modelling. (a) Relationship between lg(TOF) and the N₂ dissociative adsorption barrier. (b) Relationship between lg(TOF) and the surface energy.

To further understand the impact of the rate-determining step, we plot the relationship between lg(TOF) and the N₂ dissociative adsorption barrier, as illustrated in Fig. 9(a). This shows that the lg(TOF) value declines when the N₂ dissociative adsorption barrier increases, as expected. Moreover, Fig. 9(a) displays that these surfaces can be divided into two types, stepped surfaces and flat surfaces, showing clearly that the stepped surfaces are more active than the flat surfaces. It is worth mentioning that the actual activity value of Fe(211), considering the Fe(211) reconstruction, may be different.³³ More interestingly, the surface energy can also be linked with the lg(TOF), as shown in Fig. 9(b): as the surface energy rises, the lg(TOF) value increases, which is linearly correlated. Notably, the relationship between the surface energy and reaction barrier has been implicitly discussed,⁵¹ supporting our results. It is worth emphasizing that the surface energy is a simple property of any surface and the observed correlation between activity and surface energy is a valuable finding for future catalyst design, particularly for catalysts having strong interactions with reactants.

3.3 The microkinetic modelling with coverage effects

To carry out a more quantitative comparison with the experimental values, we performed microkinetic simulations on the most active Fe(111) surface at 673 K and 20 bar (N₂ : H₂ : NH₃ = 1 : 3 : 0.01, an experimental condition³¹), by taking the coverage effects into account. All the interactions of reaction intermediates (H*, N*, NH*, and 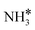), including self-interactions and cross-interactions of these surface species, were considered in the coverage-dependent kinetic simulations. In order to achieve good accuracy, we carefully calculated many structures of surface species co-adsorption at each coverage, and the most stable energy at the specific coverage was used in the kinetic modelling (see Fig. S5–S9 in the ESI†). To ensure feasibility in our calculations, we only considered the coverage effects of all the species on the N₂ dissociative adsorption barrier, which is the rate-determining step.

For the coverage effects on adsorption states, both self and cross adsorbate–adsorbate interactions of all reaction intermediates are studied (see sections S3 and S5 in the ESI†). Furthermore, the transition state energies, another critical factor, were explicitly calculated considering the coverage effects, which were found to be divided into two distinct categories (see Fig. S16 in the ESI†). Specifically, the N₂ dissociative adsorption barriers are hardly influenced by the coverage and remain nearly constant at low coverages. However, at high coverages, these barriers show an increasing trend as the total coverage is increased. Therefore, the N₂ dissociative adsorption barriers can be described by a two-line model as a function of the total coverage. All the slopes and intercepts of the interaction between the transition state and environmental species are listed in Table S3 in the ESI.†

By using the self- and cross-interactions to correct the adsorption energies and N₂ dissociative adsorption barrier, the coverage distribution on Fe(111) at the steady-state is obtained: 0.99 ML, containing 0.51 ML of N, 0.39 ML of NH₂, 0.05 ML of H and 0.04 ML of others (NH and NH₃) (Fig. 10). The TOF calculated by the coverage-dependent model is 3.6 s⁻¹ per site, in excellent agreement with the experimental result of TOF = 11.1 s⁻¹ per site.

Fig. 10 Surface coverages at the steady state for the NNR on Fe(111) using the coverage-dependent methods at 673 K and 20 bar (N₂ : H₂ : NH₃ = 1 : 3 : 0.01, an experimental condition); others including NH, NH₃ and the free site.

To simplify the calculations, we applied the coverage effects of Fe(111) to other Fe surfaces. The new activity, cosidering the coverage effects, was compared with the original activity at low coverages, as shown in Fig. 11, which indicates that the new activity trend with the coverage effects is consistent with the original coverage-independent results. We also replotted the relationships between lg(TOF) from the microkinetic modelling with the coverage effects and N₂ dissociative adsorption barrier/surface energy. As can be seen in Fig. S18 in the ESI,† linear correlations are apparent, which is similar to the results from the coverage-independent modelling (Fig. 9).

Fig. 11 Activity trend of various Fe surfaces with the coverage effects and the one from the low coverages.

3.4 Energy decomposition

Fe(111), Fe(211) and Fe(210) are all stepped surfaces that exhibit good activity. However, there are differences in their activity levels. To further understand the activity differences of these surfaces, we performed detailed analyses on the reaction energies: the energy barrier decompositions on Fe(111), Fe(211) and Fe(210) were carried out. For the N₂ dissociation reaction, starting from an N₂ molecule in the gas phase to the adsorbed N_A and N_B atoms on the surface N₂(g) → , we decomposed the energies of adsorbed atoms at the transition state (E^TS) and the final state (E^FS) as eqn (5)–(7), where E^TS_A and E^TS_B are the adsorption energies of individual species N_A and N_B at the transition state. The adsorption energies of adsorbed species N/N₂ are defined by referring to the clean surface and gaseous N₂, and E^TS_int is the repulsion energy between N_A and N_B at the transition state, which is a quantitative measure of the geometrical effect on the surfaces. Similarly, E^FS_A, E^FS_B and E^FS_int represent the corresponding energies at the final state. Hence, the barrier of N₂ dissociation (E^dis_a) and association process (E^as_a) can be expressed as:³⁵

E^dis_a = E^TS = E^TS_A + E^TS_B + E^TS_int (5)

E^FS = E^FS_A + E^FS_B + E^FS_int (6)

E^as_a = E^TS − E^FS = (E^TS_A + E^TS_B) − (E^FS_A + E^FS_B) + E^TS_int − E^FS_int (7)

where E^FS_int, under the reaction conditions we studied (low coverages), is normally very small.

The individual energy components of N₂ dissociation on the Fe stepped surfaces are listed in Table 4, and the FS chemisorption energies are also listed for comparison. Since the E^TS_A and E^TS_B mostly depend on their bonding ability to the Fe surface, which is determined by the electronic properties of the local metal, it can be suggested that E^TS_A and E^TS_B are correlated to their FS counterparts.

Table 4 Energy decompositions for the rate-determining step (N₂ + * ⇌ 2N*) on stepped surfaces (SE stands for the sum of E_A and E_B)

N2 + * ⇌ 2N*		E A (eV)	E B (eV)	SE (eV)	E int (eV)	E ^disa (eV)	E ^asa (eV)
Fe(111)	TS	−0.76	−0.76	−1.52	1.10	−0.42
	FS	−0.82	−0.83	−1.65	0.03		1.20
Fe(211)	TS	−0.61	−0.60	−1.21	0.82	−0.39
	FS	−0.91	−0.88	−1.79	−0.25		1.65
Fe(210)	TS	−0.66	−1.03	−1.68	1.58	−0.10
	FS	−0.94	−1.36	−2.31	−0.13		2.34

---

By comparing these terms, the following features can be identified:

i. For N₂ dissociation on Fe(111), it not only exhibits a high electron effect (−1.52 eV), but also a low geometrical effect (1.10 eV), resulting in the highest activity.

ii. Fe(210) has the highest electron effect (−1.68 eV) but shows the lowest activity among the stepped surfaces due to its relatively large geometrical effect (1.58 eV), as shown in Fig. 5(m–p). Its surface structure is a combination of Fe(100) and Fe(110), which leads to a strong geometrical effect.

iii. While the electron effect of N₂ dissociation on Fe(211) may not be as strong as the former two, the weak geometrical effect of Fe(211) (0.82 eV) results in a lower dissociative barrier compared to Fe(210).

We also did the following analyses on the observation that the association barriers of flat surfaces are larger than those of stepped surfaces (the average values of E^as_a are 1.73 eV and 3.02 eV for stepped surfaces and flat surfaces, respectively): according to the definitions of the dissociative (E^dis_a) and associative energy barriers (E^as_a), the relationship is:

E^as_a = E^dis_a − ΔH (8)

while the BEP relationship for the dissociation barrier is

E^dis_a = αΔH + β (9)

where α is closed to 1.^52–54 Combining these two equations, we can deduce:

E^as_a = E^dis_a − ΔH = (α − 1)ΔH + β ≈ β (10)

In general, the values of β for flat surfaces are larger than those of stepped surfaces, which explains the observation mentioned above. Nørskov and co-workers⁵⁵ studied the BEP relationship between the transition state energy and the dissociative chemisorption energy of nitrogen on the (211) surface of pure transition metals all having the fcc crystal structure, concluding that the best fit for β is 1.61 eV, which is close to our result, 1.65 eV.

4. Conclusion

In summary, nitrogen reduction reactions on various Fe surfaces have been systematically studied by DFT calculations together with microkinetic simulations, aiming at figuring out the correct activity trend of these surfaces and solving the existing puzzle in the literature. The main findings are as follows:

i. The activity order of various Fe surfaces was determined to be Fe(111) > Fe(211) > Fe(210) > Fe(100) > Fe(110). It is worth mentioning that this study primarily focuses on the intrinsic activity trends of Fe catatlysts. Surface reconstruction, although it may occur in real experiments, has not been considered in this work.

ii. The above activity order was found to be related to the rate-determining step barrier, which is the N₂ dissociative adsorption barrier, as expected. However, the finding that there is a good linear correlation between the activity order and the surface energy is slightly surprising but understandable. Hence, the surface energy of a catalyst may serve as a good indicator of activity of the catalysts especially when the rate-determining step is the dissociation of the reactants and might be of general importance in heterogeneous catalysis.

iii. For a more quantitative comparison with the experimental values, a coverage-dependent microkinetic modeling for the NNR on Fe(111) using DFT energetics was carried out under the experimental conditions (673 K, 20 bar, N₂ : H₂ : NH₃ = 1 : 3 : 0.01), from which the calculated TOF is 3.6 s⁻¹ per site, in good agreement with the experimental results (11.1 s⁻¹ per site). Furthermore, we applied the surface coverage effects on Fe(111) to other Fe surfaces as an approximation. The activity trend of various Fe surfaces considering the coverage effects we obtained remains the same as the coverage-independent model.

iv. The N₂ dissociative adsorption barriers were decomposed into electronic and geometrical effects to illustrate the differences in activity. Fe(111) exhibits the highest activity due to its strong electron effect and weak geometrical effect. In contrast, Fe(210) has the strongest electron effect but shows the lowest activity among the stepped surfaces due to its relatively large geometrical effect.

v. The association barriers of flat surfaces are larger than those of stepped surfaces. We deduced that E^as_a is approximately equal to β by combining the definition of the association barriers and the BEP relationship for the dissociation barrier, which can provide an understanding of the result: the β values from the flat surfaces are larger than those of stepped surfaces.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

NSFC (92045303, 21703067, 22202069, 21873028) and NKRDPC (2021YFA1500700) are acknowledged.

References

1. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
2. A. Valera-Medina, H. Xiao, M. Owen-Jones, W. I. F. David and P. J. Bowen, Prog. Energy Combust. Sci., 2018, 69, 63–102.
3. A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18(20), 2285–2392.
4. C. Zamfirescu and I. Dincer, Fuel Process. Technol., 2009, 90, 729–737.
5. C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111, 140–144.
6. N. J. Weise, F. Parmeggiani, S. T. Ahmed and N. J. Turner, J. Am. Chem. Soc., 2015, 137, 12977–12983.
7. Q. Wang, J. Guo and P. Chen, J. Energy Chem., 2019, 36, 25–36.
8. J. Shah, J. Harrison and M. Carreon, Catalysts, 2018, 8, 437.
9. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Norskov, ChemSusChem, 2015, 8, 2180–2186.
10. R. Hawtof, S. Ghosh, E. Guarr, C. Xu, R. M. Sankaran and J. N. Renner, Sci. Adv., 2019, 5, eaat5778.
11. X. Chen, N. Li, Z. Kong, W.-J. Ong and X. Zhao, Mater. Horiz., 2018, 5, 9–27.
12. S. Klinsrisuk, S. Tao and J. T. S. Irvine, in Membrane Reactors for Energy Applications and Basic Chemical Production, 2015, pp. 543–563,  DOI:10.1016/b978-1-78242-223-5.00018-2.
13. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500.
14. H. P. Jia and E. A. Quadrelli, Chem. Soc. Rev., 2014, 43, 547–564.
15. S. Chen, S. Perathoner, C. Ampelli and G. Centi, in Horizons in Sustainable Industrial Chemistry and Catalysis, 2019, pp. 31–46,  DOI:10.1016/b978-0-444-64127-4.00002-1.
16. A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Chem. Phys. Lett., 2014, 598, 108–112.
17. B. H. R. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Nat. Catal., 2019, 2, 290–296.
18. A. R. Singh, J. H. Montoya, B. A. Rohr, C. Tsai, A. Vojvodic and J. K. Nørskov, ACS Catal., 2018, 8, 4017–4024.
19. R. Michalsky, P. H. Pfromm and A. Steinfeld, Interface Focus, 2015, 5, 20140084.
20. H. Liu, Chin. J. Catal., 2014, 35, 1619–1640.
21. J. Fuller, Q. An, A. Fortunelli and W. A. Goddard, Acc. Chem. Res., 2022, 55, 1124–1134.
22. R. R. Schrock, Acc. Chem. Res., 2005, 38, 955–962.
23. E.-Y. Jeong, C.-Y. Yoo, C. H. Jung, J. H. Park, Y. C. Park, J.-N. Kim, S.-G. Oh, Y. Woo and H. C. Yoon, ACS Sustainable Chem. Eng., 2017, 5, 9662–9666.
24. H.-B. Wang, J.-Q. Wang, R. Zhang, C.-Q. Cheng, K.-W. Qiu, Y.-J. Yang, J. Mao, H. Liu, M. Du, C.-K. Dong and X.-W. Du, ACS Catal., 2020, 10, 4914–4921.
25. T. Spatzal, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Science, 2014, 345, 1620–1623.
26. P. Wang, F. Chang, W. Gao, J. Guo, G. Wu, T. He and P. Chen, Nat. Chem., 2017, 9, 64–70.
27. Y. Tsuji, M. Kitano, K. Kishida, M. Sasase, T. Yokoyama, M. Hara and H. Hosono, Chem. Commun., 2016, 52, 14369–14372.
28. B. Lin, Y. Qi, K. Wei and J. Lin, RSC Adv., 2014, 4, 38093–38102.
29. M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940.
30. L. M. Azofra, N. Morlanes, A. Poater, M. K. Samantaray, B. Vidjayacoumar, K. Albahily, L. Cavallo and J. M. Basset, Angew. Chem., Int. Ed., 2018, 57, 15812–15816.
31. G. A. Somorjai and N. Materer, Top. Catal., 1994, 1, 215–231.
32. J. Qian, Q. An, A. Fortunelli, R. J. Nielsen and W. A. Goddard, J. Am. Chem. Soc., 2018, 140, 6288–6297.
33. J. Fuller, A. Fortunelli, W. A. Goddard III and Q. An, Phys. Chem. Chem. Phys., 2019, 21, 11444–11454.
34. B. Y. Zhang, H. Y. Su, J. X. Liu and W. X. Li, ChemCatChem, 2019, 11, 1928–1934.
35. Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967.
36. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
37. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
38. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
39. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
40. A. Michaelides and P. Hu, J. Am. Chem. Soc., 2000, 122, 9866–9867.
41. A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653.
42. W. Xie, J. Xu, J. Chen, H. Wang and P. Hu, Acc. Chem. Res., 2022, 55, 1237–1248.
43. J.-F. Chen, Y. Mao, H.-F. Wang and P. Hu, ACS Catal., 2016, 6, 7078–7087.
44. J. Chen, M. Jia, P. Hu and H. Wang, J. Comput. Chem., 2021, 42, 379–391.
45. N. K. Razdan and A. Bhan, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(8), e2019055118.
46. W. Xie and P. Hu, Catal. Sci. Technol., 2021, 11, 5212–5222.
47. C. Guo, Y. Mao, Z. Yao, J. Chen and P. Hu, J. Catal., 2019, 379, 52–59.
48. Y. Ding, Y. Xu, Y. Song, C. Guo and P. Hu, J. Phys. Chem. C, 2019, 123, 27594–27602.
49. A. C. Lausche, A. J. Medford, T. S. Khan, Y. Xu, T. Bligaard, F. Abild-Pedersen, J. K. Nørskov and F. Studt, J. Catal., 2013, 307, 275–282.
50. N. E. Singh-Miller and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235407.
51. Q. An, M. McDonald, A. Fortunelli and W. A. Goddard, ACS Nano, 2021, 15, 1675–1684.
52. S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bligaard, F. Abild-Pedersen, C. H. Christensen and J. K. Nørskov, Catal. Lett., 2010, 141, 370–373.
53. A. Vojvodic, F. Calle-Vallejo, W. Guo, S. Wang, A. Toftelund, F. Studt, J. I. Martinez, J. Shen, I. C. Man, J. Rossmeisl, T. Bligaard, J. K. Nørskov and F. Abild-Pedersen, J. Chem. Phys., 2011, 134, 244509.
54. A. Logadottir, T. H. Rod, J. K. Nørskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, J. Catal., 2001, 197, 229–231.
55. T. R. Munter, T. Bligaard, C. H. Christensen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 5202–5206.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00462g

‡ The authors contributed equally to this work.

---