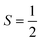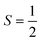Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Imperfections are not 0 K: free energy of point defects in crystals
Irea
Mosquera-Lois
 a,
Seán R.
Kavanagh
a,
Seán R.
Kavanagh
 ab,
Johan
Klarbring
ac,
Kasper
Tolborg
ab,
Johan
Klarbring
ac,
Kasper
Tolborg
 ad and
Aron
Walsh
ad and
Aron
Walsh
 *ae
*ae
aThomas Young Centre & Department of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bThomas Young Centre & Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
cDepartment of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83, Linköping, Sweden
dI-X, Imperial College London, London W12 0BZ, UK
eDepartment of Physics, Ewha Womans University, Seoul 03760, Korea
First published on 11th August 2023
Abstract
Defects determine many important properties and applications of materials, ranging from doping in semiconductors, to conductivity in mixed ionic–electronic conductors used in batteries, to active sites in catalysts. The theoretical description of defect formation in crystals has evolved substantially over the past century. Advances in supercomputing hardware, and the integration of new computational techniques such as machine learning, provide an opportunity to model longer length and time-scales than previously possible. In this Tutorial Review, we cover the description of free energies for defect formation at finite temperatures, including configurational (structural, electronic, spin) and vibrational terms. We discuss challenges in accounting for metastable defect configurations, progress such as machine learning force fields and thermodynamic integration to directly access entropic contributions, and bottlenecks in going beyond the dilute limit of defect formation. Such developments are necessary to support a new era of accurate defect predictions in computational materials chemistry.
Key learning points• Thermodynamics of point defect formation in crystals• Contributions to defect entropies (electronic, spin, vibrational, orientational) • Accounting for metastable defect configurations • Workflow for calculating defect free energies • Outstanding challenges for accurate defect predictions |
I. Introduction
The understanding and control of defects in materials are essential for the development of new technologies. Defects have the power to turn insulating materials conductive, transparent materials coloured, and inert materials reactive. In batteries, point defects determine the balance between electronic and ionic transport in solid-state components, and thus charging and degradation rates.1,2 In solar cells, imperfections in the active absorber layer provide recombination pathways for photogenerated electrons and holes that limit efficiency.3,4 In photo/electrocatalytic systems, surface layer defects provide active sites that increase reaction rates.5,6 In quantum computers, the spin states of defects can be controlled and measured as a basic unit of quantum information.7,8The microscopic theory and simulation of point defects in materials have developed over the past century. Building on the visionary 1912 work of Born and von Kármán concerning the vibrations of atoms in crystals,9 Frenkel considered the thermally activated hopping of an atom from its regular lattice site to an interstitial position in 1926.10 The subsequent ‘Frenkel pair’ formation in a silicon crystal can be described from the defect reaction
SiSi ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) VSi + Sii VSi + Sii | (1) |
In this Tutorial Review, we focus on the free energy of point defect formation at finite temperatures. The disruption of translational symmetry at a defect site induces changes in the local degrees of freedom, which can be classified into configurational, vibrational, spin and electronic terms. We explore these contributions in detail, and describe a modern computational workflow for the systematic calculation of defect free energies. Finally, we highlight some outstanding computational challenges, including the identification of global minima and the necessary timescales to describe anharmonic potential energy surfaces of defects with accessible metastable configurations.
II. Enthalpy-entropy balance
A crystal in thermal equilibrium at finite temperatures always contains a finite concentration of defects. Their formation increases the internal lattice energy of the crystal. Yet this penalty is counterbalanced by an entropy gain, so that the balance between these quantities determines the defect concentration at equilibrium. While it has become standard to estimate defect concentrations by calculating their formation energies under constant volume (isochoric) conditions in the absence of temperature, they are actually determined by the Gibbs free energy of the defect reaction, defined under constant pressure (isobaric) conditions at finite temperatures. Indeed, the equilibrium number of defects nd is determined by minimising the Gibbs free energy of the defective system at constant temperature and pressure: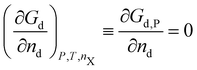 | (2) |
 | (3) |
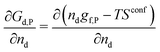 | (4) |
The main driving factor for defect formation is the mixing or configurational entropy Sconf. This arises from the many distinct ways to arrange defects in the solid and can be calculated using
Sconf = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(W) ln(W) | (5) |
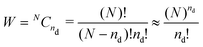 | (6) |
Sconf = kB[nd − nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(nd/N)] ln(nd/N)] | (7) |
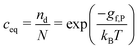 | (8) |
| gf,P = hf,P − Tsf,P | (9) |
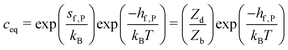 | (10) |
If Zd = Zb is assumed, one obtains
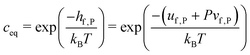 | (11) |
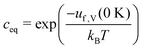 | (12) |
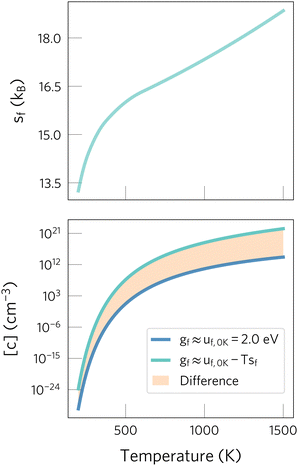 | ||
| Fig. 1 Effect of neglecting entropic contributions when predicting defect concentrations. On the top panel, the defect formation entropy of Oi2− in CeO2 is shown.24 On the bottom one, we show the concentrations predicted when neglecting the formation entropy (dark blue) or including it (light blue). The orange area highlights the error when neglecting entropic effects, which drastically changes predictions at high temperatures. Data adapted from ref. 24 and 29. | ||
III. Defect formation enthalpy
The defect formation enthalpy can be calculated from the change in internal energy using| hf,P = uf,P + Pvf,P | (13) |
| uf,P = ustaticf,P + uvibf,P | (14) |
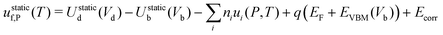 | (15) |
Firstly, eqn (14) is often evaluated by calculating the internal energies and the valence band maximum under athermal conditions – thus neglecting thermal expansion and electron–phonon interactions. Although the effect of temperature on internal energy differences is expected to be small, the energies of the band edges have a stronger temperature dependence35,36 – with band gaps changes on the order of 0.1 eV per 100 K being typical.37,38 This can affect the formation energies of charged defects at growth/annealing temperatures through the Fermi level dependence (uf,P ∝ q(EF + EVBM))39 and hence the predicted defect concentrations. While the effect has not been previously explicitly quantified to the best of our knowledge, it can be studied by calculating the band gap at the growth temperature and comparing the predicted concentrations obtained with EVBM(Vb,0K,0 K) and EVBM(Vb,Tgrowth,Tgrowth).
Another common approximation in the field involves calculating ustaticf at constant volume rather than pressure – by fixing the volume of the defect supercell to its pristine value – as discussed in ref. 19, 40 and 41. This is generally a reasonable approximation for ustaticf since the associated error is of the order of 30 meV,32 and simplifies the application of some of the finite-size corrections32 – which require similar volumes for the pristine and defective cells. However, isobaric conditions are more convenient for a consistent thermodynamic description of the atomic chemical potentials, and thus the constant pressure approach42 (i.e. volume optimisation of the defect supercell) will be used.§
Secondly, to accurately calculate Ustaticd, a stable atomic structure of the defect should be identified. Since structural reconstructions at defects can be significant, a local optimisation of an unperturbed high-symmetry defect configuration often fails to find the ground state, requiring the use of structure searching methods.43–52 A complicating factor is that hybrid non-local exchange–correlational functionals are generally required for the underlying Density Functional Theory (DFT) calculations.53–62 While local or semi-local exchange–correlation functionals often provide a good approximation for bulk properties, their self-interaction error spuriously disfavours charge localisation, in addition to underestimating the band gap energy. Since the localisation of electrons/holes in both space and energy can result in different defect structures and energies, DFT functionals that accurately describe these properties are essential. Further, for heavy element systems (period five/six and below), an accurate electronic description also involves accounting for relativistic effects like spin–orbit coupling (SOC), which is key to obtaining accurate positions of the band edges and band gap energy – and thus accurate defect levels and formation energies.53,63¶ Finally, we note that materials or dopants with highly localised electrons (d/f elements) may require further corrections.62,64–69
Third, while occasionally witnessed in the literature (particularly for semi-local DFT calculations), negative intrinsic defect formation energies at the equilibrium Fermi level are typically unphysical, as they indicate that the bulk system would spontaneously decompose through irreversible defect formation. Common causes include an unstable host crystal (e.g. VO in KCuO370) or a local phase transition triggered by the defect (e.g. VO induced local (tetragonal-like) octahedral rotations in cubic SrTiO371). A caveat to this is that a thermodynamically-unstable but kinetically-stable material (e.g. diamond), can exhibit true negative defect formation energies.
Finally, we note that recent advances in finite-size corrections have enabled the calculation of more accurate and reliable defect formation energies.72 These range from a posteriori anisotropic charge corrections73,74 to self-consistent corrections that directly modify the potential75 or charge density76 in the underlying electronic structure calculation.77
IV. Defect formation entropy
The defect formation entropy comprises the entropy change upon creating one defect at a specific lattice site. As this entropy change is defined for a given site, it does not include the mixing or off-site configurational entropy – which arises from the multiple ways of placing the defect in different lattice sites. It does, however, include the on-site configurational or orientational contribution, which results from inequivalent orientations of the defect at the same site due to a lowering of the local symmetry, as discussed below.Beyond the orientational contribution, spin can also result in an entropy change – a defect with one unpaired (collinear) electron has two equivalent electronic configurations as the electron can have up or down spin. Two additional contributions stem from changes in the vibrational and electronic entropies. The first is mainly determined by changes in the atomic vibrations of the defect environment, while the second stems from changes in the thermal occupation of electronic states.
For convenience when calculating defect concentrations, these contributions can be accounted for with the pre-exponential factor Zd/Zb, as described in eqn (10). Considering the different timescales of these degrees of freedom (Fig. 2), we can often treat them independently and thus express the partition function as a product of the different contributions:
| Z = ZelectronicZspinZvibrationalZorientational | (16) |
| sf = selectronicf + sspinf + svibrationalf + sorientationalf. | (17) |
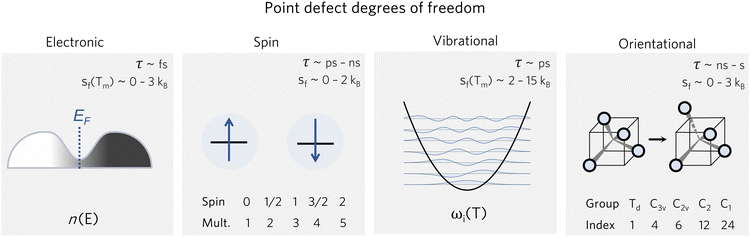 | ||
| Fig. 2 Various degrees of freedom for point defects, with their typical timescales τ78,79 and formation entropy ranges sf(T), where Tm is the melting temperature. | ||
These entropic terms and the resulting prefactors are illustrated in Fig. 2 and exemplified for a series of defects and host crystals in Table 1. The spin-degree of freedom can be described by Zspind/Zspinb = 2S + 1, where S is the total spin angular momentum.|| For example, the unpaired electron (S = 1/2) for a neutral chlorine vacancy in NaCl results in a prefactor of 2. If the orientational degrees of freedom also change, the spin prefactor is multiplied by the orientational one, with the latter determined by the number of symmetry-equivalent orientations of the defect (e.g. 4 for the C3v distorted VCd−1, resulting in Zd/Zb = 4(2(1/2) + 1) = 8). Finally, excited states are accounted for in the usual sum over levels i with energies E in 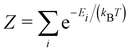 . For example, the chlorine divacancy in NaCl shows a sixfold orientational degeneracy, as well as a S = 1 spin excited state at energy E above the S = 0 ground state, resulting in the prefactor
. For example, the chlorine divacancy in NaCl shows a sixfold orientational degeneracy, as well as a S = 1 spin excited state at energy E above the S = 0 ground state, resulting in the prefactor 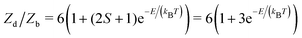 . In the following sections, we describe in detail these degrees of freedom and how to approach the calculation of the associated entropic terms.
. In the following sections, we describe in detail these degrees of freedom and how to approach the calculation of the associated entropic terms.
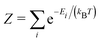 and Ei represents the energy of the available states. For simplicity, the vibrational degree of freedom is not included
and Ei represents the energy of the available states. For simplicity, the vibrational degree of freedom is not included
A. Orientational contributions
The number of equivalent defect orientations can be estimated from the change in point group symmetry at the defect site. For example, each Cd site in zinc blende-structured CdTe has a Td point group (with 24 symmetry operations). If a VCd defect maintains this environment then no additional factor is required. However, a C2v (4 symmetry operations – i.e. order 4) or C3v (order 6) distortion would lead to Zd/Zb = Nb/Nd = 24/Nd = 6 and 4, respectively, as determined by the index of the subgroup80,81 and illustrated in Fig. 3. In practice, this factor can be determined by calculating the ratio of point symmetry operations for the defect site in the pristine (Nb) and defective supercells (Nd) using materials analysis codes.82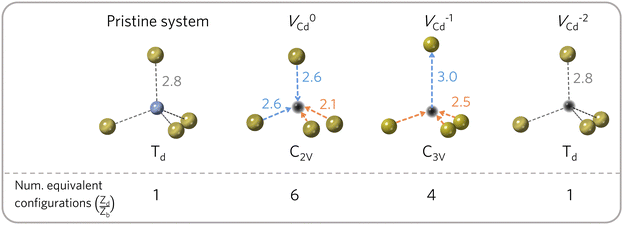 | ||
| Fig. 3 Orientational degrees of freedom for the cadmium vacancy in CdTe. The distortion undergone by the different charge states determines the number of symmetry-equivalent configurations (Zorientd/Zorientb). Cd in blue, Te in gold and vacancy in black. For each configuration, different colours are used to group bonds with equal distances (in Å), illustrating the defect site symmetry. Adapted from ref. 50. | ||
The orientational contribution can significantly increase predicted defect concentrations. For instance, a change from Td to C1 symmetry would result in a 24-fold increase in the predicted concentration. This contribution is also important for calculating the concentration of defect complexes at finite temperatures – where one has to account for the difference in orientational entropy of the complex and its associated point defects, as well as the loss in off-site configurational entropy, to predict the temperature-dependent binding energy required to overcome entropically-driven dissociation into the constituent point defects.83–85
B. Electronic contributions
The electronic density of states (DOS) can also change upon defect formation. As a first approximation for low temperatures, the electronic entropy can be estimated using the Sommerfeld approach.86 Here, one assumes that the DOS is temperature-independent and varies very slowly for energies near the Fermi level, resulting in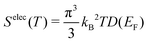 | (18) |
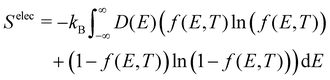 | (19) |
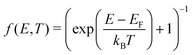 | (20) |
Generally, changes in the electronic degrees of freedom are only significant for metals or narrow band gap semiconductors at high temperatures,90,91 with absolute values of selectronicf ranging from 1 to 3kB. For instance, at the melting point of the corresponding metals, selectronicf is 1.7kB for the tungsten vacancy,90 −0.5kB for the tantalum vacancy,92 and 1.6kB for the nickel vacancy.93
C. Vibrational contributions
In early theoretical studies, the vibrational entropy was approximated by only considering the change in force constants of the defect's nearest neighbours.20,96 With increased computational power, all vibrations can be considered. The simplest approach involves applying the harmonic approximation, where the vibrational entropy is calculated by appropriately summing the phonon frequencies ω over bands v and wavevectors q
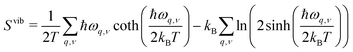 | (21) |
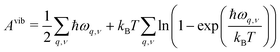 | (22) |
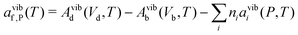 | (23) |
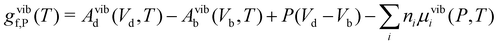 | (24) |
The vibrational contribution can significantly affect predicted defect concentrations. For example, at the melting point, svibf for the vacancy in elemental Cu, C, and Si account for 4.4kB,109 13.1kB110 and 9.1–11.6kB52,111 (Tm = 1360 K, 4100 K and 1685 K), respectively, thus increasing the predicted concentration by factors of 102, 106 and 104–105. Similarly, for VIn in In2O3, the Frenkel defects in ThO2 and CeO2, and VGa in Ga2O3, accounting for vibrations results in a 102, 102, 105 and 106 increase in the calculated concentrations at 1000 K, respectively (with svibf = 5.3kB,112 4.5kB,113 11.7kB24 and 14kB29).
Generally, the (quasi)harmonic approximation works well at low to moderately high temperatures. However, at high temperatures where the atomic vibrations significantly deviate from the perfect lattice positions, approaching a phase transition or the melting point, higher-order anharmonic effects should be included.
Thermodynamic integration (TI). Molecular dynamics (MD) simulations offer an alternative to a lattice dynamics expansion of interatomic force constants. In principle all orders of anharmonicity can be included, and TI provides a straightforward way of computing the anharmonic free energy. The most common type of TI is where integration is performed along a coupling parameter, λ, from a reference system for which the free energy can be calculated analytically – often the (quasi) harmonic reference – to the fully anharmonic system. Thus, a set of MD simulations are performed with Hamiltonians H(λ) = (1 − λ)Hqh + λHDFT, where Hqh and HDFT are the Hamiltonians of the quasiharmonic reference and the full DFT system, respectively. The anharmonic correction to the (quasi) harmonic free energy then becomes
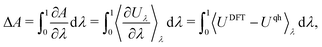 | (25) |
The TI is most conveniently performed in the NVT ensemble, thus yielding the correction to the anharmonic free energy at constant volume, but constant pressure quantities can be obtained if the simulation cell volume is first determined at the relevant temperature and pressure, using e.g. NPT dynamics. Alternatively, a mapping from the Helmholtz free energy to the Gibbs free energy can be performed following the method of Cheng & Ceriotti.115
TI can be performed from a quasiharmonic reference at each temperature of interest. However, beyond being computationally demanding, performing TI at high temperatures can be challenging due to diffusion or dynamic disorder. These issues can be avoided by carrying out the coupling constant TI only at a sufficiently low temperature, and then performing TI using temperature as the external coupling parameter to obtain the free energy as a function of temperature, i.e.
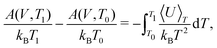 | (26) |
Since TI using ab initio MD (AIMD) can be computationally expensive due to the extensive sampling required, several methods have been devised for improving convergence, such as the UP-TILD116 (TU-TILD117) method; (two-stage) upsampled TI using Langevin dynamics. In the former, TI is performed between the quasiharmonic reference and a poorly converged, but faster, DFT method followed by thermodynamic perturbation from the low-quality DFT to high-quality DFT, while in the latter, an empirical potential is introduced as another stage in the TI to speed up the simulations even further. In both cases, one takes advantage of the fact that low-quality DFT and even empirical potential MD trajectories tend to sample the relevant phase space very well. While this has been shown to be efficient for metals and refractory materials, it is unclear if sampling with low-quality DFT or an empirical potential will be sufficient for defects with more complex electronic structure, such as competing localised and delocalised states.49,50
The importance of anharmonic contributions to the free energy of defect formation has been shown for vacancies in several metals including Cu, Al and Fe.109,115 Despite progress in improved sampling methods, AIMD may still be prohibitively expensive for more complex systems than simple metals – especially when considering the high accuracy required in the target formation free energy (≈1 meV per atom). Thus, there is promise in using machine-learned force fields (MLFF) (also called interatomic potentials) to reduce the computational cost for accurate thermodynamic calculations. MLFFs have been trained and applied for vacancies in Al, Fe and W, showing good agreement with DFT calculations and experiments.118,119 For Al, important differences between MLFFs and DFT were observed in the entropy as a function of temperature, suggesting that the DFT results may be undersampled.118 To improve accuracy, one can perform thermodynamic perturbation from the MLFF reference to the full DFT results.120
MLFFs further hold the promise of studying the thermodynamics of defects in more complex systems beyond simple metals, where hybrid DFT or more accurate electronic structure methods are necessary even for a qualitative understanding of the defect formation. While AIMD with hybrid functionals is prohibitively expensive, MLFFs trained to hybrid DFT accuracy are within reach.
Anharmonic phonon theory. Anharmonic lattice dynamics offers an alternative framework, that may overcome potential TI issues including (under-)sampling, finite-size effects, and assumptions of classical dynamics. The last decade has shown tremendous progress with methods such as temperature-dependent effective potential (TDEP),121 self-consistent phonon theory (SPCH)122 and stochastic self-consistent harmonic approximation (SSCHA)123 now being mature techniques with efficient, open source implementations. These methods have shown great results for temperature-dependent phonon spectra, phase transition temperatures in soft-mode driven transitions, and thermal conductivities, but they also allow for the calculation of anharmonic free energies.124,125 To our knowledge, these methods have not been applied to study vibrational contributions to defect formation, but it should be straightforward, although at an increased computational cost compared to using the (quasi)harmonic approximation.
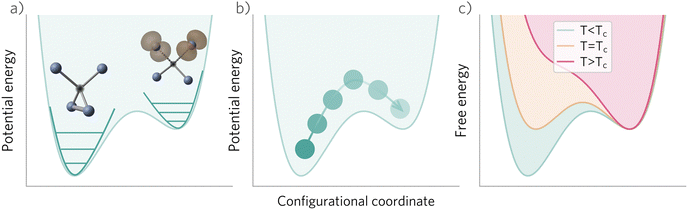
V. Metastable configurations
So far we have focused on calculating free energies for the ground state configuration of a defect species. However, defects often feature metastable states or local minima in their potential energy surface,43,47,49,50,126,127 and these will affect the associated free energy of formation. At finite temperatures under equilibrium, each configuration will have a population determined by its relative free energy, with transition rates between defect states determined by the corresponding free energy barriers. With this perspective, one may calculate the formation free energy of each configuration i and combine them to get the total defect population**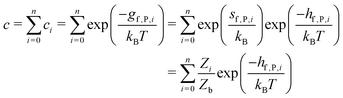 | (27) |
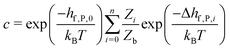 | (28) |
In these cases, defects will exhibit strong vibrational anharmonicity due to the presence of thermally accessible metastable configurations on their energy landscapes, likely requiring anharmonic treatments for accurate predictions. A TI approach may be especially applicable, as it could allow one to sample over all possible configurations of a particular type of defect, thus obtaining the total defect free energy without needing the abstraction into vibrational and orientational degrees of freedom, as illustrated in Fig. 4(a and b). This will be important when the time-scale of vibrations within each local minimum and jumps between them becomes similar. Furthermore, if the defect structure changes with temperature, as exemplified in Fig. 4(c), the total free energy will naturally emerge from this method without having to consider a possible change of the orientational entropy with temperature. Similarly, defect migration would be handled naturally by this method.
In contrast, if the barriers between configurations are large, giving rise to slow and rare transitions that would not be adequately sampled in standard MD ensembles, a TI approach would be less applicable. In these cases, one could use harmonic (or anharmonic) phonon-based methods to calculate the (an)harmonic vibrational free energy for the relevant defect configurations, as illustrated in Fig. 4(a). By yielding the temperature-dependent free energy surfaces of defective systems, these approaches allow for an understanding of defect structure as a function of temperature (Fig. 4(c)), where one may envision that thermal effects–or nuclear quantum effects-could increase the symmetry of symmetry-broken defects, as occurs for symmetry-broken bulk materials.130,131
VI. Defect free energy workflow
Drawing together the concepts discussed above, we describe how to combine these contributions for the systematic calculation of defect free energies.A. Enthalpy change
The enthalpy change upon defect formation is usually the dominant contribution and an important starting point. The first step is to construct a pristine supercell, whose size should be large enough to minimize defect-defect short-range interactions (i.e. lattice parameters >10 Å32,132). The defect structure can then be generated by adding or removing the corresponding atom(s) from the pristine supercell – which can be automated using packages such as PyCDT,133 PyLada,134 DASP,135 Spinney,136 pymatgen-analysis-defects137 or doped.138 Once the defect supercell has been created, a structure searching method43,47 should be employed to identify stable structures for each of the relevant charge states – as implemented in ShakeNBreak48 for example.From the local minimum configurations identified, one should decide whether their effect on the defect thermodynamics is likely to be relevant (depending on their relative energy and entropy). Different criteria will apply in non-equilibrium cases.81,126 For simplicity, here we assume that only the ground state structure is important, yet the procedure can be easily adapted to include metastability (see Section V). Next, the defect enthalpy of formation can be calculated for the ground state structure using eqn (13) and (15). This requires calculating the finite-size corrections using one of the available methods,73,74,76,77 as well as the chemical potentials of the relevant competing phases – steps that can be performed with the mentioned packages.
B. Entropy change
We next consider entropic contributions. Starting with the temperature-independent terms, the spin degeneracy is determined by the number of unpaired electrons (e.g. from Zspind/Zspinb = 2S + 1), while the orientational degeneracy can be estimated from the change in symmetry of the defect site using codes such as pymatgen82 (Section IV A). Within host materials that exhibit various types of disorder, such as site,139 spin,140 rotational, polar141,142 or elastic/structural,140 the introduction of defect species can lead to a reduction in configurational entropy due to short-range ordering induced by the defect, which should be accounted for if relevant. If modelling a metal or a narrow band gap semiconductor, then the (temperature-dependent) electronic contribution should be included, which can be estimated using eqn (19) with the calculated density of states for the pristine and defective supercells (Section IV B).The vibrational contribution can be calculated using an appropriate approximation (Section IV C), depending on the target system and temperature, desired accuracy and available resources. At low temperatures, vibrational contributions may be negligible, but at high operating or annealing temperatures, their effect on free energies will be significant (Section IV C). One should consider whether the harmonic approximation reasonably describes the target system at the conditions of interest. This involves assessing the importance of thermal expansion and higher-order anharmonic effects for the target system and temperature (e.g. by considering the magnitude of the volumetric thermal expansion coefficient and the existence of low-lying metastable states, respectively).
Based on these considerations, we highlight three possible approaches. The simplest is to employ the harmonic approximation to calculate the (temperature-dependent) vibrational entropy for the defective and pristine supercells at the 0 K volume, using phonopy99,143 (Section IV C1). Alternatively, thermal expansion can be accounted for using the quasiharmonic approach to calculate the vibrational entropy for a range of cell volumes for the defective and pristine supercells (Section IV C2). Finally, if higher-order anharmonic effects are expected to be important, one can use thermodynamic integration or anharmonic phonon-based methods (Section IV C3). However, their associated computational cost may prevent their application in certain cases. Here, reverting to the (quasi)harmonic approximation to include vibrational contributions will already be a significant improvement upon static methods that completely neglect finite temperature effects.
C. Chemical potentials
When defect formation involves the exchange of atoms with an external reservoir, it is essential that consistent thermodynamic potentials are employed throughout. For the special case of stoichiometric defect formation, including Frenkel and Schottky pairs, the chemical potential terms cancel out and these complications can be avoided.The atomic chemical potentials in eqn (15) must be modified to contain the same entropic contributions as considered for the defective and pristine systems, e.g.
| μ(P,T) = u(P,T) + Pv − T(sspin + svib + selec + srot + sgas/liquid) | (29) |
For gaseous/liquid reference phases, rotational (srot) and translational/configurational (sgas/liquid) entropy contributions can become significant. For gases, these quantities may be calculated analytically for arbitrary partial pressures via the ideal gas and rigid rotor approximations.144–146 For liquids or non-ideal gases on the other hand, the thermodynamic potentials can be obtained from molecular dynamics trajectories147 or taken from standardised tables of experimental data.148 These adjustments are necessary to ensure a consistent thermodynamic description when species are added or removed from the system. Chemical potential terms allow specific growth conditions to be considered, through the choice of temperature/pressure or a tabulated reference potential.
Determining the chemical potential limits by considering the free energy of all possible secondary phases would involve a significant increase in computational cost.149 A reasonable approximation here is to query a materials database to search for the phases which border the host material on the phase diagram, or are within a given energy error threshold of bordering the host, calculate their internal energy with the appropriate computational setup and then determine the relevant (nearly-)bordering competing phases based on these energies, keeping in mind that entropy contributions will be larger for gases/liquids.138 The entropic terms can then be calculated for only these competing phases that directly limit the stability region of the host.
D. Fermi level
After combining all terms into the defect formation free energy, the remaining variable is the Fermi level, EF. The position of EF is dictated by the condition of net charge neutrality, such that the sum of all excess positive charge in the material (from donor-type defects and holes) equals that of all excess negative charge (from acceptor defects and electrons). As the energies and thus concentrations of charged defects themselves depend on the Fermi level, with gf,P(T) = (…) + q(EVBM + EF(T)) − Tselec(EF) where q is the defect charge, both EF(T) and the defect free energies and concentrations must be solved self-consistently under the net neutrality constraint.150,151Typically materials are grown or processed/annealed under elevated temperatures where defects form with concentrations given by eqn (8), before the material is cooled (‘quenched’) to the operating temperature. While the total concentration of each defect is kept fixed due to kinetic trapping, the Fermi level and thus relative populations of different charge states and electron/hole carrier concentrations re-equilibrate upon cooling. This is modelled by calculating the formation free energies at the growth/annealing temperature, which gives the total concentration of each defect that forms during synthesis (using eqn (8)). To then calculate the Fermi level, free carrier concentrations and relative concentrations of the different charged defects at the operating temperature, these are solved self-consistently while fixing the total concentration of each defect.79,135,150–154†† The population of each defect with charge q at the operating temperature T is then given by
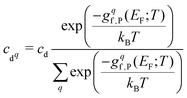 | (30) |
VII. Challenges and outlooks
The calculation of defect free energies poses a significant computational challenge, especially when considering all intrinsic defects in structurally or chemically complex systems. This complexity can lead to many inequivalent defect species that need to be considered.128 Depending on the application, one can envision different strategies to make the problem more tractable.One approach would be to filter the configurational space and only calculate the entropic terms for those defects with the lowest formation energies and thus highest concentrations. Alternatively, one could employ reasonable approximations to make the calculation of entropic terms more efficient. For instance, this could involve employing (semi-)local DFT exchange–correlation functionals for calculating vibrational entropies, instead of their hybrid counterparts often used for the energetic terms. Considering that (semi-)local functionals generally describe pristine structures and force constants accurately, this may be a reasonable approximation if the defect structure is stable at that level of theory.
Alternatively, a surrogate model could be used instead of first-principles methods. Indeed, much of the existing defect literature has been built on the development and application of classical force fields. Given the remarkable progress achieved in machine learning force fields (MLFFs), which can provide a more flexible and accurate description of the potential energy surface,155,156 they may be an optimal solution in certain cases. For instance, MLFFs may be appropriate when targeting in-depth studies of specific defects (e.g. metastable states or migration paths) or requiring high accuracies (e.g. including anharmonic interactions26,118,119). The significant cost of these calculations would justify training a model for the defective systems, which can be achieved via fine-tuning (e.g. training a model for the bulk and then re-training it for relevant configurations of the defective systems157). We highlight that further work is still required to determine the optimal approach for defect MLFF training, particularly regarding the number and diversity of defect configurations required to achieve sufficient accuracies. Additional research is also needed to investigate whether current MLFFs can describe defects with complex electronic structures and configurational landscapes, a challenge that will likely benefit from progress in fourth-generation MLFFs that include local charges and non-local effects.158
Beyond using surrogate models to reduce computational cost, other challenges include going beyond the dilute non-interacting limit that is often assumed and thus has been our focus (c ≪ 1%). At higher concentrations, interactions between defects must be considered. These can modify both the internal energy and the accessible degrees of freedom. Inspired by electrolyte models, Debye–Hückel theory has been used to account for long-range Coulombic interactions in certain highly defective ionic systems.159 Here the Coulomb interaction is modified by a screening term that depends on the concentration of charged defects, which can be formulated in terms of an activity coefficient. Future models could extend to account for the additional effects on enthalpies (e.g. elastic and bonding) and entropies arising from finite defect separations.
At shorter length scales, defect complexation can also occur, such as the combination of a vacancy and interstitial to form a bound Frenkel pair. Defect aggregation will alter the configurational landscape, in addition to vibrational, electronic, and spin terms.160 Defect complexes have been characterised in many host compounds including the NV centre in diamond.161 However, a complete description of the full ensemble of configurations that can be formed is challenging beyond certain high symmetry cases. One solution is a combinatorial evaluation of defect configurations in a radial cluster expansion, as described by Allnat and Loftus.162 At higher concentrations, the description of long-range ordering may be required with the emergence of new non-stoichiometric phases.163,164
These cases illustrate where further developments are required for accurate defect predictions. Surrogate models will enable accessing longer time and length-scales, required to describe anharmonic effects and go beyond the dilute non-interacting limit. In this Tutorial Review, we have described the different terms that contribute to defect free energies and how to calculate them. We have highlighted the importance of including entropic effects for accurate defect concentrations, and described reasonable approximations to reduce the associated computational costs. Lastly, we have discussed the remaining challenges and potential solutions for comprehensive modelling of defect free energies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. M. L. acknowledges Imperial College London for funding a Presidents PhD scholarship. S. R. K. acknowledges the EPSRC Centre for Doctoral Training in the Advanced Characterisation of Materials (CDT-ACM)(EP/S023259/1) for funding a PhD studentship. K. T. acknowledges support from the Eric and Wendy Schmidt AI in Science Postdoctoral Fellowship, a Schmidt Futures program. J. K. acknowledges support from the Swedish Research Council (VR) program 2021-00486. A. W. acknowledges support from the Leverhulme Trust.References
- J. Maier, Angew. Chem., Int. Ed., 2013, 52, 4998–5026 CrossRef CAS PubMed
.
- A. G. Squires, D. W. Davies, S. Kim, D. O. Scanlon, A. Walsh and B. J. Morgan, Phys. Rev. Mater., 2022, 6, 085401 CrossRef CAS
.
- W. Shockley and W. T. Read, Phys. Rev., 1952, 87, 835–842 CrossRef CAS
.
- S. Kim, J. A. Márquez, T. Unold and A. Walsh, Energy Environ. Sci., 2020, 13, 1481–1491 RSC
.
- W. Li, D. Wang, Y. Zhang, L. Tao, T. Wang, Y. Zou, Y. Wang, R. Chen and S. Wang, Adv. Mater., 2020, 32, 1907879 CrossRef CAS PubMed
.
- E. Pastor, M. Sachs, S. Selim, J. R. Durrant, A. A. Bakulin and A. Walsh, Nat. Rev. Mater., 2022, 7, 503–521 CrossRef CAS
.
- J. Weber, W. Koehl, J. Varley, A. Janotti, B. Buckley, C. Van de Walle and D. D. Awschalom, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8513–8518 CrossRef CAS PubMed
.
- Y. Xiong, M. Mathew, S. M. Griffin, A. Sipahigil and G. Hautier, 2023, arXiv:quant-ph/2302.10767.
- M. Born and T. von Kármán, Phys. Z., 1912, 8, 297 Search PubMed
.
- J. Frenkel, Z. Phys., 1926, 35, 652 CrossRef
.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC
.
- R. Grimes, C. R. A. Catlow and A. Stoneham, J. Phys. Condens. Matter, 1989, 1, 7367 CrossRef CAS
.
- G. Baraff and M. Schlüter, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1853 CrossRef CAS
.
- M. Leslie and M. Gillan, J. Phys. C, 1985, 18, 973 CrossRef CAS
.
- D. Morgan and Y. Zhang, Phys. Rev. B, 2020, 101, 136101 CrossRef CAS
.
- X. Zhang, S. V. Divinski and B. Grabowski, Acta Mater., 2022, 227, 117677 CrossRef CAS
.
-
M. Lannoo and J. Bourgoin, Thermodynamics of Defects, Point Defects in Semiconductors I, Springer, Berlin, 1981, pp. 191–216 Search PubMed
.
-
W. Hayes and A. Stoneham, Defects and Defect Processes in Nonmetallic Solids, Wiley, New York, 1985 Search PubMed
.
-
P. A. Varotsos and K. D. Alexopoulos, in Defects in Solids, ed. S. Amelinckx, R. Gevers and J. Nihoul, Springer, Amsterdam, 1986, vol. 14, pp. 1–470 Search PubMed
.
-
N. Hiroshi, in Physical Metallurgy, ed. D. E. Laughlin and K. Hono, Elsevier, Oxford, 5th edn, 2014, ch. 6, vol. 1, pp. 561–637
.
- C. Sutton and S. V. Levchenko, Front. Chem., 2020, 8, 2296–2646 Search PubMed
.
-
A. R. Allnatt and A. B. Lidiard, Atomic Transport in Solids, Cambridge University Press, Cambridge, 1993 Search PubMed
.
- E. G. Seebauer and M. C. Kratzer, Mater. Sci. Eng., R, 2006, 55, 57–149 CrossRef
.
- S. Grieshammer, T. Zacherle and M. Martin, Phys. Chem. Chem. Phys., 2013, 15, 15935–15942 RSC
.
- E. Rauls and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155213 CrossRef
.
- A. Forslund, J. H. Jung, P. Srinivasan and B. Grabowski, Phys. Rev. B, 2023, 107, 174309 CrossRef CAS
.
- A. Lindman, P. Erhart and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245114 CrossRef
.
- M. W. D. Cooper, S. T. Murphy and D. A. Andersson, J. Nucl. Mater., 2018, 504, 251–260 CrossRef CAS
.
- T. Zacherle, P. C. Schmidt and M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235206 CrossRef
.
- S. B. Zhang and J. E. Northrup, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed
.
- C. G. Van de Walle, D. B. Laks, G. F. Neumark and S. T. Pantelides, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9425–9434 CrossRef CAS PubMed
.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef
.
- S. Kim, S. N. Hood, J.-S. Park, L. D. Whalley and A. Walsh, JPhys Energy, 2020, 2, 036001 CrossRef CAS
.
- S. Lany and A. Zunger, Modell. Simul. Mater. Sci. Eng., 2009, 17, 084002 CrossRef
.
- P. B. Allen and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 1495–1505 CrossRef CAS
.
- D. Wickramaratne, C. E. Dreyer, B. Monserrat, J.-X. Shen, J. L. Lyons, A. Alkauskas and C. G. Van de Walle, Appl. Phys. Lett., 2018, 113, 192106 CrossRef
.
- B. Monserrat, J. Phys.: Condens. Matter, 2018, 30, 083001 CrossRef PubMed
.
- Y. Zhang, Z. Wang, J. Xi and J. Yang, J. Phys.: Condens. Matter, 2020, 32, 475503 CrossRef CAS PubMed
.
- S. Qiao, Y.-N. Wu, X. Yan, B. Monserrat, S.-H. Wei and B. Huang, Phys. Rev. B, 2022, 105, 115201 CrossRef CAS
.
- C. R. A. Catlow, J. Corish, P. W. M. Jacobs and A. B. Lidiard, J. Phys. C: Solid State Phys., 1981, 14, L121–L125 CrossRef CAS
.
- M. B. Taylor, G. D. Barrera, N. L. Allan, T. H. K. Barron and W. C. Mackrodt, Faraday Discuss., 1997, 106, 377–387 RSC
.
- B. Grabowski, T. Hickel and J. Neugebauer, Phys. Status Solidi B, 2011, 248, 1295–1308 CrossRef CAS
.
- M. Arrigoni and G. K. H. Madsen, npj Comput. Mater., 2021, 7, 1–13 CrossRef
.
- A. J. Morris, C. J. Pickard and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 144112 CrossRef
.
- J. Mulroue, A. J. Morris and D. M. Duffy, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094118 CrossRef
.
- I. Mosquera-Lois and S. R. Kavanagh, Matter, 2021, 4, 2602–2605 CrossRef
.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, npj Comput. Mater., 2023, 9, 1–11 CrossRef
.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2022, 7, 4817 CrossRef
.
- A. Kononov, C.-W. Lee, E. Shapera and A. Schleife, J. Phys. Condens. Matter, 2023, 35, 334002 CrossRef PubMed
.
- S. R. Kavanagh, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2021, 6, 1392–1398 CrossRef CAS PubMed
.
- X. Wang, S. R. Kavanagh, D. O. Scanlon and A. Walsh, 2023, arXiv:cond-mat/2302.04901.
- O. K. Al-Mushadani and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 235205 CrossRef
.
- M.-H. Du, J. Phys. Chem. Lett., 2015, 6, 1461–1466 CrossRef CAS PubMed
.
- D. Broberg, K. Bystrom, S. Srivastava, D. Dahliah, B. A. D. Williamson, L. Weston, D. O. Scanlon, G.-M. Rignanese, S. Dwaraknath, J. Varley, K. A. Persson, M. Asta and G. Hautier, npj Comput. Mater., 2023, 9, 1–12 CrossRef
.
- P. Deák, B. Aradi, T. Frauenheim, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153203 CrossRef
.
- E. Finazzi, C. Di Valentin, G. Pacchioni and A. Selloni, J. Chem. Phys., 2008, 129, 154113 CrossRef PubMed
.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085202 CrossRef
.
- M. V. Ganduglia-Pirovano, J. L. F. Da Silva and J. Sauer, Phys. Rev. Lett., 2009, 102, 026101 CrossRef PubMed
.
- S. J. Clark, J. Robertson, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115311 CrossRef
.
- P. Ágoston, K. Albe, R. M. Nieminen and M. J. Puska, Phys. Rev. Lett., 2009, 103, 245501 CrossRef PubMed
.
- A. Janotti and C. G. Van de Walle, Phys. Status Solidi B, 2011, 248, 799–804 CrossRef CAS
.
- M. Gerosa, C. E. Bottani, C. D. Valentin, G. Onida and G. Pacchioni, J. Phys.: Condens. Matter, 2017, 30, 044003 CrossRef PubMed
.
- J. Pan, W. Metzger and S. Lany, Phys. Rev. B, 2018, 98, 054108 CrossRef CAS
.
- W. Chen, S. M. Griffin, G.-M. Rignanese and G. Hautier, Phys. Rev. B, 2022, 106, L161107 CrossRef CAS
.
- C.-W. Lee, M. Singh, A. C. Tamboli and V. Stevanović, npj Comput. Mater., 2022, 8, 1–11 CrossRef
.
- V. Ivády, I. A. Abrikosov, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205201 CrossRef
.
- V. Ivády, I. A. Abrikosov and A. Gali, npj Comput. Mater., 2018, 4, 1–13 CrossRef
.
- V. Ivády, R. Armiento, K. Szász, E. Janzén, A. Gali and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035146 CrossRef
.
- A. Walsh, J. L. F. Da Silva and S.-H. Wei, Phys. Rev. Lett., 2008, 100, 256401 CrossRef PubMed
.
- M. T. Curnan and J. R. Kitchin, J. Phys. Chem. C, 2014, 118, 28776–28790 CrossRef CAS
.
- M. Choi, F. Oba, Y. Kumagai and I. Tanaka, Adv. Mater., 2013, 25, 86–90 CrossRef CAS PubMed
.
- A. Walsh, npj Comput. Mater., 2021, 7, 1–3 CrossRef
.
- Y. Kumagai and F. Oba, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195205 CrossRef
.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed
.
- M. Chagas da Silva, M. Lorke, B. Aradi, M. Farzalipour Tabriz, T. Frauenheim, A. Rubio, D. Rocca and P. Deák, Phys. Rev. Lett., 2021, 126, 076401 CrossRef CAS PubMed
.
- Z.-J. Suo, J.-W. Luo, S.-S. Li and L.-W. Wang, Phys. Rev. B, 2020, 102, 174110 CrossRef CAS
.
- J. Xiao, K. Yang, D. Guo, T. Shen, H.-X. Deng, S.-S. Li, J.-W. Luo and S.-H. Wei, Phys. Rev. B, 2020, 101, 165306 CrossRef CAS
.
- A. V. Ruban and I. A. Abrikosov, Rep. Prog. Phys., 2008, 71, 046501 CrossRef
.
- L.-P. Yang, C. Burk, M. Widmann, S.-Y. Lee, J. Wrachtrup and N. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 241203 CrossRef
.
- O. Goede, Phys. Status Solidi B, 1972, 50, 727–736 CrossRef CAS
.
- D. Krasikov and I. Sankin, Phys. Rev. Mater., 2018, 2, 103803 CrossRef CAS
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS
.
- J. M. Wynn, R. J. Needs and A. J. Morris, 2016, arXiv:cond-mat/1609.04760.
- D. Krasikov and I. Sankin, J. Mater. Chem. A, 2017, 5, 3503–3513 RSC
.
- S. L. Millican, J. M. Clary, C. B. Musgrave and S. Lany, Chem. Mater., 2022, 34, 519–528 CrossRef CAS
.
- C. Wolverton and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 8813–8828 CrossRef CAS PubMed
.
- O. Eriksson, J. M. Wills and D. Wallace, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 5221–5228 CrossRef CAS PubMed
.
- N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443 CrossRef
.
- X. Zhang, B. Grabowski, F. Körmann, C. Freysoldt and J. Neugebauer, Phys. Rev. B, 2017, 95, 165126 CrossRef
.
- A. Satta, F. Willaime and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 11184–11192 CrossRef CAS
.
- M. Youssef and B. Yildiz, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 144109 CrossRef
.
- A. Satta, F. Willaime and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7001–7005 CrossRef CAS
.
- A. Metsue, A. Oudriss, J. Bouhattate and X. Feaugas, J. Chem. Phys., 2014, 140, 104705 CrossRef PubMed
.
- N. Nickel and K. Fleischer, Phys. Rev. Lett., 2003, 90, 197402 CrossRef CAS PubMed
.
- M. Dimitrievska, H. Xie, A. Jackson, X. Fontané, M. Espndola-Rodrguez, E. Saucedo, A. Pérez-Rodrguez, A. Walsh and V. Izquierdo-Roca, Phys. Chem. Chem. Phys., 2016, 18, 7632–7640 RSC
.
-
F. Kröger, The Chemistry of Imperfect Crystals, North-Holland Publishing Company, Amsterdam, 1964 Search PubMed
.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS
.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS
.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef
.
- X. Zhang, B. Grabowski, T. Hickel and J. Neugebauer, Comput. Mater. Sci., 2018, 148, 249–259 CrossRef CAS
.
- L. Shi and L.-W. Wang, Phys. Rev. Lett., 2012, 109, 245501 CrossRef PubMed
.
- H.-S. Zhang, J. Gong and L. Shi, Phys. Status Solidi RRL, 2023, 17, 2200239 CrossRef CAS
.
- Y. Xiao, Z. Wang, L. Shi, X. Jiang, S. Li and L. Wang, Sci. China: Phys., Mech. Astron., 2020, 63, 277312 CAS
.
- S. Wu, X. Yang, H. Zhang, L. Shi, Q. Zhang, Q. Shang, Z. Qi, Y. Xu, J. Zhang, N. Tang, X. Wang, W. Ge, K. Xu and B. Shen, Phys. Rev. Lett., 2018, 121, 145505 CrossRef CAS PubMed
.
- L. Shi, K. Xu and L.-W. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205315 CrossRef
.
- H.-S. Zhang, L. Shi, X.-B. Yang, Y.-J. Zhao, K. Xu and L.-W. Wang, Adv. Opt. Mater., 2017, 5, 1700404 CrossRef
.
- Q.-J. Wang, H.-S. Zhang, L. Shi and J. Gong, J. Lumin., 2023, 255, 119561 CrossRef CAS
.
- A. Alkauskas, B. B. Buckley, D. D. Awschalom and C. G. van de Walle, New J. Phys., 2014, 16, 073026 CrossRef CAS
.
- A. Glensk, B. Grabowski, T. Hickel and J. Neugebauer, Phys. Rev. X, 2014, 4, 011018 CAS
.
- Z. S. Fatomi, A. D. Nugraheni and S. Sholihun, Comput. Condens. Matter, 2022, 32, e00708 CrossRef
.
- S. Sholihun, M. Saito, T. Ohno and T. Yamasaki, Jpn. J. Appl. Phys., 2015, 54, 041301 CrossRef
.
- P. Ágoston and K. Albe, Phys. Chem. Chem. Phys., 2009, 11, 3226–3232 RSC
.
- S. Moxon, J. Skelton, J. S. Tse, J. Flitcroft, A. Togo, D. J. Cooke, E. Lora da Silva, R. M. Harker, M. T. Storr, S. C. Parker and M. Molinari, J. Mater. Chem. A, 2022, 10, 1861–1875 RSC
.
- K. Tolborg, J. Klarbring, A. M. Ganose and A. Walsh, Digital Disc., 2022, 1, 586–595 RSC
.
- B. Cheng and M. Ceriotti, Phys. Rev. B, 2018, 97, 054102 CrossRef CAS
.
- B. Grabowski, L. Ismer, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134106 CrossRef
.
- A. I. Duff, T. Davey, D. Korbmacher, A. Glensk, B. Grabowski, J. Neugebauer and M. W. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214311 CrossRef
.
- A. S. Bochkarev, A. van Roekeghem, S. Mossa and N. Mingo, Phys. Rev. Mater., 2019, 3, 093803 CrossRef CAS
.
- A. M. Goryaeva, J. Dérès, C. Lapointe, P. Grigorev, T. D. Swinburne, J. R. Kermode, L. Ventelon, J. Baima and M.-C. Marinica, Phys. Rev. Mater., 2021, 5, 103803 CrossRef CAS
.
- B. Cheng, E. A. Engel, J. Behler, C. Dellago and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1110–1115 CrossRef CAS PubMed
.
- O. Hellman, I. Abrikosov and S. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301 CrossRef
.
- T. Tadano and S. Tsuneyuki, J. Phys. Soc. Jpn., 2018, 87, 041015 CrossRef
.
- L. Monacelli, R. Bianco, M. Cherubini, M. Calandra, I. Errea and F. Mauri, J. Condens. Matter Phys., 2021, 33, 363001 CrossRef CAS PubMed
.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104111 CrossRef
.
- Y. Oba, T. Tadano, R. Akashi and S. Tsuneyuki, Phys. Rev. Mater., 2019, 3, 033601 CrossRef CAS
.
- S. R. Kavanagh, D. O. Scanlon, A. Walsh and C. Freysoldt, Faraday Discuss., 2022, 239, 339–356 RSC
.
- J. Cen, B. Zhu, S. R. Kavanagh, A. G. Squires and D. O. Scanlon, J. Mater. Chem. A, 2023, 11, 13353–13370 RSC
.
- X. Zhang, J. Kang and S.-H. Wei, Nat. Comput. Sci., 2023, 3, 210–220 CrossRef
.
- C. P. Ewels, R. H. Telling, A. A. El-Barbary, M. I. Heggie and P. R. Briddon, Phys. Rev. Lett., 2003, 91, 025505 CrossRef CAS PubMed
.
- J. Klarbring, O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. Lett., 2020, 125, 045701 CrossRef CAS PubMed
.
- I. Errea, F. Belli, L. Monacelli, A. Sanna, T. Koretsune, T. Tadano, R. Bianco, M. Calandra, R. Arita and F. Mauri,
et al.
, Nature, 2020, 578, 66–69 CrossRef CAS PubMed
.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef
.
- D. Broberg, B. Medasani, N. E. R. Zimmermann, G. Yu, A. Canning, M. Haranczyk, M. Asta and G. Hautier, Comput. Phys. Commun., 2018, 226, 165–179 CrossRef CAS
.
- A. Goyal, P. Gorai, H. Peng, S. Lany and V. Stevanovic′, Comput. Mater. Sci., 2017, 130, 1–9 CrossRef
.
- M. Huang, Z. Zheng, Z. Dai, X. Guo, S. Wang, L. Jiang, J. Wei and S. Chen, J. Semicond., 2022, 43, 042101 CrossRef
.
- M. Arrigoni and G. K. H. Madsen, Comput. Phys. Commun., 2021, 264, 107946 CrossRef CAS
.
- J. Shen, pymatgen-analysis-defects (version 2023.04.05), 2023.
-
S. R. Kavanagh, K. Brlec, B. Zhu, A. Nicolson, S. Hachmioune, S. Aggarwal, A. Walsh and D. O. Scanlon, Defect Oriented Python Environment Distribution (DOPED) (version 1.1.2), 2023 Search PubMed
.
- Y.-T. Huang, S. R. Kavanagh, M. Righetto, M. Rusu, I. Levine, T. Unold, S. J. Zelewski, A. J. Sneyd, K. Zhang, L. Dai, A. J. Britton, J. Ye, J. Julin, M. Napari, Z. Zhang, J. Xiao, M. Laitinen, L. Torrente-Murciano, S. D. Stranks, A. Rao, L. M. Herz, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, Nat. Commun., 2022, 13, 1–13 Search PubMed
.
- O. I. Malyi and A. Zunger, Phys. Rev. Mater., 2023, 7, 044409 CrossRef CAS
.
- M. Choi, F. Oba, Y. Kumagai and I. Tanaka, Adv. Mater., 2013, 25, 86–90 CrossRef CAS PubMed
.
- Q. Zhang, T. Cagin and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14695–14700 CrossRef CAS PubMed
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- A. J. Jackson, D. Tiana and A. Walsh, Chem. Sci., 2016, 7, 1082–1092 RSC
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Condens. Matter Phys., 2017, 29, 273002 CrossRef PubMed
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
.
- C. Zhang, L. Spanu and G. Galli, J. Phys. Chem. B, 2011, 115, 14190–14195 CrossRef CAS PubMed
.
- NIST Chemistry WebBook DOI:10.18434/M32147 (accessed May 2023).
- J. Buckeridge, D. O. Scanlon, A. Walsh and C. R. A. Catlow, Comput. Phys. Commun., 2014, 185, 330–338 CrossRef CAS
.
- J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329–342 CrossRef CAS
.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, J. Open Source Softw., 2023, 8, 4962 CrossRef
.
- A. Nicolson, S. R. Kavanagh, C. N. Savory, G. W. Watson and D. O. Scanlon, J. Mater. Chem. A, 2023, 11, 14833–14839 RSC
.
- L. Villa and K. Albe, Phys. Rev. B, 2022, 106, 134101 CrossRef CAS
.
- S. Shousha, S. Khalil and M. Youssef, Phys. Chem. Chem. Phys., 2020, 22, 6308–6317 RSC
.
- J. George, G. Hautier, A. P. Bartók, G. Csányi and V. L. Deringer, J. Chem. Phys., 2020, 153, 044104 CrossRef CAS PubMed
.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed
.
- M. Pols, V. Brouwers, S. Calero and S. Tao, Chem. Commun., 2023, 59, 4660–4663 RSC
.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Acc. Chem. Res., 2021, 54, 808–817 CrossRef CAS PubMed
.
- F. K. Fong, Phys. Rev., 1969, 187, 1099 CrossRef CAS
.
- F. Kroger, Ann. Rev. Mater. Sci., 1977, 7, 449–475 CrossRef
.
- A. Lenef and S. C. Rand, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13441 CrossRef CAS PubMed
.
- A. R. Allnatt and E. Loftus, J. Chem. Phys., 1973, 59, 2541–2549 CrossRef CAS
.
- S. M. Tomlinson, C. R. A. Catlow and J. H. Harding, J. Phys. Chem. Solids, 1990, 51, 477–506 CrossRef CAS
.
- K. V. Sopiha, J. K. Larsen, J. Keller, M. Edoff, C. Platzer-Björkman and J. J. S. Scragg, Faraday Discuss., 2022, 239, 357–374 RSC
.
Footnotes |
| † Defects are often represented as Mcs with M being the defect or species occupying the lattice site s and with charge state c. |
‡ Note that in metal hosts there are only neutral defects, which simplifies eqn (15) to 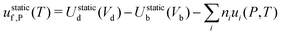 . . |
| § Finite-size corrections can still be applied by performing the geometry optimisation of the defect supercell in two steps – first optimising the atomic positions while constraining the shape and volume of the cell, then calculating the finite-size corrections, and finally performing a full optimisation. |
| ¶ While the effect of SOC on electronic structure can be significant, its role in geometry relaxation is often small; one pragmatic approach consists of geometry optimisation with scalar-relativistic DFT followed by single-point SOC calculations. |
| || When SOC is significant, for systems containing heavy elements, the total spin angular momentum should be considered to account for the possible combinations and orientations of the electron spins and their interaction with orbital motion. |
| ** Here we assume that the different configurations of a defect have the same contribution to the configurational entropy (i.e. different configurations involve the same type of lattice site). To consider defects that involve different lattice sites (e.g. Td and Oh for interstitials in cubic crystals), their respective concentrations should be calculated independently using eqn (8). |
| †† On the other hand, if the material is cooled sufficiently slowly from the growth to the operating temperature so that thermodynamic equilibrium can be assumed, then the defect concentrations should be calculated at the operating temperature without fixing the total defect populations.79,150 |
| This journal is © The Royal Society of Chemistry 2023 |