 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Issues on DFT+U calculations of organic diradicals†
Kohei
Tada
 *a and
Yasutaka
Kitagawa
*a and
Yasutaka
Kitagawa
 b
b
aResearch Institute of Electrochemical Energy, Department of Energy and Environment (RIECEN), National Institute of Advanced Industrial Science and Technology (AIST), 1-8-31 Midorigaoka, Ikeda, Osaka 563–8577, Japan. E-mail: k-tada@aist.go.jp; Tel: +81-72-751-8566
bDepartment of Materials Engineering Science, Graduate School of Engineering Science, Osaka University, Toyonaka, Osaka 560-8531, Japan
First published on 20th November 2023
Abstract
The diradical state is an important electronic state for understanding molecular functions and should be elucidated for the in silico design of functional molecules and their application to molecular devices. The density functional theory calculation with plane-wave basis and correction of the on-site Coulomb parameter U (DFT+U/plane-wave calculation) is a good candidate of high-throughput calculations of diradical-band interactions. However, it has not been investigated in detail to what extent the DFT+U/plane-wave calculation can be used to calculate organic diradicals with a high degree of accuracy. In the present study, using typical organic diradical molecules (bisphenalenyl molecules) as model systems, the discrepancy in the optimum U values between the two electronic states (open-shell singlet and triplet) that compose the diradical state is detected. The calculated results show that the reason for this U value discrepancy is the difference in electronic delocalisation due to π-conjugation between the open-shell singlet and triplet states, and that the effect of U discrepancy becomes large as diradical character decreases. This indicates that it is necessary to investigate the U value discrepancy with reference to the calculated results by more accurate methods or to experimental values when calculating organic diradicals with low diradical character. For this investigation, the local magnetic moments, unpaired beta electron numbers, and effective magnetic exchange integral values can be used as reference values. For the effective magnetic exchange integral values, the effects of U discrepancy are partially cancelled out. However, because the effects may not be completely offset, care should be taken when using the effective magnetic exchange integral value as a reference. Furthermore, a comparison of DFT+U and hybrid-DFT calculations shows that the DFT+U underestimates the HOMO–LUMO gap of bisphenalenyls, although a qualitative discussion of the gap is possible.
1. Introduction
The diradical state is important for elucidating and predicting the function of open-shell molecules.1–10 In particular, the investigation of open-shell singlet states is important for understanding chemical reactions and material functions.1,4,11–13 Open-shell structures are often stabilised in complexes with transition metal ions, whereas even pure organic compounds without transition metals can stabilise open-shell electrons owing to π-conjugation and substituents, such as phenalenyl14 and trioxotriangulen.15 The linking of these stable organic radicals spatially or through bonding provides unique open-shell singlet states.14–26 These unique electronic states lead to organic magnetic materials,16–19 environmental material functions,20–22 unique optical properties,23–25 and electronic conductivity.26,27 Hence, stable organic biradicals have been actively studied.To develop functional molecules as devices, the molecules need to be aligned on a stable substrate.28–33 However, knowledge regarding the effects of molecular/surface interactions on the open-shell singlet state is lacking. This is because analytical techniques based on theoretical calculations and experimental observations of surface diradical states have not yet been developed. Further, it is known that molecular stacking affects material properties and molecular functions, although quantum chemical calculations were performed using models cut from the crystal structure. The cut models sometimes provide insights into molecular functions,25,34–40 but the computational costs are generally too high to mimic the electronic structures of bulk systems, and high-throughput calculations are difficult. Therefore, the correlation between molecular stacking and function, as well as the influence of substrate interactions on stacking, remains unclear; it is a barrier to in silico design.
In recent years, techniques have been developed to analyse diradical states from the results of density functional theory calculations with a plane-wave basis (DFT/plane-wave calculation),10,41–43 which are high-throughput first-principle methods for surfaces and solids.44,45 The diradical character is a characteristic quantity of the open-shell singlet state, which is correlated with magnetism, optical properties, electronic conductivity, and reactivity (catalytic activity).1–10,23 It was reported that the diradical character can be estimated using the charge density distributions obtained from DFT/plane-wave calculations.10,43 Effects of surface interaction on the diradical character were investigated for model systems with s electrons in magnetic orbitals.10,46 The previous studies confirmed that diradical characters of s-electron model systems are varied by surface interactions, even when there is no clear electron transfer between the molecules and surfaces. The magnetic orbitals of the model diradicals are polarised by the surface ion species, and the polarisation causes the increase of diradical character. In addition, studies were conducted on real molecules such as p-benzyne and bisphenalenyls.47,48 Even in the real molecules, as in the model molecules, the diradical characters were varied due to the polarisation effect of the surface on the magnetic orbitals. The contribution of resonance structures of the p-benzyne is affected by the surface adsorption, and the variation causes a decrease of diradical character, which mechanism was not observed in the model molecular system.47
Although theoretical investigation using the diradical molecules in real is important, open-shell singlet states of some organic diradicals are not converged when using the pure-DFT methods.43,48,49 The self-interaction error (SIE) has a large effect in the pure-DFT,50 and the closed-shell singlet state in which electrons are delocalised is too stabilised in the calculations of organic diradicals by pure-DFT. The over-delocalisation was also detected in the calculated results of organic molecules by pure-DFT/plane-wave method.48 This indicates that the number of organic diradicals that can be studied by the pure-DFT method is severely limited, because the open-shell singlet is the key electronic structure that constitutes the diradical state. In molecular orbital calculations using atom-centred basis sets, the hybrid-DFT, post-Hartree–Fock, or both methods are essential approaches for the calculation of organic diradicals.1,49 On the other hand, the computational costs of hybrid-DFT and post-HF methods are high for band calculations of periodic systems, such as using plane-wave basis. Especially in surface adsorption state calculations, it is often difficult to perform hybrid-DFT calculations because of the large number of atoms in the calculation model, which results in a large computational cost. Therefore, in the theoretical calculations for solid-state electronic structures, on-site Coulomb parameters are used to correct the SIE in the pure-DFT method and to obtain spin-polarised states; this approach is known as DFT+U method.51–55 Since the computational costs of the DFT+U and pure-DFT methods are comparative, informatics research using high-throughput results by the DFT+U/plane-wave is very active.44,45
Data-driven study for novel molecular devices using the unique functions of diradical molecules requires computational methods that can handle both diradical states and solid-state bands with high accuracy and low cost. The DFT+U/plane-wave method would be a good candidate for such a method. However, it has not been investigated in detail to what extent the DFT+U/plane-wave method can be used to calculate organic diradicals with a high degree of accuracy. In this study, hybrid-DFT/plane-wave and DFT+U/plane-wave calculations were performed for two molecules for which experimental values of diradical character have been reported.23 The comparison detects the issues on the DFT+U calculations of organic diradical, U value discrepancy between singlet and triple states. The cause of this discrepancy is discussed to investigate how to apply DFT+U method to systems including organic biradicals.
2. Method
Fig. 1 shows the calculated molecular structure. The molecules belong to bisphenalenyl (Fig. 1(b)), in which the phenalenyl framework (Fig. 1(a)) is connected via conjugation bonds.14 Mol 1 (Fig. 1(c)) is a molecule with N = 1, and Mol 2 (Fig. 1(d)) is a molecule with N = 2, having benzene and naphthalene embedded, respectively. The diradical characters of Mol 1 and Mol 2 were experimentally determined from their absorption and fluorescence spectra,23 and the values are shown in Fig. 1. It has been clarified from both experiments and computations that Mol 2 has a larger distance between the biradicals, which results in greater spin localisation and diradical character.14,23,43 Geometries reported in previous studies23,43 were used for the calculations. | ||
| Fig. 1 (a) Phenalenyl framework, and (b) bisphenalenyl framework. Bisphenalenyl is the molecule that has two phenalenyl framework with linked five- and six-membered rings. (c) the Mol 1 that is a bisphenalenyl molecule with N = 1, and (d) the Mol 2 that is a bisphenalenyl molecule with N = 2. The experimental y values reported in the prior work23 are shown for the Mol 1 and Mol 2. The brown and white sticks represent the C and H atoms, respectively. | ||
The Vienna Ab initio Simulation Package (VASP)56–59 was used for the DFT calculations. The generalised gradient approximation proposed by Perdew, Burke, and Ernzerhof (GGA-PBE)60 was adopted for exchange–correlation functional of DFT+U calculations. The PBE0 functional61 was used for the hybrid-DFT calculations. The dependence of the diradical character of bisphenalenyl estimated by DFT on the exchange–correlation functional was discussed in a previous study, and the PBE0 functional showed good agreement with the experimental values.43 The cut-off energy of the wavefunction was 500 eV unless otherwise specified. The wavefunction was expanded using a plane-wave basis, and the core region was treated using the projector-augmented wavefunction (PAW) method.62,63 In the PAW method, the numbers of valence electrons of the C and H atoms were set to four (2s22p2) and one (1s1), respectively. A supercell with a vacuum region was used for the DFT/plane-wave calculations; the specific cell size was 30.00 × 15.00 × 45.00 Å3. The molecules calculated in this study have mirror-symmetries in the x, y and z directions (except for z direction for tertial-Bu), the artificial dipoles causing in periodic boundary conditions disappears when a sufficient vacuum region is set up in the supercell models. The orbital polarisation effects caused by the stacking of diradical molecules are negligible when using sufficient large vacuum regions.47 Therefore, in this study, a sufficient vacuum region was adapted, and no dipole correction was added. The sampled k-point was only at the Γ-points because of the calculation of molecules using the supercell. In the computational conditions and models, there was a difference of more than 104 times in the execution time between the DFT+U/plane-wave and hybrid-DFT/plane-wave calculations. The geometry and spin distributions were visualised using Visualization for Electronic and STructural Analysis (VESTA) programme.64
The diradical character is defined as the contribution of a two-electron excited configuration in the ground electronic state.1,2,6–10,43 When performing molecular orbital calculations, the diradical character can be analytically calculated from the results of natural orbital analysis.1,9 In addition, the character can be approximated using the electron-density distribution.10,43eqn (1) is based on electron density.
 | (1a) |
 | (1b) |
ρ (α)X(r) and ρ(β)X(r) represent the density of alpha electrons (electron with major spin) and of beta electrons (electrons with minor spin), respectively, while subscript “X” represents the electronic state. In this study, the low-spin state (LS) corresponds to the open-shell singlet, and the high-spin state (HS) corresponds to the triplet state. The diradical character is represented by “y”, and herein, referred to as the y value. The approximate accuracy of eqn (1) has been discussed in previous studies,10,43 and the values estimated using eqn (1) for Mol 1 and Mol 2 are in quantitative agreement with the natural orbital analysis results.43 In this study, the y values were calculated from the electron density distributions obtained by DFT+U/plane-wave and hybrid-DFT/plane-wave calculations using eqn (1).
3. Results and discussion
The energy cut-off (Ecut) dependence of the y value of Mol 1 in the DFT+U/plane-wave calculations was discussed in a previous study and was constant from 400 or 500 eV.48Fig. 2(a) and (b) show the Ecut dependence of the y values of Mol 1 and Mol 2 in the PBE0/plane-wave calculations. The difference between the y values at 400 and 500 eV was 0.002 or less; hence, it was assumed that the y values converged to a constant value. The spin density distribution at Ecut = 500 eV shown in Fig. 2(c) and (d) is similar to that reported in previous studies,14,16–18,20,21,26 and the electronic state in which antiparallel spins are localised on two phenalenyls (open-shell singlet state) was obtained as the ground electronic state. The calculated y values by PBE0/plane-wave were 0.125 for Mol 1 and 0.342 for Mol 2. These values are in qualitative agreement with the experimental results. PBE0 functional shows better agreement with experimental values when compared to the B3LYP functional which is commonly used for DFT calculations of y values.43 Hence, in this study, the results of the PBE0/plane-wave at Ecut = 500 eV were used as reference values for the DFT+U/plane-wave calculations. However, the calculated y values by the PBE0/plane-wave (Fig. 2(c) and (d)) and those experimental ones (Fig. 1(c) and (d)) are not in quantitative agreement. For a more accurate theoretical prediction, a study on “what is the best approach to quantitatively calculate the y values for in silico design” is needed (this has already been attempted by many theoretical chemists but no consensus for the method has been reached1,23).Fig. 3 shows the U dependence of the y values of Mol 1 and Mol 2. The y values on the vertical axis are plotted as differences from the values calculated using PBE0. The specific y values are shown in Fig. S1 and S2 (ESI†). The spin density distributions of the calculated singlet state are also shown in Fig. S1 and S2 (ESI†). The spin polarisation was very small (negligible) for U < 4 eV in Mol 1 and also for U = 0 eV (pure-DFT, GGA-PBE) in Mol 2 (see Fig. S1–S4, ESI†); these singlet states are regarded not as open-shell singlet but as closed-shell singlet. Thus, the bisphenalenyl molecules shown in Fig. 1 are organic diradicals for which open-shell singlet cannot be investigated by the pure-DFT method, requiring the application of the DFT+U or hybrid-DFT methods. In addition, as shown the results of Mol 1 with U = 4 eV, the spin distribution is quite different from those of U > 5 eV: the spins on the neighbouring carbon atoms of the carbon atom where the spins are predominantly localised are extremely small (it is almost zero). Hence, Fig. 3 does not show the U dependence at U < 5 eV for Mol 1 and U < 1 eV for Mol 2. Similar to the U dependence reported in a previous study,48 the optimum U values were in the range of 11–12 eV. The spin density distributions (Fig. S5 and S6, ESI†) confirm that the electronic states estimated by DFT+U/plane-wave (U = 11 and 12 eV) and PBE0/plane-wave are similar, although the U values are large. However, the results of the DFT+U/plane-wave calculations seem to show a larger localisation of spin distributions for Mol 1 and Mol 2 than those of the PBE0/plane-wave calculations.
To analyse the difference in spin localisation quantitatively, the local magnetic moment for each atom was calculated using eqn (2):65
 | (2) |
The spins on the phenalenyls are not localised to one atom but are distributed over several carbon atoms. Therefore, carbon atoms are grouped according to the amounts of localised spins: G1 atoms have relatively large spin localisation, G2 atoms have relatively small spin localisation, and G3 atoms have negligible spin polarisation. Tables S1–S4 (ESI†) summarise the groupings. Fig. S8–S11 (ESI†) show the dependence of the local magnetic moments of G1 and G2 groups on U values (Fig. S8: BS of Mol 1; Fig. S9: HS of Mol 1; Fig. S10: BS of Mol 2; S11: HS of Mol 2, ESI†). The local magnetic moments on the vertical axis differ from the PBE0 results. For both Mol 1 and Mol 2, the differences in the optimal U values between the singlet and triplet states were significant.
The results shown in Fig. S4(a, b) and S6(a, b) (ESI†) confirm that the local magnetic moment in the singlet state of the carbon atoms belonging to G1 is symmetric between the up- and down-spin; hence, it is sufficient to focus on the three carbon atoms. Specifically, the atoms are C11, C14, and C19 in Mol 1 and C28, C31, and C36 in Mol 2. Fig. 4 shows the regression curves obtained by the least-squares method using the calculated values for the carbon atoms. The values of a, b, and c in the obtained regression curves (Δmproj(i) = aU2 + bU +c) and the U value corresponding to Δmproj(i) = 0 are listed in Table 1. Discrepancies of 1.7 eV for Mol 1 and 1.1 eV for Mol 2 were detected at the optimal U values between the singlet and triplet states.
| Molecule | Atom | State | A | b | c | U [eV] |
|---|---|---|---|---|---|---|
| Mol 1 | C11 | LS | 0.0053 | 1.1659 | −9.7385 | 8.0 |
| HS | 0.0375 | 0.0960 | −2.0856 | 6.3 | ||
| C14 | LS | −0.0061 | 1.4061 | −11.761 | 8.7 | |
| HS | 0.0318 | 0.1748 | −2.7752 | 7.0 | ||
| C19 | LS | −0.0114 | 1.3123 | −11.337 | 9.4 | |
| HS | 0.0299 | 0.0739 | −2.3092 | 7.6 | ||
| Mol 2 | C28 | LS | −0.0143 | 1.3291 | −9.1250 | 7.5 |
| HS | 0.0304 | 0.2996 | −3.1023 | 6.3 | ||
| C31 | LS | −0.0159 | 1.2611 | −9.0795 | 8.0 | |
| HS | 0.0272 | 0.2629 | −3.1432 | 7.0 | ||
| C36 | LS | −0.0219 | 1.2278 | −9.1955 | 8.9 | |
| HS | 0.0222 | 0.2215 | −3.0773 | 7.8 | ||
Table 2 summarises the estimated y values using the U values listed in Table 1. When the same U value was used for the singlet and triplet states, the y values obtained by DFT+U deviated from the PBE0 result. By contrast, when the U discrepancy in the optimal value for the local magnetic moment was considered, the estimated y values approached the PBE0 value. In particular, when the singlet state was calculated at U = 8 eV, the y values agreed with a difference of less than 0.0024. This value of U = 8 eV was obtained from the fitting curves for C11 in Mol 1 and C31 in Mol 2. Furthermore, it was detected that this optimum U = 8 eV for the LS is the U value where the unpaired beta electron number of LS in eqn (1),  , estimated using the DFT+U result is equal to that of the PBE0 result (Fig. 5(a) and (b)). As shown in the U dependence of the unpaired beta electron number of HS (Fig. 5(c) and (d)), the optimum U values were different from those of LS. The specific values of the optimum U values for unpaired electron beta number were estimated by the same way as that for local magnetic moment: LS of Mol 1 (U = 8.3 eV), HS of Mol 1 (U = 7.0 eV), LS of Mol 2 (U = 8.0 eV), and HS of Mol 2 (U = 7.0 eV). For Mol 1, the y value was estimated by taking into account the discrepancy of the optimum U value in the unpaired beta electron number, and it was 0.112, whose difference from the PBE0/plane-wave result was 0.013. Hence, it can be concluded that the U value discrepancy can be estimated using the unpaired beta electron number or the local magnetic moment.
, estimated using the DFT+U result is equal to that of the PBE0 result (Fig. 5(a) and (b)). As shown in the U dependence of the unpaired beta electron number of HS (Fig. 5(c) and (d)), the optimum U values were different from those of LS. The specific values of the optimum U values for unpaired electron beta number were estimated by the same way as that for local magnetic moment: LS of Mol 1 (U = 8.3 eV), HS of Mol 1 (U = 7.0 eV), LS of Mol 2 (U = 8.0 eV), and HS of Mol 2 (U = 7.0 eV). For Mol 1, the y value was estimated by taking into account the discrepancy of the optimum U value in the unpaired beta electron number, and it was 0.112, whose difference from the PBE0/plane-wave result was 0.013. Hence, it can be concluded that the U value discrepancy can be estimated using the unpaired beta electron number or the local magnetic moment.
| Molecule | U (LS) [eV] | U (HS) [eV] | y (Δy) |
|---|---|---|---|
| Mol 1 | 8.0 | 8.0 | 0.0389 (−0.0862) |
| 8.0 | 6.3 | 0.1227 (−0.0024) | |
| 6.3 | 6.3 | 0.0126 (−0.1125) | |
| 8.7 | 8.7 | 0.0531 (−0.0720) | |
| 8.7 | 7.0 | 0.1729 (0.0478) | |
| 7.0 | 7.0 | 0.0220 (−0.1031) | |
| 9.4 | 9.4 | 0.0693 (−0.0558) | |
| 9.4 | 7.6 | 0.2554 (0.1303) | |
| 7.6 | 7.6 | 0.0317 (−0.0934) | |
| Mol 2 | 7.5 | 7.5 | 0.1525 (−0.1897) |
| 7.5 | 6.3 | 0.3322 (−0.0100) | |
| 6.3 | 6.3 | 0.1143 (−0.2279) | |
| 8.0 | 8.0 | 0.1697 (−0.1725) | |
| 8.0 | 7.0 | 0.3410 (−0.0012) | |
| 7.0 | 7.0 | 0.1361 (−0.2061) | |
| 8.9 | 8.9 | 0.2029 (−0.1393) | |
| 8.9 | 7.8 | 0.4941 (0.1519) | |
| 7.8 | 7.8 | 0.1627 (−0.1795) | |
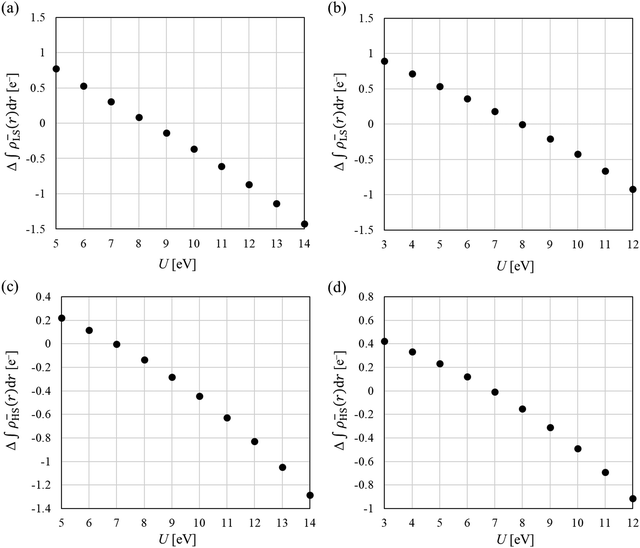 | ||
Fig. 5 Dependence of  and and  values on the U values. (a) values on the U values. (a)  of Mol 1, (b) of Mol 1, (b) 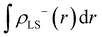 of Mol 2, (c) of Mol 2, (c)  of Mol 1, and (d) of Mol 1, and (d)  of Mol 2. of Mol 2. | ||
It was revealed that by considering the discrepancy in the optimal U value for the local magnetic moment or unpaired beta electron number, it is possible to perform DFT+U/plane-wave calculations with reasonable values of U corrections for both the local spin quantities and diradical character. Is this U discrepancy universal to organic biradicals? Is this phenomenon specific to bisphenalenyl systems? This should be clarified for the theoretical investigations of biradical molecules using DFT+U calculations.
On-site Coulomb corrections such as the DFT+U method are generally used for oxides of 3d/4f transition metals.51–55 When transition oxides are calculated at the local density approximation level (LDA), the interactions between metal ions are artificially strong, and d/f electrons are delocalised among the ions. Although this tendency still occurs at the GGA level, d/f electrons can be localised on the metal by adding repulsion among the d/f electrons as an on-site Coulomb parameter (GGA+U method). In the case of metal oxides, electron delocalisation in LDA and GGA is artificial because the electrons should be localised on the metal ions, even in the AFM state.51–55,66 By adding U parameter until the artificial delocalisation is cancelled, calculated values close to those of the hybrid-DFT and the experiment can be obtained. In the case of organic biradicals, the p electrons are delocalised on carbons; hence, the on-site Coulomb parameter U is added to their p orbitals. Organic biradical systems differ from oxides in that the neighbouring sites are composed of the same element (carbon) rather than different elements (metal and oxygen). This indicates that the spins are antiparallel coupled between neighbouring carbons. In closed-shell organic compounds, the antiparallel coupling spins are pseudo-spins, and the electrons become either π-conjugated or covalent electron pairs. Therefore, in organic biradical systems, electron delocalisation due to orbital hybridisation between neighbouring spin sites is greater than in oxide systems (there is significant non-artificial electron delocalisation). This electron delocalisation leads to diradical states in the organic biradicals. The electron delocalisation in the organic diradical differs between LS (singlet, spins are anti-parallel coupled) and HS (triplet, spins are parallel coupled) states. The electron exchange interaction in the triplet state is larger than that in the singlet state, resulting in a more localised solution and closer inter-electron distances. In DFT, on the other hand, artificial electron delocalisation occurs as described above, which is explained as SIE.50 The SIE is repulsions by the electrons themselves, which should cancel out with the exchange interaction. The effect of SIE can be significantly reduced by partially mixing the Hartree–Fock exchange term, for which the exchange interaction can be calculated correctly, into the DFT exchange functional (hybrid-DFT method such as PBE0). The pure-DFT method, such as GGA-PBE, cannot calculate the exchange interaction correctly, resulting in a solution with over-delocalised electrons in the LS state. The similar delocalisation would occur in the HS state; however, the effect of SIE is smaller than in the LS state because the HS state is an electronic state with a large exchange interaction. Therefore, the difference in the LS states between the hybrid-DFT, which has small SIE, and pure-DFT methods, which has large SIE, is not the same as that of the HS state; to fill the difference between hybrid-DFT and pure-DFT, the on-site coulomb U is added, but the required U values are not equal in the LS and HS states. This is the detected U discrepancy in the present study. Additionally, the spin localisation may differ due to the different asymmetries of orbitals other than the magnetic orbitals in the LS and HS states. In the estimation of y value using the charge density (eqn (1)), the HS state is used as a reference for the effects of SIE and broken-symmetric orbital overlaps (see the derivation in previous studies10,43,67). However, these effects could not be cancelled out due to the misalignment of the optimal U values for LS/HS.
The difference in electron delocalisation between the LS and HS states causes a U discrepancy in the local magnetic moment. When the triplet was calculated with the same U value as the singlet, a triplet state with over-localised spins was obtained due to the large exchange interactions. In addition, the values of the overlap integral associated with the broken-symmetric orbital will also differ between the LS and HS states due to the U discrepancy. Although it is unclear which the SIE or orbital asymmetries has the greater effect, they lead to an underestimation of the spin polarisation of the LS state.10,43 In fact, the results presented in Table 2 show that the y values decrease when the U value of the triplet state is calculated to be the same U value as that of the singlet (i.e., when the spin polarisation of the triplet state is overdetermined). Because of this underestimation, an unusually large U correction is required when LS and HS are calculated with the same U value to obtain the same y value as that of the hybrid-DFT.
When comparing the discrepancy in the optimal U values between Mol 1 and Mol 2, the discrepancy for Mol 2 was smaller. This can be explained by the discussion in the previous paragraph. The discrepancies in the U values at LS and HS of the bisphenalenyl were due to electron delocalisation via π conjugation affecting the localised spins. Concisely, if spin localisation is high, as in d-electron-containing oxides, the U value discrepancy will be small. Bisphenalenyl molecules exhibit larger spin localisation as the number of interconjugations linking the two phenalenyl framework increases.14 Therefore, comparing the Mol and Mol 2, Mol 2 exhibited higher spin localisation, larger y values, and smaller LS/HS U value deviations. This suggests that the influence of the LS/HS U value discrepancy on the organic biradicals was more pronounced at small y values.
Finally, U dependencies of other indicators are discussed. The effective magnetic exchange integral (J value) is a useful indicator for investigating the strength of the magnetic coupling. However, it is known that the spin contamination error affects the calculated J values by the DFT methods.3–5,9,10,37–42,68,69 The Yamaguchi equation (eqn (3)) is a formula for calculating J values with correction for spin contamination errors and is widely used in the calculation of J values of molecules.5,9,42,68
 | (3) |
 | (4) |
 | ||
| Fig. 6 Difference between the J values estimated by PBE0 and DFT+U scheme, whose U values are shown in Table 2. The red dot represent the J value was estimated by different U values of LS and HS states. (a) Mol 1, and (b) Mol 2. | ||
The Yamaguchi equation used to calculate J value (eqn (3) and (4)) includes the subtraction of LS and HS in both the denominator and numerator. Therefore, even if the optimal value of U deviates between LS and HS, it will be “partially offset”, and the effect will be small. The difference between PBE0 and DFT+U in the denominator of eqn (4) is defined as Err(ρ), and the difference in the numerator is as Err(E),
 | (5) |
| Err(E) = (ELS;DFT+U − EHS;DFT+U) − (ELS;PBE0 − EHS;PBE0). | (6) |
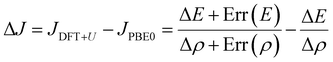 | (7) |
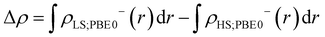 | (8) |
| ΔE = ELS;PBE0 − EHS;PBE0 | (9) |
 | (10) |
 | ||
| Fig. 7 Dependences of ΔE·Err(ρ) and Δρ·Err(E) values on on-site Coulomb parameter U. (a) Mol 1, and (b) Mol 2. | ||
Next, we discuss whether the J values can be calculated more accurately by considering the U discrepancy. Calculating the J value requires not only the charge density but also the total energy. In the DFT+U method, energy comparison between different U is not possible because of the U parameter. Hence, in this study, the charge densities were obtained for the optimal U of the HS state (Mol 1: 6.3 eV, Mol 2: 7.0 eV), and the total energy was calculated using the optimal U of the LS state with fixing the charge density. The results are shown as red circles in Fig. 6. Considering the discrepancy in the U value, the J values were calculated to be positively large, and results consistent with PBE0 were not obtained. The difference from the J value of PBE0 increased because the charge density in the HS state was not in a self-consistent field at the U values for the total energy calculation (optimum U value in the LS state). As total energies are required and the effect of U discrepancy cancels out during the calculation of J value, therefore, it can be concluded that qualitative (and in some cases quantitative) discussions are possible by using the same U values of the LS and HS states (the U values can be optimised using the local magnetic moment or unpaired β electron numbers). Moreover, because the J value is a physical quantity that can be quantified experimentally, when the J value is close to zero, it can be used to optimise the U parameter.
Fig. 8 shows the HOMO (SOMO)–LUMO gap (H–L gap) of α electrons in the LS state determined by the DFT+U method as the difference from PBE0. Here, HOMO is the highest occupied molecular orbital, SOMO is the singly occupied molecular orbital, and LUMO is the lowest occupied molecular orbital. The PBE0 method is a functional with high quantification for the calculation of the bandgap70 and was used as a reference value. The H–L gaps in the PBE0 method used in this study were 1.9684 eV for Mol 1 and 1.914 eV for Mol 2. In the range of the investigated U values (0–15 eV), the DFT+U method consistently underestimates the H–L gap. The underestimations on the H–L gaps at U = 0 eV (calculated results by pure-DFT) are the largest: specifically, 1.34 eV (Mol 1) and 1.45 eV (Mol 2). Additionally, H–L gap of Mol 1 is constant in U = 0–3 eV. This is because the stable singlet state is estimated to be the states with closed-shell structure (Fig. S1, ESI†). Thus, the pure-DFT method incorrectly estimates ground electronic states of some organic diradicals, and the H–L gaps are also greatly underestimated.
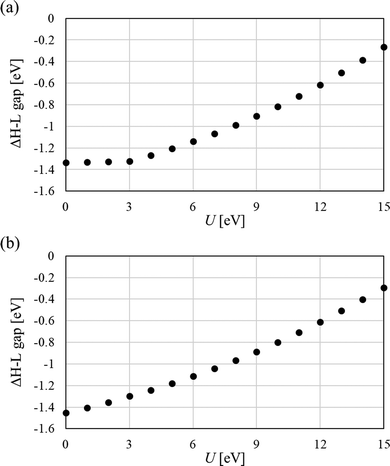 | ||
| Fig. 8 Difference between the HOMO–LUMO gap estimated by PBE0 and DFT+U scheme (U = 0 indicates pure-DFT, GGA-PBE, calculation). (a) Mol 1, and (b) Mol 2. | ||
Regression was performed using a quadratic function (values of U = 0–3 eV in Mol 1 and U = 0 eV in Mol 2 were not used in this regression analysis). The U value for which the H–L gap matches PBE0 was calculated from the regression equation: U = 17.0 eV for Mol 1 and U = 17.6 eV for Mol 2 are obtained. Additionally, the H–L gaps at the optimum U value (U = 8 eV) in y value calculation were Mol 1: 0.9787 eV and Mol 2: 0.9456 eV, respectively. These results indicate that an H–L gap close to that of the hybrid-DFT functional can be obtained by increasing U, but the DFT+U method underestimates the H–L gap. The correction to the exchange term to eliminate the effect of SIE is insufficient for the calculation of organic diradicals by the DFT+U method. Nevertheless, the DFT+U method does not give qualitatively wrong results as the pure-DFT method does (see Fig. 8(a), the calculated result for Mol 1). Therefore, quantitative calculation of the H–L gap and bandgap derived from organic biradicals requires hybrid DFT calculations or more accurate methods, whereas the DFT+U method can be used for qualitative investigation while accepting underestimation.
4. Conclusion and outlooks
The DFT+U/plane-wave method is a good candidate for a computational method that can handle both diradical states and solid-state bands with high accuracy and low cost, making high-throughput calculations of diradical-band interactions a powerful tool for molecular device development. However, the degree to which organic diradicals can be calculated with accuracy using the DFT+U/plane-wave method has not been investigated in detail. A comparison of the DFT+U and hybrid-DFT methods revealed the issues on the DFT+U method of organic diradicals, and what is the better U value to calculate the characteristic quantities of diradicals, such as diradical character, local magnetic moment, effective magnetic exchange integral value and HOMO–LUMO gap, was discussed.In DFT+U calculations of organic diradicals, the discrepancy in the optimum U values for the LS and HS states was detected by analysing the diradical character and local magnetic moment. This U value discrepancy is caused by the difference in electron delocalisation to π-conjugation in the LS/HS states. Therefore, molecules with a large spin localisation will have small U discrepancies, whereas molecules with small y values (small spin localisation) will have significant effect. When calculating organic biradicals with small y values using the DFT+U method, the U discrepancy should be investigated by referring to the calculated results of the hybrid-DFT method (or a more accurate method) and experimental values. For the optimisation of the U values using the results of hybrid DFT, the local magnetic moment, the number of unpaired β electrons  or J values can be used as reference values. When using the experimental values, the J value can be used as a reference. This is because the U discrepancy was partially cancelled out in the J value calculation. However, this does not always cancel out completely; therefore, care should be taken when using the J value as a reference. In addition, the DFT+U method underestimated the HOMO–LUMO gap compared to the hybrid-DFT method. Although this underestimation decreased by increasing the U value, excessive U values may change the electronic state significantly. A qualitative investigation of the HOMO–LUMO gap is possible even when using the DFT+U method; hence, the gap should be investigated while accepting the underestimation.
or J values can be used as reference values. When using the experimental values, the J value can be used as a reference. This is because the U discrepancy was partially cancelled out in the J value calculation. However, this does not always cancel out completely; therefore, care should be taken when using the J value as a reference. In addition, the DFT+U method underestimated the HOMO–LUMO gap compared to the hybrid-DFT method. Although this underestimation decreased by increasing the U value, excessive U values may change the electronic state significantly. A qualitative investigation of the HOMO–LUMO gap is possible even when using the DFT+U method; hence, the gap should be investigated while accepting the underestimation.
From the results and discussion, we suggested a better U values for bisphenarenyl: approximately 8 eV. However, we assume this is not the best U value. One of the causes of the issues identified in this study is that the effect of SIE is significantly differed between open-singlet and triplet states of organic diradicals. Open-singlet and triplet are the key electronic configurations that construct the diradical state of biradical systems, and discrepancy of the optimum U values in them are fatal when quantitatively investigating the organic diradicals. Unfortunately, the current DFT+U strategy cannot overcome this problem. The development of a new DFT+U scheme for calculating organic diradicals quantitatively (or a completely new approach to replace the DFT+U method) is an open question. To answer this question, (A) identifying the computational method that gives the best reference value, and (B) drawing a calibration curve (perhaps, machine learning approach will be needed) so that the DFT+U method can reproduce the reference values should be conducted. In this study, the PBE0/plane-wave calculation is used as the reference value for the PBE+U/plane-wave calculation. The reason for this adoption was that PBE0 functional gives y values relatively close to the experimental values. However, the calculated y values by PBE0 are not in quantitative agreement with the experimental values. Thus, it is important to identify a method for quantifying y values (the project A). A discussion on whether Hybrid-DFT should be used as a reference is also needed. The second-order Møller–Plesset (MP2) method71,72 is close in computational cost to the DFT method and is an alternative candidate to the hybrid-DFT method. The MP2 calculations of diradical molecules with high accuracy require the correction of spin contamination, special approaches such as APUMP2.73,74 More accurate approaches such as multi-referenced methods may also be required. Then, to put the project B into practice, it will be necessary to calculate reference values for other organic diradicals in addition to the bisphenarenyl system considered in this study. We have already performed it using several organic diradicals.75 To complete the project B, it is also important to speed up the DFT+U/plane-wave calculation. In the present study, a large vacuum region was used to reduce the influence of artificial dipoles produced by supercell models, but such a large vacuum region increases the computational cost meaninglessly. It is therefore necessary to discuss dipole correction methods when calculating organic diradicals under periodic conditions. Development of the combined scheme of the effective screening medium (ESM) method76–79 and the spin approximation projection method12,13,41,42,73 will be a promising approach. The ESM method corrects for the artificial dipole by inserting virtual electrodes and allows discussion of the effects of applying electric fields and the charged systems. The development of DFT/plane-wave with ESM and spin projection is interesting from the perspective of functional design of molecular devices, because it has been found that the diradical characters of model diradicals adsorbed on surfaces are tuned by combining the surface fields and electric fields.80 The issues on the DFT+U method identified in this study thus present an important research theme of developing the best method to study diradical–solid interactions.
Author contributions
K. T. conceived the study and performed the computations. K. T. analysed the data with input from Y. K. All authors discussed the results and commented on the manuscript, which was written by K. T.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computational work in this study was conducted at the Research Institute for Information Technology, Kyushu University (ITO). This study was conducted under the auspices of the Japan Society for the Promotion of Science (JSPS KAKENHI; Grant Number 22H02050).References
- T. Stuyver, B. Chen, T. Zeng, P. Geerlings, F. De Proft and R. Hoffinann, Do Diradicals Behave Like Radicals, Chem. Rev., 2019, 119, 11291–11351, DOI:10.1021/acs.chemrev.9b00260.
- T. Stuyver, T. Zeng, Y. Tsuji, P. Geerlings and F. De Proft, Diradical character as a guiding principle for the insightful design of molecular nanowires with an increasing conductance with length, Nano Lett., 2018, 18, 7298–7304, DOI:10.1021/acs.nanolett.8b03503.
- J. P. Malrieu, R. Coballol, C. J. Calzado, C. de Graaf and N. Guihery, Magnetic interactions in molecules and highly correlated materials: physical content, analytical derivation, and rigorous extraction of magnetic Hamiltonians, Chem. Rev., 2014, 114, 429–492, DOI:10.1021/cr300500z.
- G. David, F. Wennmohs, F. Neese and N. Ferre, Chemical tuning of magnetic exchange couplings using broken-symmetry density functional theory, Inorg. Chem., 2018, 57, 12769–12776, DOI:10.1021/acs.inorgchem.8b01970.
- S. Paul and A. Misra, Interpretation and Quantification of Magnetic Interaction through Spin Topology, J. Chem. Theory Comput., 2012, 8(3), 843–853, DOI:10.1021/ct2006506.
- M. Nakano and B. Champagne, Theoretical Design of Open-Shell Singlet Molecular Systems for Non-linear Optics, J. Phys. Chem. Lett., 2015, 6, 3236–3256, DOI:10.1021/acs.jpclett.5b00956.
- S. Muhammad, M. Nakano, A. G. Al-Sehemi, Y. Kitagawa, A. Irfan, A. R. Chaudhry, R. Kishi, S. Ito, K. Yoneda and K. Fukuda, Role of a singlet diradical character in carbon nanomaterials: a novel hot spot for efficient non-linear optical materials, Nanoscale, 2016, 8, 17998–18020, 10.1039/C6NR06097H.
- G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. P. Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Diindeno-fusion of an anthracene as a design strategy for stable organic biradicals, Nat. Chem., 2016, 8, 753–759, DOI:10.1038/nchem.2518.
- K. Yamaguchi, T. Kawakami, Y. Takano, Y. Kitagawa, Y. Yamashita and H. Fujita, Analytical and ab initio studies of effective exchange interactions, polyradical character, unpaired electron density, and information entropy in radical clusters (R)N: allyl radical cluster (N = 2–10) and hydrogen radical cluster (N = 50), Int. J. Quantum Chem., 2002, 90(1), 370–385, DOI:10.1002/qua.979.
- K. Tada, H. Ozaki, K. Fujimaru, Y. Kitagawa, T. Kawakami and M. Okumura, Can we enhance diradical character using interaction with stoichiometric surfaces of ionic oxides? A theoretical investigation using chemical indices, Phys. Chem. Chem. Phys., 2021, 23, 25024–25028, 10.1039/D1CP03439A.
- L. Noodleman, T. Lovell, W. G. Han, J. Li and F. Himo, Quantum chemical studies of intermediates and reaction pathways in selected enzymes and catalytic synthetic systems, Chem. Rev., 2004, 104, 459–508, DOI:10.1021/cr020625a.
- Y. Kitagawa, T. Saito, M. Ito, M. Shoji, K. Koizumi, S. Yamanaka, T. Kawakami, M. Okumura and K. Yamaguchi, Approximately spin-projected geometry optimization method and its application to di-chromium systems, Chem. Phys. Lett., 2007, 442, 445–450, DOI:10.1016/j.cplett.2007.05.082.
- T. Saito and W. Thiel, Analytical gradients for density functional calculations with approximate spin projection, J. Phys. Chem. A, 2012, 116, 10864–10869, DOI:10.1021/jp308916s.
- T. Kubo, Syntheses and Properties of Open-Shell π-Conjugated Molecules, Bull. Chem. Soc. Jpn., 2021, 94, 2235–2244, DOI:10.1246/bcsj.20210224.
- Y. Morita, T. Murata, A. Ueda, C. Yamada, Y. Kanzaki, D. Shiomi, K. Sato and T. Takui, Trioxotriangulene: air- and thermally stable organic carbon-centered neutral π-radical without steric protection, Bull. Chem. Soc. Jpn., 2018, 91, 922–931, DOI:10.1246/bcsj.20180074.
- A. Shimizu, T. Kubo, M. Uruichi, K. Yakushi, M. Nakano, D. Shiomi, K. Sato, T. Takui, Y. Hirao, K. Matsumoto, H. Kurata, Y. Morita and K. Nakasuji, Alternating Covalent Bonding Interactions in a One-Dimensional Chain of a Phenalenyl-Based Singlet Biradical Molecule Having Kekulé Structures, J. Am. Chem. Soc., 2010, 132(41), 1442114428, DOI:10.1021/ja1037287.
- A. Shimizu, Y. Hirao, K. Matsumoto, H. Kurata, T. Kubo, M. Uruichi and K. Yakushi, Aromaticity and π-bond covalency: prominent intermolecular covalent bonding interaction of a Kekulé hydrocarbon with very significant singlet biradical character, Chem. Commun., 2012, 48, 5629–5631, 10.1039/C2CC31955A.
- M. Nakano, N. Nakagawa, S. Ohta, R. Kishi, T. Kubo, K. Kamada, K. Ohta, B. Champagne, E. Botek, H. Takahashi, S. Furukawa, Y. Morita, K. Nakasuji and K. Yamaguchi, Second hyperpolarizabilities of polycyclic diphenalenyl radicals: effects of para/ortho-quinoid structures and central ring modification, Chem. Phys. Lett., 2006, 429, 174–179, DOI:10.1016/j.cplett.2006.07.065.
- T. Murata, M. Yokoyama, A. Ueda, Y. Kanzaki, D. Shiomi, K. Sato, T. Takui and Y. Morita, Synthesis of trioxotriangulene stable neutral π-radicals having alkyl substituent groups, and their effects on electronic-spin and π-stacking structures, Chem. Lett., 2020, 49, 95, DOI:10.1246/cl.190761.
- K. Ohashi, T. Kubo, T. Masui, K. Yamamoto, K. Nakasuji, T. Takui, Y. Kai and I. Murata, 4,8,12,16-Tetra-tert-butyl-s-indaceno[1,2,3-cd:5,6,7-c′d′]diphenalene:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Four-Stage Amphoteric Redox System, J. Am. Chem. Soc., 1998, 120(9), 2018–2027, DOI:10.1021/ja970961m.
A Four-Stage Amphoteric Redox System, J. Am. Chem. Soc., 1998, 120(9), 2018–2027, DOI:10.1021/ja970961m. - K. Nakatsuji and T. Kubo, Multi-Stage Amphoteric Redox Hydrocarbons Based on a Phenalenyl Radical, Bull. Chem. Soc. Jpn., 2004, 77, 1791–1801, DOI:10.1246/bcsj.77.1791.
- Y. Morita, S. Nishida, T. Murata, M. Moriguchi, A. Ueda, M. Satoh, K. Arifuku, K. Sato and T. Takui, Organic tailored batteries materials using stable open-shell molecules with degenerate frontier orbitals, Nat. Mater., 2011, 10, 947, DOI:10.1038/nmat3142.
- K. Kamada, K. Ohta, A. Shimizu, T. Kubo, R. Kishi, H. Takahashi, E. Botek, B. Champagne and M. Nakano, Singlet Diradical Character from Experiment, J. Phys. Chem. Lett., 2010, 1, 937–940, DOI:10.1021/jz100155s.
- K. Kamada, K. Ohta, T. Kubo, A. Shimizu, Y. Morita, K. Nakasuji, R. Kishi, S. Ohta, S. Furukawa, H. Takahashi and M. Nakano, Strong Two-Photon Absorption of Singlet Diradical Hydrocarbons, Angew. Chem., Int. Ed., 2007, 46, 3544–3546, DOI:10.1002/anie.200605061.
- Y. Ikabata, Q. Wang, T. Yoshikawa, A. Ueda, T. Murata, K. Kariyazono, M. Moriguchi, H. Okamoto, Y. Morita and H. Nakai, Near-infrared absorption of π-stacking columns composed of trioxotriangulene neutral radicals, npj Quantum Mater., 2017, 2, 27, DOI:10.1038/s41535-017-0033-8.
- T. Kubo, A. Shimizu, M. Sakamoto, M. Uruichi, K. Yakushi, M. Nakano, D. Shiomi, K. Sato, T. Takui, Y. Morita and K. Nakasuji, Synthesis, Intermolecular Interaction, and Semiconductive Behavior of a Delocalized Singlet Biradical Hydrocarbon, Angew. Chem., Int. Ed., 2005, 44, 6564–6568, DOI:10.1002/anie.200502303.
- T. Murata, C. Yamada, K. Furukawa and Y. Morita, Mixed valence salts based on carbon-centered neutral radical crystals, Commun. Chem., 2018, 1, 47, DOI:10.1038/s42004-018-0048-5.
- K. V. Raman, A. M. Kamerbeek, A. Mukherjee, N. Atodiresei, T. K. Sen, P. Lazić, V. Caciuc, R. Michel, D. Stalke, S. K. Mandal, S. Blügel, M. Münzenberg and J. S. Moodera, Interface-engineered templates for molecular spin memory devices, Nature, 2013, 493, 509–513, DOI:10.1038/nature11719.
- J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Towards single molecule switches, Chem. Soc. Rev., 2015, 44, 2998–3022, 10.1039/C4CS00377B.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Molecular-Scale Electronics: From Concept to Function, Chem. Rev., 2016, 116, 4318–4440, DOI:10.1021/acs.chemrev.5b00680.
- K. S. Kumar and M. Ruben, Sublimable spin-crossover complexes: from spin-state switching to molecular devices, Angew. Chem., Int. Ed., 2021, 60, 7502–7521, DOI:10.1002/anie.201911256.
- L. J. Martin, B. Akhavan and M. M. M. Bilek, Electric fields control the orientation of peptides irreversibly immobilized on radical-functionalized surfaces, Nat. Commun., 2018, 9, 357, DOI:10.1038/s41467-017-02545-6.
- M. Yamashita, Next generation multifunctional nano-science of advanced metal complexes with quantum effect and nonlinearity, Bull. Chem. Soc. Jpn., 2021, 94, 209–264, DOI:10.1246/bcsj.20200257.
- A. Gellé and M.-B. Lepetit, Fast calculation of the electrostatic potential in ionic crystals by direct summation method, J. Chem. Phys., 2008, 128, 244716, DOI:10.1063/1.2931458.
- A. Dittmer, R. Izsák, F. Neese and D. Maganas, Accurate band gap predictions of semiconductors in the framework of the similarity transformed equation of motion coupled cluster theory, Inorg. Chem., 2019, 58, 9303, DOI:10.1021/acs.inorgchem.9b00994.
- M. Atanasov, E.-L. Andreici Eftimie, N. M. Avram, M. G. Brik and F. Neese, First-principles study of optical absorption energies, ligand field and spin–Hamiltonian parameters of Cr3+ ions in emeralds, Inorg. Chem., 2022, 61, 178, DOI:10.1021/acs.inorgchem.1c02650.
- T. Kawakami, T. Taniguchi, Y. Kitagawa, T. Matsumoto, Y. Kamada, T. Sugimoto, M. Okumura and K. Yamaguchi, Theoretical studies on magnetic interaction in one-dimensional spin chains of hydrogen atoms (Hn) and copper bromide (CunBrm), Int. J. Quantum Chem., 2004, 100, 907, DOI:10.1002/qua.20288.
- Y. Kitagawa, Y. Nakanishi, Y. Kataoka, T. Saito, N. Yasuda, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Theoretical study of intra- and inter-chain magnetic interactions in [Ni(chxn)2Br]Br2, Polyhedron, 2011, 30, 3116, DOI:10.1016/j.poly.2011.03.006.
- K. Kinoshita, T. Kawakami, Y. Morita, T. Saito, S. Yamanaka, M. Okumura and K. Yamaguchi, Theoretical studies on the magnetic and conductive properties of crystals containing open-shell trioxotriangulene radicals, Bull. Chem. Soc. Jpn., 2016, 89, 315, DOI:10.1246/bcsj.20150322.
- K. Tada, T. Kawakami, Y. Kitagawa, M. Okumura, K. Yamaguchi and S. Tanaka, Comparison of effective exchange integrals of H–H and H–He–H chains vs. Single molecules: a theoretical study, Chem. Lett., 2020, 49, 137, DOI:10.1246/cl.190806.
- K. Tada, H. Koga, M. Okumura and S. Tanaka, Estimation of spin contamination error in dissociative adsorption of Au2 onto MgO(001) surface: first application of approximate spin projection (AP) method to plane wave basis, Chem. Phys. Lett., 2018, 701, 103–108, DOI:10.1016/j.cplett.2018.03.064.
- K. Tada, S. Tanaka, T. Kawakami, Y. Kitagawa, M. Okumura and K. Yamaguchi, Spin contamination errors on spin-polarized density functional theory/plane-wave calculations for crystals of one-dimensional materials, Appl. Phys. Express, 2019, 12, 115506, DOI:10.7567/1882-0786/ab4a37.
- K. Tada, Y. Kitagawa, T. Kawakami, M. Okumura and S. Tanaka, Electron density-based estimation of diradical character: an easy scheme for DFT/plane-wave calculations, Chem. Lett., 2021, 50, 392–396, DOI:10.1246/cl.200741.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining theory and experiment in electrocatalysis: insights into materials design, Science, 2017, 355, 6321, DOI:10.1126/science.aad4998.
- A. Urban, D.-H. Seo and G. Ceder, Computational understanding of Li-ion batteries, npj Comput. Mater., 2016, 2, 16002, DOI:10.1038/npjcompumats.2016.2.
- K. Fujimaru, K. Tada, H. Ozaki, M. Okumura and S. Tanaka, Variation in spin contamination and diradical character with distance between a singlet biradical molecule and surface, Suf. Interfaces, 2022, 33, 102206, DOI:10.1016/j.surfin.2022.102206.
- K. Tada, T. Kawakami and Y. Hinuma, Model calculations for the prediction of the diradical character of physisorbed molecules: p-benzyne/MgO and p-benzyne/SrO, Phys. Chem. Chem. Phys., 2023 10.1039/D3CP02988C.
- K. Tada, H. Ozaki, K. Fujimaru, Y. Kitagawa, T. Kawakami and M. Okumura, Diradical characters of s-indaceno [1,2,3-cd;5,6,7-c′d′] diphenalene with and without interaction with MgO(001), e-J, Surf. Sci. Nanotechnol., 2022, 20, 59–67, DOI:10.1380/ejssnt.2022-011.
- T. Saito, S. Nishihara, S. Yamanaka, Y. Kitagawa, T. Kawakami, S. Yamada, H. Isobe, M. Okumura and K. Yamaguchi, Symmetry and broken symmetry in molecular orbital description of unstable molecules IV: comparison between single- and multi-reference computational results for antiaromtic molecules, Theor. Chem. Acc., 2011, 130, 749–763, DOI:10.1007/s00214-011-0941-9.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048, DOI:10.1103/PhysRevB.23.5048.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943, DOI:10.1103/PhysRevB.44.943.
- I. V. Solovyev, P. H. Dederichs and V. I. Anisimov, Corrected atomic limit in the local-density approximation and the electronic structure of d impurities in Rb, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(16), 861, DOI:10.1103/PhysRevB.50.16861.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: orbital ordering in Mott–Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467, DOI:10.1103/PhysRevB.52.R5467.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyzyk and G. A. Sawatzky, Density-functional theory and NiO photoemission spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929, DOI:10.1103/PhysRevB.48.16929.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505, DOI:10.1103/PhysRevB.57.1505.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269, DOI:10.1103/PhysRevB.49.14251.
- G. Kresse and J. Furthmuller, Efficient interactive schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50, DOI:10.1096/0927-0256(96)00008-0.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865, DOI:10.1103/PhysRevLett.77.3865.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170, DOI:10.1063/1.478522.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276, DOI:10.1107/S0021889811038970.
- VASP online manual: https://www.vasp.at/wiki/index.php/LORBIT.
- S. Hüfner, Electronic structure of NiO and related 3d-transition-metal compounds, Adv. Phys., 1994, 43, 183–356, DOI:10.1080/00018739400101495.
- J. Wang, A. D. Becke and V. H. Smith, Evaluation of 〈Ŝ2〉 in restricted, unrestricted Hartree–Fock, and density functional based theories, J. Chem. Phys., 1995, 102, 3477–3480, DOI:10.1063/1.468585.
- K. Yamaguchi, H. Fukui and T. Fueno, Molecular-orbital (MO) theory for magnetically interacting organic-compounds-abinitio MO calculations of the effective exchange integrals for cyclophane-type carbene dimers, Chem. Lett., 1986, 625–628, DOI:10.1246/cl.1986.625.
- P. Pokhilko and D. Zgid, Broken-symmetry self-consistent GW approach: degree of spin contamination and evaluation of effective exchange couplings in solid antiferromagnets, J. Chem. Phys., 2022, 157, 144101, DOI:10.1063/5.0114080.
- I. Østrøm, Md. A. Hossain, P. A. Burr, J. N. Hart and B. Hoex, Designing 3d metal oxides: selecting optimal density functionals for strongly correlated materials, Phys. Chem. Chem. Phys., 2022, 24, 14119, 10.1039/D2CP01303G.
- C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618, DOI:10.1103/PhysRev.46.618.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506, DOI:10.1016/0009-2614(88)85250-3.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals, Chem. Phys. Lett., 1988, 149, 537–542, DOI:10.1016/0009-2614(88)80378-6.
- Y. Kitagawa, T. Saito, M. Ito, Y. Nakanishi, M. Shoji, K. Koizumi, S. Yamanaka, T. Kawakami, M. Okumura and K. Yamaguchi, Geometry optimization method based on approximate spin projection and its application to F2, CH2, CH2OO, and active site of urease, Int. J. Quantum Chem., 2007, 107, 3094–3102, DOI:10.1002/qua.21456.
- Private communication: a review article for diradical molecules co-authored by KT and YK will be submitted.
- M. Otani and O. Sugino, First-principles calculations of charged surfaces and interfaces: a plane-wave nonrepeated slab approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115407, DOI:10.1103/PhysRevB.73.115407.
- N. Bonnet, T. Morishita, O. Sugino and M. Otani, First-Principles Molecular Dynamics at a Constant Electrode Potential, Phys. Rev. Lett., 2012, 109, 266101, DOI:10.1103/PhysRevLett.109.266101.
- I. Hamada, O. Sugino, N. Bonnet and M. Otani, Improved modeling of electrified interfaces using the effective screening medium method, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155427, DOI:10.1103/PhysRevB.88.155427.
- S. Nishihara and M. Otani, Hybrid solvation models for bulk, interface, and membrane: reference interaction site methods coupled with density functional theory, Phys. Rev. B, 2017, 96, 115429, DOI:10.1103/PhysRevB.96.115429.
- Private communication: a paper entitled “Metal dimer adsorptions onto MgO (001) and BaO (001) with singlet biradical states investigated by approximate spin projected density functional theory” authored by KT is under review.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04187e |
| This journal is © the Owner Societies 2023 |



