Rotational spectra and semi-experimental structures of furonitrile and its water cluster

Abstract

Rotational spectroscopy represents an invaluable tool for several applications: from the identification of new molecules in interstellar objects to the characterization of van der Waals complexes, but also for the determination of very accurate molecular structures and for conformational analyses. In this work, we used high-resolution rotational spectroscopic techniques in combination with high-level quantum-chemical calculations to address all these aspects for two isomers of cyanofuran, namely 2-furonitrile and 3-furonitrile. In particular, we have recorded and analyzed the rotational spectra of both of them from 6 to 320 GHz; rotational transitions belonging to several singly-substituted isotopologues have been identified as well. The rotational constants derived in this way have been used in conjunction with computed rotation–vibration interaction constants in order to derive a semi-experimental equilibrium structure for both isomers. Moreover, we observed the rotational spectra of four different intermolecular adducts formed by furonitrile and water, whose identification has been supported by a conformational analysis and a theoretical spectroscopic characterization. A semi-experimental determination of the intermolecular parameters has been achieved for all of them and the results have been compared with those obtained for the analogous system formed by benzonitrile and water.

---

1 Introduction

Thanks to the discovery of several aromatic molecules in the interstellar medium (ISM), a new era of astrochemistry has just begun.¹ Recent astronomical observations reported on the first interstellar detection of various cyano-substituted rings, these including benzonitrile,^2,3 two isomers of cyanonaphtalene⁴ and of cyanocyclopentadiene,^5,6 and 2-cyanoindene.⁷ Other studies have reported the detection of ethynyl-derivatives of cyclopentadiene,⁸ pure hydrocarbon cycles,^9–11 and even the first polycyclic aromatic hydrocarbon (PAH).¹¹ Instead, searches for nitrogen-, oxygen-, and sulfur-bearing heterocycles have been unsuccessful so far.^12,13 More sensitive and broader spectral line surveys of different astrophysical objects will thus be needed in the future to secure the detection of such elusive species. However, as it occurred for the pure hydrocarbon rings, cyano-substituted heterocycles might enhance detection probabilities and they might be identified well before their unfunctionalized counterparts.

Since oxygen is the most abundant element among heteroatoms and the presence of a cyano group typically results in a large value of the molecular electric dipole moment, furonitrile (also known as furancarbonitrile or cyanofuran) represents one of the best candidates for the first detection of an interstellar heterocycle via its rotational emission. The possible presence of 2-/3-furonitrile and their protonated forms in the ISM has been recently addressed in a quantum-chemical investigation,¹⁴ which also pointed out the lack of information on rotational parameters. Indeed, an accurate spectroscopic characterization of the rotational spectra of both regioisomers of furonitrile, namely 2-furonitrile and 3-furonitrile, is mandatory in order to support their astronomical search. Surprisingly, the rotational spectrum of 3-furonitrile is completely unknown at present, while that of 2-furonitrile was limited to the frequency region below 40 GHz^15,16 until recently.¹⁷

In addition to the crucial role played by rotational spectroscopy in radioastronomy, the analysis of rotational spectra provides invaluable information to chemists. In the first place, because of its inherent precision and the intrinsic connection between rotational constants and molecular geometry, rotational spectroscopy allows for the derivation of highly accurate equilibrium structures of isolated molecules. This requires to account for the vibrational effects, which can be effectively accomplished by combining the experimental rotational constants of several isotopic species with the calculated vibration–rotation interaction constants. This is the foundation of the so-called semi-experimental approach, introduced long ago by Pulay et al.¹⁸ This methodology has been demonstrated to transfer to the derived equilibrium geometries the accuracy obtained in the experiment.^19,20 The strength of this approach has been demonstrated for a large variety of molecules^21–23 and it is easily exploited whenever experimental data are available for a sufficient number of isotopologues.

In the second place, the analysis of rotational spectra permits the identification of non-covalent interactions occurring in molecular clusters generated in a jet under supersonic expansion conditions.^24–26 In this respect, interesting information can be precisely unveiled towards the full understanding of microsolvation processes, such as (i) the favourite bonding site when several weak interactions are in competition, (ii) structural changes moving from isolated to clustered molecules with unrivaled accuracy, and (iii) interaction energies and geometries of clusters in a matrix- and collision-free environment.^27–29 While the literature on intermolecular complexes containing the cyanide group is quite vast,^30–35 to the best of our knowledge no adducts involving furonitrile have been studied so far. The investigation of the molecular cluster formed by furonitrile and water can be of great interest because of the widespread role played by water in nature and can provide insights on how water interacts with aromatic rings when a heteroatom is introduced.³⁶

In this work, we report the measurement and analysis of the rotational spectra of isolated 2- and 3-furonitrile and several of their isotopologues, as well as those of the complexes formed by 2- or 3-furonitrile with one water molecule, also including some water isotopologues. The rotational constants obtained, in combination with computed vibrational corrections, allowed us to derive the semi-experimental equilibrium structures for both the monomers and their adducts with water. Finally, we compared the interactions occurring in the furonitrile–water cluster with those reported for the analogous system formed by benzonitrile and water. In the next section, we present the computational (Section 2.1) and experimental (Section 2.2) methodologies employed in this study. Section 3 reports on the analysis of rotational spectra and the structure determination for 2- and 3-furonitrile (Section 3.1) and for their intermolecular complexes with water (Section 3.2). Finally, we summarize our results and their implications in Section 4.

2 Methodology

2.1 Computational details

In the following, the computational methodology employed for the structural and spectroscopic characterization of 2- and 3-furonitrile and their water complexes is presented. All density functional computations have been carried out using the Gaussian16 suite of programs,³⁷ while the CFOUR program package^38,39 has been employed for methodologies based on the coupled cluster and Møller–Plesset perturbation theories.

2.1.1 Isolated molecules. According to vibrational perturbation theory to second order (VPT2),⁴⁰ the rotational constants of the vibrational ground state (Bⁱ₀) can be written as the sum of two terms:where Bⁱ_e is the equilibrium rotational constant relative to the i-th inertial axis (i = a, b, c so that, for example, B^a_e ≡ A_e) and the second term is the vibrational correction, with the sum of the vibration–rotation interaction constants (αⁱ_r) running over the r vibrational modes (d_r represents the degeneracy of each mode).

Since the equilibrium rotational constants only depend on the equilibrium structure and the isotopic composition, their accurate prediction requires the determination of the equilibrium structure at the best possible level.^41–44 To this end, the so-called “jun-cheap” composite scheme,^28,45,46 hereafter denoted as junChS, has been employed. This approach is based on the geometry optimization using the CCSD(T) method⁴⁷ (the acronym standing for the CC singles and doubles approximation augmented by a perturbative treatment of triple excitations) in conjunction with the partially augmented jun-cc-pVTZ basis set,⁴⁸ within the frozen-core (fc) approximation. This level of theory is then corrected for the extrapolation to the complete basis set (CBS) limit and the core-valence (CV) correlation effects using second-order Møller–Plesset perturbation theory.⁴⁹ For a detailed account on junChS, the reader is referred to ref. 28 and 46.

As evident from eqn (1), the vibrational corrections require the calculation of the αⁱ_r constants, which in turn implies anharmonic force field computations.^20,42,50,51 These calculations have been carried out using the double-hybrid rev-DSDPBEP86⁵² functional in conjunction with the jun-cc-pVTZ basis set (hereafter, this level of theory is shortly denoted as revDSD). As a byproduct of such computations, the quartic and sextic centrifugal-distortion constants have also been obtained.^42,50

Furonitrile contains a quadrupolar nucleus, which is the nitrogen atom (¹⁴N), thus having a nuclear spin I_N = 1. This leads to an electric interaction, namely the nuclear quadrupole coupling, between the quadrupole moment of nitrogen and the electric field gradient at the nucleus itself. This interaction splits the rotational energy levels and, consequently, rotational transitions, thus giving rise to the so-called hyperfine structure of the rotational spectrum. From a computational point of view, the prediction of nuclear quadrupole coupling constants (χ_ij, with i,j being the inertial axes) requires the calculation of the electric field gradient at the quadrupolar nucleus. For details, we refer the reader to ref. 42 and 50. In this work, the elements of the electric field gradient tensor have been obtained as a byproduct of the geometry optimizations performed for the junChS scheme, thus having the junChS nuclear quadrupole coupling constants. To improve their values, the equilibrium terms have been augmented by vibrational corrections at the revDSD level, derived from the anharmonic force filed computations mentioned above. All these calculations also allow for estimating the electric dipole moment components, which are required to determine the type of rotational transitions that are observable and their intensity.

2.1.2 Intermolecular complexes. The initial computational search of the most stable structures of the molecular complex formed by 2- or 3-furonitrile with water has been carried out using the CREST software.⁵³ The output structures resulting from the CREST search were then optimized at the B3LYP-D3BJ/6-311G++(d,p) level of theory.^54,55 Thirteen different isomers have been found to lie within 1000 cm⁻¹. These correspond to different positions of the water molecule with respect to the rigid framework of furonitrile. For all of them, the water is at least partially located on the molecular plane defined by furonitrile. The structures of these minima are shown in Fig. S1 in the ESI.† As it will be discussed in the results section, among these, only the two most stable isomers for each furonitrile form have been observed in our experiment. For them, the equilibrium structure has been further refined at the revDSD level, which straightforwardly provides the equilibrium rotational constants. To predict the rotational spectra, these have been augmented by vibrational corrections at the B3LYP/SNSD level of theory,⁵⁴ § this calculation also providing the centrifugal distortion constants. Analogously to the isolated species, as a by product of the computations described above, the nuclear quadrupole coupling constants have been made available (at the revDSD level augmented by B3LYP/SNSD vibrational corrections).

2.1.3 Semi-experimental equilibrium structure. As mentioned above, the equilibrium rotational constants are immediately obtained from the equilibrium geometry. However, structural determinations from the knowledge of rotational constants are hampered by the limited number of data with respect to the number of geometrical parameters. This limitation can be overcome by considering for a given molecule different isotopic species in order to increase the number of available data. Since experimental rotational constants refer to the vibrational ground state, vibrational effects need to be excluded. For doing so, we can re-write eqn (1) and employ the computed ΔBⁱ_vib corrections, thus obtaining a set of semi-experimental (SE) equilibrium rotational constants:

Bⁱ_e(SE) = Bⁱ_0,exp − ΔB^i,calc_vib. (2)

The so-called semi-experimental equilibrium geometry^18,21 is then obtained from a least-squares fit of the semi-experimental equilibrium rotational constants of different isotopologues.

If the number of available isotopologues of a molecular system is not sufficient to allow the determination of all structural parameters, a subset of structural parameters can be kept fixed at the computed values, which can be further improved by using the linear-regression or template-molecule models.^23,56

2.2 Experimental details

In the following, the two high-resolution spectroscopic techniques employed in the present work are described in some details.

2.2.1 Microwave spectroscopy. The 2–22 GHz microwave spectra of several isotopologues of 2- and 3-furonitrile, as well as the spectra of their adducts with one water molecule, have been recorded in Chongqing with a Fourier transform microwave (FTMW) spectrometer.⁵⁷ A detailed description of this apparatus has been given elsewhere.⁵⁸

Furonitrile (97% in purity) as well as H¹⁸₂O and D₂O enriched samples were commercially obtained from Adamas and used without further purification. Furonitrile and water (or H¹⁸₂O and D₂O enriched samples) were placed at room temperature in two separate reservoirs inserted in the gas line. Helium, used as carrier gas at a stagnation pressure between 1 and 2 bar, was injected through a solenoid valve and supersonically expanded into the Fabry–Pérot cavity of the coaxially oriented beam-resonator spectrometer. Here, the molecules are polarized by strong pulses of microwave radiation and their free induction decay signal is recorded several times and co-added in order to improve the signal-to-noise ratio (S/N) of the spectrum. The spectral line positions were determined after Fourier transformation of the time-domain signal with 8k data points, recorded at 100 ns sample intervals. Because of the spectrometer arrangement, each rotational transition is split into a Doppler pair; the rest frequency of each line was then retrieved as the arithmetic mean frequency of the Doppler pair using the FTMW++ program. The assumed uncertainty on the frequency measurements is between 1 and 5 kHz, depending on the S/N of the transitions and their blending with other lines.

2.2.2 Millimeter-/submillimeter-wave spectroscopy. At higher frequency, the rotational spectra of 2- and 3-furonitrile have been recorded in Bologna with a frequency-modulation millimeter-/submillimeter-wave spectrometer (FM mm-/submm-W).^59,60 To achieve spectral coverage between 240 and 320 GHz, a Gunn diode operating in the W band (80–115 GHz) coupled to a passive frequency multiplier (WR-3.4×3 from Virginia Diodes Inc.) was used as radiation source. The frequency stability of the output radiation is ensured by exploiting a phase-lock loop circuit in which the reference signal is sine-wave modulated, while the frequency accuracy of the spectra is guaranteed by a rubidium atomic clock that provides a 5 MHz reference signal to all electronic devices. The detector system is composed by a zero-bias Schottky barrier working in the 220–330 GHz range (WR3.4ZBD, Virginia Diodes Inc.) and a lock-in amplifier set at twice the modulation frequency.

The measurements have been performed while maintaining a slow but continuous flow of furonitrile vapors at a pressure of 3 μbar inside the spectrometer cell. The cell is a 3 m long glass tube closed at both ends by two high-density polyethylene windows. The full frequency range between 240 and 320 GHz has been recorded by co-adding several spectra of 250 MHz each and employing a time constant of 10 ms, a scan rate of 5 MHz s⁻¹, a frequency step of 20 kHz, a modulation depth of 450 kHz, and a modulation frequency of f = 48 kHz. Each spectrum is the average of 2 forth-and-back scans. An excerpt of the millimeter-wave spectrum of 3-furonitrile is shown in Fig. 1.

Fig. 1 Portion of the millimeter-wave spectrum of 3-furonitrile (black trace) observed between 245.2 and 251.8 GHz with the spectrometer described in Section 2.2.2. The spectrum is dominated by a-type transitions (simulated by the red trace), approximately 100 times more intense than b-type transitions.

The assignment of the mm-/submm-W spectra has been carried out with the PGOPHER program package.⁶¹ The experimental uncertainty is estimated to be 15 kHz for all the lines measured.

2.2.3 Spectral analysis. 2- and 3-Furonitrile as well as their observed water complexes are nearly-prolate rotors. The assignment and analysis of their rotational spectra have been performed with the SPFIT program⁶² using the S-reduced Watson-type Hamiltonian for a semi-rigid nearly-prolate rotor.⁶³ All water–furonitrile adducts show a large amplitude motion that exchanges the hydrogen nuclei of water, thus leading to two inversion states which have been modelled by fitting two different set of rotational constants, while keeping a common value of all the other spectroscopic parameters. For both the isolated species and their water complexes, as mentioned in the Section 2.1, the presence of nitrogen produces a hyperfine structure of the rotational spectra. Their analysis requires the introduction of an additional quantum number, F, which originates from the coupling of the rotational quantum number J and the nuclear spin I_N.

3 Results

3.1 Rotational spectra of 2-furonitrile and 3-furonitrile

Although the microwave spectrum of 2-furonitrile was already studied in the past, we have re-measured it between 7 and 20 GHz at higher resolution and with an accuracy which is about 25 to 50 times better than that of previous works.^15,16 Instead, the rotational spectrum of 3-furonitrile was unknown so far and it has been recorded here for the first time. To guide the search of its rotational transitions in the MW region, we simulated the spectrum of 3-furonitrile using our computed rotational and centrifugal distortion constants (to predict the line positions) in combination with the electric dipole moment values (to predict the line intensities). Typically, all the transitions were found within 20 MHz from the corresponding predictions and, thus, could be assigned easily. For both regioisomers, the hyperfine structure of the rotational spectrum due to nitrogen has been resolved and the assignment of the correct hyperfine components has been supported by the computed nuclear quadrupole coupling constants. In the same frequency range, we recorded and analyzed the spectra of 7 isotopologues of both 2- and 3-furonitrile, namely all the singly-substituted ¹³C species, as well as the ¹⁵N- and ¹⁸O-containing isotopic species.

The rotational spectra of the main isotopologues of 2- and 3-furonitrile have also been measured at higher frequency. In detail, we recorded and analyzed their spectra between 240 and 320 GHz, thus assigning transitions with J and K_a quantum numbers as high as 98 and 45, respectively. The analysis of all the assigned transitions – more than 1300 for the parent species of each isomer – has been performed as explained in the methodology section (Section 2.2.3). The inclusion of both a-type and b-type transitions allowed us to determine with high accuracy the rotational and nitrogen quadrupole coupling constants as well as the entire set of centrifugal distortion constants up to the sixth order (with the exception of H_K) and two octic terms, i.e. L_JK and L_KKJ. The spectroscopic constants obtained for the main species and their isotopologues are reported in Table 1 and Table S1 of the ESI,† respectively, together with the fit statistics. For the analysis of the isotopic species, the parameters not reported in Table S1 (ESI†) were kept fixed to the values obtained for the corresponding parent species.

Table 1 Experimental and computed rotational, centrifugal distortion, and nuclear quadrupole coupling constants for 2-furonitrile and 3-furonitrile. For the former, the results from previous works are also given

Parameter	Unit	2-Furonitrile			3-Furonitrile
		Experiment^a	Theory^b	Previous^a^,^c	Experiment^a	Theory^b
a Notes: Numbers in parentheses represent the standard error in unit of the last quoted digit. b Ground state rotational constants from the junChS equilibrium rotational constants and revDSD vibrational corrections; equilibrium centrifugal distortion constants at the revDSD level; ground state nuclear quadrupole-coupling constants from junChS scheme and dipole moment components at the fc-CCSD(T)/jun-cc-pVTZ level. The last two quantities incorporate revDSD vibrational corrections. c Rotational and centrifugal distortion constants from Esselman et al.,^17 nuclear quadrupole coupling constants from Engelbrecht and Sutter,^15 and dipole moment components from Wiese et al.^64
A	MHz	9220.2507(1)	9235.10	9220.2514(1)	9296.5488(2)	9306.31
B	MHz	2029.27373(2)	2030.92	2029.27414(2)	1940.26649(2)	1942.17
C	MHz	1662.64315(3)	1664.19	1662.64352(2)	1604.63206(2)	1606.19
D J	kHz	0.059599(5)	0.0560	0.059680(2)	0.054756(4)	0.0518
D JK	kHz	2.9094(1)	2.845	2.91036(2)	2.9624(1)	2.913
D K	kHz	0.295(9)	0.272	0.2975(2)	0.405(5)	0.353
d 1	kHz	−0.015166(2)	−0.0142	−0.0151757(5)	−0.0133656(6)	−0.0125
d 2	Hz	−9.994(3)	−9.506	−9.9979(3)	−9.0840(7)	−8.692
H J	mHz	−0.0317(4)	−0.0308	−0.02801(8)	−0.0293(3)	−0.0292
H JK	mHz	4.32(1)	4.234	4.507(2)	4.330(9)	4.309
H KJ	Hz	−0.03590(9)	−0.0350	−0.03591(2)	−0.03810(9)	−0.0376
H K	mHz	0.0322	0.0322	0.0338(2)	0.0348	0.0348
h 1	μHz	−1.8(3)	−1.728	−0.851(2)	−2.004	−2.004
h 2	mHz	0.018(3)	0.0173	0.01883(3)	0.0157	0.0157
h 3	μHz	3.56(9)	3.367	3.72(1)	3.075	3.075
L JK	μHz	0.149(6)		0.1502(5)	0.154(5)
L KKJ	μHz	−1.51(2)		−1.529(4)	−1.62(2)
3/2 × χaa	MHz	−6.440(1)	−6.434	−6.39(8)	−6.338(1)	−6.588
(χbb − χcc)/4	MHz	0.2565(4)	0.269	0.24(2)	0.1579(4)	0.159
|μa|	D	…	4.483	4.51(2)	…	3.782
|μb|	D	…	0.892	0.901(5)	…	0.395
No. of lines		1314		10143	1371
rms error	kHz	23.7		40	15.1
Std. deviation		0.94		0.80	1.05

---

The inspection of Table 1 reveals an overall excellent agreement between the experimental spectroscopic constants and the computed counterparts: the discrepancy is around 0.08–0.16% for the rotational constants and below 5% for the centrifugal distortion terms; the nuclear quadrupole coupling constants and the electric dipole moment values⁶⁴ are also well-predicted by our quantum-chemical calculations. Here, it should be noted that, after the completion of our analysis, Esselman et al. reported the measurements of the rotational spectrum of 2-furonitrile from 140 to 750 GHz. In view of the wide spectral coverage and the high number of transitions analyzed by Esselman et al., it is not significant to discuss the rotational and centrifugal distortion constants derived for this species in our work. The similarity between our results and those from ref. 17 is evident from Table 1. Still, the major outcome of our analysis of 2-furonitrile is represented by the accurate determination of the nitrogen quadrupole coupling constants achieved thanks to the FTMW measurements below 20 GHz. As far as 3-furonitrile is concerned, instead, our work represents the first determination of its spectroscopic constants with an accuracy comparable to that obtained for 2-furonitrile. These data are of crucial importance for both the structure determination of this species and the possibility of obtaining accurate spectral predictions for astrochemical purposes.

3.1.1 Semi-experimental equilibrium structure. The rotational constants determined in this work for the main species of 2-furonitrile and 3-furonitrile and for seven of their isotopologues have been used to derive a semi-experimental equilibrium structure,^18,21 as explained in the methodology section (Section 2.1). Vibrational corrections to rotational constants have been evaluated at the revDSD level. Due to the lack of data on the isotopic substitution at the hydrogen nuclei, the bond distances and angles involving them were kept fixed to the corresponding junChS values. All the remaining geometry parameters, i.e. bond distances and angles involving heavy atoms, were floated in the fitting procedure. Furthermore, since both isomers are planar, all dihedral angles were constrained to be either 0° or 180°.

The planarity constraint imposes that I_cc − I_bb − I_aa = 0, so that only two principal inertia moments are linearly independent. This, in turn, implies that only two values of the three rotational constants of each isotopologue can be used in the structure determination. Therefore, the dataset available for each regioisomer is composed by 16 ground-state rotational constants from which the revDSD vibrational contributions have been subtracted, thus obtaining 16 semi-experimental equilibrium rotational constants. The fitting procedure has been performed with the XREFIT subroutine of the CFOUR package and allowed the determination of eleven structural parameters, six of which are bond-lengths and five are angles.

All geometry parameters are well constrained and are in excellent agreement with the corresponding junChS counterparts, the discrepancy being on the order of 1 mÅ for bond lengths and mostly below 0.1° for the angles. The very good quality of the fit is demonstrated by the small root-mean-square errors (ca. 2 × 10⁻⁷) and by the fact that the experimental rotational constants are reproduced with an average deviation as small as 0.1 kHz. The results of the structure determination are collected in Table 2, where the computed junChS parameters are also given. The atom numbering employed is illustrated in Fig. 2.

Table 2 Semi-experimental and junChS equilibrium structures of 2- and 3-furonitrile

2-Furonitrile			3-Furonitrile
Parameter	Semi-exp.	Theory	Parameter	Semi-exp.	Theory
Notes: the parameters involving hydrogen atoms have been kept fixed at their junChS value. Bond lengths are given in Å, angles in degrees. Numbers in parentheses represent the standard error in unit of the last quoted digit.
r(C2N1)	1.1587(1)	1.1574	r(C2N1)	1.15813(4)	1.1570
r(C2C3)	1.4173(2)	1.4177	r(C2C3)	1.4210(1)	1.4213
r(C4C3)	1.3623(5)	1.3597	r(C4C3)	1.437(2)	1.4363
r(O5C3)	1.3590(5)	1.3597	r(C5C3)	1.361(1)	1.3602
r(C7O5)	1.3544(1)	1.3535	r(C4C7)	1.3516(1)	1.3509
r(C9C7)	1.3572(1)	1.3566	r(C7O9)	1.3628(1)	1.3618
r(C4H6)	1.0747	1.0747	r(H6C4)	1.0741	1.0741
r(C7H8)	1.0737	1.0737	r(H8C7)	1.0732	1.0732
r(C9H10)	1.0744	1.0744	r(H10C5)	1.0737	1.0737
∠(C3C2N1)	179.7(2)	178.59	∠(C3C2N1)	179.42(6)	179.36
∠(C4C3C2)	131.06(9)	131.59	∠(C4C3C2)	127.4(3)	127.44
∠(O5C3C4)	110.93(2)	110.90	∠(C5C3C2)	126.2(2)	126.22
∠(C7O5C3)	106.24(2)	106.22	∠(C7C4C3)	105.47(4)	105.46
∠(C9C7O5)	111.070(4)	110.90	∠(O9C7C4)	110.812(4)	110.79
∠(H6C4C3)	125.93	125.93	∠(H6C4C3)	127.08	127.08
∠(H8C7O5)	115.65	115.65	∠(H8C7C4)	133.35	133.35
∠(H10C9C4)	127.47	127.47	∠(H10C5O9)	117.11	117.11
∠(H10C9C7)	126.49	126.49	∠(H10C9C3)	132.66	132.66
rms error	2.6 × 10^−7		rms error	1.9 × 10^−7

---

Fig. 2 Structure and atom numbering of 2-furonitrile (a) and 3-furonitrile (b). Carbon atoms are depicted in grey, oxygen in red, nitrogen in blue, and hydrogens in light grey.

3.2 Complexes with water

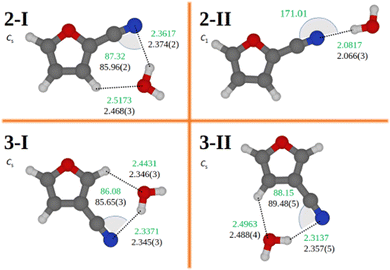
The computational search of the most stable structures of the molecular complex formed by 2- or 3-furonitrile with water has been performed as explained in the computational section (Section 2.1). Among the optimized structures, the rotational spectra recorded in our FTMW experiment revealed the presence of only the two most stable adducts for each furonitrile isomer. The molecular complexes experimentally identified are shown in Fig. 4 and hereafter labeled as 2-I, 2-II, 3-I, and 3-II. Higher energy isomers have been unsuccessfully searched for.

The assignment of the rotational spectra to the correct isomer is confirmed by the values of the rotational and quadrupole coupling constants, which have been found in agreement with those calculated at the revDSD level. Moreover, the type of transitions observed and their relative intensity agree with the computed electric dipole moment components (revDSD level). A further confirmation was then obtained by using various isotopically-enriched samples of water in our experiment (namely HDO, D₂O, and H¹⁸₂O) and by the fact that most of the transitions were observed as a doublet due to a large amplitude motion that exchanges the hydrogen nuclei of the water molecule (see Fig. 3). Accordingly, rotational transitions of the molecular complexes formed with HDO are not split because the two nuclei are no longer equivalent, and the magnitude of the splitting reduces when moving from H₂O to D₂O.

Fig. 3 Hyperfine structure of the J_Ka,Kc = 4_0,4 ← 3_0,3 transition observed for the 2-I isomer. The Doppler splittings due to the spectrometer arrangement are shown with the vertical bars and using different colors for the two inversion states. The initial F quantum number is given for each transition: only the ΔF = +1 components are visible in the spectrum.

Fig. 4 The molecular complexes formed by 2- and 3-furonitrile with water observed in the FTMW experiment. The semi-experimental (black) and theoretical (green) values of the most relevant intermolecular parameters are given. The symmetry point group of each isomer is also indicated.

For the parent species of each cluster, we have observed and analyzed at least 150 hyperfine-resolved rotational transitions (up to 366 for the 2-I species). The analysis of the spectra has been performed as explained in the methodology section (see Section 2.2.3), with the two inversion states being labelled as 0 and 1 in Tables 3 and 4. The results of the fit for the parent species of each isomer are collected in Tables 3 and 4, where the computed rotational, centrifugal distortion, and nuclear quadrupole coupling constants are also given. Thanks to the high accuracy of the FTMW measurements, the rotational constants and the nitrogen quadrupole coupling constants have been derived with great precision. As far as the quartic centrifugal distortion constants are concerned, their precision is more limited because of the reduced number of rotational energy levels accessible in a jet experiment, but their contribution is crucial to achieve a satisfactory modelling.

Table 3 Rotational, centrifugal distortion, and nuclear quadrupole coupling constants^a determined for the 2-furonitrile–water complexes

Parameter	Unit	2-I			2-II
		0	1	Theory^b	0	1	Theory^b
a Notes: Numbers in parentheses represent the standard error in unit of the last quoted digit. b Ground state rotational constants from revDSD equilibrium rotational constants and B3LYP vibrational corrections; equilibrium centrifugal distortion constants at the B3LYP level; ground state nuclear quadrupole-coupling constants at the revDSD level which incorporate B3LYP vibrational corrections.
A	MHz	3464.9751(2)	3464.4422(2)	3473.955	9018.3(3)	9011.3(3)	8896.530
B	MHz	1321.75814(7)	1321.70943(7)	1304.488	659.7708(1)	659.7989(1)	657.688
C	MHz	957.00590(5)	957.01401(5)	948.858	614.9251(1)	614.9568(1)	610.714
D J	kHz	0.5603(5)		0.4638	0.1482(2)		0.053951
D JK	kHz	−1.409(4)		−1.422	10.185(6)		4.9597
D K	kHz	13.27(2)		11.25	19.45		19.45
d 1	kHz	−0.1957(4)		−0.1673	−0.0169(3)		−0.00427
d 2	kHz	−0.0204(2)		−0.0160	−0.0069(2)		−0.00182
3/2 × χaa	MHz	−3.431(2)		−3.535	−5.98(3)		−5.992
(χbb − χcc)/4	MHz	−0.1975(6)		−0.1550	0.26(4)		0.275
Δ	amu Å^2	−0.144			−0.203
No. of lines		366			216
rms error	kHz	2.5			3.1
Std. deviation		0.49			0.62

---

Table 4 Rotational, centrifugal distortion, and nuclear quadrupole coupling constants^a determined for the 3-furonitrile–water complexes

Parameter	Unit	3-I			3-II
		0	1	Theory^b	0	1	Theory^b
a Notes: Numbers in parentheses represent the standard error in unit of the last quoted digit. b Ground state rotational constants from revDSD equilibrium rotational constants and B3LYP vibrational corrections; equilibrium centrifugal distortion constants at the B3LYP level; ground state nuclear quadrupole-coupling constants at the revDSD level which incorporate B3LYP vibrational corrections.
A	MHz	3388.4572(5)	3388.1935(5)	3388.813	3480.0341(5)	3479.7402(5)	3496.796
B	MHz	1337.0235(2)	1337.0087(2)	1322.051	1282.2758(3)	1282.2586(3)	1264.532
C	MHz	958.9058(2)	958.9091(2)	951.722	937.2953(2)	937.3007(2)	929.183
D J	kHz	0.419(2)		0.3551	0.494(2)		0.3978
D JK	kHz	−0.54(2)		−0.6159	−1.10(4)		−1.0373
D K	kHz	9.97(5)		8.4710	11.79(4)		9.8063
d 1	kHz	−0.144(2)		−0.1272	−0.169(3)		−0.1402
d 2	kHz	−0.016(2)		−0.0149	−0.015(3)		−0.0146
3/2 ×χaa	MHz	−4.093(7)		−4.188	−3.940(7)		−4.087
(χbb − χcc)/4	MHz	−0.165(1)		−0.135	−0.204(1)		−0.167
|χab|	MHz	2.1(2)		2.560	2.6(2)		2.619
Δ	amu Å^2	−0.107			−0.171
No. of lines		190			158
rms error	kHz	3.9			3.5
Std. deviation		0.79			0.69

---

Tables 3 and 4 report also the value of the inertial defect (Δ = I_c − I_a − I_b) of each complex, computed using the experimental rotational constants averaged over the two inversion states. Its value is close to zero and slightly negative for all four isomers (ranging between −0.1 and −0.2 amu Ų), thus indicating that all the structures are substantially planar in the ground state and that out-of-plane vibrations of water are more relevant than in-plane modes.

As for the clusters containing a water isotopologue (HDO, D₂O, or H¹⁸₂O), the analysis of the spectra has been carried out using the same Hamiltonian model. However, due to the lower S/N attained for these spectra, the number of measured transitions is typically smaller than that observed for the corresponding parent species. Therefore, in most cases the values of the centrifugal distortion constants as well as the quadrupole coupling constants were kept fixed to the values determined for the main isotopologue and only the rotational constants were floated. Also, the inversion splittings observed in the spectra of the complexes containing D₂O are not fully resolved: in this case, the line frequency has been taken as the average of the two transitions and, thus, a unique set of rotational constants has been derived. Finally, it should be noted that HDO can bind both 2- and 3-furonitrile in two different ways by forming the main hydrogen bond either through the deuterium atom or through the hydrogen. Consequently, the spectra of two different adducts have been observed. The spectroscopic constants determined for each isotopologue of the water adduct are given in Tables S2–S5 in the ESI.† From their inspection, it is noted that all fits are well constrained and characterized by small standard deviations. The only exception is that related to the HDO-2-II isomer, whose fit suffers from the limitation of the semi-rigid approximation. However, it has to be noted that, based on the comparison with computed and scaled (using experimental data of the other isotopologues) values, the rotational constants determined in the fit are reliable, even if affected by a larger uncertainty. Therefore, they could be safely used in the semi-experimental approach (see next section).

3.2.1 Semi-experimental equilibrium structure. The rotational constants derived for different isotopic species of the molecular complexes formed by 2- and 3-furonitrile with water were employed to derive their accurate intermolecular parameters using the semi-experimental approach (see Section 2.1) combined with the Template Molecule (TM) model.⁶⁵ The use of this latter is due to the fact that the experimental data are not sufficient for deriving the complete structure and that the intramolecular parameters affect the accuracy of the fitting procedure.

The TM approach (described in more detail in ref. 22 and 65 and successfully applied to several systems^23,66) is a computationally-affordable procedure to improve structural parameters. In the present case, it has been applied to the intramolecular parameters of the complex (r^best_intra) as follows:

r^best_intra = r^revDSD_intra + Δ^TM (3)

where Δ^TM is given by:

Δ^TM = r^SE_mono − r^revDSD_mono (4)

The r^SE_mono term denotes a generic structural parameters of the reference geometry of the monomer, while r^revDSD_mono is the corresponding revDSD optimized value. The difference between these two parameters provides the correction to the corresponding intramolecular parameter in the complex, which is computed at the revDSD level as well (r^revDSD_intra). For water, the reference geometry is the semi-experimental equilibrium structure reported in ref. 22, while for 2 and 3-furonitrile we employed those derived in this work (see Section 3.1.1). In this procedure, the initial intermolecular parameters are set to the revDSD ones.

The semi-experimental equilibrium rotational constants required to exploit the SE approach were obtained by correcting the experimental ground-state rotational constants of the five isotopologues investigated for each complex for the corresponding vibrational corrections computed at the B3LYP/SNSD level of theory. For symmetry reasons similar to those holding for the monomer species, only two rotational constants for each isotopologue could be used in the structural fit (the B and C constants have been chosen for this purpose). For all four complexes, the intermolecular distance fitted in the semi-experimental procedure is the one formed by the nitrogen atom of furonitrile with the closest hydrogen atom of water [r(H⋯N)]. With the exception of the 2-II isomer, the good quality of the fit also allowed for the determination of an intermolecular angle, i.e. that formed by the hydrogen atom of water with the two atoms of the CN group [∠(H⋯NC)]. For the 2-II complex, the attempt of determining such angle results in a large uncertainty because, at least at the revDSD level of theory, the hydrogen atom not involved in the hydrogen bond appears to be substantially free to rotate out of the molecular plane. For this species, we focused on the determination of the intermolecular distance mentioned above, while monitoring its change as the other H atom moves out of plane.

For the 2-I isomer, we obtained a r(H⋯N) value of 2.374(2) Å and a H⋯NC angle of 85.96(2)°. These quantities are quite similar to those determined for the 3-I complex, where the distance is 2.345(3) Å and the angle 85.65(3)°. Therefore, the hydrogen bond observed for 3-I is 30 mÅ shorter than that of 2-I. This can be explained in terms of higher electron density exhibited by the nitrogen atom in 3-furonitrile. The 3-II species has an intermolecular distance similar to that of 3-I, r(H⋯N) being 2.357(5) Å, while the H⋯NC angle is equal to 89.48(5)°. All these distances are about 0.3 Å longer than that observed in complex 2-II. Indeed, the fitting procedure of the intermolecular distance for the 2-II species provides a r(H⋯N) value of 2.066(3) Å with the dihedral angles HOH⋯N and OH⋯NC fixed to 173° and 4°, respectively. This distance remains unchanged (within the quoted error) if the dihedral angle changes up to ±50°, thus pointing out the flatness of the potential energy surface around this minimum. In such a determination, the CN⋯H and N⋯HO angles are fixed at the revDSD values of 171.0° and 176.8°, respectively. While the present structure determination of isomer 2-II has been carried out assuming a slightly non-planar configuration, analogous results (same H⋯N bond distance and rotational constants) could be obtained by adopting a completely planar structure with the OH⋯NC dihedral angle fixed to either 0 or 180 degree. However, since our quantum-chemical calculations indicate that the OH⋯NC angle is about 4° and the vibrational corrections, employed in the determination of the semi-experimental equilibrium structure, have been computed using this slightly non-planar geometry, we have preferred to be consistent and carried out the fitting at the non-planar structure.

The intermolecular parameters discussed above are reported in Fig. 4, while all the remaining structural parameters are listed in Tables S7 and S8 of the ESI.† For the isomers 2-I, 3-I, and 3-II, Fig. 4 also reports the values derived for the r(O⋯H) distance of the secondary hydrogen bonds.

An interesting system to compare the furonitrile–water complex with is the adduct formed by benzonitrile and water. Benzonitrile has been predicted to lead to two different van der Waals complexes with water: one with a cyclic structure and the other one with a linear structure.⁶⁷ Both structures have been observed experimentally, though the cyclic form only in the gas-phase via rotational spectroscopy³⁴ and the linear system only via matrix isolation infrared spectroscopy.⁶⁸ These isomers closely resemble those detected in our experiment, where a seven-membered cyclic structure is observed for 2-I, 3-I, and 3-II, while the 2-II structure possesses a linear form.

The intermolecular r(H⋯N) distance found for the cyclic form of benzonitrile–water is 2.257 Å,³⁴ about 0.1 Å shorter than those found for furonitrile, but in line with the value predicted by MP2 calculations (2.263 Å).⁶⁸ The same calculations predict a r(H⋯N) value of 2.066 Å in the linear form, identical to that determined for the 2-II isomer. The r(O⋯H) distances of the secondary hydrogen bond occurring in 2-I, 3-I, and 3-II (see Fig. 4 for their value) are also consistent with those found in benzonitrile–water, which has been experimentally determined to be 2.484(1) Å. The largest difference is observed for the isomer 3-I, for which the non-covalent interaction is stronger than that observed in 2-I and 3-II. Lastly, the H⋯NC angles observed in the benzonitrile–water complexes are very close to those found for furonitrile adducts, the former being 89° and 177° for the cyclic and linear forms, respectively.⁶⁸ This comparison shows how the binding sites and the overall geometries of furonitrile–water and benzonitrile–water are quite similar to each other, thus pointing out that the presence of a heteroatom in the aromatic ring does not alter significantly the nature of the non-covalent interaction.

4 Discussion and conclusions

Furonitrile represents one of the best candidates among the family of heterocycle to be searched for in the interstellar medium. Astronomical searches, however, require extremely accurate spectral line catalogs which, in turn, rely on laboratory measurements of rotational spectra. In this work, we filled the lack of data for 3-furonitrile, a species for which the rotational spectrum was completely unknown. Moreover, the high-resolution measurements carried out in the microwave domain for 2-furonitrile allowed the determination of precise nitrogen quadrupole coupling constants, thus adding an important piece of information towards an accurate and complete set of spectroscopic constants for this species. At present, the parameters reported here and in the work of Esselman et al. enable the radioastronomical search of both furonitrile isomers in a wide frequency range and in different interstellar environments, such as cold and warm gases, turbulent and quiescent clouds, early-stage and more evolved objects. Our quantum-chemical calculations (junChS electronic energy augmented by zero-point vibrational energy corrections at the revDSD level) indicate that 3-furonitrile is about 7 kJ mol⁻¹ more stable than 2-furonitrile: based on the Minimum Energy Principle,^69,70 we suggest 3-furonitrile to be the best candidate for detection in the ISM.

The analysis of the rotational spectra of several furonitrile isotopologues together with the calculation of the vibration–rotation interaction constants allowed us to determine the semi-experimental equilibrium structures of both 2- and 3-furonitrile for the first time. Our structural semi-experimental determinations agree very well with those obtained by exploiting the junChS composite scheme and reproduce, on average, the experimental rotational constants within 0.1 kHz. These structures will contribute to the extension of the SE127 database, which now collects more than a hundred semi-experimental equilibrium structures of small-/medium-size molecules.^23,56

Moving to the characterization of the clusters formed by furonitrile and one water molecule, our experiment revealed the formation of the two most stable structures for each furonitrile isomer. The assignment of the spectra has been secured by the prediction based on our quantum-chemical calculations, which provided a reliable energetic scale and accurate spectroscopic parameters for all isomers. The correct identification has also been supported by the inversion splitting observed in the spectra and through the use of several water isotopologues. In analogy to the monomers, the experimental rotational constants of these complexes have been used in combination with the corresponding computed vibrational corrections to derive semi-experimental equilibrium values of the most relevant intermolecular parameters, while the intramolecular ones have been improved by combining the Template Molecule and the semi-experimental approaches. This strategy has demonstrated to be effective and should motivate a systematic study of the structure of molecular clusters formed in the gas phase.

Finally, we have shown that the adducts formed by water and furonitrile resemble those established between water and benzonitrile, a similar system with a pure hydrocarbon ring. This similarity seems to indicate that, in these systems, the dominant non-covalent interactions are not significantly affected by the presence of a heteroatom in the aromatic ring.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by MUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds). The work in Chonqing has been supported by the National Natural Science Foundation of China (Grant No. 22073013), Chongqing Talents: Exceptional Young Talents Project (Grant No. cstc2021ycjh-bgzxm0027), and Fundamental Research Funds for the Central Universities (Grant No. 2020CDJXZ002). L. S. acknowledges the Italian Space Agency for co-funding the Life in Space project (ASI N. 2019-3-U.0). The COST Action CA21101 “COSY – Confined molecular systems: from a new generation of materials to the stars” is also acknowledged.

References

1. M. C. McCarthy and B. A. McGuire, J. Phys. Chem. A, 2021, 125, 3231–3243.
2. B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205.
3. A. M. Burkhardt, R. A. Loomis, C. N. Shingledecker, K. L. K. Lee, A. J. Remijan, M. C. McCarthy and B. A. McGuire, Nat. Astron., 2021, 5, 181–187.
4. B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst and S. Kalenskii, et al. , Science, 2021, 371, 1265–1269.
5. M. C. McCarthy, K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii and E. R. Willis, et al. , Nat. Astron., 2021, 5, 176–180.
6. K. L. K. Lee, P. B. Changala, R. A. Loomis, A. M. Burkhardt, C. Xue, M. A. Cordiner, S. B. Charnley, M. C. McCarthy and B. A. McGuire, Astrophys. J., Lett., 2021, 910, L2.
7. M. L. Sita, P. B. Changala, C. Xue, A. M. Burkhardt, C. N. Shingledecker, K. L. K. Lee, R. A. Loomis, E. Momjian, M. A. Siebert and D. Gupta, et al. , Astrophys. J., Lett., 2022, 938, L12.
8. J. Cernicharo, M. Agúndez, R. Kaiser, C. Cabezas, B. Tercero, N. Marcelino, J. Pardo and P. De Vicente, Astron. Astrophys., 2021, 655, L1.
9. J. Cernicharo, M. Agúndez, R. Kaiser, C. Cabezas, B. Tercero, N. Marcelino, J. Pardo and P. De Vicente, Astron. Astrophys., 2021, 652, L9.
10. J. Cernicharo, R. Fuentetaja, M. Agúndez, R. I. Kaiser, C. Cabezas, N. Marcelino, B. Tercero, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2022, 663, L9.
11. J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 649, L15.
12. T. J. Barnum, M. A. Siebert, K. L. K. Lee, R. A. Loomis, P. B. Changala, S. B. Charnley, M. L. Sita, C. Xue, A. J. Remijan and A. M. Burkhardt, et al. , J. Phys. Chem. A, 2022, 126, 2716–2728.
13. T. J. Barnum, K. L. K. Lee and B. A. McGuire, ACS Earth Space Chem., 2021, 5, 2986–2994.
14. R. Simbizi, D. Nduwimana, J. Niyoncuti, P. Cishahayo and G. Gahungu, RSC Adv., 2022, 12, 25332–25341.
15. L. Engelbrecht and D. Sutter, Z. Naturforsch., A: Phys. Sci., 1976, 31, 670–672.
16. T. Kojima, T. Ogata and S. Maeda, Chem. Lett., 1976, 607–610.
17. B. J. Esselman, M. A. Zdanovskaia, W. H. Styers, A. N. Owen, S. M. Kougias, B. E. Billinghurst, J. Zhao, R. C. Woods and R. J. McMahon, J. Phys. Chem. A, 2023, 127, 1909–1922.
18. P. Pulay, W. Meyer and J. E. Boggs, J. Chem. Phys., 1978, 68, 5077–5085.
19. F. Pawłowski, P. Jørgensen, J. Olsen, F. Hegelund, T. Helgaker, J. Gauss, K. L. Bak and J. F. Stanton, J. Chem. Phys., 2002, 116, 6482–6496.
20. C. Puzzarini and J. F. Stanton, Phys. Chem. Chem. Phys., 2023, 25, 1421–1429.
21. J. Demaison, J. E. Boggs and A. G. Császár, Equilibrium molecular structures: from spectroscopy to quantum chemistry, CRC Press, 2016.
22. M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058–2082.
23. G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290–7311.
24. G. Schols, Atomic and Molecular Beam Methods, Oxford University Press, 1988.
25. W. Caminati and J.-U. Grabow, in Frontiers of Molecular Spectroscopy, ed. J. Laane, Elsevier, 2009, ch. Microwave Spectroscopy: Molecular Systems.
26. J.-U. Grabow, Handbook of High Resolution Spectroscopy, Wiley, New York, 2011, ch. Fourier Transform Microwave Spectroscopy Measurement and Instrumentation, pp. 723–800.
27. E. R. Alonso, I. León and J. L. Alonso, Intra- and Intermolecular Interactions Between Non-Covalently Bonded Species, Elsevier, 2020, pp. 93–141.
28. S. Alessandrini, V. Barone and C. Puzzarini, J. Chem. Theory Comput., 2020, 16, 988–1006.
29. C. Puzzarini, L. Spada, S. Alessandrini and V. Barone, J. Phys.: Condens. Matter, 2020, 32, 343002.
30. C. Calabrese, A. Vigorito, A. Maris, S. Mariotti, P. Fathi, W. D. Geppert and S. Melandri, J. Phys. Chem. A, 2015, 119, 11674–11682.
31. F. J. Lovas and J. Sobhanadri, J. Mol. Spectrosc., 2015, 307, 59–64.
32. A. Huckauf, W. Jäger, P. Botschwina and R. Oswald, J. Chem. Phys., 2003, 119, 7749–7755.
33. K. Leopold, G. Fraser and W. Klemperer, J. Chem. Phys., 1984, 80, 1039–1046.
34. S. Melandri, D. Consalvo, W. Caminati and P. G. Favero, J. Chem. Phys., 1999, 111, 3874–3879.
35. R. Omron, A. H. Walker, G. Hilpert, G. T. Fraser and R. Suenram, J. Mol. Spectrosc., 1996, 179, 85–93.
36. A. Melli, V. Barone and C. Puzzarini, J. Phys. Chem. A, 2021, 125, 2989–2998.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
38. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
39. J. F. Stanton, J. Gauss, M. E. Harding and P. G. Szalay, CFOUR, A quantum chemical program package, 2016.
40. I. M. Mills, in Molecular Spectroscopy: Modern Research, ed. K. N. Rao and C. W. Matthews, 1972.
41. C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108.
42. C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367.
43. C. Puzzarini and V. Barone, Acc. Chem. Res., 2018, 51, 548–556.
44. S. Alessandrini, J. Gauss and C. Puzzarini, J. Chem. Theory Comput., 2018, 14, 5360–5371.
45. C. Puzzarini and V. Barone, Phys. Chem. Chem. Phys., 2011, 13, 7189–7197.
46. J. Lupi, S. Alessandrini, V. Barone and C. Puzzarini, J. Chem. Theory Comput., 2021, 17, 6974–6992.
47. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
48. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034.
49. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
50. C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191.
51. V. Barone, J. Chem. Phys., 2005, 122, 014108.
52. G. Santra, N. Sylvetsky and J. M. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143.
53. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
54. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
55. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
56. V. Barone, G. Ceselin, F. Lazzari and N. Tasinato, J. Phys. Chem. A, 2023, 127, 5183–5192.
57. J.-U. Grabow, W. Stahl and H. Dreizler, Rev. Sci. Instrum., 1996, 67, 4072–4084.
58. J. Chen, Y. Zheng, J. Wang, G. Feng, Z. Xia and Q. Gou, J. Chem. Phys., 2017, 147, 094301.
59. M. Melosso, B. Conversazioni, C. Degli Esposti, L. Dore, E. Cané, F. Tamassia and L. Bizzocchi, J. Quant. Spectrosc. Radiat. Transfer, 2019, 222, 186–189.
60. M. Melosso, L. Bizzocchi, F. Tamassia, C. Degli Esposti, E. Canè and L. Dore, Phys. Chem. Chem. Phys., 2019, 21, 3564–3573.
61. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242.
62. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377.
63. J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. Durig, Elsevier, Amsterdam, 1977, vol. 6, pp. 1–89.
64. J. Wiese, L. Engelbrecht and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1977, 32, 152–155.
65. A. Melli, F. Tonolo, V. Barone and C. Puzzarini, J. Phys. Chem. A, 2021, 125, 9904–9916.
66. H. Ye, S. Alessandrini, M. Melosso and C. Puzzarini, Phys. Chem. Chem. Phys., 2022, 24, 23254–23264.
67. E. S. Kryachko and M. T. Nguyen, J. Chem. Phys., 2001, 115, 833–841.
68. R. Gopi, N. Ramanathan and K. Sundararajan, J. Mol. Struct., 2020, 1219, 128636.
69. M. Lattelais, F. Pauzat, Y. Ellinger and C. Ceccarelli, Astrophys. J., Lett., 2009, 696, L133.
70. M. Lattelais, F. Pauzat, Y. Ellinger and C. Ceccarelli, Astron. Astrophys., 2010, 519, A30.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03984f

‡ Present address: Dipartimento di Chimica “Giacomo Ciamician”, Università di Bologna, Tecnopolo di Rimini, Via D. Campana 71, 47922 Rimini, Italy. E-mail: lorenzo.spada5@unibo.it

§ https://www.skies-village.it/smartdownload/download.php

---