 Open Access Article
Open Access ArticleEasy and accurate computation of energy barriers for carbocation solvation: an expeditious tool to face carbocation chemistry†
Antonio G.
Martínez
*a,
Hans-Ulrich
Siehl
b,
Santiago
de la Moya
 a and
Pedro C.
Gómez
a and
Pedro C.
Gómez
 *ac
*ac
aDepartamento de Química Orgánica, Facultad de Ciencias Químicas, Universidad Complutense de Madrid, 28040, Madrid, Spain. E-mail: agamar@ucm.es
bAbteilung Organische Chemie I, Universität Ulm, Albert Einstein Alee 11, 89069 Ulm, Germany
cDepartamento de Química Física, Universidad Complutense de Madrid, Facultad de Ciencias Químicas, 28040 Madrid, Spain. E-mail: pgomez@ucm.es
First published on 25th October 2023
Abstract
An expeditious procedure for the challenging computation of the free energy barriers (ΔG≠) for the solvation of carbocations is presented. This procedure is based on Marcus Theory (MT) and the popular B3LYP/6-31G(d)//PCM method, and it allows the easy, accurate and inexpensive prediction of these barriers for carbocations of very different stability. This method was validated by the fair mean absolute error (ca. 1.5 kcal mol−1) achieved in the prediction of 19 known experimental barriers covering a range of ca. 50 kcal mol−1. Interestingly, the new procedure also uses an original method for the calculation of the required inner reorganization energy (Λi) and free energy of reaction (ΔG). This procedure should pave the way to face computationally the pivotal issue of carbocation chemistry and could be easily extended to any bimolecular organic reaction.
1. Introduction
Carbocations are molecular organic ions containing positively charged carbon atoms, making them electron-deficient species and hence highly reactive electrophiles.1,2 They can be found as long-lived species in very acidic liquid-phase media,3 but they have also been found to exist in different environments such as planetary atmospheres and other astrophysical objects.4Carbocations are pivotal in organic chemistry because of their role as reactive intermediates in many organic transformations, such as the common unimolecular nucleophilic substitution (SN1) and elimination (E1) reactions.1–5 Moreover, carbocations are involved in the biosynthetic routes of a plethora of natural products like polyketides and terpenes.6
Since solvation, especially water solvation, is an essential topic for understanding conventional carbocation chemistry in solution, there has been a good deal of experimental and theoretical work devoted to the determination of solvation–reaction barriers.
Theoretical work on this issue has implied a notorious computational effort. So far, many aspects of the chemistry and properties of carbocations, such as thermochemistry, non-bonded interactions and reaction kinetics, have been studied using ab initio Density Functional Theory (DFT) and hybrid quantum mechanics-molecular mechanics (QM/MM) methods.6 However, the important subject of the reactivity with nucleophiles was performed not by computational methods but by linear free-energy relationships (LFERs),7,8 like the Mayr equation.9 The first successful computations of the pseudo-first order rate constants (kw) for the water solvation of carbocations were performed by Guthrie et al. for benzyl and benzyl-like cations based on no barrier theory (NBT).10 Unfortunately, the NBT method requires the computationally expensive optimization of eight structures, four before and four after the supposed transition state (TS) structure, according to a cubic reaction diagram.10 In this context, the need for a simple and efficient computational method, allowing the accurate prediction of the experimental outcome of these processes, is obvious and has been sought for a long time ago. Herein, we demonstrate that the free energy barriers (ΔG≠) for the solvation of carbocations with very different stability can be accurately computed by using a new procedure based on Marcus Theory (MT),11 which is much simpler than the NBT method. This simplicity should pave the way to computationally study the fundamental carbocation chemistry.
2. Theoretical background
We have previously proposed that the reaction of the tert-butyl cation with water (eqn (1); where R = t-Bu, and Haq+ represents a water solvated proton) is a two-step process,12a which is supported by the accurate computational prediction of the energy barrier for the proton transfer involved (second reaction step). This precise prediction was done by DFT calculations on the basis of the MT.12a| R+ + H2O → R-OH + Haq+ | (1) |
| R+ + :OH2 → [R+⋯:OH2 ↔ R˙···˙+OH2]≠ → R-+OH2 | (2) |
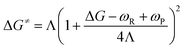 | (3) |
 | ||
| Fig. 1 Adiabatic crossing (TS) of the MT parabolas for the proposed exergonic SET-based reaction mechanism (see eqn (2)). The tunneling rate is proportional to 2H. | ||
Λ i value is usually computed by the quadratic variational method, which requires knowledge of the geometries of the initial (IS) and final (FS) reaction states.15,16 However, determining the equilibrium geometry of the IS is challenging in the case of intermolecular reactions, as our case is, and usually performed either according to time dependent DFT (TD-DFT) or scanning methods.12a,d,e These scanning methods usually guess the geometry of the TS and then determine the IS and FS geometries by following the intrinsic reaction coordinate (IRC) from the assumed TS in the proper direction.12e To address better the determination of Λi, we now propose a new and very simple procedure on the basis of using eqn (4), where G(R+) and G(RF+) are the free energies of the fully optimized carbocation and the corresponding frozen carbocation, respectively, the latter resulting from deleting the water molecule from the TS structure. This “frozen” carbocation represents the adaptation of the planar carbocation geometry to the sp3 one, which is required to enable the proposed SET process (see eqn (2)) without any further geometrical changes. In all cases, the most stable conformation of R+ is used in this approach.
| Λi = G(R+) − G(RF+) | (4) |
 | (5) |
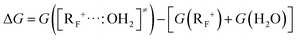 | (6) |
 | (7) |
3. Computational methods
The required computations were performed using the computationally inexpensive B3LYP/6-31G(d) method implemented in GAUSSIAN 09,17 since it has been successfully used by us in similar problems related to carbocation chemistry.12a–d Nonetheless, considering that the main drawback of the B3LYP functional when computing large species seems to be due to self-interaction effects for long range electron–electron interactions,18 and this concern could be resolved using long-range corrected (LC) functionals,19 we have also used the well-known LC MPWPPW91 method for comparison purposes.20 Additionally, both methods were combined with the popular SMD and PCM solvation models, which are also implemented in GAUSSIAN 09,17 using the default water dielectric constant value (78.3553), which is usually accepted for this solvent at 25 °C.4. Results and discussion
As a benchmark for proving our simplified MT procedure for the calculation of the energy barriers for carbocation solvation, we selected water solvation and an ample number of well-known carbocations (Fig. 2), ranging from highly stabilized carbocations (e.g., (MeO)3C+) to unstable ones (e.g., benzyl cation, Bn+). It must be noted here that, according to the classification of McClelland,21 highly stabilized carbocations are those whose pseudo-first order water solvation rates (kw) can be experimentally determined by stopped-flow spectroscopy, whereas stabilized carbocation kinetics needs to be followed by laser flash photolysis. As limit cases of instability, we included the tert-butyl (t-Bu+) and Bn+ carbocations, whose stabilities can be only determined experimentally by indirect methods (see references in Table 1).| Entry | R+ | Λ i | Λ ELo | ΔG | ΔG≠ | ΔG≠ (NBT)a | ΔG≠ (exp) |
|---|---|---|---|---|---|---|---|
| a Data from ref. 10a. b Data from ref. 22. c Data from ref. 21. d Mean value of those reported in ref. 21 and 23. | |||||||
| 1 | t-Bu+ (C3v) | 15.5 | 6.40 | −49.8 | 4.03 | — | 3.90b |
| 2 | Bn+ (C2v) | 11.0 | 5.71 | −48.4 | 1.30 | 1.26 | 1.47a |
| 3 | Ph(Me)CH+ (Cs) | 14.3 | 5.37 | −41.8 | 4.06 | 3.28 | 2.15a |
| 4 | Benzhydryl+ (C2) | 14.2 | 4.74 | −33.3 | 5.94 | — | 5.02c |
| 5 | Cumyl+ (Cs) | 13.8 | 4.85 | −37.0 | 4.73 | 4.11 | 3.2a |
| 6 | (p-MeOPh)(CF3)2C+ (Cs) | 16.9 | 4.60 | −37.2 | 8.60 | 4.80 | 7.07c |
| 7 | (p-MeOPh)(Me)2C+ (Cs) | 16.7 | 4.87 | −30.4 | 9.06 | 9.91 | 7.85c |
| 8 | Trityl+ (C3v) | 14.2 | 4.32 | −20.3 | 9.74 | — | 10.3c |
| 9 | Tropylium+ (D7) | 23.5 | 5.35 | −18.3 | 20.5 | — | 17.0c |
| 10 | Ph(MeO)2C+ (C1) | 15.7 | 5.00 | −29.0 | 9.81 | — | 10.6c |
| 11 | Ph(CH2O)2C+ (C2v) | 14.0 | 4.90 | −19.4 | 10.4 | — | 11.3c |
| 12 | (MeO)3C+ (C3h) | 17.6 | 5.35 | −20.2 | 14.0 | — | 11.8c |
| 13 | (MeO)(CH2O)2C+ (C1) | 18.8 | 5.90 | −24.0 | 14.2 | — | 11.4c |
| 14 | Me(MeO)2C+ (C1) | 20.8 | 5.77 | −27.7 | 12.4 | — | 10.5c |
| 15 | Me(CH2O)2C+ (Cs) | 16.2 | 5.60 | −26.2 | 10.6 | — | 9.1c |
| 16 | Ph(MeO)(Me)C+ (C1) | 15.2 | 5.00 | −27.2 | 8.86 | — | 6.92c |
| 17 | Me2(MeO)C+ (Cs) | 16.2 | 6.08 | −23.7 | 8.48 | — | 5.17c |
| 18 | Ph(MeO)CH+ (Cs) | 14.0 | 5.92 | −34.0 | 6.28 | — | 4.85c |
| 19 | Xanthylium+ (C2v) | 13.8 | 14.4 | −15.4 | 10.1 | — | 9.58d |
4.1. B3LYP/6-31G(d) calculations
The B3LYP/6-31G(d)//PCM-calculated ΔG≠ ΔG and Λ values, and the corresponding experimental barriers (ΔG≠(exp)), are shown in Table 1. As mentioned in Section 2, we used the computed C–O distance at the TS of highly stable (MeO)3C+ (1.688 Å) for facing the computations of all the selected carbocations (Fig. 2). Curiously enough, this distance is the same as that computationally found by us for protonated tert-butyl alcohol (an unstable carbocation) at equilibrium. On the other hand, selecting shorter distances, for example 1.522 Å, corresponding to protonated methanol at the equilibrium, produces too high computed barriers for all the selected cases (e.g., 16.8 kcal mol−1 for (MeO)3C+), whereas using larger distances (for example 1.822 Å) affords too low barriers in all the cases (e.g., 9.7 kcal mol−1 for (MeO)3C+). However, just by using critical 1.688 Å allows the accurate computation of ΔG≠ for the water solvation of the 19 selected carbocations (Fig. 2), covering an ample ΔG≠ range (between 1.3 kcal mol−1 and 20.5 kcal mol−1), as shown in Table 1.The mean absolute error (MAE) of our calculated ΔG≠ values in relation to the experimental ones is 1.51 kcal mol−1, within a range of ca. 20 kcal mol−1. This ΔG≠ range corresponds to kw values between 6.16 × 1012 s−1 and 14.3 s−1, for Bn+ and xanthylium+, respectively, at 25 °C. Hence, the accordance between experimental and calculated values can be qualified as excellent, not far away from the so-called “chemical accuracy” (1.0 kcal mol−1). It must be noted that the MAE of our computed ΔG≠ values is the same as that obtained from previously reported data computed using the more expensive NBT procedure in a more restricted set of carbocations (see Table 1).
It is worth mentioning that the ΔG≠ values computed according to our method (see Table 1) predict the kinetically stabilizing stereoelectronic effect exerted by alkyl (see Table 1 and cf. data in entries 2,3 and 5), phenyl (cf. entries 2 and 4) and alkoxyl groups (cf. entries 5 and 10) when attached to the cationic centre. These effects are cast, in quantitative terms, by plotting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwvs. the sum of the Hammett–Brown σ+ constants for the attached groups, as suggested by Kresge et al.23 However, as highlighted by McClelland, a simple linear free-energy relationship (LFER) is not clearly evident.21 Thus, for example, selecting carbocations bearing H, alkyl and alkoxyl groups attached to the carbocationic centre produces a linear correlation with a slope, ρ+, equal to 6.1; whereas selecting carbocations bearing a single phenyl produces a different LFER with a lower slope (5.5).21 Moreover, increasing the number of phenyl substituents in benzyl carbocation (Ph2CH+ and Ph3C+) generates points out of the latter line.21 In this context, it is clear that our simple computational procedure is free of these LFER inconsistencies. Even more, it is also striking that alkyl substitution at the carbocationic centre results in reactivity changes that follow neither the steric nor the electronic effects of the substituents.17
kwvs. the sum of the Hammett–Brown σ+ constants for the attached groups, as suggested by Kresge et al.23 However, as highlighted by McClelland, a simple linear free-energy relationship (LFER) is not clearly evident.21 Thus, for example, selecting carbocations bearing H, alkyl and alkoxyl groups attached to the carbocationic centre produces a linear correlation with a slope, ρ+, equal to 6.1; whereas selecting carbocations bearing a single phenyl produces a different LFER with a lower slope (5.5).21 Moreover, increasing the number of phenyl substituents in benzyl carbocation (Ph2CH+ and Ph3C+) generates points out of the latter line.21 In this context, it is clear that our simple computational procedure is free of these LFER inconsistencies. Even more, it is also striking that alkyl substitution at the carbocationic centre results in reactivity changes that follow neither the steric nor the electronic effects of the substituents.17
Another intriguing fact explained by our computations is the lack of kinetic destabilization associated with the involvement of electron-withdrawing groups directly attached to the carbocationic center. Thus, Richard et al. observed that (p-MeOPh)(CF3)2C+ is only slightly more reactive than (p-MeOPh)(Me)2C+ (see ΔG≠ (exp) in Table 1, entries 6 and 7).13 This fact was cleverly rationalized by Richard considering that the strong electron-withdrawing polar effect exerted by the trifluoromethyl groups in the case of (p-MeOPh)(CF3)2C+ (destabilizing charge-dipole interaction with the carbocationic center) is however almost relieved by an enhanced stabilizing charge-delocalization effect exerted by the methoxyl group located at para position in the aromatic ring (resonance effect).13 However, our computation of the HOMOs of the water complexes of (p-MeOPh)(CF3)2C+ and (p-MeOPh)(Me)2C+ at their solvation TSs shows that there is no enhanced resonance effect. Thus, these HOMOs (see Fig. 3 and ESI†) resemble the Ψ3 orbital of benzene, showing a through-bond nodal plane which electronically isolates the methoxyl group from the carbocation center. Moreover, our computations reveal another explanation for the unexpectedly high stability of the (p-MeOPh)(CF3)2C+ carbocation: the back-donation of the trifluoromethyl carbons to the cationic center, as supported by the significant π-bonding interaction found between the trifluoromethyl carbons and the cationic one in the computed HOMO (see Fig. 3). More importantly, our computations agree better with the experimental results than the NBT approach (cf. the corresponding ΔG≠, ΔG≠(NBT) and ΔG≠(exp) data in Table 1) and give a quantitative answer to the question: the destabilizing polar effect exerted by the trifluoromethyl groups is behind the high exergonicity of the (p-MeOPh)(CF3)2C+ water-solvation reaction when compared to that of (p-MeOPh)(Me)2C+ (ΔG = −37.2 kcal mol−1vs. −30.4 kcal mol−1; see Table 1) and such an effect is compensated by the working back-donation effect, which results in just a slightly higher solvation reactivity for (p-MeOPh)(CF3)2C+ (ΔG≠ = 8.60 kcal mol−1vs. 9.06 kcal mol−1; see Table 1).
 | ||
| Fig. 3 Electron density contour maps (ρ = 10−3) of HOMOs for the water complexes of (p-MeOPh)(Me)2C+ (left) and (p-MeOPh)(CF3)2C+ (right) at the solvation reaction TS. | ||
The relative stability of t-Bu+ and Bn+, which is an often-discussed question, can be accounted for by our procedure. From calculations of an isodesmic reaction involving both carbocations in the gas-phase, it was previously concluded that t-Bu+ is ca. 6 kcal mol−1 more stable than Bn+,24 despite the highly stabilizing resonance effect exerted by the phenyl group in the case of the Bn+.
However, according to the relative ion-stability scale of Abboud et al.,8 the relative stabilities of both carbocations in the gas-phase  are almost the same, considering the error range (
are almost the same, considering the error range ( and −5.8 ± 1.0 kcal mol−1 for Bn+ and t-Bu+, respectively). This situation is very different in solution. Thus, from extrapolation of experimental solvolytic rate results of different substrates in different solvents, tert-butyl chloride should solvolyze ca. 176 times faster than benzyl chloride at 45 °C in 50% aqueous EtOH, also suggesting that t-Bu+ is more stable than Bn+ in solution too.24 This fact could be explained by the strongly stabilizing inductive (polar) and hyperconjugative effects exerted by the methyl groups of t-Bu+, overweighing the said phenyl resonance effect. Our computations in water at 25 °C support these solvolytic conclusions. Thus, Bn+ should react with water (at 25 °C) ca. 100 times faster than t-Bu+, as calculated by us from the corresponding computed ΔG≠ values (see Table 1, entries 1 and 2) using the Eyring equation.25 In the gas phase, at the same temperature, this difference is predicted to be even larger (3.65 × 105 times faster; see Table 2). The main ground for this difference seems to be the high exergonicity of the reaction with water for Bn+ (C2v) in the gas phase (see Table 1, entries 1 and 2, and Table 2, and cf. ΔG values).
and −5.8 ± 1.0 kcal mol−1 for Bn+ and t-Bu+, respectively). This situation is very different in solution. Thus, from extrapolation of experimental solvolytic rate results of different substrates in different solvents, tert-butyl chloride should solvolyze ca. 176 times faster than benzyl chloride at 45 °C in 50% aqueous EtOH, also suggesting that t-Bu+ is more stable than Bn+ in solution too.24 This fact could be explained by the strongly stabilizing inductive (polar) and hyperconjugative effects exerted by the methyl groups of t-Bu+, overweighing the said phenyl resonance effect. Our computations in water at 25 °C support these solvolytic conclusions. Thus, Bn+ should react with water (at 25 °C) ca. 100 times faster than t-Bu+, as calculated by us from the corresponding computed ΔG≠ values (see Table 1, entries 1 and 2) using the Eyring equation.25 In the gas phase, at the same temperature, this difference is predicted to be even larger (3.65 × 105 times faster; see Table 2). The main ground for this difference seems to be the high exergonicity of the reaction with water for Bn+ (C2v) in the gas phase (see Table 1, entries 1 and 2, and Table 2, and cf. ΔG values).
| R+ | Λ i | Λ ELo | ΔG | ΔG≠ | k |
|---|---|---|---|---|---|
| a Λ EL0 is 0 because the optical (εop) and static (εs) dielectric constants of vacuum are both equal to 1 (see eqn (6)). b As calculated by applying the Eyring equation from the corresponding ΔG≠ values. | |||||
| t-Bu+ | |||||
| (C3v) | 17.3 | 0.00 | −5.40 | 14.7 | 1.03 × 102 |
| Bn+ | |||||
| (C2v) | 13.1 | 0.00 | −13.9 | 7.11 | 3.76 × 107 |
The conformational analysis of t-Bu+ is especially complex. Thus, a previous study in the gas phase at the MP2(full)/6-31G** level, conducted by v. R. Schleyer et al.,26 revealed that the energy barrier for CH3-rotation is extremely low and that the Cs conformation, which is energetically very close to the C3h one, is the global minimum, the latter being preferred by ca. 1.2 kcal mol−1 to the C3v conformation. According to our computations in the gas phase, C3h is also 1.52 kcal mol−1 more stable than the C3v structure. However, in solution (PCM), we found that the barrier to CH3-rotation is even lower than in the gas phase, but now the C3v conformation is slightly (by only 0.4 kcal mol−1) more stable than the C3h one.
The effect of cyclization on the reaction rates of acyclic oxocarbocations can also be detected by our method. Thus, McClelland explained the different water-solvation reactivity of acyclic Ph(OMe)2C+ and cyclic Ph(CH2O)2C+ (ΔG≠(exp) = 10.6 and 11.3 kcal mol−1, respectively; see entries 10 and 11 in Table 1) on the basis of a differential steric interaction involving the phenyl group, and inhibiting its full stabilizing resonance effect in the acyclic case.21 Our computations agree with a higher reactivity for acyclic Ph(OMe)2C+ (see Table 1). This differential effect does not exist in the related Me(MeO)2C+/Me(CH2O)2C+ couple bearing methyl instead of phenyl, as evidenced by the corresponding ΔG≠(exp) values (higher for the acyclic partner; cf. entries 14 and 15 in Table 1). Once again, our computational method reproduces this situation with computational accuracy (Table 1). Finally, the related (MeO)3C+/(MeO)(CH2O)2C+couple can be considered an intermediate case between the previous ones, due to the presence of a methoxyl group instead of phenyl or methyl. This group, as the phenyl one, has the ability to exert a stabilizing resonance effect, but this effect should not be significantly different for both the cyclic and the acyclic cations, due to its small steric effect. As a matter of fact, the corresponding ΔG≠(exp) values are very similar (11.8 and 11.4 kcal mol−1, respectively; see entries 12 and 13 in Table 1), and our computations reproduce this similarity within the above-said accuracy as well.
Notably, our method can be extended to other nucleophiles instead of water. As an example, we have computed ΔG≠ = 4.71 kcal mol−1 for the reaction of t-Bu+ with azide anion in water solution at 298 K. The calculated MT parameters are Λ = 30.9 kcal mol−1, ΔG = −90.6 kcal mol−1 and ΛELo = 5.28 kcal mol−1. Based on the Eyring equation, such an energy barrier allowed the calculation of a pseudo-first order rate (kw) for this reaction equal to 2.18 × 109 s−1. This value is in good agreement with that found by Richie et al. (5 × 109 s−1) for the pseudo-first order diffusion-controlled rate constant of any reactive carbocation with azide anions, which is based on the “azide clock method” for the experimental determination of rate constants for reactions of carbocations with water.21,27,28
4.2. B3LYP/6-31G(d), B3LYP/6-31+G(d,p) and MPWPW91/6-31+G(d,p) calculations
The results obtained when applying B3LYP/6-31G(d)//SMD to our benchmark set of carbocations are summarized in Table S1 in the SI. In all cases, the obtained ΔG≠ values are much higher than the experimental ones, and no correlation between both sets of values is found.In order to study the possible relevance of the long-range (LR) interactions in the studied reaction, we used the well-known MPWPW91/6-31+G(d,p) functional, which takes into account this kind of interaction.20 As an example, the hydration of Benzhydryl+ can be selected, since it exhibits intramolecular π–π and H–H interactions between the phenyl rings. For this case, MPWPW91/6-31+G(d,p)//PCM calculates Λi = 17.8 kcal mol−1 and ΔG = −35.4 kcal mol−1, giving place to ΔG≠ = 8.49 kcal mol−1 (Table 3). This computational barrier is significantly higher than the experimental one (ΔG≠(exp) = 5.02 kcal mol−1; see entry 4 in Table 1). To diminish this computational deviation, the C–O distance at the TS ([R+⋯:OH2]≠) should be enlarged with respect to the standard 1.688 Å value (see above). Moreover, this enlargement is substrate-dependent at variance with that occurring when the B3LYP functional was used. All this represents a serious complication in the computations when using the LR MPWPW91/6-31+G(d,p)//PCM method and supports the simpler use of the B3LYP/6-31G(d)//PCM one.
| Entry | Method | ΔG≠ |
|---|---|---|
| 1 | B3LYP/6-31G(d)//PCM | 5.94 |
| 2 | B3LYP/6-31+G(d,p)//PCM | 0.82 |
| 3 | MPWPW91/6-31+G(d,p)//PCM | 8.49 |
| 4 | B3LYP/6-31G(d)//SMD | 16.0 |
| 5 | MPWPW91/6-31+G(d,p)//SMD | 17.3 |
Interestingly, as shown in Table 3, the selection of the solvation model (PCM vs. SMD) is much more critical than the inclusion of LR effects in the selected functional. The origin of this fact seems to be a failure in the SMD model, giving place to more positive ΔG values than the PCM one (see Table 1, and Table S1 in the ESI,† and cf. related ΔG values). In our opinion, it is not worth using LC-corrected methods for the calculation of the ΔG≠ in systems as large as Trityl+ and Xanthylium+ (see Fig. 2) exhibiting no protobranching.29
In order to shed light on the influence of the basis set, we have also computed the energy barrier for the water solvation of benzhydryl+ using the B3LYP/6-31+G(d,p)//PCM methodology, which includes diffuse functions, while keeping the mentioned selected C–O distance and the PCM. As shown in Table 3, the computed barrier (0.82 kcal mol−1) is now extremely low, and far away from the experimental one (5.02 kcal mol−1; see Table 1). Thus, in this case, a shorter C–O distance should be used to get a reliable result, as a consequence of including diffuse functions (cf. entries 1 and 2 in Table 3). From all these results, we conclude that there is a C–O distance appropriate for each model chemistry.
5. Conclusions
The prediction of the fundamental reactivity of carbocations with nucleophiles is usually performed by using LFERs. However, this can be faulty, owing to specific stereoelectronic interactions that cannot be easily parameterized. On the other hand, the alternative azide-clock predictive method requires accurate experimental measurements. Regarding computational methods, the only computational procedure available to date for the prediction of reaction rates of carbocation solvations was the computationally expensive four-dimensional one based on the NBT. However, our methodology has been proven to be a convenient alternative to the NBT one, because it is simpler and affords a similar MAE at a much lower computational cost. On the other side, the found low MAE when computing carbocation water-solvation barriers (1.5 kcal mol−1 for 19 cases covering a very broad range of ΔG≠ values), as well as the demonstrated accuracy when predicting kinetics for reactions involving other nucleophiles different of water (azide anion), validates our method as highly appropriate to establish accurate reactivity-structure relationships in carbocation chemistry, which is central in organic chemistry.Moreover, a very simple procedure is established for computationally determining the internal reorganization energy and the free energy of the reaction of carbocations with water and other nucleophiles. In this context, it must be noted that the difficulty in determining these energies is the main drawback limiting the application of the Marcus equations to the study of a plethora of fundamental intermolecular reactions, mainly within the organic framework, which could be now rapidly and accurately addressed, from the computational point of view, on the basis of this procedure.
Also, a relevant point is the idea that the C–O distance for the transition states for carbocation water solvation shouldn’t change significantly from a study case to another. As a result, this makes affordable the application of the methodology to a good deal of organic systems with a moderate computational effort. Finally, the good agreement of the computed energy barriers with the experimental ones supports the proposed SET-based mechanism for this fundamental reaction.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge MICINN, AEI/10.13039/501100011033, of Spain (grants PID2020-114755GB-C32 and PID2021-122839NB-IT00) and UCM for supporting this work.Notes and references
- Carbonium Ion, ed. G. A. Olah, P. v R. Schleyer, J. Wiley & Sons Inc., 1972, vol. 1–4 Search PubMed.
- (a) M. Hanack, D. Lenoir, H. U. Siehl and L. R. Subramanian, in Carbokationen, Carbokation-Radikale in Methoden der Organischen Chemie (Houben Weyl), ed. M. Hanack, Georg Thieme Verlag, 1990, vol. E19c Search PubMed; (b) P. C. Gómez and P. R. Bunker, Chem. Phys. Lett., 1990, 165, 351–354, DOI:10.1016/0009-2614(90)87201-2.
- Carbocation Chemistry, ed. G. A. Olah, G. K. Surya Prakash, J. Wiley & Sons Inc., 2004 Search PubMed.
- A. Ali, E. C. Sittler Jr., D. Chornay, B. R. Rowe and C. Puzzarini, Cyclopropenyl Cation the Simplest Huckel's Aromatic Molecule and its Cyclic Methyl Derivatives in Titan's Upper Atmosphere, Planet. Space Sci., 2013, 87, 96–105 CrossRef CAS.
- Recent Developments in Carbocation and Onium Ion Chemistry, ed. K. K. Laali, ACS Symposium Series, vol. 965, American Chemical Society, 2007 Search PubMed.
- S. Zev, P. K. Gupta, E. Pahima and D. T. Major, A Benchmark Study of Quantum Mechanics and Quantum Mechanics-Molecular Mechanics Methods for Carbocation Chemistry, J. Chem. Theory Comput., 2022, 18, 167–178, DOI:10.1021/acs.jctc.1c00746 . For modern aspects of the carbocation chemistry, also see: https://www.sciencedirect.com/topics/chemistry/carbocation.
- A. G. Martínez, E. Teso, J. Osío and S. de La Moya Cerero, Comprehensive study of the methyl effect on the solvolysis rates of bridgehead derivatives, J. Am. Chem. Soc., 2002, 124, 6676–6685, DOI:10.1021/ja016583.
- J. L. Abboud, I. Alkorta, J. Z. Davalos, P. Müller, E. Quintanilla and J.-C. Rossier, Influence of Carbocation Stability in the Gas Phase on Solvolytic Reactivity:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Beyond Bridgehead Derivatives, J. Org. Chem., 2003, 68, 3786–3796, DOI:10.1021/jo026539s.
Beyond Bridgehead Derivatives, J. Org. Chem., 2003, 68, 3786–3796, DOI:10.1021/jo026539s. - J. Ammer, C. Nolte and H. Mayr, Free Energy Relationships for Reactions of Substituted Benzhydrylium Ions: From Enthalpy over Entropy to Diffusion Control, J. Am. Chem. Soc., 2012, 134, 13902–13911, DOI:10.1021/ja306522b.
-
(a) J. P. Guthrie and V. Pitchko, Reactions of carbocations with water and azide ion: calculation of rate constants from equilibrium constants and distortion energies using No Barrier Theory, J. Phys. Org. Chem., 2004, 17, 548–559, DOI:10.1002/poc.763;
(b) J. P. Guthrie, No-Barrier Theory: Calculating Rates of Chemical Reactions from Equilibrium Constants and Distortion Energies, Chem. Phys. Chem., 2003, 4, 809–816, DOI:10.1002/cphc.200200327;
(c) J. P. Guthrie and V. Pitchko, Hydration of Carbonyl Compounds, an Analysis in Terms of No Barrier Theory:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Prediction of Rates from Equilibrium Constants and Distortion Energies, J. Am. Chem. Soc., 2000, 122, 5520–5528, DOI:10.1021/ja992991q.
Prediction of Rates from Equilibrium Constants and Distortion Energies, J. Am. Chem. Soc., 2000, 122, 5520–5528, DOI:10.1021/ja992991q. - (a) R. A. Marcus, Electron transfer reactions in chemistry theory and experiment, J. Electroanal. Chem., 1997, 438, 251–259, DOI:10.1016/S0022-0728(97)00091-0; (b) R. A. Marcus, Energetic and dynamical aspects of proton transfer reactions in solution, Faraday Symp. Chem. Soc., 1975, 10, 60–68, 10.1039/FS9751000060.
- (a) S. de la Moya, H.-U. Siehl and A. G. Martínez, About the Existence of Organic Oxonium Ions as Mechanistic Intermediates in Water Solution, J. Phys. Chem. A, 2016, 120, 7045–7050, DOI:10.1021/acs.jpca.6b06216; (b) A. G. Martínez, P. C. Gómez, S. de la Moya and H.-U. Siehl, Revealing the mechanism of the water autoprotolysis on the basis of Marcus theory and TD-DFT methodology, J. Mol. Liq., 2021, 324, 115092, DOI:10.1016/j.molliq.2020.115092; (c) A. G. Martínez, P. C. Gómez, S. de la Moya and H.-U. Siehl, Structural proton transfer rates in pure water according to Marcus theory and TD-DFT computations, J. Mol. Liq., 2022, 357, 119048, DOI:10.1016/j.molliq.2022.119048; (d) A. G. Martínez, S. de la Moya, J. Osío Barcina, F. Moreno Jiménez and B. Lora Maroto, The Mechanism of Hydrolysis of Aryldiazonium Ions Revisited: Marcus Theory vs. Canonical Variational Transition State Theory, Eur. J. Org. Chem., 2013, 6098–6107, DOI:10.1002/ejoc.201300834; (e) V. K. Prasad, Z. Pei, S. Edelmann, A. Otero de la Roza and G. A. Di Labio, BH9, a New Comprehensive Benchmark Data Set for Barrier Heights and Reaction Energies: Assessment of Density Functional Approximations and Basis Set Incompleteness Potentials, J. Chem. Theory Comput., 2022, 18, 151–166, DOI:10.1021/acs.jctc.1c00694.
- (a) J. P. Richard, A consideration of the barrier for carbocation-nucleophile combination reactions, Tetrahedron, 1995, 51, 1535–1573, DOI:10.1016/0040-4020(94)01019-V; (b) T. L. Amyes and K. B. Williams, Concerted bimolecular substitution reactions of acetal derivatives of propionaldehyde and benzaldehyde, Pure & Appl. Chem., 1998, 70, 2039–2045, DOI:10.1021/ja00317a033.
- A. Fernández-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Thrular, Modeling the kinetics of bimolecular reactions, Chem. Rev., 2006, 106, 4518–4584, DOI:10.1021/cr050205w.
- (a) C. Costentin, M. Robert and J.-M. Savéant, Electrochemical concerted proton and electron transfers. Potential-dependent rate constant, reorganization factors, proton tunneling and isotope effects, J. Electroanal. Chem., 2006, 588, 197–206, DOI:10.1016/j.jelechem.2005.12.027; (b) E. Hatcher, A. V. Soudackov and S. Hammes-Schiffer, Proton-coupled electron transfer in soybean lipoxygenase: dynamical behavior and temperature dependence of kinetic isotope effects, J. Am. Chem. Soc., 2007, 129, 187–196, DOI:10.1021/ja066721.
- C. Costentin, M. Robert and J.-M. Savéant, Adiabatic and non-adiabatic concerted proton-electron transfers. Temperature effects in the oxidation of intramolecularly hydrogen-bonded phenols, J. Am. Chem. Soc., 2007, 129, 9953–9963, DOI:10.1021/ja071150d.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09, Gaussian Inc., Pittsburgh, PA, 2009. Licensed to A. G. Martínez Search PubMed.
- (a) J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections, J. Chem. Phys., 2008, 128, 084106, DOI:10.1063/1.2834918; (b) J. Tirado-Rives and W. L. Jorgensen, Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules, J. Chem. Theory Comput., 2008, 4, 297–306, DOI:10.1021/ct700248k.
- (a) G. Lars and S. A. Grimme, A General Database for Main Group Thermochemistry, Kinetics, and Noncovalent Interactions − Assessment of Common and Reparameterized (meta-)GGA Density Functionals, J. Chem. Theory Comput., 2010, 6, 107–126, DOI:10.1021/ct900489g; (b) S. N. Pieniazek, F. R. Clemente and K. N. Houk, Sources of Error in DFT Computations of C-C Bond Formation Thermochemistries: Pi-Sigma Transformations and Error Cancellation by DFT Methods, Angew. Chem., Int. Ed., 2008, 47, 7746–7749, DOI:10.1002/anie.2008801843.
- Truhlar's Group WEB: https://comp.chem.umn.edu/info/DFT.htm#m05.
- R. A. McClelland, Flash Photolysis Generation and Reactivities of Carbenium Ions and Nitremium Ions, Tetrahedron, 1996, 52, 6823–6958, DOI:10.1016/0040-4020(96)00020-8.
- Y. Chiang and A. J. Kresge, Mechanism of hydration of simple olefins in aqueous solution. cis- and trans-cyclooctene, J. Am. Chem. Soc., 1985, 107, 6363–6367, DOI:10.1021/ja00308a033.
- Y. Chiang, W. K. Chwang, A. J. Kresge, M. F. Powell and S. Szilagyi, Acid-catalyzed olefin-alcohol interconversion in the 1-methylcyclooctyl system. Strain-relief acceleration of the hydration of 1-methyl-trans-cyclooctene, J. Org. Chem., 1984, 49, 5218, DOI:10.1021/jo00200a041.
- (a) R. A. McClelland, Carbocations, in Reactive Intermediate Chemistry, ed. R. A. Moss, M. S. Platz, M. Jones Jr., J. Wiley & Sons Inc., 2004, p. 16 Search PubMed; (b) M. Jones Jr, Organic Chemistry, W. W. Norton & Co., 3rd edn, 2005, pp. 585–658 Search PubMed.
- K. J. Laidler and M. K. King, The Development of Transition-State Theory, J. Phys. Chem., 1983, 87, 2657–2664 CrossRef CAS.
- (a) S. Siber, P. Buzek, P. V. R. Schleyer, W. Koch and J. Walkimar, J. Am. Chem. Soc., 1993, 115, 259–270, DOI:10.1021/ja00054a037; (b) T. Kato and Ch. A. Reed, Angew. Chem., 2004, 116, 2968–2971, DOI:10.1002/ange.200453931.
- T. L. Amyes and W. P. Jencks, J. Am. Chem. Soc., 1989, 111, 7888–7900, DOI:10.1021/ja00202a033.
- O. Ph. Adero, T. Furukawa, M. Huang, D. Mukherjee, P. Retailleau, L. Bohé and D. Crich, J. Am. Chem. Soc., 2015, 137(32), 10336–10345, DOI:10.1021/jacs.5b06126.
- P. R. Schreiner, Angew. Chem., Int. Ed., 2007, 46, 4217–4219, DOI:10.1002/anie.200700386.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of the B3LYP optimized geometries for carbocations and carbocation–water complexes, as well as SMD energies (Table S1). See DOI: https://doi.org/10.1039/d3cp03544a |
| This journal is © the Owner Societies 2023 |

