Chiral selectivity vs. noise in spontaneous mirror symmetry breaking
Received
13th July 2023
, Accepted 10th October 2023
First published on 12th October 2023
Abstract
Mirror symmetry breaking bifurcations, that occur in nonlinear chemical systems leading to final chiral states with very large enantiomeric excess, can be exploited as an efficient chiral signal selector for even the smallest chiral polarizations. This effect of the chiral polarization requires the system's capacity for overcoming thermal noise, which is manifested as fluctuating reaction rate constants. Therefore, we investigate the chiral selectivity across a range of tiny parity-violating energy differences (PVED) in the presence of inevitable non-equilibrium temperature fluctuations. We use a stochastic differential equation simulation methodology (Ito process) that serves as a valuable tool in open systems for identifying the thresholds at which the chiral force induces chiral selectivity in the presence of non-equilibrium temperature fluctuations. This approach enables us to include and analyze chiral selectivity in the presence of other types of fluctuations, such as perturbations in the rate of fluid flow into and out of the reactor and in the clamped input concentrations. These concepts may be of practical interest (i.e., spontaneous deracemizations) but are also useful for a better understanding of the general principles governing the emergence of biological homochirality.
1 Introduction
Enantiomerism1 refers to molecular geometrical structures that break parity invariance2 The concept is related to chirality, which involves the presence of right- and left-handed objects. Chiral selectivity is the ability of a molecule or a system to recognize and differentiate between chiral forms or enantiomers. Biological homochirality, or one-handedness, refers to the uniform predominance of one and the same chiral sign of the building blocks of the functionalized biological polymers such as the L-amino acids in proteins and the D-sugars in DNA, supporting the basic functions of life such as catalysis, metabolism, self-reproduction and the ability for evolution.3 The homochirality of amino acids and sugar molecules in biosystems is a necessity for life,4,5 and has its most striking experimental manifestation regarding the question of the origin of biological homochirality.
The homochiral property of life stands in striking contrast to the characteristics of artificial chemical processes that result in chiral species. In laboratory or industrial chemistry, when there is no external chiral polarization, the final output of a reaction is typically racemic, meaning it contains an equal proportion of both enantiomeric species. However, there are a few well-known chemical experiments, such as the Soai reaction6 and Viedma deracemization,7 where the final chiral composition is often nearly homochiral rather than racemic. This phenomenon occurs in nonlinear chemical networks that exhibit enantioselective autocatalysis leading to a bifurcation when the racemic non-equilibrium stationary state (NESS) becomes unstable. In these cases, fluctuations drive the system stochastically towards one of the two possible enantiomorphic outputs. This scenario, called spontaneous mirror symmetry breaking (SMSB), bridges the gap between laboratory and prebiotic chemistries, since it is now widely accepted that enantiomeric excesses appeared very soon before the origin of life.8–12
However, due to fluctuations and in the absence of any chiral polarization, there is a stochastic distribution of chiral signs around the ideal racemic composition. It is important to emphasize that SMSB represents a genuine bifurcation scenario, which can be highly sensitive to even slight chiral biases.13 This sensitivity stands in contrast to the strong chiral polarizations that are required, for instance, in classical asymmetric synthesis.14 The Soai reaction serves as a striking example of this sensitivity, where the chiral output is directed by additives exhibiting chirality derived from isotopic substitutions such as 12C/13C, 14N/15N and 16O/18O enantiomorphs.15–17 Moreover, the presence of chiral compounds at the contaminant concentration level (cryptochirality) can select the final chiral sign.18–20 Nevertheless, it is crucial to acknowledge that in real nonlinear chemical systems, any chiral polarization competes with the unavoidable thermal and environmental fluctuations. Therefore, it is likely that there exists a critical threshold of chiral polarization capable of surpassing the racemizing effects of these fluctuations. To estimate this threshold from first principles, we assume for an ideal solution with perfect mixing that, on the one hand, the changes in the reaction rate constants are due to the thermal fluctuations and, on the other hand, that there exists a tiny but permanent chiral polarization, namely the parity-violation energy difference (PVED) between the enantiomers.21,22 In the domain of fundamental physics, violation of charge-parity (CP) symmetry determines that enantiomorphs are non-identical entities by virtue of the tiny energy difference that exists between them.8,23–31 Although PVED has not yet been detected in typical chemical experiments29,30,32–34 a logical connection exists between physical reality and biological chirality.35,36 However, the planned design and construction of ultrahigh resolution instruments for vibrational spectra, and the use of heavy atom chiral complexes, promises the possibility of successful PVED measurements being carried out in the near future.
In this paper, we follow a different approach, namely the use of SMSB37–40 as a powerful amplifier of chiral polarizations. It is well-known that some enantioselective autocatalytic systems lead to outcomes yielding large deviations from the racemic composition. A stochastic distribution of final chiral signs between successive experiments is expected on the average,41 although there was some initial doubt for both the Viedma deracemization42 and the Soai reaction.43 Therefore, for any reasonable scenario of chemical evolution, and for a relatively large number of analogous systems, the ultimate net consequence should be the racemic composition. Nevertheless, since Kondepudi's pioneering work,44 it has been assumed that weak neutral currents, extended over sufficiently long periods of time, during which there is a slow increase of the substrate concentration, could well lead to a deterministic and robust chiral bias in nonlinear chemical networks involving enantiomers, even in a randomly fluctuating environment.45 Motivated by this possibility, we developed a preliminary model46 demonstrating that the very tiny47 but permanent parity violating energy difference (PVED)22 can be sufficient to deracemize a macroscopic and out of equilibrium chemical system, even in the presence of unavoidable and permanent thermal fluctuations. These calculations were based on nonlinear stochastic differential rate equations, where the reaction rate constants involving the enantiomers are sensitive to the thermal fluctuations, and as well to the PVED bias. It was shown that when the amplitude of the thermal fluctuations times the activation enthalpy is of the same order of magnitude as the PVED bias, a resilience of the parity-violation-induced chiral selectivity to nonequilibrium temperature fluctuations is observed. Encouraged by this initial success, and being aware that there is always a risk that the influence of the fluctuations might not be taken into account sufficiently, we clarify here a number of important points not addressed or covered in our previous work.
The purpose of this paper is to focus on the details of the stochastic histories of the enantiomeric chemical compositions before and after the chiral symmetry breaking transition, showing the influence of the presence or absence of the PVED bias. Our findings demonstrate that in close proximity to the critical threshold, an increased number of simulation trials leads to a statistically more significant differentiation between the stochastic and deterministic outcomes. In the present study, we employ an improved stochastic simulation methodology that serves as a valuable tool for identifying the thresholds at which chiral forces, such as the PVED, induce chiral selectivity that remains resilient in the face of non-equilibrium temperature fluctuations in open systems. These findings shed light on the interplay between chiral forces and fluctuation effects, providing insights into the conditions under which chiral selectivity can be sustained in dynamic chemical systems. To accomplish this, we define and implement a different mathematical approach for the numerical simulation of stochastic differential rate equations which is based on Ito and Wiener processes,48 and we include the complete untruncated thermal noise spectrum. This distinct approach will allow us to consider fluctuating boundary conditions, fluctuations in the system volume and also fluctuations in the input fluid flow rates to the reactor, and distinct input/output reactor configurations or reactor architectures. To this end, we employ a stochastic version of an open-flow, fully reversible, Frank model.49 We choose this dynamical model because it is now well known that its basic ingredients, namely enantioselective autocatalysis and mutual inhibition of opposite enantiomers, lie at the heart of the Soai reaction, the first experimentally proven absolute asymmetric synthesis.6,50
This paper is organized as follows. In Section 2 we review briefly the general expression for the amplitude of the rate-constant fluctuations, the chiral selectivity criterion and the open flow reaction scheme employed. We then present the set of coupled Ito stochastic differential equations. In the present approach, the entire range of temperature fluctuations are used in the numerical simulations, in contrast to the approximation used previously, and this is commented briefly in Section 3. The inclusion of chiral bias due to PVED in the vector Ito equations is presented in Section 4. The results of varying the relative magnitude of the temperature fluctuations with respect to the fixed PVED bias are presented in Section 5 for a range of bias values. Fluctuations in the boundary conditions associated with the system volume, the fluid flow rates, and the fixed input concentrations are treated in Section 6. Conclusions are given in Section 7.
2 Chiral selectivity criterion and a stochastic open-flow model
Temperature fluctuations δT(t) about a mean value T induce corresponding fluctuations in the chemical reaction rate constants k which, to leading order in  are given by
are given by| | 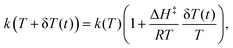 | (1) |
where ΔH‡ is the activation enthalpy of the reaction. The (non-equilibrium) temperature fluctuations δT are distributed according to a Gaussian distribution with mean T and standard deviation σ51| | 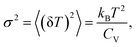 | (2) |
where kB is the Boltzmann constant and CV the constant volume specific heat. This relation allows us to characterize the T-fluctuation term in eqn (1) in terms of the root-mean-square (rms) value 〈(δT)2〉1/2 as follows. We estimate the ratio in eqn (1) according to: 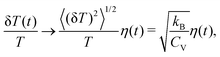 so that eqn (1) can be expressed as
so that eqn (1) can be expressed as| | | ki(T + δT(t)) = ki(T)(1 + ξiηi(t)), | (3) |
where the amplitude ξi of the fluctuation in the rate constant ki is given by| |  | (4) |
and ηi(t) is a Gaussian white noise. As the transition enthalpy can only be positive ΔH‡i > 0 we define a positive noise amplitude ξi > 0. We lose no generality in defining ξ in this way since the white noise factor it multiplies has both positive and negative fluctuations that increase or decrease the corresponding transition enthalpy factor. Both the amplitude ξi and the noise ηi depend on the individual ith reaction; the forward and reverse steps are treated as independent reactions. Note moreover that ξi in eqn (4) is a product of two independent contributions: the first one depends on the transition enthalpy divided by the mean temperature, whereas the second factor involves the relative rms temperature fluctuation. The former is a chemical property of each single reaction path, while the latter encodes the bulk thermodynamic properties of the system, via the specific heat CV at constant volume (a physical attribute).
Denote by ΔΔG‡i > 0 the minute energy difference between the two enantiomers due to their interaction with a chiral polarization, exerted for example by chiral media, or by a natural chiral physical force. Then, consider the case when g corresponds to the PVED bias in the ith rate constant. When this bias is greater than the rms temperature fluctuations times the change in enthalpy factor associated with that rate constant:
| |  | (5) |
then we would rightfully expect that the chiral bias
g can overcome the thermal noise
ξi, and therefore select deterministically the final stable chiral outcome, provided the inequality
g ≥
ξi holds for all the reactions
i in which the PVED bias intervenes. The relation
eqn (5) implies a signal-to-noise (S/N) ratio
g/
ξi ≥ 1, in which the PVED bias plays the role of the constant applied “direct current” or DC signal, and the temperature fluctuations comprise the “alternating current” or AC background noise. See Appendix A for derivation of particular cases of this chiral selectivity criterion for the kinetic model described below.
We test this chiral selectivity criterion eqn (5) with the following model. It involves four species A, L, D, P and ten one-way reactions eqn (6)–(8), in addition to the five pseudoreactions or input/output flow terms eqn (9)–(13), as defined by the following transformations:
| |  | (6) |
| |  | (7) |
| |  | (8) |
| |  | (9) |
| |  | (10) |
| |  | (11) |
| |  | (12) |
| |  | (13) |
where
kf =
q/
V, the volumetric flow rate
q is in liters per second and
V is in liters. Species
A is an achiral precursor and
P is an achiral product: the heterodimer
LD =
DL is the achiral (meso form) dimer of the two chiral enantiomers
L and
D.
The individual forward and reverse reaction rate constants in eqn (6) and (7) are constrained by the equality of the equilibrium constants for enantioselective autocatalysis and the direct production: that is,  and this relates the differences in the free energies of activation of the forward and reverse reactions for autocatalysis and direct production: ΔG‡a − ΔG‡−a = ΔG‡d − ΔG‡−d. This relation follows from inserting the expression for the rate constants k into the above constraint, and using transition state theory (the Eyring–Polanyi equation for k). This is the most general statement that can be made regarding the activation energies.
and this relates the differences in the free energies of activation of the forward and reverse reactions for autocatalysis and direct production: ΔG‡a − ΔG‡−a = ΔG‡d − ΔG‡−d. This relation follows from inserting the expression for the rate constants k into the above constraint, and using transition state theory (the Eyring–Polanyi equation for k). This is the most general statement that can be made regarding the activation energies.
The stochastic reaction rate equations that follow from the above transformations eqn (6)–(13) and using eqn (3), are written as a set of coupled Ito stochastic differential equations, see ref. 48. The noise terms follow from substituting the expression for the fluctuating reaction rate constants ki, eqn (3), into the differential reaction rate equations that follow from the above transformations. The result is then expressed as Ito stochastic differential equations, using the definition of Wiener processes to write the noise terms as indicated below. We can separate each equation into its deterministic (∝dt) and random (∝dWj(t)) parts in order to cast the equations as a vector Ito process,48 using its attendant standard notation, as follows:
| |  | (14) |
| |  | (15) |
| |  | (16) |
| |  | (17) |
There are ten independent one-way transformations in
eqn (6)–(8), hence these stochastic equations will depend on ten independent Wiener processes {
Wi}
i=110, where
dWi(
t) =
ηi(
t)
dt;
48 one such Wiener process (and Gaussian white noise
ηi) for each one of the ten independent one-way reactions. In the above, we have taken all
ξi =
ξ to be equal, a reasonable first approximation; see
eqn (4).
We comment on the scaling. The reaction rates (the coefficients of the dt) scale as the inverse volume ∼V−1. The noise terms (see coefficients of the dW) are given by the product of ξ times the reaction rates, and the noise amplitude ξ scales as the inverse square root of the heat capacity at constant volume: ξ ∼ (1/CV)1/2. The overall product, which gives the noise term thus scales as ∼V−1(1/CV)1/2. The constant volume heat capacity scales with the volume CV ∼ V. Thus the overall noise terms scale as ∼V−3/2. Thus relative to the deterministic contributions (the coefficients of dt) to the rate equation which scale as ∼V−1, the noise terms (coefficients of the dW) therefore scale as ∼V−1/2.
We remark that an attempt to estimate the individual noise amplitudes ξi would make sense if one were to consider using the rather more involved and phenomenologically realistic kinetic models of say, the Soai reaction,52 and provided of course that one could reasonably estimate the values of the transition enthalpies ΔH‡i of the individual reactions belonging to those kinetic and thermodynamic models. In that case, one could use the van't Hoff equation53 for this purpose, and would therefore need to know the equilibrium constant of a given reaction for at least two different temperatures, to be able to calculate the transition enthalpy of that reaction.
3 Thermal noise statistics
A major important difference between the stochastic differential equations used in ref. 46, and the vector Ito process used here, has to do with the treatment of the noise. For purposes of the numerical simulations, the noise was generated as continuous random functions, the latter obtained by interpolating sequences of random numbers generated from a normal distribution. These continuous random functions were then included in the differential equations. We also truncated the spectrum of the relative temperature fluctuations  so as to lie within one standard deviation of the mean temperature T. In the present paper, we employ vector Ito process to model the stochastic equations and use independent Wiener processes for the noise terms, so no such restriction is imposed on the noise. Whereas the former truncation accounted for approximately 67% of all the fluctuations, here all the fluctuations are included, see Fig. 1. The “missin” fluctuations, those beyond one standard deviation, make up for the remaining 33% of the noise spectrum. Recall that the probability distribution for non-equilibrium temperature fluctuations δT is given by ref. 46
so as to lie within one standard deviation of the mean temperature T. In the present paper, we employ vector Ito process to model the stochastic equations and use independent Wiener processes for the noise terms, so no such restriction is imposed on the noise. Whereas the former truncation accounted for approximately 67% of all the fluctuations, here all the fluctuations are included, see Fig. 1. The “missin” fluctuations, those beyond one standard deviation, make up for the remaining 33% of the noise spectrum. Recall that the probability distribution for non-equilibrium temperature fluctuations δT is given by ref. 46| |  | (18) |
where φ is the normal frequency function54 and the standard deviation σ = δTrms = 〈(δT)2〉1/2, see eqn (2). So,  corresponds to fluctuations within one standard deviation (≈67%), whereas
corresponds to fluctuations within one standard deviation (≈67%), whereas  includes all fluctuations. Using the full range of fluctuations will have an impact on the ability of the PVED bias g to overcome the thermal noise and so select a final chiral sign (see Section 5), but is not as drastic as one might suppose, since the very largest fluctuations, which are those lying beyond three standard deviations, 3σ, from the mean, have exponentially vanishing probabilities, and so are extremely rare events, see Fig. 1. Moreover, as white Gaussian noise includes all frequencies, and with equal weighting (its frequency spectrum is flat), there always exists arbitrarily large frequencies ω such that ωΔt > 1 is satisfied, where Δt is the smallest time step used in the numerical solution of the stochastic differential equations. Compliance with this inequality implies that statistical randomness between successive simulation time steps is assured.
includes all fluctuations. Using the full range of fluctuations will have an impact on the ability of the PVED bias g to overcome the thermal noise and so select a final chiral sign (see Section 5), but is not as drastic as one might suppose, since the very largest fluctuations, which are those lying beyond three standard deviations, 3σ, from the mean, have exponentially vanishing probabilities, and so are extremely rare events, see Fig. 1. Moreover, as white Gaussian noise includes all frequencies, and with equal weighting (its frequency spectrum is flat), there always exists arbitrarily large frequencies ω such that ωΔt > 1 is satisfied, where Δt is the smallest time step used in the numerical solution of the stochastic differential equations. Compliance with this inequality implies that statistical randomness between successive simulation time steps is assured.
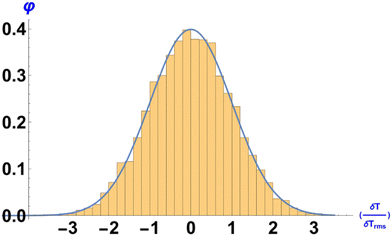 |
| | Fig. 1 The standard normal frequency function φ, eqn (18). The approximation used in ref. 46 corresponds to relative fluctuations  lying within one standard deviation from the mean. Here in this work, the full unbounded range is employed. lying within one standard deviation from the mean. Here in this work, the full unbounded range is employed. | |
4 Including PVED bias
To include a chiral bias g due to a small energy difference between enantiomers, in the above stochastic differential rate equations, we make the following substitutions in the first two equations eqn (14) and (15): and in only those terms that contain [L], but in no term containing [D]:This chiral bias favors the D-enantiomer over the L (changing the sign from −g to +g in the above favors instead the L-enantiomer over the D). This leads to the modified stochastic equations for [A] and [L]:| |  | (22) |
| |  | (23) |
The remaining two stochastic equations eqn (16) and (17) are unchanged. We can then carry out simulations of the four coupled stochastic differential equations eqn (16), (17), (22) and (23) to assess the ability of a range of PVED biases g to select deterministically final stable scalemic states in the presence of random temperature fluctuations ξ, according to eqn (5). The simulations of the set of Ito stochastic differential equations have been performed using the Euler–Maruyama method, as defined and implemented in Mathematica v13.
5 Fluctuating reaction rate constants: stochastic vs. deterministic regimes
The model parameters are taken as follows: kd = 10−4, k−d = 10−9, ka = 102, k−a = 10−3, k1 = 102, k−1 = 10−4, [A]in = 10−2 and the flow rate kf = 10−3. From eqn (6) and (7) these imply an equilibrium constant Keq = 105. We initiate all the simulations on the idealized racemic composition: [L]0 = [D]0 = 10−3, with [P]0 = 10−6 and [A]0 = [A]in. These values locate the system on the unstable racemic branch in the absence of chiral bias.
We first generate multiple runs of the system subject to the temperature fluctuations alone (no PVED bias: g = 0), and for strict racemic initial conditions. This yields a set of statistically independent random histories, a typical example of which is shown in Fig. 2. After an induction period the system bifurcates, and the times at which the concentrations of the two enantiomers separate from each other is spread out in time, this dispersion is due to the fluctuations in the rate constants. We can map these bifurcations to histograms of the final enantiomeric excesses ee = ([L] − [D])/([L] + [D]) by taking time-slices through the bifurcation curves (at the final times at t = 5000 s) in these sets of histories. Note, for each individual run, there is a majority (on the upper branch) and a minority (on the lower branch) enantiomer, which can be either the L or the D enantiomer, respectively, and we calculate the corresponding ee for this run. As each outcome is essentially homochiral (already for t = 5000 s, there are seven orders of magnitude difference in the majority vs. minority enantiomer concentrations) this single run either yields ee ≅ −1 (when the D is the majority enantiomer) or else ee ≅ +1, (when the L is the majority enantiomer). This procedure is then repeated for the entire set of all n runs, and so we calculate 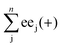 and
and  , where eej(±) = ±1, where +1 holds for the majority D-enantiomer, and −1 holds for the majority L-enantiomer, respectively. We plot the results in histograms to show the distribution of the set of all outcomes. The data slice is taken at t = 5000 s. Next, we include the PVED bias g > 0 in the stochastic equations and make multiple runs, again with racemic initial conditions. For each value of the PVED bias chosen, we test the chiral selectivity against various noise amplitudes ξ, for noise greater than, equal to, and less than the bias: ξ > g, ξ = g, ξ < g. We map the outcomes to histograms of final enantiomeric excesses ee as outlined above. Here in contrast, after the induction period the times at which the concentrations of two enantiomers separate from each other is sharply focused in time, see Fig. 3. The PVED bias has overcome the thermal fluctuations in the rate constants. See Fig. 4 for characteristic examples sampled over a wide range of g and also Table 1 for a guide to the characterization of the distinct outcomes. Very recent calculations of PVED for cinnabar crystals,55 lead to values as large as g = 2.2 × 10−12, which we include in our analysis below. Some comments regarding these results, with respect to the those obtained in ref. 46, are in order. There is now a qualitative and quantitative pattern of statistical uniformity in the outcomes of the numerical results with respect to the range of g bias values tested in that: (i) all the g's tested here select the final state deterministically when the noise level is an order of magnitude smaller than the bias: ξ < g (see Panel (a) in Fig. 4), (ii) for noise of the same order of magnitude as the bias ξ = g, the selection is still biased strongly, but is slightly skewed (see Panel (b) in Fig. 4), and for noise an order of magnitude larger than the bias ξ > g, the outcomes are bimodal, no statistically significant selection of a final scalemic state is possible, see Panel (c) in Fig. 4. Here we solve numerically for the four coupled Ito stochastic differential equations eqn (16), (17), (22) and (23). The main mathematical difference between this approach and the previous one is now the random T-fluctuations are taken from a complete normal distribution, and are not restricted to lie within (±σ) one standard deviation of the mean (see discussion in Section 3 on this point). That is, all the temperature fluctuations beyond one standard deviation from the mean are now included. This translates into a diminished chiral selectivity when the fluctuations are greater than the bias ξ > g, which is natural and is to be expected. The largest temperature fluctuations (meaning those that lie beyond three standard deviations from the mean) diminish the chiral selectivity of the PVED bias, but they are also less likely than the smaller fluctuations that lie within one standard deviation of the mean temperature, see Fig. 1. Further details of the individual numerical simulations are compiled in Table 2. For a given chiral bias g > 0, noise amplitude ξ > 0 and number of statistically independent runs n, we obtain the total numbers of final homochiral L and D outcomes, where L + D = n. From this we calculate the net enantiomeric excess 〈ee〉n = (L − D)/(L + D) averaged over the n runs, and also the fraction of homochiral D-outcomes pD = D/(L + D). We compare the latter to the 99% confidence interval (C.I.) for expecting a racemic outcome, i.e., when pD = 1/2. This C.I. eqn (24) depends on p, the confidence level and also on n. Note, in the so-called “severe” region of parameter space, for which the strength of the chiral bias is less in magnitude than the noise amplitude g < ξ, we have also further increased the number of runs n from 100 to 500 and then to 1000 in order to ascertain whether the final stationary outcomes can be regarded as either racemic or else biased. We use the 99% confidence interval (C.I.) for expecting a racemic outcome as criterion:
, where eej(±) = ±1, where +1 holds for the majority D-enantiomer, and −1 holds for the majority L-enantiomer, respectively. We plot the results in histograms to show the distribution of the set of all outcomes. The data slice is taken at t = 5000 s. Next, we include the PVED bias g > 0 in the stochastic equations and make multiple runs, again with racemic initial conditions. For each value of the PVED bias chosen, we test the chiral selectivity against various noise amplitudes ξ, for noise greater than, equal to, and less than the bias: ξ > g, ξ = g, ξ < g. We map the outcomes to histograms of final enantiomeric excesses ee as outlined above. Here in contrast, after the induction period the times at which the concentrations of two enantiomers separate from each other is sharply focused in time, see Fig. 3. The PVED bias has overcome the thermal fluctuations in the rate constants. See Fig. 4 for characteristic examples sampled over a wide range of g and also Table 1 for a guide to the characterization of the distinct outcomes. Very recent calculations of PVED for cinnabar crystals,55 lead to values as large as g = 2.2 × 10−12, which we include in our analysis below. Some comments regarding these results, with respect to the those obtained in ref. 46, are in order. There is now a qualitative and quantitative pattern of statistical uniformity in the outcomes of the numerical results with respect to the range of g bias values tested in that: (i) all the g's tested here select the final state deterministically when the noise level is an order of magnitude smaller than the bias: ξ < g (see Panel (a) in Fig. 4), (ii) for noise of the same order of magnitude as the bias ξ = g, the selection is still biased strongly, but is slightly skewed (see Panel (b) in Fig. 4), and for noise an order of magnitude larger than the bias ξ > g, the outcomes are bimodal, no statistically significant selection of a final scalemic state is possible, see Panel (c) in Fig. 4. Here we solve numerically for the four coupled Ito stochastic differential equations eqn (16), (17), (22) and (23). The main mathematical difference between this approach and the previous one is now the random T-fluctuations are taken from a complete normal distribution, and are not restricted to lie within (±σ) one standard deviation of the mean (see discussion in Section 3 on this point). That is, all the temperature fluctuations beyond one standard deviation from the mean are now included. This translates into a diminished chiral selectivity when the fluctuations are greater than the bias ξ > g, which is natural and is to be expected. The largest temperature fluctuations (meaning those that lie beyond three standard deviations from the mean) diminish the chiral selectivity of the PVED bias, but they are also less likely than the smaller fluctuations that lie within one standard deviation of the mean temperature, see Fig. 1. Further details of the individual numerical simulations are compiled in Table 2. For a given chiral bias g > 0, noise amplitude ξ > 0 and number of statistically independent runs n, we obtain the total numbers of final homochiral L and D outcomes, where L + D = n. From this we calculate the net enantiomeric excess 〈ee〉n = (L − D)/(L + D) averaged over the n runs, and also the fraction of homochiral D-outcomes pD = D/(L + D). We compare the latter to the 99% confidence interval (C.I.) for expecting a racemic outcome, i.e., when pD = 1/2. This C.I. eqn (24) depends on p, the confidence level and also on n. Note, in the so-called “severe” region of parameter space, for which the strength of the chiral bias is less in magnitude than the noise amplitude g < ξ, we have also further increased the number of runs n from 100 to 500 and then to 1000 in order to ascertain whether the final stationary outcomes can be regarded as either racemic or else biased. We use the 99% confidence interval (C.I.) for expecting a racemic outcome as criterion:
| | 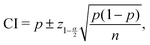 | (24) |
where
p is the proportion of interest (
e.g., for racemic proportion
p = 1/2),
n is the sample size,
α the desired confidence, and

the
Z-value for the desired confidence,

for 99% confidence.
56 These confidence interval bounds are computed and listed in the right-hand column of
Table 2. The table is based on time-slices through the bifurcation curves at the final times at
t = 5000 s.
 |
| | Fig. 2 Random outcomes. Example of n = 20 independent runs of the stochastic equations eqn (14)–(17) without PVED bias (g = 0); with ξ = 10−19. The symmetry breaking bifurcation is spread out in time by the noise, but all individual histories converge to the same asymptotic state. With no bias, both the upper and lower sets of branches are equally populated by L and D outcomes on average. Computing the enantiomeric excess ee for each individual run at time slice t = 5000 s leads to a bimodal histogram for all the runs, qualitatively similar to that in Fig. 4(c). See text for how these outcomes are mapped to histograms and see Table 1 for their interpretation. | |
 |
| | Fig. 3 Deterministic outcomes. Example of 20 independent runs of the stochastic equations eqn (16), (17), (22) and (23) with bias g = 10−18 with ξ = 10−19. The bias g reduces the spread in the bifurcation times. Compare to Fig. 2. Computing the enantiomeric excess ee at time slice t = 5000 s leads to a unimodal histogram for all the runs, qualitatively similar to that in Fig. 4(a). See text for how these outcomes are mapped to histograms and see Table 1 for their interpretation. | |
 |
| | Fig. 4 Distributions of the outcome from multiple simulations n = 100 of the competition between the PVED g and the product of the rms temperature fluctuation times the activation enthalpy factor ξj, eqn (4). The level of constant chiral bias corresponds to g = 10−n. Panel (a): ξ = 10−n−1; (b): ξ = 10−n; (c): ξ = 10−n+1. For n = 19, 18, 16, 13, 12. See Table 1 for how the outcomes are characterized. | |
Table 1 Characterization of the various outcomes: random, biased or deterministic, in terms of relationships between the sums of the enantiomeric excesses of the individual homochiral runs eej (±) = ±1. A statistically more precise discrimination between the random or biased outcomes is provided by estimating the confidence intervals (C.I.) for having a racemic outcome, as discussed in the text; see also Tables 2 and 3. Note that  holds for all outcomes. See Fig. 4
holds for all outcomes. See Fig. 4
When the results in Fig. 4 are plotted against the logarithms of the bias g and of the noise ξ, a simple pattern emerges as shown in Fig. 5. Indeed, there is a line, or separatrix, that divides the region of deterministic chiral outcomes from the region of stochastic ones, for the range of bias and noises considered. This is a linear relation between log(g) and log(ξ). We also see the effect of using the full noise noise spectrum here in contrast to the simulations of ref. 46. Also, for noise levels ξ = 10 g an order of magnitude greater that the bias, increasing the number of runs n narrows the confidence interval CI eqn (24), so what was a racemic outcome for low n can become a chiral one for larger n, since now the fraction pD lies outside the 99% CI, see Fig. 5.
 |
| | Fig. 5 Left: Influence of the calculation technique on the system output. Open circles or squares: truncated fluctuations, filled circles and squares: unrestricted fluctuations. Red round symbols: racemic output, green square symbols: chiral output. For an equivalent number of trials the stochastic Ito process is less selective than the calculations carried out in ref. 46. This can be seen at log(noise) = −11 and log(bias) = −12. For n = 100, Ito gives a racemic output (red filled dot) while truncated calculation gives a chiral output (open green square, n = 120). The same effect is also seen at log(noise) = −16 and log(bias) = −17 where truncated calculation gives a chiral output (open green square) while a red filled dot (racemic output) is expected from the Ito process. The dashed line (log(noise) = log(bias) + 0.5) is parallel to the first diagonal. It appears as a sensitive zone (separatrix between racemic and chiral domains from the Ito process) where the noise is about three times larger than the bias. Right: Statistical analysis of a series of parallel runs using a 99% confidence interval (CI) for expecting a racemic output in the presence of a noise 10 times greater than the bias. Results show that a high run number helps to unveil the tiny (but permanent) effect of the chiral bias which, otherwise would remain undetected (100 vs. 1000 runs). It is also shown that a higher bias is needed to overcome the randomizing effect of a greater noise level (bias >10−14 at 500 runs). | |
The results in Table 2 correspond to the equilibrium constant Keq = ka/k−a = kd/k−d = 105. We can consider the consequence of lowering the equilibrium constant by a factor of 102, by choosing the rate constants such that kd = 10−6 and ka = 1 keeping all other rate constants and parameters fixed, then Keq = 103. Then, mirror symmetry is still broken by temperature fluctuations, but now the reactions are less exergonic, or more reversible, than before. The results are tabulated in Table 3. For the same values of chiral bias g, noise amplitude ξ and number of runs n, the chiral selectivity of the bias is enhanced, for a lower value of the equilibrium constant, with respect to the results in Table 2. This indicates that when the reactions are more reversible (i.e., are less exergonic) the greater is the chiral selectivity of the bias g with respect to a given noise level ξ (see Table 3). We again take time-slices through the bifurcation curves at the final times at t = 5000 s.
Table 2 Summary of the simulations carried out for the open flow stochastic Frank model subject to chiral bias g and temperature fluctuations ξ, see eqn (16), (17), (22) and (23). g: the chiral bias in the rate constants; ξ: the amplitude of the temperature fluctuations, n: the number of statistically independent runs; L and D: the total number of homochiral outcomes for the L- and D-enantiomers, respectively; 〈ee〉n = (L−D)/(L + D): the net enantiomeric excess averaged over the n runs; pD = D/(L + D) is the fraction of homochiral D-outcomes for n. Final column gives the 99% confidence interval (C.I.) for expecting a racemic outcome that is, for pD = 1/2, see text for further explanation
|
g
|
ξ
|
n
|
L
|
D
|
〈ee〉n |
p
D
|
99% C.I. for racemic outcome |
| 10−19 |
10−20 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−19 |
10−19 |
100 |
10 |
90 |
−0.8 |
0.9 |
0.37 ≤ p ≤ 0.63 |
| 10−19 |
10−18 |
100 |
44 |
56 |
−0.12 |
0.56 |
0.37 ≤ p ≤ 0.63 |
| 10−19 |
10−18 |
500 |
212 |
288 |
−0.15 |
0.576 |
0.443 ≤ p ≤ 0.557 |
| 10−19 |
10−18 |
1000 |
481 |
519 |
−0.038 |
0.519 |
0.459 ≤ p ≤ 0.541 |
| 10−18 |
10−19 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−18 |
10−18 |
100 |
7 |
93 |
−0.86 |
0.93 |
0.37 ≤ p ≤ 0.63 |
| 10−18 |
10−17 |
100 |
47 |
53 |
−0.06 |
0.53 |
0.37 ≤ p ≤ 0.63 |
| 10−18 |
10−17 |
500 |
235 |
265 |
−0.06 |
0.53 |
0.443 ≤ p ≤ 0.557 |
| 10−18 |
10−17 |
1000 |
448 |
552 |
−0.104 |
0.552 |
0.459 ≤ p ≤ 0.541 |
| 10−16 |
10−17 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−16 |
10−16 |
100 |
12 |
88 |
−0.76 |
0.88 |
0.37 ≤ p ≤ 0.63 |
| 10−16 |
10−15 |
100 |
42 |
58 |
−0.16 |
0.58 |
0.37 ≤ p ≤ 0.63 |
| 10−16 |
10−15 |
500 |
244 |
256 |
−0.024 |
0.512 |
0.443 ≤ p ≤ 0.557 |
| 10−16 |
10−15 |
1000 |
452 |
548 |
−0.096 |
0.548 |
0.459 ≤ p ≤ 0.541 |
| 10−13 |
10−14 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−13 |
10−13 |
100 |
5 |
95 |
−0.9 |
0.95 |
0.37 ≤ p ≤ 0.63 |
| 10−13 |
10−12 |
100 |
52 |
48 |
+0.04 |
0.48 |
0.37 ≤ p ≤ 0.63 |
| 10−13 |
10−12 |
500 |
214 |
286 |
−0.144 |
0.572 |
0.443 ≤ p ≤ 0.557 |
| 10−13 |
10−12 |
1000 |
443 |
557 |
−0.114 |
0.557 |
0.459 ≤ p ≤ 0.541 |
| 10−12 |
10−13 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−12 |
10−12 |
100 |
13 |
87 |
−0.74 |
0.87 |
0.37 ≤ p ≤ 0.63 |
| 10−12 |
10−11 |
100 |
54 |
46 |
+0.08 |
0.46 |
0.37 ≤ p ≤ 0.63 |
| 10−12 |
10−11 |
500 |
221 |
279 |
−0.12 |
0.558 |
0.443 ≤ p ≤ 0.557 |
| 10−12 |
10−11 |
1000 |
450 |
550 |
−0.10 |
0.55 |
0.459 ≤ p ≤ 0.541 |
Table 3 Results of simulations for an equilibrium constant Keq = 103, two orders of magnitude smaller than that corresponding to Table 2. g: the chiral bias in the rate constants; ξ: the amplitude of the temperature fluctuations, n: the number of statistically independent runs; L and D: the total number of homochiral outcomes for the L- and D-enantiomers, respectively; 〈ee〉n = (L − D)/(L + D): the net enantiomeric excess averaged over the n runs; pD = D/(L + D) is the fraction of homochiral D-outcomes for n. Final column gives the 99% confidence interval (C.I.) for expecting a racemic outcome that is, for pD = 1/2. Note there is always a chiral output. Compare to Table 2
|
g
|
ξ
|
n
|
L
|
D
|
〈ee〉n |
p
D
|
99% C.I. for racemic outcome |
| 10−19 |
10−20 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−19 |
10−19 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−19 |
10−18 |
100 |
28 |
72 |
−0.44 |
0.72 |
0.37 ≤ p ≤ 0.63 |
| 10−18 |
10−19 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−18 |
10−18 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−18 |
10−17 |
100 |
29 |
71 |
−0.42 |
0.71 |
0.37 ≤ p ≤ 0.63 |
| 10−16 |
10−17 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−16 |
10−16 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−16 |
10−15 |
100 |
27 |
73 |
−0.46 |
0.73 |
0.37 ≤ p ≤ 0.63 |
| 10−13 |
10−14 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−13 |
10−13 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−13 |
10−12 |
100 |
27 |
73 |
−0.46 |
0.73 |
0.37 ≤ p ≤ 0.63 |
| 10−12 |
10−13 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−12 |
10−12 |
100 |
0 |
100 |
−1 |
+1 |
(Deterministic outcome) |
| 10−12 |
10−11 |
100 |
26 |
74 |
−0.48 |
0.74 |
0.37 ≤ p ≤ 0.63 |
The relationship between the number of experiments needed to yield an adequate CI in order to be able to distinguish between stochastic or deterministic outputs is a point that cannot be detected using common chemical kinetic methods. Despite the fact that the ratio g/ξ = 1 defines the transition from stochastic to deterministic regimes (see Tables 2 and 3 and Fig. 4), the CI (24) indicates the efficiency of the system towards chiral selectivity when the ratio between chiral induction and noise amplitude changes are >1; a large number of experiments, or in a origin of life scenario a large set of separated similar systems, is necessary to detect the chiral selection effect in SMSB. However, when g/ξ ≫ 1 only a small number of experiments, or a few separated systems, will already lead to the same final chiral sign selected by g.
6 Role of fluctuations in the boundary conditions: volume, flow rates and input concentrations
Fluctuations in the input and output rate δkf (see the pseudo-reactions in eqn (9)–(13)) can arise due to either fluctuations in the fluid flow rate itself δq and or to fluctuations in the system volume δV:| | 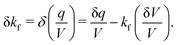 | (25) |
| | 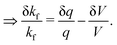 | (26) |
These are independent from the internal temperature fluctuations. We may include them in the above Ito formulation by making the following substitution in all the terms involving the flow rate:| |  | (27) |
where ηf is a Gaussian white noise, with an amplitude ξf and introducing the single Wiener process dWf[t] = ηf(t)dt for the fluctuating term. Then using eqn (27) in eqn (16), (17), (22) and (23) leads to the following replacements, where X = Ain, A, L, D, P:| | | kf[X]dt → kf[X]dt + kf[X]ξfdWf[t]. | (28) |
Whereas the rate constant fluctuations δki (due to the temperature fluctuations) for the ten individual one-way reactions eqn (6)–(8) are statistically independent, the open-flow terms eqn (9)–(13) will fluctuate coherently and in unison. This is because the input and output channels depend on one and the same flow rate constant kf. In particular, this means the fluctuations in the enantiomeric concentrations [L] and [D] due to the random flow rate δq and or volume fluctuations δV are racemic, and also of first order. So, no mirror symmetry breaking is expected due to these types of racemic, or “diagonal”, fluctuations. We have confirmed this with simulations. The outcome is similar to the Panel (a) in Fig. 4: a deterministic result. By way of example, even for very large amplitude fluctuations in the flow rate kf of the order of ξf = 0.16 (eqn (27)) and for a minuscule chiral bias g = 10−18, and in the presence of T-fluctuations, the chiral bias still selects deterministically for g > ξ, while there is a statistically significant bias when ξ = 10−18 and then no significant bias for ξ = 10−17, which is an order magnitude greater that the fixed chiral bias. Indeed, the qualitative pattern is that of the Panels (a) to (c) in Fig. 4. So, it is statistically indistinguishable from the case where the flow rate does not fluctuate. This is a consequence of the input and output flow scheme or flow architecture, for which all species concentrations are removed at the same rate in one unique output channel and where only the achiral substrate A is input to the reactor, see Fig. 6.
A distinct and realistic open-flow set-up from the chemical point of view, is to arrange for both enantiomers to flow into the reaction tank in a common shared channel and with an average racemic composition [L]in = [D]in. We can arrange for the achiral species A flow to in on a separate channel, see Fig. 6. There are thus two input channels, and a single common output channel carrying all four species A, L, D, P. In this case, the pseudo-reactions corresponding to the input flows are as follows:
| | 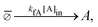 | (29) |
| |  | (30) |
where [X]
in denotes the fixed on average, or clamped, input concentration, and we define the individual input flow rates as follows:
| |  | (31) |
| |  | (32) |
| | 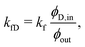 | (33) |
where the fluxes
ϕX,in satisfy the constant volume constraint

.
57 We consider fluctuations on the inflows of the enantiomers, see
Fig. 6. From
eqn (30), (32) and (33) these in turn can be due in principle to either (i) fluctuations in the individual flux fractions

and/or (ii) fluctuations about the average racemic composition [L]
in = [D]
in. This choice will depend on how we choose the Wiener processes, that is, whether they are the same process or else independent processes. Note however since the two enantiomers are being transported (by passive advection) by same fluid stream, we must rule out independent, and hence chiral, fluctuations in the L.D flux fractions. This leaves us with the possibility to consider only fluctuations in the enantiomer inflow concentrations, which are on average racemic. So we make the following replacements in the Ito stochastic equations for [L], [D] and [A] as follows using substitutions analogous to
eqn (28):
| | | (kfL[L]in − kf[L])dt + kfL[L]inζdWLin(t), | (34) |
| | | (kfD[D]in − kf[D])dt + kfD[D]inζdWDin(t), | (35) |
| | | (kfA[A]in − kf[A])dt, | (36) |
for two independent Wiener processes
WLin,
WDin.
ζ > 0 represents the amplitude of noise in the enantiomer concentrations [L]
in and [D]
in. Of course, we choose racemic input conditions:
kfL =
kfD; equal input flux fractions for both enantiomers, see
eqn (32) and (33), and [L]
in = [D]
in, so that any deviations from mirror symmetry coming from these terms
eqn (34) and (35) are thus due strictly to the independent noises on the common
L,
D-input channel, as quantified
via ζ > 0. Since
WLin,
WDin are independent Wiener processes, the fluctuations in the monomial terms
kfL[L]
in and
kfD[D]
in are therefore uncorrelated. So, they can give rise to net chiral fluctuations which can degrade the chiral selectivity of the PVED bias
g provided the input noise amplitude
ζ > 0 is sufficiently large. The constant volume constraint is

. This can be satisfied by taking the flux fractions to be
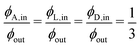
for the two input channels, this implies
kfA =
kfL =
kfD =
kf/3. Examples of the competition between chiral bias and noise on the enantiomer input channel are shown below in the
Fig. 7–9.
 |
| | Fig. 6 Left: Reversible Frank model in a continuous open-flow reactor of volume V at mean temperature T, assuming instant and perfect diffusion of all the species in solution. Achiral resource A flows in at fixed concentration [A]in. All four species A, L, D, and P flow out in a single common channel with their instantaneous concentrations, as determined inside the well-mixed reactor; see eqn (9)–(13). The matter flow maintains the system out of chemical equilibrium. Right: Here, the achiral resource A and both enantiomers L and D flow in at fixed concentrations [A]in and [L]in = [D]in, respectively, in two separate channels. The enantiomers share a common input channel and feed into the reactor with a racemic composition on average. See eqn (29) and (30). | |
 |
| | Fig. 7 Distributions of the outcomes from n = 100 simulations of the competition between the PVED g and the rms temperature fluctuation times the activation enthalpy factor ξ, eqn (4) in the presence of chiral fluctuations ζ in the racemic [L]in = [D]in input channel, see Fig. 6. The level of chiral bias corresponds to g = 10−12 and ξ = 10−13. (D,L) gives the number of homochiral outcomes for the D- and L-enantiomers. Panel (a): ζ = 10−7, (54,46); (b): ζ = 10−8, (64,36); (c): ζ = 10−9, (99,1). | |
 |
| | Fig. 8 Distributions of the outcomes from n = 100 simulations of the competition between the PVED bias g and the rms temperature fluctuation times the activation enthalpy factor ξ, eqn (4) in the presence of chiral fluctuations ζ in the racemic [L]in = [D]in input channel, see Fig. 6. The level of chiral bias corresponds to g = 10−18 and ξ = 10−19. (D,L) gives the number of homochiral outcomes for the D- and L-enantiomers. Panel (a): ζ = 10−13, (47,53); (b): ζ = 10−14, (61,39); (c): ζ = 10−15, (97,3). | |
 |
| | Fig. 9 Distributions of the outcomes from n = 100 simulations of the competition between the PVED g and the rms temperature fluctuation times the activation enthalpy factor ξ, eqn (4) in the presence of chiral fluctuations ζ in the racemic [L]in = [D]in input channel, see Fig. 6. The level of chiral bias corresponds to g = 10−18 and also ξ = 10−18. (D,L) gives the number of homochiral outcomes for the D- and L-enantiomers. Panel (a): ζ = 10−13, (53,47); (b): ζ = 10−14, (56,44); (c): ζ = 10−15, (86,14). | |
For the range of PVED biases g considered above, and for fixed thermal noise levels ξ > 0, we can estimate the maximum amplitudes of the enantiomeric input line noises ζ > 0 that can be tolerated before washing out the PVED selectivity. Deterministic outcomes can tolerate an external noise level ζ up to approximately 103 greater than the chiral bias g, and in the presence of temperature fluctuations, whereas the chiral bias gets obliterated for external noise levels on the order of approximately 105 greater than the chiral bias, see Fig. 7–9.
7 Concluding remarks
In our open flow stochastic Frank model, subject to a chiral bias g and temperature fluctuations ξ, the ratio g/ξ = 1 (see Section 4), defines the transition from stochastic to deterministic regimes. This condition represents a critical threshold for chiral sign selection in SMSB. When the ratio of chiral bias to temperature fluctuations is greater than unity g/ξ > 1, a calculated confidence interval is used to indicate the efficiency of the system towards chiral selectivity. A larger number n of experiments is necessary to detect statistically the chiral selection effect in SMSB. This relationship, depending on the system parameters, between the number of experiments needed to distinguish between stochastic or deterministic outputs, is a point that cannot be detected using common chemical kinetic methods.
Moreover, since each simulation describes the behavior of a very small volume element, the confidence interval gives a description of what occurs in a macroscopic volume resulting from addition of large numbers of small volume elements. Therefore, larger sets of small volume reactors lead to a greater confidence for the distinction between stochastic or deterministic outcomes. This result is interesting because the chemical systems description of abiotic evolution are those based on the cooperative interaction between many micro systems (e.g. ref. 58). As expected, when g/ξ ≫ 1 already a small number of experiments will lead to the g-selected final chiral sign. A large non-equilibrium system containing many interacting chiral species may behave as a collection of many microsystems. In this regard, a recent work shows a phase transition towards a homochiral state is likely to occur as the number of chiral species becomes large, see ref. 59.
Since it is expected that larger amplitude chiral fluctuations in real systems (imperfect mixing, limited diffusion rates…), occur distinctly from those originating from the temperature fluctuations in the values of the rate constants, the experimental detection of a possible PVED effect calls for a difficult and challenging experimental procedure able to eliminate or suppress the sources of the chiral fluctuations that are not due the temperature fluctuations in thermally isolated systems.
Our results show that for the range of PVED biases g considered above, and for fixed thermal noise levels ξ > 0, there exists a maximum tolerable amplitude of the enantiomeric input line noises ξ. In the presence of temperature fluctuations, deterministic outcomes can tolerate an external noise level ξ of up to approximately 10 greater that the chiral bias g. However, the PVED selectivity is washed out for external noise levels ξ about 102 times greater than the chiral bias. These refer to the thermal noise levels that can be tolerated by the chiral bias. By contrast, estimates concerning the chiral noise levels (chiral fluctuations on the ideal racemic composition that feeds into the reactor, see right hand side of Fig. 6), that can be tolerated by the chiral bias, and in the presence of fixed level of thermal noise, are notably more generous.
Results on permanent physical chiral forces overcoming chiral fluctuations are widely reported, and even in the case where the chiral force is at the order of cryptochirality.41 Cryptochirality refers to minute perturbations of the chiral symmetry which remain undetected (hence, hidden chirality) in classical physical measurements or in enantioselective reactions, but which are amplified in the bifurcation in these polarized (chiral biased) spontaneous mirror symmetry breakings. Note this definition encompasses not only PVED, but also other experimentally undetectable sources of chiral polarizations, be they of a structural, an environmental or a statistical nature. This means that the presence of a chiral polarization below the experimental limits for detecting chirality by physical methods can determine the output chiral sign. An example of cryptochirality arises from stereochemical isotopic substitutions in the Soai reaction.15–17 Note, however that contrary to such cryptochirality, whose sign can be random, the effect of PVED must always be present, and precisely because it adds to, or subtracts from, biases exerted by other chiral forces, its detection could be indirectly made by means of an accurate statistical analysis of multiple outputs of cryptochiral enantiomorphic polarizations. A detailed discussion of cryptochirality can be found in ref. 41.
Finally, it is worthwhile pointing out that this fact is contrary to the older opinions and models which supposed that biological homochirality could arise from stochasticity. Here we demonstrate that low exergonic enantioselective autocatalysis can lead to SMSB in a deterministic way.
Author contributions
D. H. conceived the idea. D. H. performed the simulations. D. H. and J.-C. M. created the figures. D. H., T. B., J.-C. M. and J. M. R. discussed the results. D. H., T. B., J.-C. M. and J. M. R. wrote the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendices
A Chiral selectivity: direct production and autocatalysis
We consider the reaction-coordinate diagrams used in ref. 46. From eqn (3), the rate constants for the reverse direct production k−d of the enantiomers eqn (7) in the presence of temperature fluctuations are given by:| | | k−d,L(T + δT(t)) = k−d,L(T)(1 + ξ−d,Lη−d,L(t)), | (37) |
| | | k−d,D(T + δT(t)) = k−d,D(T)(1 + ξ−d,Dη−d,D(t)). | (38) |
We emphasize the dependence of the rates and fluctuations on each enantiomer, L or D. The mean values, in the absence of external chiral bias satisfy the chiral constraint k−d,L(T) = 〈k−d,L(T + δT(t))〉 = 〈k−d,D(T + δT(t))〉 = k−d,D(T), since the noise satisfies 〈ηi(t)〉 = 0. But a finite chiral bias leads to a tiny free energy difference ΔΔG‡ > 0 between the two transition states, and so the ratio of the mean values of these rate constants is given by ref. 60:| |  | (39) |
in the case of higher transition state energy for the D-enantiomer with respect to the L. Substitute eqn (39) into eqn (37), expanding to leading order in g and ξ yields| | | k−d,L(T + δT(t)) = k−d,D(T)(1 + ξ−d,Lη−d,L(t) − g). | (40) |
Hence, if the chiral bias is greater (in absolute value) than the characteristic rms magnitude of the thermal fluctuationsthen according to eqn (39), which since g > 0, then k−d,D(T) > k−d,L(T), implying a faster reconversion of D back into achiral substrate A, it should be able to select for the D-enantiomer.
The chiral selection in enantioselective autocatalysis eqn (6) proceeds in a similar fashion. Here, the ratio of the corresponding rate constants is
| |  | (42) |
Then, analogous to the case of direct production, the chiral selectivity criterion is
then according to
eqn (42), which since
g > 0, then
ka,D(
T) >
ka,L(
T), implying a faster autocatalysis for
D. Hence the bias should be able to select for the
D-enantiomer. Finally, following the previous steps, the selectivity criterion for the
inverse autocatalysis is
| |  | (44) |
All the above instances
eqn (41), (43) and (44) are subsumed in
eqn (5).
Acknowledgements
D. H. and J. M. R. acknowledge the coordinated research grants PID2020-116846GB-C22 and PID2020-116846GB-C21, respectively, Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/10.13039/501100011033 and by ERDF A way of making Europe. T. B. acknowledges financial support by project CF19-2272 from the Consejo Nacional de Ciencia y Tecnología, CONACYT.
References
-
Compendium of Chemical Terminology, ed. A. D. McNaught and A. Wilkinson, IUPAC, New York, 2nd edn, 2006 Search PubMed.
-
P. Collins, A. Martin and E. Squires, Particle Physics and Cosmology, Wiley, New York, 1st edn, 1989 Search PubMed.
-
Biochirality: Origins, Evolution and Molecular Recognition, ed. P. Cintas, Springer-Verlag, Heidelberg, 2013 Search PubMed.
-
L. Barron, in Chirality and Life, ed. O. Botta, J. L. Bada, J. Gomez-Elvira, E. Javaux, F. Selsis and R. Summons, Springer US, Boston, MA, 2008, pp. 187–201 Search PubMed.
- S. Toxvaerd, Int. J. Mol. Sci., 2009, 10, 1290–1299 CrossRef CAS PubMed.
-
K. Soai, T. Kawasaki and A. Matsumoto, Asymmetric Autocatalysis: The Soai Reaction, RSC, Cambridge, 2022 Search PubMed.
- C. Viedma, Phys. Rev. Lett., 2005, 94, 065504 CrossRef PubMed.
- A. J. MacDermott, Chirality, 2012, 24, 764–769 CrossRef CAS PubMed.
- J.-I. Takahashi and K. Kobayashi, Symmetry, 2019, 11, 919 CrossRef CAS.
- C. D. Stevenson and J. P. Davis, J. Phys. Chem. A, 2019, 123, 9587–9593 CrossRef CAS PubMed.
- C. D. Stevenson and J. P. Davis, ACS Earth Space Chem., 2021, 5, 2817–2826 CrossRef CAS.
-
A. Guijarro, The Origin of Chirality in the Molecules of Life, Royal Society of Chemistry, Cambridge, 2nd edn, 2022 Search PubMed.
- D. Kondepudi, I. Prigogine and G. Nelson, Phys. Lett. A, 1985, 111, 29–32 CrossRef.
-
T. Akiyama and I. Ojima, Catalytic Asymmetric Synthesis, Wiley, 2022 Search PubMed.
- T. Kawasaki, Y. Matsumura, T. Tsutsumi, K. Suzuki, M. Ito and K. Soai, Science, 2009, 324, 492–495 CrossRef CAS PubMed.
- A. Matsumoto, H. Ozaki, S. Harada, K. Tada, T. Ayugase, H. Ozawa, T. Kawasaki and K. Soai, Angew. Chem., Int. Ed., 2016, 55, 15246–15249 CrossRef CAS PubMed.
- T. Kawasaki, Y. Okano, E. Suzuki, S. Takano, S. Oji and K. Soai, Angew. Chem., Int. Ed., 2011, 50, 8131–8133 CrossRef CAS PubMed.
- T. Kawasaki, M. Shimizu, D. Nishiyama, M. Ito, H. Ozawa and K. Soai, Chem. Commun., 2009, 4396–4398 RSC.
- R. R. E. Steendam, B. Harmsen, H. Meekes, W. J. P. van Enckevort, B. Kaptein, R. M. Kellogg, J. Raap, F. P. J. T. Rutjes and E. Vlieg, Cryst. Growth Des., 2013, 13, 4776–4780 CrossRef CAS.
- I. Alkorta and J. Elguero, Struct. Chem., 2019, 30, 633–636 CrossRef CAS.
- A. MacDermott, G. Tranter and S. Trainor, Chem. Phys. Lett., 1992, 194, 152–156 CrossRef CAS.
- L. Barron, Rend. Fis. Acc. Lincei, 2013, 24, 179–189 CrossRef.
- A. Bakasov and M. Quack, Chem. Phys. Lett., 1999, 303, 547–557 CrossRef CAS.
- R. Berger and M. Quack, ChemPhysChem, 2000, 1, 57–60 CrossRef CAS PubMed.
- L. D. Barron and A. D. Buckingham, Acc. Chem. Res., 2001, 34, 781–789 CrossRef CAS PubMed.
-
M. Quack, Molecular Parity Violation and Chirality: The Asymmetry of Life and the Symmetry Violations in Physics, Springer, Dordrecht, 1st edn, 2012 Search PubMed.
- A. Dorta-Urra and P. Bargueño, Symmetry, 2019, 11, 661 CrossRef CAS.
- M. Quack, G. Seyfang and G. Wichmann, Chem. Sci., 2022, 13, 10598–10643 RSC.
- G. Rauhut and P. Schwerdtfeger, Phys. Rev. A, 2021, 103, 042819 CrossRef CAS.
- M. R. Fiechter, P. A. B. Haase, N. Saleh, P. Soulard, B. Tremblay, R. W. A. Havenith, R. G. E. Timmermans, P. Schwerdtfeger, J. Crassous, B. Darquié, L. F. Pašteka and A. Borschevsky, J. Phys. Chem. Lett., 2022, 13, 10011–10017 CrossRef CAS PubMed.
- N. Kuroda, T. Oho, M. Senami and A. Sunaga, Phys. Rev. A, 2022, 105, 012820 CrossRef CAS.
- C. Daussy, T. Marrel, A. Amy-Klein, C. T. Nguyen, C. J. Bordé and C. Chardonnet, Phys. Rev. Lett., 1999, 83, 1554–1557 CrossRef CAS.
- J. Crassous, F. Monier, J.-P. Dutasta, M. Ziskind, C. Daussy, C. Grain and C. Chardonnet, ChemPhysChem, 2003, 4, 541–548 CrossRef CAS PubMed.
- R. Bast, A. Koers, A. S. P. Gomes, M. Iliaš, L. Visscher, P. Schwerdtfeger and T. Saue, Phys. Chem. Chem. Phys., 2011, 13, 864–876 RSC.
- Y. Yamagata, J. Theor. Biol., 1966, 11, 495–498 CrossRef CAS PubMed.
-
A. J. MacDermott, Perspective and Concepts: Biomolecular Significance of Homochirality: The Origin of the Homochiral Signature of Life, in Comprehensive Chirality, ed. E. M. Carreira and H. Yamamoto, Elsevier, Amsterdam, 2012, vol. 8, pp. 11–38 Search PubMed.
- H. Wang, W. Yang, K. K. Baldridge, C.-H. Zhan, T. U. Thikekar and A. C.-H. Sue, Chem. Sci., 2021, 12, 10985–10989 RSC.
- G. Yin, T. Namikoshi, M. Teraguchi, T. Kaneko and T. Aoki, Polymer, 2022, 245, 124673 CrossRef CAS.
- M. Mauksch, Phys. Chem. Chem. Phys., 2023, 25, 1734–1754 RSC.
- S. Y. Bak, G. Coquerel, W.-S. Kim and B. J. Park, J. Phys. Chem. Lett., 2023, 14, 785–790 CrossRef CAS PubMed.
- T. Buhse, J.-M. Cruz, M. E. Noble-Terán, D. Hochberg, J. M. Ribó, J. Crusats and J.-C. Micheau, Chem. Rev., 2021, 121, 2147–2229 CrossRef CAS PubMed.
- C. Viedma, Cryst. Growth Des., 2007, 7, 553–556 CrossRef CAS.
- B. Barabas, L. Caglioti, C. Zucchi, M. Maioli, E. Gál, K. Micskei and G. Pályi, J. Phys. Chem. B, 2007, 111, 11506–11510 CrossRef CAS PubMed.
- D. K. Kondepudi and G. W. Nelson, Phys. Rev. Lett., 1983, 50, 1023–1026 CrossRef CAS.
- D. Kondepudi and G. Nelson, Nature, 1985, 314, 438–441 CrossRef CAS.
- D. Hochberg, T. Buhse, J.-C. Micheau and J. M. Ribó, Phys. Rev. Res., 2022, 4, 033183 CrossRef CAS.
- Q. Sallembien, L. Bouteiller, J. Crassous and M. Raynal, Chem. Soc. Rev., 2022, 51, 3436–3476 RSC.
-
C. Gardiner, Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences, Springer, Berlin, 2nd edn, 1985 Search PubMed.
- F. Frank, Biochem. Biophys. Acta, 1953, 11, 459–463 CAS.
- T. Shibata, H. Morioka, T. Hayase, K. Choji and K. Soai, J. Am. Chem. Soc., 1996, 118, 471–472 CrossRef CAS.
-
I. Prigogine and D. Kondepudi, Modern Thermodynamics From Heat Engines to Dissipative Structures, Wiley, Chichester, 2nd edn, 2015 Search PubMed.
- M. E. Noble-Terán, J.-M. Cruz, J.-C. Micheau and T. Buhse, ChemCatChem, 2018, 10, 642–648 CrossRef.
-
R. Chang, Physical Chemistry for the Chemical and Biological Sciences, University Science, Sausaulito, 1st edn, 2000 Search PubMed.
-
G. Korn and T. Korn, Mathematical Handbook for Scientists and Engineers, Dover, New York, 1st edn, 2000 Search PubMed.
- D. Vadivel and D. Dondi, Orig Life Evol Biosph, 2023, 53, 61–69 CrossRef CAS PubMed.
- L. D. Brown, T. T. Cai and A. DasGupta, Statistical Sci., 2001, 16, 101–133 CrossRef.
- A. Blokhuis, D. Lacoste and P. Gaspard, J. Chem. Phys., 2018, 148, 144902 CrossRef PubMed.
-
S. Kauffman, The origin of order: Self-organization and selection in evolution, Oxford, New York, 1st edn, 1993 Search PubMed.
- G. Laurent, D. Lacoste and P. Gaspard, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–6 Search PubMed.
- J. M. Ribó, C. Blanco, J. Crusats, Z. El-Hachemi, D. Hochberg and A. Moyano, Chem. – Eur. J., 2014, 20, 17250–17271 CrossRef PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Thomas
Buhse
*a,
Thomas
Buhse
 b,
Jean-Claude
Micheau
b,
Jean-Claude
Micheau
 c and
Josep M.
Ribó
c and
Josep M.
Ribó
 *d
*d
 are given by
are given by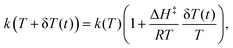
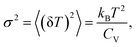
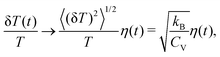 so that eqn (1) can be expressed as
so that eqn (1) can be expressed as









 and this relates the differences in the free energies of activation of the forward and reverse reactions for autocatalysis and direct production: ΔG‡a − ΔG‡−a = ΔG‡d − ΔG‡−d. This relation follows from inserting the expression for the rate constants k into the above constraint, and using transition state theory (the Eyring–Polanyi equation for k). This is the most general statement that can be made regarding the activation energies.
and this relates the differences in the free energies of activation of the forward and reverse reactions for autocatalysis and direct production: ΔG‡a − ΔG‡−a = ΔG‡d − ΔG‡−d. This relation follows from inserting the expression for the rate constants k into the above constraint, and using transition state theory (the Eyring–Polanyi equation for k). This is the most general statement that can be made regarding the activation energies.



 so as to lie within one standard deviation of the mean temperature T. In the present paper, we employ vector Ito process to model the stochastic equations and use independent Wiener processes for the noise terms, so no such restriction is imposed on the noise. Whereas the former truncation accounted for approximately 67% of all the fluctuations, here all the fluctuations are included, see Fig. 1. The “missin” fluctuations, those beyond one standard deviation, make up for the remaining 33% of the noise spectrum. Recall that the probability distribution for non-equilibrium temperature fluctuations δT is given by ref. 46
so as to lie within one standard deviation of the mean temperature T. In the present paper, we employ vector Ito process to model the stochastic equations and use independent Wiener processes for the noise terms, so no such restriction is imposed on the noise. Whereas the former truncation accounted for approximately 67% of all the fluctuations, here all the fluctuations are included, see Fig. 1. The “missin” fluctuations, those beyond one standard deviation, make up for the remaining 33% of the noise spectrum. Recall that the probability distribution for non-equilibrium temperature fluctuations δT is given by ref. 46
 corresponds to fluctuations within one standard deviation (≈67%), whereas
corresponds to fluctuations within one standard deviation (≈67%), whereas  includes all fluctuations. Using the full range of fluctuations will have an impact on the ability of the PVED bias g to overcome the thermal noise and so select a final chiral sign (see Section 5), but is not as drastic as one might suppose, since the very largest fluctuations, which are those lying beyond three standard deviations, 3σ, from the mean, have exponentially vanishing probabilities, and so are extremely rare events, see Fig. 1. Moreover, as white Gaussian noise includes all frequencies, and with equal weighting (its frequency spectrum is flat), there always exists arbitrarily large frequencies ω such that ωΔt > 1 is satisfied, where Δt is the smallest time step used in the numerical solution of the stochastic differential equations. Compliance with this inequality implies that statistical randomness between successive simulation time steps is assured.
includes all fluctuations. Using the full range of fluctuations will have an impact on the ability of the PVED bias g to overcome the thermal noise and so select a final chiral sign (see Section 5), but is not as drastic as one might suppose, since the very largest fluctuations, which are those lying beyond three standard deviations, 3σ, from the mean, have exponentially vanishing probabilities, and so are extremely rare events, see Fig. 1. Moreover, as white Gaussian noise includes all frequencies, and with equal weighting (its frequency spectrum is flat), there always exists arbitrarily large frequencies ω such that ωΔt > 1 is satisfied, where Δt is the smallest time step used in the numerical solution of the stochastic differential equations. Compliance with this inequality implies that statistical randomness between successive simulation time steps is assured.

 lying within one standard deviation from the mean. Here in this work, the full unbounded range is employed.
lying within one standard deviation from the mean. Here in this work, the full unbounded range is employed.

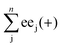 and
and  , where eej(±) = ±1, where +1 holds for the majority D-enantiomer, and −1 holds for the majority L-enantiomer, respectively. We plot the results in histograms to show the distribution of the set of all outcomes. The data slice is taken at t = 5000 s. Next, we include the PVED bias g > 0 in the stochastic equations and make multiple runs, again with racemic initial conditions. For each value of the PVED bias chosen, we test the chiral selectivity against various noise amplitudes ξ, for noise greater than, equal to, and less than the bias: ξ > g, ξ = g, ξ < g. We map the outcomes to histograms of final enantiomeric excesses ee as outlined above. Here in contrast, after the induction period the times at which the concentrations of two enantiomers separate from each other is sharply focused in time, see Fig. 3. The PVED bias has overcome the thermal fluctuations in the rate constants. See Fig. 4 for characteristic examples sampled over a wide range of g and also Table 1 for a guide to the characterization of the distinct outcomes. Very recent calculations of PVED for cinnabar crystals,55 lead to values as large as g = 2.2 × 10−12, which we include in our analysis below. Some comments regarding these results, with respect to the those obtained in ref. 46, are in order. There is now a qualitative and quantitative pattern of statistical uniformity in the outcomes of the numerical results with respect to the range of g bias values tested in that: (i) all the g's tested here select the final state deterministically when the noise level is an order of magnitude smaller than the bias: ξ < g (see Panel (a) in Fig. 4), (ii) for noise of the same order of magnitude as the bias ξ = g, the selection is still biased strongly, but is slightly skewed (see Panel (b) in Fig. 4), and for noise an order of magnitude larger than the bias ξ > g, the outcomes are bimodal, no statistically significant selection of a final scalemic state is possible, see Panel (c) in Fig. 4. Here we solve numerically for the four coupled Ito stochastic differential equations eqn (16), (17), (22) and (23). The main mathematical difference between this approach and the previous one is now the random T-fluctuations are taken from a complete normal distribution, and are not restricted to lie within (±σ) one standard deviation of the mean (see discussion in Section 3 on this point). That is, all the temperature fluctuations beyond one standard deviation from the mean are now included. This translates into a diminished chiral selectivity when the fluctuations are greater than the bias ξ > g, which is natural and is to be expected. The largest temperature fluctuations (meaning those that lie beyond three standard deviations from the mean) diminish the chiral selectivity of the PVED bias, but they are also less likely than the smaller fluctuations that lie within one standard deviation of the mean temperature, see Fig. 1. Further details of the individual numerical simulations are compiled in Table 2. For a given chiral bias g > 0, noise amplitude ξ > 0 and number of statistically independent runs n, we obtain the total numbers of final homochiral L and D outcomes, where L + D = n. From this we calculate the net enantiomeric excess 〈ee〉n = (L − D)/(L + D) averaged over the n runs, and also the fraction of homochiral D-outcomes pD = D/(L + D). We compare the latter to the 99% confidence interval (C.I.) for expecting a racemic outcome, i.e., when pD = 1/2. This C.I. eqn (24) depends on p, the confidence level and also on n. Note, in the so-called “severe” region of parameter space, for which the strength of the chiral bias is less in magnitude than the noise amplitude g < ξ, we have also further increased the number of runs n from 100 to 500 and then to 1000 in order to ascertain whether the final stationary outcomes can be regarded as either racemic or else biased. We use the 99% confidence interval (C.I.) for expecting a racemic outcome as criterion:
, where eej(±) = ±1, where +1 holds for the majority D-enantiomer, and −1 holds for the majority L-enantiomer, respectively. We plot the results in histograms to show the distribution of the set of all outcomes. The data slice is taken at t = 5000 s. Next, we include the PVED bias g > 0 in the stochastic equations and make multiple runs, again with racemic initial conditions. For each value of the PVED bias chosen, we test the chiral selectivity against various noise amplitudes ξ, for noise greater than, equal to, and less than the bias: ξ > g, ξ = g, ξ < g. We map the outcomes to histograms of final enantiomeric excesses ee as outlined above. Here in contrast, after the induction period the times at which the concentrations of two enantiomers separate from each other is sharply focused in time, see Fig. 3. The PVED bias has overcome the thermal fluctuations in the rate constants. See Fig. 4 for characteristic examples sampled over a wide range of g and also Table 1 for a guide to the characterization of the distinct outcomes. Very recent calculations of PVED for cinnabar crystals,55 lead to values as large as g = 2.2 × 10−12, which we include in our analysis below. Some comments regarding these results, with respect to the those obtained in ref. 46, are in order. There is now a qualitative and quantitative pattern of statistical uniformity in the outcomes of the numerical results with respect to the range of g bias values tested in that: (i) all the g's tested here select the final state deterministically when the noise level is an order of magnitude smaller than the bias: ξ < g (see Panel (a) in Fig. 4), (ii) for noise of the same order of magnitude as the bias ξ = g, the selection is still biased strongly, but is slightly skewed (see Panel (b) in Fig. 4), and for noise an order of magnitude larger than the bias ξ > g, the outcomes are bimodal, no statistically significant selection of a final scalemic state is possible, see Panel (c) in Fig. 4. Here we solve numerically for the four coupled Ito stochastic differential equations eqn (16), (17), (22) and (23). The main mathematical difference between this approach and the previous one is now the random T-fluctuations are taken from a complete normal distribution, and are not restricted to lie within (±σ) one standard deviation of the mean (see discussion in Section 3 on this point). That is, all the temperature fluctuations beyond one standard deviation from the mean are now included. This translates into a diminished chiral selectivity when the fluctuations are greater than the bias ξ > g, which is natural and is to be expected. The largest temperature fluctuations (meaning those that lie beyond three standard deviations from the mean) diminish the chiral selectivity of the PVED bias, but they are also less likely than the smaller fluctuations that lie within one standard deviation of the mean temperature, see Fig. 1. Further details of the individual numerical simulations are compiled in Table 2. For a given chiral bias g > 0, noise amplitude ξ > 0 and number of statistically independent runs n, we obtain the total numbers of final homochiral L and D outcomes, where L + D = n. From this we calculate the net enantiomeric excess 〈ee〉n = (L − D)/(L + D) averaged over the n runs, and also the fraction of homochiral D-outcomes pD = D/(L + D). We compare the latter to the 99% confidence interval (C.I.) for expecting a racemic outcome, i.e., when pD = 1/2. This C.I. eqn (24) depends on p, the confidence level and also on n. Note, in the so-called “severe” region of parameter space, for which the strength of the chiral bias is less in magnitude than the noise amplitude g < ξ, we have also further increased the number of runs n from 100 to 500 and then to 1000 in order to ascertain whether the final stationary outcomes can be regarded as either racemic or else biased. We use the 99% confidence interval (C.I.) for expecting a racemic outcome as criterion: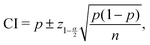
 the Z-value for the desired confidence,
the Z-value for the desired confidence,  for 99% confidence.56 These confidence interval bounds are computed and listed in the right-hand column of Table 2. The table is based on time-slices through the bifurcation curves at the final times at t = 5000 s.
for 99% confidence.56 These confidence interval bounds are computed and listed in the right-hand column of Table 2. The table is based on time-slices through the bifurcation curves at the final times at t = 5000 s.



 holds for all outcomes. See Fig. 4
holds for all outcomes. See Fig. 4

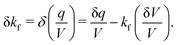
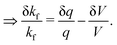

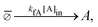



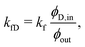
 .57 We consider fluctuations on the inflows of the enantiomers, see Fig. 6. From eqn (30), (32) and (33) these in turn can be due in principle to either (i) fluctuations in the individual flux fractions
.57 We consider fluctuations on the inflows of the enantiomers, see Fig. 6. From eqn (30), (32) and (33) these in turn can be due in principle to either (i) fluctuations in the individual flux fractions  and/or (ii) fluctuations about the average racemic composition [L]in = [D]in. This choice will depend on how we choose the Wiener processes, that is, whether they are the same process or else independent processes. Note however since the two enantiomers are being transported (by passive advection) by same fluid stream, we must rule out independent, and hence chiral, fluctuations in the L.D flux fractions. This leaves us with the possibility to consider only fluctuations in the enantiomer inflow concentrations, which are on average racemic. So we make the following replacements in the Ito stochastic equations for [L], [D] and [A] as follows using substitutions analogous to eqn (28):
and/or (ii) fluctuations about the average racemic composition [L]in = [D]in. This choice will depend on how we choose the Wiener processes, that is, whether they are the same process or else independent processes. Note however since the two enantiomers are being transported (by passive advection) by same fluid stream, we must rule out independent, and hence chiral, fluctuations in the L.D flux fractions. This leaves us with the possibility to consider only fluctuations in the enantiomer inflow concentrations, which are on average racemic. So we make the following replacements in the Ito stochastic equations for [L], [D] and [A] as follows using substitutions analogous to eqn (28): . This can be satisfied by taking the flux fractions to be
. This can be satisfied by taking the flux fractions to be  for the two input channels, this implies kfA = kfL = kfD = kf/3. Examples of the competition between chiral bias and noise on the enantiomer input channel are shown below in the Fig. 7–9.
for the two input channels, this implies kfA = kfL = kfD = kf/3. Examples of the competition between chiral bias and noise on the enantiomer input channel are shown below in the Fig. 7–9.












