 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An effective model for sodium insertion in hard carbons
Huy Sy
Nguyen
 *ab and
Arnulf
Latz
*ab and
Arnulf
Latz
 abc
abc
aDepartment of Electrochemistry, University of Ulm, Albert-Einstein-Allee 47, 89081 Ulm, Germany. E-mail: huy.nguyen@dlr.de; Arnulf.Latz@dlr.de
bInstitute of Engineering Thermodynamics, German Aerospace Center (DLR), Wilhelm-Runge-Str. 10, 89081 Ulm, Germany
cHelmholtz Institute Ulm (HIU), Helmholtzstr. 11, 89081, Ulm, Germany
First published on 11th October 2023
Abstract
Sodium ion batteries (NIBs) are a potential alternative to Lithium ion batteries (LIBs) because of their lower cost and greater availability. As anodes, hard carbons (HCs) seem to be the most promising candidates for NIBs. Previous numerical theoretical research studies have focussed on the general conditions for Na insertion in HCs, while experiments have shown that the properties of Na insertion in HCs depend strongly on specific material properties of HCs. Our target is building an effective model based on experimental data and the volume expansion phenomenon as a base for constructing chemical potentials and free energies efficiently as the starting point for continuum modeling of intercalation in HCs. In our effective model, HC is treated implicitly, while Na is simulated in a confined space, created by the HC. To reproduce the complex intercalation behavior of Na, different intercalation sites at different energy levels must be introduced. The results show good agreement with the experimental data and clarify the contribution of different Na insertion sites and the exchange between different sites of Na to the open circuit voltage as well as their contribution to the reversible and irreversible capacity of Na in HCs.
1. Introduction
Lithium ion batteries (LIBs) have many applications in commercial electronic devices1 and vehicles, energy storage, military2 and others, due to their high energy density and low self-discharge.2 However, limited Li resources on the Earth lead to high costs of LIBs3,4 while the demand for energy storage capacity continues to increase. Sodium ion batteries (NIBs) are a potential alternative to LIBs because NIBs have similar electrochemical properties to LIBs but at a much lower cost since Na is an Earth abundant material.3,4 Unfortunately, graphite, the traditional anode of LIBs5–9 is not suitable for NIBs10 because of low capacity3 and high volume expansion.11 Among several anodes for NIBs, such as MXenes,3 C6B4,12 blue – phosphorene,13 and 1H-BeP2,14 hard carbon (HC) is a promising anode for NIBs because of stable cycling, large specific capacity,15 and low-cost biomass product precursors.15,16Besides experimental studies,17–20 there are several theoretical investigations of Na-insertion in HCs. At the atomic level, the simplest models use density functional theory (DFT) to calculate the adsorption energy of Na in a graphite layer with some heteroatoms.21–23 DFT results can be combined with operando Raman spectra to study the mechanism of Na insertion in HCs.24,25 For further calculations, Cai et al. studied the insertion of Na between two graphitic layers26 and Youn et al. suggested the crystalline phase of Na inside HCs at high capacity.27
While DFT studies reveal the separate atomistic mechanisms of Na insertion in HCs, continuum models are used for quantitative simulation of Na insertion in HCs on larger scales. Previous continuum models for Na insertion in HCs used 2-level models describing intercalation + pore filling28 or 3-level models for capturing adsorption, intercalation, and pore filling.29 However, a complete understanding of Na insertion in HCs is more complicated than this. Reddy et al.24 suggested 4 types of Na insertion in HCs, including adsorption of Na on the surface of the graphitic layer, on defect sites of HCs, intercalation of Na in graphitic sheets and interpore Na, filling the pores of HCs. Both the 2-level model and the 3-level model ignored the defect Na, but the defect Na should not be neglected for 2 reasons: on the one hand, the heteroatom defects always appear in HCs,23 and on the other hand, some experimental studies use heteroatom doping defects to increase the capacity.30–33
Moreover, these models investigated the generic case of Na insertion in HCs, while experiments proved that the properties of Na insertion in HCs depends strongly on the specific material properties of HCs.34–37 Bommier et al. predicted Na capacity based on the pore volume and surface area of HCs; however, the mechanism of Na insertion in HCs is not considered in their study.38 The picture is more complicated when the HC structure can change during the charge/discharge process: Sauerteig et al. observed that the volume of HC expanded by up to 10% in the first charge/discharge cycle and 5% in the later cycles.39
Besides the insertion mechanism, the reversible and irreversible capacity are also important factors for battery applications. Olsson et al. calculated the adsorption energy of Na atoms at the defect points to study the irreversible contribution of defect Na.22 Jensen et al. studied migration barriers to estimate the mobility of Na atoms in HCs.40 However, these studies are qualitative and do not provide the full picture of reversible and irreversible effects for each type of Na in HCs.
In this work, we develop an effective model to investigate the Na insertion into HCs dependent on structural features of hard carbon and the energetic properties of different insertion mechanisms. The purpose of our model is to provide a frame in which known experimental materials data and results from ab initio simulations can be used to relate the SOC to the internal states of the inserted Na ions and to create a base for future continuum simulations, in which the OCV and the distribution of Na over internal states also in non-equilibrium (charge and discharge) situations is needed. Our effective model is therefore a crucial step for the development of a multi-scale approach for Na batteries based on materials data and ab initio simulations. This model is based on the experimental data and includes volume expansion to cover all aspects of Na insertion in HCs. In this model, Na atoms are simulated in the confined space created by HCs, where the full energetics of the different insertion mechanisms are covered.
This paper is arranged as follows. The effective model and the different energy states of Na in HCs are described in detail in Section 2. The results are shown and compared with experiments in Section 3. The mechanism and interchange between different states of Na are also clarified in this section. Finally, the conclusion is provided in Section 4.
2. Model
2.1 Effective model
 | (1) |
| μout = μHC | (2) |
In our simulation, it is convenient to use the energy εout and εHC for the outer zone and HC, respectively. The relationship between the energy and chemical potential is μout = ∂εout/∂Nout and μHC = ∂μHC/∂NHC.
2.2 Model hard carbon
To model specific HC materials, we use property data obtained from their characterization, including the length of the graphitic layer La, the layer thickness Lc, the pore volume Vp, and the swelling coefficient KSW. The La, Lc, and Vp values are used to model the unit cell of HC while KSW is used to describe the interaction between Na and HC.In this simulation, the number of boundary layers adjacent to a pore is set to 3 for simplicity. La and Lc0 are obtained from Raman spectra and Vp is obtained from BET.37 The figure and parameters of the unit cell are shown in Table 1 and Fig. 4.
| Parameters, unit | Value |
|---|---|
| L a, nm | 2.06 |
| L c0, nm | 1.10 |
| V p, cm3 g−1 | 0.10 |
| Lc = Lc0[1 + ΔSW(C)] | (3) |
| dl = Lc/(n − 1) | (4) |
The distance between 2 graphitic layers dl is in the range of 0.309–0.404 nm.23 In the effective model, n is set to 4 and the layer distant dl is about:
| dl = Lc/(n − 1) ≈ Lc0/3 ≈ 0.367 nm | (5) |
2.3 Model Na
 | ||
| Fig. 5 Schematic of effective model: outer Na (green) in the outer zone (light green); interpore Na (blue), interlayer Na (orange), adsorption Na (black) and defect Na (yellow) in HC zone (grey). | ||
• Outer Na: in the outer zone.
• Interpore Na: inside the pore.
• Interlayer Na: in between 2 graphitic layers.
• Adsorption Na: close to a graphitic layer.
• Defect Na: close to defect points in the graphitic layer.
a. The total energy. The total energy in the system is
| Etot = Noutεout + Npεp + Nlεl + Ndεd + Nfεf | (6) |
ε out, εp, εl, εd, and εf are the energies per Na atom in the corresponding states. In the effective model, the total Na atoms, Ntot is kept as constant, but the number of Na atoms in each energy state can fluctuate, which means Na can switch between states.
| Nout + Np + Nl + Nd + Nf = Ntot = constant | (7) |
| εd, εf < εl < εp | (8) |
In the effective model, the Na atoms are modelled as hard spheres with radius rNa = 0.106 nm.47 Using the mean-field theory,28 the energy per Na atom in different states depends on the number of Na atoms in each other state.
b. The energy in the outer state εout. In the effective model, all atoms in the outer state have the same energy εout. The energy level in the outer state is regulating the state of charge (SOC) of the electrode i.e., for εout < εd, εf < εl < εp all Na are in the outer zone. For εd, εf < εl < εp < εout, all Na are in HC zone. By varying εout, the SOC is varying smoothly from zero to one.
c. Defect energy εf. Experimental XPS measurements identify commonly a 4% oxygen defect in HC.23 There are 4 possible types of defects: single substitutional oxygen defect (OC), single substitutional oxygen defect and carbon vacancy (OCVC), double substitutional oxygen defect (2OC) and triple substitutional oxygen defect (3OC). OC and 2OC are purely substitutional in nature23 and more common than others.22
Based on these results, we set the number of defect points to 4% of the number of the total carbon atom, nCarbon in the system. The coordinates of the defect points are fixed. Every defect point of OC has the same energy εf1 and every defect point of 2OC has the same energy εf2.
| nOC + n2OC + nOCVC + n3OC ≈ nOC + n2OC = 0.04nCarbon | (9) |
 | (10) |
d. Adsorption energy εd. In DFT calculations,21 the adsorption energy of Na adsorption εd is a function of Na concentration. In this work, we use the fitted equation, which εd can be approximated as:
 | (11) |
The DFT data and fit with eqn (11) are shown in Fig. 6.
 | ||
| Fig. 6 Adsorption energy as a function of the number of Na atoms. Dots and lines are obtained from DFT21 and eqn (11), respectively. | ||
In our effective model, we distinguish between Na adsorbed on the outer graphitic layer and Na inserted between the graphitic layer (“interlayer Na”). The energy scale ad and the particle scale bd are adjusted so that the interlayer position becomes energetically preferable for Nd > bd, if the number Nd of adsorbed Na atoms are exceeding bd, Na preferentially occupy interlayer positions.
e. Interlayer energy εl. The value of εl not only depends on the number of interlayer Na, Nl28 but also on the distance between 2 graphitic layers, dl.26 The value εl can be expressed as:
| εl = ε0l + l1(dl) + l2(xl) | (12) |
 | (13) |
The function l1(dl) diverges when dl = dmin, which means the layer spacing is too narrow and Na cannot intercalate.
The dl value is calculated from the graphitic layer thickness:
 | (14) |
 | (15) |
N SW is all Na causing layer thickness swelling. In Fig. 6, they include defect Na, adsorbed Na and interlayer Na.
| NSW = Nf + Nd + Nl | (16) |
| NmaxSW = Nmaxf + Nmaxd + Nmaxl | (17) |
 | (18) |
f. Interpore energy εp. According to the literature, the properties of εp are complicated compared with those of εl:
• In DFT calculations,26 the insertion energy of Na into the confined space between graphitic layers decreases with the distance between Na and the nearest graphitic layer. Note that the pore radius, rp is larger than the thickness of the layer dl which implies εp < εl.
• Interpretations from experiments24 suggest that Na fills the pore after intercalating between graphitic layers which implies εp > εl.
To combine these statements, εp is expressed as follows:
| εp = p1(rp)p2(Np) + p3(xp) | (19) |
 | (20) |
 | (21) |
p 3(xp) mimics the interaction between Na in the pore. In our effective model, this term is approximated using the pore occupation fraction xp = Np/Nmaxp
| p3(xp) = bpxp | (22) |
| Type | Parameters | Equation | 1st cycle | 10th cycle |
|---|---|---|---|---|
| Outer Na | ε out | (6) | ε out = −3.0 to 0.0 eV | |
| Defect Na | ε f1 | (10) | −2.2 eV | 0.0 eV |
| ε f1 | (10) | 0.0 eV | 0.0 eV | |
| Adsorption Na | ε 0d | (11) | 0.0 eV | 0.0 eV |
| a d | (11) | −3.0 eV | −3.0 eV | |
| Interlayer Na | ε 0l | (12) | −1.3 eV | −1.3 eV |
| l 2(xl) | (12) | l 2(xl) = clxl + elxl2 + flxl3 | l 2(xl) = glxl0.5 | |
| c l = 0.3 eV, el = −0.34 eV fl = 0.18 eV | g l = 0.74 eV | |||
| a l | (13) | 0.01 eV | 0.01 eV | |
| d min | (13) | 0.3383 nm | 0.3383 nm | |
| L c0 | (14) | 1.1 nm | 1.155 nm | |
| K SW | (15) | 0.1 | 0.05 | |
| Interpore Na | a p | (21) | 0.2 | 0.13 |
| b p | (22) | 0.1 eV | 0.06 eV | |
2.4 Simulation
Monte Carlo NVT simulation is applied for simulating the effective model. As mentioned in Section 2.3.1, the total volume V contains the outer zone and the HC zone, while the total number of Na in both the outer zone and the HC zone, Ntot = 648, is also kept constant, while the number Na in each state of Na will change. The temperature is chosen at T = 25 °C. The outer potential energy εout is varied to find the equilibrium condition of Na. The Monte Carlo simulation is run with Markov chain48,49 including 107 steps. Each step loops over all 648 Na atoms. In this work, we do not compare with ab initio NVT simulation. Alternatively, we compare directly with experiments.The cell voltage is calculated as:44
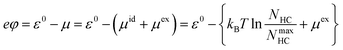 | (23) |
ε 0 (eV) is the interaction between Na and the counter electrode that shifts the voltage scale, kB = 8.61733 × 10−5 eV K−1 is the Boltzmann constant, T = 25 °C = 298.15 K, NHC = Np + Nl + Nd + Nf is the total Na in HC, NmaxHC is the maximum Na in HC, and μex (eV) is the excess chemical potential obtained from Widom's insertion method.48,49 In our effective model, ions are only inserted in HCs, while the total number of ions in the outer zone and HCs are constant, eqn (7).
3. Results and discussion
3.1 Comparison with experiment
In Fig. 7, the OCV results of the 1st and 10th cycles are compared with the experiment. The capacities determined from simulation in the 1st and 10th cycles are 537 mA h g−1 and 325 mA h g−1, respectively, compared with 507 mA h g−1 and 322 mA h g−1 from experiments. This excellent agreement with our effective model based on specific material properties motivates us to study in detail the insertion mechanism and the cause of the reversible – irreversible capacity of Na insertion in HC.3.2 Mechanism of Na insertion in HCs
The order of the different mechanisms of Na insertion in HC is illustrated in Fig. 8. In the 1st cycle, at first, Na adsorbs on defect OC of HC. At a capacity of C = 10 mA h g−1, Na adsorbs on the surface of graphitic layers. The adsorption Na has a dip in this zone from C = 25 mA h g−1 to C = 210 mA h g−1 due to the interchange between adsorption Na and interlayer Na, Na atoms intercalate until the structure NaC15.3 is formed (xl ∼ 1.57). This value is close to other DFT results for NaC16.50–52 Finally, Na can only be filled in the pore of HC from a capacity of C > 210 mA h g−1. Na is not adsorbed on 2OC defects. The mechanism of Na insertion in HCs in the 10th cycle is similar to that in the 1st cycle. However, there are no insertions to defect OC sites in the 10th cycle, which means that all adsorption to defect sites OC are irreversible.3.3 The relationship between the upper limit of adsorption Na bd and the energy in the outer state εout
In simulation, we vary εout and change bd to fit with experiments. Interestingly, we found a linear relationship between εout and bd, Fig. 9. The value of bd increases with εout and we can estimate bd from εout. Moreover, the value of bd in the 1st cycle is much higher than the 10th cycle, which means that most of adsorption Na are trapped inside HC during the charge – discharge process. This will be discussed further in the next section.3.4 Approximating reversible and irreversible capacities
As shown in Fig. 10, Na atoms adsorb irreversibly on defect points. The degree of reversibility of Na at adsorption sites is also relatively small because their mobility is restricted by interlayer Na, Fig. 5. The fraction of reversible capacity of interlayer Na is very high, about 80%, due to the weak interaction between graphitic layers and inserted Na, whereas the adsorption energy of Na on graphitic layers is relatively large. Therefore, interlayer Na can move freely as does the interpore Na. This can be inferred from the comparable reversibility of interlayer Na and interpore Na. The larger reversibility of the Interpore Na capacity is due to the larger mobility of interpore Na compared to interlayer Na.These results are consistent with DFT calculations,40 where the interpore Na has the highest reversibility, while the average irreversibility of other types is about 80%. However, our effective model helps to clarify the relative contributions of Na on defect sites, and Na adsorbed to graphitic layers to the capacity.
3.5 Comparison with Langmuir theory
The comparison between simulation and Langmuir theory53 of the 1st cycle is shown in Fig. 11. Initially, Na adsorbs quickly on defect points. After that, the adsorbed Na follows the Langmuir theory. When Na starts to intercalate between graphitic layers, the amount of adsorbed Na decreases due to the interchange between adsorption Na and interlayer Na. When the interlayer sites for Na are saturated and the Na starts to fill the pore, the adsorbed Na follows Langmuir theory again. At very high capacity, the number of adsorbed Na ions is much higher than in the Langmuir theory. | ||
| Fig. 11 The cover of the 1st cycle obtained from Langmuir theory (blue line) and simulation (red dots). | ||
4. Conclusions
To the best of our knowledge, we present the first effective model for Na insertion in the hard carbon anode, which comprises all known insertion mechanisms. Using specific material properties, combined with volume expansion and previous DFT calculations from the literature, we create an effective model with non – aligned graphitic domains and all possible energetically different insertion sites in the disordered structure. Our results agree with experiments for the OCV by taking into account the different mechanisms of Na insertion and the transitions between different insertion sites of Na. Also, the increase of irreversible capacity is captured within our model.By comparing insertion for different cycles, a complete understanding of the capacity loss is gained. In the 1st cycle, four different insertion sites are accessible. Na atoms adsorb first on defect points OC until the capacity C = 10 mA h g−1 is reached. Then, Na will adsorb to the graphitic layers adjacent to pores. For capacities larger than C = 25 mA h g−1, Na atoms continue to adsorb to graphitic layers but some of the adsorbed Na interchange to the type interlayer Na until the interlayer structure NaC15.3 is formed at capacity C = 250 mA h g−1. Finally, Na can only fill the pore at a higher capacity. There are no Na atoms adsorbing on defect points 2OC, which means that 2OC defects prevent Na insertion in HC. The OCV results of the 10th cycle show similar behaviour to that of the 1st cycle, but there is no insertion to defect sites in 10th cycle anymore, since all sites remain occupied.
By comparing the 1st and 10th cycles, we can approximate the degree of reversibility of each type of Na in HC. The defect Na is irreversible due to the very strong interaction between Na and defect points. The fraction of reversibly adsorbed Na is also low because of the strong interaction between Na and graphite layers, while the proportion of reversible interlayer Na is high because of the weak interaction between Na and graphitic layers. This is clarified using DFT calculations:40 only defect Na and adsorption Na are irreversible, while interlayer Na is highly mobile. Interpore Na is nearly reversible because the pore is large, compared with Na size, which means that they can move freely without restriction.
In future work, our model can be further developed to study transport properties as well as the diffusion pathway of Na+ from the cathode/electrolyte to HCs by using kinetic Monte Carlo simulation (KMC). The model can also be extended by combining many unit cells of HCs with different directions to describe the random structure of HCs.
Author contributions
Huy Sy Nguyen contributed to conceptualization, data curation, formal analysis, investigation, methodology, designing computer program and writing original draft. Arnulf Latz contributed to project administration, supervision, validation, visualization, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work contributes to the research performed at CELEST (Center for Electrochemical Energy Storage Ulm – Karlsruhe) and was funded by German Research Foundation (DFG) under project ID 390874152 (POLiS Cluster of Excellence). This study was also supported by computer resources from the University of Ulm and German Aerospace Center (DLR).References
- A. Belgibayeva, A. Rakhmetova, M. Rakhatkyzy, M. Kairova, I. Mukushev, N. Issatayev, G. Kalimuldina, A. Nurpeissova, Y. K. Soon and Z. Bakenov, J. Power Sources, 2023, 15, 232550 CrossRef.
- Y. Qiao, H. Zhao, Y. Shen, L. Li, Z. Rao, G. Shao and Y. Lei, EcoMat, 2023, e12321, DOI:10.1002/eom2.12321.
- S. Özcan and B. Biel, J. Appl. Phys., 2023, 133, 044301, DOI:10.1063/5.0131621.
- W. Zou, A. Innocenti, M. Zarrabeitia, D. Bresser, Y. Yang and S. Passerini, Acc. Chem. Res., 2023, 56(3), 284–296, DOI:10.1021/acs.accounts.2c00690.
- K. Askaruly, M. Yeleuov, A. Taurbekov, B. Sarsembayeva, A. Tolynbekov, N. Zhylybayeva, S. Azat, A. Abdisattar and C. Daulbayev, Mater. Today Commun., 2023, 34, 105136 CrossRef CAS.
- B. S. Lee, S. H. Oh, Y. J. Choi, M. J. Yi, S. H. Kim, S. Y. Kim, Y. E. Sung, S. Y. Shin, Y. Lee and S. H. Yu, Nat. Commun., 2023, 14, 150 CrossRef CAS PubMed.
- Y. Lai, X. Zhu, J. Li, Q. Guo, M. Li, A. Xia, Y. Huang, X. Zhu and Q. Liao, Chem. Eng. J., 2023, 457, 141196 CrossRef CAS.
- B. Biber, S. Sander, J. Martin, M. W. Mehrens and M. Mancini, Carbon, 2023, 201, 847–855 CrossRef CAS.
- B. Heidrich, M. Stamm, O. Fromm, J. Kauling, M. Börner, M. Winter and P. Niehoff, J. Electrochem. Soc., 2023, 170, 010530 CrossRef CAS.
- A. F. Cuesta, S. A. M. Dickson, A. B. Naden, C. Longdale and J. T. S. Irvine, J. Phys. Energy, 2023, 5, 015004 CrossRef.
- A. V. Desai, V. R. Seymour, R. Ettlinger, A. Pramanik, A. S. Manche, D. N. Rainer, P. S. Wheatley, J. M. Griffin, R. E. Morris and A. R. Armstrong, Chem. Commun., 2023, 59, 1321–1324 RSC.
- D. Kong, M. Tang, X. Wang, Z. Yuan and Y. Wang, Appl. Surf. Sci., 2023, 616, 156468 CrossRef CAS.
- Z. Mansouri, A. A. Shami, A. Sibari, S. Lahbabi, A. E. Kenz, A. Benyoussef, A. E. Fatimi and O. Mounkachi, Phys. Chem. Chem. Phys., 2023, 25, 3160–3174 RSC.
- C. Chen, S. Guo, S. Gao, W. Chen, E. Abduryim, Y. Kuai, G. Wu, X. Guan and P. Lu, Colloids Surf., A, 2023, 662, 131037 CrossRef CAS.
- A. Vasileiadis, Y. Li, Y. Lu, Y. S. Hu and M. Wagemaker, ACS Appl. Energy Mater., 2023, 6(1), 127–140 CrossRef CAS PubMed.
- H. Darjari, L. Bottoni, H. R. Moazami, S. J. Rezvani, L. Balducci, L. Sbrascini, A. Staffolani, A. Tombesi and F. Nobili, Mater. Today Sustainability, 2023, 21, 100313 CrossRef.
- H. Zhu, D. Wu, G. Zhang, W. Xu, A. Wang and K. Sun, J. Energy Storage, 2023, 57, 106172 CrossRef.
- B. Feng, L. Xu, Z. Yu, G. Liu, Y. Liao, S. Chang and J. Hu, Electrochem. Commun., 2023, 148, 107439 CrossRef CAS.
- S. Cho, J. C. Hyun, S. Ha, Y. Choi, H. Seong, J. Choi, H. J. Jin and Y. S. Yoon, Carbon Energy, 2023, 5, e288, DOI:10.1002/cey2.288.
- A. Jo, B. Lee, B. G. Kim, H. Lim, J. T. Han, S. Y. Jeong, J. Kim, S. H. Seo, H. J. Jeong, G. W. Lee, K. J. Baeg, B. Jeong and J. H. Park, Carbon, 2023, 5, 549–560 CrossRef.
- K. C. Wasalathilake, G. A. Ayoko and C. Yan, Carbon, 2018, 140, 276–285 CrossRef CAS.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Nanoscale, 2019, 11, 5274–5284 RSC.
- E. Olsson, G. Cottom and Q. Cai, Small, 2021, 17(18), 2007652, DOI:10.1002/smll.202007652.
- M. A. Reddy, M. Helen, A. Groβ, M. Fichtner and H. Euchner, ACS Energy Lett., 2018, 3, 2851–2857 CrossRef.
- H. Euchner, B. P. Vinayan, M. A. Reddy, M. Fichtner and A. Groβ, J. Mater. Chem. A, 2020, 8, 14205–14231 RSC.
- C. Cai, Y. Chen, P. Hu, T. Zhu, X. Li, Q. Yu, L. Zhou, X. Yang and L. Mai, Small, 2022, 18, 2105303, DOI:10.1002/smll202105303.
- Y. Youn, B. Gao, A. Kamiyama, K. Kubota, S. Komaba and Y. Tateyama, npj Comput. Mater., 2021, 4, 48, DOI:10.1038/s41524-021-00515-7.
- M. C. Mercer, S. Affleck, E. M. Gavilán-Arriazu, A. A. Zülke, P. A. Maughan, S. Trivedi, M. Fichtner, A. R. Munnangi, E. P. M. Leiva and H. E. Hoster, Chem. Phys. Chem., 2022, 23, e202100748 CrossRef CAS PubMed.
- X. Chen, Y. Zheng, W. Liu, C. Zhang, S. Li and J. Li, Nanoscale, 2019, 11, 22196–22205 RSC.
- J. Zhang, Y. Huang, C. Chen and K. She, Enery Fuels, 2023, 37(3), 2379–2386 CrossRef CAS.
- I. Jeon, D. Yang, D. Yadav, J. Seo, H. Zhang, L. Yin, H. S. Ahn and C. R. Cho, Electrochim. Acta, 2023, 439, 141730 CrossRef CAS.
- D. Qin, L. Wang, X. Zheng, J. Sheng, F. Huang, G. Xu, M. Zhu and Z. Dai, Energy Storage Mater., 2023, 54, 498–507 CrossRef.
- N. T. Aristote, Z. Song, W. Deng, H. Hou, G. Zou and X. Ji, J. Power Sources, 2023, 558, 232517 CrossRef CAS.
- B. Zhang, C. M. Ghimbeu, C. Laberty, C. V. Guterl and J. M. Tarascon, Adv. Energy Mater., 2016, 6(1), 1501588 CrossRef.
- E. Irisarri, A. Ponrough and M. R. Palacin, J. Electrochem. Soc., 2015, 162(14), A2476–A2482 CrossRef CAS.
- L. Yang, M. Hu, H. Zhang, W. Yang and R. Lv, J. Colloid Interface Sci., 2020, 566, 257–264 CrossRef CAS PubMed.
- X. Chen, Y. Fang, H. Lu, H. Li, X. Feng, W. Chen, X. Ai, H. Yang and Y. Cao, Small, 2021, 17(34), 2102248, DOI:10.1002/smll.202102248.
- C. Bommier, W. Luo, W.-Y. Gao, A. Greaney, S. Ma and X. Ji, Carbon, 2014, 76, 165–174 CrossRef CAS.
- D. Sauerteig, S. Ivanov, H. Reinshagen and A. Bund, J. Power Sources, 2017, 342, 939–946 CrossRef CAS.
- A. C. S. Jensen, E. Olsson, H. Au, H. Alptekin, Z. Yang, S. Cottrell, K. Yokoyama, Q. Cai, M. M. Titirici and A. J. Drew, J. Mater. Chem. A, 2020, 8, 743–749 RSC.
- M. Schammer, B. Hortstmann and A. Latz, J. Electrochem. Soc., 2021, 168, 026511 CrossRef CAS.
- J. Lück and A. Latz, Phys. Chem. Chem. Phys., 2018, 20, 27804–27821 RSC.
- L. von Kolzenberg, A. Latz and B. Horstmann, ChemSusChem, 2020, 13, 3901–3910 CrossRef CAS PubMed.
- J. Newman and K. E. Thomas-Alyea, Electrochemical System, John Wiley & Sons, Inc., New Jersey, 2004 Search PubMed.
- J. Hao, Y. Wang, K. Sheng, Z. Tian, Y. Liu, W. Li and J. Li, Fuel, 2023, 332(2), 126158 CrossRef CAS.
- L. Tao, P. Sittisomwong, B. Ma, A. Hu, D. Xia, S. Hwang, H. Huang, P. Bai and F. Lin, Energy Storage Mater., 2023, 55, 826–835 CrossRef.
- F. Xie, Z. Xu, Z. Guo and M. M. Titirici, Prog. Energy, 2020, 2, 042002 CrossRef.
- H. S. Nguyen, J. Forsman and C. E. Woodward, Soft Matter, 2018, 14, 6921–6928 RSC.
- H. S. Nguyen, J. Forsman and C. E. Woodward, J. Chem. Phys., 2019, 150, 044906 CrossRef PubMed.
- S. Qiu, L. Xiao, M. L. Sushko, K. S. Han, Y. Shao, M. Yan, X. Liang, L. Mai, J. Feng and Y. Cao, Adv. Energy Mater., 2017, 7, 1700403, DOI:10.1002/aenm.201700403.
- P. C. Tsai, S. C. Chung, S. K. Lin and A. Yamada, J. Mater. Chem. A, 2015, 3, 9763–9768, 10.1039/C5TA01443C.
- S. Alvin, D. Yoon, C. Chandra, H. S. Cahyadi, J. H. Park, W. Chang, K. Y. Chung and J. Kim, Carbon, 2019, 145, 67–81, DOI:10.1016/j.carbon.2018.12.112.
- O. Ziaee, N. Zolfaghari, M. Baghani and M. Baniassadi, Phys. Scr., 2021, 96, 125841 CrossRef.
| This journal is © the Owner Societies 2023 |








