Open Access Article
Open Access ArticleCorrelation of magnetic resonance (EPR, ssNMR) parameters and crystal-microstrain in marbles as a tool to probe their provenance†
Loukas
Belles‡
 a,
Christos
Dimitriou‡
a,
Christos
Dimitriou‡
 a,
Constantinos
Moularas
a,
Maria
Solakidou
a,
Constantinos
Moularas
a,
Maria
Solakidou
 a,
Marinos
Theorodakopoulos
a,
Marinos
Theorodakopoulos
 b,
Maria
Louloudi
b and
Yiannis
Deligiannakis
b,
Maria
Louloudi
b and
Yiannis
Deligiannakis
 *a
*a
aLaboratory of Physical Chemistry of Materials & Environment, Department of Physics, University of Ioannina, 45110, Ioannina, Greece. E-mail: ideligia@uoi.gr
bLaboratory of Biomimetic Catalysis & Hybrid Materials, Department of Chemistry, University of Ioannina, 45110 Ioannina, Greece
First published on 9th November 2023
Abstract
Marbles constitute a significant family of materials, for antiquities, as well as modern constructions. Herein, we have studied Greek marbles, using electron paramagnetic resonance (EPR) and solid-state nuclear magnetic resonance (ssNMR) spectroscopies, focusing on their structural microenvironment. Spin-Hamiltonian parameters derived from EPR spectra of naturally occurring 55Mn2+ (S = 5/2, I = 5/2) atoms in marbles, were studied as structural-probes. EPR data at 300 K provide a library of 55Mn2+ zero-field-splitting parameters (E, D). The effect of temperature (300 up to 700 K) on 55Mn2+-ZFS (E, D) and the strain of the D-tensor (Dstrain) was studied by high-temperature EPR spectroscopy. The EPR data, combined with 13C-ssNMR, provide detailed physicochemical information of the calcite and dolomite crystal phases in the marbles. In parallel, we have analyzed the lattice-microstrain (ε0) of the marbles’ crystallites using high-resolution XRD data. Analysis of the correlation between the D-values of Mn2+ centers and (ε0)-XRD, reveals trends that reflect the provenance of the marbles. In this context, we discuss the correlation between the D-values of Mn2+ centers and (ε0)-microstrain as a novel tool to elucidate the provenance of marbles.
1. Introduction
The use of Greek marble in ancient architecture and sculpture has fascinated researchers and historians for centuries.1 The physicochemical properties of Greek marbles, including their mineral composition, texture, and color, have rendered them a subject of intense study in the field of materials science.2,3 Identification of the origin of marbles used in monuments is very important.3 Moreover, the effects of environmental factors, such as temperature and mechanical stress, if properly measured and analyzed, are expected to provide insights into their historical evolution.1 In fact, it is well recognized that the precise attribution of geographical origin and environmental fingerprints to ancient marbles can provide useful information about cultural linkages.3–5 A closely related task is to establish scientific tools that allow the interlinking of parts or fragments from various monuments, that have been shattered or separated.6 In this context, so far, the characterization of marbles and the determination of their provenance, constitute important archaeological challenges that require use of specific petrographical and physicochemical techniques.7 Marble is defined as a carbonate rock that has undergone regional or contact metamorphism, according to petrography,4 in which calcite [CaCO3] or dolomite [CaMg(CO3)2] composes its crystal lattice.8 Apart from calcite and dolomite, which are the structural minerals, marble can also contain trace amounts of accessory minerals such as quartz, aluminosilicate minerals (muscovite, chlorite, phlogopite, etc.), and in some cases, Fe-oxides and graphite, giving veins of orange or dark color, respectively.9 Calcite and dolomite are responsible for the typical white color of marble, while impurities and other minerals often contribute to different colors, which vary from white to blue, gray, or even black.10,11 The whiter the marble stones, the lower the accessory mineral content, and this renders their distinction more difficult. Thus, white marbles are among the most difficult to differentiate with regard to their origin, i.e., due to their broad use in antiquity and lack of distinguishing macroscopic characteristics.3,5,6Calcite is calcium carbonate with a trigonal crystal structure. Insertion of divalent cations, such as Mg2+, Mn2+, Fe2+ and Fe3+, creates defects in the calcite microstructure.12 Thus, techniques such as instrumental neutron activation analysis (INAA),13 trace element analysis,14 analysis of stable-isotope ratios using mass spectroscopy,15 cathodoluminescence,16 and X-ray diffraction (XRD),17 have been utilized as high-resolution tools to analyze the composition, structure, and ultimately the origin and geochemical itinerary of white marbles. Magnetic resonance spectroscopies, i.e. electron paramagnetic resonance (EPR)6,8,18 and solid-state NMR (ssNMR) spectroscopies19 can offer high-precision, high resolution information on the local environment of the marble structures. For example, the 13C-ssNMR spectrum for calcite identified crystal flaws as well as the presence of trace elements, establishing the origin of marble.19 In a more recent study, in addition to 13C, two extra nuclei, i.e., 25Mg-ssNMR and 43Ca-ssNMR, were shown to provide specific information about variations among dolomitic marbles that can assist in their discrimination.20 It should be underlined, however, that a combination and correlation of information is necessary, not a single technique, to address the complex issue of marble provenance and geochemical itinerary.21–24
Herein, we propose a methodological approach based on the concurrent use of magnetic resonance (EPR and ssNMR spectroscopy) together with high-resolution XRD to establish a methodology that will contribute to the analysis of the microstructure of white marbles and their provenance identification. Previously, Maniatis et al.22 and Mandi et al.,18 conducted more in-depth and systematic research on the EPR spectrum of marble. Their findings were subjected to hierarchical aggregative cluster analysis, and 170 marbles constituted the first EPR database.18 To date, this database has been extended significantly,5,9,23 and a considerable number of archaeological marbles have been analyzed, with encouraging results.2,4,14,24
The underlying solid-state physics of this EPR-based information, is as follows: EPR identifies Mn2+ and Fe3+ in substitution of Ca2+ in the CaCO3 of aged marble's surface.9 Because the radius of Mn2+ (0.91 Å) is closer to that of Ca2+ (1.00 Å), it fits more easily into the calcite lattice without causing considerable disturbance. In contrast, Fe3+ (0.67 Å) generates far-greater crystallographic distortion and tends to access non-lattice locations in calcite rather than substitutional sites.25 Re-crystallization results in the formation of freshly produced calcite crystals, which are anticipated to have lower impurity concentrations than marble crystals.26 Water penetration induces re-crystallization but also enables Mn2+ and Fe3+ to enter marble surfaces in various oxidation states in clay minerals.27 Additionally, the presence of fungi or bacteria promotes the entry of water and crystal dissolution, in addition to microbial oxidation or reduction of Fe and Mn on marbles’ surfaces.28
Hereinafter, our working hypothesis was that all these geochemically or environmentally induced micro-alterations of the marble structures, could provide a correlating fingerprint of the marble's provenance. On this front, we focus on the study of local micro-alterations in marble crystals by combining EPR spectroscopy, ss-NMR spectroscopy, and XRD. In contrast to the classical use of XRD17,29,30i.e. as the standard method for crystal-phase identification in marbles, herein we elaborated on high-resolution analysis of the XRD focusing on the analysis of the microstrains of the crystallites.31 Recently Yakaboylu et al.31 have reported that strain analysis can provide distinct information on Marcellus Shales. Hereafter, our method relies on the assessment of structural microstrain by two methods (see conceptual Fig. 1 and 2): [i] X-ray diffraction line-broadening and [ii] zero-field-splitting (ZFS) tensor32 from the EPR spectra of Mn2+ centers, naturally occurring in the marbles. The full details of the two methods and the definitions of the parameters are provided in Section 2.1, hereafter.
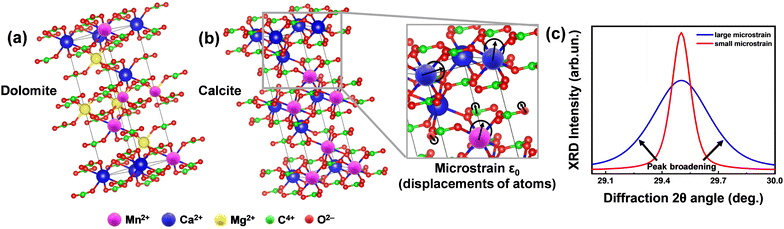 | ||
| Fig. 1 Concept of microstrain analysis using XRD. (a) The unit cells of the predominant phases in Greek marbles, i.e. calcite (Ca(CO3)) and dolomite (CaMg(CO3)2). (b) Magnified region of calcite's unit cell demonstrating the displacement of atoms. The degree of this relocation is captured by the microstructural (ε0) analysis utilizing XRD and TOPAS software. (c) Theoretical XRD pattern of a crystallite under small (red line) and large (blue line) microstrain. We underline that since the size of the marble crystallite is in the micrometers range, see data in Table 4, the observed XRD-broadening in not due to nano-size effects, but exclusively due to lattice-strains. | ||
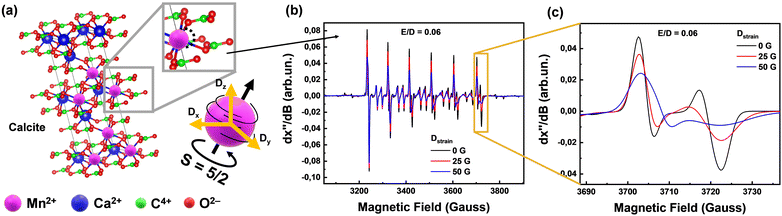 | ||
| Fig. 2 Phase composition of all collected Greek marbles contain calcite and dolomite. (a) Calcite unit cell of any marble, generated using VESTA software,36 where we present a local displacement of Mn2+ in the lattice and therefore the strain which can be described as Dstrain (orange arrows) versus the spin tensor (black arrows) direction. (b) EPR spectra which have different D distribution which displays changes of linewidths according to the Dstrain value. (c) Magnified region of the last transition of the EPR Mn2+ sextet, demonstrating the Dstrain linewidths changes. | ||
In brief, we define lattice-microstrain as an inhomogeneity of the lattice parameters, i.e., the unit cell vector's alterations, with no change in the XRD diffraction angle position (Fig. 1), i.e., no change in the average distance of the calcite or dolomite Miller planes {h k l}, see more explanation in Fig. 1. In this context, microstrain analysis through X-ray diffraction (XRD) provides information about the examination of the displacements of lattice-atoms from their ideal positions within a crystalline material. This provides valuable insights into the level of lattice distortions within the marbles, aiding in the understanding of their mechanical properties, durability, and potential susceptibility to environmental factors.
The EPR signals from the 55Mn2+ (S = 5/2, I = 5/2) ions provide valuable information about their concentration and local environment, contributing to a deeper understanding of the composition and origin of the marbles.22 Zero field splitting (ZFS) is a phenomenon that arises from the interaction between electron-spins in atoms with more than one-unpaired electron33i.e.55Mn2+ has five-unpaired electrons, thus S = 5/2. Moreover, the isotope 55Mn has 100% natural abundance and is characterized by I = 5/2. Thus, the S = 5/2 and I = 5/2 of 55Mn2+ provide a highly sensitive spin–probe system that sheds light on its immediate structural environment.34 By analyzing the ZFS-tensor D (fully detailed in Section 2.1) of marbles, by EPR spectroscopy, we can gain insights into the atomic-level characteristics of the materials, such as the orientation of the magnetic-tensors and the distribution of the principal values of the D-tensor, that we define as Dstrain, see more explanation in Fig. 2. Our key-hypothesis was that the ZFS-tensor D values and Dstrain can act as sensitive probes to detect variations in the local microstructure among various homologous marble materials i.e., reflecting their geochemical history and provenance.
In this context, herein we used electron paramagnetic resonance (EPR) spectroscopy in-tandem with X-ray diffraction (XRD) to study, on a systematic-comparative basis, a family of white marbles from various regions in Greece, see the map shown in Fig. 3. In addition, we have used high-temperature EPR35 as an advanced, non-conventional, EPR technique to study the Mn2+-ZFS in marbles in situ at elevated temperatures up to 700 K. This allowed us to investigate the possible role of temperature-induced strains in the materials and distinguish it from its interference with its geochemical EPR fingerprint.
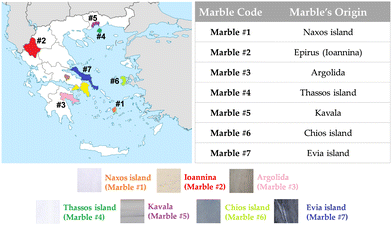 | ||
| Fig. 3 Map with selected colored locations, from where marbles were collected. The Greek marbles were collected according to their color and historic importance. | ||
Overall, the key aims of the present work were [i] to present a comprehensive correlation analysis of the structural, spectroscopic, and magnetic properties of various types of Greek marbles, including their crystal structure, lattice microstrain and 55Mn2+ zero-field-splitting tensor strain and [ii] to propose the concurrent use of high-resolution-XRD and EPR as a novel methodological protocol to address questions of provenance, and thermal and geochemical history of marbles.
2. Experimental methods
2.1 Description of microstrain-analysis methods using XRD and EPR
The prevailing crystal phases for marbles are calcite [Ca(CO3)] and dolomite [CaMg(CO3)2]. Their unit cells are depicted in Fig. 2(a). The relocations of atoms from their ideal positions within the Ca(CO3) lattice (Fig. 2(b)) lead to XRD peak broadening, with no shift of the Bragg-diffraction angles. Microstrain represents displacements of atoms from their ideal positions, generated by any lattice imperfection (dislocations, vacancies interstitials and similar defects), eqn (1). It can be conceived by considering two extreme values of the lattice spacing d, namely d + Δd and d − Δd, where ε0 = Δd/d is attributed as the mean deviation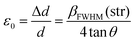 | (1) |
Hereinafter, we have used high-resolution detection of the XRD signals, with angular steps of 0.01 degrees, and the use of TOPAS37 software, to implement Rietveld analysis and microstructure analysis. The concept of microstrain (ε0) entails the deviations of atoms from their equilibrium positions within a crystal lattice, which are generated by different lattice imperfections such as dislocations, vacancies, interstitials, and similar defects.38 By analyzing the broadening and shifting of diffraction peaks in the XRD pattern using TOPAS, the magnitude and distribution of microstrain in calcite and dolomite crystals can be quantitatively assessed.
The zero field splitting tensor (D-tensor) has three principal values (Dx, Dy, Dz) in its principal-axes system32,33 see Fig. 2(a). The Dx,y,z values are influenced by the electron–electron interactions within the 55Mn2+ atom, which in turn are influenced by the immediate chemical environment of the atom.23,33,34 Typically, the Dx,y,z values are influenced by factors such as ligand field strength, crystal symmetry, and local distortions.32,34 These changes in D can be traced by EPR spectra i.e., see examples of numerically simulated EPR spectra in Fig. 2(b) and (c). Importantly, as we exemplify in Fig. 2(b) and (c), Dstrain can be reliably traced by EPR spectroscopy via alteration of certain spectral features e.g. the high-field transitions.
In this way, we have quantified and analyzed the lattice-microstrain (ε0) by XRD and the ZFS, (Dstrain), by EPR based on the definition and conventions defined herein.
2.2 Preparation of marble materials
The marble samples were collected as raw materials from different quarries in Greece, according to their historical locations and their color, choosing from a colorful palette of Greek marbles that were used by many artists all over the centuries. In Fig. 3, we present a map of the regions where marbles were collected from. Marbles of different colors [marble #2 (Ioannina) yellowish, marble #6 (Chios Island) dark grey, marble #4 (Thassos Island) white] have different historic importance, i.e., marble #1 from Naxos Island and marble #4 from Thassos Island are the two of great importance due to their large use in classical monuments and sculptures.Firstly, the collected marbles were cleaned up by soft-tissue wiping, so that dirt and surface weathering were removed appropriately. Afterwards, the marbles were crushed to coarse powder of millimeter-size to avoid artefacts induced by the treatment. Comparison with intact pieces shows that coarse powders did not have additional treatment-induced signals. Therefore, the marbles used through all experiments for EPR, ssNMR and XRD analysis were in a coarse-powder form. In order to characterize the materials, we have collected samples from three different spots from the same quarry site. The standard error is 5%.
2.3 Material characterization methods
Ĥ = β![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0042_20d1.gif) ĝ ĝ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0053_20d1.gif) + + ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0053_20d1.gif) ![[D with combining circumflex]](https://www.rsc.org/images/entities/char_0044_0302.gif) ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0053_20d1.gif) + + ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0049_20d1.gif) Â Â![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0053_20d1.gif) | (2) |
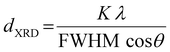 | (3) |
3. Results and discussion
EPR and HT EPR spectroscopy
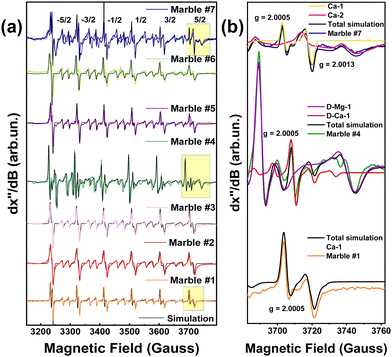
Fig. 4(a), presents a broad scan 77 K EPR spectra of all marbles. In all cases, the EPR spectrum characteristic of 55Mn2+ (S = 5/2, I = 5/2) is detected.34 A typical 55Mn2+ EPR spectrum is characterized by six main peaks, corresponding to the allowed 2I + 1 hyperfine splitting of –1/2 up to 1/2 transitions. Between each hyperfine, a pair of “forbidden” ΔMI = 234 peaks are present. In accordance with the original analyses conducted by Reed and Markham, their relative intensity and line shape, are governed by the numerical values of the components of tensors D and A.34 In marble structures, all these factors depend on the type of marble, its geological history, and the location of the marble.4–6 The EPR spectra in Fig. 4 are due to Mn2+ ions occupying Ca-sites, in the unit cells of calcite or dolomite, see Fig. 2(a). The black lines in Fig. 4(a) are theoretically calculated 55Mn2+ EPR spectra, using the spin Hamiltonian parameters listed in Table 1. Noticeably the hyperfine tensor anisotropy of all marbles did not vary significantly despite the different phase composition.| Marble | g (±0.0001) | [D, E] (Gauss) (±0.5) | D strain (Gauss) (±1) | [Ax, Ay, Az] (Gauss) (±1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ca-site | Mg-site | Ca-site | Mg-site | Ca-site | Mg-site | Ca-site | Mg-site | |||||
| #1 | 2.0004 | — | — | [90, 5.4] | — | — | 21 | — | — | [94, 94, 93] | — | — |
| #2 | 2.0005 | — | — | [86, 4.3] | — | — | 23 | — | — | [95, 94, 93] | — | — |
| #3 | 2.0005 | — | — | [82, 5.3] | — | – | 18 | — | — | [95, 95, 93] | — | — |
| #4 | 2.0005 | — | 2.0005 | [5.4, 0.1] | — | [160, 5.4] | 10 | — | 15 | [94.5, 95, 96] | — | [93, 93, 90] |
| #5 | 2.0005 | — | — | [82, 4.6] | — | — | 12 | — | — | [93, 96, 93] | — | – |
| #6 | 2.0005 | — | – | [90, 3.6] | — | — | 28 | — | — | [94, 96, 94] | — | — |
| #7 | 2.0005 | 2.0013 | — | [107, 8.9] | [86, 5.4] | — | 18 | 4 | — | [88, 99, 95] | [95, 94, 93] | — |
In Fig. 4(b), we show the EPR spectra of marbles #1, #4, and #7 that show significant differences. Such analysis, see the spin-Hamiltonian parameters in Table 1, provides two pieces of information as follows: [i] the hyperfine-tensor A values of the 55Mn2+ (I = 5/2), and [ii] the D-tensor parameters together with its Dstrain values. Accordingly, marble #7 shows two EPR spectral components corresponding to two types of Mn-atoms. Marble #7 is a pure calcite. Based on literature data,42,43 the two Mn-atoms occupy two different calcium sites in the calcite structure, marked Ca-1 and Ca-2, in Fig. 4(b). As seen in Table 1 these two Mn2+ species are distinguishable by their different g-values, D-tensors and A-tensors. Site Ca-2 is characterized by smaller D-tensor values and lower Dstraini.e., 4 vs. 18 for the Ca-1 site. From the simulation of the EPR spectra, see Fig. 4(b), the relative population of these Mn2+-centers is Ca-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca-2 = 0.7
Ca-2 = 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3.
0.3.
Their specific spin-Hamiltonian parameters are responsible for the clear differences seen in the EPR spectrum of marble #7, and, as we show in the following, can serve as fingerprints together with the XRD microstrain parameter (ε0). Regarding marble #4, with a different phase composition, i.e. both calcite and dolomite, see XRD data in Table 4, we see that its 55Mn-EPR spectrum can be deconvoluted into two sub-spectra, see Table 1. Based on literature data,21–23 one 55Mn-type (D-Mg-1 in Fig. 2(b) and (c)) refers to 55Mn atoms occupying Mg-atom sites in dolomite, while D-Ca-1 in Fig. 2(b), corresponds to 55Mn atoms occupying the Ca-atom sites in dolomite. From the EPR spectra, we estimate the relative populations of the two Mn2+ sites to be Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca = 0.96
Ca = 0.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04.
0.04.
Both sites in marble #4 show moderate Dstrain values of 10 and 15, respectively, see Table 1. Then, marble #1 which is pure calcite, shows a single EPR signal, see Table 1, from 55Mn atoms occupying a Ca-atom site, see Ca-1 in Fig. 2(b). Marble #1 has a high Dstrain of 21, see Table 1.
Based on the data listed in Table 1, hereafter we discuss four of them, according to their distinct phase compositions: marbles #2, #5, and #6 have a higher percentage of the calcite phase, in comparison with marble #4 with the dolomitic phase. The Dstrain of these marbles spans a wide range of 10 up to 28, for Ca-sites and 15 for Mg-site in the dolomitic marble #4. We underline that the hyperfine tensor anisotropy of all marbles did not vary significantly, despite the different phase compositions.
In addition to the EPR analysis of pristine materials, the selected marbles #2, #4, #5, and #6 were studied using our high-temperature EPR spectrometer (see the EPR spectra in Fig. S2a–d of the ESI†). The protocol was as follows: for each material EPR spectra were recorded in situ for temperatures up to 700 K, under an equilibration time of 2 hours for each temperature. After measurements the marbles were allowed to cool for 4 hours at room temperature (Tresting = 300 K) and measured again (Fig. S3a–d, ESI†). In each case the EPR parameters measured at Tresting were similar to those at high-T i.e. the changes in the value of D due to heat-stress were not reversible.
In Table 2, we present the Spin Hamiltonian parameters derived from the theoretical simulation of all experimental spectra for the four selected marbles at variable temperatures (300–700 K). For simplicity we discuss only the Ca-sites. The trends in D-parameters and the Dstrain can be observed in Fig. 5(a) and (b) respectively, where we observe the following: [i] minor changes in the D-values for all marbles. Similarly, the rhombicity parameter E is not sensitive to the marble type, see Table 2. [ii] A significant increase of Dstrain at increasing temperatures for all marbles. [iii] the Dstrain increase was always more prominent in the calcite sites than in dolomite sites. Therefore, the present data exemplify that high-temperature electron paramagnetic resonance (EPR) provides a new tool to unravel microstrain trends in marbles. As shown in Fig. 5(a) an interesting fact is that with the increase in temperature all marbles show an increase in Dstrain parameters, while D does not change. More specifically, marble #5 showed the most significant Dstrain increase i.e., 70% on heating from 300 to 700 K.
| Temperature (K) (±1) | A [Ax, Ay, Az] (Gauss) (±1) | [D, E] (Gauss) (±0.5) | D strain (Gauss) (±1) | g (±0.0001) |
|---|---|---|---|---|
| Marble #2 | ||||
| 300 | [95, 94, 93] | [86.0, 4.3] | 23 | 2.0005 |
| 400 | [96, 94, 93] | [81.5, 4.4] | 28 | 2.0005 |
| 500 | [95, 94, 92] | [80.8, 4.6] | 26 | 2.0005 |
| 600 | [95, 94, 92] | [110.1, 4.5] | 32 | 2.0005 |
| 700 | [95, 94, 92] | [94.2, 4.3] | 42 | 2.0005 |
| Marble #4 | ||||
| 300 | [94, 95, 95] | [5.4, 0.1] | 10 | 2.0005 |
| 400 | [95, 95, 95] | [5.6, 0.1] | 14 | 2.0005 |
| 500 | [95, 95, 95] | [5.8, 0.1] | 16 | 2.0005 |
| 600 | [95, 95, 95] | [5.3, 0.1] | 17 | 2.0005 |
| 700 | [95, 95, 95] | [5.5, 0.1] | 20 | 2.0005 |
| Marble #5 | ||||
| 300 | [93, 96, 93] | [82.0, 4.6] | 12 | 2.0005 |
| 400 | [95, 95, 94] | [90.9, 4.6] | 17 | 2.0005 |
| 500 | [94, 95, 94] | [86.3, 4.6] | 21 | 2.0005 |
| 600 | [93, 95, 94] | [88.9, 4.6] | 30 | 2.0005 |
| 700 | [93, 95, 94] | [93.3, 4.6] | 40 | 2.0005 |
| Marble #6 | ||||
| 300 | [94, 96, 94] | [90.0, 3.6] | 28 | 2.0005 |
| 400 | [94, 94, 93] | [87.8, 3.6] | 29 | 2.0005 |
| 500 | [94, 94, 93] | [88.3, 3.6] | 30 | 2.0005 |
| 600 | [94, 94, 93] | [96.2, 3.6] | 38 | 2.0005 |
| 700 | [94, 94, 93] | [92.8, 3.6] | 47 | 2.0005 |
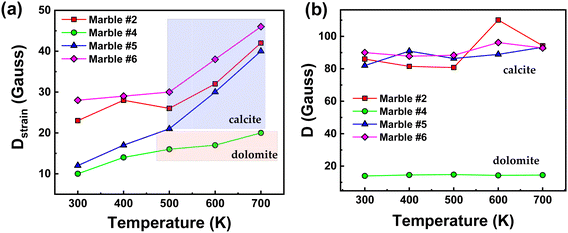 | ||
| Fig. 5 Variations of (a) Dstrainvs. temperature and (b) ZFS (D-tensor) vs. temperature, for marbles #2, #4, #5, and #6. | ||
Marble #6 also showed a significant Dstrain increase of 39% and marble #2 showed an increase of 45%. Marble #4 with a lower Dstrain value showed an increase of 49%. Noticeably, a more careful perusal allows us to observe that the similarities between the Dstrain trends for marbles #2, #5, #6 and their distinction vs. marble #4, might correlate with the [calcite/dolomite] phase ratio, for example, the dolomitic (calcite/dolomite = 3/96), marble #4 with low-initial D and Dstrain, is more resistant to distortions at higher temperatures. On the other hand, marbles #2, #5, and #6 with mostly calcite phase composition show increased values of both Dstrain and D, as well as Dstrain sensitivity under thermal stress.44
To further peer into the microstructural features of these materials, marbles #2, #4, #5 and #6, we have studied their long-term exposure at 700 K for 30 minutes, 3 hours and 3 days. The XRD and EPR data are presented in Fig. S4 and S5 (ESI†), respectively, and the strain-trends vs. calcination time are listed in Tables S1 and S2 (ESI†). The plot of microstrain vs. the heating time (Fig. S6 and S7, ESI†) shows that in the first 3 hours an important strain increase occurs, while a minor change occurs upon further heating for up to 3 days. The high-T EPR data provide an additional piece of information, which further demonstrates that the Dstrain (not D) is the parameter of pertinence that is sensitive to the changes in the local environment.
13C-Solid-state NMR
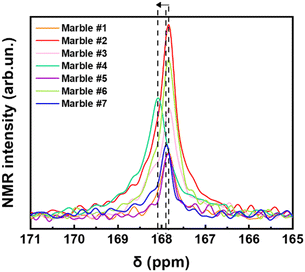
Fig. 6 shows a selected part of the 13C-NMR spectra, (from 171 ppm to 165 ppm), the full spectra are shown in Fig. S8 (ESI†). In Fig. 6, we can decipher three parameters: the peak-position (δ in ppm), its width at half maximum (Δν1/2), and the integrated area of resonance (Table S3, ESI†). The δ (ppm) and Δν1/2 values are listed in Table 3. The calibrated δ-values show rather small variations of around 167–168 ppm that are assigned to 13C of structural carbonates.45 These structural carbonates in dolomite [CaMg(CO3)2] or calcite [Ca(CO3)], are clearly distinct from free carbonates that are typically detected at 170.5 ppm.20 The linewidths (Δν1/2) listed in Table 3, vary in the range from 32.4 to 60.6 Hz depending on the marble. The carbonate peak broadening (Δν1/2) may be caused either by the different distribution of the carbonates due to the presence of other atoms like Fe, Mn, and Mg, which can substitute Ca in the crystal lattice of calcite, or/and due to the presence of para/ferromagnetic substances/impurities.46 From Table 3, we see that marble #4 has the highest percentage of dolomite with few ferro/paramagnetic impurities (see Table 4). This material shows higher Δν1/2 = 60.6 Hz and 13C δ shift. We see that these 13C-strains are correlated with the highest structural microstrains (ε0), see XRD data in Table 5. Noticeably, the dolomitic marble #4 shows the lowest D and Dsrtain values of 55Mn centers. All other marbles have almost the same δ-ppm and lack of dolomite phase. Marble #2 and #6, have Fe3+ ions and lastly marbles #1, #5 and #7 have the lowest concentration of ions in their structure.47 Overall, the 13C-NMR data provide additional information about the microstructure of the studied marbles. We underline that EPR, NMR and XRD probe different aspects of the marble structure, therefore, not a single method can provide material-discriminating information alone. As we show in the following, it is the correlation of the trends of the parameters that allows a better material-discriminating strategy to be built up.| Marble | δ (ppm) | Δν1/2 (Hz) |
|---|---|---|
| #1 | 167.83 | 39.6 |
| #2 | 167.83 | 47.5 |
| #3 | 167.82 | 54.2 |
| #4 | 168.07 | 60.7 |
| #5 | 167.84 | 32.5 |
| #6 | 167.83 | 46.9 |
| #7 | 167.88 | 33.2 |
| Marble | Grain size dXRD (μm) | Phase composition (%) (±0.5) | ||||||
|---|---|---|---|---|---|---|---|---|
| Calcite | Dolomite | Calcite | Dolomite | Magnetite | Quartz | Akermanite | Ankerite | |
| CaCO3 | CaMg(CO3)2 | CaCO3 | CaMg(CO3)2 | Fe3O4 | SiO2 | Ca2Mg(Si2O7) | Ca(Fe,Mg,Mn)(CO3)2 | |
| #1 | 2.80 ± 0.27 | — | 95 | — | — | 5 | – | — |
| #2 | 2.82 ± 0.12 | — | 96 | — | 1 | 1.5 | 1.5 | — |
| #3 | 1.94 ± 0.12 | 2.63 ± 0.61 | 83 | 12 | — | 2 | 2 | 1 |
| #4 | 2.81 ± 0.11 | 1.91 ± 0.16 | 3 | 96 | — | 1 | — | — |
| #5 | 1.54 ± 0.14 | — | 96 | — | — | 4 | — | — |
| #6 | 1.91 ± 0.12 | — | 95.5 | — | — | 2.5 | 1 | 1 |
| #7 | 1.91 ± 0.16 | – | 94 | — | 1 | 2.5 | 2.5 | — |
| Marble | Microstrain ε0 (×10−4) | |
|---|---|---|
| Calcite | Dolomite | |
| CaCO3 | CaMg(CO3)2 | |
| #1 | 4.1 ± 0.7 | — |
| #2 | 4.7 ± 0.2 | — |
| #3 | 7.1 ± 0.6 | 11.4 ± 1.1 |
| #4 | 8.6 ± 0.4 | 9.6 ± 0.6 |
| #5 | 2.9 ± 0.3 | — |
| #6 | 4.0 ± 0.2 | — |
| #7 | 3.2 ± 0.4 | — |
Lattice-microstrain probed by X-ray diffraction
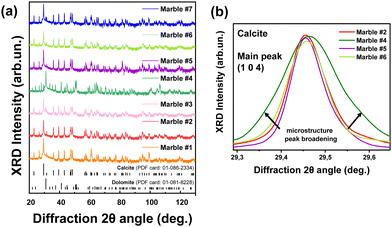
The XRD patterns for all marbles are presented in Fig. 7(a). As expected, they show that the predominant phases are calcite (CaCO3) and dolomite (CaMg(CO3)2), with traces of quartz, magnetite, akermanite and ankerite (Table 4). All the observed diffraction peaks can be indexed to CaCO3 with face-centered rhombohedral cell with trigonal symmetry (![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), a = 5.01 Å, b = 5.01 Å, and c = 16.99 Å (JCPDS card no. 86-2340). The peaks at 23.06°, 29.44°, 31.43°, 35.98°, 39.42°, and 43.16° are indexed to the (012), (104), (006), (110), (113), and (202) Miller planes, respectively. Likewise, the dolomite peaks correspond to its trigonal phase with a rhombohedral lattice system, a = 4.87 Å, b = 4.87 Å, and c = 16.19 Å (JCPDS card no. 36-0426). The reflections centered at 24.04°, 30.94°, 33.54°, 35.32°, 37.38°, and 41.13° with the corresponding (101), (012), (104), (006), (015), and (110) Miller planes belong to dolomite. The XRD data for all calcined materials are shown in Fig. S3 in the ESI.† In Table 4, the crystallite-size and phase composition are listed, as derived from analysis of the XRD data. The pure calcitic marbles are #1, #2, #5, #6 and #7, i.e. ‘pure’ means the majority of their composition is calcite, and in addition they possess traces of magnetite, quartz, akermanite and ankerite. Marble #3 is calcitic with a 12% dolomite, and marble #4 is pure dolomitic with a minimal CaCO3 percentage of 3%.
m), a = 5.01 Å, b = 5.01 Å, and c = 16.99 Å (JCPDS card no. 86-2340). The peaks at 23.06°, 29.44°, 31.43°, 35.98°, 39.42°, and 43.16° are indexed to the (012), (104), (006), (110), (113), and (202) Miller planes, respectively. Likewise, the dolomite peaks correspond to its trigonal phase with a rhombohedral lattice system, a = 4.87 Å, b = 4.87 Å, and c = 16.19 Å (JCPDS card no. 36-0426). The reflections centered at 24.04°, 30.94°, 33.54°, 35.32°, 37.38°, and 41.13° with the corresponding (101), (012), (104), (006), (015), and (110) Miller planes belong to dolomite. The XRD data for all calcined materials are shown in Fig. S3 in the ESI.† In Table 4, the crystallite-size and phase composition are listed, as derived from analysis of the XRD data. The pure calcitic marbles are #1, #2, #5, #6 and #7, i.e. ‘pure’ means the majority of their composition is calcite, and in addition they possess traces of magnetite, quartz, akermanite and ankerite. Marble #3 is calcitic with a 12% dolomite, and marble #4 is pure dolomitic with a minimal CaCO3 percentage of 3%.
Table 5 lists the derived microstrain values (ε0) from the analysis of the XRD data. In all cases the microstrains are in the range ε0 = 3–11 × 10−4. In Fig. 8, we present correlation plots of the lattice-microstrain values (ε0) derived from XRD vs. the D and Dstrain values derived from EPR. We see that the microstrain ε0 is larger for marbles #3 and #4 where dolomite or akermanite phases i.e., Mg atoms are introduced in the crystal phase. When we examine the correlation trends (D vs. ε0) and (Dstrainvs. ε0) in Fig. 8(a) and (b), we observe a diaspora of the points: marble #7 with its two 55Mn Dstrain values clearly identified at the left-hand part of Fig. 8(b). Marble #4 with its two species of 55Mn2+, D and Dstrain values is classified at the upper and lower parts of Fig. 8(a). Marble #1 with its two calcitic ε0 values is shown in the middle parts of Fig. 8(a) and (b). More specifically, marble #4 where dolomite is 96% and calcite is 4%, has a low ZFS D-value of 12 Gauss while all marbles with more than 83% of calcite have a D range from 80 Gauss up to 110 Gauss. Microstrain analysis shows that all marbles with more calcite than dolomite phase composition, are in the range from 2.8 × 10−4 to 7.5 × 10−4. Regarding the Dstrainversus microstrain ε0, we observe similar correlation i.e., for small microstrain values ε0 < 8.0 × 10−4 we have calcitic marbles while for large ε0 > 8.0 × 10−4 we have the interference of dolomite. The Dstrain for pure calcitic marbles has a range of 0–30 Gauss, whilst the dolomitic marbles have a small range of 10–20 Gauss.
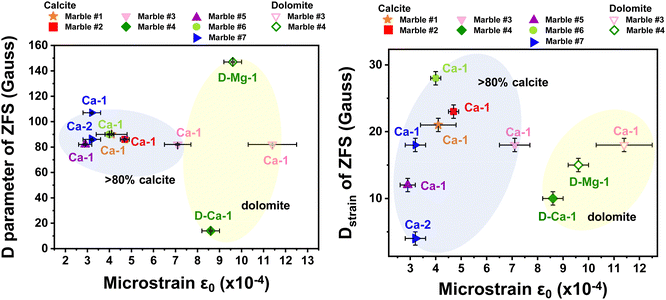 | ||
| Fig. 8 Correlation plot ZFS-XRD microstrain. (a) D axial parameter versus XRD-microstrain ε0 and (b) Dstrainversus XRD-microstrain ε0 for all the Greek marbles. We observe that when the marble is calcitic is positioned inside the blue bubble in the graph, while the dolomitic marbles are located in the yellow bubble. The points are notated as follows: Ca-1 for one species of calcite, Ca-2 for second species of calcite, D-Ca-1 for one species of calcite in dolomitic marble and D-Mg-1 for one species of dolomite in dolomitic marble (see Fig. 4(b)). | ||
4. Conclusions
A novel methodology is suggested that correlates magnetic resonance properties with crystal-microstrain in order to reveal a trend that reflects the provenance of the marble. Greek marbles from different places along Greece, have been selected according to their historical importance and provenance and studied using our EPR, ssNMR and XRD methods. Theoretical simulation of the EPR spectra using the spin-Hamiltonian formalism, provides numerical values of the zero field splitting tensor (D-tensor) and its Dstrain for each marble. High-temperature EPR provides, for the first time to our knowledge, important insight into the structural behavior of marbles under heat-stress that can be related to environmental events through history. Marbles with different phase compositions, i.e., calcite and dolomite, show an increment of Dstrainversus temperature. A pattern for marbles with more than 95% calcite is emerging which indicates a considerable Dstain for 12 Gauss up to 47 Gauss versus a temperature of 700 K. On the other hand, dolomitic marble #4 shows a lower range of D-tensor from 10 Gauss to 20 Gauss. XRD shows that calcitic marbles have low microstrain (ε0), whilst the dolomitic ones have larger lattice-microstrain (ε0) which indicates that the interference of Mg atoms (marbles #3 and #4) into the carbonate lattice affects the local crystal environment enhancing the lattice distortions. Finally, we propose a correlation plot between lattice-microstrain (ε0) and the D-tensor strain from XRD data and EPR data, respectively. We consider that this correlation tool can be of broader use i.e., to other marbles, as well as other cultural materials including ceramics and glasses with specific aims of deciphering the provenance and possibly historical path.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support of this work by the project “Center For Research, Quality Analysis Of Cultural Heritage Materials And Communication Of Science” (MIS 5047233) which is implemented under the Action “Reinforcement of the Research and Innovation Infrastructure”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund).Notes and references
- Ancient stones: quarrying, trade and provenance: interdisciplinary studies on stones and stone technology in Europe and Near East from the prehistoric to the early Christian period, ed. M. Waelkens, N. Herz, L. Moens and Association for the Study of Marble and Other Stones used in Antiquity, Leuven University Press, Leuven, Belgium, 1992 Search PubMed.
- W. Prochaska, D. Attanasio and J. Archaeol., Sci. Rep., 2021, 35, 102676 Search PubMed.
- Y. Maniatis, D. Tambakopoulos, L. Lazzarini and M. C. Sturgeon, Archaeometry, 2021, 63, 685–704 CrossRef CAS.
- D. Attanasio, M. Bruno, W. Prochaska and A. B. Yavuz, Archaeometry, 2015, 57, 217–245 CrossRef CAS.
- K. Polikreti and Y. Maniatis, Archaeometry, 2002, 44, 1–21 CrossRef CAS.
- V. Baïetto, G. Villeneuve, M. Schvoerer, F. Bechtel and N. Herz, Archaeometry, 1999, 41, 253–265 CrossRef.
- N. Herz and E. Garrison, Treatise on Geochemistry, Elsevier, 2014, pp. 241–253 Search PubMed.
- D. Attanasio, R. Platania and P. Rocchi, J. Archaeol. Sci., 2005, 32, 311–319 CrossRef.
- K. Polikreti and Y. Maniatis, Atmos. Environ., 2004, 38, 3617–3624 CrossRef CAS.
- I. Badouna, P. Koutsovitis, C. Karkalis, K. Laskaridis, N. Koukouzas, P. Tyrologou, M. Patronis, C. Papatrechas and P. Petrounias, Minerals, 2020, 10, 507 CrossRef CAS.
- G. Charalampides, N. Arvanitidis, K. I. Vatalis and S. Platias, Procedia Econ. Finance, 2013, 5, 143–151 CrossRef.
- K. Al-Bashaireh, J. Archaeol. Sci. Rep., 2021, 35, 102777 Search PubMed.
- L. Moens, J. De Rudder, P. De Paepe and M. Waelkens, Bull. Soc. Chim. Belg., 2010, 95, 399–406 CrossRef.
- G. Poretti, M. Brilli, C. De Vito, A. M. Conte, A. Borghi, D. Günther and A. Zanetti, J. Cult. Herit., 2017, 28, 16–26 CrossRef.
- M. L. Gerdes, L. P. Baumgartner and J. W. Valley, J. Petrol., 1999, 40, 853–872 CrossRef CAS.
- P. Blanc, M. P. Lapuente Mercadal and A. Gutiérrez Garcia-Moreno, Minerals, 2020, 10, 381 CrossRef CAS.
- J. D. Lynn, All Days, SPE, Al-Khobar, Saudi Arabia, 2011, p.SPE-149091-MS Search PubMed.
- Y. Maniatis and V. Mandi, J. Appl. Phys., 1992, 71, 4859–4867 CrossRef CAS.
- A. Gutiérrez Garcia-M., M. C. Savin, N. Cantin, S. Boudoumi, P. Lapuente, R. Chapoulie and I. Pianet, Archaeometry, 2019, 61, 795–808 CrossRef.
- I. Pianet, A. Gutiérrez Garcia-Moreno, M.-C. Savin, N. Frerebeau, J. Trebosc, P. Florian and M. P. Lapuente Mercadal, Materials, 2023, 16, 1468 CrossRef CAS PubMed.
- K. Polikreti, Archaeometry, 2007, 49, 603–619 CrossRef CAS.
- Y. Maniatis, V. Mandi and A. Nikolaou, in Classical Marble: Geochemistry, Technology, Trade, ed. N. Herz and M. Waelkens, Springer, Netherlands, Dordrecht, 1988, pp.443–452 Search PubMed.
- Y. Maniatis, Proc. Int. Sch. Phys. LdquoEnrico Fermirdquo, 2004, 154, 179–202.
- S. Khrissi, L. Bejjit, M. Haddad, C. Falguères, S. Ait Lyazidi and M. El Amraoui, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 353, 012013 Search PubMed.
- J. D. Rimstidt, A. Balog and J. Webb, Geochim. Cosmochim. Acta, 1998, 62, 1851–1863 CrossRef CAS.
- R. G. C. Bathurst, Carbonate sediments and their diagenesis, Elsevier, Amsterdam, 2nd edn, 1975 Search PubMed.
- D. Camuffo, M. Del Monte, C. Sabbioni and O. Vittori, Atmos. Environ., 1982, 16, 2253–2259 CrossRef CAS.
- D. A. Brown, D. C. Kamineni, J. A. Sawicki and T. J. Beveridge, Appl. Environ. Microbiol., 1994, 60, 3182–3191 CrossRef CAS PubMed.
- B. Bakruddin and A. R. Sembiring, J. Inotera, 2019, 4, 79 CrossRef.
- D. Covaci, C. Costea, D. Dumitras and O. G. Duliu, Geophys. Res. Lett., 2012, 14(EGU2012), 8771 Search PubMed.
- G. A. Yakaboylu, N. Gupta, E. M. Sabolsky and B. Mishra, Int. J. Rock Mech. Min. Sci., 2020, 130, 104345 CrossRef.
- J. R. Pilbrow, Appl. Magn. Reson., 1994, 6, 161–181 CrossRef CAS.
- J. R. Pilbrow and G. R. Hanson, Methods in Enzymology, Academic Press, 1993, vol. 227, pp.330–353 Search PubMed.
- G. H. Reed and G. D. Markham, in Biological Magnetic Resonance, ed. L. J. Berliner and J. Reuben, Springer, US, Boston, MA, 1984, pp.73–142 Search PubMed.
- S. Zheng, J.-W. Feng and G. E. Maciel, Energy Fuels, 2005, 19, 1201–1210 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- R. E. Dinnebier, A. Leineweber and J. S. O. Evans, Rietveld Refinement: Practical Powder Diffraction Pattern Analysis using TOPAS, Berlin, Boston: De Gruyter, 2019 DOI:10.1515/9783110461381.
- Y. Zhao and J. Zhang, J. Appl. Crystallogr., 2008, 41, 1095–1108 CrossRef CAS.
- D. Sanna, G. Delogu, M. Mulas, M. Schirra and A. Fadda, Food Anal. Methods, 2012, 5, 759–766 CrossRef.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- C. R. Byfleet, D. P. Chong, J. A. Hebden and C. A. McDowell, J. Magn. Reson., 1969, 1970(2), 69–78 Search PubMed.
- C. R. De Abreu, T. C. Cordeiro, A. A. G. Carrasquilla, E. S. De Souza and A. O. Guimarães, J. Pet. Sci. Eng., 2021, 203, 108847 CrossRef CAS.
- R. A. Shepherd and W. R. M. Graham, J. Chem. Phys., 1984, 81, 6080–6084 CrossRef.
- C. Ionescu, V. Hoeck, C. Gruian and V. Simon, Appl. Clay Sci., 2014, 97–98, 138–145 CrossRef CAS.
- K. Beshah, C. Rey, M. J. Glimcher, M. Schimizu and R. G. Griffin, J. Solid State Chem., 1990, 84, 71–81 CrossRef CAS.
- V. J. Witherspoon, J. Xu and J. A. Reimer, Chem. Rev., 2018, 118, 10033–10048 CrossRef CAS PubMed.
- H. Nebel, M. Neumann, C. Mayer and M. Epple, Inorg. Chem., 2008, 47, 7874–7879 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02974c |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2023 |