Open Access Article
Open Access ArticleDynamics and local ordering of pentachloronitrobenzene: a molecular-dynamics investigation†
Jonathan F.
Gebbia
 *ab,
Andrés Henao
Aristizabal
c,
Philippe
Negrier
d,
David
Aguilà
ef,
Josep Lluis
Tamarit
*ab,
Andrés Henao
Aristizabal
c,
Philippe
Negrier
d,
David
Aguilà
ef,
Josep Lluis
Tamarit
 ab and
Luis Carlos
Pardo
ab and
Luis Carlos
Pardo
 ab
ab
aGrup de Caracterizació de Materials, Departament de Física, EEBE, Universitat Politècnica de Catalunya, Eduard Maristany, 10-14, 08019 Barcelona, Catalonia, Spain. E-mail: jonathan.fernando.gebbia@upc.edu
bBarcelona Research Center in Multiscale Science and Engineering, Universitat Politècnica de Catalunya, Eduard Maristany, 10-14, 08019 Barcelona, Catalonia, Spain
cDribia Data Research Sociedad Limitada, Carrer Llacuna, 162, 08018, Barcelona, Spain
dLaboratoire Ondes et Matière dAquitaine, Université de Bordeaux, UMR 5798, F-33400 Talence, France
eInstitute of Nanoscience and Nanotechnology (IN2UB), Universitat de Barcelona, Barcelona, Spain
fDepartament de Química Inorgànica i Orgànica, Facultat de Química, Secció de Química Inorgànica, Universitat de Barcelona, Martí i Franquès, 1-11, 08028, Barcelona, Spain
First published on 6th November 2023
Abstract
Plastic phases are constituted by molecules whose centers of mass form a long range ordered crystalline lattice, but rotate in a more or less constrained way. Pentachloronitrobenzene (PCNB) is a quasi-planar hexa-substituted benzene formed by a benzene ring decorated with a –NO2 group and five chlorine atoms that displays below the melting point a layered structure of rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) planes in which the molecules can rotate around a six-fold-like axis. Dielectric spectroscopy [Romanini et al., The Journal of Physical Chemistry C, 2016, 120, 10614] of this highly anisotropic phase revealed a complex relaxation dynamics with two coupled primary α processes, initially ascribed to the in-plane and out-of-plane components of the molecular dipole. In this work, we perform a series of molecular dynamics simulations together with single crystal X-ray synchrotron diffraction experiments to investigate the puzzling dynamics of PCNB. We conclude that the molecule undergoes very fast movements due to the high flexibility of the –NO2 group, and two slower movements in which only the in-plane rotation of the whole ring is involved. These two movements are related to fast attempts to perform a 60° in-plane rotation, and a diffusive motion that involves the rotation of the molecule completely decorrelating the dipole orientation. We have also investigated whether a homogeneous or a heterogeneous scenario is better suited to describe the restricted orientational disorder of this anisotropic phase both from a structural and dynamical point of view.
) planes in which the molecules can rotate around a six-fold-like axis. Dielectric spectroscopy [Romanini et al., The Journal of Physical Chemistry C, 2016, 120, 10614] of this highly anisotropic phase revealed a complex relaxation dynamics with two coupled primary α processes, initially ascribed to the in-plane and out-of-plane components of the molecular dipole. In this work, we perform a series of molecular dynamics simulations together with single crystal X-ray synchrotron diffraction experiments to investigate the puzzling dynamics of PCNB. We conclude that the molecule undergoes very fast movements due to the high flexibility of the –NO2 group, and two slower movements in which only the in-plane rotation of the whole ring is involved. These two movements are related to fast attempts to perform a 60° in-plane rotation, and a diffusive motion that involves the rotation of the molecule completely decorrelating the dipole orientation. We have also investigated whether a homogeneous or a heterogeneous scenario is better suited to describe the restricted orientational disorder of this anisotropic phase both from a structural and dynamical point of view.
The dynamics of disordered materials in general, and amorphous solids in particular, is far from being understood. With the aim of simplifying the study of such materials we can assume that the removal of some degrees of freedom of a fully disordered state, such as the liquid state, in which both translational and orientational long-range disorder are present, would simplify the process of unraveling the main and intrinsic dynamical features. However this is not the case: all features of the dynamics of liquids can also be observed in phases where the translational disorder has been suppressed as in the so-called orientationally disordered crystals (ODICs) or plastic phases composed of globular shaped molecules.1 This phase, having the whole richness of dynamical features of the liquid state, displays microscopic movements which involve only rotations lacking the inherent translational diffusion of the fully disordered liquids.
The common overall quasi-isotropic rotations observed in ODICs can be impeded: spatial or dynamical constraints give rise to more restricted movements which concern only a subset of the degrees of freedom. For these systems, at least in a certain temperature range, thermal energy is not enough to allow free rotations. The molecules rather perform reorientational jumps between well-defined distinguishable orientations compatible with the symmetry operations of the site of the lattice in which they are located.2–8
This is the case of the quasi-planar molecules of pentachloronitrobenzene (hereinafter PCNB). This molecule, with chemical formula C6Cl5NO2, consists of a quite rigid benzene ring in which hydrogen atoms have been substituted by chlorine atoms, except for one site that is occupied by a nitro group (see Fig. 1 and a simplified scheme in the inset of Fig. 2).
PCNB exhibits a single solid phase from the melting temperature of 417 K down to the lowest temperature experimentally reached.9 The solid phase of PCNB displays a stacked rhombohedral structure (spatial group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) of molecular planes in which the molecules lie flat on each plane occupying the sites of a hexagonal lattice with occupational factors of 5/6 for chlorine atoms and 1/6 for the nitro group.10–12
) of molecular planes in which the molecules lie flat on each plane occupying the sites of a hexagonal lattice with occupational factors of 5/6 for chlorine atoms and 1/6 for the nitro group.10–12
Usually, when the liquid state is cooled without inducing crystallization, a conventional structural glass (SG) can be obtained, in which all degrees of freedom (translational and rotational) become frozen. Similarly, when cooling an ODIC, the freezing of only the orientational disorder of molecules takes place and an orientational glass (OG) appears. This transformation occurs if the transition into a more ordered crystalline phase is suppressed, as it occurs for PCNB. The glass transition temperature was determined to be Tg = 185 K by means of adiabatic calorimetry,7,13 which is confirmed later by DSC and thermally stimulated currents.14,15
Despite the fact that only the molecular orientations are completely disordered, while the periodicity of the network is preserved, the main properties of SGs (existence of thermal conductivity plateau, excess low-energy vibrational modes in the density of states and consequently in the specific heat capacity, acoustic attenuation, etc.) are shared with OGs.9,16–19
The dynamics of the highly anisotropic molecules of PCNB aroused particular interest because the restricted number of possible molecular orientations imposed by the symmetry operations of the lattice site strongly reduces the number of degrees of freedom when compared to the most typical OGs analysed so far.14,20
As for the dynamics, when the dielectric susceptibility is studied, SGs and OGs also share the most common features, as the slowing down of the collective dynamics gives rise to the transition to the glassy state, the well-known α (primary) relaxation process, and the less cooperative Johari–Goldstein (JG) (secondary) relaxation process. Early dielectric spectroscopy studies of PCNB revealed the existence of a collective molecular motion initially attributed to rotations around a 6-fold-like axis perpendicular to the stacking planes along the rhombohedral c axis. Even excess wing was also observed as a shoulder of the main α-relaxation process which was finally treated as a secondary β-like JG process.21
In order to unveil the JG character of the excess wing, complete broadband dielectric spectroscopy and structural characterization of the two relaxations as a function of temperature and pressure were carried out by some of the authors of this work.14 The main finding was that these two processes correspond to two distinct cooperative motions of the molecular dipole moment (called α and α′) and that both processes verify the so-called temperature–volume (TVγ) scaling with a different exponent for each one of the α and α′ relaxations. The two processes were ascribed to in-plane large-angle reorietational motions (α), which freeze at Tg = 193 K, and a faster out-of-plane (α′) contribution. This description is opposite to that of a previous work21 in which the two relaxations were explained in terms of the anisotropic intermolecular interaction.22–24
The existence of two collective α relaxations has also been found in systems displaying high anisotropy.25–28
In this work, we have performed a series of molecular dynamics simulations on the OD phase of PCNB accompanied by single crystal synchrotron X-ray diffraction experiments, in order to disclose the physical origin of the dynamics and to account for the local order consequences. This work is organized as follows. First, we describe the main results concerning the single crystal X-ray diffraction, in particular those concerning the atomic thermal displacement ellipsoids. Second, we analyse the dynamics of the OD phase through two vectors which enable us to distinguish between the dynamics of the rigid benzene ring and that of the molecular dipole itself. We then use a statistical method previously used by N. B. Caballero et al.29 to distinguish orientational jumps from the rattling movement to obtain characteristic residence times. We finally dissect the obtained results and compare it with the features concerning local molecular ordering and the single-crystal X-ray diffraction that leads to an explanation of the physical origin of the double primary relaxations.
1 Experiments and simulations
1.1 Diffraction experiments
Crystals of PCNB were obtained by recrystallizing the solid in MeOH. Data for the compound were collected on a colorless plate at the BL13-XALOC beamline30 of the ALBA synchrotron (λ = 0.72931 Å) at 100 and 200 K. The crystal was mounted with Paratone N grease on a MiTegen kapton loop and placed in the N2 stream of an Oxford Cryosystems Cryostream. The structures were solved by intrinsic phasing with SHELXT31 and refined by full-matrix least-squares on F2 with SHELXL.32 Two twin components were found in the crystal, which were assessed with TWIN and BASF commands. At 200 K, C1 and N1 atoms were refined using SIMU and DELU instructions. Several attempts were made in order to collect data for a non-twinned crystal. However, the compound crystallizes as thin stacked plates, precluding the selection and manipulation of a single crystal. CIF files were deposited at the Cambridge Crystallographic Data Centre as 2266449 and 2266450 at 100 and 200 K, respectively.†1.2 Molecular dynamics
MD simulations were performed with the GROMACS code, version 2021 using the CHARMM27 force field.33 The leap-frog algorithm was used as an integrator with a 2 fs time step. Temperature control was realized via velocity rescaling34 using a time constant of 0.5 ps. The pressure was set to 1 bar with a compressibility of 4.5 × 10−5 bar−1 and kept constant via a new stochastic-cell rescaling method35 (available in Gromacs version 2021 and higher) with a time constant of 2 ps. The Verlet list scheme36 was employed with a neighbor list updated every 100 steps. The calculation of electrostatic interactions was done using the particle mesh Ewald method37 with a cut-off distance of 1.0 nm for the real-space contribution. The aforementioned CIF file 2266450† (200 K) of the diffraction experiment of this study was used to prepare the initial configuration. In order to avoid directional anisotropy in the system, the orientations of all molecules were randomized by means of an in-house developed open-software, ANGULA.38 Subsequently, a simulation was performed under NTP conditions until potential energy stabilized. Moreover, to ensure the randomness of the initially randomized system, additional simulation was carried out for a duration of 20 ns, reaching the decorrelation time.The production run lasted for 0.5 μs recording frames every 2 ps. The time scale of the simulation was limited by the long time required to perform the simulation up to μs. We needed in this study, however, a time scale large enough to obtain the whole relaxation of the molecular dipole. We have performed thus a first set of simulations in order to guess the temperature at which we would obtain the full decay of the autocorrelation curve. As can be seen in Fig. 2 the temperature chosen (T = 500 K) does follow this requirement.
2. Results and discussion
2.1 Diffraction of PCNB
X-Ray and neutron diffraction experiments have previously shown that the six different orientations of the molecule in each crystallographic site have equal probability, thus providing a six-fold site symmetry.10,11 Such an orientational disorder is independent of the temperature, i.e., 1/6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5/6 NO2
5/6 NO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
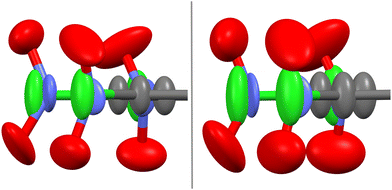
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl occupation factors at each substitution site remain constant, whereas the atomic displacements due to thermal librations strongly depend on temperature (see Fig. 1 and Table 1). Our single crystal measurements (see Table S1, ESI†) at 100 and 200 K confirm those results. The anisotropic displacement parameters accounted for by the components of the thermal ellipsoid (Table 1) obtained at 100 and 200 K from the structure refinement, evidence a large amplitude vibration of C and Cl atoms along the normal of the molecular benzene ring (i.e., along the c crystallographic axis). This would entail the hypothesis that thermal displacement of the molecular dipole should appear along the [001] hexagonal direction, as argued in the previous work of Romanini et al.14
Cl occupation factors at each substitution site remain constant, whereas the atomic displacements due to thermal librations strongly depend on temperature (see Fig. 1 and Table 1). Our single crystal measurements (see Table S1, ESI†) at 100 and 200 K confirm those results. The anisotropic displacement parameters accounted for by the components of the thermal ellipsoid (Table 1) obtained at 100 and 200 K from the structure refinement, evidence a large amplitude vibration of C and Cl atoms along the normal of the molecular benzene ring (i.e., along the c crystallographic axis). This would entail the hypothesis that thermal displacement of the molecular dipole should appear along the [001] hexagonal direction, as argued in the previous work of Romanini et al.14
| 100 K | ||||||
|---|---|---|---|---|---|---|
| Atom | U 11 | U 22 | U 33 | U 23 | U 13 | U 12 |
| C1 | 19.8(7) | 22.3(7) | 67.4(8) | −0.1(4) | 0.3(4) | 9.2(5) |
| Cl1 | 18.5(6) | 25.0(5) | 116.9(8) | −0.3(2) | 1.0(2) | 8.8(3) |
| N1 | 12(6) | 39(8) | 63(5) | 8(4) | 1(3) | 12(5) |
| O1 | 53(5) | 75(6) | 54(3) | 6(3) | 11(3) | 9(4) |
| O2 | 47(5) | 98(8) | 80(5) | 30(5) | −35(4) | −3(5) |
| 200 K | ||||||
|---|---|---|---|---|---|---|
| Atom | U 11 | U 22 | U 33 | U 23 | U 13 | U 12 |
| C1 | 26.8(7) | 29.9(8) | 101.4(13) | 0.4(7) | −0.4(6) | 12.3(6) |
| Cl1 | 25.5(5) | 36.7(5) | 169.2(13) | 0.2(4) | 1.7(4) | 11.7(3) |
| N1 | 14(3) | 58(6) | 92(5) | 2(5) | −2(3) | 22(3) |
| O1 | 67(7) | 109(12) | 89(6) | 0(5) | 5(5) | 8(6) |
| O2 | 82(9) | 115(11) | 126(9) | 18(7) | −59(8) | 13(8) |
A close look at the atomic displacements reveals that the Uii values for the two oxygen atoms are quite similar and that at least two Uij (i ≠ j) values are one order of magnitude higher than the respective values for the rest of the atoms. It thus means that they display quasi-isotropic thermal displacements. As for the nitrogen atom, the Uii values are overall the smallest values, with the atomic vibration along the c hexagonal axis being the largest. We thus conclude that the nitrogen atom acts in some way as a pivot center for the nearly isotropic vibration of the adjacent oxygens.
2.2 Dynamics of PCNB
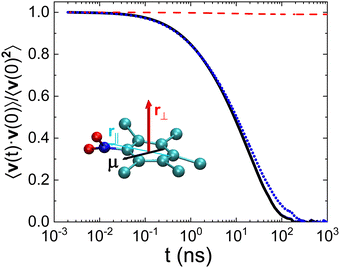
The dynamics of PCNB can be studied in depth by separating movements of different parts of the molecule. Concerning the ring we can define two vectors, one parallel to the ring (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖) shown as a blue vector in Fig. 2 and one perpendicular to the ring (
‖) shown as a blue vector in Fig. 2 and one perpendicular to the ring (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥) shown as a red vector in the same figure. The parallel vector has been chosen to point to the nitro group, being its origin in the carbon atom at the other extreme of the benzene ring. The vector
⊥) shown as a red vector in the same figure. The parallel vector has been chosen to point to the nitro group, being its origin in the carbon atom at the other extreme of the benzene ring. The vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥ has been chosen as the vectorial product of the vector
⊥ has been chosen as the vectorial product of the vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ and a vector pointing from the center of the molecular ring to one of the carbon atoms.
‖ and a vector pointing from the center of the molecular ring to one of the carbon atoms.
In order to compare our simulations with the results of dielectric spectroscopy, we have also plotted in Fig. 2 the dipole of the molecule ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) . The dynamics of this last vector is indeed the result of the combination of the molecular movements of the ring as a whole and the intra-molecular movements of the nitro group. This fact will be of utter importance throughout the analysis of both the dynamics and structure of the OD phase of PCNB.
. The dynamics of this last vector is indeed the result of the combination of the molecular movements of the ring as a whole and the intra-molecular movements of the nitro group. This fact will be of utter importance throughout the analysis of both the dynamics and structure of the OD phase of PCNB.
In Fig. 2 we show the rescaled autocorrelation of the three aforementioned vectors. We can extract two conclusions from this figure:
• The decay of the vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥ (red) is negligible. This fact proves that molecular tumbling is minimal. Thus, regardless of the temperature-inherent atomic displacements (vibrations) along the perpendicular direction of the ring (c-axis), only in-plane rotations appear.
⊥ (red) is negligible. This fact proves that molecular tumbling is minimal. Thus, regardless of the temperature-inherent atomic displacements (vibrations) along the perpendicular direction of the ring (c-axis), only in-plane rotations appear.
• When comparing the (rescaled) results of ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and the vector
and the vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ we observe that both autocorrelation functions are very similar. The dynamics observed by dielectric spectroscopy is thus dictated by the rotation of the ring as a whole, and not by an out-of-plane component of the dipole as suggested in the work of Romanini et al.14 In order to simplify the notation, and given the fact that vector
‖ we observe that both autocorrelation functions are very similar. The dynamics observed by dielectric spectroscopy is thus dictated by the rotation of the ring as a whole, and not by an out-of-plane component of the dipole as suggested in the work of Romanini et al.14 In order to simplify the notation, and given the fact that vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥ plays no role in the dynamics of PCNB, we will assign the name “ring vector” to that parallel to the ring
⊥ plays no role in the dynamics of PCNB, we will assign the name “ring vector” to that parallel to the ring ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ shown in Fig. 2 hereafter.
‖ shown in Fig. 2 hereafter.
Once stated that in-plane correlations govern the dynamics of PCNB in the OD phase, and thus dipole dynamics, we will investigate whether their autocorrelation functions can be described by a single component, or by two of them. In order to decide which model better describes our results, we use the following equation to perform the fittings:
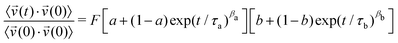 | (1) |
![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) in the equation stands, thus, for any of the three possibilities, i.e.
in the equation stands, thus, for any of the three possibilities, i.e. ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) =
= ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖,
‖, ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) =
= ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥ or
⊥ or ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) =
= ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) . In eqn (1), τi (i = a, b) is the correlation time, a and b are the long-time correlation asymptotes, βa and βb are the stretching exponents and F is an overall rescaling factor. The fitted function is a multiplicative combination of two movements. We assume here a homogeneous scenario where each molecule performs two movements, as opposed to an additive ansatz that considers the existence of patches with molecules exhibiting different dynamics (heterogeneous scenario). The rationale behind choosing the homogeneous scenario will become evident throughout this work (vide infra).
. In eqn (1), τi (i = a, b) is the correlation time, a and b are the long-time correlation asymptotes, βa and βb are the stretching exponents and F is an overall rescaling factor. The fitted function is a multiplicative combination of two movements. We assume here a homogeneous scenario where each molecule performs two movements, as opposed to an additive ansatz that considers the existence of patches with molecules exhibiting different dynamics (heterogeneous scenario). The rationale behind choosing the homogeneous scenario will become evident throughout this work (vide infra).
We want to compare two models, with one having a single process (setting a = 1), and the second one setting a, βa, and τa as fitting parameters. Model selection has been performed by calculating the reduced χ2 for both models, with one among the two processes clearly favoured as seen in Table 2.
| One process model | χ red 2 = 100.73 |
| Two processes model | χ red 2 = 7.2 |
We have performed the fittings for both the autocorrelation functions of the dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and of the ring vector
and of the ring vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖. The results of the fittings parameters can be found in Table 3, and the comparison with the obtained data is shown in Fig. 3.
‖. The results of the fittings parameters can be found in Table 3, and the comparison with the obtained data is shown in Fig. 3.
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ and dipole
‖ and dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ) and from dielectric spectroscopy.14 In the second case, the time window of the experiment does not allow us to access the nanosecond region and, therefore, the values are an extrapolation (see the text for details)
) and from dielectric spectroscopy.14 In the second case, the time window of the experiment does not allow us to access the nanosecond region and, therefore, the values are an extrapolation (see the text for details)
| Vector | β fast | τ fast (ns) | β slow | τ slow (ns) |
|---|---|---|---|---|
Dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |
1 | 1.6 | 0.7 | 19 |
Parallel ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ ‖ |
0.67 | 6.6 | 0.65 | 28.3 |
| Poisson | 3 | 33 | ||
| Dielectrics (exp.) | 1 | 4 | 0.72 | 6 |
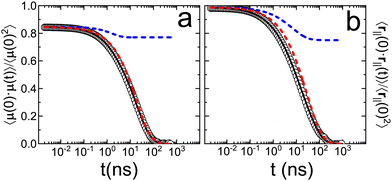 | ||
Fig. 3 Fits of auto-correlation curves associated with (panel a) the molecular dipole moment (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i) and (panel b) the ring vector ( i) and (panel b) the ring vector (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖) depicted in Fig. 2. Empty circles represent the auto-correlation results of MD simulations, solid black line shows the result of total fit, dashed blue and red lines show the results of the fast confined motion and the slow free motion, respectively. ‖) depicted in Fig. 2. Empty circles represent the auto-correlation results of MD simulations, solid black line shows the result of total fit, dashed blue and red lines show the results of the fast confined motion and the slow free motion, respectively. | ||
Results evidence that in the case of the ring vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖ the short-time value of the autocorrelation function is 1, while in the case of the dipole
‖ the short-time value of the autocorrelation function is 1, while in the case of the dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is 0.8. Therefore, there is a fast movement occurring in a time scale of pico-seconds in the case of the dipole correlation function. It cannot be related to the movement of the molecule as a whole, described by the ring vector
is 0.8. Therefore, there is a fast movement occurring in a time scale of pico-seconds in the case of the dipole correlation function. It cannot be related to the movement of the molecule as a whole, described by the ring vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖, otherwise, the autocorrelation of this vector would also start at circa 0.8. The only option is thus that the reason for this decay at short times is the fast movement of the nitro group carrying the charge of the dipolar moment of PCNB. We conclude then that, contrary to what happens to the rigid benzene ring, the –NO2 group should be very flexible. This fact agrees with the diffraction results. We will, however, come back again to this point in subsequent sections of this work.
‖, otherwise, the autocorrelation of this vector would also start at circa 0.8. The only option is thus that the reason for this decay at short times is the fast movement of the nitro group carrying the charge of the dipolar moment of PCNB. We conclude then that, contrary to what happens to the rigid benzene ring, the –NO2 group should be very flexible. This fact agrees with the diffraction results. We will, however, come back again to this point in subsequent sections of this work.
From the fitting results, we have concluded that for both the dipole and the ring vector, two processes exist: fast and slow. The fast process is linked to confined motion (a ≠ 0), while the slow process completely decorrelates the vectors over long times. This is unequivocally associated with the rotation of the ring as a whole. Table 3 demonstrates the similarity of parameters for this slow process in both the dipole and the ring vector. Consequently, this implies that the main factor contributing to the loss of dipole correlation is the in-plane rotation of the molecule as a whole.
For the fast movement, although there is agreement in the time scale for ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and
and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖, there is a slight difference that can be related to the intrinsic flexibility of the nitro group, which strongly contributes to the molecular dipole of the PCNB.
‖, there is a slight difference that can be related to the intrinsic flexibility of the nitro group, which strongly contributes to the molecular dipole of the PCNB.
Finally, the agreement between the extrapolation of the experimental data and any of the autocorrelation functions is hard to assess: the extrapolation must be done in a temperature range as wide as 100 K, involving the change of two decades in the time scale. This extrapolation leads to two processes that are very close (almost indistinguishable). The correlation time of the fast process found in the simulation (1.6 ns for the dipole vector) is in good agreement with the values reported from dielectric spectroscopy (4 ns).14 However this agreement is not so accurate for the slow process. This discrepancy may reflect the mono/poly-crystalline character of the system: in the experiments for PCNB, powder samples were used, whereas the simulated system corresponds to an infinite monocrystalline structure due to the periodic boundary conditions. In the first case, molecular rotations may be easier to produce since nanocrystalline domains confer the system additional degrees of freedom.
In order to go deeper in the study of the OD phase we have first studied the rotational movement of PCNB molecules with respect to the laboratory frame. As can be seen in Fig. 1 as well as in the snapshot of Fig. 4, PCNB is arranged in sheets and, as we have already seen, there is no “flip” movement of PCNB that would involve a change in the direction of a vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ⊥, regardless of the fast thermal atomic displacements. Therefore the only movement that will be studied is the rotation of the ring around the z-axis of the lab frame.
⊥, regardless of the fast thermal atomic displacements. Therefore the only movement that will be studied is the rotation of the ring around the z-axis of the lab frame.
 | ||
| Fig. 4 Snapshot of a configuration of the OD phase of PCNB together with the laboratory reference system used to calculate the rotation of PCNB of Fig. 5. Red, green and blue vectors defining the laboratory reference frame are axis x, y and z (c-axis), respectively. | ||
In Fig. 5 we show the rotation angle, defined as the angle between the x-axis and the vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖, as a function of time. Three different types of movements are observed:
‖, as a function of time. Three different types of movements are observed:
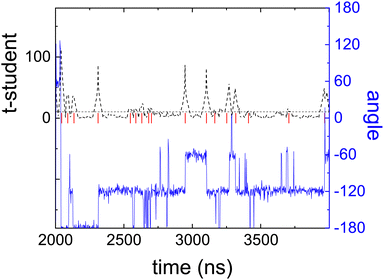 | ||
| Fig. 5 Angle of the ring vector of a molecule with respect to the laboratory frame (αring) as a function of time (blue line) and the running t-student function (dashed black line) used as a statistical estimator for the detection of rotational jumps.29 Red vertical lines show the jumps detected. | ||
• Changes between equilibrium states in the orientation of the molecules from one equilibrium angle to the next.
• Short time attempts to go from one equilibrium position to another one seen as spikes in the figure, that occur between changes between equilibrium states in orientation.
• A rattling movement of small amplitude (less than 5°) of the molecule around its equilibrium orientation.
For the purpose of detecting rotational jumps we have used the statistical method developed by Caballero et al.29 This method calculates a running average and detects, by calculating a t-student function, when a statistically relevant jump in the angle occurs (for further details see ref. 29). Fig. 5 clearly shows the success of detecting the 60° orientational jumps by this method.
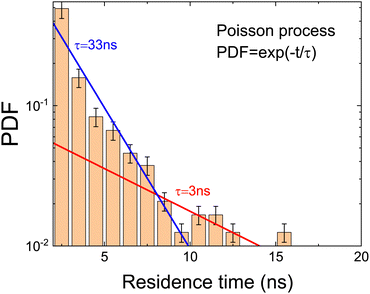
In order to analyze the jumps, we have calculated the probability distribution function (PDF) of the residence time between jumps.29 The obtained distribution (Fig. 6) has been fitted using two different models with one and two processes. In order to know which model better describes the data, the reduced χ2, derived from the fitting, has been calculated. The simplest model corresponds to a unique Poisson distribution (PDF ∝ e−t/τ) which can be seen as a straight line in Fig. 6. This model has an associated reduced chi-square χ1p,red2 = 1.83. The second model including two processes has been built using a composition of two independent Poisson distributions: one for the range 0 < t < 5 (ns) and another one in the range 5 < t < 20 (ns). In this case, the corresponding χ2p,red2 takes a value of 1.02. The model selection clearly supports the necessity of using two Poisson processes to describe the data. This is in agreement with the results of the autocorrelation function (see Table 2). We have then calculated, from the values of the slopes, the values of the residence time (see Table 3). The results are compatible with the relaxation times obtained for the dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and the ring vector
and the ring vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖.
‖.
Taking into account Fig. 5, the fast process can be associated with the time between attempts of performing an orientational jump, and the slow process is thus related to the elapsed time between changes in the “equilibrium” positions. It must be pointed out, though, that given the results shown in Fig. 5, there is n sharp distinction between the two movements. The smooth transition between the two dynamics can easily be explained by the fact that “an attempt” to perform a rotational jump, can also be viewed as a “short stay” in an “equilibrium” orientation. What is indisputable is that the spikes seen in Fig. 4, no matter whether regarded as “attempts” or as “short stays”, occur more often than jumps between equilibrium positions and can thus be linked to the fast movements characterized by τslow (see Table 3).
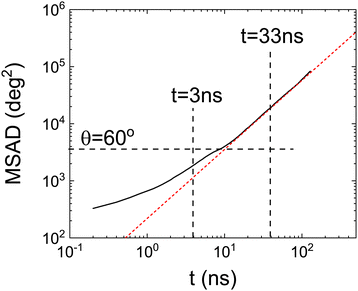
To further investigate whether there is a (smooth) change between two kinds of dynamics we have also calculated the mean squared angle displacement (MSAD) as a function of time. It is important to note that, in order to calculate the MSAD, the angle cannot be wrapped in the range 0° < θ < 360°. This function is therefore always increasing, i.e. no periodic boundary conditions are applied to the time-dependent angular trajectories. This must be done in order to investigate if long-time dynamics can be well described by a diffusive mechanism.
It must be noted that the calculation of this quantity is completely independent of the previously calculated residence times: it does not involve the use of any statistical tool and is a straightforward calculation of the molecular rotation. It serves, thus, as a consistency test of the obtained results.
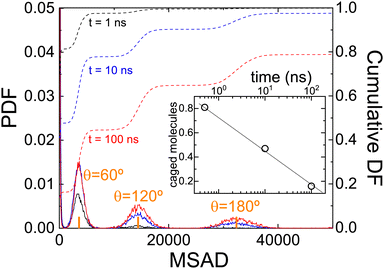
Fig. 7 clearly shows a (smooth) change in the angular dynamics of PCNB from a subdiffusive movement to an angular diffusive movement, the change between the two regimes is observed at about t ≈ 10 ns. In fact, the time exponent of the long-time regime of MSAD is 1.2 ± 0.1, which is consistent with a diffusive process. We have marked in the figure the times obtained from the Poisson distribution of residence times in abscissa, and of an angle θ = 60° in the ordinate axis. As can be seen in the figure the subdiffusive movement takes place only during the first jump (θ < 60°), the rotations involved are more than one jump diffusive in nature, thus allowing the full decorrelation of the molecular orientation. This result completely agrees with the previous analysis based on the study of the distribution of residence times.
MSAD is, indeed, an average of the unwrapped squared rotation angle of PCNB. For this reason, we have also calculated the PDF of angle θ at some selected times that is hidden behind the averaged single-valued MSAD as shown in Fig. 8. As expected, for short times all molecules are rattling around the equilibrium position, however, even at the shortest time scale, a very small fraction of molecules have already performed a 60° jump. As time evolves, the number of molecules exploring greater angles increases: This is clearly seen by the PDF of angles as a function of time: peaks appear in the angle distribution at increasing angles of 60°, 120°, 180°, etc. We show also in the inset the proportion of molecules with an angle θ < 60°, i.e. caged molecules as a function of time. For time scales of ns, 80% of molecules are caged, i.e. with an angle αring < 60°. After two decades of time (hundreds of nano-seconds) the number of caged molecules has decreased to 20%.
These results agree, and round off our previous results. Attempts to jump over equilibrium positions are molecules that “come back” to the original position, and therefore they can be seen as caged molecules: their MSAD is less than that related to θ = 60°. The dynamics of these molecules are seen as spikes in Fig. 5. Moreover, from the calculated MSAD, we have obtained that this movement is subdiffusive. For times a decade longer there is a smooth transition to a movement, diffusive in nature, that completely decorrelates PCNB orientation with respect to the initial one.
A question that still needs to be answered is which scenario better describes the molecular dynamics of PCNB in the OD phase, a homogeneous or a heterogeneous one? In more specific terms, are there two patches of molecules, some moving fast and others moving slowly?
We plot in Fig. 8 the residence time of a molecule (interarrival time, τi) as a function of the next residence time (τi+1). As can be seen in the figure there is neither a correlation between these two magnitudes, nor two groups of fast and slow moving molecules. (The fact that there is a concentration of points at short times is due to the (trivial) Poisson distribution of residence times). We conclude that concerning the dynamics, the homogeneous scenario is clearly favoured. However, this does not exclude short-time congregation of molecules with a correlation in their orientation, i.r., a spatially heterogeneous scenario. For this reason we will study in the next section the spatial orientational correlation of PCNB molecules.
2.3 Local orientational ordering of PCNB
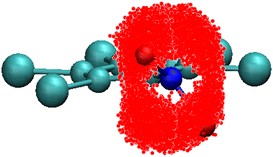
The first decay in the dipole autocorrelation function in the pico-second time-scale seen in Fig. 3 has been assigned to the high mobility of the –NO2 group in a previous section. In order to test this assessment we have calculated the positions of oxygen atoms with respect to the ring structure. As can be seen in Fig. 10 oxygen atoms are distributed in a very large portion of space. The elongated-disk shape of the cloud formed by possible positions of oxygen atoms is a convolution of the libration movement of the nitrogen atom in a plane perpendicular to that of the ring (not shown for clarity) and the rotation movement of the oxygen atoms. The high flexibility of the –NO2 group is thus clear and compatible with the results of the atomic displacements determined through X-ray single crystal diffraction (see Table 1). This result supports the previous explanation of the initial decay of the dipole correlation (see Fig. 2) which was assigned to the fast movement of the flexible –NO2 group.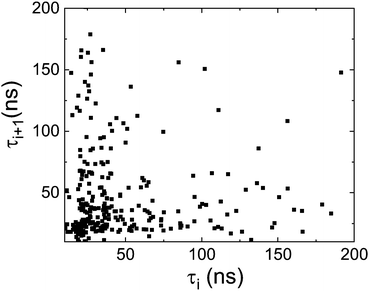 | ||
| Fig. 9 Residence time between two successive jumps i+1 (τi+1) as a function of the previous interarrival time i (τi) as a measure of the correlation of consecutive reorientational processes. | ||
Finally, we have studied whether there is a correlation between the rotational dynamics and the structure, that is, if there is any angular correlation between neighboring molecules. We have defined two angles that are aimed to describe the relative orientation of two neighboring molecules:
• αring angle is that formed between two ring vectors ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖.
‖.
• θdip angle is that formed between the dipoles of two molecules.
In Fig. 11 panel a, we show the PDF (in the z axis) of the cosines of the angle αring between two molecules as a function of their distance. The cosines must be used to take into account the differences in solid angles as a function of angle αring, which is minimum at the poles (strictly zero indeed) and maximum at the equator.
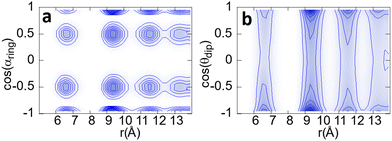 | ||
Fig. 11 Relative orientation of two neighbouring molecules as a function of the distance. Panel (a) shows this correlation taking into account the ring vector (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ‖), and panel (b) taking into account the dipole ( ‖), and panel (b) taking into account the dipole (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ) (see vectors in Fig. 2). ) (see vectors in Fig. 2). | ||
As previously determined, PCNB is jumping between six equivalent positions with respect to the laboratory frame. However, this does not imply that the same result will be obtained when the reference frame is set in a (moving) molecule. As an example, two molecules avoiding an antiparallel orientation of the –NO2 groups would result in the missing of one of the six possible angles between molecules when regarded from the molecular moving frame. With regards to Fig. 11 this is not the case, the six possible relative orientations can be seen, no matter the distance between molecules. No ring correlation between molecules is thus detected and, therefore, when regarding the molecule as a whole, there are no patches of fast and slow-moving molecules.
It must be pointed out that given the definition of the angle between molecules, the six orientations are seen as four spots in the plot because the scalar product is constrained between 1 and −1 (angles of 60° and −60° between two vectors result in the same scalar product).
We have performed the same procedure with the angle between dipoles θdip expecting to see the same result as for the ring orientation, i.e. four spots in the angle–distance PDF plot. However, as can be seen in Fig. 11b there are two clear maxima for dipole orientations at cos(θdip) = ±1. This result is in clear contradiction to that of the ring vector. The only explanation for this fact is that the dipoles of the molecule, mainly governed by the nitro group, tend to be parallel or anti-parallel thanks to the high flexibility of the –NO2 group. To understand this result is crucial to point out that the dipole is not coplanar with the ring (see Fig. 2): it has a component perpendicular to it. Therefore, the observed parallel-antiparallel conformation is well explained by the combination of the libration of the nitrogen atom, and the rotation of the two oxygen atoms.
Finally, as shown in Fig. 11, the dipole has a continuum of relative orientations, contrary to what happens with the ring orientations. This, again, has to be understood taking into account that dipole direction is a convolution of the ring orientation and the movement of the high flexible –NO2 group that tends to orient the dipole parallel or antiparallel with the neighbouring molecules.
We have concluded (from the structural analysis) that there is a correlation between dipoles. This fact, however, seems not to agree with the previous result shown in Fig. 9, i.e. there are no regions with fast and slow-moving molecules. Orientational correlation between molecules could cause a molecule to rotate faster or slower depending on the relative orientation of its neighbours. Therefore, it is imperative to assess whether this correlation exists only between particular pairs of molecules or the correlation creates regions where all molecules have the dipole parallel or antiparallel. In other words, whether the correlation is homogeneous throughout the structure or heterogeneous.
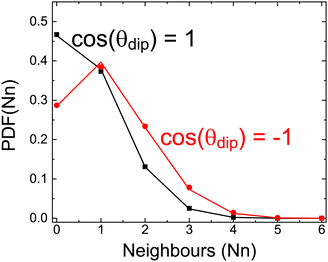
For this reason, we have calculated how many of the first six neighboring molecules surrounding a central one have a given relative orientation. We have calculated this for all possible orientations dividing cos(θdip) in regions of Δ[cos(θdip)] = 0.2 (symbols in Fig. 12). We show in the figure only two cases as follows: where molecules are parallel 1 < cos(θdip) < 0.8 and when the orientation is antiparallel −0.8 < cos(θdip) < −1. Similar results (not shown) are obtained for all orientations. We have also calculated the results coming from a completely random distribution of possible orientations (lines in the same figure).
There are no differences between our simulation and a random distribution as seen in Fig. 12. We thus conclude that although there is a dipole correlation, there are no patches of molecules with a given relative orientation, and thus the homogeneous scenario is undoubtedly favored also from the point of view of the local structural ordering.
3. Conclusions
The goal of our work was to find the microscopic mechanism behind the dynamics of PCNB molecules in their plastic phase, as obtained by dielectric spectroscopy.14We have performed this study by the concurrent use of single crystal X-ray synchrotron diffraction and molecular dynamics (MD) simulation.
Concerning the structure, our X-ray single crystal diffraction experiments of PCNB confirm the existence of statistical disorder previously reported10,11 for this plastic phase. Furthermore, we have presented new data for the anisotropic displacement parameters that agree with the high thermal flexibility of the molecules shown in the MD simulations.
Concerning the dynamics, two relaxations were obtained in the aforementioned dielectric spectroscopy experiments. These were tentatively associated with in-plane and out-of-plane movements of the dipole.14 Our results indicate that the interpretation of the experimental results is not accurate.
We identify the two relaxations to a fast attempt of the molecule to jump between “equilibrium” orientations, which is subdiffusive in nature, and a slower process associated with the jump between “equilibrium” positions that completely decorrelates the molecular orientation and that is diffusive in nature. Quasi Elastic Neutron experiments are planned to be performed in order to corroborate our MD results.
Moreover, the high thermal flexibility of the –NO2 group obtained both by simulation and experiment explains the initial correlation decay of the dipole correlation obtained by MD simulations.
We have also investigated if the two relaxations are better described by a homogeneous or by a heterogeneous scenario, both from the point of view of molecular movements and the local structure. We clearly obtain that the homogeneous scenario is better for describing the plastic phase of PCNB: there are neither regions of fast (slow) moving molecules nor patches of molecules with a given orientation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the MINECO through the PID2020-112975GB-I00 grant and the Catalan government for the 2021SGR-00343 grant. This research used resources of the ALBA synchrotron. The corresponding crystallographic measurements were performed with the collaboration of ALBA staff at the BL13-XALOC beamline.Notes and references
- J. N. Sherwood, The Plastically Crystalline State: Orientationally-Disordered Crystals, Wiley, New York, 1979 Search PubMed.
- M. Romanini, P. Negrier, J. L. Tamarit, S. Capaccioli, M. Barrio, L. C. Pardo and D. Mondieig, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134201 CrossRef.
- M. Zuriaga, L. C. Pardo, P. Lunkenheimer, J. L. Tamarit, N. Veglio, M. Barrio, F. J. Bermejo and A. Loidl, Phys. Rev. Lett., 2009, 103, 075701 CrossRef CAS PubMed.
- M. Zuriaga, S. Perez, L. Pardo and J. L. Tamarit, J. Chem. Phys., 2012, 137, 054506 CrossRef CAS PubMed.
- P. Negrier, M. Barrio, J. L. Tamarit, L. C. Pardo and D. Mondieig, Cryst. Growth Des., 2012, 12, 1513–1519 CrossRef CAS.
- S. C. Pérez, M. Zuriaga, P. Serra, A. Wolfenson, P. Negrier and J. L. Tamarit, J. Chem. Phys., 2015, 143, 134502 CrossRef PubMed.
- P. Negrier, M. Barrio, J. L. Tamarit, D. Mondieig, M. J. Zuriaga and S. C. Perez, Cryst. Growth Des., 2013, 13, 2143–2148 CrossRef CAS.
- Y. Miyazaki, M. Nakano, A. Krivchikov, O. Koroyuk, J. F. Gebbia, C. Cazorla and J. L. Tamarit, J. Phys. Chem. Lett., 2021, 12, 2112–2117 CrossRef CAS PubMed.
- J. F. Gebbia, M. Ramos, D. Szewczyk, A. Jezowski, A. Krivchikov, Y. V. Horbatenko, T. Guidi, F. J. Bermejo and J. L. Tamarit, Phys. Rev. Lett., 2017, 119, 215506 CrossRef CAS PubMed.
- A. Aihara, C. Kitazawa and A. Nohara, Bull. Chem. Soc. Jpn., 1970, 43, 3750–3754 CrossRef CAS.
- L. H. Thomas, T. R. Welberry, D. J. Goossens, A. P. Heerdegen, M. J. Gutmann, S. J. Teat, P. L. Lee, C. C. Wilson and J. M. Cole, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 663–673 CrossRef CAS PubMed.
- J. M. Cole, H.-B. Bürgi and G. J. McIntyre, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 224202 CrossRef.
- Z.-C. Tan, Y. Nakazawa, K. Saito and M. Sorai, Bull. Chem. Soc. Jpn., 2001, 74, 1221–1224 CrossRef CAS.
- M. Romanini, M. Barrio, S. Capaccioli, R. Macovez, M. D. Ruiz-Martin and J. L. Tamarit, J. Phys. Chem. C, 2016, 120, 10614–10621 CrossRef CAS.
- N. T. Correia, J. J. M. Ramos and H. P. Diogo, J. Phys. Chem. Solids, 2002, 63, 1717–1722 CrossRef CAS.
- D. Szewczyk, A. Jezowski, G. Vdovichenko, A. Krivchikov, F. Bermejo, J. L. Tamarit, L. Pardo and J. Taylor, J. Phys. Chem. B, 2015, 119, 8468–8474 CrossRef CAS PubMed.
- A. Vispa, M. Romanini, M. A. Ramos, L. C. Pardo, F. J. Bermejo, M. Hassaine, A. I. Krivchikov, J. W. Taylor and J. L. Tamarit, Phys. Rev. Lett., 2017, 118, 105701 CrossRef CAS PubMed.
- D. Szewczyk, J. F. Gebbia, A. Jeżowski, A. I. Krivchikov, T. Guidi, C. Cazorla and J.-L. Tamarit, Sci. Rep., 2021, 11, 18640 CrossRef CAS PubMed.
- A. I. Krivchikov, A. Jeżowski, D. Szewczyk, O. A. Korolyuk, O. O. Romantsova, L. M. Buravtseva, C. Cazorla and J. L. Tamarit, J. Phys. Chem. Lett., 2022, 13, 5061–5067 CrossRef CAS PubMed.
- R. Brand, P. Lunkenheimer and A. Loidl, J. Chem. Phys., 2002, 116, 10386–10401 CrossRef CAS.
- A. K. Singh and S. Murthy, Thermochim. Acta, 2015, 604, 33–44 CrossRef CAS.
- J. C. Dyre, J. Phys. Chem. B, 2014, 118, 10007–10024 CrossRef CAS PubMed.
- D. E. Albrechtsen, A. E. Olsen, U. R. Pedersen, T. B. Schrøder and J. C. Dyre, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094106 CrossRef CAS.
- C. Roland, Soft Matter, 2008, 4, 2316–2322 RSC.
- M. Elmahdy, G. Floudas, M. Mondeshki, H. W. Spiess, X. Dou and K. Müllen, Phys. Rev. Lett., 2008, 100, 107801 CrossRef CAS PubMed.
- M. Marik, A. Mukherjee, D. Jana, A. Yoshizawa and B. Chaudhuri, Phys. Rev. E, 2013, 88, 012502 CrossRef PubMed.
- A. Yildirim, C. Krause, R. Zorn, W. Lohstroh, G. J. Schneider, M. Zamponi, O. Holderer, B. Frick and A. Schönhals, Soft Matter, 2020, 16, 2005–2016 RSC.
- C. Krause, R. Zorn, F. Emmerling, J. Falkenhagen, B. Frick, P. Huber and A. Schönhals, Phys. Chem. Chem. Phys., 2014, 16, 7324–7333 RSC.
- N. B. Caballero, M. Zuriaga, M. Carignano and P. Serra, J. Phys. Chem. B, 2016, 120, 860–865 CrossRef CAS PubMed.
- J. Juanhuix, F. Gil-Ortiz, G. Cun, C. Colldelram, J. Nicolás, J. Lidón, E. Boter, C. Ruget, S. Ferrer and J. Benach, J. Synchrotron Radiat., 2014, 21, 679–689 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct, Chem., 2015, 71, 3–8 Search PubMed.
- V. Zoete, M. A. Cuendet, A. Grosdidier and O. Michielin, J. Comput. Chem., 2011, 32, 2359–2368 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107 CrossRef CAS PubMed.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- L. C. Pardo, ANGULA, 2010, https://gcm.upc.edu/en/members/luis-carlos/angula/ANGULA.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2266449 and 2266450. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cp02633g |
| This journal is © the Owner Societies 2023 |