Competition between the H-abstraction and the X-abstraction pathways in the HX (X = Br, I) + C₂H₅ reactions

Abstract

The recently-developed high-level full-dimensional spin–orbit-corrected potential energy surfaces based on ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for the Br and I atoms) energy points for the reactions of HX (X = Br, I) with C₂H₅ are improved by adding three to four thousand new geometries with higher energies at the same ab initio level to cover a higher-energy range. Quasi-classical trajectory simulations in the 30–80 kcal mol⁻¹ collision energy range on the new surfaces are performed and show that as collision energy increases, the reaction probability of the submerged-barrier H-abstraction reaction pathway decreases a bit but the reactivity of the X-abstraction reaction, which has an apparent barrier, increases significantly, which leads to the co-domination of the two reaction pathways at high collision energies. The excitation in HX vibrational mode helps both reaction pathways, but more for X-abstraction. The mode-specific excitations in C₂H₅ inhibit the H-abstraction, especially for CH₂ wagging mode, but almost no effect is found for X-abstraction. The deuterium effect is similar for both pathways. The sudden vector projection model can only predict the HX-stretching vibrational enhancements in X-abstraction. Forward/backward scattering is favored for H/X-abstraction, indicating the dominance of the direct stripping/rebound mechanism. The decrease of reactivity for the H-abstraction reaction pathway partly comes from the fact that the H-abstraction is much pickier about the initial attack angle. The reactivity of both reaction pathways increases when side-on CH₃CH₂ attack happens. The major part of the initial translational energy is preserved as translational energy in the products in H-abstraction, while for X-abstraction a large amount of it is transferred into the internal energy of C₂H₅X.

---

1. Introduction

Reactions of hydrogen halide with alkyl radical^1–8 and the backward process (halogen with alkane)^9–16 have become benchmark systems to study the dynamics and mechanisms of polyatomic chemical reactions. The main reaction pathway of the former is a hydrogen abstraction process leading to X + alkane:

HX + CH₂R → X + CH₃R. (1)

Here X stands for halogen and R could be H, CH₃, CH₂CH₃, etc. At higher temperature or collision energy, however, a new reaction pathway may become available:^17–20 halogen abstraction which leads to hydrogen + alkyl halide

HX + CH₂R → H + CH₂XR. (2)

Recently we reported two high-level ab initio full-dimensional spin–orbit-corrected potential energy surfaces (PESs) for two reactions, HBr/HI + C₂H₅, separately,^15,16 which are built from 11 364/10 921 geometries and energies at the following composite level of theory: ManyHF-based²¹ UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12),²² where a small-core relativistic effective core potential (ECP)²³ is used for the Br and I atoms. The multireference computations utilized a minimal active space of 5 electrons on 3 spatial 4p/5p-like orbitals, and the higher-order correlation energy effects were estimated by the Q Davidson-correction.²⁴ The SO computations made use of the Breit–Pauli operator for the HBr + C₂H₅ system and spin–orbit pseudopotential for the HI + C₂H₅ system in the interacting-states approach,²⁵ where the SO eigenstates were determined by diagonalizing the 6 × 6 SO matrix whose diagonal elements were replaced by the Davidson-corrected MRCI energies. The Monomial Symmetrization Approach (MSA)²⁶ was used in the fitting process of the energy points of the PES. During the PES development the ROBOSURFER program²⁷ was used and the potential energies were calculated by the MOLPRO program package,²⁸ and quasi-classical trajectory (QCT) computations²⁹ were run to obtain new geometries, where the E_coll was set from 1 to 60 kcal mol⁻¹. Later we performed vibrational mode-specific QCT studies on those analytical PESs.^19,20 In the present work we plan to extend our previous work by improving the two PESs so that they cover a higher energy range. Then we can investigate the X-abstraction reaction pathways in the HBr/HI + C₂H₅ reactions requiring higher E_coll.

2. Theory and methods

2.1. Potential energy surface

The PESs used in this work are improved versions of the potential energy functions worked out by the current author^15,16 for dynamical calculations on the HBr/HI + C₂H₅ reactions. The high-energy regions were not accurately described by those PESs. To correct this deficiency, the ROBOSURFER program was restarted and the QCTs were run at collision energies of 60 to 100 kcal mol⁻¹ to obtain new geometries, where the energies were calculated at the same ab initio level and were re-fitted with the same fitting procedure. We stopped adding more geometries when the percentage of broken trajectories was less than 1%. The new PESs are built from 14 630/14 649 geometries and the corresponding composite energies (see Section 1), whose distributions are shown in Fig. 1.

Fig. 1 Distribution of the data points. Energies are given with respect to the asymptote of the corresponding reactants and the bin size is 1 kcal mol⁻¹. The new data points are obtained in the present study and the old ones are taken from ref. 15 and 16 for the HBr/HI + C₂H₅ systems.

To make sure that the new geometry sets, which include more high-energy points, can cover the range of interest in this study, we have added 415 more data points for the HBr + C₂H₅ system, and have compared the cross sections at E_coll = 80 kcal mol⁻¹ on the PES with 14 630 data points (used in this work) and the PES with 15 045 data points. We have found that for the H-abstraction pathway, the cross sections are 5.59 bohr² and 5.67 bohr² on the PES with 14 630 and 15 045 data points, respectively, while for the X-abstraction pathway, the corresponding cross sections are 4.10 bohr² and 3.82 bohr², in order. The differences are within 10% and thus do not affect the analysis of the results. We have also performed QCT simulations on the previous PES (taken from ref. 15) of the HBr + C₂H₅ system at E_coll = 80 kcal mol⁻¹. However, the percentage of the unphysical trajectories reaches 10% at this high E_coll on the old PES, whereas this probability is negligible (0.2%) on the new PES, which means that the previous PES was not “smooth” and accurate enough at the high-energy range, and it was necessary to improve the PES.

The root-mean-square (RMS) errors of the new PESs are 0.39/0.34, 1.15/1.04, and 2.32/2.13 kcal mol⁻¹ in the energy intervals of 0–30, 30–80, 80–150 kcal mol⁻¹ relative to the global minimum of the fitting set, for the HBr/HI + C₂H₅ systems, respectively.

As shown in Fig. 2, for the H-abstraction reaction pathway, a pre-reaction minimum is located very near to the submerged transition state (TS) and the reaction is exothermic. For the X-abstraction reaction pathway, a post-reaction minimum is located below the corresponding products and it is endothermic. Fig. 2 also shows the comparison of the classical relative energies of the stationary points of the HBr/HI + C₂H₅ reactions obtained on the analytical PESs and the ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) energies computed for the geometries optimized on the PES. The comparison of two sets of energies indicates a good fitting behavior, in accordance with the small RMS values reported above.

Fig. 2 Potential energy of the HX + C₂H₅ (X = Br, I) reactions comparing the classical relative energies obtained on the present PESs and the ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for Br and I atoms) energies at geometries optimized on the PESs. Four single-excited vibrational energy levels (in parentheses, at UCCSD(T)-F12a/cc-pVDZ-F12 level of theory) of the reactants are also shown. All the energies are given in kcal mol⁻¹.

2.2. Quasi-classical trajectory

At the beginning of the trajectories, the initial vibrational excitation energies and the zero-point energies (ZPEs) of HX and C₂H₅ are set by standard normal-mode sampling²⁹ and the initial rotational angular momentum of each reactant is adjusted to zero. The spatial orientations of the reactants are randomly sampled. The initial distance between the center of mass of HX and the center of mass of C₂H₅ is (x² + b²)^1/2, where x = 16 bohr (distance along the relative center of mass velocity direction) and the impact parameter (b) is varied between 0 and b_max (where the reaction probability vanishes) with a step size of 0.5 bohr. The collision energy is set from 30 to 80 kcal mol⁻¹, with a step size of 10 kcal mol⁻¹. Simulations for the ground-state reactions as well as vibrationally excited-state reactions are performed by exciting the HX-stretching, the CH₂ wagging, the symmetric CH-stretching, and the asymmetric CH-stretching modes at the beginning of the trajectories, each with one quantum. 1000 trajectories are run at each b value. The trajectories are propagated with a 0.0726 fs time step until the largest interatomic distance becomes larger than the largest initial one by 1 bohr.

The motions corresponding to the normal-mode vibrations of C₂H₅ mentioned above are represented in Fig. 3. The imaginary mode of the H-abstraction transition state (v_{HA_TS}) and that of the X-abstraction transition state (v_{XA_TS}) are also shown.

Fig. 3 Schematic representation of the normal-mode vibrations of C₂H₅ studied in the present work: v₉ CH₂ wagging, v₁ symmetric CH-stretching, and v₁₀ asymmetric CH-stretching, where v_x [x = 9, 1, 10] refer to the standard Mulliken notations, as well as imaginary-mode vibrations of the H-abstraction and X-abstraction transition states.

3. Result and discussion

3.1. Reaction probability

The opacity functions (reaction probabilities as a function of the impact parameter) obtained at E_coll = 40 kcal mol⁻¹ using the old and new PESs, for the ground-state and HX-excited H-abstraction reaction pathways, are shown in Fig. 4. The differences of reaction probabilities between the old and new PESs are within 10%, and the excitation in HX-stretching promotes more than 20% in both PESs in both reactions, which means the same results can be obtained from the old and new PESs and a small statistical uncertainty lies in our results. The fluctuations come from statistical errors and within 10% of differences thus do not affect the analysis of the results.

Fig. 4 Reaction probabilities as a function of the b impact parameter for the H-abstraction channels of the ground-state and HX-excited (X = Br, I) reactions on the old^15,16 and new PESs at E_coll = 40 kcal mol⁻¹.

The opacity functions of H-abstraction and X-abstraction in the HBr/HI + C₂H₅ reactions obtained at the different E_coll are shown in Fig. 5. The reaction probability decreases a little for the H-abstraction reaction pathway but increases significantly for the X-abstraction reaction pathway with increasing E_coll, in accordance with the negative/positive barrier height of the two reaction pathways. A threshold energy of 40/30 kcal mol⁻¹ is observed for the Br/I-abstraction reaction pathway to proceed, which is much higher than the reaction barrier shown in Fig. 2 (around 21/16 kcal mol⁻¹). By checking the trajectories, we found out that before the Br/I connects with the C atom, it usually (not always) connects to one or two H atom(s) first, which dissipates a part of the energy thus the system needs more energy to complete the reaction.

Fig. 5 Reaction probabilities as a function of the b impact parameter for the HBr/HI + C₂H₅ reactions at different collision energies (given in kcal mol⁻¹).

The maximum b where reactivity vanishes is nearly independent of E_coll. The b_max value is 7–8 bohr for the H-abstraction reaction pathway and 4–5 bohr for the X-abstraction reaction pathway. This is because the Br/I atom is much heavier than H atom. The H atom is more flexible to approach the C atom but Br/I is too heavy and can only proceed to reaction when the b value is small.

3.2. Normal-mode excitation and deuterium effect

Competition between the H-abstraction and the X-abstraction reaction pathways in the HX + C₂H₅ reactions, for the ground-state and v_HX = 1 state, are presented in Fig. 6. At low E_coll the H-abstraction reaction pathway dominates but at high E_coll the two reaction pathways co-dominate the system. We can also observe that the excitation in HX vibrational mode helps both reaction pathways, but the enhancement is more substantial for the X-abstraction.

Fig. 6 Integral cross sections for the HX(v_HX = 0, 1) + C₂H₅(v = 0) (X = Br, I) reactions as a function of the collision energy.

Fig. 7 shows the inhibition effect of mode-specific excitations in C₂H₅ for the H-abstraction. Among them the v₉ = 1 (CH₂ wagging) inhibits the hydrogen abstraction most efficiently, because this wagging prevents HBr/HI to approach the CH₂ group. But for X-abstraction the excitations in C₂H₅ have almost no effect. The deuterium effect for both H-abstraction and X-abstraction reaction pathways is also investigated by replacing the reactant HX with DX (X = Br, I). Due to the fact that QCT cannot capture the tunneling effect, the only kinetic isotope effect comes from the ZPE and/or mass difference. Therefore, the effect, i.e., decrease in reactivity, is similar for both pathways.

Fig. 7 Integral cross sections for the HX(v_HX = 0) + C₂H₅(v_x = 0, 1) (X = Br, I and x = 9, 1, 10) and DX(v_DX = 0) + C₂H₅(v = 0) (deut) reactions as a function of the collision energy.

The sudden vector projection (SVP)^30,31 values, i.e., the overlaps of the vibrational modes of the reactants with the reaction coordinate (imaginary mode) at the TS structure calculated using the UCCSD/cc-pVDZ optimized geometries and the corresponding normal-mode vectors of the TS and the two reactants placed far, are listed in Table 1. The SVP values vary between 0 and 1, where 0 means no overlap between that vibrational mode of the reactant and the imaginary mode at the TS structure, while 1 means total overlap between them. The larger the SVP value is, the more efficient reactivity enhancement is expected upon the excitation of that mode.

Table 1 SVP values of the reactant vibrational normal modes (and translation) for the HX (X = Br, I) + C₂H₅ reactions calculated at the UCCSD/cc-pVDZ level of theory

Mode	Habs (Br)	Xabs (Br)	Habs (I)	Xabs (I)
v HX	0.151	0.903	0.055	0.955
v 9	0.187	0.098	0.096	0.053
v 1	0.017	0.044	0.011	0.027
v 10	0.000	0.056	0.000	0.032
Translation	0.768	0.317	0.806	0.208

---

We noticed that only for the X-abstraction, the HX-stretching vibrational enhancements are consistent with the predictions of the SVP model. The reason is that the imaginary frequency of the H-abstraction transition state is only 230/114 cm⁻¹ for the Br/I system and the mode is more like both of the two atoms (H and X) approaching C₂H₅, instead of only the H atom approaching C₂H₅ and the X atom heading to the opposite direction (when the reaction could happen) (see Fig. 3), which could not represent the reaction coordinate very well. Furthermore, it also explains the suspiciously large SVP values of the translational mode in the hydrogen-abstraction channels shown in Table 1. In addition, the reactivity is inhibited by the mode-specific excitations in C₂H₅, but the SVP model is unable to predict the inhibition effect, as described above. For X-abstraction, however, the imaginary frequency of the transition state is 851/652 cm⁻¹ and the imaginary mode shows forming C–X and breaking H–X bonds, which can represent the reaction process very well.

Certainly one of the limitations of QCT is that it is actually based on classical Newtonian dynamics, which means that it cannot account for the tunneling effect, and the probability distribution at low temperatures can be qualitatively wrong compared to the true quantum distribution. However, this problem is not expected to affect the present results as we consider high collision energies in this study. As for the zero-point energy (ZPE) leakage, it is a well-known issue that in the QCT simulations, the initial ZPE of all the normal modes and the excitation energy of the selected normal mode of the reactants may mix between the different modes. However, the intramolecular vibrational redistribution (IVR) may be well described classically, and as our group showed for the Cl + C₂H₆ reaction,³² the IVR does not necessarily prevent the system from keeping its mode-specific character.

3.3. Scattering and initial attack angle distribution

In this section we only show the results from E_coll = 80 kcal mol⁻¹ since little collision energy dependence is observed. The scattering angle distributions are obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the center of masses of the products and those of the reactants into 10 equidistant bins from −1 to 1. cos(θ) = 1 (θ = 0°) corresponds to forward scattering and cos(θ) = −1 (θ = 180°) corresponds to backward scattering. Differential cross sections showing the scattering angle distributions for both H-abstraction and X-abstraction of the HBr/HI + C₂H₅ reaction at E_coll = 80 kcal mol⁻¹ are shown in Fig. 8.

Fig. 8 Normalized scattering angle distributions for the HBr/HI + C₂H₅ reactions for both H-abstraction and X-abstraction pathways at E_coll = 80 kcal mol⁻¹.

It is clear that forward scattering is favored for H-abstraction, indicating the dominance of the direct stripping mechanism. In the case of X-abstraction, we can see the clear dominance of backward scattering indicating the direct rebound mechanism. This is consistent with the smaller b_max in the case of X-abstraction (Fig. 5).

The initial attack angle distributions for the reactants are calculated by binning the cosine of the angle (α for HX and β for C₂H₅) of the velocity vector of the center of mass of the examined reactant and an interatomic vector that is considered as the X–H bond for HX and the C–C bond for C₂H₅. We also use 10 equidistant bins between −1 to 1 like in the case of scattering angle distributions. For HX cos(α) = –1 means that HX approaches with its X atom side and in the situation of cos(α) = 1 HX goes with its H atom towards C₂H₅. While for C₂H₅ cos(β) = –1 means that C₂H₅ approaches HX with its CH₃ side and in the situation of cos(β) = 1 C₂H₅ goes with its CH₂ side towards the HX. Normalized initial attack angle distributions for the HX + C₂H₅ reaction at E_coll = 80 kcal mol⁻¹ are plotted in Fig. 9.

Fig. 9 Normalized initial attack angle distributions for the HBr/HI + C₂H₅ reactions at E_coll = 80 kcal mol⁻¹.

The H-abstraction reaction pathway favors H-side attack over side-on HX and the least-preferred I-side approach, as expected, because an H–C bond forms in the H-abstraction process. In the case of X-abstraction reaction pathway, it is not as obvious as H-abstraction but we can still observe that X-side attack is the most favored, because an X–C bond forms in the X-abstraction process. Comparing the two reaction pathways we see that H-abstraction is much pickier about the initial attack angle distributions for HX than X-abstraction, which leads to a decrease of reactivity for the H-abstraction reaction pathway. That is one reason why the reaction probability of X-abstraction is even a little higher than H-abstraction when b = 0 (Fig. 5), even though the X-abstraction pathway is less energy favored (Fig. 2). Both the H-abstraction and X-abstraction reaction pathways favor side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach.

3.4. The post-reaction distribution of energy

In this section we only show the results from the HI + C₂H₅ reaction since there is not much difference between the HBr + C₂H₅ and HI + C₂H₅ reactions.

As shown in the upper panels of Fig. 10, the translational energy distributions of the products I + C₂H₆ become broader as the E_coll increases, and their maxima are shifted by almost the total increment of the E_coll, indicating that the major part of the initial translational energy ends up in translational recoil, while for the products H + C₂H₅I there is little collision energy dependence and only a small part of the initial translational energy ends up in translational recoil.

Fig. 10 Normalized product relative translational energy distributions and product internal energy distributions for the HI + C₂H₅ reaction at different collision energies (given in kcal mol⁻¹).

In consistence with the upper panels, the E_coll dependence of the internal energy distributions of the products C₂H₆/C₂H₅I, plotted in the lower panels of Fig. 10, also suggests that only a small portion of the collision energy is transferred into the vibrational and rotational degrees of freedom of C₂H₆ but a large amount of collision energy is transferred into C₂H₅I. The internal energy excitations of the product C₂H₆ mainly come from the reaction energy.

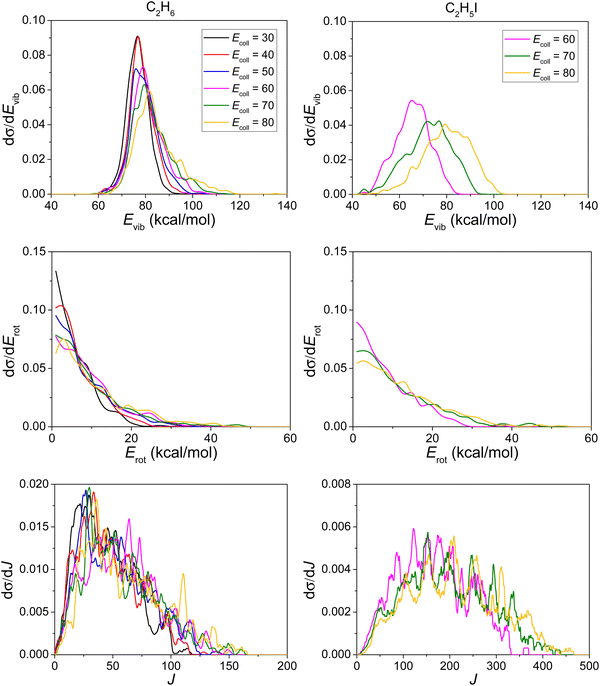
As expected, most of the internal energy is in the form of vibrational energy while a small part is restored in the rotational degrees of freedom, as shown in Fig. 11. Considering that the ZPE of C₂H₆ and C₂H₅I is 47 and 41 kcal mol⁻¹, respectively, only a few reactive trajectories in our simulations violate the ZPE constraint, in accord with the upper panels of Fig. 11.

Fig. 11 Vibrational energy (E_vib), rotational energy (E_rot), and rotational quantum number (J) value distributions for the products C₂H₆/C₂H₅I of the HI + C₂H₅ reaction at different collision energies (given in kcal mol⁻¹).

Rotational quantum numbers are obtained by rounding the lengths of classical rotational angular momentum vectors to the nearest integer values. While the rotational energy distribution is similar for C₂H₆ and C₂H₅I, the rotational quantum number value distributions of C₂H₅I are much broader than in the case of C₂H₆, since the mass of atom I is so heavy that the moment of inertia of C₂H₅I is much larger than that of C₂H₆.

4. Comparison with X + CH₄ systems

The phenomenon that at high collision energies the new channel (Br-/I-abstraction in the present reaction system) can compete with the main channel (H-abstraction in the present reaction system) happens in the X + CH₄^33–36 reactions too, in which the products of the main channel are HX + CH₃, but at high E_coll the new channel forming H + CH₃X opens. For example, in the case of H′ + CH₄, the main channel forms HH′ + CH₃, but at 1.4 eV the exchange reaction channel producing H + H′CH₃ opens and makes up a large proportion at 2.5 eV.³³ Shao et al.³⁴ investigated the O(¹D) + CH₄ multichannel reaction (main channel OH + CH₃, second channel H + CH₂OH/CH₃O, and third channel H₂ + HCOH/H₂CO) and calculated the branching ratios of product channels at E_coll = 6.8 kcal mol⁻¹. Their theoretical results are in good agreement with the experimental ones. Chen et al.³⁵ reported a full-dimensional PES for the F + CH₄ reaction covering both the abstraction and substitution channels. Compared with the abstraction channel, the classical barrier of the substitution reaction is much higher, being 1.129 eV at the UCCSD(T)-F12a/aug-cc-pVTZ level. Krotos and Czakó³⁶ plotted the integral cross sections as a function of collision energy for the abstraction (forming HCl + CH₃) and substitution (forming H + CH₃Cl) channels of the Cl(²P_3/2) + CH₄(v = 0) reaction and found out that the substitution channel opens around E_coll = 40 kcal mol⁻¹.

5. Conclusions

New high-level ab initio full-dimensional spin–orbit-corrected PESs for the HX (X = Br, I) + C₂H₅ reactions are presented in this paper. QCT calculations are used to study properties of these reactions, such as reaction probabilities, cross sections, normal-mode excitations on the reactivity, deuterium effects, mechanisms, and the post-reaction energy flow. The present new high-level ab initio full-dimensional study has found the following important features for these reactions.

(1) The reaction probability decreases a little for the H-abstraction reaction pathway but increases significantly for the X-abstraction reaction pathway with increasing E_coll, all of which is in accordance with the negative/positive barrier height of the two reaction pathways. By checking the trajectories, it is found that before Br/I atom meets the C atom, it usually (not always) connects to one or two H atom(s) first, which dissipates a part of the energy and thus makes harder to complete the reaction. The maximum b is almost independent of E_coll for both pathways. At low E_coll the H-abstraction reaction pathway dominates while the two reaction pathways co-dominate the system at high E_coll.

(2) It is observed that the excitation in the HX vibrational mode helps both reaction pathways, but the promotion is more efficient for X-abstraction. The mode-specific excitations in C₂H₅ inhibit the H-abstraction, especially for the CH₂ wagging mode. However, for X-abstraction the excitations in C₂H₅ have almost no effect. Besides, it is also noticed that the HX-stretching vibrational enhancements are consistent with the predictions of the SVP model only for the X-abstraction. In addition, the reactivity is inhibited by the mode-specific excitations in C₂H₅, but the SVP model is unable to predict the inhibition effect.

(3) Forward/backward scattering is favored for H/X-abstraction, indicating that the dominance of the direct stripping/rebound mechanism is in consistence with the larger/smaller b_max. Comparing the two reaction pathways brings us the conclusion that H-abstraction is much pickier about the initial attack angle distributions for HX than X-abstraction. This could explain why the reaction probability of X-abstraction is even a little higher than H-abstraction when b = 0. Both the H-abstraction and X-abstraction reaction pathways favor side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach.

(4) The translational energy distributions of the products X + C₂H₆ become broader as the E_coll increases, and their maxima are shifted by almost the total increment of the E_coll, whereas the translational energy release for the products H + C₂H₅X has little collision energy dependence. The internal energy distributions of the products C₂H₆/C₂H₅X suggest that only a small portion of the collision energy is transferred into the vibrational and rotational degrees of freedom of C₂H₆ but a large amount of collision energy flows into C₂H₅X.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office-NKFIH, K-125317; project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.

References

1. C. Rangel, M. Navarrete, J. C. Corchado and J. Espinosa-García, J. Chem. Phys., 2006, 124, 124306.
2. F. Meng, W. Yan and D. Y. Wang, Phys. Chem. Chem. Phys., 2012, 14, 13656.
3. K. Liu, J. Chem. Phys., 2015, 142, 080901.
4. J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, J. Chem. Phys., 2016, 144, 171101.
5. J. Chen, X. Xu, S. Liu and D. H. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 9090.
6. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
7. D. Papp and G. Czakó, J. Chem. Phys., 2020, 153, 064305.
8. D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762.
9. Y. H. Chen and E. Tschuikow-Roux, J. Phys. Chem., 1993, 97, 3742.
10. J. A. Seetula, J. Chem. Soc., Faraday Trans., 1998, 94, 891.
11. J. A. Seetula, Phys. Chem. Chem. Phys., 2000, 2, 3807.
12. L. Sheng, Z. S. Li, J. Y. Liu, J. F. Xiao and C. C. Sun, J. Comput. Chem., 2004, 25, 423.
13. D. M. Golden, J. P. Peng, A. Goumri, J. Yuan and P. Marshall, J. Phys. Chem. A, 2012, 116, 5847.
14. N. Leplat, A. Wokaun and M. J. Rossi, J. Phys. Chem. A, 2013, 117, 11383.
15. C. Yin, V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 24784.
16. C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 29084.
17. C. K. Westbrook, Proc. Combust. Inst., 1982, 19, 127.
18. J. Yuan, L. Wells and P. Marshall, J. Phys. Chem. A, 1997, 101, 3542.
19. C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 3083.
20. C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 9944.
21. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
22. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
23. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
24. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
25. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
26. Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26.
27. T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51.
28. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
29. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407.
30. B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104.
31. H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679.
32. D. Papp, J. Li, H. Guo and G. Czakó, J. Chem. Phys., 2021, 155, 114303.
33. J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302.
34. K. Shao, B. Fu and D. H. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 24098.
35. J. Chen, X. Xu, S. Liu and D. H. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 9090.
36. L. Krotos and G. Czakó, J. Phys. Chem. A, 2017, 121, 9415.

---