Ligand binding of interleukin-8: a comparison of glycosaminoglycans and acidic peptides

Abstract

Recognition and binding of regulatory proteins to glycosaminoglycans (GAGs) from the extracellular matrix is a process of high biological importance. The interaction between negatively charged sulfate or carboxyl groups of the GAGs and clusters of basic amino acids on the protein is crucial in this binding process and it is believed that electrostatics represent the key factor for this interaction. However, given the rather undirected nature of electrostatics, it is important to achieve a clear understanding of its role in protein–GAG interactions and how specificity and selectivity in these systems can be achieved, when the classical key-lock binding motif is not applicable. Here, we compare protein binding of a highly charged heparin (HP) hexasaccharide with four de novo designed decapeptides of varying negative net charge. The charge density of these peptides was comparable to typical GAGs of the extracellular matrix. We used the regulatory protein interleukin-8 (IL-8) because its interactions with GAGs are well described. All four peptide ligands bind to the same epitope of IL-8 but show much weaker binding affinity as revealed in ¹H–¹⁵N HSQC NMR titration experiments. Complementary molecular docking and molecular dynamics simulations revealed further atomistic details of the interaction mode of GAG versus peptide ligands. Overall, similar contributions to the binding energy and hydrogen bond formation are determined for HP and the highly charged peptides, suggesting that the entropic loss of the peptides upon binding likely account for the remarkably different affinity of GAG versus peptide ligands to IL-8.

---

Introduction

Glycosaminoglycans (GAGs) represent a particular class of linear anionic periodic polysaccharides made up of disaccharide repetitive units containing a hexosamine and an uronic acid or galactose in the case of keratan sulfate.^1,2 These molecules present varying net degrees and patterns of sulfation.³ GAGs are major components of the extracellular matrix and play important roles in numerous cellular processes such as signaling,^4,5 anticoagulation,^6,7 angiogenesis,^8,9 and communication.¹⁰ Their biological role is executed though intermolecular interactions with protein partners such as growth factors, chemokines, proteases and collagen.^11–13 Disruptions of protein–GAG interactions can cause a variety of pathologies including cancer,^14–16 Alzheimer's¹⁷ and prion diseases,¹⁸ autoimmune¹⁹ and inflammatory disorders.^14,20 All this renders GAGs to be very promising molecules for the design of new biomaterials in regeneration therapies.²¹

Binding of protein to GAGs has been studied extensively and different mechanism to regulate this interaction have been shown to be important.^13,22–24 The first and most important mechanism is via specific interactions, where the classical picture of a highly specific binding motif applies, e.g. via hydrogen bonds. In particular, for antithrombin III, a very specific short GAG sequence was discovered to exhibit the strongest binding with important pharmaceutical implications.²⁵ This system represents the best example studied so far of the highly specific protein–GAG interactions. Several hydrogen bonds have been identified in the crystal structure.²⁶ Second, low-affinity binding governed entirely by electrostatics has been reported for many protein targets, including BMP-2,²⁷ CXCL-12,²⁸ TIMP-3,²⁹ or TGF-β1.³⁰ Here, the most important parameter that affects the binding strength is the net charge per GAG disaccharide unit. Although a clear GAG binding epitope on the protein is also defined in this case, the discrimination between different GAG-ligands and thus the binding strength is solely dependent on the charge per disaccharide unit and not the exact position of the charge. Hence, this mechanism results in a rather low affinity and a rather fuzzy structural ensemble of protein-bound GAGs. Nevertheless, such a non-directed interaction may be of high biological relevance due to the highly ubiquitous abundance of GAGs, e.g. in the case of heperansulfate–thrombin interaction.^22,31 Third — and most challenging to study in detail — GAGs bind to proteins via contributions of both aforementioned mechanisms. GAG binding by such a mechanism is characterized by a rather low-affinity and is believed to have the largest contribution from electrostatics and solvation energy. However, some distinct differences in the binding strength of ligands of the same net charge but different sulfation patterns are observed. These result in specificity or discrimination between ligands with the same charge density.^13,32,33 For cathepsin S, chondroitin sulfates with varying sulfation patterns were predicted to bind to different sites, suggesting the underlying molecular mechanism of its inhibition.³⁴ For CXCL-14, binding poses for dermatan sulfate and chondroitin sulfate of the same net charge are clearly distinguishable both in the experiment and in the computational analysis.³⁵ This is also known as the “sulfation code”, where the sulfation pattern is suggested to be crucial for defining the recognition by protein targets and the involvement in particular biochemical processes.³⁶

Unfortunately, protein–GAG interactions are still insufficiently characterized at the molecular level due to the highly repetitive nature and high variability of GAGs, and relatively few GAG structures are available. Consequently, both experimental and computational approaches experience challenges when dealing with these systems because of GAGs’ particular properties such as limited availability of experimental structures, high length, high flexibility, conformational variability, periodicity, pseudosymmetry of the charged groups distribution, multipose binding³⁷ and high variation in the sulfation pattern.^13,32,33 Considering these challenges, there is a central question in protein–GAG research that remains unanswered: How is specificity in protein–GAG interaction achieved? This specificity itself could be understood within several contexts: GAG type (glycosidic linkage and monosaccharide components of a periodic unit), GAG net sulfation (the amount of the GAG sulfate groups defining the charge and, therefore, potential strength of electrostatic interactions established by the molecules), GAG sulfation pattern (particular positions of the sulfate groups in a GAG periodic unit). Despite the central role of GAG binding specificity, this issue is far from being completely understood.

In the current work, we aim to get deeper insights into the particular aspect of the specificity of protein–GAG binding by specifically analyzing the role of electrostatics for the binding affinity and structural properties of the protein–polyelectrolyte complexes. In this generalization, we approach the question by asking: would other molecules with a comparable net charge but of very different chemical nature represent similarly binding behavior with the same protein receptor? Answering this question could yield an improved understanding of the extent to which pure electrostatic interactions in protein–GAG binding are decisive, and could, therefore, affect the molecular mechanisms behind their biological functions. To this end, we chose the small chemokine IL-8, a well-known regulatory protein, for which the interactions with GAGs were extensively studied previously and discussed in terms of its potential specificity.^37–50 We performed comparative analysis of the interaction of IL-8 with the hexameric heparin (HP) and a series of acidic decapeptides with varying charge density (Fig. 1). We applied a combination of solution NMR and molecular modeling (molecular docking, molecular dynamics, free energy calculations) approaches that were previously demonstrated to be successful in the characterization of the interfaces of ligand binding to small proteins.^13,51 Although we confirm the strong impact of electrostatics on the binding characteristics of this system, there are also different structural, dynamic and energetic/entropic features that distinguish HP from peptide binding to IL-8 suggesting that electrostatics is not the only driving force responsible for GAG recognition of proteins. Our results contribute to the basic understanding of protein–GAG interactions and represent a fundamental step on the way to deciphering the molecular basis of the molecular specificity in these complex systems.

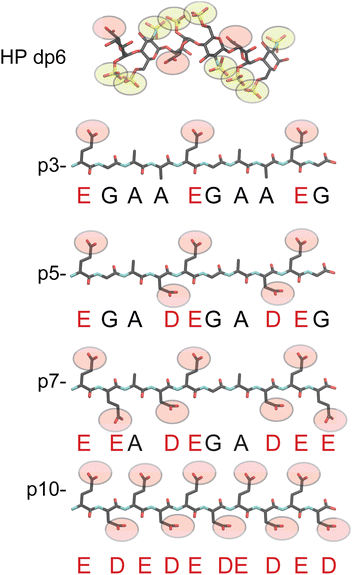Fig. 1 Chemical structures of HP dp6 and the 4 acidic peptides used in this study. Carboxylate groups are depicted as red and sulfate groups as yellow spheres.

Materials and methods

Experimental studies

Materials. Heparin hexasaccaride (HP, degree of polymerization of 6; dp6) was purchased from Iduron (Manchester, UK). The four different peptides, varying in their net charge (p3-: EGAAEGAAEG, p5-: EGADEGADEG, p7-: EEADEGADEE and p10-: EDEDEDEDED, see Fig. 1), were synthesized by the Peptide Synthesis Core Unit (Leipzig University, Germany). The ¹⁵N-labeled ammonium salts were purchased from Eurisotop (Saarbrücken, Germany) and all other chemicals from Carl Roth (Karlsruhe, Germany).

Protein production. Human IL-8 (1–77) was expressed, purified, and refolded as previously described,⁴⁵ except the final dialyzing step was against a buffer containing 22.2 mM sodium phosphate and 55.5 mM NaCl at pH 7.0 or only 22.2 mM sodium phosphate at ph 7.0 without any additional NaCl.

Circular dichroism spectroscopy. Peptides were dissolved in the measuring buffer containing 20 mM sodium phosphate and 50 mM NaCl (pH 7.0) to a final concentration of 5 mM. After dissolving the peptides, the pH value of the solution had to be carefully adjusted to pH 7.0 using NaOH. The CD analysis was performed with 70 μM peptide in 20 mM sodium phosphate buffer (pH 7.0) on a Jasco J-1500 spectropolarimeter (Pfungstadt, Germany). All experiments were carried out using a sample size of 350 μl in a 0.1 cm quartz cell at 25 °C and CD spectra were recorded from 190 nm to 260 nm with a scanning rate of 50 nm min⁻¹, 2 nm bandwidth and 0.2 nm data pitch averaged in five scans for each sample. The molar ellipticity (Θ) was calculated using the following equation, where m° represents the measured data (mdeg), M the average molecular weight, C the peptide concentration, and L the path length of the cell:

[Θ] = m° × M/(10 × L × C)

NMR spectroscopy. The NMR experiments were performed on Bruker Avance Neo 700 MHz or Avance III 600 MHz spectrometers (Bruker BioSpin GmbH, Rheinstetten, Germany) equipped with 5 mm inverse triple resonance probes with z-gradient. For data acquisition and spectrum processing, the Bruker software Topspin™ and for the analysis of the chemical shift perturbation (CSP) and plotting the software NMRFAM-Sparky was used.⁵²

The peptides were dissolved in 22.2 mM sodium phosphate buffer (0 mM NaCl, pH 7.0) to a concentration between 30 (p3-) and 50 (p10-) mg ml⁻¹ and the pH-value was carefully adjusted to 7. Afterwards, an extensive dialysis of roughly 100 μl of the peptide solution against two times 1 l of the buffer without NaCl using Spectrum™ Micro Float-A-Lyzer™ with a MWCO of 100–500 Da was performed. The concentration of the resulting peptide solutions (∼300 μl) was determined using ¹H NMR. For each peptide 10 μl of the solution was mixed with 100 μl valine (c = 1.7 mM) and filled up to 500 μl including 10% D₂O. A 1D ¹H NOESY with low power water presaturation during the mixing time (10 ms) and a 5 s period during the recycle delay of 40 s were collected, with a 64 scans each. Concentrations of the peptide solutions were determined using the internal valine standard (H_γ signal) and the alanine H_β signals. For p10- the H_β and H_γ of glutamic acid and H_β of aspartate were integrated and the concentration was determined. Finally, these solutions were mixed with phosphate buffer (either 0 mM NaCl or 1000 mM NaCl) and D₂O to obtain stem solutions of the peptides with 10 mM concentration (p3-, p5-), 9 mM (p7-) and 7 mM (p10-) in two different buffers. Both buffer systems contained 20 mM sodium phosphate at a pH of 7 including 10% D₂O. One contained no additional NaCl, while the other contained 50 mM NaCl.

The fully ¹⁵N-labeled IL-8 (100 μM) sample was measured at a temperature of 30 °C in 20 mM sodium phosphate buffer (pH 7.0) containing 10% D₂O and 4 μM TSP-d₄ with or without additional 50 mM NaCl. The acquired ¹H–¹⁵N HSQC spectra were comparable with published data of the homodimeric form of IL-8,⁵³ and the previously reported assignment was used.⁴⁵ For CSP experiments, increasing amounts of HP hexasaccharide (only in buffer with 50 mM NaCl) or the respective peptides were titrated. Furthermore, pure buffer was titrated in to exclude chemical shift pertubations due to protein dilution. For each titration step, a ¹H–¹⁵N Fast HSQC spectrum,⁵⁴ using a watergate 3919 water suppression⁵⁵ and globally optimized alternating phase rectangular pulse (GARP) for heteronuclear decoupling,⁵⁶ was acquired. For each NMR spectrum, typical pulse lengths of 8.9–10.2 μs for ¹H (depending on the salt concentration of the buffer), 35 μs for ¹⁵N 90° pulses and 240 μs for the ¹⁵N decoupling were used. In total, 32 scans per increment were acquired with a spectral with of 16 ppm as well as complex 3072 data points in the direct, and 25 ppm as well as real 128 data points in the indirect dimension. To reduce the sample size to 350 μl for p10-, a Shigemi® tube matched to D₂O (Shigemi Co., Tokyo, Japan), was used. The resulting weighted chemical shift change for each NH signal of the IL-8 backbone was calculated using the following equation, where Δδ represent the chemical shift perturbation (CSP):

To determine the apparent k_D value for the binding peptide, the calculated CSP was plotted against the ligand concentration and fitted using the following equation,⁵⁷ where Δδ_obs is the observed chemical shift change from the free state, Δδ_max is the maximum chemical shift change on saturation, [P]_t and [L]_t are the respective protein/ligand concentrations:
For the mean k_D only the five most affected amino acids (by CSP) were taken into account, as they most likely represent the binding to the ligand instead of effects due to tertiary structure changes. From this the mean k_D and its standard deviation was calculated.

For visualization of the CSP on the tertiary protein structure USCF Chimera was used.⁵⁸

Computational studies

Structures. The structure of the dimeric IL-8 protein used for all simulations was obtained from the PDB (PDB ID: 1IL8).⁵⁹ The N-terminal missing residues were built in xLeap module of AMBER16.⁶⁰ The structure of hexameric HP dp6 used for molecular docking simulations was taken from the PDB (PDB: 1HPN).⁶¹ The four anionic peptides, p3-, p5-, p7-, and p10- were built using the xLeap module of AMBER16⁶⁰ based on their amino-acid sequence.

Molecular docking. Docking simulations were performed with Autodock 3 (AD3),⁶² using a grid box with the grid step of 0.375 Å centered on the two α-helices of the IL-8 dimer (the heparin-binding site as described by ref. 39), of the following sizes: 60 × 60 × 60 and 80 × 80 × 60 grid points for the IL-8/HP complex and the IL-8/anionic peptide complexes, respectively. The number of rotatable bonds of the ligands was set to 29 for p3-, 32 for p5-, p7-, p10-, and HP dp6, respectively. IL-8 was kept rigid throughout the docking simulation. Each docking experiment was carried out in 100 independent runs, employing the Lamarckian Genetic Algorithm with an initial population size of 300, set to terminate after 10⁵ generations. The 50 docking solutions with the best AD3-score were clustered using the DBSCAN algorithm.⁶³ The metric used was root mean square atom type distance (RMSatd metric), which is used to calculate distances between atoms in the same manner as RMSD, but uses pairs of atoms of the same type which are spatially close. The neighborhood search radius was determined manually for each complex in order to maximize the amount of identified clusters. For subsequent molecular dynamics (MD) simulations, the cluster representative(s), cluster members with the best AD3-score within the cluster, and docking solutions with the best AD3-score that did not belong to a cluster were used, amounting to a total of 10 solutions per complex. No experimental data was used as a restraint for either docking or MD simulations.

Molecular dynamics

Molecular dynamics of protein–ligand complexes. MD simulations of the complexes obtained from docking experiments were carried out in AMBER16.⁶⁰ The ff14SB force field⁶⁴ parameters were used for the protein and peptide molecules, while GLYCAM06 parameters were used for HP. The simulated IL-8/peptide and IL-8/HP complexes were solvated in a periodic TIP3P octahedron water box with at least 15 Å distance between atoms of the analyzed complex and box boundaries. Charges of the complexes were neutralized by adding Na⁺ and Cl⁻ counterions. Prior to the MD analysis, two energy minimization steps, with and without harmonic restraints on the solute atoms, were performed, followed by heating the system up to 300 K for 10 ps, and an equilibration step at 300 K in an isothermal isobaric ensemble (NTP) for 100 ps. Subsequently, the 20 ns-long productive MD run was carried out with snapshots of the trajectories being written every 10 ps. The entire protocol used for the MD simulation can be found in detail in ref. 28.

Long MD simulations of unbound ligands. The unbound ligand structures were analyzed in a separate 1 μs-long MD simulation. The anionic peptides were solvated in a TIP3PBOX with minimum distance of 7 Å between box boundaries and the solute, and Na⁺ counterions were added to the system. The same protocol for the minimization, heating, and equilibration steps was as described above, followed by the productive MD run. The corresponding simulation of HP dp6 was taken from our previous work.⁶⁵

Free energy calculations. Calculations of the free energy of the IL-8/peptide and IL-8/HP complex trajectories as well as per-residue energy decomposition were performed using the Molecular Mechanics-Generalized Born Surface Area (MM-GBSA) approach in AMBER16 with igb = 2. The analysis was performed for all frames as well as for the last 5 ns of the productive MD run, however no significant difference was observed between the results of those subsets; hence, the energy calculation results for all frames are presented and analyzed. The mean values for total, electrostatic, and van der Waals energy components were compared between the ligands and the statistical significance of the differences was determined using Welch's t-test for unpaired samples.⁶⁶ Bonferroni correction for multiple comparisons was applied. The MD simulation length of 20 ns was shown to be sufficient for statistically significant MD-based free energy calculations for another protein–GAG system of a similar size when an ensemble of trajectories starting from multiple docked poses are analyzed.⁶⁷

Comparison of bound and unbound ligand structures

The RMSD (root mean square deviation) of heavy atoms of the same ligand between bound (docked) and unbound states was calculated to make a qualitative estimate of how much the conformation of the ligand changes upon binding to IL-8. Per ligand, the bound structures were taken from all of the 1000 solutions obtained from the docking of the ligand to IL-8 from all AD3 runs. The unbound structures consisted of the 10⁸ conformations obtained from the 1 μs-long MD simulation.

The number of structures considered similar was calculated for each ligand by counting the amount of bound and unbound structures that were within a certain RMSD cutoff after structural superposition of the structures. The RMSD cutoff value was incremented by a step of 1 Å from 0 Å to 12 Å. The results of this comparison were used to estimate the total energy of the system as a function of the reaction coordinate, which was expressed as the number of structures below the RMSD cutoffs (RMSDi). The resulting Potential of Mean Force (PMF) curves were plotted, and the free energy values were used to obtain an estimate of the dissociation constant k_D using the relationship:

where R is the universal gas constant and T is the temperature of the system, k_D is the binding constant and N is the number of corresponding structures.

The radius of gyration (R_gyr) of each ligand was calculated in cpptraj⁶⁸ using default parameters for all atoms and compared between the bound (docked) and unbound states in order to assess the compactness of the structures. Per ligand, the bound structures were taken from all 1000 AD3 solutions obtained from the docking of the ligand to IL-8. The unbound structures consisted of the 10⁸ conformations obtained from the 1 μs-long MD simulation. The kernel density estimates of R_gyr values were calculated and plotted for all ligands in R.⁶⁹

H-Bonds. Hydrogen bonds (H-bonds) established between IL-8 and the ligand molecules were identified from all frames of the 20 ns MD trajectories using cpptraj.⁶⁸ The default parameters were used to determine the presence of a H-bond (bond distance cutoff of 3.0 Å and hydrogen bond angle cutoff of 135°). For each donor–acceptor pair, the fraction of frames in which they formed a H-bond was calculated; the obtained fractions were averaged across the 10 replicates of MD runs per IL-8/ligand complex and subsequently summarized and visualized in Python 3.8.5 using the numpy 1.19.2,⁷⁰ pandas 1.1.3,⁷¹ and matplotlib 3.3.2⁷² libraries as well as in the R package.⁶⁹

Ligand flexibility and secondary structure analysis. The 1 μs-long MD simulation of the unbound ligands was used to analyze the ligands’ flexibility and secondary structure composition using cpptraj.⁶⁸ The secondary structure content of the peptide ligands was determined using the secstruct command and subsequently visualized using gnuplot.⁷³ The atomic fluctuations of HP dp6 and the four peptides were obtained using the rmsd command, applied to all atoms of the superimposed trajectories. The variation of the rmsd value for the whole trajectory was used as a measure of the ligand flexibility.

Data analysis and visualization. Postprocessing analysis of the trajectories was performed using cpptraj module of AMBER16.⁶⁸ Visualization of the analyzed structures was carried out in VMD.⁷⁴ The R package⁶⁹ was used for data analysis and statistical analysis (Welch t-test for unpaired samples and Bonferroni corrections for multiple testing).

Results

Interaction of IL-8 with charged ligands

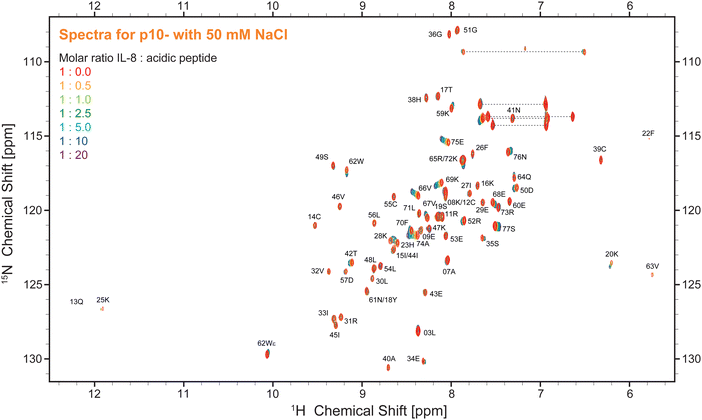
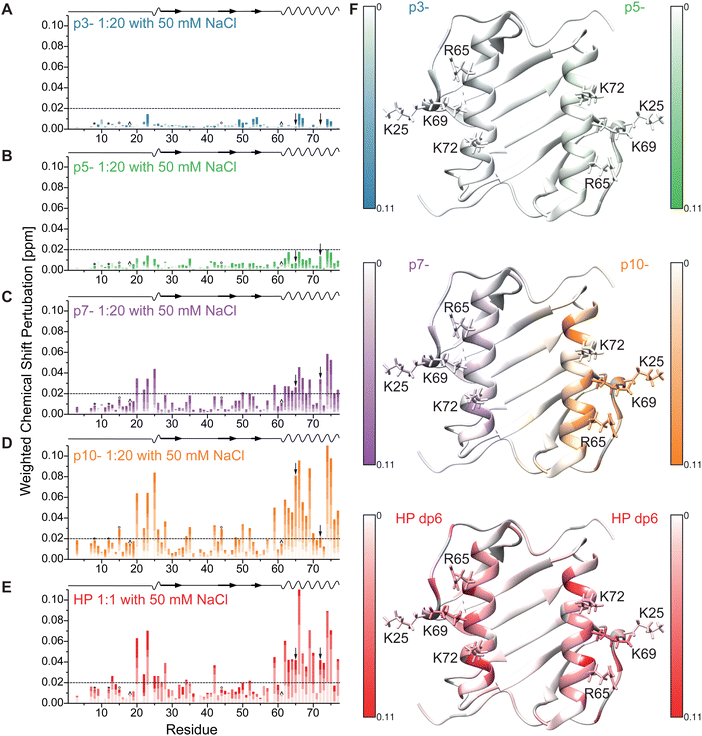
The ¹H–¹⁵N HSQC NMR spectrum of IL-8 shows well dispersed, high-resolution signals (red contours in Fig. 2). Titration of the five ligands (HP dp6 and the four negatively charged peptides, see Fig. 1) to the protein caused specific peak shifts in the ¹H–¹⁵N HSQC NMR spectra indicating changes in the chemical environment of the respective amino acid. Fig. 2 shows as example the ¹H–¹⁵N HSQC NMR spectra for the titration of the highest charged peptide ligand, featuring ten negative net charges (p10-). The final titration step used a 20-fold excess of the titrated peptides over IL-8, while for HP only an equimolar GAG/protein ratio was used. Higher HP dp6 concentration leads to a loss of signal intensity in the ¹H–¹⁵N HSQC spectra combined with an increased turbidity of the sample. However, after some incubation time, the solution became clear again and no aggregated protein was observable, while the NMR signal intensity remained the same. All ligands changed the chemical shifts of several residues of IL-8; the affected amino acids were similar, but the magnitude of the chemical shift perturbation (CSP) varied. The CSP increased with increasing net charge of the ligands (Fig. S1, ESI†).

Fig. 2 ¹H–¹⁵N HSQC NMR spectra of ¹⁵N-labeled IL-8 (100 μM, 50 mM NaCl, 20 mM NaP, pH 7.0; red) in the presence of the p10- peptide at varying molar ratios of IL-8 to p10- (orange 0.5, light green 1, dark green 2.5 light blue 5, dark blue 10 and purple 20 fold molar excess of p10-).

To map out these chemical shift changes for each residue of IL-8, the weighted chemical shift perturbations (CSP) (Δδ(¹H,¹⁵N)) were calculated as described in the methods section. The threshold for the significance level was set to 0.02 ppm, which was well above 2σ of the CSP for all control spectra. Fig. 3 shows these CSPs of the IL-8 for each peptide as well as for HP dp6 as a function of sequence. By comparing the overall pattern of peak shifts for each ligand, some similarities but also specific differences are observable. The residues with the highest CSP magnitude are concentrated in two regions of IL-8, including (i) residues K20–K28 and (ii) K59–S77. Especially residues V66 and A74 of the C-terminal α-helix show a strong response in the titration experiments for all ligands. Close to the shorter α-helix of IL-8, the titration with the peptides leads to a similarly pronounced shift of residue K25, H23 and K20, whereby HP dp6 influences predominantly residue H23 and K20. Fig. 3F shows the CSP plotted on the structure of the IL-8 dimer, indicating an overall similar region of IL-8 affected by the binding of p7-, p10- and HP dp6, where the degree of perturbation due to the ligands on IL-8 is ordered as p3- < p5- < p7- < p10- < HP dp6. Please note, that at 20-fold ligand excess, p10-shows similar effects like HP dp6 at equimolar ratio between protein an GAG. Nevertheless, for p5-, only A74 shows a CSP above the threshold and for p3- no significant CSP was reached.

Fig. 3 Weighted chemical shift perturbation of IL-8 in buffer containing 50 mM NaCl upon addition of (A-D) the four peptides (0.5, 1, 2.5, 5, 10 and 20-fold molar excess relative to IL-8 with increasing color) and of (E) HP dp6 (0.2, 0.5, 0.75 and equimolar ratio with IL-8) plotted for each residue of IL-8. The black dashed line denotes the significance threshold of 0.02 ppm. On the top of each graph, the secondary structure of IL-8 is shown, where waves represent α-helical and arrows β-sheet regions. *, ° and ^ denote overlapping peak pairs – K8/C12, 15I/44I and 18Y/61N respectively – which have therefore the same CSP, as they did not separate during the course of titration. Please note, that the arrows indicate the overlapping peak pair R65/72K which separated during the course of titration but could therefore not unambiguously assigned. (F) Shows the highest observed CSP of all ligands (uniform scale from 0 to 0.11 ppm) plotted on the tertiary structure of dimeric IL-8 (pdb: 1IL8). Residues without information about the CSP are colored grey, sidechains of the important residues K25, R65, K69 and K72 are shown and labelled.

Next, we performed the same titration experiments in a NaCl-free buffer because this reduced salt concentration strengthens electrostatic interactions due to reduced screening of the charges. The CSPs for the same titrations steps as in Fig. 3 are shown in Fig. 4 under NaCl-free buffer conditions. As expected, the overall magnitude of the CSPs was increased for each peptide ligand in the absence of NaCl (note the different scaling of the y-axis in Fig. 3 and 4). The regions most influenced by ligand binding remain the same (residues K20–K28 and K59–S77) and the overall pattern in the helical region is comparable to the buffer conditions with higher ionic strength. However, especially the CSP pattern for p10- shows some distinct changes for residues K20–K28. Fig. 4E shows the maximal CSP during titration enlarging this region. This time, the full color represents the maximum CSP of the respective titration to allow for a better distinction of the effects on the influenced amino acid pattern. While for p7- (left) nearly no difference without (top panel) and with 50 mM NaCl (middle panel) is observed, for p10- (right side) no influence on the helical pattern is detected, but in the absence of NaCl a reduced effect on K25 (side chain shown and labeled) is observed compared to 50 mM NaCl. Interestingly, the sequence of residues with maximum CSP in this region changed from K25 > H23 ∼ K20 in the presence to K20 > H23 ∼ K25, S19 in the absence of NaCl. However, using HP as ligand, an even more reduced influence on K25 and no influence on S19 is observed. Taken together, this shows that the only three charged amino acids in this region (K20, H23, K25) are influenced by the peptide binding, while HP binding clearly perturbs the chemical shift of K20 and H23 more than K25 (see also Fig SI1 and SI2 lowest panel for enlarged spectra of this region, ESI†). Supporting this binding of the peptides governed mostly by the charged side chains of IL-8, the most highly charged peptide also shows a strong influence on either R65 or K72 (labelled by arrows in Fig. 3 and 4 and side chains shown, see also Fig. SI1 and SI2 upper panel, ESI†), which are adjacent to the K20–K25 region.

Fig. 4 Weighted chemical shift perturbation of IL-8 in NaCl-free buffer upon addition of (A-D) the four peptides (0.5, 1, 2.5, 5, 10 and 20-fold molar excess relative to IL-8 with increasing color) plotted for each residue of IL-8. The black dashed line denotes the significance threshold of 0.02 ppm. On the top of each graph, the secondary structure of IL-8 is shown, where waves represent α-helical and arrows β-sheet regions. ° and ^ denote overlapping peak pairs 15I/44I and 18Y/61N – which have therefore the same CSP, as they did not separate during the course of titration. * represents the initially slightly close peak pair K8/C12, whose CSPs where evaluated using integration. Please note, that the arrows indicate the overlapping peak pair R65/72K which separated during the course of titration but could therefore not unambiguously assigned. (E) Shows the highest observed CSP in the helical region and from K20–K25 for p7- and p10- in buffer without additional NaCl (top), in buffer with 50 mM additional NaCl (middle) and for HP dp6 in buffer with 50 mM NaCl (scale from 0.02 ppm to the respective maximum CSP) plotted on the tertiary structure of dimeric IL-8 (pdb: 1IL8). Residues without information about the CSP are colored grey, sidechains of K25, R65, K69 and K72 are shown.

Determination of apparent k_D values

We analyzed the binding strength of the negatively charged ligands by plotting the CSP of each titration step of the five most perturbed amino acids against the ligand concentration and calculated the apparent dissociation constant (k_D) for the interaction of IL-8 with each ligand (Fig. 5). Normally, the k_D values determined from the NMR experiments do not represent the intrinsic k_D because the protein concentration necessary for solution NMR measurements is much higher than the intrinsic k_D. However, taking the starting protein concentration of 100 μM and the end titration step with 20 fold excess for the peptides into account, a determination of the k_D in the range from 20 μM to 2000 μM is reasonable.⁵⁷Fig. 5A shows exemplarily the plots for residues V66 and A74, which were highly influenced by all ligands, when the CSP threshold was reached (see Fig. 5B). The apparent k_D values ( ± standard deviation) obtained from the fits are (1774 ± 570) μM for p5-, (1024 ± 400) μM for p7- and (194 ± 21) μM for p10- and thus show the expected effect of the net charge in buffer containing 50 mM NaCl. Because the titration experiment with HP dp6 in the same buffer was only possible up to an equimolar ratio, saturation of the CSP was not reached and a k_D could not be determined. However, given the fast increase of the CSP at low ratios, an apparent k_D much smaller than 25 μM is expected. Hence, even the highest charged peptide p10- shows at least an order of magnitude higher k_D at higher salt concentration (50 mM).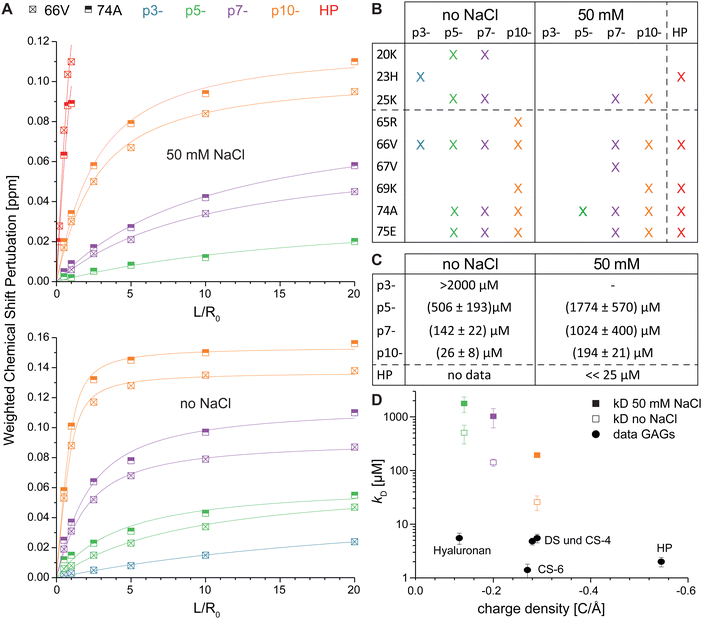

Fig. 5 Plot of the weighted CSP of residue V66 and A74 for the titration experiment with HP dp6 and the four peptide ligands in buffers with different ionic strength (A). Solid lines represent best fits to a 1 : 1 binding model. In (B) the up-to-five amino acids with largest CSP by the binding are shown, from which the k_D were calculated (C). (D) Shows the k_D from this work and data adapted from literature for different hexasaccharides,^45,46 where the same high ionic strength buffer (filled symbols), but a concentration of 1 μM IL-8 was used.

The apparent k_D values for ligand binding in the absence of NaCl are larger than 2000 μM for p3- as no saturation was reached, (506 ± 193) μM for p5-, (142 ± 22) μM for p7- and (26 ± 8) μM for p10-. They show again the clear influence on the net charge of the peptide ligand confirming the stronger binding at reduced ionic strength of the buffer.

Ligand docking to dimeric IL-8

In order to predict the structures of the complexes of IL-8 with HP dp6 and the anionic peptides, the molecular docking approach was applied. Docking simulations were performed with the grid box centered on and encompassing only the C-terminal helical regions of IL-8 dimer. Fig. S3 (ESI†) shows the results of the docking; while most ligand molecules were placed parallel to the α-helices of IL-8, the solutions appear to be more narrow for HP and p3-, while for p5-, p7- and p10- the docked structures are more spread out along the helices. The results obtained for HP dp6 are in agreement with the previous data we obtained for this system as an alternative binding pose⁴⁵ and by Joseph et al.,³⁷ where for longer HP poses, in which HP bound to both C_β-terminal helices, were proposed.

Clustering the 50 top-scoring solutions for each ligand identified two clusters in the case of peptides and only one cluster for HP. For subsequent MD simulations, the cluster representative(s) (the structure(s) closest to the cluster center), high-scoring cluster members, and high-scoring structures not belonging to any cluster were taken, resulting in a total of 10 docking solutions per docking experiment chosen (Fig. 6). Apart from p7-, no clear visual difference in the representative binding poses within the clusters could be determined. For p7- several binding poses stand out from the rest of the structures.

Fig. 6 The docking poses used as input for the MD for IL-8 complexed with HP dp6 and p3-, p5-, p7-, and p10-. The protein is shown in cartoon and the ligands in stick representation. Ligand structures are colored according to cluster membership as identified using DBSCAN clustering, with cluster 1 in red, cluster 2 in light green, and structures not belonging to any cluster in dark blue.

Molecular dynamics

MD simulations of the IL-8/ligand complexes obtained from AD3 docking experiments were performed. To consider the conformational variety of the structural ensemble obtained by molecular docking, 10 different representative initial structures for each ligand were used in the MD simulation. Fig. 7 shows the results of one of the MD simulations for each ligand, while Fig. S4 (ESI†) shows the poses of the ligand at the start of the MD simulations (red) and at the end of the 20 ns MD simulation (blue). In many cases, the ligand molecules dissociated from the initial binding pose either to move along the α-helices of IL-8 or to bind to the side of IL-8. However, no clear trend in neither binding site nor binding pose preference could be identified for the ligands when compared to each other. Nevertheless, peptide p5- moved the least in all of the 10 simulations performed for the given ligand, suggesting that the initial pose was energetically favorable.

Fig. 7 Representative MD trajectory frames (every 100 ps for ligand, and every 1 ns for the protein) of IL-8 complex with HP dp6 and p3-, p5-, p7-, and p10-. Protein is shown in cartoon and ligand in stick representation (red corresponds to the beginning and blue to the end of the simulation).

Energetic analysis of the complexes revealed differences in binding strength between the ligands as shown in Fig. 8. A clear difference between HP and the peptides was seen in terms of the total free energy, with IL-8/HP complexes being on average more favorable. The differences were statistically significant between HP and p3- as well as HP and p7-, while between the peptides the only statistically significant difference was between p10-, which had the lowest average total free energy of binding, and p7-. The in vacuo electrostatic component of the total energy became more favorable with increasing charge of the ligand molecule, with HP and p10- having similar average electrostatic energies, while IL-8/p3-complexes were the least favorable in terms of electrostatic energy. The differences were statistically significant between HP and p3-, p5-, and p7-, between p10- and p3-, p5-, and p7-, as well as between p3- and p5-, p3- and p7-, and p5- and p7-. The van der Waals interaction energy was the lowest for p5-, and the least favorable for p10-, while HP, p3-, and p7-average energies were comparable. The only differences that remained statistically significant after multiple-testing correction were between p10- and HP dp6, p3-, and p5-. The total electrostatic energy made up of the in vacuo and implicit solvation generalized Born component follows the same trend as the electrostatics in vacuo for the peptide series. Only for p10- is the total electrostatic impact favorable. Interestingly, it is significantly more favorable than for the HP dp6, which has a more negative charge than p10-. This analysis allowed to conclude that HP dp6 and p10- are comparable in terms of electrostatics which justifies the design of the used peptides to meet our original aim which was to analyze if there are substantial differences in binding for representatives of essentially different classes of molecules that are similar in terms of their electrostatic properties.

Fig. 8 Boxplots representation of the electrostatic energy in vacuo (top left), total electrostatic energy (bottom left), van der Waals energy (top right) and total free energy (bottom right) for the IL-8/ligand complexes determined using MM/GBSA. Statistical significance of differences is shown as (*) for statistical significance when compared to all other groups, (1) statistical significance when compared to p3-, (2) statistical significance when compared to p5-, (3) statistical significance when compared to p7-, (4) statistical significance when compared to p10-.

In order to identify key residues of IL-8 involved in the binding of HP dp6 and the anionic peptides, a per-residue decomposition of the total free binding energy was performed. The residues that contribute most favorably to the binding energy, R65, K69 and K72, are common to all of the studied systems (Table 1). Residue K25 was important for IL-8/HP dp6 and IL-8/p10- complexes, however the magnitude of its influence was greater for the HP-containing complex.

Table 1 Residues of IL-8 with mean contributions to ΔG below −1.5 kcal mol⁻¹ for the complexes IL-8/HP and IL-8/peptides, averaged over 10 replicates. Residues with more favorable free energy contributions than −2.0 kcal mol⁻¹ are shown in bold

	IL-8 residues
	IL-8 monomeric unit 1	IL-8 monomeric unit 2
HP dp6	R65, K69, K72	K25, R65, K69, K72
p3-	R65, K72	R65
p5-	R65, K69, K72	K72
p7-	R65, K69, K72	R65, K69, K72
p10-	K25, R65, K69, K72, R73	R65, K69, K72

---

The acidic residues E68 and E75 of IL-8, on average, had a strongly unfavorable impact on binding HP dp6, contributing on average more than +1.50 kcal mol⁻¹ to the binding free energy. Only residue E68 had a similar contribution in the IL-8/p10- complex (average energy contribution equal to +1.55 kcal mol⁻¹), while in case of IL-8 complexed with the other peptides, this influence of E68 was not greater than +1.50 kcal mol⁻¹. This could be attributed to the higher flexibility of the peptides in comparison to HP dp6, which allowed them to reduce the unfavorable interactions with the negatively charged residues. While all of the HP residues had negative average binding free energy contributions, peptide residue E1 had an unfavorable (positive) average binding free energy contribution above +1.50 kcal mol⁻¹ for all of the IL-8/peptide complexes.

Comparison of bound and unbound ligand conformations

To explore the changes in conformation and compactness of the ligand structures upon binding to IL-8, the distributions of radii of gyration (R_gyr) were compared for each ligand between its bound and unbound state and those differences were compared between ligands. R_gyr has been used as a measure for the description of structural specificity of both binding site and the ligand.^75–77Fig. 9 shows the differences between the bound and unbound state for each ligand. The distribution of the HP R_gyr does not essentially change upon binding, while there is a clear increase of R_gyr values for all the peptides. With the increase of the peptide charge, this difference in the R_gyr distributions between the bound and unbound states are smaller. This can be explained by the fact that more charged peptides are less likely to be folded into particularly compact structures when unbound due to the intramolecular electrostatic repulsion. This analysis underlines the principal structural differences between the peptides and the HP molecule in IL-8 binding and could potentially be a factor explaining the specificity of HP binding.

Fig. 9 Comparison of distributions of R_gyr values (kernel density estimation) between bound and unbound states in continuous and dashed lines, respectively, for HP dp6, p3-, p5-, p7-, and p10-.

The secondary structures of the unbound acidic peptides were analyzed with the DSSP (Dictionary of Secondary Structure of Proteins) approach applied to the corresponding MD trajectories (Fig. S5, ESI†). Neither peptide revealed significant secondary structure elements in the course of the simulation. This was also in agreement with the CD experiments (Fig. S6, ESI†).

The atomic fluctuation analysis of the unbound ligands revealed substantial differences in flexibility between HP dp6 and the peptide ligands. The flexibility of the HP dp6 in terms of the RMSD variance was equal to 0.7 Å and lower in comparison to the flexibility values of p3- (4.1 Å), p5- (2.3 Å), p7- (1.9 Å) and p10- (1.1 Å). Among the peptides, higher rigidity is observed for more charged peptides as it was also suggested by the analysis of R_gyr distributions.

Analysis of hydrogen bonds

Fig. 10 shows the patterns of H-bond formation during MD simulations between IL-8, acting as H-bond donor, and the ligands. The C-terminal helix region (residues 64–73) was an important site of H-bond formation for all of the complexes, especially for residues R65, K69, and K72. A second site of H-bond formation was identified for residues 23–26, located at the side loop of IL-8. Noteworthy is that HP dp6 was more likely to form H-bonds in this site compared to the peptides. In the case of the ligands acting as H-bond donors and IL-8 as H-bond acceptor (Fig. S7, ESI†), only residues belonging to the C-terminal helical region of IL-8 were involved in H-bonds with occupancy over 0.1. The average frequency of H-bond formation was similar for all of the examined IL-8/ligand complexes. When ligands act as H-bond donors, the participation of the less charged peptides is higher, while p10- behaves similarly to HP dp6, establishing the fewest H-bonds.

Fig. 10 Heatmap of hydrogen bond interactions between IL-8 (hydrogen atom donor) and HP dp6, p3-, p5-, p7- and p10-, averaged over IL-8 dimer subunits and across replicates of MD simulations. Protein residue numbers are shown on the x-axis, ligand residue numbers are shown on the y-axis. Color intensity corresponds to the frequency of the H-bond, i.e. the average fraction of MD trajectory frames in which the bond was formed.

Furthermore, we analyzed the differences in the distribution of the number of simultaneously established H-bonds for these particular residues depending on the bound ligand. When considering only the 14 IL-8 residues that establish most H-bonds as donors (i.e., residues 23–26, 59–61, 64–66, 69, 70, 72, 73) based on Fig. 10, there is a clear difference between the distributions for p5- and especially for p10- in comparison to HP dp6, p3-, p7- (Fig. 11). Peptides p5- and p10- form more H-bonds simultaneously, which could be the explanation for the observation that these peptides are more stable during the course of the MD simulation in terms of their movements on the protein surface. When analyzing contributions of each individual residue of IL-8 as an H-bond donor, certain patterns of specificity could be revealed (Fig. S8, ESI†). For H23 and K25, there is a clear trend of higher H-bond propensity with the increase in peptide charge, with the similarities between HP dp6 and p10-. In contrast, while the trend for the peptides remains the same for K59 (except for p10-), negligible number of H-bonds with this residue are established by HP dp6. Peptide p10- specifically interacts with H23, K25, and R73, while p5- interacts with E60, N61, Q64, K72. V66 and F70 establish specific H-bonds with HP dp6, although the normalized frequencies of these H-bonds are very low. Interestingly, when considering the amino acids of the known binding motif of IL-8 and HP (K25, R65, K69 and K72) especially p7- resembles the H-bond donor pattern overall very well, while the other high propensity amino acids are either in good agreement (H23) or in closest agreement considering the other peptide ligands (N61 and Q64).

Fig. 11 Frequency of H-bonds established in each frame for 14 IL-8 residues that establish most H-bonds as donors (23–26, 59–61, 64–66, 69, 70, 72, 73). On the x-axis the number of H-bonds simultaneously observed in the same MD frames is provided.

Discussion

Recognition of regulatory proteins by GAGs on the cell surface is a key molecular process critically related to wound healing, cell growth, hemostasis, anticoagulation, tumor progression, inflammation and others.⁷⁸ The molecular characteristics of that interaction is the electrostatic attraction between GAGs, rich in negatively charged sulfate groups, and clusters of positively charged amino acids on the respective protein.⁷⁹ As electrostatic forces represent a rather undirected mode of interaction, the question arises how it can play the key role in such important biological processes. For instance, both pro- and anti-inflammatory cytokines, which induce highly adverse biological effects, expose clusters of basic amino acids on their surface and would be equally attracted by negatively charged GAGs on the cell surface. Although GAGs feature varying charge densities and distributions of negatively charged groups, their interactions strengths with the same protein are not too different.⁴⁵ Furthermore, also other negatively charged polyelectrolytes (i.e. peptides, nucleic acids and nucleotides etc.) are found in the extracellular space and could also interact electrostatically with basic proteins. This triggers the question what factors other than electrostatics could provide an additional contribution to the recognition of proteins by GAG molecules.

We approached this question by a combination of experimental and computational methods comparing binding of a classical GAG HP dp6 to IL-8 with a small library of de novo designed short acidic decapeptides of varying charge density. Here, the most highly charged peptide is comparable with HP dp6 in terms of its net charge (Fig. 1). While HP is certainly one of the most highly charged GAG with 4 negative charges on average per dp (charge density: −0.52 to −0.57 C Å⁻¹ depending on conformation⁸⁰), also other GAGs with lower charge density such as hyaluronan (1 negative charge per dp, charge density −0.13 C Å⁻¹) or dermatan sulfate (2 negative charges per dp, charge density −0.29 C Å⁻¹) and chondroitin sulfate (2 negative charges per dp, charge density −0.28 or −0.27 C Å⁻¹ for chondoritin-4-sulfate and chondroitin-6-sulfate, respectively) are part of the extracellular matrix. The decapeptides varied in their number of charges between −3 and −10, representing comparable charge densities between non-sulfated hyaluronan and monosulfated chondroitin or dermatan sulfate. The charge densities of the peptides are −0.09 C Å⁻¹ for p3-, −0.14 C Å⁻¹ for p5-, −0.2 C Å⁻¹ for p7-, and −0.29 C Å⁻¹ for p10- and thus well comparable to typical GAGs (Fig. 5D). Furthermore, we included two different negatively charged amino acids, aspartate and glutamate, which differ in the sidechain length similarly to 4-O and 6-O sulfation, where the latter is one CH₂ group further away from the sugar ring. The uncharged amino acids in the peptides had small sidechains (Gly, Ala) to avoid steric effects. For IL-8, it was shown that the binding strength for chondroitin sulfate with the same net charge but an altered position of the sulfate group, differs significantly – e.g. a sulfation in the 6-O position leads to higher affinity (black circles in Fig. 5D).^45,46

At the same time, it is worth taking into account that the chemical nature (the absence of sulfate groups in the peptides) and conformational preferences of peptides and GAGs as molecular classes in general are essentially different and, therefore, their recognition elements are also likely to be distinguishable because of the differences in terms of degrees of freedom, charges distribution and as a consequence solvent-mediated interactions. All these factors could potentially affect the specificity features of their interactions with proteins.

Both GAG and the acidic peptides bind to an epitope defined by similar amino acid residues on IL-8 as shown by NMR titration (Fig. 3 and 4) and MD-based analysis (Table 1). Furthermore, binding is enhanced with increasing net charge from p3- to p10- and highly dependent on the ionic strength of the buffer (Fig. 4D and Table 2). This suggests that non-specific electrostatics may indeed be the key interaction for the formation of GAG/IL-8 complexes. The most involved IL-8 residues in peptide binding are R65, K69, and K72, which are part of the well-known α-helical BxxxBxxBB motif (including R73), where B stands for a basic residue.^39,41,42 The second known GAG binding motif of IL-8 is localized in the loop connecting the N-terminal regions with the first β-strand and involves residues K20, H23 and K25. Here, all positively charged residues respond to peptide binding, while K25 responds strongest (Table 1 and Fig. 2–4, except for p10- in buffer without NaCl). These two binding motifs combined make the binding parallel to the helix on the side of IL-8 more favorable for HP and the peptides than the binding between the two helices, although both are observed in the MD.

Table 2 Estimate of the free energy of the system based on the comparison of bound and unbound ligand structures and the determined mean dissociation constant k_D for the analyzed complexes

	p3-	p5-	p7-	p10-
Calculated free energy [kcal mol^−1] (derived kD [μM])	1.93 (26.0)	1.79 (20.4)	1.58 (14.3)	1.46 (11.7)

---

Although similar values for the NMR CSP of IL-8 were induced by HP and the four model peptides, the ligand to protein ratio corresponding to the maximal achieved CSP varied drastically. For HP, the final titration step was achieved at a molar 1 : 1 ratio between HP and IL-8, higher GAG to IL-8 ratios lead to unspecific aggregation and loss of NMR signal intensity. In contrast, an up to 20-fold peptide excess still allowed reasonable NMR measurements. This experimental result suggests very different affinities of HP and the acidic peptides. Indeed, from plots of CSP vs. ligand concentration, apparent k_D values could be determined for three peptides (except p3-) varying between ∼0.2 and 1.8 mM in high ionic strength buffer. As no saturation of the CSP was measured in the presence of HP, such an apparent k_D value could not be determined from the NMR measurements. Using Trp fluorescence at much lower protein concentration of 1 μM in the same buffer, Schlorke et al. determined the k_D for GAG binding to IL-8, which varied between 5.5 μM for HA and 2.0 μM for HP dp6.^45,46 These k_D values for GAGs and our NMR values for the acidic decapeptides are not directly comparable because very different protein concentrations were used. It is also known that IL-8 forms dimers with a monomer/dimer dissociation constant of 18 ± 6 μM.⁸¹ Thus, the NMR measurements are determined for the IL-8 dimer while the Trp fluorescence data was acquired for monomers. Nevertheless, it is clear from Fig. 5D (closed symbols) that GAGs bind with much higher affinity to IL-8, which is also clearly suggested by the MD-based free energy calculations (Fig. 8). This is remarkable, since the charge density of the peptides and the lowly charged GAGs is comparable. Strikingly, the k_D values vary in the high ionic strength buffer from p5- to p10- by a factor of roughly 10, while in the low ionic strength buffer a factor of 20 is observed. This once again suggests that electrostatics play an important role, as ligand binding is improved in the absence of NaCl.

Since net electrostatics cannot fully explain the very different affinity of the negatively charged GAG or peptides for IL-8, the question arises what other factors contribute to the higher affinity of GAG for the protein. Our computational analysis can provide detailed insight into this question. Free energy calculations (Fig. 8) allowed the separation of electrostatic and van der Waals contributions as well as the impact of solvent that was previously demonstrated to be key in the protein–GAG interfaces.⁸² While the in vacuo electrostatic contribution scales approximately proportionally with the ligand charges, the van der Waals contribution is less favorable for the more charged peptides. Total electrostatic contributions are also essentially different for HP dp6 and acidic peptides: in the implicit solvent model, the solvent contribution compensates the electrostatic interactions between HP dp6 and the protein more effectively than between the peptide p10- and the protein. This could be explained by the substantially more hydrated nature of protein-HP interfaces in comparison to protein-peptide interfaces.⁸² Such energetic pattern differences could provide one of the clues for the GAG binding specificity.

An important difference between GAG and acidic peptides is also the nature of the negatively charged groups on either molecule. While sulfated GAGs contain both carboxylate and sulfate groups, the model peptides only feature carboxylate groups. The pK_a value of the Glu sidechain is 4.1 at 25 °C⁸³ and between 2.5 and 0.5 for the sulfate group of mucopolysaccharides.^84,85 While shifts in these pK_a values can be observed, our results suggest that both groups are relatively strong electrolytes that should be fully charged at neutral pH used in our experiments. However, both functional groups vary in their physical properties as well as their hydrogen bond capacity. The carboxylate group is smaller (V = 40.6 ų) than the sulfate group (V = 57.7 ų) as determined by quantum chemical calculations (https://www.spartan.com). This results in a lower charge density of the sulfate group (−11.5 mC Å⁻²) compared to the carboxylate group (−16.6 mC Å⁻²). Also, the sulfate group has a higher dipole moment (4.7 D) than the carboxylate group (3.1 D). All these differences influence the charge–charge, charge–dipole, and dipole–dipole electrostatics. However, this hardly explains the difference in binding strength over three orders of magnitude between Hyaluronan dp6 (5.5 ± 1.3 μM)⁴⁵ and p5- (∼1.7 ± 0.6 mM), which both only exhibit carboxylate groups and have a comparable charge density.

The conformational changes of the ligands between free and bound form also play a role in the formation of ligand/IL-8 complexes. While HP is considered to be already relatively elongated in free solution, CD experiments confirm that all peptides are in random coil conformation in solution (Fig. S6, ESI†). While backbone flexibility may help for the ligand to assume the ideal binding pose on the protein surface, the entropic change a coiled peptide ligand undergoes upon binding to a well-defined pose on the protein is rather unfavorable. This could be explained qualitatively by the entropic component of binding. As HP does not alter its radius of gyration or conformation upon protein binding (Fig. 9), it already represents a perfect ligand for IL-8 without the need for further structural adaption and binds with the highest affinity by far. In contrast, a remarkable adaptation of all peptides upon binding to a more elongated structure is observed (Fig. 9); R_g increases by ∼2.4 Å for p3-, ∼1.9 Å for p5-, and ∼1.4 Å for p7- and p10- upon IL-8-binding. This is accompanied with a decrease in entropy due to the loss of motional freedom, which also contributes to the lower binding energy. The suggestion that entropy may be a very important factor is also supported by the fuzzier binding poses assumed by the peptides in comparison to HP (Fig. 6). This looser and more flexible binding mode has more favorable entropy but also results in less optimal binding geometry and thus in overall lower affinity.

The MD results also show that the R_g of the free peptides increases with increasing charge density. This suggests that the entropic loss associated with IL-8-binding is reduced for the more highly charged peptides, in agreement with the higher affinity of these molecules for the protein. As the peptide charges are less screened in the absence of NaCl in the buffer, one would assume that the peptides are even more elongated under these conditions and thus closer to the peptide-bound conformation, which would also result in a smaller entropy loss contributing to the higher affinity of the peptides for IL-8 under these conditions, which amounts to a factor of 3.5, 7.2 and 7.4 for p5-, p7- and p10-, respectively.

The last but very important descriptor of the interaction of IL-8 with these ligands is hydrogen bonding. Based on the MD simulation, we could analyze and compare the hydrogen bond pattern of HP vs. the four negatively charged decapeptides (Fig. 10). At first sight, no major differences in hydrogen bond formation are observed between the individual ligands and the C-terminal binding motif of IL-8. However, our analysis reveals that the hydrogen bonds with residues from the more N-terminal binding motif are much less frequent (Fig. 10). There are more H-bonds observed at the same frames of the trajectory for p5- and p10- in comparison to HP dp6, p3- and p7-. But taking only the H-bonds of the binding motive into account, p7- resembles the pattern of HP closest.

Conclusion

Taken together, although long ranged electrostatics is clearly a key player in IL-8/ligand interaction, it cannot fully explain the much higher affinity of GAGs for regulatory proteins compared to other polyelectrolytes, i.e., acidic peptides. Further aspects such as the ligand flexibility and conformational changes upon binding associated with an entropic contribution, ligand structural adaptability, hydrogen bond capacity, participation of the solvent in the establishment of the interface, and exact localization of negatively charged groups as well as their (chemical) nature have to be taken into account. Physiologically, it is highly important that regulatory proteins do not bind polyacidic ligands — which are found abundantly in extracellular fluids — as strongly as the cell surface GAGs. It appears that a fine balance of physical interactions favors GAG binding over binding of other ligands such as polyions, nucleic acid, or peptide fragments. To describe each of the relevant factors in more detail, investigations with more similar functional groups should be conducted. Nevertheless, all aforementioned factors act synergistically in providing some specificity of certain GAGs to preferentially bind regulatory proteins and direct them to the respective cells. This directed motion, mediated by a well-balanced network of GAGs of varying charge density and distribution, has been referred to as the “electrostatic bandpass”.⁸⁶ While in principle an appealing concept, the current comparison between negatively charged GAGs and peptides suggests that additional factors than electrostatics need to be considered to adequately describe the filtering of regulatory proteins by the extracellular matrix. This contributes a step towards understanding the specificity of protein–GAG biomolecular systems and the sulfation code, which remain highly challenging for analysis at the atomistic level.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the German Research Foundation (DFG) project numbers 426256511 and 58397982 and the National Science Centre of Poland (Narodowe Centrum Nauki, grant number UMO-2018/31/G/ST4/00246). The molecular docking calculations were performed on the ZIH cluster at TU Dresden (grant p_gag). The molecular dynamics simulations were performed on the PROMETHEUS cluster provided by Polish Grid Infrastructure (PL-GRID, grants kchtkat, plggagi, PLG/2020/014274 and PLG/2020/014275) as well as on the local “piasek” cluster. We thank Dr Albert Smith-Penzel for proof reading of the manuscript.

References

1. J. D. Esko, K. Kimata and U. Lindahl, in Essentials of Glycobiology, ed. A. Varki, R. D. Cummings, J. D. Esko, H. H. Freeze, P. Stanley, C. R. Bertozzi, G. W. Hart and M. E. Etzler, Cold Spring Harbor (NY), 2nd edn, 2009, Proteoglycans and Sulfated Glycosaminoglycans.
2. J. Schiller and D. Huster, New methods to study the composition and structure of the extracellular matrix in natural and bioengineered tissues, Biomatter, 2012, 2, 115–131.
3. H. Habuchi, O. Habuchi and K. Kimata, Sulfation pattern in glycosaminoglycan: does it have a code?, Glycoconjugate J., 2004, 21, 47–52.
4. J. Gallagher, Fell-Muir Lecture: heparan sulphate and the art of cell regulation: a polymer chain conducts the protein orchestra, Int. J. Exp. Pathol., 2015, 96, 203–231.
5. N. K. Karamanos, Z. Piperigkou, A. D. Theocharis, H. Watanabe, M. Franchi, S. Baud, S. Brézillon, M. Götte, A. Passi, D. Vigetti, S. Ricard-Blum, R. D. Sanderson, T. Neill and R. V. Iozzo, Proteoglycan Chemical Diversity Drives Multifunctional Cell Regulation and Therapeutics, Chem. Rev., 2018, 118, 9152–9232.
6. M. S. G. Pavão, Glycosaminoglycans analogs from marine invertebrates: structure, biological effects, and potential as new therapeutics, Front. Cell. Infect. Microbiol., 2014, 4, 123.
7. K. Karamanou, D. C. R. Espinosa, A. Fortuna-Costa and M. S. G. Pavão, Biological function of unique sulfated glycosaminoglycans in primitive chordates, Glycoconjugate J., 2017, 34, 277–283.
8. P. Chiodelli, A. Bugatti, C. Urbinati and M. Rusnati, Heparin/Heparan sulfate proteoglycans glycomic interactome in angiogenesis: biological implications and therapeutical use, Molecules, 2015, 20, 6342–6388.
9. F. M. Spinelli, D. L. Vitale, G. Demarchi, C. Cristina and L. Alaniz, The immunological effect of hyaluronan in tumor angiogenesis, Clin. Transl. Immunol., 2015, 4, e52.
10. S. D. Vallet, O. Clerc and S. Ricard-Blum, Glycosaminoglycan-Protein Interactions: The First Draft of the Glycosaminoglycan Interactome, J. Histochem. Cytochem., 2021, 69, 93–104.
11. Y. Monneau, F. Arenzana-Seisdedos and H. Lortat-Jacob, The sweet spot: how GAGs help chemokines guide migrating cells, J. Leukoc. Biol., 2016, 99, 935–953.
12. A. E. I. Proudfoot, Z. Johnson, P. Bonvin and T. M. Handel, Glycosaminoglycan Interactions with Chemokines Add Complexity to a Complex System, Pharmaceuticals, 2017, 10, 70.
13. G. Künze, D. Huster and S. A. Samsonov, Investigation of the structure of regulatory proteins interacting with glycosaminoglycans by combining NMR spectroscopy and molecular modeling – the beginning of a wonderful friendship, Biol. Chem., 2021, 402, 1337–1355.
14. S. Morla, Glycosaminoglycans and Glycosaminoglycan Mimetics in Cancer and Inflammation, Int. J. Mol. Sci., 2019, 20, 1963.
15. D. Vitale, S. Kumar Katakam, B. Greve, B. Jang, E.-S. Oh, L. Alaniz and M. Götte, Proteoglycans and glycosaminoglycans as regulators of cancer stem cell function and therapeutic resistance, FEBS J., 2019, 286, 2870–2882.
16. N. Afratis, C. Gialeli, D. Nikitovic, T. Tsegenidis, E. Karousou, A. D. Theocharis, M. S. Pavão, G. N. Tzanakakis and N. K. Karamanos, Glycosaminoglycans: key players in cancer cell biology and treatment, FEBS J., 2012, 279, 1177–1197.
17. T. Hosono-Fukao, S. Ohtake-Niimi, H. Hoshino, M. Britschgi, H. Akatsu, M. M. Hossain, K. Nishitsuji, T. H. van Kuppevelt, K. Kimata, M. Michikawa, T. Wyss-Coray and K. Uchimura, Heparan sulfate subdomains that are degraded by Sulf accumulate in cerebral amyloid β plaques of Alzheimer's disease: evidence from mouse models and patients, Am. J. Pathol., 2012, 180, 2056–2067.
18. N. Iwahashi, M. Ikezaki, T. Nishikawa, N. Namba, T. Ohgita, H. Saito, Y. Ihara, T. Shimanouchi, K. Ino, K. Uchimura and K. Nishitsuji, Sulfated glycosaminoglycans mediate prion-like behavior of p53 aggregates, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 33225–33234.
19. C. M. Simonaro, M. D’Angelo, X. He, E. Eliyahu, N. Shtraizent, M. E. Haskins and E. H. Schuchman, Mechanism of glycosaminoglycan-mediated bone and joint disease: implications for the mucopolysaccharidoses and other connective tissue diseases, Am. J. Pathol., 2008, 172, 112–122.
20. P. Johnson, A. A. Arif, S. S. M. Lee-Sayer and Y. Dong, Hyaluronan and Its Interactions With Immune Cells in the Healthy and Inflamed Lung, Front. Immunol., 2018, 9, 2787.
21. D. Scharnweber, L. Hübner, S. Rother, U. Hempel, U. Anderegg, S. A. Samsonov, M. T. Pisabarro, L. Hofbauer, M. Schnabelrauch, S. Franz, J. Simon and V. Hintze, Glycosaminoglycan derivatives: promising candidates for the design of functional biomaterials, J. Mater. Sci.: Mater. Med., 2015, 26, 232.
22. D. Xu and J. D. Esko, Demystifying heparan sulfate-protein interactions, Annu. Rev. Biochem., 2014, 83, 129–157.
23. D. Shi, A. Sheng and L. Chi, Glycosaminoglycan-Protein Interactions and Their Roles in Human Disease, Front. Mol. Biosci., 2021, 8, 639666.
24. in Essentials of Glycobiology, A. Varki, R. D. Cummings, J. D. Esko, P. Stanley, G. W. Hart, M. Aebi, D. Mohnen, T. Kinoshita, N. H. Packer, J. H. Prestegard, R. L. Schnaar and P. H. Seeberger, (ed.) Cold Spring Harbor (NY), 4th edn, 2022.
25. M. Guerrini, S. Guglieri, B. Casu, G. Torri, P. Mourier, C. Boudier and C. Viskov, Antithrombin-binding octasaccharides and role of extensions of the active pentasaccharide sequence in the specificity and strength of interaction. Evidence for very high affinity induced by an unusual glucuronic acid residue, J. Biol. Chem., 2008, 283, 26662–26675.
26. L. Jin, J. P. Abrahams, R. Skinner, M. Petitou, R. N. Pike and R. W. Carrell, The anticoagulant activation of antithrombin by heparin, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14683–14688.
27. V. Hintze, S. A. Samsonov, M. Anselmi, S. Moeller, J. Becher, M. Schnabelrauch, D. Scharnweber and M. T. Pisabarro, Sulfated glycosaminoglycans exploit the conformational plasticity of bone morphogenetic protein-2 (BMP-2) and alter the interaction profile with its receptor, Biomacromolecules, 2014, 15, 3083–3092.
28. N. Panitz, S. Theisgen, S. A. Samsonov, J.-P. Gehrcke, L. Baumann, K. Bellmann-Sickert, S. Köhling, M. T. Pisabarro, J. Rademann, D. Huster and A. G. Beck-Sickinger, The structural investigation of glycosaminoglycan binding to CXCL12 displays distinct interaction sites, Glycobiology, 2016, 26, 1209–1221.
29. S. Rother, S. A. Samsonov, T. Hofmann, J. Blaszkiewicz, S. Köhling, S. Moeller, M. Schnabelrauch, J. Rademann, S. Kalkhof, M. von Bergen, M. T. Pisabarro, D. Scharnweber and V. Hintze, Structural and functional insights into the interaction of sulfated glycosaminoglycans with tissue inhibitor of metalloproteinase-3 – A possible regulatory role on extracellular matrix homeostasis, Acta Biomater., 2016, 45, 143–154.
30. L. Koehler, S. Samsonov, S. Rother, S. Vogel, S. Köhling, S. Moeller, M. Schnabelrauch, J. Rademann, U. Hempel, M. T. Pisabarro, D. Scharnweber and V. Hintze, Sulfated Hyaluronan Derivatives Modulate TGF-β1:Receptor Complex Formation: Possible Consequences for TGF-β1 Signaling, Sci. Rep., 2017, 7, 1210.
31. S. T. Olson, H. R. Halvorson and I. Björk, Quantitative characterization of the thrombin-heparin interaction. Discrimination between specific and nonspecific binding models, J. Biol. Chem., 1991, 266, 6342–6352.
32. V. H. Pomin and B. Mulloy, Current structural biology of the heparin interactome, Curr. Opin. Struct. Biol., 2015, 34, 17–25.
33. A. Almond, Multiscale modeling of glycosaminoglycan structure and dynamics: current methods and challenges, Curr. Opin. Struct. Biol., 2018, 50, 58–64.
34. J. Sage, F. Mallèvre, F. Barbarin-Costes, S. A. Samsonov, J.-P. Gehrcke, M. T. Pisabarro, E. Perrier, S. Schnebert, A. Roget, T. Livache, C. Nizard, G. Lalmanach and F. Lecaille, Binding of chondroitin 4-sulfate to cathepsin S regulates its enzymatic activity, Biochemistry, 2013, 52, 6487–6498.
35. A. Penk, L. Baumann, D. Huster and S. A. Samsonov, NMR and molecular modeling reveal specificity of the interactions between CXCL14 and glycosaminoglycans, Glycobiology, 2019, 29, 715–725.
36. C. I. Gama, S. E. Tully, N. Sotogaku, P. M. Clark, M. Rawat, N. Vaidehi, W. A. Goddard, A. Nishi and L. C. Hsieh-Wilson, Sulfation patterns of glycosaminoglycans encode molecular recognition and activity, Nat. Chem. Biol., 2006, 2, 467–473.
37. P. R. B. Joseph, P. D. Mosier, U. R. Desai and K. Rajarathnam, Solution NMR characterization of chemokine CXCL8/IL-8 monomer and dimer binding to glycosaminoglycans: structural plasticity mediates differential binding interactions, Biochem. J., 2015, 472, 121–133.
38. A. D. Cardin and H. J. Weintraub, Molecular modeling of protein-glycosaminoglycan interactions, Arteriosclerosis, 1989, 9, 21–32.
39. G. S. Kuschert, A. J. Hoogewerf, A. E. Proudfoot, C. W. Chung, R. M. Cooke, R. E. Hubbard, T. N. Wells and P. N. Sanderson, Identification of a glycosaminoglycan binding surface on human interleukin-8, Biochemistry, 1998, 37, 11193–11201.
40. D. Spillmann, D. Witt and U. Lindahl, Defining the interleukin-8-binding domain of heparan sulfate, J. Biol. Chem., 1998, 273, 15487–15493.
41. W. Bitomsky and R. C. Wade, Docking of Glycosaminoglycans to Heparin-Binding Proteins: Validation for aFGF, bFGF, and Antithrombin and Application to IL-8, J. Am. Chem. Soc., 1999, 121, 3004–3013.
42. H. Lortat-Jacob, A. Grosdidier and A. Imberty, Structural diversity of heparan sulfate binding domains in chemokines, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1229–1234.
43. E. Krieger, E. Geretti, B. Brandner, B. Goger, T. N. Wells and A. J. Kungl, A structural and dynamic model for the interaction of interleukin-8 and glycosaminoglycans: support from isothermal fluorescence titrations, Proteins, 2004, 54, 768–775.
44. N. S. Gandhi and R. L. Mancera, Molecular dynamics simulations of CXCL-8 and its interactions with a receptor peptide, heparin fragments, and sulfated linked cyclitols, J. Chem. Inf. Model., 2011, 51, 335–358.
45. A. Pichert, S. A. Samsonov, S. Theisgen, L. Thomas, L. Baumann, J. Schiller, A. G. Beck-Sickinger, D. Huster and M. T. Pisabarro, Characterization of the interaction of interleukin-8 with hyaluronan, chondroitin sulfate, dermatan sulfate and their sulfated derivatives by spectroscopy and molecular modeling, Glycobiology, 2012, 22, 134–145.
46. D. Schlorke, L. Thomas, S. A. Samsonov, D. Huster, J. Arnhold and A. Pichert, The influence of glycosaminoglycans on IL-8-mediated functions of neutrophils, Carbohydr. Res., 2012, 356, 196–203.
47. K. Möbius, K. Nordsieck, A. Pichert, S. A. Samsonov, L. Thomas, J. Schiller, S. Kalkhof, M. Teresa Pisabarro, A. G. Beck-Sickinger and D. Huster, Investigation of lysine side chain interactions of interleukin-8 with heparin and other glycosaminoglycans studied by a methylation-NMR approach, Glycobiology, 2013, 23, 1260–1269.
48. K. Nordsieck, A. Pichert, S. A. Samsonov, L. Thomas, C. Berger, M. T. Pisabarro, D. Huster and A. G. Beck-Sickinger, Residue 75 of interleukin-8 is crucial for its interactions with glycosaminoglycans, ChemBioChem, 2012, 13, 2558–2566.
49. T. Hofmann, S. A. Samsonov, A. Pichert, K. Lemmnitzer, J. Schiller, D. Huster, M. T. Pisabarro, M. von Bergen and S. Kalkhof, Structural analysis of the interleukin-8/glycosaminoglycan interactions by amide hydrogen/deuterium exchange mass spectrometry, Methods, 2015, 89, 45–53.
50. P. R. B. Joseph, K. V. Sawant, J. Iwahara, R. P. Garofalo, U. R. Desai and K. Rajarathnam, Lysines and Arginines play non-redundant roles in mediating chemokine-glycosaminoglycan interactions, Sci. Rep., 2018, 8, 12289.
51. G. Paiardi, M. Milanesi, R. C. Wade, P. D’Ursi and M. Rusnati, A Bittersweet Computational Journey among Glycosaminoglycans, Biomolecules, 2021, 11, 739.
52. W. Lee, M. Tonelli and J. L. Markley, NMRFAM-SPARKY: enhanced software for biomolecular NMR spectroscopy, Bioinformatics, 2015, 31, 1325–1327.
53. S. Berkamp, S. H. Park, A. A. de Angelis, F. M. Marassi and S. J. Opella, Structure of monomeric Interleukin-8 and its interactions with the N-terminal Binding Site-I of CXCR1 by solution NMR spectroscopy, J. Biomol. NMR, 2017, 69, 111–121.
54. S. Mori, C. Abeygunawardana, M. O. Johnson and P. C. van Zijl, Improved sensitivity of HSQC spectra of exchanging protons at short interscan delays using a new fast HSQC (FHSQC) detection scheme that avoids water saturation, J. Magn. Reson., Ser. B, 1995, 108, 94–98.
55. V. Sklenar, M. Piotto, R. Leppik and V. Saudek, Gradient-Tailored Water Suppression for ¹H–¹⁵N HSQC Experiments Optimized to Retain Full Sensitivity, J. Magn. Reson., Ser. A, 1993, 102, 241–245.
56. A. Shaka, P. Barker and R. Freeman, Computer-optimized decoupling scheme for wideband applications and low-level operation, J. Magn. Reson., 1985, 64, 547–552.
57. M. P. Williamson, Using chemical shift perturbation to characterise ligand binding, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 73, 1–16.
58. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, UCSF Chimera—a visualization system for exploratory research and analysis, J. Comput. Chem., 2004, 25, 1605–1612.
59. G. M. Clore, E. Appella, M. Yamada, K. Matsushima and A. M. Gronenborn, Three-dimensional structure of interleukin 8 in solution, Biochemistry, 1990, 29, 1689–1696.
60. D. A. Case, R. M. B. D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, 2016.
61. B. Mulloy, M. J. Forster, C. Jones and D. B. Davies, N.m.r. and molecular-modelling studies of the solution conformation of heparin, Biochem. J., 1993, 293, 849–858.
62. G. M. Morris, D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew and A. J. Olson, Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function, J. Comput. Chem., 1998, 19, 1639–1662.
63. M. Ester, H.-P. Kriegel, J. Sander and X. Xu, Proceedings of 2^nd International Conference on Knowledge Discovery and Data Mining (KDD), AAAI Press, Portland, Oregon, 1996, pp. 226–231.
64. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713.
65. K. K. Bojarski, A. K. Sieradzan and S. A. Samsonov, Molecular dynamics insights into protein-glycosaminoglycan systems from microsecond-scale simulations, Biopolymers, 2019, 110, e23252.
66. B. L. Welch, The generalisation of student's problems when several different population variances are involved, Biometrika, 1947, 34, 28–35.
67. M. Marcisz, B. Huard, A. G. Lipska and S. A. Samsonov, Further analyses of APRIL/APRIL-receptor/glycosaminoglycan interactions by biochemical assays linked to computational studies, Glycobiology, 2021, 31, 772–786.
68. D. R. Roe and T. E. Cheatham, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095.
69. R Core Team, R: A language and environment for statistical computing, http://www.R-project.org/, (accessed 19 August 2022).
70. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. Del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Array programming with NumPy, Nature, 2020, 585, 357–362.
71. W. McKinney, in Proceedings of the 9^th Python in Science Conference SciPy 2010, ed. S. van der Walt and J. Millman, 2010, pp. 56–61.
72. J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9, 90–95.
73. T. Williams and C. Kelley, Gnuplot 4.5: An interactive plotting program, http://gnuplot.inf, (accessed 19 August 2022).
74. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(33–38), 27–28.
75. K. W. Walker and R. A. Bradshaw, Yeast methionine aminopeptidase I. Alteration of substrate specificity by site-directed mutagenesis, J. Biol. Chem., 1999, 274, 13403–13409.
76. L. He, S. André, H.-C. Siebert, H. Helmholz, B. Niemeyer and H.-J. Gabius, Detection of Ligand- and Solvent-Induced Shape Alterations of Cell-Growth-Regulatory Human Lectin Galectin-1 in Solution by Small Angle Neutron and X-Ray Scattering, Biophys. J., 2003, 85, 511–524.
77. S. Baranova, F. V. Tuzikov, O. D. Zakharova, N. A. Tuzikova, C. Calmels, S. Litvak, L. Tarrago-Litvak, V. Parissi and G. A. Nevinsky, Small-angle X-ray characterization of the nucleoprotein complexes resulting from DNA-induced oligomerization of HIV-1 integrase, Nucleic Acids Res., 2007, 35, 975–987.
78. N. S. Gandhi and R. L. Mancera, The structure of glycosaminoglycans and their interactions with proteins, Chem. Biol. Drug Des., 2008, 72, 455–482.
79. A. Imberty, H. Lortat-Jacob and S. Pérez, Structural view of glycosaminoglycan-protein interactions, Carbohydr. Res., 2007, 342, 430–439.
80. S. A. Samsonov, L. Bichmann and M. T. Pisabarro, Coarse-grained model of glycosaminoglycans, J. Chem. Inf. Model., 2015, 55, 114–124.
81. S. D. Burrows, M. L. Doyle, K. P. Murphy, S. G. Franklin, J. R. White, I. Brooks, D. E. McNulty, M. O. Scott, J. R. Knutson and D. Porter, Determination of the monomer-dimer equilibrium of interleukin-8 reveals it is a monomer at physiological concentrations, Biochemistry, 1994, 33, 12741–12745.
82. S. A. Samsonov, J. Teyra and M. T. Pisabarro, Docking glycosaminoglycans to proteins: analysis of solvent inclusion, J. Comput.-Aided Mol. Des., 2011, 25, 477–489.
83. D. L. Nelson and M. M. Cox, Lehninger Biochemie, Springer, Berlin, Heidelberg, New York, Barcelona, Hongkong, London, Mailand, Paris, Tokio, 3rd edn, 2001.
84. K. E. Kuettner and A. Lindenbaum, Analysis of mucopolysaccharides in partially aqueous media, Biochim. Biophys. Acta, 1965, 101, 223–225.
85. M. Remko, R. Broer and P. T. van Duijnen, How acidic are monomeric structural units of heparin?, Chem. Phys. Lett., 2013, 590, 187–191.
86. O. Lieleg, R. M. Baumgärtel and A. R. Bausch, Selective filtering of particles by the extracellular matrix: an electrostatic bandpass, Biophys. J., 2009, 97, 1569–1577.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02457a

‡ These authors contributed equally.

---