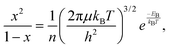Can photoluminescence quenching be a predictor for perovskite solar cell efficiencies?

Abstract

Bromide-based perovskites have large bandgaps, making them attractive for tandem solar cells developed to overcome the Shockley–Queisser limit. A perovskite solar cell architecture employs transporting layers to improve charge extraction and transport. Due to the wide variety of materials and preparation methods, it is critical to devise fast screening methods to rank transporting layers. Herein, we evaluate perovskite fluorescence quenching followed by time- and energy-resolved photoluminescence (TER-PL) and analyse the intensity dependence as a potential method to qualify charge-transporting layers rapidly. The capability of the technique was evaluated with TiO₂/FAPbBr₃ and SnO₂/FAPbBr₃, the most commonly used electron transporting layers, which were prepared using standard protocols to make best-performing devices. The results revealed that TiO₂ is the most effective quencher due to the higher density of states in the conduction band, consistent with Marcus-Gerischer's theory. However, record-performance devices use SnO₂ as the electron transport layer. This shows that the relationship between photoluminescence quenching and device performance is not bidirectional. Therefore, additional measurements like conductivity are also needed to provide reliable feedback for device performance.

---

Introduction

The current need for renewable energy has never been greater. Mankind faces a climate crisis due to the massive amount of greenhouse gases released into the atmosphere from burning fossil fuels. This has led to global warming, rising sea levels, and extreme weather events. Renewable energy sources such as solar, wind, hydro, geothermal, and biomass have become essential in the fight against climate change. They provide clean, abundant, and sustainable energy sources that can replace fossil fuels and reduce carbon emissions. The transition to renewable energy is critical to securing a sustainable future for ourselves and the planet. Significant research efforts are underway to improve and develop photovoltaics and wind-turbine technologies that can produce our electricity needs (ca. 26 000 TWh in 2020 and is forecast to grow 2.5–4% annually).¹

Solar cell technology has significantly advanced in recent years, increasing efficiency and lowering costs. New materials and manufacturing processes, such as perovskite solar cells and thin-film technologies, are being developed to improve performance further and reduce production costs. These developments make solar energy accessible and viable as a mainstream renewable energy source.

Lead perovskites, especially hybrid organic–inorganic lead halide perovskites, are promising materials for solar cells due to their high efficiency and low production cost. In 2009, Kojima et al.² introduced this class of materials as potential active materials for photovoltaics, reporting a device with an efficiency of around 9%, which has increased rapidly to more than 25%^3–5 in a short amount of time compared to other photovoltaic technology developments. Lead perovskites exhibit unique optoelectronic properties, such as high carrier mobility and tunable bandgaps, enabling the conversion of a large portion of sunlight into electricity. However, lead perovskites are also toxic materials, and their use poses environmental and health risks.⁶ Scientists are researching alternative materials that can replace lead and maintain the performance of lead perovskite solar cells, making them safer and more sustainable. There has been considerable progress in blocking the lead leakage,⁷ by introducing polymeric interlayers,^8–10 engineering material dimensionality,^11,12 and using tin as an alternative to lead.^13,14

Iodine-based perovskites dominate the performance records of photovoltaic cells. Still, bromide-based perovskites are gaining interest^15–21 due to their high V_oc, good chemical stability in ambient air,^22–24 and larger bandgap (around 2.3 eV), making them promising candidates for top cells in tandem devices. Perovskite solar cells utilise n–i–p or p–i–n architectures, in which the perovskites are ‘sandwiched’ between two transporting layers. Due to the variety of materials, developing fast methods to rank them and guide device development is paramount.

Transient and static photoluminescence quenching studies are widely performed to investigate the radiative charge recombination of light-absorbing materials. In the context of perovskite solar cell development, the photoluminescence quenching efficiency of the perovskite by a transporting layer is then correlated with photovoltaic performance.^25,26 Commonly, higher solar cell performances are obtained on devices with higher quenching efficiencies.^27–30 Indeed, Campanari et al. showed recently that quenching of photoluminescence under short-circuit conditions is an excellent parameter to assess the device efficiency.³¹

Invariably, photoluminescence quenching experiments are performed at the end of the development cycle to rationalize the obtained performance trends. This raises an important scientific question: is the relationship between photoluminescence quenching and device performance bidirectional? In other words, can photoluminescence quenching experiments performed at the start of the development cycle be used to predict device performance? An affirmative answer would offer a powerful strategy to screen materials without the need for the complex and labour-intensive process of device manufacturing. Additionally, it would enable standardised protocols for materials screening, less reliant on the operator's ability to make devices.

In this work, we test the hypothesis of using time and energy-resolved photoluminescence (TER-PL) with femtosecond pulse excitation studies.^32–36 As a proof-of-concept, we used the two most commonly used electron transport layers (ETLs), SnO₂ and TiO₂, and FAPbBr₃ as the light absorber but assumed that nothing was known about their performance in photovoltaic devices. Quenching studies revealed that TiO₂ is a better quencher, which aligns with Marcus-Gerischer's theory but does not reflect the solar cell performance records. Therefore, we argue that TER-PL alone cannot be used as a predictor and needs additional data like conductivity; thus, the relationship is not bidirectional.

Experimental section

Preparation of perovskite samples

A colloidal dispersion of tin oxide (15% in H₂O, Alfa Aesar) was diluted with deionised water, and the volume ratio of water to SnO₂ was 4 : 1. Deposition of the SnO₂ dispersion on the glass slide was carried out using a spin coating method at 3000 rpm for 30 seconds. The film was then annealed at 150 °C for 30 minutes, followed by UV/ozone treatment for 20 minutes. The TiO₂ film was prepared on the glass slide using the spray pyrolysis method. The precursor solution was made by mixing 600 μL titanium diisopropoxide bis(acetylacetonate) with 400 μL acetylacetone in 9 mL ethanol solvent. The TiO₂ film was finally annealed at 500 °C for 30 minutes.

FAPbBr₃ was fabricated using a two-step solution method. 1.1 M PbBr₂ solution was prepared in a mixture solvent of DMF and DMSO with a volume ratio of 9 : 1 and stirred at 60 °C overnight. The first step was spin-coating the PbBr₂ solution on different substrates at 1500 rpm for 20 seconds, followed by 5000 rpm for 30 seconds. Then, the films were transferred to a hot plate and annealed at 70 °C for 1 min. The second step was depositing FABr (65 mg mL⁻¹ in methanol) solution over the PbBr₂ films (2000 rpm, 30 s), and perovskite films were annealed at 140 °C for 25 min in the air. Devices for measuring the conductivity were fabricated on the FTO glass, and 100 nm Ag was deposited by thermal evaporation as the electrode.

Characterisation of films

Time- and energy-resolved photoluminescence measurements were performed using a 515 nm excitation wavelength generated from the fundamental 1030 nm laser (200 kHz, Jasper 10, Fluence). The fluorescence was collected through a streak camera detection system (C5680 + M5675, Hamamatsu). A graduated neutral density filter adjusted the pump power. And the angle of the excitation beam hitting the perovskite side was 45°. After being transmitted through an extended pass filter, PL emission was detected by the streak camera. The temporal resolution of the camera is ca. 10 ps.

I–V curves for the conductivity experiment were obtained using an Ossila Solar Cell I–V Test System. The applied voltage range was from 1 V to −1 V, and the voltage increment was 20 mV.

Results and discussion

FAPbBr₃ is a wide-band gap perovskite (around 2.2 eV) with a cubic crystal structure after thermal annealing.³⁷ Compared with the FAPbI₃ perovskite, the FAPbBr₃ counterpart has a higher exciton binding energy, ranging from 24 to 80 meV.^38,39 Previously, we estimated our exciton binding energy to be ca. 60 meV.³⁷ Therefore, with an excitation energy of 2.4 eV (i.e. 515 nm), the coexistence of free charges and bounded excitons in FAPbBr₃ is to be expected. This work focuses on energy-resolved transient photoluminescence (PL) studies under variable laser fluencies. The stability of FAPbBr₃ was evaluated by exposing it to the highest illumination power for several hours. There was no significant change in the shape of PL spectra (see the ESI,† Fig. S1), suggesting that FAPabBr₃ has good stability and can tolerate the laser condition employed in this study. Additionally, there were no measurable differences in the optical and structural data of the perovskite grown on glass, TiO₂ and SnO₂, suggesting that the light-absorbing material is by and large the same, at least when it comes to its bulk.

Based on our previous study,³⁷ deconvolutions of the PL spectrum revealed two peaks resulting from the recombination of free carriers (high energy emission, in the presence study ca. 520 nm) and excitons (low energy emission, in the presence study ca. 550 nm) (Fig. 2a inset). There is a conversion between free charges and excitons and equilibrium between these two states. The binding energy and excitation density determine the fraction of free charges and excitons. When the number of free carriers increases, electrons have more chance to encounter holes and, consequently, more excitons will be formed. This behaviour can be described by the Saha-Langmuir equation,^40,41 which is

where x is the ratio of free charges (electrons) over the total excitation density, E_B is the exciton binding energy, h is the Planck constant, T is the temperature, and k_B is the Boltzmann constant, and μ is the reduced mass of the exciton. Four binding energies, higher than the energy at room temperature (25 meV), were chosen to simulate the Saha-Langmuir equation (Fig. 1a). The dissociation of excitons into free charges tends to be less efficient in materials with higher exciton binding energy, consistent with the simulated data.

Fig. 1 The population of excited species in the FAPbBr₃ film under various excitation densities. (a) Simulation of the free charge according to the Saha-Langmuir equation with a binding energy E_B of 60 meV and a reduced mass of exciton μ of 0.15 m_e. (b) Simulation data calculated by multiplying the species fraction with the excitation density and experimental data of the exciton and free charge densities calculated from PL^max.

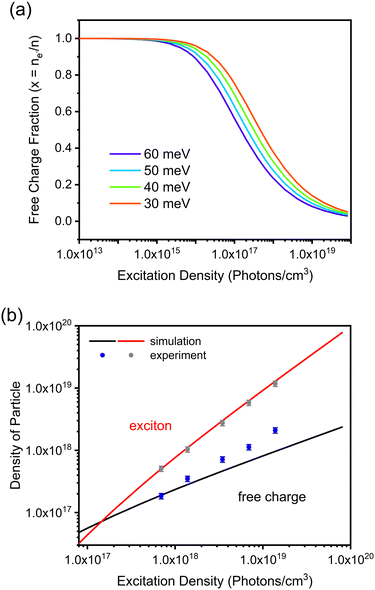
Considering the exciton binding energy (60 meV) and assuming a reduced mass of the exciton to be μ = 0.15 m_e,⁴² it is possible to estimate the densities of free carriers and excitons as a function of laser fluence (Fig. 1b). The increase in laser fluency increases the proportion of excitons in the material, consistent with what has been reported for other perovskites.^41,43,44 To see how well the simulated data represent the experimental results, the PL^max signal was deconvoluted and over-plotted on the simulated data (Fig. 1b). There is considerable agreement between the simulated and experimental data, supporting the values of exciton binding energy and reduced mass used. Moreover, under the used excitation energies, the (10¹⁷ to 10¹⁹ photons per cm³) excitons are the dominant species in the perovskite material.

Before proceeding with the results and their discussion, two important notes should be made. First, there are other processes like the Auger process, exciton–exciton interactions and electron–hole plasma that can affect the population of free carriers and exciton in the material. To minimize their contribution, the excitation wavelength was kept close to the bandgap, and the laser fluencies below levels can induce non-linear processes and multiple excitons per unit cell. Therefore, it is reasonable to assume that these processes play a minor role in the population of free carriers and bound excitons. Second, free carriers are the preferred charges for extraction by the transport material. Excitons form free carriers, so by increasing the exciton population, one can study the transporting layers' true capabilities in charge extraction since free carriers are not limiting.

Time- and energy-resolved PL (TER-PL) is a powerful tool to investigate charge extraction since it analyses the changes in radiative recombination induced by quenching of the light absorber with a charge acceptor. The measurements of fluorescent materials, such as perovskites, are very sensitive because the radiative recombination is very high.^45,46 As the study deals with systems used in solid-state solar cells, the quenching of the FAPbBr₃ perovskite was evaluated using TiO₂ and SnO₂ semiconductors, the most widely used materials in the electron transport layer, which quench the PL by acting as electron acceptors. Following the generation of free charge carriers or excitons, charge carriers are transferred to the electron transport layer, decreasing the PL intensity from the perovskite material.

The rising edge on the transient part of the data showed little to no difference between the two studied systems, suggesting that quenching occurs faster than our temporal resolution (ca. 10 ps), and thus cannot be used to discriminate the systems. Conversely, the decays require complex deconvolution, as shown elsewhere, limiting their use for rapid screening. Therefore, this work focus is to evaluate if the energy-resolved intensity profiles can be used as predictors.

Fig. 2 compares the PL quenching efficacy of SnO₂ and TiO₂ at different laser fluencies. We studied the transient PL of the FAPbBr₃ thin film on different ETLs using a planar structure (i.e. compact ETL layer) to enable direct comparisons. The integrated PL spectra after 1000 ps show a higher quenching efficiency of TiO₂, especially at lower fluencies. This becomes even more apparent in the ratio between the unquenched PL of the perovskites (Fig. 3). It is also noticeable that the differences in quenching efficiencies narrow as the laser fluencies increase, which indicates some saturation of both materials. The first 1000 ps of the PL decay encompasses the charge transfer from perovskite to ETL, which one is trying to evaluate if it is a good predictor of material performance in solar cell devices.

Fig. 2 The integrated TER-PL spectra (1000 ps) of the FAPbBr₃/ETL films under various excitation densities were normalised by the exposure time and the scan number. (a) ∼1.4 × 10¹⁷ photons per cm³, (b) ∼1.4 × 10¹⁸ photons per cm³, and (c) ∼1.4 × 10¹⁹ photons per cm³. Inset figure (a) shows the deconvolution of the integrated TER-PL spectra (1000 ps) of the FAPbBr₃ films under an excitation density of 1.4 × 10¹⁷ photons per cm³.

Fig. 3 The ratio of PL intensity from the unquenched perovskite layer as a function of laser fluencies.

Higher PL quenching reflects the more efficient charge transfer process, often used as an indicator for higher solar cell performance.^47,48 However, it is widely known that SnO₂ devices’ performance^49,50 is rationalised based on the better band alignment and higher conductivity (Fig. 4). A larger band offset, as observed in the FAPbBr₃/SnO₂ system, provides the additional driving force for electron transfer. The rate of electron transfer reactions, the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor), is described by Marcus' theory, for which he received the Noble prize in Chemistry in 1992.⁵¹ The energy difference between the donor and the acceptor in these reactions drives electron transfer. This energy difference is quantified by the Gibbs free energy of the reaction (ΔG). According to Marcus's theory, the rate of an electron transfer reaction depends on the electronic coupling between the donor and acceptor, the reorganisation of the solvent and the energy difference between the donor and the acceptor.⁵² Since our systems are solid-state, solvent rearrangement does not play a role.

Fig. 4 Dark I–V curves for the FTO/ETL/Ag (100 nm) devices. When measured in this configuration, the ETL conductivity can be extracted from the curve slope in accordance to what has been published elsewhere.⁵³

While the theory was developed for molecular systems, the approach can be adapted and applied to solid-state systems, the so-called Marcus-Gerischer model.⁵⁴ For example, the Marcus theory successfully described electron transfer from the quantum dot to metal oxide.⁵⁵ Considering the conduction band offsets (the conduction band edge of SnO₂ is 0.2–0.3 eV lower than that of TiO₂),⁵⁶ a significant difference in the driving force between the systems is not expected. Therefore, the explanation for a higher transfer rate must be related to the electronic coupling between the donor and the acceptor and the density of states (DOS). The system with a higher DOS should be the one with higher transfer rates. The theoretical calculation has revealed that these two n-type semiconductors have different band-edge structures. TiO₂ has a higher DOS from the onset of the conduction band edge.⁵⁷ This justifies TiO₂'s higher quenching rate compared to SnO₂.

SnO₂ proficiency is related not only to the number of electrons it extracts from the perovskite but also to what it does with the ones that extract. The higher conductivity, as revealed by the higher slope in the I–V curve,⁵⁸ points to more efficient charge transport and, consequently, lower interfacial recombination. This has also been reported for other systems, such as plasmonic/semiconductors interfaces.⁵⁹ More importantly, the reported result shows that PL quenching measurements must be considered carefully as predictors of solar cell efficiencies.

Having established the motives for differences in quenching efficiencies, the accumulated time-resolved PL spectra after 1000 ps were carefully analysed to evaluate the difference between TiO₂ and SnO₂ when it comes to extraction of free carriers and bounded excitons. As mentioned, the free carriers have PL and bounded excitons at lower energy. Therefore, the analysis of the normalised PL band edge shifts should indicate the proportion of carrier extraction and provide information if free carriers have higher selectivity than bounded excitons. Fig. 5 shows that the PL band edges shift asymmetrically with increased laser fluency, confirming the hypothesis's validity.

Fig. 5 Normalized PL spectra of the FAPbBr₃/ETL films under various excitation densities: (a) FAPbBr₃/SnO₂ and (b) FAPbBr₃/TiO₂.

With the increment of excitation density, PL peaks in both systems become broader, with the FAPbBr₃/SnO₂ system showing broader peaks. Fig. 6 shows the differences in the asymmetric shifts. Starting with the lower energy region (bounded excitons), there is no significant difference in their proportion between the two systems. This indicates that exciton quenching, either directly or through their dissociated free carriers, is relatively the same in both systems and, thus, not the culprit for the quenching rate differences. This is, however, contrasted with what is observed in the high energy region (free carriers), where SnO₂ is less effective in their quenching (i.e., higher band edge shift) compared to TiO₂. This is once more consistent with the hypothesis that higher DOS provides a better overlap and, thus, higher transfer rates between the donor and the acceptor.

Fig. 6 Edge shifts of the FAPbBr₃/ETL films at various excitation densities and the reference sample was measured under the lowest excitation density: (a) Left edge and (b) right edge.

Conclusions

In conclusion, the transfer rates from FAPbBr₃ to SnO₂ and TiO₂ were studied by time- and energy-resolved PL at various illumination intensities as a means of evaluating if the relationship between photoluminescence quenching and device efficiency is bidirectional, which would enable PL to be used as a performance predictor. The transient part of the data did not provide a quick way to discriminate between systems, and thus one needs to focus on evaluating the energy-resolved intensity profiles. From these, it was possible to establish that the electron transfer rate was higher for TiO₂, which was surprising considering that SnO₂ performs better as a solar cell electron transporting layer. The result is, however, well understood based on Marcus-Gerischer theory and related to the higher DOS of TiO₂, which improves the overlap between the donor and the acceptor. The proficiencies of SnO₂ are related to better use of the charge injected because of its higher conductivity. The result shows that PL alone is not a good predictor of solar cell performance, and thus the relationship between photoluminescence quenching and device efficiency is not bidirectional. Consequently, PL analysis alone at the start of the device development cannot be used as a device performance predictor. Finally, analysis of PL peak asymmetric broadening is an excellent approach to determine what carriers are being transferred and how they change with excitation fluency.

Author contributions

All the authors participated in the planning of the study. Mr Geng and Ms Liu synthesised and prepared the samples and films. Mr Geng performed all the standard and transient characterisation methods, the latter with the help of Dr Zou. The data were analysed and curated by Mr Geng. Mr Geng drafted the manuscript with inputs from all the authors. Mr Geng prepared all the figures and tables. All the authors contributed to the final version of the manuscript and approved its submission.

Conflicts of interest

The authors declare that there are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the Physical Chemistry unit of the Department of Chemistry-Angström, Uppsala University, the Knut & Alice Wallenberg Foundation (grant no. 2019-0071) and the Swedish Energy Agency (grant no. 46330-19) for the financial support.

References

1. https://www.aljazeera.com/news/2022/1/20/interactive-how-much-of-your-countrys-electricity-is-renewable-infographic, Accessed on April the 24th, 2023.
2. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050.
3. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643.
4. H. S. Jung and N. G. Park, Small, 2015, 11, 10.
5. https://www.nrel.gov/pv/cell-efficiency.html, Accessed on April the 24th, 2023.
6. A. Extance, Nature, 2019, 570, 429.
7. J. Dou, Y. Bai and Q. Chen, Mater. Chem. Front., 2022, 6, 2779.
8. L. Zuo, H. Guo, D. W. deQuilettes, S. Jariwala, N. De Marco, S. Dong, R. DeBlock, D. S. Ginger, B. Dunn, M. Wang and Y. Yang, Sci. Adv., 2017, 3, e1700106.
9. M. Yavari, M. Mazloum-Ardakani, S. Gholipour, M. M. Tavakoli, N. Taghavinia, A. Hagfeldt and W. Tress, ACS Omega, 2018, 3, 5038.
10. M. Zhang, F. Wu, D. Chi, K. Shi and S. Huang, Mater. Adv., 2020, 1, 617.
11. J.-W. Lee, Z. Dai, T. H. Han, C. Choi, S.-Y. Chang, S.-J. Lee, N. De Marco, H. Zhao, P. Sun, Y. Huang and Y. Yang, Nat. Commun., 2018, 9, 3021.
12. M. Shao, T. Bie, L. Yang, Y. Gao, X. Jin, F. He, N. Zheng, Y. Yu and X. Zhang, Adv. Mater., 2022, 34, 2107211.
13. N. Sun, W. Gao, H. Dong, Y. Liu, X. Liu, Z. Wu, L. Song, C. Ran and Y. Chen, ACS Energy Lett., 2021, 6, 2863.
14. K. Gahlot, S. de Graaf, H. Duim, G. Nedelcu, R. M. Koushi, M. Ahmadi, D. Gavhane, A. Lasorsa, E. De Luca, P. Rudolf, P. C. A. van der Wel, M. A. Loi, B. J. Kooi, G. Portale, J. Calbo and L. Protesescu, Adv. Mater., 2022, 34, 2201353.
15. J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764.
16. E. Edri, S. Kirmayer, D. Cahen and G. Hodes, J. Phys. Chem. Lett., 2013, 4, 897.
17. Y. Zhang, Y. Liang, Y. Wang, F. Guo, L. Sun and D. Xu, ACS Energy Lett., 2018, 3, 1808.
18. N. Arora, M. I. Dar, M. Abdi-Jalebi, F. Giordano, N. Pellet, G. Jacopin, R. H. Friend, S. M. Zakeeruddin and M. Grätzel, Nano Lett., 2016, 16, 7155.
19. N. Arora, S. Orlandi, M. I. Dar, S. Aghazada, G. Jacopin, M. Cavazzini, E. Mosconi, P. Gratia, F. De Angelis, G. Pozzi, M. Grätzel and M. K. Nazeerudin, ACS Energy Lett., 2016, 1, 107.
20. J. Das, A. S. Subbiah, N. Mahuli, R. Singh and S. K. Sarkar, Energy Technol., 2017, 5, 1807.
21. H. Xu, Z. Liang, J. Ye, S. Xu, Z. Wang, L. Zhu, X. Chen, Z. Xiao, X. Pan and G. Liu, Chem. Eng. J., 2022, 437, 135181.
22. S. Albrecht, M. Saliba, J. P. Correa Baena, F. Lang, L. Kegelmann, M. Mews, L. Steier, A. Abate, J. Rappich, L. Korte, R. Schlatmann, M. K. Nazeerudin, A. Hagfeldt, M. Grätzel and B. Rech, Energy Environ. Sci., 2016, 9, 81.
23. J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584.
24. X. Zheng, B. Chen, M. Yang, C. Wu, B. Orler, R. B. Moore, K. Zhu and S. Priya, ACS Energy Lett., 2016, 1, 424.
25. F. C. Hanusch, E. Wiesenmayer, E. Mankel, A. Binek, P. Angloher, C. Fraunhofer, N. Giesbrecht, J. M. Feckl, W. Jaegermann, D. Johrendt, T. Bein and P. Docampo, J. Phys. Chem. Lett., 2014, 4, 2791.
26. S. Li, C. Deng, L. Tao, Z. Lu, W. Zhang and W. Song, J. Phys. Chem. C, 2021, 125, 12551.
27. H. Zhang, J. Cheng, F. Lin, H. He, J. Mao, K. S. Wong, A. K.-Y. Jen and W. C. H. Choy, ACS Nano, 2016, 10, 1503.
28. T. Du, W. Xu, M. Daboczi, J. Kim, S. Xu, C.-T. Lin, H. Kang, K. Lee, M. J. Heeney, J.-S. Kim, J. R. Durrant and M. A. McLachlan, J. Mater. Chem. A, 2019, 7, 18971.
29. L. Wagner, P. Schygulla, J. P. Herterich, M. Elshamy, D. Bogachuk, S. Zouhair, S. Mastroianni, U. Würfel, Y. Lie, S. M. Zakeeruddin, M. Grätzel, A. Hinsch and S. W. Glunz, Matter, 2022, 5, 2352.
30. S. Hu, X. Yan, Y. Zhang, B. Yang, H. Li and C. Sheng, Appl. Sci., 2021, 11, 2683.
31. V. Campanari, F. Martelli, A. Agresti, S. Pescetelli, N. Y. Nia, F. Di Giacomo, D. Catone, P. O’Keeffe, S. Turchini, B. Yang, J. Suo, A. Hagfeldt and A. Di Carlo, Sol. RRL, 2022, 6, 2200049.
32. Z. Zhang, X. Wang, Y. Chen, Z. Zheng, W. Xu, W. Liu, Y. Yang, J. Zhao, T. Chen and H. Zhu, Nat. Commun., 2019, 10, 4540.
33. X. Liu, Y. Zhang, L. Shi, Z. Liu, J. Huang, J. S. Yun, Y. Zeng, A. Pu, K. Sun, Z. Hamieri, J. A. Stride, J. Seidel, M. A. Green and X. Hao, Adv. Energy Mater., 2018, 8, 1800138.
34. P. Zhu, S. Gu, X. Luo, Y. Gao, S. Li, J. Zhu and H. Tan, Adv. Energy Mater., 2020, 10, 1903083.
35. V. C. Nair, C. Muthu, A. L. Rogach, R. Kohara and V. Biju, Angew. Chem., Int. Ed., 2017, 56, 1214.
36. X. Tang, M. Khurana, D. Rossi, L. Luo, A. V. Akimov and D. H. Son, J. Phys. Chem. C, 2022, 126, 18366.
37. X. Geng, Y. Liu, X. Zou, E. M. J. Johansson and J. Sá, J. Phys. Chem. C, 2023, 127, 3085.
38. M. Baranowski and P. Plochocka, Adv. Energy Mater., 2020, 10, 1903659.
39. M. Jain, D. Gill, P. Bhumia, P. Basera and S. Bhattacharya, Appl. Phys. Lett., 2021, 118, 192130.
40. V. D’Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani and H. J. Snaith, Nat. Commun., 2014, 5, 3586.
41. N. Droseros, G. Longo, J. C. Brauer, M. Sessolo, H. J. Bolink and N. Banerji, ACS Energy Lett., 2018, 3, 1458.
42. K. Tanaka, T. Takahashi, T. Ban, T. Kondo, K. Uchida and N. Miura, Sol. State Commun., 2003, 127, 619.
43. S. D. Stranks, V. M. Burlakov, T. Leijtens, J. M. Ball, A. Goriely and H. J. Snaith, Phys. Rev. Appl., 2014, 2, 034007.
44. S. Draguta, S. Thakur, Y. V. Morozov, Y. Wang, J. S. Manser, P. V. Kamat and M. Kuno, J. Phys. Chem. Lett., 2016, 7, 715.
45. Y. Zu, J. Xi, L. Li, J. Dai, S. Wang, F. Yun, B. Jiao, H. Dong, X. Hou and Z. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 2835.
46. A. Perumal, S. Shendre, M. Li, Y. K. E. Tay, V. K. Sharma, S. Chen, S. Wei, Q. Liu, Y. Gao, P. J. S. Buenconsejo, S. T. tan, C. L. Gan, Q. Xiong, T. C. Sun and H. V. Demir, Sci. Rep., 2016, 6, 36733.
47. Q. Jiang, L. Zhang, H. Wang, X. Yang, J. Meng, H. Liu, Z. Yin, J. Wu, X. Zhang and J. You, Nat. Energy, 2017, 2, 16177.
48. D. Yang, R. Yang, K. Wang, C. Wu, X. Zhu, J. Feng, X. Ren, G. Fang, S. Priya and S. Liu, Nat. Commun., 2018, 9, 3239.
49. H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin. and S. I. Seok, Nature, 2021, 598, 444.
50. J. Kim, K. W. Kim and C. W. Myung, Npj Comput. Mater., 2020, 6, 100.
51. https://www.nobelprize.org/prizes/chemistry/1992/marcus/lecture/, Accessed on April the 15th, 2023.
52. R. A. Marcus, J. Chem. Phys., 1956, 24, 966.
53. Y. Liu, Z. Liu and E.-C. Lee, ACS Appl. Energy Mater., 2019, 2, 1932.
54. R. Memming, Electron transfer theories, Semiconductor Electrochemistry, Wiley-VCH Verlag GmbH, vol. 24, ch. 6, 2015.
55. K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 29.
56. J. P. C. Baena, L. Steier, W. Tress, M. Saliba, S. Neutzner, T. Matsui, F. Giordano, T. J. Jacobsson, A. R. S. Kandada, S. M. Zakeeruddin, A. Petrozza, A. Abate, M. K. Nazeeruddin, M. Grätzel and A. Hagfeldt, Energy Environ. Sci., 2015, 8, 2928.
57. M. Dou and C. Persson, J. Appl. Phys., 2013, 113, 083703.
58. J. Obrzut and K. A. Page, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195211.
59. Y. Hattori, S. G. Ávarez, J. Meng, K. Zheng and J. Sá, ACS Appl. Nano Mater., 2021, 4, 2052.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02190d

---