The role of covalency in enhancing stability of Eu and Am complexes: a DFT comparison of BTP and BTPhen

Abstract

We compare the stabilities and bonding nature of [Eu/Am(BTPhen)₂(NO₃)]²⁺ complexes to those previously reported for [Eu/Am(BTP)₃]³⁺, and investigate whether more accurately reflecting the reaction conditions of the separation process by considering [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes instead of aquo complexes increases the selectivity of the separation ligands BTP and BTPhen for Am over Eu. The geometric and electronic structures of [Eu/Am(BTPhen)₂(NO₃)]²⁺ and [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) have been evaluated using density functional theory (DFT) and used as the basis for analysis of the electron density through the application of the quantum theory of atoms in molecules (QTAIM). Increased covalent bond character for the Am complexes of BTPhen over Eu analogues was found, with this increase more pronounced than that found in BTP complexes. BHLYP-derived exchange reaction energies were evaluated using the hydrated nitrates as a reference and a favourability for actinide complexation by both BTP and BTPhen was found, with the BTPhen ligand found to be more selective, with relative stability ≈0.17 eV greater than BTP.

---

1 Introduction

The processing of spent nuclear fuel has been an area of great focus since the inception of nuclear energy. While initial processing had militaristic aims, focus has shifted in later decades to minimising the environmental impact of spent nuclear fuel storage and maximising fuel resources. This focus remains today, with particular regard to the development of next-generation nuclear reactors. PUREX (Plutonium Uranium Redox EXtraction) remains the process by which uranium and plutonium is recovered from spent fuel, producing a raffinate which contains lanthanides (Ln) and the minor actinides (MA, typically considered to comprise Np, Am, Cm), the latter of which are responsible for most of the residual radioactivity. Removal of these minor actinides can reduce the radiotoxicity of the eventual waste product derived from PUREX raffinate, reducing the environmental impact of any subsequent geological disposal. The challenge, however, lies in the separation of the minor actinides from the lanthanides, the chemistry of the latter strongly resembling that of Am^III and Cm^III.

Despite this challenge, which is further exacerbated by the requirement that any process must stand up to highly acidic conditions with significant radioactivity, several ligands for Am/Eu separation have been identified and successfully tested, such as the N-donor ligand ‘trio’ developed for the European Selective ActiNide EXtraction (SANEX) process: the bis-triazinylpyridines (BTPs, 1), a family of ligands with high Am^III/Eu^III separation factors, with the drawback of problematic stripping of the ligands due to their strong binding with the actinide;^1–6 bis-triazinylbipyridines (BTBPs, 2), which show good selectivity and increased back-extraction capability in comparison to the BTPs, with the drawback of slow kinetics without the use of a phase-transfer agent;^4–7 and the bis-triazinylphenanthrolines (BTPhens, 3), which have much faster reaction kinetics than the BTBPs, owing to the cis-locked nature of the 1,10-phenanthroline moiety which replaces the 2,2,-bipyridine of the BTBPs, as well as high selectivity and efficiency (Fig. 1).^6,8,9

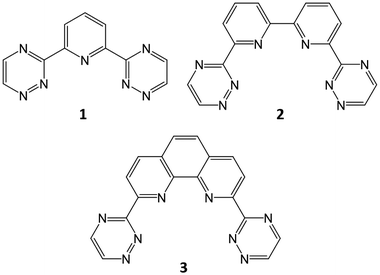Fig. 1 N-donor ligands for An/Ln separation: BTP (1); BTBP (2); and BTPhen (3). BTP and BTPhen (1 and 3) are considered in this study.

The tridentate BTP ligand forms symmetrical 3 : 1 ligand : metal complexes with the Ln/An centre with an overall charge of 3+. The existing literature shows that a wide range of computational and analytical methods have been used to investigate the differences in structure between selected Ln^III and An^III complexes. A combined effort of electrospray mass spectroscopy,^11,12 time-resolved laser-induced fluorescence spectroscopy (TRLFS),^13–19 X-ray photoelectron spectroscopy (XPS) and extended X-ray absorption fine structure spectroscopy (EXAFS)^{13,16,20–24} with complementary DFT studies^16,21,25,26 have probed the structure of [Ln/An(BTP)_n]³⁺ (n = 1–3), with a general focus on the complexes of Ln = Eu, Gd and An = U–Cm due to their relevance to the separation process. A trend of decreasing metal–ligand bond length with decreasing Ln^III ionic radius was observed spectroscopically across the lanthanides,^{13,16,20–24} in contrast to the bond lengths of the actinide complexes, which were observed to be largely independent of An^III ionic radius.^13,21,27,28

Additionally, there are many examples of computational investigations into the selective binding of these ligands, both for the BTP ligand and other nitrogen donor ligands, such as BTBP (6,6′-bis(1,2,4-triazin-3-yl)-2,2′-bipyridine) and BTPhen (2,9-bis(1,2,4-triazin-3-yl)-1,10-phenanthroline).^26,29–41 Focal to many of these studies are the differences in energies of the Ln^III and An^III complexes. Despite the large separation factors exhibited by these ligands, these energetic differences amount to only hundredths to tenths of an electronvolt;^31,32,34,38 for instance, Lan et al.^31–33 report that for the reaction M(NO₃)₃ (H₂O)₄ + L → M(L)(NO₃)₃ + 4H₂O, (L = BTBPs) the formation of M(L)(NO₃)₃ is favoured energetically when M = Am compared to M = Eu by 0.13 eV in the DFT-calculated Gibbs free energy for L = BTBP and 0.07 eV for L = CyMe₄-BTBP, obtained using the B3LYP xc-functional.³¹ For BTP, Trumm et al.³⁴ report the formation of the Cm complex to be 2.3 kcal mol⁻¹ (≈0.1 eV) more favourable than Gd in the gas-phase, calculated at the MP2 level on DFT structures optimised using the BHLYP xc-functional.

The high Am^III/Eu^III separation factors exhibited by these three families of ligands is thought to be due to an enhanced covalent interaction in the actinides due to the increased radial extent, and hence chemical availability, of the 5f orbitals, compared to the more core-like 4f orbitals of the lanthanides. In support of this, recent studies have shown growing evidence of correlations between covalent bond character and bond stability.^10,42–45 Our previous work employing Bader's quantum theory of atoms in molecules (QTAIM)⁴⁶ applied to density functional theory (DFT) derived electron densities has demonstrated an increase in the covalent character of the metal–ligand bonds of [An(H₂O)₉]³⁺ and [An(BTP)₃ ]³⁺ complexes (An = Am, Cm) compared to their Ln analogues (Ln = Eu, Gd), which was more pronounced in the BTP complexes than in the aquo complexes.¹⁰ Additionally, [An(H₂O)₉]³⁺ + [Ln(BTP)₃]³⁺ → [Ln(H₂O)₉]³⁺ + [An(BTP)₃]³⁺ exchange reaction energies were shown to favour An complexation by BTP for the Eu ↔ Am and Gd ↔ Cm reactions. Together, this selectivity of the BTP ligand and increase in covalent bonding character for Am over Eu and Cm over Gd implies a small but significant electronic contribution to An–BTP bond stability and the selectivity found experimentally.

Here, we present the results of DFT-based quantum chemical simulations and subsequent QTAIM analysis of [Eu/Am(BTPhen)₂(NO₃)]²⁺, in order to provide insight into the origin of the experimentally observed selectivity of the BTPhen ligand for the actinide through the evaluation of exchange reaction energies and the quantification of covalent character in equivalent Am–N and Eu–N bonds. We continue to present an analysis into the stability of [Eu/Am(BTP)₃]³⁺ complexes relative to the corresponding nitrate complexes.

Additionally, we investigate whether the properties of the [Eu/Am(BTPhen)₂(NO₃)]²⁺ are greater in magnitude than those previously reported for the BTP ligand.¹⁰ We also present the results of the same simulation and analysis applied to the [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes, in an effort to better replicate the conditions of the separation process.

2 Methods

All calculations were performed using version 6.6 of the TURBOMOLE quantum chemistry code⁴⁷ using scalar-relativistic DFT. Three xc-functionals were employed: BLYP,^48,49 B3LYP^50,51 and BHLYP.⁵² BLYP is a functional based on the generalised gradient approximation (GGA), whereas B3LYP and BHLYP are hybrid GGA functionals, incorporating 20% and 50% of exact exchange, respectively. All optimisations were performed using the def-SVP (Eu and Am) and def2-SVP (H, C, N and O) basis sets of polarised double-ζ quality,⁵³ which is referred to from here onwards as def(2)-SVP. Single-point-energy calculations were performed at these optimised geometries using the def(2)-TZVP basis sets of polarised triple-ζ quality.⁵³ All calculations were performed in the presence of a water-like continuum solvent defined using the COSMO model⁵⁴ with the default radii r_O = 1.72 Å, r_C = 2.00 Å, r_N = 1.83 Å, r_H = 1.30 Å, r_Eu = 2.22 Å, and r_Am = 2.22 Å. Scalar relativistic effects were accounted for by replacing Eu and Am core electrons with the small-core pseudopotentials of Dolg and co-workers:^55–57 28 and 60 core electrons were replaced, respectively. Topological and integrated properties of the electron density were investigated with version 14 of the AIMAll code.⁵⁸

During the analysis of the topological and integrative properties (Tables 3 and 4), Δ_Am/Eu is taken as the percentage by which a given metric is greater for Am over Eu, N(Ω) = integrated electron density in atomic basin Ω, q(Ω) = total charge of basin Ω, λ(Ω) = localization index of basin Ω, [small rho, Greek, macron]_BCP = mean magnitude of the electron density at the M–N BCPs, [small delta, Greek, macron](Ω₁,Ω₂) = mean delocalisation index between atomic basins Ω₁ and Ω₂ and = mean Laplacian of ρ at the M–N BCPs. B3LYP-derived values are given in parentheses. All values are in atomic units (a.u.).

2.1 Structural characterisation

We have previously reported the structures of [Ln(H₂O)₉]³⁺ and [Ln(BTP)₃]³⁺ for Ln = Ce–Lu obtained using the BLYP, B3LYP and BHLYP xc-functionals.¹⁰ For [Ln(H₂O)₉]³⁺, the B3LYP and BHLYP functionals gave Ln–O bond lengths typically ≈0.01–0.03 Å shorter than those obtained with BLYP, with a more pronounced difference in the middle of the series (Gd–Dy); additionally, BHLYP-derived [Eu(BTP)₃]³⁺ bond lengths lay closer to EXAFS literature values than those derived using B3LYP. Similar functional differences were observed for Ln–N bond lengths in [Ln(BTP)₃]³⁺, with BLYP significantly overestimating bond lengths for the middle of the series. High expectation values of 〈S²〉 (in comparison to formal values) for these poor-quality BLYP structures was indicative of significant spin contamination, which the inclusion of exact exchange was found to significantly reduce.¹⁰ These overestimated expectation values, along with the poor performance of the BLYP functional when compared to experimentally determined structural data, indicated that the origin of this poor performance lay in the description of the electronic structure of the Ln ion, leading us to focus only on the electronic structures of the B3LYP and BHLYP-optimised complexes. As such, throughout this paper, we report only results obtained with the B3LYP and BHLYP functionals; due to the performance when compared to similar experimental systems^{10,31,32,34,38} and the production of better S² values, the primary focus of the discussion will be on BHLYP values.

For [Eu/Am(BTPhen)₂(NO₃)]²⁺ and [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) geometries were obtained through optimisation with B3LYP and BHLYP. Additionally, in our previous study, bond lengths were found to be typically ≈0.05 Å shorter in the presence of a continuum aqueous solvent than in the gas phase, and in better agreement with experimental values. For this reason, we also employed the COSMO solvent model when optimising the present complexes.

3 Results & discussion

3.1 Structure – [Eu/Am(BTPhen)₂(NO₃)]²⁺

Unlike the 3 : 1 complexes formed by the tridentate BTP ligands, the larger tetradentate BTPhen ligand forms 2 : 1 complexes with Eu and An ions.⁸ The [Eu/Am(BTPhen)₂]³⁺ complex has a coordination number of only 8 and can accommodate solvent molecules to achieve a coordination number of 9 or 10.⁸ As the ions to be separated by the SANEX process are maintained in a nitric acid solution, we have here investigated the [Eu/Am(BTPhen)₂(NO₃)]²⁺ complex, which incorporates a bidentate nitrate ligand, as reported for the [Ln(CyMe₄-BTPhen)₂(NO₃)]²⁺ complexes isolated and characterised by Lewis et al. (Ln = Eu) and Whittaker et al. (Ln = Pr, Eu, Tb, Yb) (Fig. 2).^8,59 Average optimised M–N and M–O_nitrate bond lengths for [Eu/Am(BTPhen)₂(NO₃)]²⁺ are reported in Table 1.

Fig. 2 BHLYP/def(2)-SVP optimised geometries of [Am(BTPhen)₂(NO₃)]²⁺.

Table 1 Average M–N and M–O_N (M = Eu/Am) bond lengths of BHLYP//def(2)-SVP- and B3LYP//def(2)-SVP-calculated [Eu/Am(BTP)₃]³⁺ (previous work)¹⁰ and [Eu/Am(BTPhen)₂(NO₃)]²⁺ geometries. B3LYP-derived values are given in parentheses. All values are in angstroms (Å)

Complex	R̄(MN)	R̄(MON)
[Eu(BTP)3]^3+	2.57
	(2.59)
[Am(BTP)3]^3+	2.60
	(2.61)
[Eu(BTPhen)2NO3]^2+	2.61	2.55
	(2.63)	(2.55)
[Am(BTPhen)2NO3]^2+	2.63	2.60
	(2.65)	(2.58)

---

The BHLYP- and B3LYP-calculated Eu–N bond lengths in BTPhen are ≈0.03–0.05 Å longer than the mean [Eu(CyMe₄-BTPhen)₂(NO₃)]²⁺ Eu–N bond lengths (2.587, 2.582 Å) reported by Lewis et al.⁸ Additionally, it would appear that B3LYP is overestimating M–N and underestimating M–O compared to BHLYP.

As in the BTP complexes, the BHLYP- and B3LYP-calculated bond lengths for the BTPhen complexes are similar, with at most a 0.02 Å difference. The Am–N bond lengths are ≈0.02 Å longer than the Eu–N bond lengths in the BTPhen complexes, consistent with the ≈0.03 Å Eu/Am–N bond length difference in the BTP complexes and Eu/Am–N bond length differences seen in other theoretical studies, for example that of Trumm et al. in 2015 in which the bond lengths for thirteen Gd complexes were all 0.02–0.05 Å shorter than their Cm analogues.⁶⁰ Additionally, while the M–N bond lengths in the BTPhen complexes are ≈0.03–0.04 Å longer than in the BTP complexes, the Eu–O_N bond lengths are 0.03–0.05 Å shorter than the corresponding Am–O_N bond lengths in the BTPhen complexes.

3.2 Structure – [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4)

In our previous study, we compared the BTP and aqueous complexes of Eu and Am. However, in the SANEX process, the ions must be extracted from the nitric acid environment of the PUREX raffinate. As such, we have optimised structures of [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes, to investigate whether the separation ligands exhibit greater An affinity when the ions are initially bound by nitrate ligands. In these complexes the nitrate ligands were modelled in a bidentate coordination mode, which is more favourable than the monodentate mode.⁶¹ Water was added in order to complete the first coordination sphere, with hydration numbers of 3 and 4 chosen to achieve coordination numbers of 9 and 10, matching the coordination numbers of the BTP and BTPhen complexes, respectively (Fig. 3). Average optimised M–O_N and M–O_W bond lengths for the [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes are reported in Table 2.

Fig. 3 BHLYP/def(2)-SVP optimised geometries of [Am(NO₃)₃(H₂O)_x] (x = 3 (A), 4 (B)).

Table 2 Average M–O_N and M–O_W bond lengths of BHLYP/def(2)-SVP and B3LYP/def(2)-SVP calculated [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) geometries. B3LYP-derived values are given in parentheses. All values are in angstroms (Å)

Complex	R̄(MON)	R̄ (MOW)
[Eu(NO3)3(H2O)3]	2.47	2.41
	(2.48)	(2.43)
[Am(NO3)3(H2O)3]	2.51	2.46
	(2.51)	(2.48)
[Eu(NO3)3(H2O)4]	2.51	2.47
	(2.51)	(2.50)
[Am(NO3)3(H2O)4]	2.54	2.52
	(2.54)	(2.54)

---

As in the BTP and BTPhen complexes, B3LYP-calculated bond lengths are similar to those obtained with BHLYP, with at most 0.03 Å difference. In both the x = 3 and x = 4 complexes, the average M–O_W bond lengths are shorter than the M–O_N bond lengths, by ≈0.03–0.05 Å when x = 3 and up to 0.04 Å when x = 4. Bond lengths are consistently longer by ≈0.03–0.07 Å when x = 4 than when x = 3, likely due to additional steric crowding caused by the additional bound water. The bond lengths in the Eu complexes are ≈0.03–0.05 Å shorter than their Am counterparts.

3.3 Eu vs. Am bonding in BTP and BTPhen complexes

To investigate the bonding character in the [Eu/Am(BTPhen)₂ (NO₃)]²⁺ and [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes, we have again employed the QTAIM, which we have previously used to investigate the bonding character in the [Eu/Am(H₂O)₉]³⁺ and [Eu/Am(BTP)₃]³⁺ complexes.¹⁰ These calculations were based on single-point-energy calculations using a SARC all-electron basis sets of polarised triple-zeta quality^62–65 along with the second-order Douglas–Kroll–Hess Hamiltonian in order to account for scalar relativistic effects; however, recently added functionality in our chosen analysis software has allowed us to instead use densities generated using the def(2)-TZVP basis sets, employing effective core potentials (ECP) (Tables 3 and 4), which we also employ when evaluating our reaction energies. For consistency we have therefore repeated the analysis of the [Eu/Am(H₂O)₉]³⁺ and [Eu/Am(BTP)₃]³⁺ complexes with these densities. Comparison of QTAIM values calculated utilising an ECP with those determined using an all electron basis set¹⁰ produces only small variations for the [Eu/Am(H₂O)₉]³⁺ and [Eu/Am(BTP)₃]³⁺ complexes; this similarity lends credence to both the appropriateness of the def(2)-TZVP//ECP model chemistry as well as to the robust transferability of the QTAIM analysis.

Table 3 Topological and integrated properties of BHLYP/def(2)-TZVP//BHLYP/def(2)-SVP and B3LYP/def(2)-TZVP//B3LYP/def(2)-SVP (parentheses) calculated electron densities of [Eu/Am(BTP)₃]³⁺ and [Eu/Am(BTPhen)₂(NO₃)₂]²⁺

Complex	q(M)	q̄(N)	N(M) − λ(M)	[small delta, Greek, macron](M,N)	[small rho, Greek, macron] BCP(M–N)
[Eu(BTP)3]^3+	2.29	−0.99	1.02	0.204	0.0422	0.131
	(2.18)	(−0.84)	(1.12)	(0.221)	(0.0416)	(0.122)
[Am(BTP)3]^3+	2.25	−0.98	1.21	0.240	0.0451	0.137
	(2.13)	(−0.84)	(1.36)	(0.264)	(0.0453)	(0.128)
Δ Am/Eu			18%	17%	7%
			(21%)	(19%)	(9%)
[Eu(BTPhen)2(NO3)]^2+	2.31	−1.07	1.00	0.187	0.0386	0.121
	(2.19)	(−0.91)	(1.12)	(0.201)	(0.0377)	(0.112)
[Am(BTPhen)2(NO3)]^2+	2.27	−1.06	1.18	0.222	0.0417	0.128
	(2.15)	(−0.91)	(1.33)	(0.240)	(0.0414)	(0.120)
Δ Am/Eu			18%	19%	8%
			(19%)	(20%)	(10%)

---

QTAIM partitions a molecular system into a contiguous space-filling set of atomic volumes bound by a zero flux surface which satisfies the condition ∇ρ(r)·n(r) = 0, where ρ(r) is the magnitude of the electron density at a point r and n(r) is a vector normal to the surface at that point. Molecular structure is revealed by critical points (CPs) in the electron density, i.e. points in space at which the first derivatives of ρ vanish. Two types of CPs are nuclear critical points (NCPs), which are local maxima of ρ(r) at the atomic nuclei, and bond critical points (BCPs), which lie at the points at which a minimum in ρ(r) between nuclei coincides with the interatomic surface defined by the zero-flux condition. Early characterisation of chemical bonding in QTAIM focused on the concept by which a bond path can be defined by two NCPs with a BCP situated on the line of minimum ρ(r), and the properties of the electron density at the BCP can be used to characterise the bonding interaction; however, in recent years a number of molecules have been presented in which a BCP and, as a result, a bond path is missing between two bonded atoms, leading to the need for refinement in QTAIM bond characterisation.^66–68 Three QTAIM metrics are typically used for this characterisation:⁶⁹ the magnitude of the electron density, ρ_BCP, the Laplacian of the electron density, ∇²ρ_BCP, and the energy density at the BCP, H_BCP. For a covalent interaction, a rule of thumb is that ρ_BCP is large and positive (>0.2 a.u.), while ∇²ρ_BCP and H_BCP are negative.

To enhance our ability to accurately characterise both existing bonds and their character, and to supplement this topological analysis, we also consider several integrated properties of the electron density: the atomic charge (q(M)), the localisation (λ(M)) and delocalisation (δ(M,N)) indices⁷⁰ due to their relation to the interatomic exchange–correlation energy, and the difference between the total electron density in the atomic basin and the localisation index (N(M) − λ(M)). Additionally, we have discounted H_BCP; as we have previously argued, H_BCP can be considered effectively equal to 0 in these complexes.¹⁰ Reported in Table 3 are the topological and integrated properties of [Eu/Am(BTPhen)₂(NO₃)]²⁺ as well as those derived from the repeated analysis of [Eu/Am(BTP)₃]³⁺ discussed above.

There is a slight excess of 0.04 (0.05) a.u. in the atomic charge on the metal centres of the Eu complexes compared to the Am complexes with both B3LYP and BHLYP; however, as we have previously argued, the localisation indices are more informative than q(M) with regard to bonding.^71–73 The difference between the total electron density in the atomic basin and the localisation index, N(M) − λ(M), provides the number of non-localised electrons in the atomic basin. Δ(N(M) − λ(M))v_Am/Eu, the percentage by which N(M) − λ(M) is greater for the Am complexes over that of the Eu complexes, is significant in both the BTP and BTPhen complexes – 18% (21%) and 18% (19%), respectively.

For both the BTP and BTPhen complexes, the small values of [small rho, Greek, macron]_BCP and the positive values of their Laplacian indicate that the metal–ligand interaction is predominantly ionic, as would be expected. While M–N [small rho, Greek, macron]_BCP values of the BTPhen complexes are lower than those of the BTP complexes, the lengths of the M–N bonds are longer in the BTPhen complexes. Instead we can consider Δ[small rho, Greek, macron]_Am/Eu, the percentage by which the Am [small rho, Greek, macron]_BCP values are larger than their Eu counterparts. Despite the Eu–N bond lengths being shorter than the Am–N bond lengths, Δ[small rho, Greek, macron]_Am/Eu is 7% (9%) for the BTP complexes, while Δ[small rho, Greek, macron]_Am/Eu for the BTPhen complexes is slightly larger at 8% (10%). In the same way, we can consider Δ[small delta, Greek, macron]_Am/Eu, the percentage by which [small delta, Greek, macron](Am, N) is greater than [small delta, Greek, macron](Eu, N), which is 17% (19%) for the BTP complexes and 19% (20%) for the BTPhen complexes.

Altogether, the QTAIM analysis of the BTP and BTPhen complexes show a slightly greater difference in covalency for the BTPhen complexes than seen in the BTP complexes. While these percentages are small, we have previously reported a 4% increase in the BHLYP-derived value of [small rho, Greek, macron]_BCP for An (An = Am, Cm) which is ≈3 standard deviations larger than the mean Ln (Ln = Ce–Lu) value (corresponding B3LYP-derived [small rho, Greek, macron]_BCP values are 6% larger and 4% standard deviations from the mean Ln value).¹⁰

3.4 Eu vs. Am bonding in aquo and nitrate complexes

We have previously argued that if covalent stabilisation of the An–N bond plays a role in the actinide selectivity of BTP, and hence BTPhen, complexes, then the difference in covalent character between the An–N and Ln–N bonds should be expected to be more pronounced than in the M–O bonds of the aquo complexes.¹⁰ QTAIM analysis of the nona-aquo complexes of Eu and Am confirmed that this was the case, with Δ(N(M) − λ(M))_Am/Eu, Δ[small rho, Greek, macron]_Am/Eu and Δ[small delta, Greek, macron]_Am/Eu values which were all lower than their equivalents in the BTP complexes.¹⁰ Here, we extend this argument to the [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes of Eu and Am, the topological and integrated properties for which are tabulated in Table 4, as well as the repeated analysis of [Eu/Am(H₂O)₉]³⁺.

Table 4 Topological and integrated properties of BHLYP/def(2)-TZVP//BHLYP/def(2)-SVP and B3LYP/def(2)-TZVP//B3LYP/def(2)-SVP (parentheses) calculated electron densities of [Eu/Am(H₂O)₉]³⁺ and [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4)

Complex	q(M)	q̄(ON)	q̄(OW)	N(M) − λ(M)	[small delta, Greek, macron](M,O)	[small rho, Greek, macron] BCP
[Eu(H2O)9]^3+	2.46		−1.27	0.91	0.196	0.0422	0.187
	(2.37)		(−1.20)	(1.00)	(0.213)	(0.0440)	(0.177)
[Am(H2O)9]^3+	2.45		−1.27	1.05	0.225	0.0455	0.188
	(2.36)		(−1.20)	(1.14)	(0.244)	(0.0455)	(0.178)
Δ Am/Eu				15%	15%	3%
				(15%)	(14%)	(4%)
[Eu(H2O)3(NO3)3]	2.40	−0.67	−1.27	0.98	0.205	0.0470	0.185
	(2.27)	(−0.62)	(−1.20)	(1.09)	(0.227)	(0.0465)	(0.172)
[Am(H2O)3(NO3)3]	2.38	−0.67	−1.27	1.12	0.234	0.0484	0.185
	(2.25)	(−0.62)	(−1.20)	(1.25)	(0.259)	(0.0485)	(0.173)
Δ Am/Eu				14%	14%	3%
				(14%)	(14%)	(4%)
[Eu(H2O)3(NO3)4]	2.41	−0.67	−1.26	0.96	0.182	0.0421	0.167
	(2.28)	(−0.62)	(−1.20)	(1.08)	(0.213)	(0.0440)	(0.177)
[Am(H2O)3(NO3)4]	2.38	−0.67	−1.26	1.11	0.210	0.0438	0.170
	(2.26)	(−0.62)	(−1.19)	(1.24)	(0.244)	(0.0455)	(0.178)
Δ Am/Eu				16%	15%	4%
				(15%)	(15%)	(6%)

---

While N(M) − λ(M), Δ[small delta, Greek, macron]_Am/Eu, [small rho, Greek, macron]_BCP and values vary in magnitude slightly between complexes, they are broadly similar, and the small values of [small rho, Greek, macron]_BCP and positive again indicate an ionic metal–ligand interaction. Looking once more at the percentage differences, Δ(N(M) − λ(M))_Am/Eu values are 14–16% (14–15%) for the nona-aquo and hydrated nitrate complexes, compared to the 18% increase (19–21%) in the BTP and BTPhen complexes; Δ[small rho, Greek, macron]_Am/Eu values are 3–4% (4–6%) compared to 7–8% (9–10%) and Δ[small delta, Greek, macron]_Am/Eu values are 14–15% (14–15%) compared to 17–19% (19–20%). Altogether, a trend in the Δ(N(M) − λ(M))_Am/Eu values emerges, as follows:

[Eu/Am(BTPhen)₂(NO₃)]²⁺ > [Eu/Am(BTP)₃]³⁺ > [Eu/Am(NO₃)₃(H₂O)₄] > [Eu/Am(H₂O)₉]³⁺ > [Eu/Am(NO₃)₃(H₂O)₃] (1)

However, the differences in these values between the nona-aquo and the hydrated nitrate complexes is even more slight than the differences between the BTP and BTPhen complexes. This would suggest that the presence of a harder (oxygen) or softer (nitrogen) coordinating atom may have a more significant effect on the character of the bonds in question. Nevertheless, we observe a weaker increase in covalent bonding character in the nona-aquo complexes and both hydrated nitrate complexes than in the BTP and BTPhen complexes.

3.5 Stabilities of BTP and BTPhen complexes relative to aquo and hydrated trinitrate complexes

BHLYP/def(2)-TZVP single-point energy calculations were performed at BHLYP/def(2)-SVP optimised geometries. Results from these calculations were used to calculate self-consistent-field (SCF) energies of the exchange reactions (1–7), tabulated in Table 5. To investigate the stability of the BTP complexes of Am over Eu analogues, we have previously considered the exchange reaction (1) (Table 5). To more accurately reflect the conditions of the separation process, here we also consider the exchange reactions (2) and (3), which replace the nona-aquo complexes in eqn (1) with M[(H₂O)₃(NO₃)_x] (x = 3, 4) complexes. Further, to investigate the stability of the BTPhen complexes of Am over Eu, we also consider the exchange reactions (4–6), as well as an exchange reaction between the BTP and BTPhen complexes, reaction (7).

Table 5 SCF energies of reactions (1–7), calculated using the BHLYP/def(2)-TZVP//BHLYP/def(2)-SVP and B3LYP/def(2)-TZVP//BHLYP/def(2)-SVP model chemistries. B3LYP-derived values are given in parentheses

Reaction		E r (eV)
(1)	[Eu(BTP)3]^3+ + [Am(H2O)9]^3+ → [Eu(H2O)9]^3+ + [Am(BTP)3]^3+	−0.01
		(−0.05)
(2)	[Eu(BTP)3]^3+ + [Am(NO3)3(H2O)3] → [Eu(NO3)3(H2O)3] + [Am(BTP)3]^3+	−0.09
		(−0.04)
(3)	[Eu(BTP)3]^3+ + [Am(NO3)3(H2O)4] → [Eu(NO3)3(H2O)4] + [Am(BTP)3]^3+	−0.03
		(0.02)
(4)	[Eu(BTPhen)2NO3]^2+ + [Am(H2O)9]^3+ → [Eu(H2O)9]^3+ + [Am(BTPhen)2NO3]^2+	−0.19
		(−0.22)
(5)	[Eu(BTPhen)2NO3]^2+ + [Am(NO3)3(H2O)3] → [Eu(NO3)3(H2O)3] + [Am(BTPhen)2NO3]^2+	−0.26
		(−0.21)
(6)	[Eu(BTPhen)2NO3]^2+ + [Am(NO3)3(H2O)4] → [Eu(NO3)3(H2O)4] + [Am(BTPhen)2NO3]^2+	−0.21
		(−0.14)
(7)	[Eu(BTP)3]^3+ + [Am(BTPhen)2NO3]^2+ → [Eu(BTPhen)2NO3]^2+ + [Am(BTP)3]^3+	−0.17
		(−0.17)

---

As we have stated previously, the reaction energies required to give significant separation factors are not large; an energy difference of 0.12 eV corresponds to a separation factor of 100, or a 99% separation of species.⁷⁴ In our previous study we reported E_r values of −0.01 eV (−0.05 eV) for reaction (1). Here we report that when [Eu/Am(NO₃)₃(H₂O)_x] replaces the aqueous complexes in reaction (1) (reactions (2) and (3)), the reaction energy is shifted in favour of the formation of the actinide BTP complex, to −0.09 eV when x = 3 and −0.03 eV when x = 4, although it is worth noting that the B3LYP-derived reaction energies shift in the opposite direction, by 0.01 when x = 3 and by 0.07 when x = 4, leading to a positive reaction energy for the latter (0.02 eV). With these opposing trends in mind, consideration should be given to BHLYP which presents more accurate structural metrics than the equivalent B3LYP calculations; when considering reaction energies of the scale shown here, these small geometric deviations can explain the discrepancy in trends observed.

Most notably, when the separation ligand is BTPhen instead of BTP, the reaction energy is shifted in favour of the actinide by 0.17 eV (with both B3LYP and BHLYP), as seen in reaction (7). While the reaction energy for the BTP ligand is evident of weak selectivity, those of the BTPhen ligand are much higher. This is in accordance to experimental results, which show a much larger separation factor for the BTPhen ligand than BTP,^75–78 as well as our QTAIM analysis, which shows a slightly greater difference in covalency for the BTPhen complexes than seen in the BTP complexes. The same shifts in reaction energy are observed for when [Eu/Am(NO₃)₃(H₂O)_x] replaces the aqueous complexes in reaction (4), although unlike the BTP ligand all B3LYP derived reaction energies are in favour of the actinide. A potential cause for this could be that the shift in favour of the lanthanide is outweighed by the greater selectivity of the BTPhen ligand.

4 Conclusions

In this work, we have investigated the stability and bonding nature of the separation ligands BTP and BTPhen with Eu^III and Am^III, performing QTAIM analysis on DFT-optimised electron densities of [Eu/Am(BTPhen)₂(NO₃)]²⁺ with BHLYP/def(2)-TZVP//BHLYP/def(2)-SVP and B3LYP/def(2)-TZVP//B3LYP/def(2)-SVP model chemistries. This analysis has revealed an increased covalent bonding character for the Am complexes of BTPhen over Eu which was slightly more than the increase seen for the BTP complexes. Additionally, exchange reaction energies for the BTPhen ligand utilising nona-aquo complexes as a reference show evidence for stronger selectivity of the BTPhen ligand for Am over Eu than the BTP ligand by ≈0.17 eV at the SCF level.

The values presented within this work suggest that while differences in covalent character may present a partial explanation for the trends in selectivity, it cannot account for the full picture; instead, it is suggested that structural differences also represent a significant factor. There is a 0.04 Å increase in the Eu–N bond of [Eu(BTPhen)₂(NO₃)]²⁺ when compared to the equivalent BTP complex while Am–N bond lengths for the same complexes only show a 0.03 Å increase. In comparison the 0.02 Å difference Eu–N and Am–N bonds of the [Eu/Am(BTPhen)₂(NO₃)]²⁺ complexes can be contrasted to a significantly larger 0.05 Å difference in the Eu/Am–O_N bonds; these observations suggest that the stronger Eu–nitrate interactions may act to weaken the corresponding Eu–BTPhen interactions, which in turn acts to promote the stability of the Am–BTPhen complex.

As these ligands were designed to operate in ≥1 M nitric acid solutions, we have also performed this same analysis on [Eu/Am(NO₃)₃(H₂O)_x] (x = 3, 4) complexes as a better reference than the nona-aquo complexes. QTAIM analysis revealed only slight differences in any increased covalent bonding character for Am over Eu between these hydrated nitrate complexes (for both x = 3 and 4) and the nona-aquo complexes. However, BHLYP-derived exchange reaction energies using the hydrated nitrates as a reference shift in favour of the actinide for both BTP and BTPhen.

Recent work in the field of Ln/An separation via solvent extraction has investigated how functionalisation effects the selectivity of the BTPhen ligand.^79–83

We find that the increase in covalent bonding character for the BTPhen complex of Am over that of Eu is slightly greater than that seen for the BTP complexes, reaction energies which show the BTPhen ligand to be more actinide-selective than BTP, and that when the nona-aquo complexes previously used to calculate Eu ↔ Am exchange reaction energies are replaced with hydrated nitrate complexes the reaction energies shift further in favour of the An species.

While this increase in An covalent character from BTP to BTPhen complexes readily explains the differences in the exchange reaction energies (Table 5), that alone fails to fully describe the exceptionally high separation factor observed through experiment, given the small relative difference in exchange energy on the overall thermodynamics of the system. There are a number of possibilities through which the extent of this separation factor may be explained: while having minimal effect on the relative exchange energy, these values fail to take into account the dissociative barriers involved in the removal of each ligand from the relative An and Ln complexes; additionally, while the relative stabilities of each complex are assessed here in their completely coordinated states (M(BTP)₃³⁺ and M(BTPhen)₂NO₃²⁺), the intermediate structures have yet to be investigated in terms of their relative properties. In addition to the findings presented here, filling in a piece of the overall puzzle, the questions raised in turn warrant further, and dedicated investigation to better shed light on the full picture.

In parallel, given the results presented in this work, further investigation into the effect of functionalisation of the BTPhen ligands⁸⁴ has on both exchange reaction and QTAIM based measure, such as the recently investigated substitution at the 5,6- and 4,7-positions of the 1,10-phenanthroline moiety,^85,86 is warranted.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Nuclear Decommissioning Authority for financial support and the National Nuclear Laboratory for industrial supervision. I. F.-K., T. M., and A. K. thank The High End Computing facility at Lancaster University.

Notes and references

1. M. J. Hudson, C. E. Boucher, D. Braekers, J. F. Desreux, M. G. B. Drew, M. R. S. J. Foreman, L. M. Harwood, C. Hill, C. Madic, F. Marken and T. G. A. Youngs, New J. Chem., 2006, 30, 1171.
2. Z. Kolarik, U. Müllich and F. Gassner, Solvent Extr. Ion Exch., 1999, 17, 1155.
3. Z. Kolarik, U. Müllich and F. Gassner, Solvent Extr. Ion Exch., 1999, 17, 23.
4. P. J. Panak and A. Geist, Chem. Rev., 2013, 113, 1199.
5. Z. Kolarik, Chem. Rev., 2008, 108, 4208.
6. M. J. Hudson, L. M. Harwood, D. M. Laventine and F. W. Lewis, Inorg. Chem., 2013, 52, 3414.
7. A. Geist, C. Hill, G. Modolo, M. R. S. J. Foreman, M. Weigl, K. Gompper and M. J. Hudson, Solvent Extr. Ion Exch., 2006, 24, 463.
8. F. W. Lewis, L. Harwood, M. J. Hudson, M. G. B. Drew, J. Desreux, G. Vidick, N. Bouslimani, G. Modolo, A. Wilden, M. Sypula, T. Vu and J. Simonin, J. Am. Chem. Soc., 2011, 133, 13093.
9. F. W. Lewis, L. M. Harwood, M. J. Hudson, M. B. Drew, V. Hubscher-Bruder, V. Videva, F. Arnaud-Neu, K. Stamberg and S. Vyas, Inorg. Chem., 2013, 52, 4993.
10. I. Fryer-Kanssen, J. Austin and A. Kerridge, Inorg. Chem., 2016, 55, 10034.
11. M. Steppert, C. Walther, A. Geist and T. Fanghänel, New J. Chem., 2009, 33, 2437.
12. S. Colette, B. Amekraz, C. Madic, L. Berthon, G. Cote and C. Moulin, Inorg. Chem., 2002, 41, 7031.
13. M. Steppert, C. Walther, A. Geist and T. Fanghänel, New J. Chem., 2009, 33, 2437.
14. S. Trumm, P. J. Panak, A. Geist and T. Fanghänel, Eur. J. Inorg. Chem., 2010, 3022.
15. S. Trumm, G. Lieser, M. R. S. J. Foreman, P. J. Panak, A. Geist and T. Fanghänel, Dalton Trans., 2010, 39, 923.
16. M. A. Denecke, P. J. Panak, M. Weigl, B. Schimmelpfennig and A. Geist, Inorg. Chem., 2005, 44, 8418.
17. S. Colette, B. Amekraz, C. Madic, L. Berthon, G. Cote and C. Moulin, Inorg. Chem., 2004, 43, 6745.
18. C. M. Ruff, U. Müllich, A. Geist and P. J. Panak, Dalton Trans., 2012, 41, 14594.
19. B. B. Beele, E. Rüdiger, F. Schwörer, U. Mullich, A. Geist and P. J. Panak, Dalton Trans., 2013, 42, 12139.
20. N. L. Banik, M. a Denecke, A. Geist, G. Modolo, P. J. Panak and J. Rothe, Inorg. Chem., 2009, 33, 2437.
21. N. L. Banik, B. Schimmelpfennig, C. M. Marquardt, B. Brendebach, A. Geist and M. A. Denecke, Dalton Trans., 2010, 39, 5117.
22. J. Berthet, Y. Miquel, P. B. Iveson, M. Nierlich, P. Thuéry, C. Madic and M. Ephritikhine, J. Chem. Soc., Dalton Trans., 2002, 2, 3265.
23. M. G. B. Drew, D. Guillaneux, M. J. Hudson, P. B. Iveson, M. L. Russel and C. Madic, Inorg. Chem. Commun., 2001, 4, 12.
24. P. B. Iveson, C. Riviére, M. Nierlich, P. Thuéry, M. Ephritikhine, D. Guillaneux and C. Madic, Chem. Commun., 2001, 1512.
25. F. Gutierrez, C. Rabbe, R. Poteau and J. P. Daudey, J. Phys. Chem. A, 2005, 109, 4325.
26. L. Petit, C. Adamo and P. Maldivi, Inorg. Chem., 2006, 45, 8517.
27. M. Hülsen, A. Weigand and M. Dolg, Theor. Chem. Acc., 2008, 112, 23.
28. A. Moritz, X. Cao and M. Dolg, Theor. Chem. Acc., 2006, 117, 473.
29. F. W. Lewis, L. Harwoord, M. J. Hudson, M. G. B. Drew, V. Hubscher-Bruder, V. Videva, F. A. K. Stamberg and S. Vyas, Inorg. Chem., 2013, 52, 4993.
30. D. Guillaumont, J. Phys. Chem., 2004, 108, 6893.
31. J. Lan, W. Shi, L. Yuan, Y. Zhao, J. Li and Z. Chai, Inorg. Chem., 2011, 50, 9230.
32. J. Lan, W. Shi, L. Yuan, Y. Feng, Y. Zhao and Z. Chai, J. Phys. Chem. A, 2012, 116, 504.
33. J. Lan, W. Shi, L. Yuan, Y. Zhao, J. Li and Z. Chai, Coord. Chem. Rev., 2012, 256, 1406.
34. M. Trumm, B. Schimmelpfennig and A. Geist, Nukleonika, 2015, 60, 847.
35. C. de Sahb, L. a Watson, J. Nadas and B. P. Hay, Inorg. Chem., 2013, 52, 10632.
36. Y. Yang, S. Hu, Y. Fang, H. Wei, S. Hu, D. Wang, L. Yang, H. Zhang and S. Luo, Polyhedron, 2015, 95, 86.
37. A. Zaiter, B. Amine, Y. Bouzidi, L. Belkhiri, A. Boucekkine and M. Ephritikhine, Inorg. Chem., 2014, 53, 4687.
38. Y. Yang, J. Liu, L. Yang, K. Li, H. Zhang, S. Luo and L. Rao, Dalton Trans., 2015, 44, 8959.
39. V. S. Bryantsev and B. P. Hay, Dalton Trans., 2015, 44, 7935.
40. C. Mari, M. Miguirditchian, D. Guillaumont, A. Tosseng, C. Berthon, P. Guilbaud, M. Duvail, J. Bisson, D. Guillaneux, M. Pipelier and D. Dubreuil, Inorg. Chem., 2011, 50, 6557.
41. M. Trumm and B. Schimmelpfennig, Mol. Phys., 2016, 114, 876.
42. Q. Huang, J. R. Kingham and N. Naltsoyannis, Dalton Trans., 2015, 44, 2554.
43. S. D. Woodall, A. N. Swinburne, A. Kerridge, P. D. Pietro, C. Adam, P. Kaden and L. S. Natrajan, Chem. Commun., 2015, 51, 5402.
44. P. D. Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573.
45. P. D. Pietro and A. Kerridge, Phys. Chem. Chem. Phys., 2016, 18, 16830.
46. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990.
47. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165.
48. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200.
49. C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, 37, 785.
50. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
51. A. D. Becke, Phys. Rev., 1988, 38, 3098.
52. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
53. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
54. A. Klamt and G. Schüürmann, Perkins Trans., 1993, 2, 799.
55. M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730.
56. X. Cao and M. Molg, J. Chem. Phys., 2001, 115, 7348.
57. W. Küchle, M. Dolg, H. Still and H. Preuss, J. Chem. Phys., 1994, 100, 7535.
58. K. A. Keith, AIMAll (Version 19.02.13), aim.tkgristmill.com.
59. D. M. Whittaker, T. L. Griffiths, M. Helliwell, A. N. Swinburne, L. S. Natrajan, F. W. Lewis, L. M. Harwood, S. A. Parry and C. A. Sharrad, Inorg. Chem., 2013, 52, 3429.
60. M. Trumm, B. Schimmelpfennig and A. Geist, Nukleonika, 2015, 60, 847.
61. J. Xi, J. Lan, G. Lu, Y. Zhao, Z. Chai and W. Shi, Mol. Simul., 2014, 40, 379.
62. D. A. Pantazis and F. J. Neese, J. Chem. Theory Comput., 2009, 5, 2229.
63. D. A. Pantazis, X. Y. Chen, C. R. Landis and F. J. Neese, J. Chem. Theory Comput., 2008, 4, 908.
64. M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. J. Neese, J. Chem. Theory Comput., 2008, 4, 1449.
65. D. A. Pantazis and F. J. Neese, J. Chem. Theory Comput., 2011, 7, 677.
66. C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem. – Eur. J., 2014, 20, 10140.
67. C. Foroutan-Nejad, Angew. Chem., Int. Ed., 2020, 59, 20900.
68. S. Sowlati-Hashjin, V. Šadek, S. Sadjadi, M. Karttunen, A. Martín-Pendás and C. Foroutan-Nejad, Nat. Commun., 2022, 13, 2069.
69. A. Kerridge, Chem. Commun., 2017, 53, 6685.
70. C. Foroutan-Nejad, Z. Badri and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 30670.
71. A. Kerridge, RSC. Adv., 2014, 4, 12078.
72. P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573.
73. R. Beekmeyer and A. Kerridge, Inorganics, 2015, 3, 482.
74. K. L. Nash, Metal-Ion Separation and Preconcentration, ed. A. H. Bond, M. L. Dietz and R. D. Rogers, ACS Publications, 1999, pp. 52–78.
75. H. Wu, Q. Wu, C. Wang, J. Lan, Z. Liu, Z. Chai and W. Shi, Dalton Trans., 2016, 45, 8107.
76. P. Zsabka, K. V. Hecke, L. Adriaensen, A. Wilden, G. Modolo, M. Verwerft, K. Binnemans and T. Cardinaels, RSC Adv., 2021, 11, 6014.
77. P. Zsabka, K. V. Hecke, A. Wilden, G. Modolo, M. Verwerft, K. Binnemans and T. Cardinaels, Solvent Extr. Ion Exch., 2020, 38, 194.
78. F. W. Lewis, L. M. Harwood, M. J. H. Adn, A. Afsar, D. M. Laventine, K. Stastna, J. John and P. Distler, Solvent Extr. Ion Exch., 2018, 36, 115.
79. M. A. Higginson, N. D. Kyle, O. J. Marsden, P. Thompson, F. R. Livens and S. L. Heath, Dalton Trans., 2015, 44, 16547.
80. A. Afsar, D. M. Laventine, L. M. Harwood, M. J. Hudson and A. Geist, Chem. Commun., 2013, 49, 8534.
81. M. A. Higginson, O. J. Marsden, P. Thompson, F. R. Livens and S. L. Heath, React. Funct. Polym., 2015, 91, 93.
82. A. Afsar, P. Distler, L. M. Harwood, J. John and J. Westwood, Chem. Commun., 2017, 53, 4010.
83. N. J. Williams, J. Dehaudt, V. S. Bryantsev, H. Luo, C. W. Abney and S. Dai, Chem. Commun., 2017, 53, 2744.
84. I. Fryer-Kanssen, Advancing solvent extraction technology for improved management of contaminated liquors, PhD thesis, Lancaster University, 2017.
85. A. Afsar, D. M. Laventine, L. M. Harwood, M. J. Hudson and A. Geist, Chem. Commun., 2013, 49, 8534.
86. A. C. Edwards, C. Wagner, A. Geist, N. A. Burton, C. A. Sharrad, R. W. Adams, R. G. Pritchard, R. C. Whitehead and L. M. Harwood, Dalton Trans., 2016, 45, 18102.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01832f

---