Experimental and theoretical study of resonant core-hole spectroscopies of gas-phase free-base phthalocyanine

Abstract

We studied N 1s⁻¹ inner-shell processes of the free base Phthalocyanine molecule, H₂Pc, in the gas-phase. This complex organic molecule contains three different nitrogen sites defined by their covalent bonds. We identify the contribution of each site in ionized, core–shell excited or relaxed electronic states by the use of different theoretical methods. In particular, we present resonant Auger spectra along with a tentative new theoretical approach based on multiconfiguration self-consistent field calculations to simulate them. These calculations may pave the road towards resonant Auger spectroscopy in complex molecules.

---

1. Introduction

Phthalocyanine molecules (Pc) have been extensively studied for their potential applications in solar batteries^1,2 and organic light-emitting devices.^3,4 Regardless of whether Pc contains a metal in its center or not, these molecules are of interest in conducting, magnetic or optical materials,^5–10 and their resemblance to porphyrins, which are ubiquitous molecules in living cells, makes them biomimetics that can be used in medical treatments, for instance in photodynamic therapy.¹¹ The free-base phthalocyanine's (H₂Pc) structure is represented in Fig. 1. It is a plane aromatic macrocycle composed of four pyrole rings linked together by four imine bridges. Due to different chemical environments, H₂Pc contains three types of nitrogen atoms: the first type is located on the imine bridge and labeled Np; it occurs twice as often as the other two types. These other types are located in the pyrole ring and labeled NH or Nc, with NH being the one bond to the hydrogen atom. H₂Pc is mostly represented in its trans form as shown in Fig. 1, i.e. with the two H atoms facing each other at the center of H₂Pc. Finally, 4 benzene rings are also part of H₂Pc.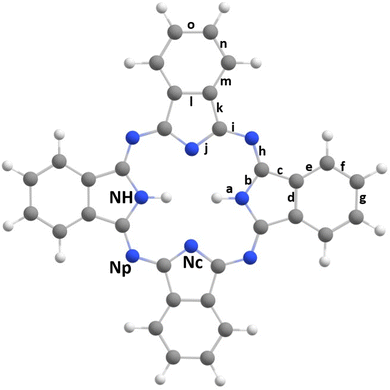

Fig. 1 Geometrical structure of the trans-H₂-phthalocyanine. The letters from “a” to “o” define the distances used in Section 3.1. The three types of N atoms are indicated as NH, Np and Nc.

Phthalocyanines have been widely studied and, in particular for H₂Pc, one can find many articles treating of its molecular structure,^12–18 as well as its electronic properties¹⁹ or structure through various X-ray techniques.^19–24 X-Ray photoelectron spectroscopy (XPS) was performed to study the valence shells,^19,22,24 as well as the C 1s and the N 1s shells.^20–22,24 The latter two core holes were also studied by X-ray Absorption spectroscopy (XAS).^22,23 Moreover, valence excitations were also used to investigate the electronic structure.^15,25,26 For the mentioned studies, the complementary theoretical simulations usually imply density functional theory (DFT) or time-dependent DFT (TD-DFT) calculations.

Beside Edwards and Gouterman,²⁵ who measured H₂Pc in the vapor phase and in the optical and the near-UV region, all other experimental studies mentioned above used either crystalline H₂Pc or films on a substrate. In the present study, we have investigated valence photoelectron and resonant Auger spectra at the N 1s edge of H₂Pc in the gas phase, free of any environment perturbation. The resonant Auger relaxation represents the predominant decay channel of the states which contribute to the X-ray absorption spectrum. However, the analysis of their spectra can provide more detailed information, both on the character of the core-hole states (see e.g. ref. 27), and on the topology of the final states of the relaxation decay (see e.g. ref. 28).

For larger molecules, spectral congestion due to the many transitions leading to Auger emission prevents reaching such a high level of details. For example, H₂Pc possesses 186 valence electrons, which leads to more than 15 000 possible Auger transitions for each of the N 1s sites, without accounting for correlation and shake effects, which would again drastically increase this number. Although it is well-known that for molecules with small bond distances and low Auger-energies non-local effects,^29–32i.e. inter-atomic Auger transitions, can contribute to the Auger decay, the Auger rates are normally dominated by local effects, more precisely by intra-atomic transitions where only valence orbitals located close to the core-hole site contribute. In this approximation we still expect that at least several hundred transitions contribute to the Auger spectrum of H₂Pc.

Despite this complexity, resonant Auger spectra of large molecules can still provide valuable information. These spectra can serve as a benchmark for extended theoretical approaches. As mentioned above, the Auger process is basically localized at the formed core hole. Because of this, calculations of Auger spectra are often performed in the so-called one-center approximation, i.e. only the electron density at the core-hole site is taken into account. Such simplified calculations help to identify Auger decays based on non-local processes like interatomic Coulomb decay (ICD) in molecules^31,32 or charge transfer from the surrounding (see e.g. ref. 33), where several atomic centers can participate to the relaxation of inner-holes. From a more practical point of view, resonant Auger spectra allow to resolve core-excited states, which overlap in the X-ray absorption spectrum. They also help to identify contributions from impurities in the X-ray absorption spectrum. Both aspects will be addressed in the present work.

In order to obtain first calculations for the resonant Auger spectra of H₂Pc, we propose to revisit a relatively simple approach used by Ramaker et al.³⁴ in the 1970's to calculate normal Auger transitions, and modify it for application to the resonant decay.

This proposed methodology paves the road to using resonant Auger spectroscopy to elucidate the electronic structure of medium-size molecular systems, as well as deciphering the molecular orbitals' contributions to the spectra.

2. Methods

2.1 Experimental

The experiments have been performed on the PLEIADES' beamline of the french synchrotron radiation facility SOLEIL. This beamline provides access to monochromatic light in the 10–1000 eV energy range. This broad energy range permits probing valence as well as core–shell orbitals. A home-made oven specifically designed for this beamline was used to evaporate the molecules at ≈700 K. We used a wide-angle lens VG-Scienta R4000 electron spectrometer at the magic angle of 54.7° to avoid influence of the photoelectron angular distribution on the ionization cross sections. H₂Pc has been provided by Porphychem as a sublimated product, mostly free of synthesis pollutants.

The Auger spectra measured around the N 1s ionization threshold have been obtained by varying the photon energy from 396 eV to 407 eV with a stepwidth of 0.2 eV and for each photon energy, the electrons were detected in the binding-energy range between 5 and 62 eV using the same stepwidth of 0.2 eV. These small and constant stepwidths allow to display the Auger spectra as a 2D-map where the photon energy is given on the y-axis and the binding energy on the x-axis, as shown in Fig. 8; and the colorscale represents the Auger intensity. In this map we idenfitied some impurities caused by the N 1s → π* excitation of N₂, which for the v′′ = 0 → v′′ = 0 vibrational excitation is located at hν = 400.88 eV;³⁵ this allows to calibrate the photon energy with an accuracy of ≅0.1 eV. The overall resolution consisting of the photon energy bandwidth and the spectrometer resolution was set at about 670 meV, which is a good compromise between spectral resolution and signal intensity.

Since the N 1s core hole relaxes predominantly via Auger decay, and since we measured almost the entire resonant Auger spectrum, we assume that the partial electron-yield spectrum, which is obtained by integrating the 2D-map along the binding-energy axis, is equivalent to the absorption spectrum.

Furthermore, to be able to interpret the low-binding energy side of our spectra, we measured the valence photoelectron spectrum, at a photon energy hν = 100 eV using a binding energy of 6 to 20 eV and a stepwidth of 0.01 eV. The spectrum has been linearly calibrated on the binding energy scale by using the intense ionization peak of water at 12.62 eV,³⁶ which is a pollutant originating from the oven, see Fig. 3. The overall experimental resolution was set to a nominal value of 55 meV.

2.2 Theoretical

The theoretical valence photoelectron spectrum has been obtained by calculating the density of states (DOS) in the ground state. In a first step, the molecular structure of H₂Pc has been optimized with the Gaussian 16 software³⁷ at the DFT B3LYP/cc-pVTZ level of theory constraining a D_2h symmetry. The ionization potentials were calculated by the Maximum Overlap Method (MOM),³⁸ imposing a single electron occupation to each molecular orbital per calculation, at the DFT B3LYP/def2-TZVP level of theory. The MOM approach avoids the variational collapse for electronic excited states with non-Aufbau occupation numbers, i.e. where not only the lowest available energy subshells are populated, by restricting the occupation during the SCF procedure according to the one given in the initial guess. These calculations were done using the PySCF software.^39,40

In a second step, the partial DOS (pDOS) was calculated using the geometrical structure optimized for the electronic ground state, and the percentages of each atomic group to the molecular orbitals were calculated through Mulliken population analysis. To simulate the photoelectron spectrum, we followed the method described in Brena et al.⁴¹ and used the Gelius model,⁴² which consists in weighting each atomic contribution to the molecular orbitals by its subshell photoionization cross section at the corresponding experimental photon energy; in the present case a photon energy of hν = 100 eV was used. These cross sections are taken from the calculations of Yeh and Lindau.^43,44 Finally, we convoluted the theoretical intensities with Gaussian functions of 3 widths depending on their binding energies, i.e. 82.5 meV full width at half maximum (FWHM) for binding energies (E_b) < 7 eV, 450 meV FWHM for 7 ≤ E_b < 11 eV and 600 meV FWHM for E_b > 11 eV. These different widths are used to partially account for the contributions of 2-holes 1-electron final states corresponding to simultaneous ionization and excitation, which become more important at higher binding energies.

The N 1s absorption spectrum has been calculated at the multi-configurational self-consistent field (MCSCF) level of theory⁴⁵ with a def2-TZVP basis set. We used the density-fitting approximation⁴⁶ implemented in the Molpro 2021.2 software^47,48 and the def2-TZVP uncontracted auxiliary basis set. Three different calculations in total have been performed, i.e. one for each type of N atoms, namely NH, Nc, and Np. In each of these calculation, the active space consisted of the corresponding N 1s orbital, the molecular orbitals involving the N 2s and 2p electrons, and the molecular orbitals involving the direct C neighbours' 2s and 2p electrons as well as the HOMO (highest occupied molecular orbital). The calculation consisted of two restricted active spaces (RAS), with a total of 30 electrons and 21 orbitals (30e,21o). The first space is a RAS(29e,15o), containing the investigated core orbital plus the higher energy doubly occupied molecular orbitals. The second space is a RAS(1e,6o), which means that only single excitations were taken into account, resulting in 91 configurations. To avoid the variational collapse during the self-consistent optimization, the core orbitals added to the active space were kept frozen. This kind of approach has been successfully applied to obtain core transition energies.^49–53 To match the experimental spectrum, we convoluted the oscillators strength by a Gaussian function of 750 meV of FWHM. We also added an error function to represent the ionization continuum. Moreover, the theoretical peaks have been shifted by ≅3.7 eV to higher energies to match the experimental ones.

For the case that the lifetime of the final state is long compared to the lifetime of the core-hole state, the double differential cross section for resonant core excitation and Auger decay is defined as:⁵⁴

withHere Ψ_o,c,f are the initial, intermediate and final states respectively, ω is the photon energy, ω′ corresponds to the energy of the emitted electron, ω_co and ω_fo are the energy differences between the ground and core-excited states and the ground and final states, respectively. Moreover, Q is the Coulomb operator for the Auger transition, D is the dipole operator for the excitation and Γ_c is the half-width at half maximum lifetime broadening for the core-hole state. Finally, the delta function carries the energy conservation throughout the whole process, i.e. the core-excitation and resonant Auger decay. A more general discussion of eqn (1) and in particular a different treatment of normal and resonant Auger decay is given in ref. 55. The dipole matrix elements were extracted from the calculations of the core excitations, see above.

In the Born–Oppenheimer's approximation, the electronic and nuclear degrees of freedom can be decoupled, so that the total wavefunction can be expressed as |Ψ_i〉 = |Φ_i〉 ⊗ |χ_i〉, where |Φ_i〉 is the electronic wavefunction of the state i and |χ_i〉 is the nuclear wavefunction. Then, eqn (1) has the form:

The third line of eqn (3) describes the so-called direct terms, i.e. the terms which only have to be taken into account when the excitation and the decay process are considered separately; this approach is widely used for the interpretation of Auger spectra. The term LIC describes the so-called lifetime interference contributions, which are relevant if the lifetime broadening of the resonances is comparable or larger than the splitting between the resonances. In this case the population of a given Auger final state can occur via different intermediate states so that the exact excitation and decay pathway is not known. This leads to interference terms in the cross section comparable to those well known from the textbook example of a double slit. For a more detailed discussion of such terms, see e.g. ref. 56–58. In the present approximation, where both holes of the Auger final state are located in the same orbital, the symmetry of the outgoing Auger electron is determined by the symmetry of the core excited state so that the lifetime interference contributions can be calculated in a simple manner and they are fully taken into account. In the course of the present work, the calculations were performed in two ways, namely with the two effects of shake transitions and lifetime interference contributions as well as by neglecting both effects, and we found that these two effects have only minor influence on the results. Nevertheless, for reasons of completeness, in the present publication we show the results where the shake processes and lifetime interferences are taken into account.

To calculate the intensity of the resonant Auger decay, we approximated the Coulomb matrix element by using a formalism employed by Ramaker et al.³⁴ as:

with |ϕ_c〉 and |ϕ_f〉 being virtual orbitals of the core-excited and final state.

Here I_KXY describes a normal Auger decay as defined in the ref. 34. In detail,

is a transition intensity involving a core 1s hole (the index K) and 2 electrons issued from the molecular orbitals X and Y. c_Xn² (respectively c_Ym²) corresponds to the population of the N atomic orbital n (m) in the molecular orbital X (Y) and P_Knm is the theoretical Auger rate obtained for the nitrogen atom by Walters and Bhalla.⁵⁹ Finally, 〈ϕ_f|ϕ_c〉 is the overlap between virtual molecular orbitals, where the N 1s electron was initially promoted and the virtual orbital occupied in the final state. This term allows taking into account the spectator resonant Auger decay, where the excited electron remains in the same molecular orbital during the relaxation, and shake processes, i.e. when the electron is promoted to another virtual orbital during the Auger decay.

Note that a similar approach has been used recently by Fouda et al.⁶⁰ to calculate the Auger decay after single and double core–shell excitations in the N₂ O molecule, after interaction with a X-ray free electron laser pulse, as well as by Tenorio et al.⁶¹ for simulating resonant Auger decay in a series of simple systems. The main difference with the present calculations is that the excitation and relaxation steps are decoupled, i.e. the LIC term in eqn (3) is neglected. Nevertheless, it is a sound approach to calculate normal Auger decay as shown by ref. 34 and the closely related article from Mitani et al.⁶² on a more complex series of molecules.

The electronic structures were calculated using the same active space as for the N 1s absorption spectrum, however, only selected configurations for the final states, namely those that correspond to spectator resonant Auger, i.e. with 2 holes and 1 excitation in the valence shell were taken into account.

We summarize the main calculated structures in Fig. 2, where (A) corresponds to the electronic ground state of the molecule (optimization through DFT calculation). (B) Represents the MCSCF calculation for the core-excited states for each type of N atoms; in these calculations single excitations to 6 virtual orbitals were taken into account. (C) Illustrates Auger decay, restricted to the spectator decay, i.e. the excited electron remains on the same orbital during the relaxation, and where the two electrons involved in the relaxation belong to the same molecular orbital. As a first approximation, one can consider the Auger decay following the N 1s excitations should be localized at the N site, since it fills a core-hole.

Fig. 2 The electronic structures taken into account in our calculations. (A) Represents the ground state, (B) corresponds to the core–shell photoexcitation for which we considered 6 unoccupied orbitals. Then (C) schematizes the spectator Auger decay; here we consider only transitions where the two electrons participating to the decay originate from the same molecular orbital.

This approximation was required to be able to fairly represent the entire energy range of relaxation pathways in order to compare with our experimental spectra's binding energy range. However, the calculations were restricted to a limit of 100 transitions per N atom, which we consider to be a reasonable compromise between computational resources and calculation time needed and the necessary ingredients to simulate the resonant Auger spectra. Furthermore, it is also the limit number of transitions which can be calculated in the MCSCF module of MOLPRO 2021.2.

A second de-excitation pathway for the core excited states is the participator Auger decay. In this case, the excited electron participates in the decay, which leads also to a singly ionized molecule as in Fig. 2C, but with one vacancy in the valence shell, i.e. the final states are identical to those after photoionization in the valence region. To interpret our resonant Auger spectra in terms of such participator decays as well, we used the results of the pDOS calculation and took for each type of N atom the excitation probability into account; in this way we were able to reproduce the participator decay as a function of the incident energy. In more details, since the final states after participator decay and direct valence ionization are the same, we used the calculated energies from our MOM approach, extracted the intensities belonging to the N atoms and multiplied the spectrum by the various N 1s intensities as a function of the incident energy, as given by the calculated absorption spectrum. Finally, we multiplied the participator's contribution by a factor of 0.35 as compared to the calculated spectator's contribution. This factor has been chosen so that the intensity of the participator decay matches the experimental spectrum at the top of the most intense resonance energy.

3. Results and discussion

3.1 Valence spectroscopy and DFT calculations

Fig. 3 represents the valence photoelectron spectrum measured at hν = 100 eV. The grey circles correspond to the experimental spectrum in the binding-energy range between 6 and 20 eV. The black solid line corresponds to the simulated DOS spectrum, which is shifted by 0.31 eV to higher energies so that the most intense peak superimposes the experimental one located at ≈8.85 eV; the intensities are also normalized to this peak. In blue, we show the background spectrum, which was measured using a heated oven, however, without H₂Pc powder. This blue spectrum corresponds mainly to the gas-phase water photoelectron spectrum³⁶ and explains the main discrepancies between our simulation (black line) and the experimental (grey) spectrum. The remaining discrepancies at higher binding energies are probably due to correlation effects, which are typical for inner-valence states, and are not taken into account in the present calculations.

Fig. 3 Valence photoelectron spectrum in the binding-energy range from 6 to 20 eV measured at the photon energy hν = 100 eV. The experimental spectrum is plotted as grey circles, along with the simulated one (black solid line) and individual intensities (black sticks). Moreover, the blue line is a background spectrum measured with a heated oven, which is not filled with the H₂Pc. It is mainly composed of gas-phase water, as discussed in Section 3.1.

In our previous study on FePc,⁶³ we noted that a good agreement between simulated DOS and the experimental spectrum is sensitive to the correct molecular structure. Therefore, we compare the optimized geometry of our DFT calculation with experimental data from Hoskins et al.,¹⁶ see Table 1. For comparison, we also present the DFT results of Day et al.¹⁵ and Cortina et al.¹⁸ One can observe that, apart from the distance “a” between the NH atom and the H atom, see Fig. 1, the agreement with the experimental data is quite good for all presented calculations.

Table 1 Summary of the distances “a” to “o” defined in Fig. 1. Given are the optimized structures of the present work, of Day et al.¹⁵ and Cortina et al.,¹⁸ as well as the experimental values from ref. 16. δr is the average deviation to the experimental values (see text) and Δr_max is the maximum deviation between a single calculated and experimental values, both in Å. For the calculation of these quantities the distance “a” is not taken into account, see footnote

	Expt.^16 (Å)	This work (Å)	Cortina et al.^18 (Å)	Day et al.^15 (Å)
a For H2Pc two trans-tautomers exist since the two hydrogen atoms can hop as a pair from one nitrogen atom to the other, i.e. NH becomes Nc and vice versa. This hopping occurs at 300 K on a timescale of ≅50 ns.^64 Because of this we assume that the discrepancy for the distance “a” is due to the fact that the experimental data are obtained by neutron scattering,^16 which averages over a larger timescale than 50 ns and, therefore, results in an averaged distance for the two tautomeres. This is fully in line with the explanation of Hopkins et al.,^16 who suggest that their results can be better described with 4 half-covalent N–H bonds in the center of the phthalocyanine. In contrast to this, we probe the H2Pc by the absorption of photons, which occurs on the attosecond timescale. Because of this, the hopping of the hydrogen atoms is frozen and the molecules is in the calculated trans form with two covalent bonds, see Fig. 1.
a^a	0.923	1.009	1.014	1.035
b	1.377	1.373	1.378	1.367
c	1.453	1.448	1.453	1.436
d	1.398	1.408	1.411	1.402
e	1.388	1.392	1.398	1.385
f	1.380	1.386	1.392	1.384
g	1.399	1.405	1.411	1.400
h	1.326	1.312	1.318	1.309
i	1.330	1.330	1.336	1.326
j	1.376	1.360	1.365	1.362
k	1.462	1.463	1.467	1.447
l	1.395	1.399	1.406	1.395
m	1.384	1.387	1.393	1.383
n	1.386	1.392	1.397	1.389
o	1.393	1.400	1.406	1.396
δr	—	0.006	0.009	0.007
Δrmax	—	0.016	0.013	0.017

---

In Table 1, the quantities δr, i.e.: the average deviation to the experimental values and Δr_max, the maximum deviation between a calculated and an experimental values are also given. For the calculation of these quantities, the distance “a” was not taken into account, see above footnote in Table 1.

In the following we discuss the features of the spectrum. The present theoretical results identify the HOMO as a π orbital formed by the carbon 2p orbitals; this is in full agreement with the references^19,22 and the seminal paper of Berkowitz,⁶⁵ who performed gas-phase valence photoelectron spectroscopy of phthalocyanines.

For a more detailed discussion of the valence region, we display in Fig. 4 the total simulated DOS spectrum, together with the atomic contributions of C atoms as well as each type of N atoms. Note that the present valence photoelectron spectrum differs in the peak intensities from previously published spectra, see e.g. ref. 19 and 22. However, these differences can readily be explained with different photon-energy dependencies of the photoionization cross sections of the atomic orbitals involved (C 2p, C 2s, N 2p, N 2s) recorded at a different excitation energy, as well as differences in the experimental resolution. Berkowitz⁶⁵ measured the photoelectron spectra of various metallophthalocyanines, and described the spectral features in the binding-energy region between 6.41 and 13.92 eV. Berkowitz used the photoelectron spectrum of H₂Pc mainly to discriminate the contributions originating from the phthalocyanine and the ones from the 3d orbitals of the metals and did not detail the type of molecular orbitals involved in the observed peaks.

Fig. 4 Simulated DOS spectrum (black solid line on top) along with individual atomic contributions from NH (red line), Np (blue line), Nc (green line) and C (black line) atoms. The two vertical dotted lines are located at 8.9 eV and 10 eV and will be referred to in the subsection dealing with resonant Auger spectroscopy.

As already described above, the peak at 6.42 eV is due to the HOMO orbital, which is mainly composed by the π orbitals formed by the carbon atoms located close to the center of H₂Pc, as shown in Fig. 5. The broad band at 8.75 eV already observed by Berkowitz⁶⁵ actually consists of 3 main regions, as can be seen in the high-resolution spectrum we report in Fig. 3. Based on the present calculations the low-energy shoulder at ≈8.20 eV is mainly due to molecular orbitals located at the C and Nc atoms, the central peak at ≈8.80 eV due to molecular orbitals mainly located at the C, Np and NH atoms and the high-energy shoulder at 9.3 eV corresponds to orbitals which are predominantly formed by the C, Np and Nc atoms. Moreover, the calculations show that the broad but distinct contributions at ≈10 eV are largely due to orbitals located on Np atoms, with some admixing from the Nc atoms. Finally, in the energy range of 10 to 20 eV, the photoelectron spectrum is mainly dominated by contributions from orbitals formed by the C atoms.

Fig. 5 Representation of the highest occupied molecular orbital of H₂Pc, which is mainly formed by the π orbitals of C atoms close to the center of the molecule.

Note that the two vertical dotted lines at binding energies of 8.9 and 10 eV are important for the interpretation of the resonant Auger spectra and will be discussed further below.

3.2 N 1s absorption spectroscopy and MCSCF calculations

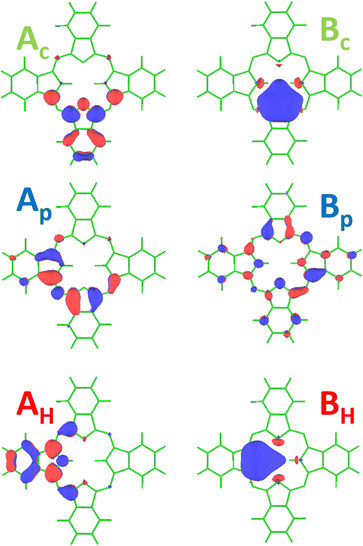
In Fig. 6, we represented on the top the experimental partial electron yield (grey hollow circles and line) below the different N 1s⁻¹ thresholds at 403.6 eV (Nc 1s⁻¹), 405.1 eV (Np 1s⁻¹), and 407.4 eV (NH 1s⁻¹). These values are obtained by adding 4.7 eV to the values given by Alfredsson et al.²² in order to account for different binding energy scales used for gas-phase and condensed-phase spectra; the value for the shift was obtained by comparing the binding energies of the HOMO obtained in the different phases. The figure also displays the simulated spectrum (black solid line), which represents the intensities for the transitions from the different N 1s core holes to the first six virtual orbitals, convoluted with a Gaussian of 0.75 eV FWHM and shifted by +3.27 eV to match the experimental spectrum. This shift is in the order of one percent of the photon energy, which is typical for MCSCF calculations. It can be related to the fact that our electronic structure approach still lacks the dynamic correlation energy, which is responsible for a significant portion of this shift. Finally, to compare with the experimental spectrum, an error function (black dotted line) was used in order to account for the contributions of the continuum. The contributions for each type of N atoms are displayed on the bottom of the graph with the same color-code as used in the Fig. 4, i.e. the contributions of Np atoms are displayed in blue, the Nc contributions are displayed in green and NH ones are in red. The excited-state orbitals for the 6 most intense transitions of the absorption spectrum are shown in Fig. 7. The orbitals labeled A_c, A_p, B_p, as well as A_H possess a π-symmetry and the orbitals labeled B_c as well as B_H possess a σ-symmetry. Note that the A_c/A_H and B_c/B_H virtual orbitals are identical, showing no contribution from the H atom in the LUMO and LUMO+1 orbitals.

Fig. 6 Partial electron yield spectrum at the N 1s threshold (top graph, grey hollow circles and line) obtained by integrating the 2D-map, see Fig. 8, along the binding energy axis. The simulated spectrum (black solid line) is composed of oscillator strengths for the transitions to the six lowest singly excited core-hole states, along with an error function (black dotted line) used to simulate the continuum's contribution. At the bottom, the contributions for the individual transitions are given. The blue line indicates transitions with a Np core hole, the green one with a Nc core hole and the red line with a NH 1s hole. The letters next to the transition refer to the excited-state orbitals shown in Fig. 7. Note that at ≅400.9 eV the experimental spectrum contains some impurities from the N 1s → π* excitation of N₂, indicated by a black arrow.

Fig. 7 Excited-state orbitals of the six most intense N 1s⁻¹ excitations. The orbitals A_c, A_p, B_p, as well as A_H possess π-symmetry and the orbitals B_c as well as B_H possess σ-symmetry. These are canonical orbitals representing configurations with higher coefficients for each of the assigned states.

The overall agreement between the present MCSCF calculations and experimental spectra is better than with the TD-DFT or DFT^19,22,23 methods. In particular, all references cited above overestimate the intensity of the second isolated peak at ≅400 eV, which is assigned to the first excited state from the NH core hole. The present calculations agree with the previous result in the sense that the spectrum is dominated by excitations into π-orbitals. However, in contrast to literature we find already in the low-energy region some contributions of excitations to σ-orbitals. In this context we want to point out that in the course of the present work, we performed TD-DFT calculations, which also do not show contributions of excitations to σ-orbitals for the N 1s excitations. In summary, we consider DFT-based calculations a valuable first approach to core-level spectra (XAS and XPS). In comparison to such calculations, MCSCF calculations are more difficult to perform since it is necessary to define for each calculation the active space and because they require more computational resources.

Nevertheless, MCSCF calculations are a prerequisite to calculating the relaxation process subsequent to core–shell excitations. As the resonant Auger decay processes (see panel C of Fig. 2) contain excited and ionized states simultaneously, it becomes fundamentally a multireference problem, and most DFT-based methods cannot describe them accurately.

Finally we shall discuss a process which has an influence on the X-ray absorption spectrum, namely core-valence double excitations. These excitations have not been taken into account in calculations, neither in the present work nor in literature. As we will discuss in the following, these double excitations are expected to contribute in the photon energy region above hν ≅ 400 eV. They should contribute to the spectrum in a twofold manner. First they should lead to an additional absorption intensity and second they can influence the energy positions and intensities of the single core-excited states by configuration interaction.

In detail, such core-valence double excitations can be understood based on the shake-up structures visible in the photoelectron spectrum. For H₂Pc such shake-up structures are calculated for the C 1s ionization threshold by Brena et al.²¹ These calculations predict total shake probabilities of 15 to 20% with respect to the corresponding main line; the exact value depends on the site of the non-equivalent carbon atom. Moreover, their calculated energy positions are located between 1.5 and 3.7 eV above the main lines. For the N 1s photoelectron spectrum of H₂Pc, calculations the shake-up structures are not available. However, experimental XPS spectra²⁴ show clearly such shake-up structures and one can expect that their relative intensities and energy positions are comparable to the values given for the carbon atoms. Such shake processes can also accompany resonant excitations leading to doubly excited states of the type N 1s⁻¹V⁻¹V′V′′ with V⁻¹ describing a normally occupied valence orbital and V′ as well as V′′ being virtual orbitals; note, that V′ and V′′ can describe the same virtual orbital.

3.3 Resonant Auger spectroscopy

The resonant Auger spectra were measured by recording electrons in 4.5–61.5 eV E_b range for photon energies varied between 396 and 407 eV. These spectra are displayed in the bottom panel of Fig. 8 as a 2D-map where the photon energy is indicated on the y-axis and the binding energy is the x-axis. Furthermore, a colorscale represents the intensity. Note that in this figure only the spectra measured with photon energies up to ≅405 eV, i.e. up to the Np 1s⁻¹ ionization threshold are shown. This photon energy range corresponds to the N 1s → OM* excitations, where OM* stands for an unoccupied molecular orbital. Moreover, the binding energies are limited to 50 eV. The top panel is the result of our simulation, which will be discussed further below.

Fig. 8 Experimental (bottom panel) and theoretical (top panel) resonant Auger spectra measured below N 1s ionization thresholds at ≅405 eV and plotted as 2D-maps. The photon energy is displayed on the y-axis, the binding energy on the x-axis and the intensity is represented by a colorscale going from dark blue (minimum) to white (maximum) as plotted in-between the two 2D-maps. Moreover, rectangle boxes show the contributions of the pollution from molecular nitrogen in the experimental 2D-map. See text for details.

The major contribution occurs at the photon energy of ≈398 eV, which corresponds to the most intense transition in the absorption spectrum discussed above. Therefore, the Auger final states visible in Fig. 8 at this photon energy are predominantly due to the relaxation from the first excited state of Np 1s transitions, see first green peak in Fig. 6. The corresponding resonant Auger spectrum is dominated by the spectator Auger decays as described in panel C of the Fig. 2, i.e. the process involved is: GS → Np(1s⁻¹)LUMO⁺¹ → Np(V⁻²)LUMO⁺¹. Here GS stands for the ground state, LUMO for the lowest unoccupied molecular orbital and V for valence orbitals. Its dominance over the participator decay can be explained by two factors: (i) in the spectator decay, there is more combination of relaxation pathways available, since in the participator decay, the promoted electron has to intervene in the decay. (ii) The overlap between the two electrons involved in the spectator decay with the core-hole is bigger than with the promoted electron. In the spectator Auger decay, the core electron, promoted during the excitation process to the LUMO remains in its orbital, while a bi-electronic mechanism occurs with one electron filling the core hole and another being ejected in the continuum. This relaxation pattern is common to the Auger decay and explains the nomenclature “spectator Auger”. However, three more processes participate to the spectrum at this photon energy; (i) the participator decay; (ii) the resonant Auger decay of the lowest Nc 1s⁻¹ excitation, see green peak at a photon energy of 398 eV in Fig. 6, which overlaps with lowest Np 1s⁻¹ excitation. (iii) Shake-up processes, i.e. processes according to the pathway GS → Np(1s⁻¹)LUMO⁺¹ → Np(V⁻²)LUMO(+n)⁺¹ with LUMO(+n) describing a higher-lying virtual orbital; in these shake processes the excited electron is promoted into a different virtual orbital. Note that for the latter Auger process the corresponding lines will, due to energy conservation, appear at higher binding energies than the spectator decay.

The main difference between participator, spectator, as well as shake-up and shake down decays is that in the first case the final states of the Auger lines are identical to those of the valence photoelectron lines, i.e. their binding energies are independent of the photon energy and thus appear as vertical lines in the 2D-map. In contrast to this, the structures of spectator decays are more complex since the dispersion with the photon energy reflects many competing dynamical processes as described in detail in our recent article.⁵⁵

Unlike the photoelectron lines caused by direct ionization, contributions due to a participator decay will show a resonance behaviour in intensity when the photon energy is crossing the energy of the excited states. At hν ≈ 398 eV, one can observe from the experimental 2D-map two lines showing an increase of intensity at E_b = 8.9 and 10 eV. These binding energies have been highlighted in the Fig. 4. The final state with E_b = 8.9 eV corresponds to an orbital, which is located mostly at the Np and the C atoms and the final state with E_b = 10 eV corresponds to an orbital located at the Np atoms only. This result is consistent with the above-discussed fact that at this photon energy, the dominant excitation possess a 1s core hole at a Np site.

For the simulated 2D-map shown on the top panel of Fig. 8 the calculated intensities are convoluted with a Gaussian function of 0.75 eV FWHM along the photon energy direction and a Gaussian function of 2 eV FWHM along the binding energy dimension, in order to account for nuclear dynamics and compare with the experimental results. The obtained structures of the map agree qualitatively with the most intense spectral features of the experimental 2D-map.

The present calculations show that the molecular orbitals possess, at the nitrogen sites, either 2s or 2p character, i.e. there is very little sp mixing. The present simulations describe only the KL_2,3L_2,3 and the KL₁L₁ Auger decays, but not the KL₁L_2,3 Auger decays. For the Auger decay following the excitation to the first peak in the absorption spectrum at hν = 398 eV we found from our calculations the KL_2,3L_2,3 Auger final states in the binding energy range of 15 to 48 eV and for the KL₁L₁ states in the range from 18 to 48 eV, i.e. the ranges overlap almost completely. Note that the KL_2,3L_2,3 Auger final states dominate the lower energy part and the KL₁L₁ states the higher energy part of this region. Based on these results we expect that the KL₁L_2,3 are also present in the same binding-energy region, i.e. they should not give significant new structures in the simulated spectrum.

In Fig. 9 we present three selected resonant Auger spectra, which are used to produce the 2D-maps shown in the Fig. 8. The grey line and circles represent the experimental spectra along with the theoretical results. In order to indicate the Auger transitions occurring at the different non-equivalent nitrogen atoms we use the same color code as above. Note that, in contrast with the previous discussed results, the theoretical data are not shifted to match better the experimental ones. The top panel displays the spectrum measured at hν = 397 eV, i.e. 1 eV below the most intense spectral feature, which consists mainly of a Nc 1s⁻¹ → OM* excitation, with some admixing of a Np 1s⁻¹ → OM* excitation, see the N 1s absorption spectrum (Fig. 6). Note that the Auger decays of the Nc core-excited state (green line) is more intense than that of the Np core-excited state (blue line), which can readily be explain by the fact that the corresponding resonance is lower in energy and posses a higher cross section at hν = 397 eV. The center panel shows the resonant Auger spectrum measured at hν = 398 eV, i.e. 1 eV above the spectrum shown in the upper panel. Here, the contributions from the Np atoms is larger than from the Nc atoms since the photon energy is close to the resonance position of the Np 1s⁻¹ → OM* excitation. The different shapes of the spectra between binding energies of 20 and 30 eV in the spectra measured at 397 and 398 eV, which is reasonably well reproduced by the simulations, clearly suggests that the first peak in the photoabsorption spectrum, see Fig. 6, consists of two different resonances.

Fig. 9 Three selected Auger spectra taken from the 2D-maps shown in the Fig. 8. The experimental spectra (grey line and circles) are displayed along with the simulated ones (black solid lines). The contributions of the individual nitrogen sites Nc (green), Np (blue), and NH (red) are plotted beneath. The grey solid lines correspond to participator Auger decay.

The spectrum in the bottom panel is measured at hν = 403.6 eV and the preponderant contributions originate from the decays of a NH 1s⁻¹ → OM* excitation. The grey solid lines indicate the contributions of the participator decay. Since the calculations of the spectator and participator Auger decays were performed in a different way, the intensities of the participator decay are multiplied by a constant factor of 0.35 in order to find for both decay pathways a good agreement with the experimental results.

For all excitation energies, the simulations reproduce well the participator Auger regions visible at a binding energy of about 10 eV as well as in the main region, which is located between 20 and 35 eV for the spectra recorded at hν = 397 and 398 eV and between 25 and 35 eV for the spectrum recorded at 403.6 eV. The small width of the calculated Auger spectra is due to the fact that the valence orbitals with strong N 2s or N 2p contributions can mainly be found in the binding energy region of 8 to 11 eV.

For all photon energies there are disagreements between experiment and theory between the participator Auger region and the main region (around 15 eV for the spectra recorded at 397 and 398 eV and around 20 eV for the spectrum measured 403.6 eV) as well as for binding energies above 35 eV. These disagreements can be explained with our simplified theoretical approach. For this we want to recall that the spectra measured at 397 and 398 eV comprises more than 35 000 Auger transitions and the spectrum at hν = 403.6 eV around 17 000 transitions, while the simulated spectra take into account only about 800 transitions in total, i.e. only a small fraction of the possible transitions. As discussed above, we applied the so-called one-center approximation, i.e. we took into account only valence-orbital contributions, which are formed by the atomic orbitals of the nitrogen atom, at which the core hole is located. Moreover, only Auger transitions with two holes in the same valence orbital are taken into account. Obviously, these transitions are sufficient to describe the main features of the Auger spectra.

However, as already pointed out by Siegbahn et al.⁶⁶ the one-center approximation is only a good approximation if the molecular orbital coefficients at the other atoms are not too large. This is not valid for the molecular orbitals, which are mainly localized at the carbon atoms, like e.g. the HOMO. Because of this, we can expect minor contributions of Auger transitions where such orbitals are involved. In particular, we assume that the missing intensity at a binding energy about 10 eV in the spectra measured at 397 and 398 eV as well as at about 15 eV in the spectrum measured 403.6 eV can be explained by Auger transitions where the HOMO is involved. This assumption is in line with an observation for the building block molecule pyridine.⁶⁷ The N KVV Auger spectrum of this molecule shows a weak low-energy shoulder, while in the same binding-energy region of the C KVV Auger spectrum a significantly more intense shoulder can be seen; this behaviour can be understood in the model of Matthew and Komninos,²⁹ which predicts for the non-local processes a ω⁻⁴ dependence with ω being the energy difference between the core hole and the valence electron that fills this hole. Based on this observation this shoulder is assigned to transitions which involve an orbital with low binding energy, which is localized at the carbon sites. In the same way we explain the missing intensity in the calculated spectra in the binding energy region above 35 eV with transitions to final states, where one orbital with higher binding energies located at the carbon sites is involved.

Finally, the sharp spectral features indicated with rectangular boxes in the experimental 2D-map of Fig. 8 at ≈401 eV of photon energy and at binding energies of ≈17 eV as well as 24 eV are due to a pollution with N₂.⁶⁸ Such pollutions lead to contributions in the X-ray absorption spectrum as indicated by the vertical arrow in Fig. 6, which can be identified by resonant Auger spectroscopy due to the additional information provided by this process.

4. Conclusion

In conclusion, we have measured emission spectra of H₂Pc at various edges and showed through two different types of calculations that we can extract the contributions of the three different N atoms to the measured electronic states. This holds for valence transitions where we used the well-known PDOS approach combined with the Gelius model to simulate our spectrum, for the N 1s absorption spectrum where we summed the MCSCF calculations for each type of N atoms (within their corresponding active spaces) and even for the complex resonant Auger decay case.

For the latter, we propose an approximated approach to simulate the spectra which provides a qualitative agreement that is good enough to interpret our data. The approach is based on a method originally suggested by Ramaker et al.³⁴ for normal Auger spectra, but is extended to the present case of resonant Auger decay. The overall agreement between the experimental and simulated spectra indicate that it is, indeed, possible to decompose the resonant Auger spectra in terms of decays originating from the individual types of nitrogen atoms. This is similar to what we achieved for the valence photoelectron spectrum and strengthens our point that one can consider the resonant Auger spectrum of complex molecule as a combination of a local excitation step, and a relaxation part where the intensities of the Auger process are proportional to the population of the molecular orbitals involved. Our results also show that when the decay involves delocalized valence orbitals, one has to go beyond the one-center approximation to be able to reproduce, at least qualitatively, all regions of the Auger spectra. To interpret the KVV Auger experimental spectra of such complex molecular systems, our results point out the complementary of valence photoelectron spectra that allowed assigning the energy location of these two-centers decays in the spectra. In contrast to other related theoretical approaches, where the excitation and Auger relaxation steps are uncoupled,^60–62 we took into account LIC, which originates from the cross terms between different intermediate electronic states leading to the same final state. Indeed, after its promotion to an unoccupied orbital in the photoabsorption process, the electron can remain in the same molecular orbital or shake to another one (see eqn (4)). Although in the present study, these effects are negligible in regard of the contribution of the several ten thousands transitions at play, they may turn out to be important in case of simpler systems or well separated electronic transitions as we showed recently in Goldsztejn et al.⁵⁵

Furthermore, we identified a significant contribution of double excitations to the N 1s absorption spectrum. In atoms and simple molecular systems, these effects are known to be visible at energies well above the ionization potential,^69–73 whereas in the present case they already contribute below threshold.

This new calculation methodology may pave the way towards resonant Auger spectroscopy of complex molecules. However, a full description of the Auger spectra obviously requires future more sophisticated theoretical approaches.

Author contributions

N. S., B. S., M. S. and G. G. conceived and planned the experiment, J. B., M. B., P. C., D. C., A. M., N. S., B. S. and G. G. performed the experiment, J. L. and G. G. analyzed the data, C. E. V. M. and G. G. performed the theoretical simulations, C. E. V. M., R. P. and G. G. interpreted the findings, C. E. V. M., R. P. and G. G. drafted the manuscript and all authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

G. G. and R. P. acknowledge financial support from Université Paris-Saclay through the “Missionnaires Invités” program.

Notes and references

1. M. Hiramoto, M. Kubo, Y. Shinmura, N. Ishiyama, T. Kaji, K. Sakai, T. Ohno and M. Izaki, Electronics, 2014, 3, 351.
2. M. Walter, A. Rudine and C. Wamser, J. Porphyrins phthalocyanines, 2010, 14, 759.
3. Y. Tomita, Alternative transparent electrodes for organic light emitting diodes, PhD thesis, Technische Universität Dresden, 2008.
4. H. Kanno, High-Efficiency Organic Electroluminescent devices, PhD thesis, The University of Tokyo, 2006.
5. T. Nyokong, Coord. Chem. Rev., 2006, 251, 1707.
6. C. Claessens, W. Blau, M. Cook, M. Hanack, R. Nolte, T. Torres and D. Wöhrle, Monatsh. Chem., 2001, 132, 3.
7. C. Schramm, R. Scaringe, D. Stojakovic, B. Hoffman, J. Ibers and T. Marks, J. Am. Chem. Soc., 1980, 102, 6702.
8. H. Hasegawa, T. Naito, T. Inabe, T. Akutagawa and T. Nakamura, J. Mater. Chem., 1998, 8, 1567.
9. T. Inabe and H. Tajima, Chem. Rev., 2004, 104, 5503.
10. D. Rittenberg, L. Baars-Hibbe, A. Böhm and J. Miller, J. Mater. Chem., 2000, 10, 241.
11. E. Reddi, G. L. Castro, R. Biolo and G. Jori, Br. J. Cancer, 1987, 56, 597.
12. P. Zugenmaier, T. Bluhm, Y. Deslandes, W. Orts and G. Hamer, J. Mater. Sci., 1997, 32, 5561.
13. N. Amar, R. Gould and A. Saleh, Curr. Appl. Phys., 2002, 2, 455.
14. S. Yim, T. Jones, Q. Chen and N. Richardson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 235402.
15. P. Day, Z. Wang and R. Pachter, J. Mol. Struct. THEOCHEM, 1998, 455, 33.
16. B. Hoskins, S. Mason and J. White, Chem. Commun., 1969, 554.
17. S. Matsumoto, K. Matsuhama and J. Mizuguchi, Acta Cryst., 1999, C55, 131.
18. H. Cortina, M. Senent and Y. Smeyers, J. Phys. Chem. A, 2003, 107, 8968.
19. M. Nardi, F. Detto, L. Aversa, R. Verucchi, G. Salviati, S. Iannotta and M. Casarin, Phys. Chem. Chem. Phys., 2013, 15, 12864.
20. Y. Niwa, H. Kobayashi and T. Tsuchiya, J. Chem. Phys., 1974, 60, 799.
21. B. Brena, Y. Luo, M. Nyberg, S. Carniato, K. Nilson, Y. Alfredsson, J. Åhlund, N. MÅrtensson, H. Siegbahn and C. Puglia, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195214.
22. Y. Alfredsson, B. Brena, K. Nilson, J. Åhlund, L. Kjeldgaard, M. Nyberg, Y. Luo, N. MÅrtensson, A. Sandell, C. Puglia and H. Siegbahna, J. Chem. Phys., 2005, 122, 214723.
23. G. Semushkina, L. Mazalov and T. Basova, J. Struct. Chem., 2016, 57, 1334.
24. G. Semushkina, L. Mazalov, S. Lavrukhina, T. Basova and R. Gulyaev, J. Struct. Chem., 2015, 56, 523.
25. L. Edwards and M. Gouterman, J. Mol. Spectrosc., 1970, 33, 292–310.
26. K. Toyota, J.-Y. Hasegawa and H. Nakatsuji, J. Phys. Chem. A, 1997, 101, 446.
27. J. Mursu, H. Aksela, O.-P. Sairanen, A. Kivimäki, E. N. ommiste, A. Ausmees, S. Svensson and S. Aksela, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 4387.
28. C. Miron, C. Nicolas, O. Travnikova, Y. P. Sun, F. Gel'mukhanov, N. Kosugi and V. Kimberg, Nature Phys., 2012, 8, 135.
29. J. A. D. Matthew and Y. Komninos, Surf. Sci., 1975, 53, 716.
30. T. D. Thomas, C. Miron, K. Wiesner, P. Morin, T. X. Carroll and L. J. Sæthre, Phys. Rev. Lett., 2002, 89, 223001.
31. C. Buth, R. Santra and L. S. Cederbaum, J. Chem. Phys., 2003, 119, 10575.
32. R. Püttner, T. Marchenko, R. Guillemin, L. Journel, G. Goldsztejn, D. Céolin, O. Takahashi, K. Ueda, A. F. Lago, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2019, 21, 8827.
33. D. Céolin, N. Kryzhevoi, C. Nicolas, W. Pokapanich, S. Choksakulporn, P. Songsiriritthigul, T. Saisopa, Y. Rattanachai, Y. Utsumi, J. Palaudoux, G. Öhrwall and J.-P. Rueff, Phys. Rev. Lett., 2017, 119, 263003.
34. D. E. Ramaker, N. H. Turner, G. Moore, M. G. Lagally and J. Houston, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 5375.
35. R. N. S. Sodhi and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1984, 34, 363.
36. J. Reutt, L. Wang, Y. Lee and D. Shirley, J. Chem. Phys., 1986, 85, 6928.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian – 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
38. A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171.
39. Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340.
40. Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109.
41. B. Brena, C. Puglia, M. de Simone, M. Coreno, K. Tarafder, V. Feyer, R. Banerjee, E. Göthelid, B. Sanyal, P. M. Oppeneer and O. Eriksson, J. Chem. Phys., 2011, 134, 074312.
42. U. Gelius, J. Electron Spectrosc. Relat. Phenom., 1974, 5, 985–1057.
43. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155.
44. J. Yeh, Atomic Calculation of Photoionization Cross-Sections and Asymmetry Parameters, Gordon and Breach Science Publishers, Langhorne, PE (USA), 1993.
45. D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2020, 152, 074102.
46. F. R. Manby, P. J. Knowles and A. W. Lloyd, J. Chem. Phys., 2001, 115, 9144–9148.
47. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242.
48. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
49. C. E. V. d Moura, R. R. Oliveira and A. B. Rocha, J. Mol. Model., 2013, 19, 2027–2033.
50. M. Guo, L. K. Sørensen, M. G. Delcey, R. V. Pinjari and M. Lundberg, Phys. Chem. Chem. Phys., 2015, 18, 3250–3259.
51. I. Corral, J. González-Vázquez and F. Martín, J. Chem. Theory Comput., 2017, 13, 1723–1736.
52. D. Bhattacharya, K. R. Shamasundar and A. Emmanouilidou, J. Phys. Chem. A, 2021, 125, 7778–7787.
53. J. B. Martins, C. E. V. d Moura, G. Goldsztejn, O. Travnikova, R. Guillemin, I. Ismail, L. Journel, D. Koulentianos, M. Barbatti, A. F. Lago, D. Céolin, M. L. M. Rocco, R. Püttner, M. N. Piancastelli, M. Simon and T. Marchenko, Phys. Chem. Chem. Phys., 2022, 24, 8477–8487.
54. F. Gel'mukhanov and H. Ågren, Phys. Rev. A, 1996, 54, 379.
55. G. Goldsztejn, R. Guillemin, T. Marchenko, O. Travnikova, D. Céolin, L. Journel, M. Simon, M. Piancastelli and R. Püttner, Phys. Chem. Chem. Phys., 2022, 24, 6590–6604.
56. R. Püttner, V. Pennanen, T. Matila, A. Kivimäki, M. Jurvansuu, H. Aksela and S. Aksela, Phys. Rev. A, 2002, 65, 042505.
57. G. Goldsztejn, T. Marchenko, D. Céolin, L. Journel, R. Guillemin, J.-P. Rueff, R. K. Kushawaha, R. Püttner, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2016, 18, 15133.
58. G. Goldsztejn, R. Püttner, L. Journel, R. Guillemin, O. Travnikova, R. K. Kushawaha, B. C. de Miranda, I. Ismail, D. Céolin, M. N. Piancastelli, M. Simon and T. Marchenko, Phys. Rev. A, 2017, 95, 012509.
59. D. L. Walters and C. P. Bhalla, Atomic Data, 1971, 3, 301.
60. A. Fouda, D. Koulentianos, L. Young, G. Doumy and P. Ho, Mol. Phys., 2022, e2133749.
61. B. N. C. Tenorio, T. A. Voß, S. I. Bokarev, P. Decleva and S. Coriani, J. Chem. Theory Comput., 2022, 18, 4387.
62. M. Mitani, O. Takahashi, K. Saito and S. Iwata, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 103.
63. J. Laurent, J. Bozek, M. Briant, P. Çarçabal, D. Cubaynes, A. Milosavljević, R. Püttner, N. Shafizadeh, M. Simon, B. Soep and G. Goldsztejn, Phys. Chem. Chem. Phys., 2022, 24, 2656.
64. B. Wehrle and H.-H. Limbach, Chem. Phys., 1989, 136, 223–247.
65. J. Berkowitz, J. Chem. Phys., 1979, 70, 2819.
66. H. Siegbahn, L. Asplund and P. Kelfve, J. Chem. Phys., 1975, 35, 330.
67. R. R. Rye, J. A. Kelber, G. E. Kellogg, K. W. Nebesny and D. L. Lichtenberger, J. Chem. Phys., 1987, 86, 4375.
68. R. Feifel, M. Andersson, G. Öhrwall, S. Sorensen, M. Piancastelli, M. Tchaplyguine, O. Björneholm, L. Karlsson and S. Svensson, Chem. Phys. Lett., 2004, 383, 222.
69. J. M. Esteva, B. Gauthé, P. Dhez and R. C. Karnatak, J. Phys. B: At. Mol. Phys., 1983, 16, L263.
70. T. K. Sham, B. X. Yang, J. Kirz and J. S. Tse, Phys. Rev. A, 1989, 40, 652.
71. A. Filipponi and A. D. Cicco, Phys. Rev. A, 1995, 52, 1072.
72. A. Filipponi, Physica B, 1995, 208 & 209, 29.
73. M. Kitajima, R. Püttner, S. L. Sorensen, M. Hoshino, H. Fukuzawa, A. D. Fanis, Y. Tamenori, R. Sankari, M. N. Piancastelli, H. Tanaka and K. Ueda, Phys. Rev. A, 2008, 78, 033422.

---