Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phonon mechanism for the negative thermal expansion of zirconium tungstate, ZrW2O8
Leila H. N.
Rimmer
b,
Keith
Refson
 c and
Martin T.
Dove
c and
Martin T.
Dove
 *abd
*abd
aCollege of Computer Science, Sichuan University, Chengdu, Sichuan 610065, China. E-mail: martin.dove@icloud.com
bSchool of Physical and Chemical Sciences, Queen Mary University of London, Mile End Road, London, E1 4NS, UK
cISIS Facility, Harwell Campus, Chilton, Didcot OX11 0QX, UK
dSchool of Mechanical Engineering, Dongguan University of Technology, 1st Daxue Road, Songshan Lake, Dongguan, Guangdong 523000, China
First published on 13th June 2023
Abstract
Negative thermal expansion (NTE) in ZrW2O8 was investigated using a flexibility analysis of ab initio phonons. It was shown that no previously proposed mechanism adequately describes the atomic-scale origin of NTE in this material. Instead it was found that the NTE in ZrW2O8 is driven, not by a single mechanism, but by wide bands of phonons that resemble vibrations of near-rigid WO4 units and Zr–O bonds at low frequency, with deformation of O–W–O and O–Zr–O bond angles steadily increasing with increasing NTE-phonon frequency. It is asserted that this phenomenon is likely to provide a more accurate explanation for NTE in many complex systems not yet studied.
1 Introduction
The last two decades have seen a considerable upsurge of interest in materials that have the counter-intuitive and potentially technologically important property of negative thermal expansion (NTE).1–4 This interest was prompted by the discovery, in 1996, that NTE in ZrW2O8, which was first observed 3 decades earlier,5 actually exists over a very wide range of temperatures (0–1050 K).6,7 Since then a number of other materials have been shown to exhibit NTE,1,2,8–11 with research initially focusing on oxides before being extended to other ceramics and hybrid metal–organic materials. There now exists a considerable body of work on the ‘archetypal’ NTE material ZrW2O8, including experiments based on characterisation, diffraction and spectroscopy,12–25 together with simulations based on force field and ab initio methods.26–36 However, despite the wealth of studies, NTE in this material is still not understood, suffering, perhaps, from a surfeit of simplified yet untested ideas, as we discuss below.In this paper we offer an advance in our understanding of NTE in ZrW2O8 using an approach we have successfully applied to a number of other NTE materials, including ScF3,37 Zn(CN)2,38 Cu2O,39 MOF-5,40 and Y2W3O12.41 The idea is to model the dynamics of ZrW2O8 in terms of different flexibility models, and then to map the vibrational modes of these models onto the vibrational spectrum of the real material computed using accurate ab initio methods. These are then compared with the contribution of each mode to the NTE, and from this comparison we are able to determine how NTE arises from specific flexibilities in the material. In some cases the NTE can be mapped against very specific phonon modes and specific types of flexibility, but in the case of ZrW2O8 discussed here we are able to show that its NTE is caused not by a single mechanism but, rather, by a much wider range of phonons.
Thermal expansion of materials is generally understood in terms of the Grüneisen model.42–44 Normally, the anharmonicity of atomic bonding causes phonon frequencies to decrease with an increase in volume, due to a corresponding decrease in the effective interatomic force constants as neighbouring atoms are pulled slightly apart. This leads to the normal positive thermal expansion, as the increase in energy due to increasing the crystal volume is offset by an increase in entropy through the resultant decrease in phonon frequencies. However, in the case of NTE materials, we expect to find a significant number of phonons whose frequencies increase with an increase in volume. Given that the thermodynamic weighting of any vibration typically scales as the inverse of the square of its frequency, we expect to find that the most influential phonons for NTE will be those that exist at lower frequencies.
Quite why a particular vibration might have a frequency that decreases on decreasing volume is often understood in terms of the ‘tension effect’.2,3 In the case of ZrW2O8, for which this was first articulated,6 the crystal structure – illustrated in Fig. 1 – shows nearly linear Zr–O–W linkages. Since it is envisaged that the Zr–O and W–O bonds are relatively rigid, it follows that transverse vibrations of an oxygen atom in a Zr–O–W linkage might pull the structure inwards, thereby giving rise to NTE.6,28,34 The question that this idea poses is whether there are specific phonons generating this motion with sufficient thermodynamic weighting. In this regard, the discussion of the tension effect in the simpler material ScF3 is interesting, where the specific phonons can easily be identified,45 but the issue of why there is sufficient thermodynamic weighting hinges on the bending flexibility of the ScF6 octahedra.37,46
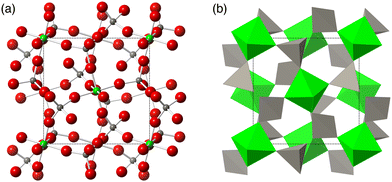 | ||
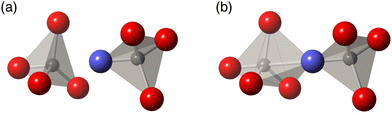
| Fig. 1 The crystal structure of the ordered phase of ZrW2O8.6 (a) The structure in ball-and-stick representation. Green spheres are Zr atoms, grey spheres are W atoms, and red spheres are O atoms. (b) The same structure represented as green ZrO6 octahedra and grey WO4 tetrahedra. The space group of this material is P213. | ||
In the case of ZrW2O8, experimental and computational evidence has led to several different proposals for the realisation of the tension effect and the mechanism of NTE mechanism. The Rigid Unit Mode (RUM) model29,30,47–50 suggests that the low frequencies can be accomplished by normal modes that show minimal deformation of coordination polyhedra, namely the ZrO6 octahedra and WO4 tetrahedra.18–20,29,30 An alternative model proposed that the Zr⋯W distance remains unchanged, but significant deformation in one or more of the ZrO6 and WO4 tetrahedra may be allowed.21–23,31 A further possibility was that adjacent WO4 tetrahedra may have some additional interaction between each other33 which would, in turn, mean that both tetrahedra may move as a single unit for low frequency NTE phonons; this model is illustrated in Fig. 2. However, thus far, no proposed mechanism has been comprehensively tested against the overall phonon spectrum in this material—an omission which we now rectify.
In the next section we describe our methodology in detail, namely the methods of calculation, the analysis of NTE, and the analysis of structure flexibility. In Section 3 we examine the phonon spectrum to identify which modes contribute to NTE. Then in Section 2.3 we interpret the phonon spectrum in terms of 16 different models of network flexibility. The analysis is then assessed in the Discussion (5) and Conclusions (6) sections. Finally, the analysis of the flexibility models is presented in an Appendix.
2 Methods
2.1 Simulation method
In this work we obtained the phonon spectrum of ZrW2O8 using plane-wave Density Functional Theory calculations using the CASTEP software.51,52 The Perdew–Burke–Ernzehof (PBE) functional53,54 was used with optimised norm-conserving pseudo-potentials.55,56 A plane-wave cutoff energy of 750 eV was used, and a Monkhorst–Pack grid57 of size 3 × 3 × 3 was used to carry out reciprocal-space integration of electronic states.The unit cell was relaxed at a set pressure of 0 GPa to give a lattice parameter of a = 9.26705 Å. Full details of the crystal structure are given in Table 1, comparing the optimised and experimental6 (room temperature) crystal structures. The optimised structure has a lattice parameter that is only 1.2% larger than the experimental structure, which is well within the usual tolerance of DFT with the PBE functional. The nearest-neighbour W–O and Zr–O distances, given in Table 2, agree to around 0.5% in almost all cases, with one Zr–O distance differing by 2.3%. This too is within the usual tolerance.
| a (Å) | DFT calculation (this study) | Neutron diffraction at 293 K | ||||
|---|---|---|---|---|---|---|
| 9.26705 | 9.15993(5) | |||||
| x | y | z | x | y | z | |
| Zr | 0.0000 | 0.0000 | 0.0000 | 0.0003(4) | 0.0003(4) | 0.0003(4) |
| W1 | 0.3428 | 0.3428 | 0.3428 | 0.3412(3) | 0.3412(3) | 0.3412(3) |
| W2 | 0.5980 | 0.5980 | 0.5980 | 0.6008(3) | 0.6008(3) | 0.6008(3) |
| O1 | 0.2055 | 0.4383 | 0.4452 | 0.2071(3) | 0.4378(4) | 0.4470(3) |
| O2 | 0.7833 | 0.5654 | 0.5545 | 0.7876(3) | 0.5694(4) | 0.5565(3) |
| O3 | 0.4895 | 0.4895 | 0.4895 | 0.4916(5) | 0.4916(5) | 0.4916(5) |
| O4 | 0.2360 | 0.2360 | 0.2360 | 0.2336(3) | 0.2336(3) | 0.2336(3) |
| W1–O (Å) | W2–O (Å) | Zr–O (Å) | ||||
|---|---|---|---|---|---|---|
| DFT | 1.714 | 1.817 | 1.742 | 1.790 | 2.052 | 2.158 |
| Experiment | 1.707 | 1.798 | 1.733 | 1.782 | 2.042 | 2.109 |
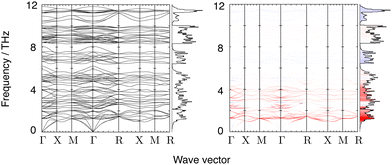
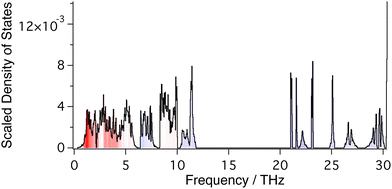
Phonon frequencies were calculated using Density Functional Perturbation Theory.58 A Monkhorst–Pack grid of phonon wave vectors of size 3 × 3 × 3 was used to compute the dynamical matrix, and Fourier interpolation of the resulting dynamical matrices was used to calculate frequencies for any point within the Brillouin zone. Calculated phonon dispersion curves for the frequency range 0–12 THz are shown in Fig. 3, together with the corresponding phonon density of states. The phonon spectrum shows a gap that extends to 21.5 THz, above which it shows a set of sharp bands of frequencies corresponding to W–O and Zr–O stretch motions up to around 31 THz (Fig. 4).
Phonon frequencies were calculated for wave vectors along the main symmetry directions in reciprocal space for plotting dispersion curves. Frequencies were also calculated for 757 wave vectors distributed randomly in reciprocal space for the calculation of the phonon density of states, giving nearly 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent frequency values (Fig. 4).
000 independent frequency values (Fig. 4).
2.2 Methodology for analysis of phonon contributions to thermal expansion
Here we recall that the Grüneisen theory of thermal expansion42–44 leads to a simple expression for the volumetric thermal expansivity, αV = CV![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) /BV, where CV is the constant–volume heat capacity, and B is the bulk modulus, V is the volume. The fourth quantity
/BV, where CV is the constant–volume heat capacity, and B is the bulk modulus, V is the volume. The fourth quantity ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is the weighted average of the individual mode Grüneisen parameters γi,k,
is the weighted average of the individual mode Grüneisen parameters γi,k,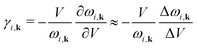 | (1) |
2.3 Flexibility modelling
The existence of a tension effect acting as the mechanism for NTE hinges on the existence of some degree of rigidity in the structure. This may be as simple as single bonds, as advocated in some other works,34,59 but, as we argued in the case of Cu2O,39 this can be too simplistic because it effectively assigns a tension effect to far too many phonons, including those that have clearly positive values of their mode Grüneisen parameters. The reason why such a mode may have positive thermal expansion is often associated with correlations of the motion of a single bond with the motions of other bonds, typically through the effects of bond-bending interactions. Thus neglecting such correlations prevents a clear understanding of how the tension effect operates to give NTE. For the tension effect to operate, the normal modes must be able to allow easy flexing of the structure whilst taking account of correlations across the crystal, with corresponding low frequency. Thus here we have set up a number of flexibility models, following a similar approach used in previous studies,39,41 and which we now describe.The ZrO6 octahedra and WO4 tetrahedra were modelled in two ways. The first was to have rigid bonds (Zr–O or W–O) but flexible bond angles, and the second was to create rigid polyhedra through addition of bond-bending forces within the polyhedra. The two models for the ZrO6 octahedra are illustrated in Fig. 5, and the models for the WO4 tetrahedra are shown in the upper part of Fig. 6.
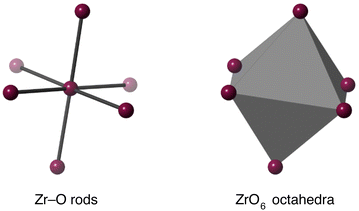 | ||
| Fig. 5 Flexibility models of the ZrO6 unit. Grey octahedra represent rigid ZrO6 units, and grey rods represent rigid Zr–O bonds. In both cases purple spheres represent flexible linkages. | ||
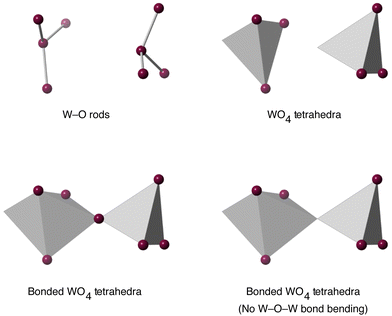 | ||
| Fig. 6 Flexibility models of the WO4 unit. Grey tetrahedra represent rigid WO4 or WO5 units, and grey rods represent rigid W–O bonds. In all cases purple spheres represent flexible linkages. | ||
Models were also developed to take account of possible bonding between adjacent WO4 units, as shown in Fig. 2. Bonding between adjacent rigid WO4 tetrahedra was modelled in three different ways. First, trivially, was to have no bonding. Second was to have a rigid bond between adjacent rigid WO4 tetrahedra, with a flexible W–O–W angle. Thirdly was to have a rigid bond between adjacent rigid WO4 with a rigid W–O–W angle. These last two are shown in the lower pane of Fig. 6.
The two models for the ZrO6 octahedra coupled with the four models for the WO4 tetrahedra give a total of 8 models. However, It has also been suggested that there is a rigidity regarding the distances between Zr and W distances. Cao et al.21,22 proposed the existence of rigid groups consisting of three Zr centres and a single W centre, forming a tent shape. Thus to each of the 8 models we also added a Zr–W constraint, giving a total of 16 different flexibility models. The rigidity and flexibility for each of these combinations is analysed in the Appendix.
In practice here, bonds and bond angles are described as either effectively rigid or completely flexible, and the models were implemented in the lattice simulation program GULP,60,61 which is able to calculate equilibrium structures and lattice dynamics. Rigidity within the flexibility models was enforced using harmonic potential energy functions of the form ½k(r − r0)2 for bonds (r is the distance between neighbouring atoms, and values of r0 were chosen to correspond to the DFT bond lengths) and ½K(θ − θ0)2 for bond angles (θ, with ideal values of θ0 for the two types of polyhedra), with large values used for the force constants k and K.† No additional functions, such as Coulomb interactions, were used. Given the manner in which the flexibility models were constructed, any phonon that does not require deformation of any of the designated rigid units of a specific model will be calculated to have zero frequency. Phonon spectra using these simple functions were calculated for each model at the same wave vectors as used in the ab initio calculations using GULP.
The frequencies ω and eigenvectors e of the model phonons j were then mapped on to the ab initio phonons i at each wave vector k using the equation
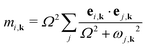 | (2) |
3 Distribution of mode Grüneisen parameters
Fig. 3 also shows the phonon dispersion curves along high symmetry directions coloured according to the values of the corresponding mode Grüneisen parameter (eqn (1)). The dispersion curves are accompanied by the calculated phonon density of states coloured by the mean value of the mode Grüneisen parameter within each frequency bin (a wider version of the density of states encompassing the high frequency modes is shown in Fig. 4). It can be seen from Fig. 3 that the values of the mode Grüneisen parameters for different phonon branches span the entire Brillouin zone such that the density of states captures a large part of the detail of the phonon spectrum.The strongest NTE modes exist around 1.2 THz with NTE character weakening slightly as the frequency increases to 2 THz. Bands of weaker NTE modes range from 2–6 THz and from 8–10 THz. There are also some low-frequency, positive thermal expansion (PTE) phonons at wave vectors near Γ and X at 2.5 THz, and near Γ and R at 5 THz. In all, there are 48 phonon branches in the 0–6 THz range which mostly drive NTE (with some driving PTE in the upper frequencies); 12 PTE branches in the 6.5–8 THz range; 28 weak NTE branches in the 8.5–10 THz range; 12 PTE branches in the 10–12 THz range; and (not pictured) 32 weak PTE branches above 12 THz.
A similar distribution of NTE and PTE phonon branches was found in Y2W3O12,41 with the exception of the PTE branches at around 2.5 THz. This is in striking contrast to simpler materials such as ScF3,37,45 Zn(CN)238 and Cu2O39 where the NTE can be seen to be associated with a relatively small number of phonon modes (in some cases, with a set of acoustic modes).
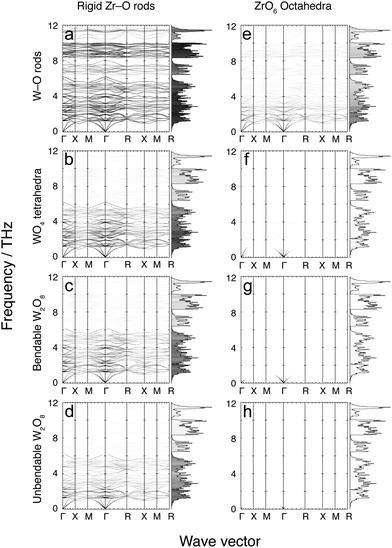
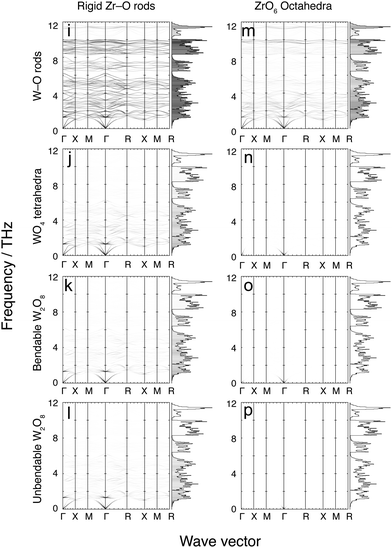
4 Flexibility models
Fig. 7 and 8 show the phonon dispersion curves calculated by DFT (same as Fig. 3) shaded according to the corresponding values of mi,k for each of the 16 models. Fig. 7 shows results for the 8 models without the Zr–W constraint (labelled as models a–h), and Fig. 8 shows the corresponding models with the Zr⋯W constraint (labelled as models i–p). The dispersion curves in both figures are accompanied by the corresponding phonon density of states, shaded by the average value of mi,k over all modes within each frequency bin. We noted above that the analysis of the flexibility of the different models is discussed in the Appendix, and Table 3 presented there summarises the quantitative flexibility analysis for each case.| Model | F atoms | F poly | C bonds | C links | F–C |
|---|---|---|---|---|---|
| a | 33 | 0 | 14 | 0 | 19 |
| b | 3 | 12 | 6 | 0 | 9 |
| c | 3 | 12 | 6 | 3 | 6 |
| d | 3 | 12 | 7 | 3 | 5 |
| e | 12 | 6 | 8 | 0 | 10 |
| f | 0 | 18 | 0 | 18 | 0 |
| g | 0 | 18 | 0 | 21 | −3 |
| h | 0 | 18 | 1 | 21 | −4 |
| i | 33 | 0 | 17 | 0 | 16 |
| j | 3 | 12 | 9 | 0 | 6 |
| k | 3 | 12 | 9 | 3 | 3 |
| l | 3 | 12 | 10 | 3 | 2 |
| m | 12 | 6 | 11 | 0 | 7 |
| n | 0 | 18 | 3 | 18 | −3 |
| o | 0 | 18 | 3 | 21 | −6 |
| p | 0 | 18 | 4 | 21 | −7 |
4.1 Model a: rigid Zr–O rods with rigid W–O rods
This model is the simplest and most flexible. It has mi,k ≈ 1 for nearly the entire low-frequency spectrum, but with some decline for frequencies in the ranges 6–8 and 10–12 THz, indicating a degree of bond stretching for these modes. Nevertheless, most bond stretching is clearly associated with the higher-frequency modes. In addition, there is some reduction in mi,k values for the weak PTE modes around 5 THz. The contributions to PTE at 5, 6–8 and 10–12 THz are therefore the result of part of the motions involving bond stretching with reduced tension effect.This model, by design, does not give any account of correlated rotations of bonds. However the results of this model show unambiguously that that NTE in ZrW2O8 arises from a tension effect involving nearly-rigid Zr–O and W–O bonds.
4.2 Model b: rigid Zr–O rods with rigid independent WO4 tetrahedra
This model shows values of mi,k ≈ 1 for frequencies lower than 6 THz, but with significant reduced values of mi,k for frequencies above 6 THz compared to model a with rigid W–O rods but flexible O–W–O bond angles. This result, coupled with the result for model a, shows that much of the motion for frequencies below 6 THz involves whole-body rotations of the WO4 tetrahedra.4.3 Model c: rigid Zr–O rods, rigid and bonded pairs of WO4 tetrahedra, and flexible inter-tetrahedral W–O–W bond bending
The flexibility of this model covers much of the same part of the phonon spectrum as for model b, but with a slight decrease in overall mi,k values. One interesting feature is that mi,k values fall significantly for phonons around 2.5 THz at the specific wave vectors where the same modes drive PTE rather than NTE. This suggests, firstly, that the distance between two WO4 units in a pair does not undergo significant change at low energy; secondly, that any change in distance that does occur is not a high-energy process; and, thirdly, that modes involving non-trivial change in the W–W distance contribute to PTE.4.4 Model d: rigid Zr–O rods, rigid and bonded pairs of WO4 tetrahedra, and no inter-tetrahedral W–O–W bond bending
This model covers much of the same part of the phonon spectrum as models b and c, but with another slight decrease in overall mi,k values. Additionally, there is a further slight decrease in mi,k values around 4 THz, indicating that W–O–W bond-angle bending occurs to some extent around this frequency. This motion, however, does not lead to any drastic change in the NTE contribution of the phonons in that portion of the full vibrational spectrum. It appears that W–O–W bond angle bending does not occur to a significant extent in the low-frequency phonon spectrum of ZrW2O8.Models e–h, which now follow, have the same constraints for the WO4 tetrahedra as for models a–d, but have rigid ZrO6 octahedra rather than rigid Zr–O bonds and flexible O–Zr–O angles.
4.5 Model e: rigid ZrO6 octahedra with rigid W–O rods
This model has small, non-zero values of mi,k for the entire low frequency phonon spectrum, with mi,k values largest in the 0–2.5 THz region. This shows that O–Zr–O angle bending is a relatively low-energy process and thus occurs to some extent throughout the phonon spectrum. The energy cost associated with bending of O–Zr–O bonds means that this deformation is smaller for the phonons with lower frequencies.4.6 Model f: rigid ZrO6 octahedra with rigid WO4 tetrahedra; rigid unit modes
This is the traditional RUM model, which was initially explored for insights into the flexibility of the ZrW2O8 structure to support the tension effect.29 The flexibility analysis, given in Table 3 in the Appendix, shows that there is an exact balance between the numbers of degrees of freedom and constraints. As a result, the RUM analysis showed a curved surface of RUMs. This model has large mi,k for modes surrounding the Γ point. However it has very weak values of mi,k for the rest of the phonon spectrum, including the reciprocal space regions where RUMs of this model were previously located. Furthermore, even when specific wave vectors known to harbour RUMs were individually inspected, no significant increase in mi,k was observed. In general, the (small) mi,k values are slightly larger at the lower frequencies, indicating that there is less overall polyhedral deformation at the lowest frequency modes.The result here is consistent with an observation about RUMs in relatively complex systems.50 ZrW2O8 has 132 normal modes per wave vector, and relatively low symmetry (compared to other cubic space groups). This means that there are many modes of the same symmetry and similar frequency, which allows for mixing of eigenvectors between such modes – this point has been discussed recently.49 Therefore, although model b shows that WO4 tetrahedra often move as rigid units, and model e shows that ZrO6 octahedra deform less in the eigenvectors of modes with lower frequencies, the combination of both types of rigid-unit motion are both limited as shown by the RUM analysis, and are diluted by eigenvector mixing.
4.7 Models g, h: rigid ZrO6 octahedra with rigid, bonded WO4 tetrahedra without (g) and with (h) inter-tetrahedral W–O–W bond bending
Model f represents the cross-over between flexible and constrained models, as shown in the flexibility analysis of Table 3 in the Appendix. Models g and h are shown by the same analysis to be over-constrained, and this is confirmed by the extremely low of zero values of mi,k ≈ 0 for all phonons. The results for these two final cases in this suite of models without constraints on the Zr⋯W distances indicate that modes with rigid ZrO6 and WO4 units cannot exist without some relative displacement of the WO4 units within a pair.Models i–p which now follow use exactly the same sets of constraints used in models a–h respectively, but now with the addition of the Zr⋯W constraint implemented as a rigid rod.
4.8 Models i–m: flexible models with Zr⋯W bonding
Fig. 8 shows the results of mi,k mapping for the eight flexibility models described above when a rigid Zr⋯W bond, corresponding to the proposed tent mode,21,22 is incorporated. In cases i–m, namely the four models with rigid Zr–O bonds without O–Zr–O angular constraints, and the model with rigid ZrO6 octahedra and rigid W–O bonds but no O–W–O angular constraints. In these cases the distributions of values of mi,k over the entire vibrational spectrum replicate what is seen in the corresponding models without Zr⋯W bonds, but with a significant overall reduction in the values of mi,k. This outcome conflicts suggests that W–O–Zr bond bending will occur across the range of frequencies, and offers little support for the operation of the tent model.4.9 Models n–p: over-constrained models with Zr⋯W bonding
These three models with rigid ZrO6 octahedra and WO4 tetrahedra are seen from Table 3 in the Appendix to be over-constrained, and the lack of any flexibility in the vibrations is shown by the near-zero values of mi,k for all phonons in the corresponding panels in Fig. 8.5 Discussion
Unlike simpler systems such as Zn(CN)2,38 Cu2O39 or ScF3,37 flexibility-model eigenvectors do not neatly map onto a small number of specific modes identified in the ab initio calculations. Instead, a high degree of eigenvector mixing is present, so that a given type of flexibility ends up being spread over multiple ab initio phonons, a phenomenon made possible by the low symmetry of the structure and large number of modes. For example, as noted above, eigenvector mixing is particularly evident for the rigid ZrO6 and WO4 model – the RUM model – mapped in Fig. 7f, where the RUMs are spread so widely across the phonon spectrum that all modes have low values of mi,k.These results show that the 48 phonons in the 0–6 THz range correspond to the motions of near-rigid WO4 tetrahedra and Zr–O rods. O–W–O and O–Zr–O bond bending are minimised (although the O–Zr–O angle distorts more) at the lowest frequencies. As the frequency increases, so too does the degree of both types of bond bending, with O–Zr–O bond bending increasing steadily, whilst O–W–O bond bending increases slowly before experiencing a jump at 6 THz. This implies that the O–W–O bond angle is stiffer than the O–Zr–O, even though both distort. Neither the RUM model nor the rigid Zr⋯W model corresponding to the tent model correlates well with any of the NTE modes.
Some NTE modes around 4 THz involve additional bending of the W–O–W angle between two WO4 units in a pair. However, since there is no effect on the values of the mode Grüneisen parameters, this additional angle bending appears to make no extra contribution to thermal expansion behaviour. Meanwhile the small number of PTE modes in the 0–6 THz range appear to correlate with changes in the distance between two WO4 units in a pair at 2.5 THz and to a small amount of bond stretching within the coordination polyhedra at 5 THz. From the dispersion curves shown in Fig. 7 it can be seen that both sets of modes (and thus the PTE that they drive) have a strong dependence on wave vector, appearing around Γ and X, and at Γ and R points respectively. The fact that the occasional separation of adjacent WO4 units does not significantly affect mode frequency suggests that there is no strong bonding between them, but that they do move in tandem more often than not, most likely as a consequence of constraints imposed by the wider ZrW2O8 framework.
The 12 PTE phonons in the range 6–8 THz involve further O–Zr–O and O–W–O bond-angle bending, as well as a significant amount of Zr–O and W–O bond stretching. This latter effect is a well-known mechanism for PTE and is what ultimately gives these phonons their PTE character. The 28 weak NTE modes in the range 8–10 THz involve negligible bond stretching but increased bending of both O–Zr–O and O–W–O bond angles. This band of modes resembles the traditional tension effect, but they exist at high frequency and thus only contribute to NTE relatively weakly due to the large amount of energetically-costly bond bending they incur. The 12 phonons in the 10–12 THz range comprise another band of weak PTE modes that involve similar distortions to those seen in the 6–8 THz range but with a much greater degree of bond stretching that gives these modes both their high frequency and their PTE behaviour. PTE modes above 12 THz consist of the remaining bond stretches.
As a result of this detailed analysis, we conclude that the NTE in ZrW2O8 cannot be described by a mechanism that involves a small set of normal modes, in contrast to other NTE materials that have been studied in similar depth.37–40 Instead, NTE is driven by a broad spectrum of phonons extending over a wide range of energies. The strongest of these exist around 1.2 THz and involve minimal deformation of the WO4 and ZrO6 polyhedral units, with the O–Zr–O bond deforming more than the relatively rigid O–W–O bond. As frequency increases, the level of O–Zr–O and O–W–O bond bending gradually increases. The behaviour of ZrW2O8 is reminiscent of that found in Y2W3O12.41
6 Conclusions
Our study of ZrW2O8 presented in this paper, together with the previous work on other NTE in Y2W3O12,41 strongly suggests that the wide expectation that NTE might always be explained in terms of simple mechanisms will not hold for all framework materials. In the simplest of cases such mechanisms can provide an elegant description of observed behaviour. For instance, the specific modes shown to drive NTE in ScF337,45 and Zn(CN)238 look like RUMs, and in Cu2O the important modes are those in which linear O–Cu–O rods move as rigid entitites.39 This seems logical given that deformation of a coordination polyhedron is an energetically-costly process, and a tension effect in which the important modes have minimal polyhedral deformation will exist at the necessary low frequency. However with added complexity, such as a large number of phonon branches in a low symmetry structure, we find that simple mechanisms are not sufficient to explain the NTE, even though such modes can be supported by the atomic structure of the material. Mode mixing is always present in the vibrational spectra of real materials but, in less-complex high-symmetry structures, these effects are minimal, and simpler mechanisms can be sufficient to explain NTE.It is only through the in-depth study of phonons in NTE framework materials with structural complexity that the more complete picture can be drawn out. Since many NTE materials are also have relatively complex structures,10 the authors offer the identification of this more complete explanation of NTE in ZrW2O8 as the key contribution of this paper to a general understanding of NTE across all framework materials.
Author contributions
Leila Rimmer: investigation, formal analysis, validation, software, writing (original draft), writing (review & editing), visualisation. Keith Refson: investigation, formal analysis, software, writing (review & editing). Martin T Dove: conceptualisation, methodology, software, validation, formal analysis, resources, software, writing (original draft), writing (review & editing), supervision, project administration, funding acquisition.Data and code availability
The main CASTEP code is available for academic use. Information is available from https://www.castep.org/CASTEP/GettingCASTEP. The GULP code is also available for academic use and can be obtained from https://gulp.curtin.edu.au/download.html. The software used for the analysis of the results presented here is available from https://osf.io/bcauq/files/osfstorage/6425168f63995b07eae19a58.Conflicts of interest
There are no conflicts to declare.Appendix: flexibility analysis
We consider the flexibility of rigidity of the models discussion in Section 2.3 in terms of both the Thorpe–Phillips constraint counting approach62–66 and the approach developed for analysis of polyhedral structures and rigid unit modes,47–49 both of which have been more recently reviewed in a paper on rigid unit modes.49 The main task is to count the number of degrees of freedom, F, and the number of constraints C, per formula unit. The difference F−C gives the number of normal modes per formula unit in which the structure can buckle without the constraints being broken. That is, these normal modes will not stretch bonds or bend constrained bond angles. If F > C, the structure is floppy in some ways, and there will be a set of normal modes calculated by diagonalisation of the dynamical matrix to have zero frequency. If C > F, the structure is over-constrained and unlikely to have any floppy modes. In the special case F = C, symmetry can make some constraints degenerate, so there will be some floppy modes.For atoms that are bonded but not constrained by bond-bending forces, the model assigns 3 degrees of freedom to each atom, and 1 constraint per bond. Thus in the case were we consider ZrW2O8 to consist of bonds with no angular forces (Section 4.1), the 11 atoms give rise to three degrees of freedom each, and hence F = 33. The Zr–O bonds give 6 constraints, and the W–O bonds from the two WO4 tetrahedra give 8 constraints, so that in total C = 14.
When we consider rigid polyhedra, it would be possible to add bond-bending constraints (for a polyhedra with r bonds, there are 2r − 3 angular constraints), but we prefer to count each polyhedron as a rigid entity with 6 degrees of freedom (now allowing for rotations). Where one vertex is connected to the vertex of another polyhedron, we assign 3 constraints per shared vertex. Where the vertex is bonded to another cation without angular constraints, the bond itself is the constraint as before. In the case where we have rigid ZrO6 and WO4 polyhedra, we have F = 3 × 6 = 18. Each WO4 polyhedron has only 3 linked apices to consider. Avoiding double-counting, we count the number of constraints from both set of polyhedra as C = 18/2 + 18/2 = 18. Thus we have the marginal case F = C, which was discussed in the initial analysis of ZrW2O8 in terms of RUMs,29,30 and as discussed above in Section 4.6.
In Section 4 we consider two variations of the model. In the first, it is recognised that in the crystal structure of ZrW2O8 a pair of neighbouring WO4 tetrahedra have one oxygen atom on one tetrahedron that is unusually close to the W centre of the other tetrahedron. Thus it is possible to add bonding between this atom and the second tetrahedron, making a WO5 polyhedron with a shared vertex. With no additional constraints, we can still associate 12 degrees of freedom to the W2O8 unit, but we now have 3 additional constraints at the shared vertex (Fig. 6). The second variant is to add a constraint that prevents bending of the W–O–W bond, which can be achieved by adding a single constraint on the W⋯W distance.
It has also been proposed that there are effectively rigid WZr3 groups of atoms, in what has been called the ‘tent’ model.21,22 We take account of this by adding Zr–W bond constraints, with three such connections for each Zr and W atom. In this model, we add 3 constraints per Zr atom.
For a final example of mixing different types of constraint, let us consider the case of Zr–O bonds (no angular constraints within the ZrO6 octahedra), and rigid WO4 tetrahedra with the additional W–O bond to form a linkage of WO5 and WO4 (Section 4.3). The Zr atom gives 3 degrees of freedom and 6 bond constraints. The W2O8 unit gives 12 degrees of freedom and 3 constraints. Thus in total F = 15 and C = 9. If the W–O–W is made unbendable, we have C = 10. If additionally we have the constraints of the tent model, we then have C = 13. In all cases F > C.
Analyses for all 16 cases considered in this paper, namely models a–h as shown in Fig. 7 and models i–o as shown in Fig. 8, are given in Table 3.
Acknowledgements
LHNR was supported by a quota studentship funded by NERC with addition support from CrystalMaker Software Ltd. Access to high performance computer facilities was obtain through membership of the UKs HPC Materials Chemistry Consortium, which was funded by EPSRC (Grant No. EP/F067496), The calculations were performed on the facilities of HECToR, a former UK national high-performance computing service, which was provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, and funded by the Office of Science and Technology through EPSRCs High End Computing Programme. We also acknowledge financial support from National Natural Science Foundation of China, grant number 12174274 (MTD).Notes and references
- C. P. Romao, K. J. Miller, C. A. Whitman, M. A. White and B. A. Marinkovic, Comprehensive Inorganic Chemistry II: From Elements to Applications, Elsevier, 2013, pp. 127–151 Search PubMed.
- G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, J. Phys.: Condens. Matter, 2005, 17, R217–R252 CrossRef CAS.
- M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503 CrossRef PubMed.
- K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef PubMed.
- C. Martinek and F. A. Hummel, J. Am. Ceram. Soc., 1968, 51, 227–228 CrossRef CAS.
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef CAS.
- J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8, 2809–2823 CrossRef CAS.
- C. Lind, Materials, 2012, 5, 1125–1154 CrossRef CAS PubMed.
- J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567 RSC.
- N. Shi, Y. Song, X. Xing and J. Chen, Coord. Chem. Rev., 2021, 449, 214204 CrossRef CAS.
- E. Liang, Q. Sun, H. Yuan, J. Wang, G. Zeng and Q. Gao, Front. Phys., 2021, 16, 53302 CrossRef.
- A. P. Ramirez and G. R. Kowach, Phys. Rev. Lett., 1998, 80, 4903–4906 CrossRef CAS.
- J. Boerio-Goates, R. Stevens, B. Lang and B. F. Woodfield, J. Therm. Anal. Calorim., 2002, 69, 773–783 CrossRef CAS.
- Y. Yamamura, N. Nakajima, T. Tsuji, M. Koyano, Y. Iwasa, S. Katayama, K. Saito and M. Sorai, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 014301 CrossRef.
- G. Ernst, C. Broholm, G. R. Kowach and A. P. Ramirez, Nature, 1998, 396, 147–149 CrossRef CAS.
- R. Mittal, S. L. Chaplot, H. Schober and T. A. Mary, Phys. Rev. Lett., 2001, 86, 4692–4695 CrossRef CAS PubMed.
- T. R. Ravindran, A. K. Arora and T. A. Mary, Phys. Rev. Lett., 2000, 84, 3879–3882 CrossRef CAS PubMed.
- J. N. Hancock, C. Turpen, Z. Schlesinger, G. R. Kowach and A. P. Ramirez, Phys. Rev. Lett., 2004, 93, 225501 CrossRef PubMed.
- M. G. Tucker, A. L. Goodwin, M. T. Dove, D. A. Keen, S. A. Wells and J. S. O. Evans, Phys. Rev. Lett., 2005, 95, 255501 CrossRef PubMed.
- M. G. Tucker, D. A. Keen, J. S. O. Evans and M. T. Dove, J. Phys.: Condens. Matter, 2007, 19, 335215 CrossRef PubMed.
- D. Cao, F. Bridges, G. R. Kowach and A. P. Ramirez, Phys. Rev. Lett., 2002, 89, 215902 CrossRef CAS PubMed.
- D. Cao, F. Bridges, G. R. Kowach and A. P. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 014303 CrossRef.
- F. Bridges, T. Keiber, P. Juhas, S. J. L. Billinge, L. Sutton, J. Wilde and G. R. Kowach, Phys. Rev. Lett., 2014, 112, 045505 CrossRef CAS PubMed.
- W. I. F. David, J. S. O. Evans and A. W. Sleight, Europhys. Lett., 1999, 46, 661 CrossRef CAS.
- K. Wang and R. R. Reeber, Appl. Phys. Lett., 2000, 76, 2203–2204 CrossRef CAS.
- R. Mittal and S. L. Chaplot, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7234–7237 CrossRef CAS.
- V. Gava, A. L. Martinotto and C. A. Perottoni, Phys. Rev. Lett., 2012, 109, 195503 CrossRef CAS PubMed.
- M. K. Gupta, R. Mittal and S. L. Chaplot, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014303 CrossRef.
- A. K. A. Pryde, K. D. Hammonds, M. T. Dove, V. Heine, J. D. Gale and M. C. Warren, J. Phys.: Condens. Matter, 1996, 8, 10973 CrossRef CAS.
- A. K. Pryde, K. D. Hammonds, M. T. Dove, V. Heine, J. D. Gale and M. C. Warren, Phase Trans., 1997, 61, 141–153 CrossRef CAS.
- C. A. Figueirêdo and C. A. Perottoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 184110 CrossRef.
- A. K. A. Pryde, M. T. Dove and V. Heine, J. Phys.: Condens. Matter, 1998, 10, 8417 CrossRef CAS.
- A. Kojima, Y. Kuroiwa, S. Aoyagi, A. Sawada, Y. Yamamura, N. Nakajima and T. Tsuji, J. Korean Phys. Soc., 2003, 42, S1257–S1260 CAS.
- A. Sanson, Chem. Mater., 2014, 26, 3716–3720 CrossRef CAS.
- P. F. Weck, E. Kim, J. A. Greathouse, M. E. Gordon and C. R. Bryan, Chem. Phys. Lett., 2018, 698, 195–199 CrossRef CAS.
- P. F. Weck, M. E. Gordon, J. A. Greathouse, C. R. Bryan, S. P. Meserole, M. A. Rodriguez, C. Payne and E. Kim, J. Raman Spectrosc., 2018, 49, 1373–1384 CrossRef CAS.
- M. T. Dove, Z. Wei, A. E. Phillips, D. A. Keen and K. Refson, APL Mater., 2023, 11, 041130 CrossRef CAS.
- H. Fang, M. T. Dove, L. H. N. Rimmer and A. J. Misquitta, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 104306 CrossRef.
- L. H. N. Rimmer, M. T. Dove, B. Winkler, D. J. Wilson, K. Refson and A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214115 CrossRef.
- L. H. N. Rimmer, M. T. Dove, A. L. Goodwin and D. C. Palmer, Phys. Chem. Chem. Phys., 2014, 16, 21144–21152 RSC.
- L. H. N. Rimmer and M. T. Dove, J. Phys.: Condens. Matter, 2015, 27, 185401 CrossRef PubMed.
- E. Grüneisen, Ann. Phys., 1912, 39, 257–306 CrossRef.
- E. Grüneisen, in Thermische Eigenschaften der Stoffe, ed. C. Drucker, E. Grüneisen, P. Kohnstamm, F. Körber, K. Scheel, E. Schrödinger, F. Simon, J. D. van der Waals and F. Henning, Springer Berlin Heidelberg, Berlin, Heidelberg, 1926, pp. 1–59 Search PubMed.
- E. Grüneisen, NASA technical report, 1959, RE 2-18-59W, 1–76 Search PubMed.
- C. W. Li, X. Tang, J. A. Muñoz, J. B. Keith, S. J. Tracy, D. L. Abernathy and B. Fultz, Phys. Rev. Lett., 2011, 107, 195504 CrossRef PubMed.
- M. T. Dove, J. Du, Z. Wei, D. A. Keen, M. G. Tucker and A. E. Phillips, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 094105 CrossRef CAS.
- A. P. Giddy, M. T. Dove, G. S. Pawley and V. Heine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 697–703 CrossRef.
- K. D. Hammonds, M. T. Dove, A. P. Giddy, V. Heine and B. Winkler, Am. Mineral., 1996, 81, 1057–1079 CAS.
- L. Tan, V. Heine, G. Li and M. T. Dove, Rep. Prog. Phys., 2023 DOI:10.1088/1361-6633/acc7b7.
- M. T. Dove, Philos. Trans. R. Soc., A, 2019, 377, 20180222 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230 CrossRef PubMed.
- N. J. Ramer and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12471–12478 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, R4954 CrossRef.
- A. Sanson, Solid State Sci., 2009, 11, 1489–1493 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- J. C. Phillips, J. Non-Cryst. Solids, 1979, 34, 153–181 CrossRef CAS.
- J. C. Phillips, Phys. Today, 1982, 35, 27–33 CrossRef CAS.
- M. F. Thorpe, J. Non-Cryst. Solids, 1983, 57, 355–370 CrossRef CAS.
- H. He and M. F. Thorpe, Phys. Rev. Lett., 1985, 54, 2107–2110 CrossRef CAS PubMed.
- Y. Cai and M. F. Thorpe, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 10535–10542 CrossRef PubMed.
Footnote |
| † The exact values of k and K are unimportant. It is only important that they are either large or zero, depending on the specific flexibility model. A large value needs to give largest frequencies in the calculations of the lattice dynamics of the flexibility models that are considerably bigger than the value of Ω used in eqn (2). |
| This journal is © the Owner Societies 2023 |