Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
HOMER: a reparameterization of the harmonic oscillator model of aromaticity (HOMA) for excited states†
Enrique M.
Arpa
 * and
Bo
Durbeej
* and
Bo
Durbeej
 *
*
Division of Theoretical Chemistry, IFM, Linköping University, SE-581 83 Linköping, Sweden. E-mail: enrique.arpa@liu.se; bodur@ifm.liu.se
First published on 12th June 2023
Abstract
Excited-state aromaticity (ESA) and antiaromaticity (ESAA) are by now well-established concepts for explaining photophysical properties and photochemical reactivities of cyclic, conjugated molecules. However, their application is less straightforward than the corresponding process by which the thermal chemistry of such systems is rationalized in terms of ground-state aromaticity (GSA) and antiaromaticity (GSAA). Recognizing that the harmonic oscillator model of aromaticity (HOMA) provides an easy way to measure aromaticity on geometric grounds, it is therefore notable that this model is yet to be parameterized for excited states. Against this background, we here present a new parameterization of HOMA – termed HOMER – for the T1 state of both carbocyclic and heterocyclic compounds based on high-level quantum-chemical calculations. Considering CC, CN, NN and CO bonds and testing the parametrization using calculated magnetic data as reference, we find that the description of ESA and ESAA by HOMER is superior to that afforded by the original HOMA scheme, and that it reaches the same overall quality as HOMA does for GSA and GSAA. Furthermore, we demonstrate that the derived HOMER parameters can be used for predictive modeling of ESA and ESAA at very different levels of theory. Altogether, the results highlight the potential of HOMER to facilitate future studies of ESA and ESAA.
1. Introduction
Despite the undisputed role of aromaticity in shaping the structures and controlling the chemical reactivities of cyclic, conjugated π-electron systems, a precise definition of this concept and a general approach to directly quantify aromaticity are elusive.1–5 In principle, the reason for this situation is the lack of a quantum-mechanical operator that would make aromaticity a proper observable and, therefore, amenable to direct experimental measurement.5 Consequently, aromaticity is usually probed in an indirect fashion by calculating or measuring a physicochemical property that reflects its manifestation4 and relates to, e.g., induced ring currents, energetic stabilization or electron delocalization.5 For example, the ability of NMR spectroscopy to detect diamagnetic ring currents in aromatic compounds through their effect (downfield) on proton chemical shifts6 is the basis for the calculation of nucleus-independent chemical shift (NICS) indices.7,8 In the isomerization stabilization energy (ISE) approach, in turn, the energetic stabilization associated with aromaticity is quantified in terms of the energy difference between a methylated derivative of the aromatic system at hand and its non-aromatic, exocyclic methylene isomer.9 Other indices, such as the para-delocalization (PDI),10 aromatic fluctuation (FLU)11 and multicenter (MCI)12 ones, probe aromaticity based on different measures of electron delocalization.13Besides magnetism-, energy- and electron delocalization-based measures, there are also geometry-based aromaticity indices that rely on the typical characteristic of aromatic systems to show equalization of bond lengths.14,15 Of these models, perhaps the most effective is the harmonic oscillator model of aromaticity (HOMA).14–16 Originally developed for carbocyclic π-electron systems, this model assumes that the energy required to extend/compress a carbon–carbon (CC) bond in such a system depends quadratically on the extension/compression relative to the equilibrium bond length.16 Under this assumption, the original HOMA index was defined as
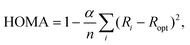 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the initial estimate of Ropt (1.397 Å) in 197216 is very close to the experimental value of 1.398 Å subsequently obtained for benzene by neutron diffraction at 15 K.17 Moreover, by setting HOMA = 0 in eqn (1), this estimate was then used to obtain a value of α as
2, the initial estimate of Ropt (1.397 Å) in 197216 is very close to the experimental value of 1.398 Å subsequently obtained for benzene by neutron diffraction at 15 K.17 Moreover, by setting HOMA = 0 in eqn (1), this estimate was then used to obtain a value of α as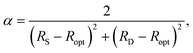 | (2) |
Perhaps the most appealing feature of the HOMA index is the ease with which its values can be obtained,18,19 requiring only information about molecular geometry (Ri) that oftentimes is accessible from both experiments and quantum-chemical calculations. Throughout the years, various extensions of the original model have been proposed.20–24 In 1993, Krygowski20 made it applicable to heterocyclic π-electron systems by introducing a modified HOMA index as
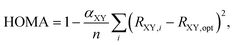 | (3) |
The HOMA index also has a few well-known shortcomings, such as its tendency to exaggerate aromatic character in cases where bonds have similar lengths,14 which by itself clearly is not a sufficient sign of aromaticity. Furthermore, by relying on parameterization, it is less broadly applicable than many of the other indices mentioned above. For example, because of the need of model aromatic/non-aromatic/antiaromatic reference systems from which to derive suitable Ropt and α parameters, HOMA has not yet been applied to aromatic all-metal clusters25,26 in the same way that electron delocalization-based indices have.27 Additionally, there are both positive28 and negative29 results on the ability of HOMA to describe changes in aromatic character along a reaction path.
So far, our presentation has pertained to different ways to probe aromaticity and antiaromaticity in the electronic ground state (S0), i.e., to ground-state aromaticity (GSA) and antiaromaticity (GSAA). However, already in 1972, following earlier work by Dewar30 and Zimmerman,31 the concepts of excited-state aromaticity (ESA) and antiaromaticity (ESAA)32–36 were given a solid theoretical foundation through the discovery by Baird37 that annulenes with 4n and 4n + 2 π-electrons are respectively aromatic and antiaromatic in their lowest triplet ππ* excited state (T1), thus implying a reversal of (anti)aromatic character in this state relative to the ground state as asserted by Hückel's rule. With time, and particularly since the past decade or so,38,39 ESA and ESAA have established themselves as very useful concepts for explaining and predicting photophysical properties40–43 and photochemical reactivities28,44–56 of both triplet and singlet excited states of organic molecules.
A major hurdle for the use of the ESA and ESAA concepts as tools in rational design in photophysics and photochemistry is that conventional experimental measurements (by, e.g., NMR spectroscopy and X-ray crystallography) required to probe aromaticity are much more difficult to perform for molecules in an excited state,35 although developments in time-resolved spectroscopy and electron diffractometry have proven to offer new possibilities in this regard.35,45 As a result, most studies on ESA and ESAA to date have relied on the possibility to calculate aromaticity indices using quantum-chemical methods. Nevertheless, this is generally more challenging for excited states than for ground states, as the former (especially singlet excited states) call for more elaborate modeling and because there is a relative lack of benchmark data for assessing how well different indices measure ESA and ESAA57 (the accuracy of different indices for GSA and GSAA, on the other hand, has been thoroughly investigated13,58–61).
In this light, it is of particular interest to establish how the HOMA index performs for excited states, as this index is probably the easiest to calculate, requiring only a quantum-chemical geometry optimization. Indeed, for this reason, HOMA has often been employed to highlight photochemical consequences of ESA and ESAA,28,45–47,49,52–54 despite that it is yet to be parameterized for excited states. Against this background, we here present a parameterization of HOMA for the T1 state of both carbocyclic and heterocyclic compounds (throughout this work, the “T1 state” refers to the lowest-lying 3ππ* state). Terming the parameterization as the Harmonic Oscillator Model of Excited-state aRomaticity (HOMER) and considering CC, CN, NN and CO bonds (which are the most abundant sources of π-conjugation in heterocyclic compounds62), its performance is tested for a set of 28 molecules across a large portion of the aromatic–antiaromatic spectrum. Thereby, it is found that HOMER offers a vast improvement over standard parameterizations of HOMA20 in the description of ESA and ESAA, as judged from a comparison of how well the two indices correlate with calculated NICS values, which are widely considered as among the most dependable measures of aromaticity and antiaromaticity.60,63 Furthermore, by the same token, it is demonstrated that HOMER is about as accurate for ESA and ESAA as HOMA is for GSA and GSAA. Altogether, these findings pave the way for the use of HOMER to probe ESA and ESAA by means of geometry optimizations.
2. Results and discussion
2.1. Parameterization of HOMER
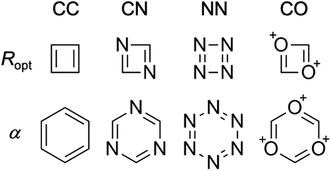
In the same way that benzene is the S0 aromatic reference system for the application of HOMA to carbocyclic compounds, our parameterization of HOMER requires selecting a suitable T1 aromatic reference system for determining the Ropt value for each bond included in the parameterization (i.e., CC, CN, NN and CO). Here, for the CC bond, T1 cyclobutadiene was chosen as reference, which is natural given Karadakov's demonstration that cyclobutadiene, which is antiaromatic in S0, becomes square-symmetric and aromatic in T1,33 in line with Baird's original prediction for 4n π-electron systems.37 For the same reason, the parameterization of CN, NN and CO bonds made use of the T1 aza- and oxo-analogues of cyclobutadiene shown in Fig. 1, which only contain CN, NN or CO bonds in their rings. In order to obtain as accurate Ropt parameters as possible for the different bonds, the T1 geometries of cyclobutadiene and its aza- and oxo-analogues were optimized with the gold standard64,65ab initio multiconfigurational complete active space second-order perturbation theory (CASPT2) method66 in combination with the large cc-pVQZ basis set.67 Since each individual bond type XY was parameterized according to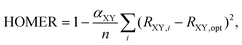 | (4) |
Besides selecting T1 aromatic reference systems for determining the Ropt parameters, it is also necessary to choose appropriate references systems for deriving the corresponding α parameters employed by HOMER. Here, rather than using model non-aromatic systems (as HOMA does14–16), we invoked model T1 antiaromatic systems for this task. Specifically, following the well-known result that benzene changes character from aromatic in S0 to antiaromatic in T1,33,37 the different bonds were parameterized based on T1 benzene and the T1 aza- and oxo-analogues of benzene, which also are shown in Fig. 1 and only contain CN, NN or CO bonds in their rings. By optimizing the T1 geometries of these reference systems, using again CASPT2/cc-pVQZ, the α parameters for the different bonds were obtained from the condition that
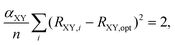 | (5) |
2.2. Probing GSA and GSAA with HOMA
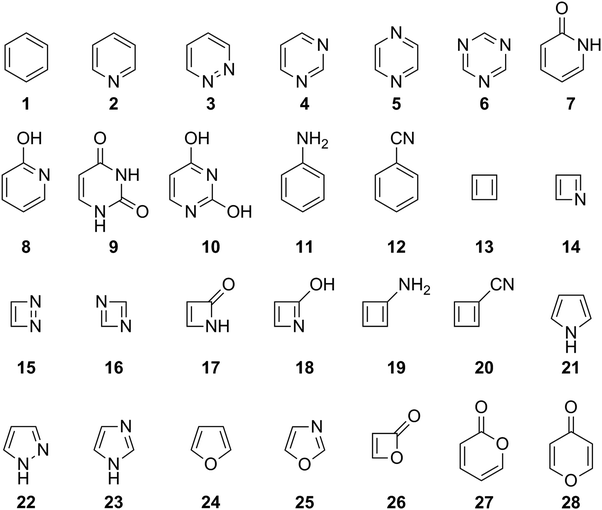
Before assessing the description of ESA and ESAA by HOMER, it is necessary to first test how well HOMA performs for GSA and GSAA, as reference. To this end, the 1993 parameterization of HOMA20 (see eqn (3) and Table 1) was used to probe the aromatic character of the 28 compounds shown in Fig. 2, which cover a large portion of the aromatic-antiaromatic spectrum and comprise four-, five- and six-membered carbocyclic and N,O-heterocyclic species with different substitution patterns. The underlying calculations (i.e., the S0 geometry optimizations) were carried out with the CASPT2 method66 and a medium-sized basis set – cc-pVDZ67 – that represents a typical choice for such calculations. The performance of HOMA was evaluated based on a comparison with S0 NICSzz values (corresponding to the zz-component of the magnetic shielding tensor8) calculated with the complete active space self-consistent field (CASSCF) method68 and the same basis set (cc-pVDZ) that was used to obtain HOMA values. Besides calculating NICSzz values at 1 Å distances above the geometric centers of the rings (NICSzz(1)), which is a proven approach,8 distances of 0 (NICSzz(0)) and 2 Å (NICSzz(2)) were also considered, so as to minimize bias in the comparison of HOMA and NICS values. In addition to testing HOMA in this way, the same exact approach was also used to assess the potency of HOMER in describing GSA and GSAA. Here, however, it should be kept in mind that HOMER is parameterized for ESA and ESAA. Also, for the sake of accuracy, the parameterization is based on geometries optimized with the CASPT2 method, with which NICS values cannot be calculated. Instead, NICS values are calculated with the closest possible method to CASPT2, which is CASSCF.Before going through the results of the calculations, it should be noted that HOMA and HOMER on the one hand and NICS on the other reflect different properties of an aromatic system (the static geometry and the response to a magnetic field, respectively). However, this does not mean that it is inappropriate to use NICS as reference in evaluating the performance of HOMA and HOMER. Contrarily, given the multidimensional character of the aromaticity concept, such an approach is even desirable, and good correlations between HOMA and NICS have indeed been documented in numerous studies of many different compounds.1,14,69–72 Here, it may also be emphasized that this work is primarily concerned with assessing the relative performance of HOMA and HOMER, for which the different origins of HOMA/HOMER and NICS are expected to be a minor issue, rather than the absolute performance of either index relative to NICS.
The results of the calculations are presented in Fig. 3, which uses the NICSzz(1) values for comparing HOMA and HOMER with NICS. For both comparisons, the correlation between the two sets of data was quantified by the R2 value resulting from a linear regression analysis. The corresponding results obtained with the NICSzz(0) and NICSzz(2) values as reference are given in Fig. S1 and S3, respectively, in the ESI.† Furthermore, all raw data underlying these analyses are summarized in Table S1 in the ESI.† From Fig. 3, it is clear that HOMA on the whole agrees quite well with NICS, showing an R2 value of 0.82 (the R2 values relative to the NICSzz(0) and NICSzz(2) data are of similar magnitude, 0.75 and 0.84, see Fig. S1 and S3, ESI†). Hence, in line with many previous studies,1,14,69–72 the easily calculable HOMA index appears to be a viable alternative to the dependable60,63 but more elaborate NICS index in probing GSA and GSAA, which well motivates the goal of the present work to parameterize HOMER for the description of ESA and ESAA. Notably, the most prominent HOMA outliers in Fig. 3 (compounds 15, 16 and 26), whose exclusion from the analysis would increase the R2 value from 0.82 to 0.93, are all four-membered heterocyclic species. Accordingly, it could well be that such species pose a special challenge for HOMA, although the three other of them among the 28 test systems (compounds 14, 17 and 18) follow the overall HOMA/NICS correlation much more closely. Another possibility is that the NICS values of either 15/16 or 26 are skewed by a ring-size dependence. Still, because of its local nature, NICS is generally found to exhibit a modest ring-size dependence.7,72 This is in contrast to global magnetic aromaticity indices, such as those based on magnetic susceptibilities, which show a pronounced ring-size dependence.7,72
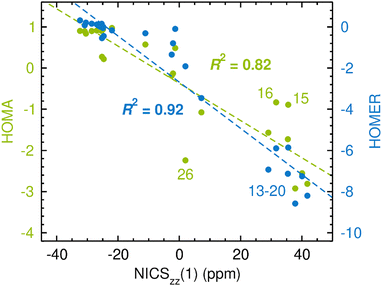 | ||
| Fig. 3 Correlation between CASPT2-based HOMA (in green font)/HOMER (in blue font) values and CASSCF-based NICSzz(1) values in probing GSA and GSAA. The data points for some compounds deserving particular attention are highlighted by their numbers according to Fig. 2. | ||
As an aside, it is striking in Fig. 3 that HOMER actually achieves a better correlation with NICS (R2 = 0.92) than HOMA does (R2 = 0.82), despite that HOMER is parameterized exclusively for ESA and ESAA. While this may be a coincidence, it could also reflect an advantage in our approach to employ cyclic, aromatic and antiaromatic compounds in deriving the Ropt and α parameters of HOMER, as opposed to using non-cyclic, non-aromatic systems, as done in the 1993 parameterization of HOMA.20 At the same time, it should be noted that the HOMER values for GSA and GSAA are somewhat wayward, being, for example, much more negative than −1 for the antiaromatic compounds 13–20. This means that while HOMER provides a surprisingly balanced assessment of GSA and GSAA in a series of different molecules, its value for an individual molecule should not be taken as a quantitative measure of the GSA or GSAA in that system without comparison with the values for a few related molecules.
2.3. Probing ESA and ESAA with HOMER
Having tested the performance of HOMA for GSA and GSAA, we turn next to the assessment of how well HOMER describes ESA and ESAA. This part of the work was carried out in a completely analogous fashion as the previous part, except that the CASPT2 geometry optimizations and the CASSCF NICS calculations were now done for the T1 state of the 28 compounds in Fig. 2. The results of the assessment, including a parallel test of HOMA, are given in Fig. 4, with NICSzz(1) values as reference. The corresponding results obtained with NICSzz(0) and NICSzz(2) values as reference are presented in Fig. S1 and S3 (ESI†), respectively, and all raw data for the analyses are summarized in Table S2 in the ESI.† Before going through the results, it should be noted that HOMA and HOMER, by considering relaxed T1 geometries, cannot describe the aromatic character of the T1 state in the vertically excited Franck–Condon region. As a consequence, if an antiaromatic T1 state is formed upon vertical excitation, this antiaromaticity might be reduced by the geometric relaxation.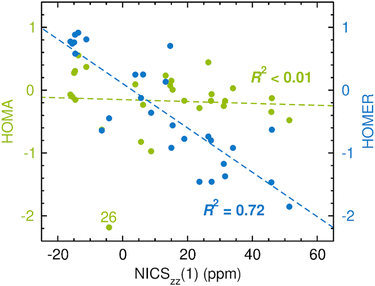 | ||
| Fig. 4 Correlation between CASPT2-based HOMA (in green font)/HOMER (in blue font) values and CASSCF-based NICSzz(1) values in probing ESA and ESAA. | ||
From Fig. 4, it is firstly apparent that HOMA does not correlate at all with NICS (R2 < 0.01), which is also the case when the comparison is made with the NICSzz(0) (see Fig. S1, ESI†) or NICSzz(2) (see Fig. S3, ESI†) data. Hence, using HOMA with standard parameters20 to probe variations in ESA and ESAA between different molecules does not yield reliable results. HOMER, on the other hand, fares much better, achieving a correlation with an R2 value of 0.72 (the R2 values relative to the NICSzz(0) and NICSzz(2) data are quite comparable, 0.57 and 0.69, see Fig. S1 and S3, ESI†). Accordingly, our parameterization of HOMER appears to have been successful and seemingly offers a means to measure ESA and ESAA that is about as consistent with NICS calculations as HOMA is for measuring GSA and GSAA (see Fig. 2).
Interestingly, further scrutiny of the results in Fig. 4 reveals that both the HOMA and the HOMER R2 values increase if lactones (compounds 26 and 27) and lactams (compounds 7, 9 and 17) are excluded from the analysis (the HOMER R2 value increases from 0.72 to 0.81). In fact, as can be seen in Table 2, a similar effect is observed for all correlations tested up to this point. Thus, the rather complex electronic features shown by many ester and amide bonds73 may require a more specific model than those afforded by the 1993 parameterization of HOMA20 or the present parameterization of HOMER. Designing such models is beyond the scope of this work. Of the five lactone/lactam compounds, the most prominent HOMA outlier in Fig. 4 is 26, a four-membered lactone. Since we have already seen that a common characteristic of the three HOMA outliers in Fig. 3 (15, 16 and 26) is that they are four-membered rings, the behavior of 26 in Fig. 4 may stem from an enhancement of complex ester bonding by the four-membered ring.
| Index | Probing of | R 2 with lactones/lactams | R 2 without lactones/lactams |
|---|---|---|---|
| HOMA | GSA and GSAA | 0.82 | 0.90 |
| HOMER | GSA and GSAA | 0.92 | 0.97 |
| HOMA | ESA and ESAA | <0.01 | 0.12 |
| HOMER | ESA and ESAA | 0.72 | 0.81 |
As noted in the Introduction, a main advantage of geometry-based aromaticity indices is that their values are easy to derive once atomic-level resolution structures of the compounds of interest have been obtained, either experimentally or computationally. Up to this point, the performance of HOMER has been tested based on geometries optimized with the CASPT2 method.66 The reason for using CASPT2 for this task is its status as a highly accurate method64,65 that is generally applicable to both ground and excited states, owing to the inclusion of both static and dynamic electron correlation. At the same time, CASPT2 is an expensive method with many subtleties, which means that it is yet to be adopted as a workhorse by non-experts in the field. Instead, for many years, this role has been played by density functional theory (DFT) methods, which offer a much more favorable cost-performance ratio and are easier to use. In this light, we decided to also test HOMER for the description of ESA and ESAA based on geometries and NICSzz(1) values for the T1 state of the 28 compounds calculated with M06-2X74 and CAM-B3LYP,75 which are two popular hybrid density functionals of different types. These results are presented in Fig. 5. The corresponding results testing HOMA for the description of GSA and GSAA are given in Fig. S4 and S5, respectively, in the ESI.† Furthermore, all raw data for the calculations are summarized in Tables S3 and S4 (M06-2X) and in Tables S5 and S6 (CAM-B3LYP) in the ESI.†
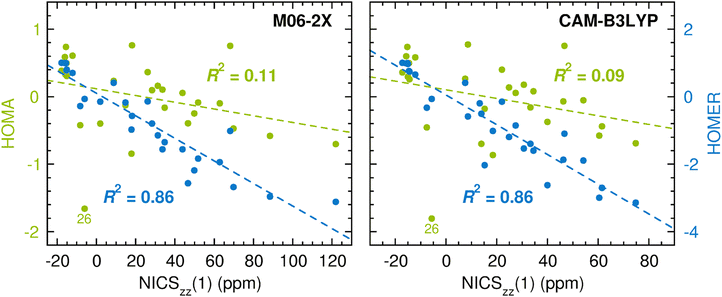 | ||
| Fig. 5 Correlation between DFT-based HOMA (in green font)/HOMER (in blue font) values and DFT-based NICSzz(1) values in probing ESA and ESAA. | ||
Notably, the DFT results in Fig. 5 fully corroborate the previous CASPT2/CASSCF results in Fig. 4 by showing that HOMER (R2 = 0.86) enables a considerably more reliable measurement of ESA and ESAA than HOMA (R2 = 0.09–0.11). In fact, the HOMER R2 values of 0.86 are even better than that of 0.72 assigned to the calculations in Fig. 4, despite that HOMER was parameterized through CASPT2 calculations. Moreover, the HOMER R2 values are virtually identical to those of 0.85–0.86 in Fig. S4 and S5 (ESI†) that quantify how well HOMA measures GSA and GSAA at the DFT level. Given that the T1 geometry optimizations were carried out using unrestricted DFT (UDFT), it is also pleasing to note from Table S7 in the ESI† that the geometries and HOMER values for the 28 compounds obtained at the UM06-2X level are generally close to those instead obtained with M06-2X in the framework of time-dependent DFT (TD-DFT).76 Altogether, these results show that HOMER can also be used successfully at other levels of theory than that employed for the parameterization, which is a very appealing characteristic in terms of applicability (but has been considered difficult to achieve by HOMA-related aromaticity indices77). Thus, while this work has focused on small molecular systems, it will be worthwhile in future studies to test the HOMER parameters derived herein also for molecular systems of varying sizes, using levels of theory of varying sophistication.
3. Conclusions
In summary, recognizing the need for an easily calculable, geometric measure of ESA and ESAA, we have presented a parameterization of the HOMA index for application to the T1 state of both carbocyclic and heterocyclic compounds, which we term HOMER (the Harmonic Oscillator Model of Excited-state aRomaticity). Focusing on CC, CN, NN and CO bonds, the corresponding Ropt and α parameters are derived from high-level ab initio (CASPT2/cc-pVQZ) calculations on cyclic, model T1 aromatic and antiaromatic systems, rather than from experimental bond lengths of non-cyclic, non-aromatic systems (which is the more common procedure in the development of HOMA-related aromaticity indices). Collecting suitable reference data by calculating S0 and T1 NICSzz values for a panel of 28 small molecules across the aromatic-antiaromatic spectrum, the quality of the parameterization is assessed by quantifying its correlation with these NICSzz values, and by comparing this correlation with that achieved by the 1993 parameterization of HOMA.20 Thereby, it is found that while HOMA cannot reliably describe variations in ESA and ESAA between different molecules, the good performance of HOMER at the same task is fully comparable to that HOMA contrarily shows when used to probe variations in GSA and GSAA. Moreover, by employing both ab initio and cheaper DFT methods in the assessment, another important result that further paves the way for HOMER in studies of ESA and ESAA is the observation that the ab initio Ropt and α parameters can be used for predictive calculations at very different levels of theory. Indeed, this will facilitate the future application of HOMER to larger molecular systems than those considered herein. Besides such applications, another worthwhile extension of the present work would be to test how well these parameters, derived here for the T1 state, describe ESA and ESAA in the S1 state. For the sake of generality, one would of course hope that the parameters can be used for all low-lying excited states of organic molecules, regardless of their spin multiplicity. If this is not possible, then a specific parameterization for the S1 state is certainly feasible, as model compounds that are aromatic/non-aromatic/antiaromatic in this state are readily available.334. Computational methods
All calculations except where otherwise noted were done with the medium-sized cc-pVDZ basis set.67 All CASPT2 calculations were carried out based on CASSCF reference wave functions optimized with active spaces including only π and π* orbitals, which correspond to (4,4), (6,5) and (6,6) active spaces for compounds with four-, five- and six-membered rings, respectively.The CASPT2 T1 geometry optimizations performed to derive the Ropt and α parameters of HOMER were done with the large cc-pVQZ basis set67 and using convergence criteria that are considerably tighter (maximum component of the gradient vector: 0.00001 hartree bohr−1; maximum component of the displacement vector: 0.00004 bohr; maximum energy change: 0.000001 hartree) than the default ones in the BAGEL 1.1.2 software78 employed for these calculations.
The CASPT2 S0 and T1 geometry optimizations performed to assess HOMA and HOMER relative to NICS were done using the default convergence criteria in BAGEL 1.1.2. Based on the resulting geometries, HOMA and HOMER values were calculated with the Multiwfn 3.7 software,79 employing a standard version (with the 1993 HOMA parameters20) for the former and a modified version (with our derived HOMER parameters) for the latter. These values were compared with NICSzz values8 calculated from CASSCF S0 and T1 wave functions with the Dalton 2016.2 software,80,81 using gauge-including atomic orbitals and the aforementioned (4,4), (6,5) and (6,6) active spaces for compounds with four-, five- and six-membered rings, respectively.
The complementary S0 and T1 geometry optimizations that were performed to also compare HOMA and HOMER with NICS at the DFT level were carried out with the M06-2X74 and CAM-B3LYP75 hybrid density functionals, using UDFT for the T1 state. Furthermore, in control calculations, T1 geometries and HOMER values were also derived through TD-M06-2X optimizations. All DFT calculations were done with the Gaussian 16 software.82 Again, the associated HOMA and HOMER values were obtained with the use of standard (HOMA) and modified (HOMER) versions of Multiwfn 3.7. As for the corresponding DFT NICSzz values, finally, they too were calculated by employing gauge-including atomic orbitals.
As for frequency calculations at the optimized geometries, it should first be noted that all S0 and T1 geometries considered in this work were optimized to be planar, because such structures are the ideal ones for assessing aromaticity and antiaromaticity. For any given geometry, the corresponding frequency calculation was always performed at the same level of theory used to optimize the geometry in question. At the CASPT2 (DFT) level, the frequency calculations were carried out numerically (analytically) with BAGEL 1.1.2 (Gaussian 16). Thereby, all S0 geometries were found to be potential-energy minima with real vibrational frequencies only. For some of the 28 compounds used to assess the performance of HOMA and HOMER, the corresponding T1 geometries were found to be first-order saddle points with one imaginary vibrational frequency. Importantly, this has no bearing on the evaluation of ESA or ESAA by HOMA and HOMER, which can be done as long as the geometries in question are stationary points (which they are).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Olle Engkvist Foundation (grant 204-0183), the Swedish Research Council (grant 2019-03664), ÅForsk (grant 20-570) and the Carl Trygger Foundation (grant CTS 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102). The calculations were enabled by resources provided by (a) the Swedish National Infrastructure for Computing at the National Supercomputer Centre partially funded by the Swedish Research Council (grant 2018-05973) and (b) the National Supercomputer Centre funded by Linköping University.
102). The calculations were enabled by resources provided by (a) the Swedish National Infrastructure for Computing at the National Supercomputer Centre partially funded by the Swedish Research Council (grant 2018-05973) and (b) the National Supercomputer Centre funded by Linköping University.
References
- T. M. Krygowski, M. K. Cyrański, Z. Czarnocki, G. Häfelinger and A. R. Katritzky, Tetrahedron, 2000, 56, 1783–1796 CrossRef CAS.
- P. V. R. Schleyer, Chem. Rev., 2001, 101, 1115–1118 CrossRef CAS PubMed.
- A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Chem. Rev., 2004, 104, 2777–2812 CrossRef CAS PubMed.
- M. Solà, Front. Chem., 2017, 5, 22 Search PubMed.
- M. Solà, WIREs Comput. Mol. Sci., 2019, 9, e1404 Search PubMed.
- R. H. Mitchell, Chem. Rev., 2001, 101, 1301–1315 CrossRef CAS PubMed.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS PubMed.
- P. V. R. Schleyer and F. Pühlhofer, Org. Lett., 2002, 4, 2873–2876 CrossRef CAS.
- J. Poater, X. Fradera, M. Duran and M. Solà, Chem. – Eur. J., 2003, 9, 400–406 CrossRef CAS PubMed.
- E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2005, 122, 014109 CrossRef PubMed.
- P. Bultinck, R. Ponec and S. van Damme, J. Phys. Org. Chem., 2005, 18, 706–718 CrossRef CAS.
- F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434–6451 RSC.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1419 CrossRef CAS.
- T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Chem. Rev., 2014, 114, 6383–6422 CrossRef CAS PubMed.
- J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef.
- G. A. Jeffrey, J. R. Ruble, R. K. McMullan and J. A. Pople, Proc. R. Soc. London, Ser. A, 1987, 414, 47–57 CAS.
- J. C. Dobrowolski, ACS Omega, 2019, 4, 18699–18710 CrossRef CAS PubMed.
- H. Szatylowicz, P. A. Wieczorkiewicz and T. M. Krygowski, in Aromaticity: Modern Computational Methods and Applications, ed. I. Fernández, Elsevier, 2021, pp. 71–99 Search PubMed.
- T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78 CrossRef CAS.
- T. M. Krygowski and M. K. Cyrański, Tetrahedron, 1996, 52, 1713–1722 CrossRef CAS.
- E. D. Raczyńska, M. Hallman, K. Kolczyńska and T. M. Stępniewski, Symmetry, 2010, 2, 1485–1509 CrossRef.
- C. P. Frizzo and M. A. P. Martins, Struct. Chem., 2012, 23, 375–380 CrossRef CAS.
- R. Kalescky, E. Kraka and D. Cremer, J. Phys. Chem. A, 2014, 118, 223–237 CrossRef CAS PubMed.
- A. I. Boldyrev and L.-S. Wang, Chem. Rev., 2005, 105, 3716–3757 CrossRef CAS PubMed.
- F. Feixas, E. Matito, J. Poater and M. Solà, WIREs Comput. Mol. Sci., 2013, 3, 105–122 CrossRef CAS.
- F. Feixas, E. Matito, M. Duran, J. Poater and M. Solà, Theor. Chem. Acc., 2011, 128, 419–431 Search PubMed.
- J. Wang, B. Oruganti and B. Durbeej, ChemPhotoChem, 2019, 3, 450–460 Search PubMed.
- E. Matito, J. Poater, M. Duran and M. Solà, THEOCHEM, 2005, 727, 165–171 CrossRef CAS.
- M. J. S. Dewar, Tetrahedron, 1966, 8, 75–92 CrossRef.
- H. E. Zimmermann, J. Am. Chem. Soc., 1996, 88, 1564–1565 CrossRef.
- P. Wan and E. Krogh, J. Chem. Soc., Chem. Commun., 1985, 1207–1208 RSC.
- P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 7303–7309 CrossRef CAS.
- H. Ottosson, Nat. Chem., 2012, 4, 969–971 CrossRef CAS.
- J. Oh, Y. M. Sung, Y. Hong and D. Kim, Acc. Chem. Res., 2018, 51, 1349–1358 CrossRef CAS PubMed.
- L. J. Karas and J. I. Wu, Nat. Chem., 2022, 14, 719–727 CrossRef PubMed.
- N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948 CrossRef CAS.
- M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425 CrossRef CAS PubMed.
- J. Kim, J. Oh, A. Osuka and D. Kim, Chem. Soc. Rev., 2022, 51, 268–292 RSC.
- B. J. Lampkin, Y. H. Nguyen, P. B. Karadakov and B. VanVeller, Phys. Chem. Chem. Phys., 2019, 21, 11608–11614 RSC.
- K. J. Fallon, P. Budden, E. Salvadori, A. M. Ganose, C. N. Savory, L. Eyre, S. Dowland, Q. Ai, S. Goodlett, C. Risko, D. O. Scanlon, C. W. M. Kay, A. Rao, R. H. Friend, A. J. Musser and H. Bronstein, J. Am. Chem. Soc., 2019, 141, 13867–13876 CrossRef CAS PubMed.
- O. El Bakouri, J. R. Smith and H. Ottosson, J. Am. Chem. Soc., 2020, 142, 5602–5617 CrossRef CAS PubMed.
- H. Kim, W. Park, Y. Kim, M. Filatov, C. H. Choi and D. Lee, Nat. Commun., 2021, 12, 5409 CrossRef CAS PubMed.
- L. Gutiérrez-Arzaluz, F. Cortés-Guzmán, T. Rocha-Rinza and J. Peón, Phys. Chem. Chem. Phys., 2015, 17, 31608–31612 RSC.
- M. Hada, S. Saito, S. Tanaka, R. Sato, M. Yoshimura, K. Mouri, K. Matsuo, S. Yamaguchi, M. Hara, Y. Hayashi, F. Röhricht, R. Herges, Y. Shigeta, K. Onda and R. J. D. Miller, J. Am. Chem. Soc., 2017, 139, 15792–15800 CrossRef CAS PubMed.
- B. Oruganti, J. Wang and B. Durbeej, Org. Lett., 2017, 19, 4818–4821 CrossRef CAS PubMed.
- B. Durbeej, J. Wang and B. Oruganti, ChemPlusChem, 2018, 83, 958–967 CrossRef CAS PubMed.
- T. Yamakado, S. Takahashi, K. Watanabe, Y. Matsumoto, A. Osuka and S. Saito, Angew. Chem. Int. Ed., 2018, 57, 5438–5443 CrossRef CAS PubMed.
- J. Toldo, O. El Bakouri, M. Solà, P.-O. Norrby and H. Ottosson, ChemPlusChem, 2019, 84, 712–721 CrossRef CAS PubMed.
- C.-H. Wu, L. J. Karas, H. Ottosson and J. I. Wu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20303–20308 CrossRef CAS PubMed.
- L. J. Karas, C.-H. Wu, H. Ottosson and J. I. Wu, Chem. Sci., 2020, 11, 10071–10077 RSC.
- B. Oruganti, P. P. Kalapos, V. Bhargav, G. London and B. Durbeej, J. Am. Chem. Soc., 2020, 142, 13941–13953 CrossRef CAS PubMed.
- R. Kotani, L. Liu, P. Kumar, H. Kuramochi, T. Tahara, P. Liu, A. Osuka, P. B. Karadakov and S. Saito, J. Am. Chem. Soc., 2020, 142, 14985–14992 CrossRef CAS PubMed.
- E. M. Arpa and B. Durbeej, Phys. Chem. Chem. Phys., 2022, 24, 11496–11500 RSC.
- B. Oruganti, J. Wang and B. Durbeej, J. Org. Chem., 2022, 87, 11565–11571 CrossRef CAS PubMed.
- J. Yan, T. Slanina, J. Bergman and H. Ottosson, Chem. – Eur. J., 2023, 29, e202203748 CrossRef CAS PubMed.
- J. Pedersen and K. V. Mikkelsen, J. Phys. Chem. A, 2023, 127, 122–130 CrossRef CAS PubMed.
- F. Feixas, E. Matito, J. Poater and M. Solà, J. Comput. Chem., 2008, 29, 1543–1554 CrossRef CAS PubMed.
- M. Solà, F. Feixas, J. O. C. Jiménez-Halla, E. Matito and J. Poater, Symmetry, 2010, 2, 1156–1179 CrossRef.
- R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615 RSC.
- J. Pedersen and K. V. Mikkelsen, RSC Adv., 2022, 12, 2830–2842 RSC.
- N. N. Makhova, L. I. Belen’kii, G. A. Gazieva, I. G. Dalinger, L. S. Konstantinova, V. V. Kuznetsov, A. N. Kravchenko, M. M. Krayushkin, O. A. Rakitin, A. M. Starosotnikov, L. L. Fershtat, S. A. Shevelev, V. Z. Shirinian and V. N. Yarovenko, Russ. Chem. Rev., 2020, 89, 55–124 CrossRef CAS.
- A. Stanger, Eur. J. Org. Chem., 2020, 3120–3127 CrossRef CAS.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed.
- Š. Budzák, G. Scalmani and D. Jacquemin, J. Chem. Theory Comput., 2017, 13, 6237–6252 CrossRef PubMed.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- M. K. Cyrański and T. M. Krygowski, Tetrahedron, 1998, 54, 14919–14924 CrossRef.
- M. K. Cyrański and T. M. Krygowski, Tetrahedron, 1999, 55, 6205–6210 CrossRef.
- M. K. Cyrański, B. T. Stępień and T. M. Krygowski, Tetrahedron, 2000, 56, 9663–9667 CrossRef.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- C. R. Kemnitz and M. J. Loewen, J. Am. Chem. Soc., 2007, 129, 2521–2528 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- M. Andrzejak, P. Kubisiak and K. K. Zborowski, Struct. Chem., 2013, 24, 1171–1184 CrossRef CAS.
- T. Shiozaki, WIREs Comput. Mol. Sci., 2018, 8, e1331 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- Dalton A Molecular Electronic Structure Program, Release Dalton 2016.2, 2016, https://daltonprogram.org (accessed February 10, 2023).
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Complementary results (Fig. S1–S5 and Tables S1–S7) and Cartesian coordinates and electronic energies of optimized molecular geometries. See DOI: https://doi.org/10.1039/d3cp00842h |
| This journal is © the Owner Societies 2023 |