Open Access Article
Open Access ArticleIn silico screening of nanoporous materials for urea removal in hemodialysis applications†
Thomas
Fabiani
a,
Eleonora
Ricci‡
 b,
Cristiana
Boi
b,
Cristiana
Boi
 b,
Simone
Dimartino
b,
Simone
Dimartino
 c and
Maria Grazia
De Angelis
c and
Maria Grazia
De Angelis
 *a
*a
aInstitute for Materials and Processes, School of Engineering, University of Edinburgh, Sanderson Building, Robert Stevenson Road, EH9 3FB, Edinburgh, Scotland, UK. E-mail: grazia.deangelis@ed.ac.uk
bDepartment of Civil, Chemical, Environmental and Materials Engineering, University of Bologna, Via Terracini 28, 40131 Bologna (BO), Italy
cInstitute for Bioengineering, School of Engineering, University of Edinburgh, King's Buildings Colin Maclaurin Road, EH9 3DW, Edinburgh, Scotland, UK
First published on 24th August 2023
Abstract
The design of miniaturized hemodialysis devices, such as wearable artificial kidneys, requires regeneration of the dialysate stream to remove uremic toxins from water. Adsorption has the potential to capture such molecules, but conventional adsorbents have low urea/water selectivity. In this work, we performed a comprehensive computational study of 560 porous crystalline adsorbents comprising mainly covalent organic frameworks (COFs), as well as some siliceous zeolites, metal organic frameworks (MOFs) and graphitic materials. An initial screening using Widom insertion method assessed the excess chemical potential at infinite dilution for water and urea at 310 K, providing information on the strength and selectivity of urea adsorption. From such analysis it was observed that urea adsorption and urea/water selectivity increased strongly with fluorine content in COFs, while other compositional or structural parameters did not correlate with material performance. Two COFs, namely COF-F6 and Tf-DHzDPr were explored further through Molecular Dynamics simulations. The results agree with those of the Widom method and allow to identify the urea binding sites, the contribution of electrostatic and van der Waals interactions, and the position of preferential urea–urea and urea–framework interactions. This study paves the way for a well-informed experimental campaign and accelerates the development of novel sorbents for urea removal, ultimately advancing on the path to achieve wearable artificial kidneys.
Introduction
Hemodialysis (HD) replaces kidney functionality by removing uremic toxins (UTs), rebalancing electrolytes and draining excess fluid. The technology relies on the extracorporeal exchange of compounds in the blood stream through a semipermeable membrane with a buffered solution called dialysate. Traditionally, HD is administered in hospital, in 4–5 hours sessions, two or three times a week;1 due to the discontinuous treatment, the patient is subject to fluctuating concentrations of toxins and fluid accumulation, resulting in severe vascular and post-treatment stress. These drawbacks are a serious concern, especially for patients with comorbidities (e.g. cardiovascular disease or diabetes), which are generally associated with chronic kidney disease (CKD).2A significant improvement in the patient's lifestyle and health could come from home dialysis or through a wearable device. The biggest challenge lies in the downsizing of the water supply unit by which dialysis water needs to be purified and recirculated. In fact, after HD the spent dialysate contains the UTs removed from the blood stream, mostly low molecular weight compounds such as urea, creatinine, uric acid and others.3 Urea is the hardest compound to be removed from the spent dialysate, due to its similarity with water, as the two molecules have similar size and are both polar and weakly nucleophilic. Furthermore, urea has a very low concentration in the dialysate;3–5 with reference values in many experimental works ranging between 2 and 41 mM.6–12 For this reason, the removal of urea from aqueous solutions, as a proxy for spent dialysate fluid, has been investigated by many research groups.13–15
A dialysate regeneration unit that rebalances ions and captures uremic toxins could solve this problem, enable the design of a wearable artificial kidney (WAK)14 and reduce the water consumed in the process. Attempts at such portable systems have mostly been based on the concept of enzymatic decomposition of urea, using immobilised urease, such as in the REDY®, a commercial device based on a multi-cartridge system.16 Urea was converted by urease into ammonium and carbon dioxide, activated carbon was used to capture uremic toxins such as creatinine, uric acid and part of the urea, while ion exchangers served to capture and rebalance the ammonium ions and CO2 in the dialysate. Due to safety issues related to leaching of aluminium ions, REDY® was withdrawn from the market. Subsequent portable prototypes followed a similar concept of urea decomposition (e.g. the WAK™, NeoKidney, AWAK, Dharma™, Medtronic, Fresenius), using different supports for urease or other designs, but only few of them reached the clinical trials so far.1 Other devices relied on electro-oxidation of urea, but the formation of by-products, such as nitrogen oxides (NO3−, NO2−), ammonia (NH3), chloramines and active chlorine species, is still an open issue.17
A technology based solely on an adsorption mechanism and without chemical reactions would be intrinsically free of by-products generation and thus safer. Indeed, many studies focused on the removal of urea from diluted solution, such as dialysate, using adsorption on nanoporous materials, as activated carbon (AC), zeolites, metal organic frameworks (MOFs) or inorganic nanosheets, the most relevant results reported in Table 1. A discussion of the literature on the adsorption of urea on porous particles is beyond the scope of this article, as there are several reviews dealing with this topic.13–15 Based on a back of the envelope calculation, the ideal sorbent should have a urea binding capacity of 100 mg g−1 for a light wearable device, which could remove the daily urea production with 250 g of sorbent. Such a goal still represents a challenge for the materials tested so far.
| Urea binding capacity (mg g−1) | Urea equilibrium concentration (mM) | Ref. | ||
|---|---|---|---|---|
| a PS nanoparticles ninhydrin groups rely on a chemical reaction of urea with functional groups. | ||||
| Activated carbon | Amorphous carbon | 8.8 | 10 | 19 |
| Silicalite (MFI) | Zeolite | 28.97 | 8.6 | 8 |
| Mordenite (MOR) | Zeolite | 2.49 | 8.6 | 8 |
| ZSM-5 (Si/Al ratio 400) | Zeolite | 6.36 | 20 | 41 |
| ZSM-5 (Si/Al ratio 400) | Zeolite | 6.63 | 10 | 42 |
| PS nanoparticles ninhydrin groupsa | Functional polymer | 126 | 20 | 12 |
| MXene (Ti3C2Tx) | Inorganic nanosheets | 13.8 | 20 | 6,7 |
| MoS2 with widened interlayer spacing | Inorganic nanosheets | 63.9 | 2.3 | 43 |
| Cu-BTC | MOF | 128 | 2 | 44 |
Computational tools offer the possibility of testing conditions and materials that would require an extensive experimental campaign. Erucar et al. performed a computational screening focusing on bio-MOFs for the separation of UTs,18,19 showing that structures based on adenine, dicyanamide and methionine could outperform conventional materials such as AC or zeolites. A similar approach was used to select six out of 354 MOFs with high uptake of indoxyl sulphate, a protein-bound UT.20
Covalent organic frameworks (COFs) are based on covalently bound organic building blocks. The stability of COFs in water under extreme conditions of temperature and pH has been demonstrated experimentally.21 COFs represent an interesting class of nanoporous materials to be simulated at the molecular level. The enormous number of combinations of ligands and functionalisations allow a free design of nano-cavities with the desired size and chemical environment. Furthermore, the structure of new hypothetical COFs, which have not yet been synthesised, can be generated through an in silico assembly of rigid blocks.22 This would allow a much broader computational screening, enabling the design of materials with specific properties and advancing the understanding of the behaviour of COFs.23 Despite these features, to the best of our knowledge, only a few works have focused on molecular simulations of COFs for UTs sorption, and they refer to the sorption of urea on single COF monolayers, which differ from the nanoporous structures object of the present study. Others examined creatinine and uric acid adsorption on ACA-COF, but no experimental work has tested COFs for urea removal.24,25
The present work aims to evaluate and classify nanostructured materials for the selective adsorption of urea, with a focus on COFs. Similar approaches have been attempted to evaluate the performance of large COF libraries for gas separations.26,27 No experimental data on urea removal are available for this class of materials, therefore it is believed that a well-informed experimental campaign of such a wide set of materials should start with molecular screening rather than with random, expensive, and time-consuming tests. Other materials are also considered in this analysis, such as graphites, siliceous zeolites and metal organic frameworks (MOFs) for a total of 560 porous crystals.
A preliminary screening is carried out with the fast Widom insertion method to evaluate the interaction energies between individual sorbate molecules (urea or water) and the crystal frameworks. Such analysis allows to classify materials according to preferential interactions for urea over water, in relation to their pore diameter, surface area and elemental composition. Based on these results, two structures were selected and analysed more in detail with molecular dynamics (MD) at different urea concentrations.
Methods
Database selection
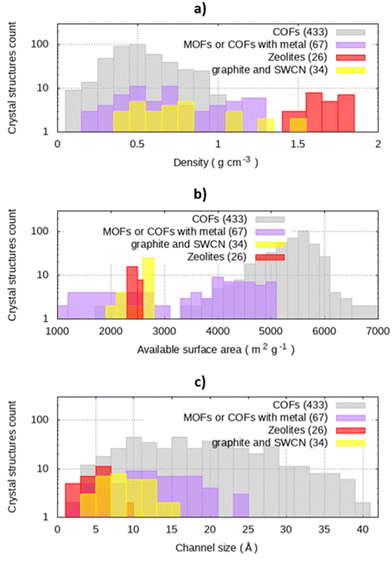
The database selected comprised 26 zeolites, 34 graphite sheets and single wall carbon nanotubes (SWCNs), 433 COFs, and 67 MOFs or COFs coordinating a transition metal. The latter materials were treated separately from the other COFs, as the presence of a metal could cause potential issues in biomedical application, such as hemodialysis.For zeolites, a subset of the database provided by the International Zeolite Association (IZA) was used as a benchmark, as these structures were tested in the literature.8 The 26 frameworks (AHT, EON, ERI, ESV, EUO, FAU, FER, ITE, IWV, LTJ, MEI, MEL, MFI, MON, MOR, MSE, MSO, MTT, MTW, MVY, NES, NSI, PTY, SFS, TON, VFI) are zeolites with high silica content (Si/Al ratio > 10), with few or devoid of acid sites. The choice was made because experimental evidence showed that hydrophobic zeolites were those with better performance in urea capture.28 In fact, the removal of aluminium from the structure through acid treatment is commonly performed to augment the hydrophobicity of the framework.28 Moreover, the presence of aluminium is a concern for its potential release in the patient's blood stream. The structures chosen may be modelled without any cation pairing or substitution of Si atoms, i.e. as purely siliceous structures.
Graphite sheets, graphite square channels and SWCNs (34 structures) present in the RASPA database29 were used as a benchmark for modelling of nanoporous materials with high hydrophobicity.
Although MOFs were not the main focus of this work due to their instability in water, we included them in the database, together with COFs coordinating a transition metal as a reference to consider the impact of transition metals in the structure. The list of MOFs studied is reported in the ESI.† Finally, 433 COFs from CoreCOF database26 were considered, excluding all structures containing boron (namely those based on boroxine, borazine and boronic ester) for their susceptibility to hydrolysis in water and for low stability in the final application.
Simulation conditions
Pore size and available surface area of the frameworks were calculated with Zeo++ version 0.330 by using a probe with a 1.4 Å radius, compatible with a water molecule. Crystal frameworks and penetrant molecules were considered to be rigid, as motivated by the limited degrees of freedom of the crystal structures and of the small adsorbates molecules without rotatable bonds. In fact, COFs are based on building blocks based on aromatic rings, lacking flexibility, favouring the stacking during the synthesis. Therefore, the energy functional form collapses to the inter-molecular contribution alone, according to eqn (S1) (ESI†). Lennard Jones 12–6 (LJ) and Ewald electrostatic potential were used to model the non-bonded interactions. The van der Waals (VdW) and charge–charge cut-off values was set to 12 Å. Lorentz–Berthelot mixing rule was used. Crystals were parametrized by using the DREIDING force field31 and assigning partial charge by EQeq method,32 as reported in Section S1 (ESI†). For zeolites, fixed partial charges were assigned to Si and O (Si = +2.05 and O = −1.025) according to the results described in literature33 since the EQeq implemented in RASPA failed to produce a parametrization in accordance with literature. The TIP5P-E model parameters were used for the calculation of water excess chemical potential, as such model proved to be superior in predicting the water adsorption in zeolites.34,35 Urea was modelled as a rigid molecule (Table S1, ESI†) using the parameters obtained by Weerasinghe and Smith to match the behaviour of urea in water solution.36,37The excess chemical potential μex was calculated through the Widom insertion method38,39 in RASPA,29,40 according to eqn (1).
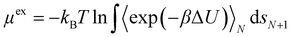 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 insertions were performed in each simulation at random positions. The simulations were carried out probing the individual molecules (urea and water) in the empty framework. The excess chemical potential μex represents the average binding energy of molecule i with the framework, at infinite dilution. Free energy profiles were calculated with RASPA as the projection of μex calculated through Widom method along each crystallographic dimension, with the toolkit provided in the suite29,40
000 insertions were performed in each simulation at random positions. The simulations were carried out probing the individual molecules (urea and water) in the empty framework. The excess chemical potential μex represents the average binding energy of molecule i with the framework, at infinite dilution. Free energy profiles were calculated with RASPA as the projection of μex calculated through Widom method along each crystallographic dimension, with the toolkit provided in the suite29,40
The Henry's law constants KH,i can be computed from μexi as:
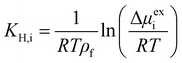 | (2) |
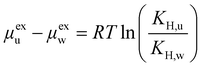 | (3) |
The calculation of infinite dilution excess chemical potentials required only 1.69 ± 1.3 h per molecule and structure. After this fast screening, two selected COF structures (COF-F6 and Tf-DHzDPr) were studied through MD simulations, carried out in RASPA. Urea molecules (1, 10, 100) were initially placed randomly in the framework, reaching an equilibrium position at the end of the simulation. Such loadings of urea correspond to, respectively, 0.53, 5.3 and 53 mg g−1 in COF-F6 and 0.73, 7.3 and 73 mg g−1 in Tf-DHzDPr. Simulation boxes were built to guarantee a minimum box side length of twice the cut-off for both COF-F6 (2 × 2 × 12, 48 unit cells, 174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 Å3) and Tf-DHzDPr (2 × 2 × 18, 78 unit cells, 185
123 Å3) and Tf-DHzDPr (2 × 2 × 18, 78 unit cells, 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 Å3) with a similar total volume. Each canonical ensemble, with constant number of molecules, volume and temperature (NVT), was simulated for 500 ps with 1000 cycles for initialization and up to 500 ps until equilibration was observed, with a time step to 0.5 fs. Nose–Hoover thermostat was used to keep temperature at 310 K (time scale parameter 0.15 ps). Two trajectories were analysed for each condition. Radial distribution functions g(r) were calculated in RASPA with the toolkit provided in the suite.29,40 All simulations were run on Precision 5820 Tower XCTO Base (Intel Core i9-10980XE 3.0 GHz, 4.8 GHz Turbo, 18C, 24.75 MB Cache, HT).
169 Å3) with a similar total volume. Each canonical ensemble, with constant number of molecules, volume and temperature (NVT), was simulated for 500 ps with 1000 cycles for initialization and up to 500 ps until equilibration was observed, with a time step to 0.5 fs. Nose–Hoover thermostat was used to keep temperature at 310 K (time scale parameter 0.15 ps). Two trajectories were analysed for each condition. Radial distribution functions g(r) were calculated in RASPA with the toolkit provided in the suite.29,40 All simulations were run on Precision 5820 Tower XCTO Base (Intel Core i9-10980XE 3.0 GHz, 4.8 GHz Turbo, 18C, 24.75 MB Cache, HT).
Results and discussion
Database analysis and description
The dataset used in our analysis was designed to study the COFs available on repositories, using other classes of materials as a reference. In the whole dataset of nanoporous crystals, densities range from 0.10 g cm−3 to 2.09 g cm−3, with a median value of 0.58 g cm−3 (Fig. 1(a)). In particular, zeolites have density comprised between 1.33 and 2.09 g cm−3 with a median 1.72 g cm−3. The graphites and SWCNs present a scattered distribution of densities, ranging from 0.38 g cm−3 to 1.79 g cm−3. COFs have a lower density with respect to zeolites, with a median density equal to 0.56 g cm−3.Surface area is a key parameter for the application, representing the area available for adsorption, and it is reported in Fig. 1(b). The calculated available surface areas of zeolites, graphite, and SWCN are in the left side of the histogram, while COFs have larger values of surface per gram of materials. For instance, zeolites surface areas range between 2185 m2 g−1 and 2685 m2 g−1 with median value 2541 m2 g−1, while COFs has a median surface area of 5529 m2 g−1, with a standard deviation of 664.6 m2 g−1.
The calculated channel sizes ranges from 3.0 Å to 11.2 Å (median 6.2 Å) for zeolites, while carbon-based materials have a broader distribution (between 5.1 and 16.7 Å, median 9.9 Å). For graphite sheets and graphite square channels, pore size calculations with Zeo++ agree with the structural features of the materials, namely the interlamellar distance for graphite sheets and the channel size for graphite square channels. (Fig. S1, ESI†). The whole database spans from 3.0 Å up to 60.8 Å, in the case of COF-122-2. Conversely from the other materials, with a limited span of pore size, COFs cover the whole range of pore sizes of the dataset, with a median value of 18.5 Å (Fig. 1(c)), confirming the aforementioned tunability of pore size.
Urea and water excess chemical potential at infinite dilution
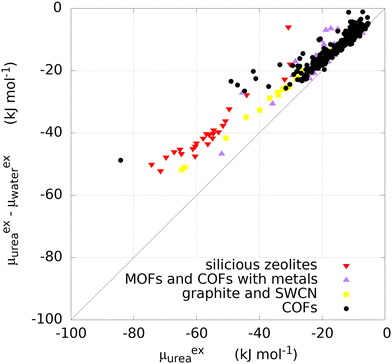
For most of the materials considered, and in particular for COFs, no experimental data on urea removal capacity are available to verify, even if only qualitatively, the simulation results. The only two data available in literature for the materials considered refer to two zeolites, silicalite (MFI) (Si/Al∞) and mordenite (MOR) (Si/Al equal to 10). Such sorbents experimentally adsorb 28.97 mg g−1 and 2.49 mg g−1 of urea from a solution of 8.6 mM, respectively.8 Other materials were tested experimentally for urea sorption and they are summarized in Table 1. Interestingly, Cu-BTU, a metal organic framework, showed an adsorption capacity higher than 100 mg g−1, with a performance attributable to a chemisorption mechanism. Erucar et al.18 screened a set of Bio-MOFs for urea adsorption, following a similar protocol, but using a different model for urea. A comparison in term of μexu and μexu − μexw, between two MOFs simulated in this work and the ones from the literature is reported in Table S2 (ESI†). The calculations of the materials density, channel pore size, available surface area, urea and water excess chemical potential are reported in the SI Excel files SI_COFs, SI_MOFs, SI_C-materials and SI_Zeolites.The infinite dilution performance of the materials was evaluated with the Widom insertion method, considering the excess chemical potential of urea μexu as a measure for urea binding strength, and the difference between excess chemical potential of urea and water μexu − μexw, as a measure of urea/water selectivity (Fig. 2). The bisecting line in Fig. 2 represents a condition in which interaction between framework and water is zero, since μexu − μexw = μexu.
Carbonaceous materials like graphites and SWCNs (yellow squares in Fig. 2) have no electronic polarization and they interact only through VdW forces with urea and water. The deviation from the bisecting line might be attributed to the VdW interactions with water. Furthermore, they lay roughly on a straight line, as the variation in interaction is purely given by structural reasons. Specifically, graphite sheets with the smallest interlamellar distance have the lowest value of μexu (−32.0 kJ mol−1) decreasing monotonically with increasing distance between sheets (Fig. S2, ESI†). A similar trend was observed with graphite square channels, with lowest μexu of −63.6 kJ mol−1 for the structure with the smallest channel size. The monotonic trend may be explained by the fact that two layers of carbon atoms interact more with the urea molecule when lamellae are closer together.
The excess chemical potential of urea in zeolites (red triangles in Fig. 2) ranges between −74.3 kJ mol−1 (PTY) and −30.15 kJ mol−1 (LTJ), with a median value of −56.16 kJ mol−1. One structure (MVY) shows a repulsive energy, due to the sieving effect related to the size of the pores, as small as 3.0 Å (not shown in Fig. 2 and not included in the statistics). MOFs and COFs containing a transition metal (violet triangles in Fig. 2) do not show preferential binding of urea with respect to COFs (black circles in Fig. 2). Most COFs own a μexu not greater than 22.96 kJ mol−1 in absolute value but some of them show higher absolute values with a maximum of 84.2 kJ mol−1.
The key features of the 12 COFs with highest absolute value of urea Excess Chemical Potential are reported in Table 2, while the complete list of values for all materials inspected is reported in the ESI.† These structures (Fig. S3, ESI†) have a channel diameter ranging from 4.1 Å to 26.9 Å and a broad distribution of surface area (2184 to 5932 m2 g−1). On the chemical point of view, all of them contain highly electronegative atoms, such as fluorine, oxygen, nitrogen and sulphur. Interestingly, the top-5 COFs contain fluorine as a functional group, usually grafted as pre or post-synthetic modification of the linker. Each of the twelve contain nitrogen, as it is required for the building blocks reaction, and 9 of them have oxygen in their structure.
Interestingly, some of the structures reported in Table 2 have a corresponding COFs structure with a different linker functionality. For instance, COF-F6, synthetized to be a proton conductor, is based on the same linkers of Tf-DHz COFs54 (Tf-DHzDPr-COF, Tf-DHzDAll-COF, Tf-DHzDM-COF, Tf-DHzDM-COF-1, Tf-DHzDAll-COF-1, Tf-DHzDAll-COF-2) with μexu ranging from −27.8 to −6.2 kJ mol−1. In this series, the fluorination enhances dramatically the binding strength toward urea with respect to groups like propyl, allyloxyl or methyl.
| Framework name | Density | Pore size | ASA | μ exu | μ exw | μ exu − μexw | Oxygen content | Nitrogen content | Fluorine content | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| g cm−3 | Å | m2 g−1 | kJ mol−1 | kJ mol−1 | kJ mol−1 | % | % | % | ||
| COF-F6 | 1.09 | 10.6 | 4568 | −84.2 | −35.4 | −48.7 | 5.9 | 5.9 | 26.5 | 45 |
| CF3-TFP-TTA | 0.59 | 19.0 | 5102 | −49.0 | −25.6 | −23.4 | 0.0 | 6.5 | 9.7 | 46 |
| CF3-TFP-TAPB | 0.52 | 19.4 | 5217 | −47.0 | −22.4 | −24.6 | 0.0 | 3.1 | 9.4 | 46 |
| TpPa-F4 | 1.02 | 14.9 | 3979 | −44.7 | −18.1 | −26.6 | 8.3 | 8.3 | 16.7 | 47 |
| COF-F | 0.56 | 26.9 | 4851 | −41.1 | −18.6 | −22.6 | 0.0 | 10.0 | 10.0 | N/A |
| NUS-3 | 0.69 | 16.7 | 5090 | −37.1 | −12.0 | −25.1 | 13.6 | 9.1 | 0.0 | 48 |
| DAPH-TFP | 0.54 | 23.5 | 5290 | −33.4 | −15.4 | −18.1 | 5.9 | 11.8 | 0.0 | 49 |
| NPN-1 | 1.05 | 4.1 | 4772 | −31.5 | −5.9 | −25.6 | 8.2 | 8.2 | 0.0 | 50 |
| PP-TzDa-AB | 0.70 | 7.3 | 5932 | −30.3 | −5.9 | −24.4 | 5.1 | 5.1 | 0.0 | 51 |
| COF-318 | 1.14 | 13.0 | 2184 | −29.0 | −7.8 | −21.2 | 14.3 | 7.1 | 0.0 | 52 |
| COF-316 | 1.14 | 13.0 | 3091 | −28.1 | −7.8 | −20.3 | 13.3 | 6.7 | 0.0 | 52 |
| CCOF-6 | 0.89 | 5.7 | 5177 | −27.9 | −5.0 | −22.9 | 6.8 | 3.4 | 0 | 53 |
| Tf-DHzDPr-COF | 0.74 | 15.8 | 5651 | −27.8 | −9.4 | −18.5 | 8.0 | 8.0 | 0 | |
Following the same comparison between analogues, TpPa COFs family,47,55–58 based on ketoenamine linkage (TpPa-F4, TpPa-NO2, TpPa-SO3H, TpPa-SO3H-Py, TpPA-2, CCOF-TpPa-1, TpPa-(OH)2, TpPa-Py, TpPa-1, TpPa-1-2F, TpPa-OMe2 in increasing order according with their μexu) show an important effect of the functionalization of the pore on the μexu ranging from −44.7 to −7.1 kJ mol−1. Specifically, highly electronegative functionalization of the COF, such as fluorine, nitric, sulphonyl groups appears to promote the binding strength toward urea.
Similarly, the NUS family,48,59,60 based on ketoenamine linkage, have a trend of μexu according to heteroatoms on the structure increasing from −37.1 to −6.3 kJ mol−1 in the following order: NUS-3, NUS-10, NUS-50, NUS-9, NUS-51, NUS-2, NUS-15, NUS-14. Structures NUS-14 and NUS-15 contain only nitrogen as heteroatom, while NUS-2, NUS-3, NUS-50, NUS-51 contain also oxygen as hydroxyl, ketonic or ether groups. NUS-9 and NUS-10 have sulfonic groups in their structure.
Only few of the materials in this database were tested for separation purposes, for instance NUS-3 and NUS-2 were used in a MMM for CO2 separation,48 while CCOF-6 was synthetized to be used in chromatography of enantiomers. Other applications of the COFs in Table 2 are proton conduction, sensing or catalysis. Interestingly, most of the TpPa-COF,47 as well as COF-318, COF-316,52 CF3-TFP-TAA, CF3-TFP-TAPB,46 CCOF-653 proved to be stable in boiling water and extreme acid and basic conditions, retaining their crystalline structure. Furthermore, all of them, excepting NPN-1, showed to retain their structure up to 300 °C during the thermogravimetric analysis. The 12 COFs were obtained through solvothermal synthesis, for instance COF-F6 was obtained after 3 days in 1,4-dioxane and mesitylene using acetic acid, as a catalyst, at 120 °C.45 The entire list of values of μexu calculated is reported in the ESI† in the various spreadsheets.
Correlation of structure performance with elemental composition and structural parameters
Nitrogen content and oxygen content in COFs did not correlate with the excess chemical potential of urea, as reported in Fig. S4 (ESI†). The top 12 COF structures, in terms of excess chemical potential over urea, reported in Table 2, have molar nitrogen content between 3.2% and 11.8% and molar oxygen content as high as 14.3%. On the other hand, the fluorine content has a clear quantitative impact, as reported in Fig. 3, with the highest values recorded in COF-F6 containing 25% of F atoms. A similar trend is observed between the urea/water selectivity and fluorine content, with increasing selectivity as fluorine content increases.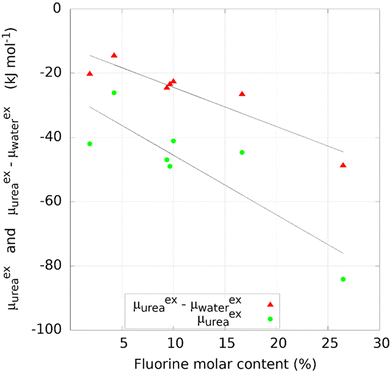 | ||
| Fig. 3 Effect of fluorine molar content on the urea binding and selectivity of COFs with fluorine atoms in the structure. | ||
The excess chemical potential and urea/water selectivity of COF structures showed no clear correlation with pore size and available surface area (Fig. S5, ESI†). While these parameters are traditionally used for the description of nanoporous materials, the positioning, orientation, and quality of functional groups, as well as the intermolecular interactions formed upon adsorption of the urea/water species, are hardly described by pore size and available surface area. This highlights the need for more meaningful descriptors able to capture the properties of the crystalline structure and the chemical environment of the pore.
MD simulation of urea adsorption in COF-F6 and Tf-DHzDPr
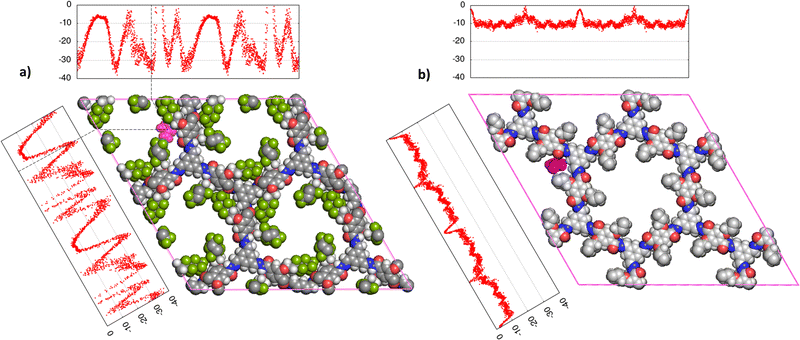
The screening carried out through the chemical potential at infinite dilution showed the impact of functionalization on the COFs pores on the promotion of selective interaction toward urea. To highlight the role played by fluorine atoms, two COF materials, COF-F6 and Tf-DHzDPr-COF were comparatively investigated at higher loading through MD simulations.COF-F6 is the best performing crystal in terms of urea binding strength at infinite dilution, while Tf-DHzDPr-COF, based on the same building blocks as COF-F6, has a propyl chain connected to the oxygen, instead of the fluorinated tail (see Fig. 4). In particular, COF-F6 and Tf-DHzDPr share the same node monomer (benzene-1,3,5-triyltrimethanol) and a similar linker; the former is based on 2,5-di-(6,6,6,5,5,4,4,3,3-nonafluoro-hexoxy)-terephthalohydrazide (Fig. 4(a)), while the latter uses the 2,5-dipropoxyterephthalohydrazide (Fig. 4(b)), differing from the chain attached to the aromatic ring. The resulting crystal structures are reported in Fig. 4(c) for COF-F6 and Fig. 4(d) for Tf-DHzDPr. The presence of a bulky functional group in COF-F6 results in a reduction of pore size and surface area with respect to Tf-DHzDPr, shifting from to 15.83 Å to 10.56 Å and from 5651 m2 g−1 to 4568 m2 g−1.
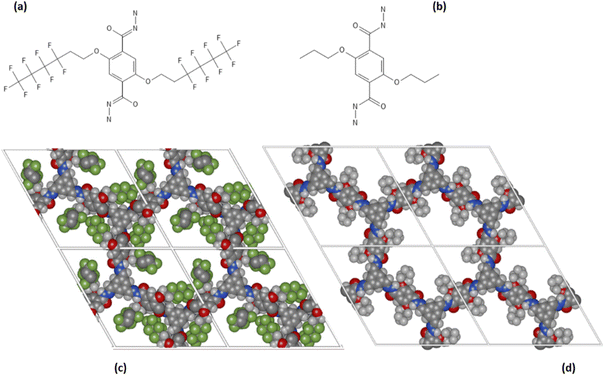 | ||
| Fig. 4 (a) 2,5-di-(6,6,6,5,5,4,4,3,3-nonafluoro-hexoxy)-terephthalohydrazide, (b) 2,5-dipropoxyterephthalohydrazide, (c) Structure of COF-F6 (z-projection) (d) Structure of Tf-DHzDPr (z-projection). | ||
Simulations were carried out in the absence of water molecules as solvent for urea in the framework. In general, the simultaneous presence of both species would result in water molecules competing with urea for interactions with the adsorbent. At the same time, water partially hydrates urea in the bound states, providing favourable intermolecular stabilization of adsorbed urea molecules. The impact of water needs to be thoroughly investigated and will be the object of future study.
MD NVT simulations locate the equilibrium position of the urea molecule in the framework and to calculate the potential energy in that position. The excess chemical potential calculated through the Widom approach, on the other hand, evaluates the average value of the potential energy estimated at different random positions of one molecule in the crystal.
The equilibrium position of the urea molecule in the framework resulting from the MD simulation corresponds to the location of one of the free energy minima obtained with Widom mapping (Fig. 5), indicating the agreement of the two methodologies. Multiple minima are evidenced by MD runs and they refer to equivalent binding sites, due to the symmetry of the crystal structure. In particular, the MD simulation yields a potential energy of the system of −115.0 kJ mol−1 (±0.01%) in COF-F6 and −45.9 kJ mol−1 (±0.50%) in Tf-DHzDPr, versus values of −84.2 kJ mol−1 and −27.8 kJ mol−1 evaluated with the Widom method. The difference is due to the fact that MD simulation evaluates the energy of the most favourable binding site, while the Widom insertion procedure averages the excess chemical potential over a uniform sampling of the unit cell, according to eqn (1). The sampling of Tf-DHzDPr with the insertion method provided an almost flat trend over the two directions of the unit cell (Fig. 5), with values mostly comprised between −5 kJ mol−1 and −15 kJ mol−1. This difference between the two materials may be addressed with the absence of strong polar centers in the Tf-DHzDPr defining preferential site in terms of position and orientation for the urea molecule.
The adsorption of a urea molecule in the nanoporous materials, at a given concentration in the bulk, requires chemical (together with thermal and mechanical) equilibrium. This condition implies the equality between the chemical potentials of urea in the external water solution and in the nanoporous materials. Kokubo et al. reported chemical potential for urea in a water solution, equal to −85.57 kJ mol−1 with the model used in this work, at a concentration of 42.86 mM (2.71 g L−1), considered in many works as an upper bound for urea concentration in CKD patients’ blood. Particularly, the excess chemical potential μex is equal to −41.31 kJ mol−1 (with a contribution from van der Waals and electrostatic terms that are respectively 2.14 kJ mol−1 and −46.40 kJ mol−1). The ideal chemical potential, due to the urea concentration in water is equal to −44.26 kJ mol−1.37
The infinite dilution chemical potential μexu calculated with the insertion method does not include the stabilization due to the partial solvation of water in the framework and the ideal contribution of the chemical potential, that are by definition negative. Nonetheless, urea in COF-F6, according to the Widom insertion method reaches a μexu equal to −84.2 kJ mol−1, showing the compatibility of binding strengths in COFs with the adsorption of urea at the concentration of interest.
To consider the effect of a larger number of urea molecules in the structure we designed systems for COF-F6 and Tf-DHzDPr, as explained in the methods sections. Upon increasing the number of molecules, a slight decrease of the absolute value of potential energy per molecule is observed for COF-F6, while Tf-DHzDPr displays a less definite trend.
Fig. 6 shows the different contributions to the total potential energies. The VdW interaction term is smaller for COF-F6 (less than 24%), while for Tf-DHzDPr it represents up to 54% of the total interactions between urea and the framework. Fluorine in COF-F6 binds urea molecules primarily through electrostatic forces. The urea–urea interactions, also reported in Fig. 6, arise only when there are at least 100 molecules in the system. This is compatible with a progressive filling of the materials, with urea molecules occupying the most favourable binding sites first, and then opting for less favourable interactions on the framework. This concept is corroborated by the slight decrease of the average interaction of urea molecules with the framework and the increasing urea–urea intermolecular interactions. The urea–urea intermolecular interactions are, in both cases, mostly electrostatic.
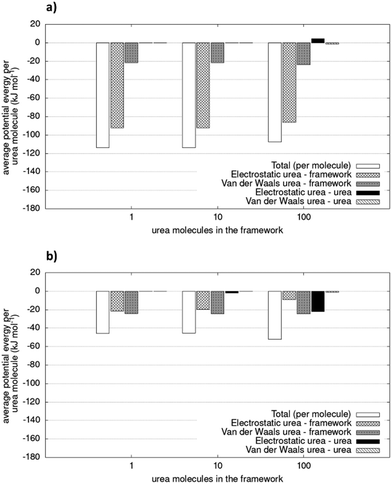 | ||
| Fig. 6 Potential energy of simulated system (per urea molecule) for (a) COF-F6 and (b) Tf-DHzDPr. The values are average of two simulations. Relative errors of duplicate is lower than 1.2%. | ||
Intermolecular interactions between 100 urea molecules in COF-F6 are repulsive, while for Tf-DHzDPr they are attractive. In the latter material, the loss in interaction between urea molecules and framework is compensated by attractive interactions of adsorbate molecules which increase with their concentration. The urea molecules distribution in the two materials can be seen in Fig. S6 and S7 (ESI†).
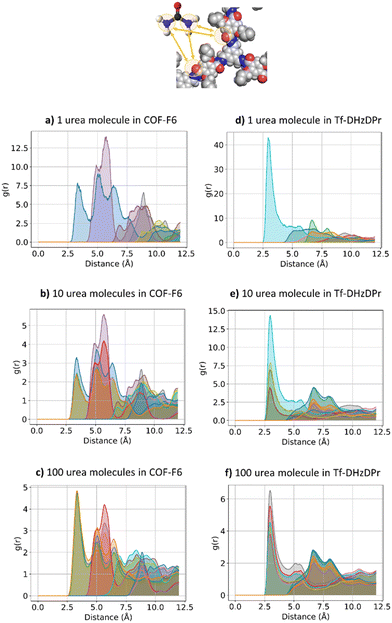
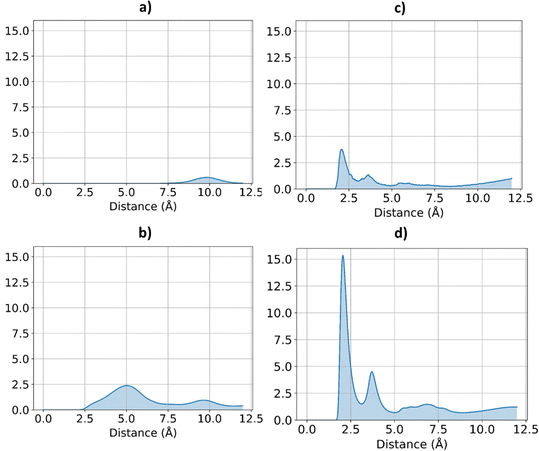
The effect of increasing urea loading on the resulting interactions can be also studied analysing the radial distribution functions (RDF), describing the pairwise distance between atoms in the system. Interestingly, all individual urea atoms preferentially interact with COF-F6 fluorine, oxygen and hydrogen atoms. For instance, as shown in Fig. 7, hydrogen atoms bound to nitrogen in the urea structure interact tightly with fluorine atoms in COF-F6 (shown by the peak at a distance of 2 Å in Fig. 7(a)). The oxygen atom in the urea molecule seems to privilege the interaction with hydrogen in the COF-F6 structure (shown by the peak at a distance of 2.5 Å in Fig. 7(c)). Thus, urea owns a preferential orientation while adsorbing, supporting the presence of a binding site on COF-F6 provided by both atoms of the bone structure (hydrogens) and the tails (fluorines). This is testified by the peaks’ positions of RDFs (reported in Fig. S8, ESI†) between 2 Å and 4 Å, showing relative position of urea atoms with respect to the framework. On the other hand, nitrogen atoms in the framework appear to be more distant from urea with distances higher than 4 Å. The quality and the distance between electronegative atoms of urea and of the framework support the classification of such interactions as hydrogen bonds, in which the urea nitrogen behaves as a hydrogen bonds’ acceptor.
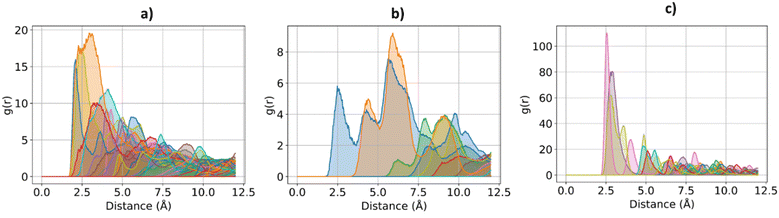 | ||
| Fig. 7 RDF for the system of COF-F6 with 1 urea molecule: (a) urea H atoms with F atoms on COF-F6, in (b) urea H atoms with O atoms of COF-F6 and in (c) urea O atoms with H atoms of COF-F6. | ||
The interactions established by the urea N atoms with O atoms in the framework, at increasing number of urea molecules, are reported in Fig. 8. Introducing 1 and 10 molecules of urea in COF-F6, oxygen in the framework binds urea nitrogen atoms, testified by the broad peak at 3.70 Å, with soft and wide shape. With 100 molecules, the first peak is slightly shifted increasing its height (with respect to the other peaks) and many peaks emerge between 2.5 and 10 Å. This means that, increasing the number of molecules in the framework, urea starts to establish tighter interactions with O atoms therein.
In Tf-DHzDPr the behaviour is different, as the framework lacks electronegative atoms on the exposed propyl tail. In this case, urea binds through its amine groups with the oxygen available on the framework, forming hydrogen bonding, while the carbonyl group in urea interacts with hydrogens on the framework surface. This is showed by the peaks’ position in Fig. S8 (ESI†): in this case oxygen atoms play a prominent role in binding urea, when only one molecule is placed in the framework. A sharp peak between 2.5 and 4 Å in the radial distribution function computed between oxygens of the sorbent, and hydrogens and nitrogens of the urea molecule confirms the previous statement. Even in this case, nitrogen atoms in the framework appear far from the urea molecules, in fact RDF with C atoms in urea do not show a peak closer than 4 Å. Also in Tf-DHzDPr, upon increasing the number of urea molecules, the RDF undergo a modification (Fig. 8). In this case, the peaks at closest distance remains unperturbed, with an increasing number of overlapping peaks at the same distance, due to the progressive filling of preferential binding locations. Conversely from COF-F6, additional peaks, overlapping or shifted at higher distance with respect to the others, appear with 100 molecules, showing the interaction of urea in other sites.
Therefore, COF-F6 and Tf-DHzDPr bind urea differently; the former has fluorine atoms providing strong electronegative sites that prevail over the other hydrogen bonding donors and acceptors on the structure. Multiple atoms of urea in these crystals interact with each other, arranging in order to minimize repulsion. Specifically, a concentration of 53 mg g−1 in COF-F6 results in urea molecules interacting with each other, at a distance of 4.8 Å (Fig. S10, ESI†), but there is no specific relative orientation, confirming that the interaction with the framework is strong enough to compensate the energetic penalty of repulsion between urea molecules (Fig. 6). Such evidence agrees with the energetic contributions to the potential energy reported in Fig. 6. For Tf-DHzDPr at 73 mg g−1 of urea in the framework, the molecules are 4.53 Å apart and they orient themselves to maximize their attraction. This is suggested by the defined peaks at 2.08 Å and 3.73 Å in Fig. 9(d), proof of an orientation of urea molecules while they are bound to the framework (oxygen atoms in urea are oriented toward hydrogen atoms of other urea molecules).
Although partial charge parametrisation showed to be a source of uncertainty in the reproduction of adsorption performance in organic frameworks,61,62 the chemical pore environment in COFs seems to strongly influence the urea binding strength, demonstrating their potential as sorbents for urea removal.
However, functionalisation could reduce the pore space available for sorption, thus limiting the maximum theoretical amount of urea molecules in the system.
Conclusions
In this study, a database of 560 porous crystals containing zeolites, graphitic materials, MOFs and COFs was screened to assess their potential as urea adsorbents to regenerate dialysate. The focus was put on COF materials which can guarantee high stability in water and low safety issues. The Widom insertion approach for excess chemical potential at infinite dilution allowed to rank the frameworks according to their affinity and selectivity towards urea. Fluorine content in the COF structures promotes the adsorption of urea and favours urea/water selectivity, with the framework COF-F6 having the best performance. Other structural parameters (e.g. pore size, surface area, etc.) or composition of other elements were not correlated to urea removal performance.The results are consistent with MD simulations carried on COF-F6 and its non-fluorinated equivalent, Tf-DHzDP. The analysis of the radial distribution functions allowed to understand that electronegative atoms, such as fluorine or nitrogen atoms in the framework structure are crucial in forming hydrogen bonds with the sorbate. However, fluorination reduces the pores volume and the maximum number of urea molecules that can be theoretically loaded in the framework.
In conclusion, the screening indicates that the large freedom in linkers’ selection gives space for optimizing and tailoring the frameworks on the desired application.
Furthermore, the computational method here presented is suitable for a fast preliminary screening of large materials databases and consistent with longer MD simulations. Such procedure can be used to inform and shorten the experimental campaign and also to explore hypothetical structures, not yet synthesised, assisting the design of new materials with target performance. Future work will inspect the competitive effect of water on the urea removal performance of selected materials.
Author contributions
Thomas Fabiani: conceptualization, data curation, investigation, formal analysis, software, writing – original draft. Eleonora Ricci: supervision, writing – review & editing. Cristiana Boi: writing – review & editing. Simone Dimartino: writing – review & editing. Maria Grazia De Angelis: conceptualization, funding acquisition, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by Kidney Research UK through the programs Kidney Medtech Competition Award 2022 and Kidney Research UK – Stoneygate Research Project Grant KS_RP_012_20221129. We also acknowledge financial support from the Royal Society of Edinburgh (RSE) through the Saltire Facilitation Workshop Award 2021 (Funder reference number 1898), and the RSE Scottish Government SAPHIRE Grant: 2022 (Funder reference number 2816). The School of Engineering at the University of Edinburgh has supported the PhD scholarship of Mr Thomas Fabiani.Notes and references
- M. K. van Gelder, S. M. Mihaila, J. Jansen, M. Wester, M. C. Verhaar, J. A. Joles, D. Stamatialis, R. Masereeuw and K. G. F. Gerritsen, Expert Rev. Med. Devices, 2018, 15, 323–336 CrossRef CAS PubMed.
- W. G. Couser, G. Remuzzi, S. Mendis and M. Tonelli, Kidney Int., 2011, 80, 1258–1270 CrossRef PubMed.
- R. A. Pollock, G. Yu Gor, B. R. Walsh, J. Fry, I. T. Ghampson, Y. B. Melnichenko, H. Kaiser, W. J. DeSisto, M. C. Wheeler and B. G. Frederick, J. Phys. Chem. C, 2012, 116, 22802–22814 CrossRef CAS.
- H. D. Lehmann, R. Marten and C. A. Gullberg, Artif. Organs, 1981, 5, 278–285 CrossRef CAS PubMed.
- J. T. Olesberg, M. A. Arnold and M. J. Flanigan, Clin. Chem., 2004, 50, 175–181 CrossRef CAS PubMed.
- F. Meng, M. Seredych, C. Chen, V. Gura, S. Mikhalovsky, S. Sandeman, G. Ingavle, T. Ozulumba, L. Miao, B. Anasori and Y. Gogotsi, ACS Nano, 2018, 12, 10518–10528 CrossRef CAS PubMed.
- Q. Zhao, M. Seredych, E. Precetti, C. E. Shuck, M. Harhay, R. Pang, C.-X. Shan and Y. Gogotsi, ACS Nano, 2020, 14, 11787–11798 CrossRef CAS PubMed.
- V. Wernert, O. Schäf, H. Ghobarkar and R. Denoyel, Microporous Mesoporous Mater., 2005, 83, 101–113 CrossRef CAS.
- M. N. Z. Abidin, P. S. Goh, A. F. Ismail, N. Said, M. H. D. Othman, H. Hasbullah, M. S. Abdullah, B. C. Ng, S. H. S. A. Kadir and F. Kamal, Carbohydr. Polym., 2018, 201, 257–263 CrossRef CAS PubMed.
- W.-K. Cheah, Y.-L. Sim and F.-Y. Yeoh, Mater. Chem. Phys., 2016, 175, 151–157 CrossRef CAS.
- C.-H. Ooi, W.-K. Cheah and F.-Y. Yeoh, Adsorption, 2019, 25, 1169–1175 CrossRef CAS.
- I. Geremia, J. A. W. Jong, C. F. van Nostrum, W. E. Hennink, K. G. F. Gerritsen and D. Stamatialis, Sep. Purif. Technol., 2021, 277, 119408 CrossRef CAS.
- W.-K. Cheah, K. Ishikawa, R. Othman and F.-Y. Yeoh, J. Biomed. Mater. Res., Part B, 2017, 105, 1232–1240 CrossRef CAS PubMed.
- Y. Ma, S. Li, M. Tonelli and L. D. Unsworth, Microporous Mesoporous Mater., 2021, 319, 111035 CrossRef CAS.
- C. Gao, Q. Zhang, Y. Yang, Y. Li and W. Lin, Biomater. Res., 2022, 26, 5 CrossRef PubMed.
- M. Roberts, Nephrology, 1998, 4, 275–278 CrossRef CAS.
- M. K. van Gelder, J. A. W. Jong, L. Folkertsma, Y. Guo, C. Blüchel, M. C. Verhaar, M. Odijk, C. F. Van Nostrum, W. E. Hennink and K. G. F. Gerritsen, Biomaterials, 2020, 234, 119735 CrossRef CAS PubMed.
- B. Akkoca Palabıyık, M. Batyrow and I. Erucar, Sep. Purif. Technol., 2022, 281, 119852 CrossRef.
- T. Yıldız and I. Erucar, Chem. Eng. J., 2022, 431, 134263 CrossRef.
- B. Li, S. Gong, P. Cao, W. Gao, W. Zheng, W. Sun, X. Zhang and X. Wu, Ind. Eng. Chem. Res., 2022, 61, 6618–6627 CrossRef CAS.
- X. Huang, C. Sun and X. Feng, Sci. China: Chem., 2020, 63, 1367–1390 CrossRef CAS.
- F. Haase and B. V. Lotsch, Chem. Soc. Rev., 2020, 49, 8469–8500 RSC.
- Y. Lan, X. Han, M. Tong, H. Huang, Q. Yang, D. Liu, X. Zhao and C. Zhong, Nat. Commun., 2018, 9, 5274 CrossRef PubMed.
- A. M. Jahromi, M. Khedri, M. Ghasemi, S. Omrani, R. Maleki and N. Rezaei, Sci. Rep., 2021, 11, 12085 CrossRef CAS PubMed.
- T. Skorjanc, D. Shetty, F. Gándara, S. Pascal, N. Naleem, S. Abubakar, L. Ali, A. K. Mohammed, J. Raya, S. Kirmizialtin, O. Siri and A. Trabolsi, ACS Appl. Mater. Interfaces, 2022, 14, 39293–39298 CrossRef CAS PubMed.
- M. Tong, Y. Lan, Q. Yang and C. Zhong, Chem. Eng. Sci., 2017, 168, 456–464 CrossRef CAS.
- C. Kessler, J. Eller, J. Gross and N. Hansen, Microporous Mesoporous Mater., 2021, 324, 111263 CrossRef CAS.
- H. L. Jamieson, H. Yin, A. Waller, A. Khosravi and M. L. Lind, Microporous Mesoporous Mater., 2015, 201, 50–60 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511 CrossRef CAS PubMed.
- J. M. Castillo, D. Dubbeldam, T. J. H. Vlugt, B. Smit and S. Calero, Mol. Simul., 2009, 35, 1067–1076 CrossRef CAS.
- Y. Khalak, B. Baumeier and M. Karttunen, J. Chem. Phys., 2018, 149, 224507 CrossRef PubMed.
- S. W. Rick, J. Chem. Phys., 2004, 120, 6085–6093 CrossRef CAS PubMed.
- S. Weerasinghe and P. E. Smith, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS.
- H. Kokubo, J. Rösgen, D. W. Bolen and B. M. Pettitt, Biophys. J., 2007, 93, 3392–3407 CrossRef CAS PubMed.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, Inc., USA, 2nd edn, 2001 Search PubMed.
- RASPA2 iRASPA 2022.
- M. De Pascale, M. G. De Angelis and C. Boi, Membranes, 2022, 12, 203 CrossRef CAS PubMed.
- Y.-C. Cheng, C.-C. Fu, Y.-S. Hsiao, C.-C. Chien and R.-S. Juang, J. Mol. Liq., 2018, 252, 203–210 CrossRef CAS.
- H. Zhao, J. Huang, L. Miao, Y. Yang, Z. Xiao, Q. Chen, Q. Huang and K. Ai, Chem. Eng. J., 2022, 438, 135583 CrossRef CAS.
- W. Li, S. Chao, Y. Li, F. Bai, Y. Teng, X. Li, L. Li and C. Wang, J. Membr. Sci., 2022, 642, 119964 CrossRef CAS.
- X. Wu, Y. Hong, B. Xu, Y. Nishiyama, W. Jiang, J. Zhu, G. Zhang, S. Kitagawa and S. Horike, J. Am. Chem. Soc., 2020, 142, 14357–14364 CrossRef CAS PubMed.
- Structural Engineering of Two-Dimensional Covalent Organic Frameworks for Visible-Light-Driven Organic Transformations|ACS Applied Materials & Interfaces, https://pubs.acs.org/doi/10.1021/acsami.0c00013, (accessed 26 June 2023).
- S. Chandra, S. Kandambeth, B. P. Biswal, B. Lukose, S. M. Kunjir, M. Chaudhary, R. Babarao, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2013, 135, 17853–17861 CrossRef CAS PubMed.
- Z. Kang, Y. Peng, Y. Qian, D. Yuan, M. A. Addicoat, T. Heine, Z. Hu, L. Tee, Z. Guo and D. Zhao, Chem. Mater., 2016, 28, 1277–1285 CrossRef CAS.
- E. Vitaku, C. N. Gannett, K. L. Carpenter, L. Shen, H. D. Abruña and W. R. Dichtel, J. Am. Chem. Soc., 2020, 142, 16–20 CrossRef CAS PubMed.
- D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830–834 CrossRef CAS PubMed.
- M. Huang, J. Chong, C. Hu and Y. Yang, Inorg. Chem. Commun., 2020, 119, 108094 CrossRef CAS.
- B. Zhang, M. Wei, H. Mao, X. Pei, S. A. Alshmimri, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 12715–12719 CrossRef CAS PubMed.
- X. Han, J. Huang, C. Yuan, Y. Liu and Y. Cui, J. Am. Chem. Soc., 2018, 140, 892–895 CrossRef CAS PubMed.
- X. Li, Q. Gao, J. Wang, Y. Chen, Z.-H. Chen, H.-S. Xu, W. Tang, K. Leng, G.-H. Ning, J. Wu, Q.-H. Xu, S. Y. Quek, Y. Lu and K. P. Loh, Nat. Commun., 2018, 9, 2335 CrossRef PubMed.
- J.-B. Liao, J.-S. Chang and D.-J. Lee, Mater. Lett., 2023, 338, 134061 CrossRef CAS.
- Q. Sun, B. Aguila and S. Ma, Mater. Chem. Front., 2017, 1, 1310–1316 RSC.
- S. Kandambeth, A. Mallick, B. Lukose, M. V. Mane, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2012, 134, 19524–19527 CrossRef CAS PubMed.
- S. Chandra, T. Kundu, K. Dey, M. Addicoat, T. Heine and R. Banerjee, Chem. Mater., 2016, 28, 1489–1494 CrossRef CAS.
- Y. Peng, G. Xu, Z. Hu, Y. Cheng, C. Chi, D. Yuan, H. Cheng and D. Zhao, ACS Appl. Mater. Interfaces, 2016, 8, 18505–18512 CrossRef CAS PubMed.
- T. Kundu, J. Wang, Y. Cheng, Y. Du, Y. Qian, G. Liu and D. Zhao, Dalton Trans., 2018, 47, 13824–13829 RSC.
- D. Ongari, P. G. Boyd, O. Kadioglu, A. K. Mace, S. Keskin and B. Smit, J. Chem. Theory Comput., 2019, 15, 382–401 CrossRef CAS PubMed.
- C. Cleeton, F. Lopes de Oliveira, R. Neumann, A. Farmahini, B. Luan, M. Steiner and L. Sarkisov, Chemical Engineering and Industrial Chemistry.
Footnotes |
| † Electronic supplementary information (ESI) available: SI_screening. See DOI: https://doi.org/10.1039/d3cp01510f |
| ‡ Current address: National Centre for Scientific Research “Demokritos”, Athens, Greece. |
| This journal is © the Owner Societies 2023 |