 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase equilibria of symmetric Lennard-Jones mixtures and a look at the transport properties near the upper critical solution temperature†
Ivan
Antolović
 a,
Jens
Staubach
b,
Simon
Stephan
a,
Jens
Staubach
b,
Simon
Stephan
 b and
Jadran
Vrabec
b and
Jadran
Vrabec
 *a
*a
aThermodynamics, Technical University Berlin, 10587 Berlin, Germany. E-mail: vrabec@tu-berlin.de; Tel: +49 30 314 22755
bLaboratory of Engineering Thermodynamics (LTD), RPTU Kaiserslautern, Kaiserslautern, Germany
First published on 5th June 2023
Abstract
This study investigates phase equilibria and transport properties of five symmetric binary Lennard-Jones mixtures using molecular simulation and equation of state models. The mixtures are selected for their representation of different types of phase behavior and the research contributes to the development of simulation techniques, mixture theories and understanding of thermophysical mixture properties. A novel method is introduced for determining the critical end point (CEP) and critical azeotropic end point (CAEP) by molecular simulation. The van der Waals one-fluid theory is assessed for its performance in conjunction with Lennard-Jones equation of state models, while addressing different phase equilibrium types simultaneously. An empirical correlation is introduced to account for deviations between the equation of state and simulation that arise when using the same binary interaction parameter. This study also investigates the influence of the liquid–liquid critical point on thermophysical properties, which are found to exhibit no significant anomalies or singularities. System-size effects of diffusion coefficients are addressed by extrapolating simulation data to the thermodynamic limit and applying analytical finite-size corrections.
1. Introduction
For the fundamental understanding of fluid mixture properties and the development of theories, Lennard-Jones (LJ) model systems have been successfully studied for many decades. They are an attractive tool because they are on one hand simple and well-defined and, on the other hand, exhibit a large variety of phase behavior types that can be found in real substances.Consequently, LJ systems have been employed for the development of theories, like for bulk phases via conformal solution theory,1–4 interfacial properties5–7 or models for transport properties.8–11 Moreover, binary LJ mixtures have been extensively studied with molecular simulation to gain a better fundamental understanding of the thermophysical properties of mixtures and their relation to the molecular interactions, like excess properties,12–14 phase equilibria,15–18 interfacial properties,19–24 entropic properties,8,25 Joule–Thomson inversion26 and transport properties.27–29 Despite their simplicity, LJ mixtures exhibit a wealth of phase behavior types, such as azeotropy and aneotropy,30 isopycnic inversion,31 barostatic inversion32 as well as different types of criticality.33 Moreover, LJ mixtures are frequently used for the development of simulation techniques.25,28
This work contributes to all three of the addressed aspects, i.e. (i) simulation techniques, (ii) mixture theories and (iii) fundamentals of thermophysical mixture properties. For these purposes, five binary LJ mixtures were selected that exhibit different types of phase behavior. These mixtures are throughout symmetric, i.e. both components have identical size, energy and mass parameters. The five mixtures only differ in their cross-interaction parameter. Symmetric systems are a particularly simple and well-defined mixture class so they were studied occasionally.31,34,35
First, this work contributes to the development of simulation techniques (i) for studying phase equilibria. Various methods are available in the literature for determining vapor–liquid (VLE), liquid–liquid (LLE), vapor–liquid–liquid equilibria (VLLE), azeotropic points as well as liquid–liquid and vapor–liquid critical points, cf. ref. 36.
However, to the best of our knowledge, no method has been proposed yet for determining the critical end point (CEP) and critical azeotropic end point (CAEP). These points bear substantial significance in the context of phase behavior, as they refer to a specific combination of temperature, pressure and composition where two distinct phases cease to exist. Moreover, special thermodynamic and particularly characteristic conditions hold at these points (see Section 2.2 for details). A binary mixture may exhibit a single CEP and a single CAEP, which makes these points similarly characteristic as the critical point of a pure fluid. A new method is presented here for determining CEP and CAEP data by molecular simulation. For the studied mixtures, VLE, LLE, VLLE and the azeotropic line are also studied such that a comprehensive data set becomes available.
Second, this work contributes to mixture theories (ii) by studying the applicability of van der Waals one-fluid theory to different phase equilibrium types. In van der Waals one-fluid theory, the properties of a mixture are estimated by considering a hypothetical pure component with interaction parameters derived from those of the individual pure components.3 For modeling the thermodynamic properties of mixtures, conformal solution theory in the form of the van der Waals one-fluid theory3,37–40 has become a central element. Yet, for modeling more complex phase behavior, problems often arise upon simultaneously modeling different phase equilibrium types (i.e. VLE, LLE and VLLE). Hence, it seems that describing such equilibria simultaneously poses conflicting objectives. The origin of this issue is not fully understood, i.e. it might be in general due to deficiencies of the underlying equation of state (EOS) or due to the employed mixture theory. The performance of conformal solution theory in the form of van der Waals one-fluid theory is systematically assessed in this work. Accurate molecular simulation data obtained under (i) are taken as a reference. This information is used to test the performance of this theory in conjunction with several EOS. The deviations arising from this theory used in the EOS are compensated by adjusting the binary interaction parameter ξEOS of the EOS models such that good agreement with the simulation data is obtained. Based on this approach, the conflicting objectives for simultaneously describing VLE, LLE and VLLE are rigorously quantified for the first time. This provides insights into the performance of the van der Waals one-fluid mixing rule applied to mixtures exhibiting different phase equilibrium types.
Under (iii), the influence of a liquid–liquid critical point on thermophysical properties is investigated, cf.Fig. 1. At critical points, a phase equilibrium terminates in a sense that two coexisting phases become equal, which is closely related to fluctuations.42,43 While there is a wealth of information on the influence of vapor–liquid critical points on different thermophysical properties, cf. ref. 44 for a review, less is known about this issue for liquid–liquid critical points.24,45 At vapor–liquid critical points, the heat capacities exhibit a pole and the thickness of fluid interfaces diverges. Also, the shear viscosity and the thermal conductivity exhibit peculiarities in the vicinity of vapor–liquid critical points.44
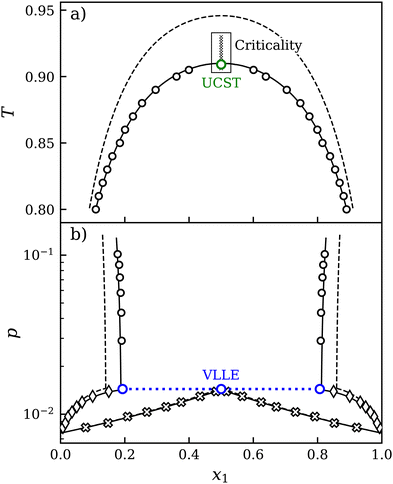 | ||
| Fig. 1 T–x diagram at constant pressure p = 0.0724 (a) and p–x diagram at constant temperature T = 0.85 (b) of mixture C (ξ = 0.80). Transport and equilibrium properties were studied in the vicinity of the upper critical solution temperature (UCST). EOS:41 predictive (dashed line) and adjusted (solid line), simulation data: LLE (circles), VLE (crosses: vapor, diamonds: liquid). | ||
This work is structured as follows: the simulation and modeling methods are introduced together with the specification of the LJ mixtures studied in this work. The results section consists of three parts: (i) the simulation results for the phase equilibria and characteristic points are presented and discussed; (ii) the van der Waals one-fluid theory is assessed in conjunction with different EOS models; and (iii) the behavior of various thermophysical properties in the vicinity of a liquid–liquid critical point is investigated.
2. Modeling and simulation
Five symmetric binary LJ mixtures were considered in this work, which are defined by the shared size (σ1 = σ2), energy (ε1 = ε2) and mass (m1 = m2) parameters of their pure components, while variations are introduced by different cross-interactions. Interactions between unlike LJ particles were described with the modified Lorentz–Berthelot combining rules46,47 | (1) |
 | (2) |
Note that the size, energy and mass parameters of the LJ interaction potential of the components were used to reduce all thermodynamic properties to dimensionless numbers on the order of unity, e.g. temperature T* = TkB/ε, pressure p* = pσ3/ε or self-diffusion coefficient 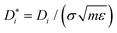 . For brevity, the asterisk is omitted in the following with the understanding that reduced quantities are reported throughout.
. For brevity, the asterisk is omitted in the following with the understanding that reduced quantities are reported throughout.
2.1 Simulation techniques for characteristic lines
Depending on the value of the binary interaction parameter ξ, the LJ mixtures belong to varying types according to the classification of van Konynenburg and Scott50 and have different characteristic lines and points. Three mixture types were considered in this work: type I-A, type II-A and type III-H, cf.Table 1. The characteristics of these mixtures were investigated with molecular simulation, which involved analyzing five specific lines and points: VLLE line, critical LLE line, azeotropic line, CEP and CAEP, cf.Fig. 2. Horizontal (a) and vertical (b) cuts in the p–T plane were predominantly used to obtain these lines with simulative means. The steep slope of the critical LLE line required horizontal cuts in the T–x diagram, while the VLLE and azeotropic lines were analyzed vertically in p–x diagrams as presented in Fig. 1. | ||
| Fig. 2 Characteristic lines and points of mixture C in the p–T projection. Horizontal (a) and vertical (b) cuts correspond to T–x and p–x diagrams shown in Fig. 1. The labeled lines and points were the subject of this work – lines: VLLE (blue), critical LLE (green) and azeotropic line (red) – points: CEP (triangle down), CAEP (plus sign) and CP (star). | ||
While the characteristic lines and points can be obtained rather straightforwardly from the EOS, the molecular simulation tool ms2 used in this work does not allow for their direct sampling. Therefore, dedicated techniques were required to extract the characteristic lines and points from simulation data, for which the symmetry of the mixtures was extensively utilized.
The three-phase VLLE incorporates both the VLE and LLE and it is worth taking a closer look at the latter before moving on to the VLLE conditions. In addition to thermal and mechanical equilibrium, the equality of chemical potentials is required. For LLE and VLE in a symmetric binary mixture, this requirement is expressed as follows:
| μL11 = μL21 = μL12 = μL22, | (3) |
| μL1 = μV1, μL2 = μV2. | (4) |
| μL11 = μL21 = μV1, | (5) |
| μL12 = μL22 = μV2. | (6) |
| μLLE = μV1 = μV2. | (7) |
| μLLE = μVLE1 = μVLE2 = μV(x1 = 0.5). | (8) |
The critical line of the LLE is constituted by the upper critical solution temperature (UCST), which is a function of pressure. Fig. 2 depicts the projection of this line on the p–T plane, and it can be seen that it is very steep, almost parallel to the pressure axis. At the critical point, the binodal and spinodal, which are characterized by a vanishing thermodynamic factor Γ = 0, meet. For a binary mixture, the thermodynamic factor is given by
 | (9) |
The composition at the UCST is generally unknown, but due to the mixtures' symmetry, it is clear that it must be equimolar, cf.Fig. 1b. Therefore, the thermodynamic factor at the UCST will vanish there
| Γ(TUCST, x1 = 0.5) = 0. | (10) |
Due to this limitation that obstructs direct simulations, a model-based approach was used instead. The NRTL model was selected and fitted to the chemical potential data sampled with simulation in the stable liquid region to obtain an analytical expression for the chemical potential from which the thermodynamic factor can be extracted. This approach not only allowed for the determination of the LLE but also provided a solution to the issue of glancing intersections, which may lead to inaccurate results.52 After fitting the NRTL model to simulation data, values for the thermodynamic factor at x1 = 0.5 were calculated. A model-based approach generally raises concerns about model dependence. However, the present findings indicate that such concerns are unfounded here, as discussed below.
Fig. 3b shows a Γ–T diagram with an exemplary isobar at equimolar composition. Inside the miscibility gap of the LLE, the thermodynamic factor is negative and has a positive, linear slope. The zero crossing of Γ as a function of temperature marks the UCST because it satisfies condition (10). UCST data calculated in this work are listed in the ESI.†
2.2 Simulation techniques for characteristic points
The CEP marks the point where the VLLE ceases to exist and where the LLE and VLE phase envelopes start to diverge. This point is also characteristic of a specific mixture, lending itself as a reference point. Once the VLLE line and the critical line of the LLE have been determined as discussed above, their stark slope difference was utilized to identify the CEP. While the VLLE line has a slight bend near the CEP, the critical line of the LLE is locally linear, cf.Fig. 3c. Fitting both lines and finding their intersection yields a reasonable approximation of the CEP. A direct simulation of the exact CEP location might be possible and was tried for mixture C (ξ = 0.8) once its approximate location was determined. However, this trial and error approach was found to be ineffective compared to the one followed in this work.The CAEP marks the end point of the azeotropic line and is the last contact point between the two symmetric VLE envelopes. They separate and each exhibits a critical point. Approaching the CAEP along the azeotropic line, the liquid and vapor phases become increasingly indistinguishable as their densities converge. In order to determine the critical temperature Tc, pressure pc and density ρc at the CAEP, the scaling law for density and the rectilinear diameter were employed53,54
| ρL − ρV = A·(Tc − T)β, | (11) |
 | (12) |
| Mixture | B | C | D | E |
|---|---|---|---|---|
| ξ | 0.75 | 0.80 | 0.85 | 1.20 |
| T CEP | 1.000 | 0.904 | 0.776 | — |
| p CEP | 0.049 | 0.022 | 0.006 | — |
| T CAEP | 1.153 | 1.181 | 1.211 | 1.439 |
| p CAEP | 0.111 | 0.112 | 0.114 | 0.135 |
2.3 Equations of state
For modeling purposes, four LJ EOS were used that were found to yield a reasonable overall agreement with pure fluid reference data.57–59 These EOS were developed by Johnson et al.,60 Kolafa and Nezbeda,41 Lafitte et al.61 and Stephan et al.58 The EOS of Johnson et al.60 is of modified Benedict–Webb–Rubin (MBWR)62,63 type, whereas the remaining ones41,58,61 are based on the perturbation theory of Barker and Henderson (BH).64,65 All four are formulated in terms of the Helmholtz energy41,58,61 or can be transformed into it.60MBWR-type EOS are based on an empirically modified virial expansion. For the three perturbation theory-based EOS, the Helmholtz energy per molecule is split into a reference aref and a perturbation term apert
| a = aref + apert, | (13) |
| aref = aid + ahs. | (14) |
All four EOS were extended to mixtures using the van der Waals one-fluid mixing rule.1,66 The binary interaction parameter ξEOS was introduced through the modified Berthelot combination rule46,47 in the same way as for the force fields, cf.eqn (1) and (2). The p–T diagrams of the binary mixtures were calculated with an algorithm proposed by Deiters and Schneider.38,67
In the first step, all four EOS were applied to one mixture. Based on these results, the most suitable EOS was chosen for subsequent steps.
3. Results and discussion
Simulation results for phase equilibria and transport properties are presented, discussed and compared to EOS results. First, it is focused on the characteristic lines and points, which serve as a “fingerprint” for a given mixture and are particularly useful for comparison purposes. The results are presented in the following order: (1) simulation data are evaluated in terms of phase equilibria which served as a benchmark for EOS. (2) The critical point is then approached by simulation with a focus on transport properties while incorporating an EOS for equilibrium properties.3.1 Simulation results for characteristic lines and points
Three characteristic lines and two characteristic points were investigated for five mixtures, cf.Table 1. Each line is comprised of several points that in turn were obtained through a series of simulations and calculations involving numerous state points and intermediate steps. For example, the VLLE line consists of individual three-phase points that were derived from preceding VLE, LLE and vapor phase simulations. The critical LLE line consists of several UCST, each obtained by the thermodynamic factor route. The azeotropic line consists of individual azeotropic points as well. The critical points CEP and CAEP require all of the above. Therefore, the presentation of these characteristic lines and points in a p–T projection provides a highly condensed summary of the available data and allows for a thorough comparison between simulation and EOS. The number, curvature and location of the characteristic lines and points provide distinguishing features of each investigated mixture, allowing both for classification into mixture types and differentiation within a particular mixture type.Fig. 4 presents the results for the mixtures B, C and E according to Table 1, as well as the results obtained from the EOS by Kolafa and Nezbeda.41 The variation of the binary interaction parameter ξ causes the characteristic lines and points to shift along the pressure and temperature axes, either above or below the pure component vapor pressure curve (for ξ < 1 or ξ > 1, respectively). For ξ = 1, all lines and points coincide with the pure component vapor pressure curve. The CEP and CAEP exhibit opposing trends, approaching each other as ξ decreases. Below a certain threshold, CEP, CAEP and the connecting azeotropic line disappear, leaving only a tricritical point (TCP). This threshold is known as the “shield region”, within which CEP, CAEP, TCP and a quadruple point can coexist, as demonstrated by Garrido et al.31 The values of ξ were chosen in this study such that all mixtures fall outside of the shield region, with mixture A being below and mixtures B to E above it.
 | ||
| Fig. 4 p–T projection of the phase behavior of mixtures B, C and E compared to the EOS of Kolafa and Nezbeda41 in predictive mode. Characteristic lines and points: VLLE (blue), critical LLE line (green), azeotropic line (red), CEP (triangle down), CAEP (plus sign). EOS (solid lines and markers), simulation data (empty markers). LLE simulation matrix (+). | ||
The VLLE and azeotropic lines show a good agreement between EOS and simulation results in terms of temperature and pressure, with only minor deviations. However, the mole fraction along these lines does not match well, as can be seen in Fig. 1b for the three-phase line. To address these deviations, a modified binary interaction parameter ξEOS was introduced into the EOS that differs from the force field parameter ξ. This topic is discussed below in more detail.
For mixture B, the simulation matrix used for the LLE calculations is provided as an example in Fig. 4a. The results of numerous trial simulations have shown that a 4 × 4 grid is sufficient to accurately obtain the VLLE, critical LLE lines and the CEP through horizontal and vertical cuts. In addition, further VLE simulations were carried out at constant temperature to accurately locate the three-phase point and the azeotropic points.
It was observed that the critical LLE line is very sensitive to variations of the binary interaction parameter ξ. This is demonstrated by the significant difference in the rate with which it propagates through the p–T plane compared to the VLLE and azeotropic lines.
The results presented in Fig. 5 demonstrate that the CEP and CAEP exhibit opposing trends. As ξ increases, the temperature of the CEP falls progressively, while the temperature of the CAEP rises linearly. The simulation results suggest that the EOS overestimates the temperature of these points, but the general trends are in good agreement. The systematic overestimation of simulation results by the EOS could be attributed to its failure in exhibiting an appropriate scaling behavior near a critical point. It should be noted that it is not possible to simply shift the EOS to match one of these points without causing the other to move in the opposite direction. The data indicate that the CEP and CAEP may converge for some value ξ < 0.70. Extrapolating the simulation data leads to an estimate of ξ ≈ 0.68 for the intercept. However, this estimate should be viewed with caution because the accurate location of the shield region was not the focus of this work. CEP and CAEP data of the investigated mixtures are listed in Table 2.
 | ||
| Fig. 5 Temperature of the critical points as a function of the binary interaction parameter ξ. Comparison between EOS41 in predictive mode (solid lines) and simulation results for the type II mixtures B, C and D: CEP (orange, triangles down) and CAEP (red, plus signs). | ||
3.2 van der Waals one-fluid theory
The five mixtures studied in this work were modeled with four LJ EOS, which were carefully selected among the large number of such models available in the literature.58 For pure components, a systematic evaluation of LJ EOS using a comprehensive computer experiment database57 showed that the one of Kolafa and Nezbeda41 presently provides the best compromise of robustness and accuracy.58,59 It exhibits a reasonable behavior in the vapor–liquid two-phase region, i.e. it has a single van der Waals loop and extrapolates well to extreme temperature and pressure conditions with respect to Brown's characteristic curves.59As can be seen in Fig. 4, the UCST along the critical LLE line was consistently overestimated by the EOS of Kolafa and Nezbeda41 when using the same binary interaction parameter ξ. Fig. 6 shows the adjusted binary interaction parameter ξEOS that was optimized with respect to the molecular simulation results for mixture C. Results are shown for the EOS of Johnson et al.,60 Kolafa and Nezbeda,41 Lafitte et al.61 and Stephan et al.58 Both VLE and LLE data from simulation were considered in the fitting procedure for lower temperatures T ≤ 0.92. For higher temperatures, only VLE data were used for the fit. For each temperature studied by molecular simulation, the ξEOS value was fitted individually. Thereby, the temperature dependence of ξEOS(T) was obtained, which can be taken as a measure for the deficiencies of the mixture model. The values of ξEOS close to the true value ξ = 0.8 indicate a good predictive capability of the mixture model. All studied EOS show the same qualitative behavior of ξEOS: in the low-temperature regime, it increases linearly with rising temperature and the slope is approximately the same. The EOS of Johnson et al.60 and Kolafa and Nezbeda41 require very similar ξEOS values, which are significantly lower than those for the EOS of Lafitte et al.61 and Stephan et al.58 in the low temperature regime. The EOS of Stephan et al.58 exhibits the largest ξEOS values.
 | ||
| Fig. 6 Binary interaction parameter of the EOS ξEOS for mixture C (ξ = 0.8) adjusted to simulation data as a function of temperature. VLE and LLE data were included for T ≤ 0.92 and VLE data only for T > 0.92. Results are shown for the EOS of Johnson et al.60 (triangles), Kolafa and Nezbeda41 (squares), Lafitte et al.61 (crosses) and Stephan et al.58 (diamonds). The temperature of the CEP obtained from simulation is indicated by the vertical line. | ||
In the temperature range where only VLE data were considered in the fitting procedure (T > 0.92), only a minor temperature dependence of ξEOS was observed. For the EOS of Stephan et al.,58 there is hardly any temperature dependence of ξEOS. The EOS of Lafitte et al.61 exhibits the largest ξEOS values in the high temperature regime, whereas the smallest ξEOS values were obtained for the Kolafa and Nezbeda41 EOS.
Important differences were observed for the ξEOS values in the low temperature regime (fitted to VLE and LLE data) and the high temperature regime (only fitted to VLE data). In particular, ξEOS values obtained from the fit to the simulation data exhibit a discontinuity in the vicinity of the CEP. This is the case for all four considered EOS and might indicate deficiencies of the van der Waals one-fluid mixing rule, which is reminiscent of EOS not consistently describing VLE and LLE with a given parameter set. Subsequently, only the EOS of Kolafa and Nezbeda41 was used as its binary interaction parameter ξEOS required the smallest adjustments.
Fig. 7 shows the results for the ξEOS fit for all five mixtures studied in this work. Results are shown for one type III mixture (A), three type II mixtures (B, C, D) and one type I mixture (E). For mixtures of type I and III, only a minor temperature dependence of ξEOS is observed. The binary interaction parameter ξEOS for the type II mixtures, on the other hand, was fitted to VLE and LLE data, but shows no temperature dependence. The average offset of ξEOS from ξ is much larger for the mixture of type III than for the mixture of type I. For all type II mixtures, a discontinuity was observed in the vicinity of the CEP.
 | ||
| Fig. 7 Binary interaction parameter ξEOS for mixtures A to E adjusted to simulation data as a function of temperature. Results were obtained by fitting ξEOS to VLE and LLE simulation data and are shown for the EOS of Kolafa and Nezbeda41 (squares). The temperature of the CEP is indicated by the triangles. | ||
3.3 Equilibrium properties near the UCST
The attention is now turned to the Helmholtz energy derivatives, which have been obtained with the formalism of Lustig,68 and the thermodynamic factor, which serves for conversion between transport diffusion coefficients. The details of these methods are outlined in the ESI.†For the study of the critical point, one binary mixture and one EOS were selected, namely mixture C and the EOS of Kolafa and Nezbeda,41cf.Table 1. In particular, it was focused on the UCST as depicted in Fig. 1. The UCST was previously located from the two-phase region (Γ < 0) and is now approached from the homogenous region (Γ > 0), yielding a value of TUCST = 0.9084 in both cases.
The partial derivatives of the reduced Helmholtz energy, denoted as  , can be used to determine all thermodynamic equilibrium properties, such as the isochoric heat capacity cv, speed of sound w or the Joule–Thomson coefficient μJT. For additional information on the subject, the reader is referred to the ESI.†Fig. 8 shows the results for the residual contributions
, can be used to determine all thermodynamic equilibrium properties, such as the isochoric heat capacity cv, speed of sound w or the Joule–Thomson coefficient μJT. For additional information on the subject, the reader is referred to the ESI.†Fig. 8 shows the results for the residual contributions  to the reduced Helmholtz energy derivatives. The respective ideal gas contributions for the same states are given in the ESI.† EOS and simulation results indicate that the derivatives
to the reduced Helmholtz energy derivatives. The respective ideal gas contributions for the same states are given in the ESI.† EOS and simulation results indicate that the derivatives  exhibit a linear trend with respect to temperature. Upon the approach to the UCST, no notable changes were observed. When comparing the simulation results and the EOS for the given mixture, it was found that the slopes of the derivatives are similar, but there are offsets. This deviation is more pronounced for derivatives that are associated with caloric properties
exhibit a linear trend with respect to temperature. Upon the approach to the UCST, no notable changes were observed. When comparing the simulation results and the EOS for the given mixture, it was found that the slopes of the derivatives are similar, but there are offsets. This deviation is more pronounced for derivatives that are associated with caloric properties  ,
,  than for the ones associated with thermal properties
than for the ones associated with thermal properties  ,
,  . The application of the adjusted binary interaction parameter ξEOS to the EOS resulted in curves that are much closer to the simulation results. No significant system size dependence was observed for the Helmholtz energy derivatives.
. The application of the adjusted binary interaction parameter ξEOS to the EOS resulted in curves that are much closer to the simulation results. No significant system size dependence was observed for the Helmholtz energy derivatives.
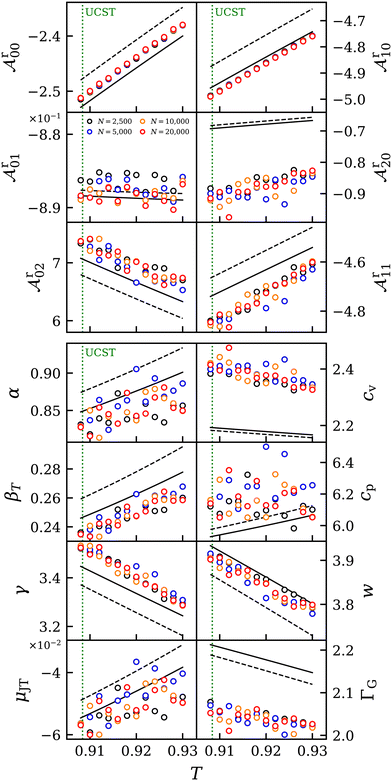 | ||
Fig. 8 Residual Helmholtz energy derivatives  (top) and thermophysical properties α, β, γ, cv, cp, w, ΓG, μJT (bottom) near the UCST of mixture C at p = 0.0724 and x1 = 0.5. Results from simulation (circles) are compared to predictive (dashed line) and adjusted EOS (solid line).41 The error bars of the simulation data were omitted for visibility reasons. (top) and thermophysical properties α, β, γ, cv, cp, w, ΓG, μJT (bottom) near the UCST of mixture C at p = 0.0724 and x1 = 0.5. Results from simulation (circles) are compared to predictive (dashed line) and adjusted EOS (solid line).41 The error bars of the simulation data were omitted for visibility reasons. | ||
At the critical point, the thermodynamic factor vanishes (Γ = 0), which has specific implications for the Maxwell-Stefan (MS) and Fick diffusion coefficients and their finite-size corrections. Fig. 9 shows the results for the thermodynamic factor obtained from simulation and EOS. It is apparent that both approaches predict a linear temperature dependence. This linearity largely persists as the system transitions from the LLE to the homogenous phase. Moreover, the simulation results from below and above the UCST show a good agreement in terms of the zero crossing and slope, considering that these regions were accessed in a different manner. This validates the methodologies applied in this work and the NRTL-based approach to obtain the thermodynamic factor. It also demonstrates that the UCST could have been equivalently calculated from simulations in the homogenous phase only. The combined use of both simulative approaches in this study allowed for a comprehensive exploration of phase equilibria, capitalizing on the unique advantages offered by each method.
 | ||
Fig. 9 Thermodynamic factor around the UCST (green circle) of mixture C at p = 0.0724 and x1 = 0.5. Results from predictive (dashed line) and adjusted EOS (solid line)41 have a linear slope below and above the UCST. Simulation results were obtained from chemical potential data below (crosses) and above the UCST (diamonds). KBI results are depicted as a shaded point-cloud (●) for three system sizes. Results for N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 based on RDF vdV + shf and extrapolated (white circles) were extended further into the homogenous region. 000 based on RDF vdV + shf and extrapolated (white circles) were extended further into the homogenous region. | ||
Fig. 1 and 9 show the deviation between simulation data and EOS in predictive mode, which is off by approximately ΔT = 0.04 in terms of the critical temperature. After applying the adjusted ξEOS to the EOS, the results coincide with the simulation data, only the ascending slopes are not fully aligned.
The results from KBI show a strong system size dependence. For clarity, the system size N = 2500 was left out in Fig. 9, showing only the results for the larger systems N = 5000, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 20
000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. It is apparent that KBI data for larger systems tend toward smaller values of Γ and thereby better agree with the reference curve obtained from the chemical potential data. This trend is reinforced by the choice of the underlying radial distribution function (RDF) type and whether extrapolation was applied. Three types of RDF were used to calculate the KBI: the standard RDF, and two modifications – RDF corrected according to Ganguly and van der Vegt69 (vdV) and a shifted version thereof (vdV + shf).25 More details can be found in the ESI.† The vdV-corrected and extrapolated version consistently led to the lowest values of Γ, often improved by its shifted form. Simulations for N = 20
000. It is apparent that KBI data for larger systems tend toward smaller values of Γ and thereby better agree with the reference curve obtained from the chemical potential data. This trend is reinforced by the choice of the underlying radial distribution function (RDF) type and whether extrapolation was applied. Three types of RDF were used to calculate the KBI: the standard RDF, and two modifications – RDF corrected according to Ganguly and van der Vegt69 (vdV) and a shifted version thereof (vdV + shf).25 More details can be found in the ESI.† The vdV-corrected and extrapolated version consistently led to the lowest values of Γ, often improved by its shifted form. Simulations for N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 were additionally extended further into the homogenous phase. It appears that the KBI values slowly converge to the reference curve for higher temperatures further away from the critical point.
000 were additionally extended further into the homogenous phase. It appears that the KBI values slowly converge to the reference curve for higher temperatures further away from the critical point.
It is worth noting that all Γ values are relatively close to zero, but the difference among them can be significant. Variations due to different RDF types, correction methods and system size can be large. For example, while the thermodynamic factor of the largest system at T = 0.91 is as low as Γ ≈ 0.06, it can be three to four times larger for smaller systems, cf.Table 3. This is particularly relevant for transport properties, as Γ is typically used as a factor or divisor.
| RDF | |||
|---|---|---|---|
| N | Standard | vdV | vdV + shf |
| 2500 | 0.214(3) | 0.194(3) | 0.206(2) |
| 5000 | 0.160(3) | 0.14(2) | 0.155(8) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.137(4) | 0.125(3) | 0.123(2) |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.100(2) | 0.091(1) | 0.092(1) |
| Extrapolated to N → ∞ | |||
| 2500 | 0.139(3) | 0.118(3) | 0.129(2) |
| 5000 | 0.104(3) | 0.09(2) | 0.098(8) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.096(4) | 0.081(3) | 0.079(2) |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.069(2) | 0.059(1) | 0.059(1) |
3.4 Transport properties near the UCST
In the vicinity of the studied liquid–liquid critical point, the self-diffusion coefficient exhibits a linear temperature dependence, cf.Fig. 10 (top left). The results show a consistent behavior across all four system sizes, i.e. the curves have the same slope but are vertically displaced. As the temperature rises, the self-diffusion coefficient also increases as expected. | ||
| Fig. 10 Simulation results (left) and finite size correction (right) for the self- (top), MS (center) and Fick (bottom) diffusion coefficients near the critical solution point of mixture C at p = 0.0724. Simulation data (circles), correction proposed by Yeh and Hummer70 (black squares), extrapolation to the thermodynamic limit (purple squares). Linear (dash-dotted lines) and constant (dashed lines) fits. MS diffusion coefficient data from extrapolated Onsager coefficients (green cross). | ||
Unlike the self-diffusion coefficient, the results for the MS diffusion coefficient display no notable temperature dependence in this limited range of states, cf.Fig. 10 (center left). While the data suggest a dependence on system size, the presence of statistical uncertainties makes this relationship less discernible. To overcome this issue, the scattered data for each system size were averaged, effectively revealing a clear dependence on system size, cf.Fig. 10 (center right).
Since the Fick and MS diffusion coefficients are related by the thermodynamic factor according to Dij = Γ· Đij, the Fick diffusion coefficient traces the same linear trajectory as the thermodynamic factor (cf.Fig. 9) multiplied by the constant MS diffusion coefficient. Hence, the Fick diffusion coefficient is zero at the UCST solely due to the thermodynamic factor. The resulting set of curves highlights the system size dependence through different slopes rather than displacements as observed for the self-diffusion coefficient, cf.Fig. 10 (bottom left).
When examining the impact of system size in Fig. 10 (top right), the self-diffusion coefficient reveals a linear relationship with the inverse of the edge length of the simulation volume L−1. By fitting a linear function to the simulation data and extrapolating to the thermodynamic limit L−1 → 0, the value for D∞i coincides with the intercept. Yeh and Hummer70 investigated the system size dependence of the self-diffusion coefficient and proposed a correction term to account for finite-size effects far from the thermodynamic limit. Their correction term scales linearly with the inverse of the edge length of the simulation volume L−1
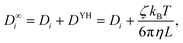 | (15) |
After applying the correction to the self-diffusion coefficient, the average value of the corrected data demonstrates an overestimation in comparison to the value of D∞i obtained from extrapolated simulation data. However, a more accurate comparison can be made by considering the slopes of the curves instead of their intercepts. The correction term DYH aims to equalize the slope of the self-diffusion coefficient so that only the intercept D∞i remains. To obtain a horizontal fit curve for the results in this work, DYH must be scaled down by approximately 22%.
Similar to the self-diffusion coefficient, a finite-size correction for the MS diffusion coefficient was proposed by Jamali et al.71
| Đ∞ij = Đij + DYH/Γ. | (16) |
The present simulation results suggest that there must be other factors at play when approaching the UCST so that a division by Γ is not advisable. These findings highlight the need for a more comprehensive approach to correcting the MS diffusion coefficient near the critical point. Further research into the system size effects of the MS diffusion coefficient in this region is worthwhile.
In addition to the correction proposed by Jamali et al.,71 the finite-size corrected MS diffusion coefficient can also be obtained by extrapolating the Onsager coefficients to the thermodynamic limit.72 Recently, Celebi et al.73 published a comprehensive overview of finite-size corrections for diffusion coefficients.
The system size correction for the Fick diffusion coefficient can be calculated by applying Dij = Γ·Đij to eqn (16)
| D∞ij = Dij + DYH, | (17) |
The shear viscosity shown in Fig. 11 (top) appears to be constant in this limited range of states and independent of system size, which is in accordance with the findings in ref. 70 and 71. It has a weighted mean of 1.168 ± 0.118, with an uncertainty of approximately 10%. Taking the average value of the shear viscosity and its uncertainty into account, the parameter ζ ≈ 2.837297 of the correction DYH would need to be adjusted to 2.2 ± 0.3 in order to obtain a horizontal correction as aspired by Yeh and Hummer.70
In this limited range of states, the thermal conductivity also remains independent of temperature, cf.Fig. 11 (bottom). Moreover, there is no observable effect on thermal conductivity as the system size increases and statistical accuracy improves. Note that the thermal conductivity for large systems with N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 could not be obtained with the Green–Kubo formalism due to technical memory usage limitations.
000 could not be obtained with the Green–Kubo formalism due to technical memory usage limitations.
4. Conclusions
This study presents a detailed investigation of phase equilibria and transport properties of five symmetric binary Lennard-Jones mixtures, using molecular simulation and different EOS models. Utilizing dedicated techniques, the study obtained characteristic phase equilibrium lines and points, including the CEP and CAEP. The simulation results for the VLLE and the azeotropic line demonstrate a good agreement with EOS results in terms of temperature and pressure. However, the critical LLE line is significantly overestimated by the EOS due to a strong sensitivity of the CEP and UCST on the binary interaction parameter ξ. To address this issue, an empirical correlation between the binary interaction parameter of the EOS ξEOS and the true ξ value was introduced. The CEP and CAEP were found to have opposing trends, which exacerbates the challenge of representing them concurrently with EOS, compared to the already demanding task of characterizing several phase equilibrium types simultaneously.Unlike the vapor–liquid critical points, the transport and thermophysical properties near the liquid–liquid critical point were found to exhibit no significant anomalies or singularities, such as local extrema or poles. Instead, all properties approach the critical point either linearly with temperature or are independent of it. The Fick diffusion coefficient is zero there only because the thermodynamic factor vanishes. To address system-size effects on diffusion coefficients, the simulation data were extrapolated to the thermodynamic limit and analytical finite-size corrections were applied. However, these analytical corrections showed an overestimation, particularly when they incorporate the thermodynamic factor near the liquid–liquid critical point.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support by the BMBF under the grant WindHPC. The authors I. A. and J. V. gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) under grant no. VR 6/16. Equilibrium molecular dynamics simulations were performed on the Atos BullSequana XH2000 system (Noctua 2) at the Paderborn Center for Parallel Computing (PC2), contributing to the project MMHBF2. The authors S. St. and J. S. gratefully acknowledge financial support by the DFG within IRTG 2057 “Physical Modelling for Virtual Manufacturing Systems and Processes”. The EOS calculations were carried out on the ELWE computer at Regional University Computing Center Kaiserslautern (RHRK) under the grant TUKL-TLMV.Notes and references
- T. W. Leland, J. S. Rowlinson and G. A. Sather, Trans. Faraday Soc., 1968, 64, 1447–1460 RSC.
- S. Stephan and H. Hasse, Phys. Rev. E, 2020, 101, 012802 CrossRef CAS PubMed.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, Cambridge, 4th edn, 2013 Search PubMed.
- G. A. Mansoori, Fluid Phase Equilib., 1993, 87, 1–22 CrossRef CAS.
- J. K. Lee, J. A. Barker and G. M. Pound, J. Chem. Phys., 1974, 60, 1976–1980 CrossRef CAS.
- B. S. Carey, L. E. Scriven and H. T. Davis, AIChE J., 1980, 26, 705–711 CrossRef CAS.
- T. Wadewitz and J. Winkelmann, Ber. Bunsenges. Phys. Chem., 1996, 100, 1825–1832 CrossRef CAS.
- D. Fertig, H. Hasse and S. Stephan, J. Mol. Liq., 2022, 367, 120401 CrossRef CAS.
- O. Loetgering-Lin, M. Fischer, M. Hopp and J. Gross, Ind. Eng. Chem. Res., 2018, 57, 4095–4114 CrossRef CAS.
- K. C. Mo and K. E. Gubbins, Mol. Phys., 1976, 31, 825–847 CrossRef CAS.
- K. C. Mo, K. E. Gubbins, G. Jacucci and I. R. McDonald, Mol. Phys., 1974, 27, 1173–1183 CrossRef CAS.
- R. Fingerhut, G. Herres and J. Vrabec, Mol. Phys., 2020, 118, e1643046 CrossRef.
- D. Fertig and S. Stephan, Mol. Phys., 2023, e2162993 CrossRef.
- F. Blas and I. Fujihara, Mol. Phys., 2002, 100, 2823–2838 CrossRef CAS.
- J. Vrabec, A. Lotfi and J. Fischer, Fluid Phase Equilib., 1995, 112, 173–197 CrossRef CAS.
- S. Stephan and H. Hasse, Mol. Phys., 2020, 118, e1699185 CrossRef.
- J. J. Potoff and A. Z. Panagiotopoulos, J. Chem. Phys., 1998, 109, 10914–10920 CrossRef CAS.
- A. Z. Panagiotopoulos, N. Quirke, M. Stapleton and D. J. Tildesley, Mol. Phys., 1988, 63, 527–545 CrossRef CAS.
- S. P. Protsenko and V. G. Baidakov, Fluid Phase Equilib., 2016, 429, 242–253 CrossRef CAS.
- S. P. Protsenko, V. G. Baidakov and V. M. Bryukhanov, Fluid Phase Equilib., 2016, 430, 67–74 CrossRef CAS.
- J. B. Buhn, P. A. Bopp and M. J. Hampe, Fluid Phase Equilib., 2004, 224, 221–230 CrossRef CAS.
- P. Geysermans, N. Elyeznasni and V. Russier, J. Chem. Phys., 2005, 123, 204711 CrossRef CAS PubMed.
- M. Mecke, J. Winkelmann and J. Fischer, J. Chem. Phys., 1999, 110, 1188–1194 CrossRef CAS.
- S. Stephan and H. Hasse, Phys. Chem. Chem. Phys., 2020, 22, 12544–12564 RSC.
- R. Fingerhut and J. Vrabec, Fluid Phase Equilib., 2019, 485, 270–281 CrossRef CAS.
- J. Vrabec, A. Kumar and H. Hasse, Fluid Phase Equilib., 2007, 258, 34–40 CrossRef CAS.
- R. S. Chatwell, M. Heinen and J. Vrabec, Int. J. Heat Mass Transfer, 2019, 132, 1296–1305 CrossRef CAS.
- S. Stephan, D. Schaefer, K. Langenbach and H. Hasse, Mol. Phys., 2021, 119, e1810798 CrossRef.
- V. G. Baidakov, S. P. Protsenko and V. M. Bryukhanov, Fluid Phase Equilib., 2019, 481, 1–14 CrossRef CAS.
- J. Staubach and S. Stephan, J. Chem. Phys., 2022, 157, 124702 CrossRef CAS PubMed.
- J. M. Garrido, M. M. Piñeiro, A. Mejía and F. J. Blas, Phys. Chem. Chem. Phys., 2016, 18, 1114–1124 RSC.
- E. L. Granados-Bazán, S. E. Quiñones-Cisneros and U. K. Deiters, J. Chem. Phys., 2021, 154, 084704 CrossRef PubMed.
- I. Nezbeda, J. Kolafa and W. R. Smith, J. Chem. Soc., Faraday Trans., 1997, 93, 3073–3080 RSC.
- F. J. Martinez-Ruiz, A. I. Moreno-Ventas Bravo and F. J. Blas, J. Chem. Phys., 2015, 143, 104706 CrossRef CAS PubMed.
- M. Heier, S. Stephan, F. Diewald, R. Müller, K. Langenbach and H. Hasse, Langmuir, 2021, 37, 7405–7419 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1989 Search PubMed.
- D. A. Jonah and U. K. Deiters, Mol. Phys., 1992, 77, 1071–1083 CrossRef CAS.
- U. K. Deiters and T. Kraska, High-Pressure Fluid Phase Equilibria - Phenomenology and Computation, Elsevier, Amsterdam, 2012 Search PubMed.
- V. Harismiadis, N. Koutras, D. Tassios and A. Panagiotopoulos, Fluid Phase Equilib., 1991, 65, 1–18 CrossRef CAS.
- A. M. Georgoulaki, L. V. Ntouros, D. P. Tassios and A. Z. Panagiotopoulos, Fluid Phase Equilib., 1994, 100, 153–170 CrossRef CAS.
- J. Kolafa and I. Nezbeda, Fluid Phase Equilib., 1994, 100, 1–34 CrossRef CAS.
- J. Binney, The Theory of Critical Phenomena: An Introduction to the Renormalization Group, Clarendon Press, Oxford, 1992 Search PubMed.
- D. I. Uzunov, Introduction to the theory of critical phenomena: mean field, fluctuations and renormalization, World Scientific, Singapore, 1993 Search PubMed.
- M. Barmatz, I. Hahn, J. A. Lipa and R. V. Duncan, Rev. Mod. Phys., 2007, 79, 1–52 CrossRef CAS.
- M. M. Telo da Gama and R. Evans, Mol. Phys., 1983, 48, 229–250 CrossRef CAS.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703–1706 Search PubMed.
- V. A. Mazur, L. Z. Boshkov and V. G. Murakhovsky, Phys. Lett. A, 1984, 104, 415–418 CrossRef.
- U. K. Deiters, High-pressure fluid phase equilibria: Phenomenology and computation, Elsevier, Amsterdam, 1st edn, 2012, vol. 2 Search PubMed.
- P. H. van Konynenburg and R. L. Scott, Philos. Trans. R. Soc., A, 1980, 298, 495–540 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- I. Antolović and J. Vrabec, Ind. Eng. Chem. Res., 2022, 61, 3104–3112 CrossRef.
- B. Smit, J. Chem. Phys., 1992, 96, 8639–8640 CrossRef CAS.
- J. Algaba, B. Mendiboure, P. Gómez-Álvarez and F. J. Blas, RSC Adv., 2022, 12, 18821–18833 RSC.
- D. M. Heyes, Comput. Methods Sci. Eng., 2015, 21, 169–179 Search PubMed.
- A. Lotfi, J. Vrabec and J. Fischer, Mol. Phys., 1992, 76, 1319–1333 CrossRef CAS.
- S. Stephan, M. Thol, J. Vrabec and H. Hasse, J. Chem. Inf. Model., 2019, 59, 4248–4265 CrossRef CAS PubMed.
- S. Stephan, J. Staubach and H. Hasse, Fluid Phase Equilib., 2020, 523, 112772 CrossRef CAS.
- S. Stephan and U. K. Deiters, Int. J. Thermophys., 2020, 41, 147 CrossRef CAS PubMed.
- J. K. Johnson, J. A. Zollweg and K. E. Gubbins, Mol. Phys., 1993, 78, 591–618 CrossRef CAS.
- T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, J. Chem. Phys., 2013, 139, 154504 CrossRef PubMed.
- M. Benedict, G. B. Webb and L. C. Rubin, J. Chem. Phys., 1940, 8, 334–345 CrossRef CAS.
- R. T. Jacobsen and R. B. Stewart, J. Phys. Chem. Ref. Data, 1973, 2, 757–922 CrossRef CAS.
- J. A. Barker and D. Henderson, Annu. Rev. Phys. Chem., 1972, 23, 439–484 CrossRef CAS.
- J. A. Barker and D. Henderson, J. Chem. Phys., 1967, 47, 2856–2861 CrossRef CAS.
- T. W. Leland, P. S. Chappelear and B. W. Gamson, Trans. Faraday Soc., 1962, 8, 482–489 CAS.
- U. Deiters and G. M. Schneider, Ber. Bunsenges. Phys. Chem., 1976, 80, 1316–1321 CrossRef CAS.
- R. Lustig, Mol. Phys., 2012, 110, 3041–3052 CrossRef CAS.
- P. Ganguly and N. F. A. van der Vegt, J. Chem. Theory Comput., 2013, 9, 1347–1355 CrossRef CAS PubMed.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- S. H. Jamali, L. Wolff, T. M. Becker, A. Bardow, T. J. H. Vlugt and O. A. Moultos, J. Chem. Theory Comput., 2018, 14, 2667–2677 CrossRef CAS PubMed.
- G. Guevara-Carrion, R. Fingerhut and J. Vrabec, J. Phys. Chem. B, 2020, 124, 4527–4535 CrossRef CAS PubMed.
- A. T. Celebi, S. H. Jamali, A. Bardow, T. J. H. Vlugt and O. A. Moultos, Mol. Simul., 2021, 47, 831–845 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01434g |
| This journal is © the Owner Societies 2023 |




















![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) mn,
mn, 



