On the antiaromatic–aromatic–antiaromatic transition of the stacked cyclobutadiene dimer

Abstract

We have studied the changes in the aromatic nature of two cyclobutadiene (C₄H₄) molecules on decreasing the intermolecular distance and approaching the cubane structure in a face-to-face fashion. The analysis based on the calculations of the magnetically induced current density and the induced magnetic field shows that the aromaticity of the two C₄H₄ rings changes from a strongly antiaromatic character at long distances to an aromatic transition state of stacked C₄H₄ rings at intermediate internuclear distances when approaching the antiaromatic state of cubane.

---

1 Introduction

Non-covalent π–π stacking interactions of aromatic rings play a crucial role in stabilizing biological systems.^1–3 However, chemical concepts like π–π stacking and aromaticity are difficult to measure. Therefore, they are mainly characterized by using computational approaches.^3–6 The molecular magnetic response is one of the commonly used methods to identify the aromatic nature of molecules.^7–11 In the presence of an external magnetic field, aromatic molecules sustain a diatropic ring current flowing in the classical direction that induces a secondary magnetic field in the opposite direction to the applied external one.^12–14 Antiaromatic molecules sustain a paratropic ring current flowing in the non-classical direction. The paratropic ring current induces a secondary magnetic field strengthening the applied external magnetic field. Non-covalent π–π stacking can also affect the aromaticity or vice versa.^15–18 Ring currents usually flow along covalent bonds around molecular rings.^19–21 However, there are also examples of molecules with stacked rings exhibiting through-space current densities.^16,22–26

An interesting property of π stacked molecules is the dependence of the tropicity of the ring current on the distance between the antiaromatic rings. The ring current is paratropic representing antiaromaticity when the face-to-face stacked molecules weakly interact far away from each other and diatropic indicating aromaticity when they strongly interact at a shorter distance between the molecular rings.^15,16,27,28 Bean and Fowler found that at short interring distances the rotational transitions between the occupied and virtual frontier orbitals of the dimer are forbidden, whereas the translationally allowed transitions dominate resulting in a diatropic ring current.¹⁶ There is also a significant current density between the rings suggesting a through-space delocalization of the π electrons.^15,16

The distance dependence of the aromaticity of the C₄H₄ dimer is even more complicated. The global minimum of the C₄H₄ dimer is cubane (C₈H₈), which is a cage structure belonging to the O_h point group with single C–C bonds between C₄H₄ rings. Cubane has single sp³ hybridized bonds between the C atoms and pyramidal C–H bonds.²⁹ In the presence of an external magnetic field, cubane exhibits a paramagnetic response and sustains a paratropic ring current like C₄H₄.^30,31

Li and Houk studied the dimerization of cyclobutadiene in detail.³² They noted that the face-to-face stacked structure is a transition state with two degenerate imaginary vibrational modes.³² Later, Alonso et al. showed that there is a change in the degree of antiaromaticity along the face-to-face reaction coordinate.³³ They employed the harmonic oscillator model of aromaticity (HOMA)³⁴ to determine the degree of aromaticity. For this purpose, they also calculated the fluctuation aromatic (FLU)³⁵ and nucleus-independent chemical shift (NICS)³⁶ indices. The three approaches yielded somewhat inconsistent interpretations. The HOMA and FLU calculations showed that the rings are aromatic when they are between 3.4 Å and 1.9 Å apart, while the NICS values suggested that the dimer is antiaromatic in this interval.³³ However, these calculations were performed for structures belonging to the D_4h point group, which prevents analyzing changes originating from the transition from the rectangular (D_2h) structure of the non-interacting C₄H₄ molecules to the octahedral (O_h) structure of cubane.³³

It is known that calculations of single NICS values can lead to misinterpretations of the aromatic character of three-dimensional molecules and the aromatic character of molecules containing stacked rings.^18,37–39 Although a change in the degree of aromaticity of the C₄H₄ dimer in the face-to-face stacking process has been suggested, it has not been elucidated to what extent it happens and at what distance between the C₄H₄ rings it occurs.

Qualitative and quantitative analyses of global and local aromaticity can be addressed by calculating and visualizing the magnetic response and the magnetically induced current density of the studied molecule.^19,40 In this work, we analyze the changes in the aromatic character by calculating the magnetic response for a number of steps of the process in which two face-to-face oriented C₄H₄ rings approach each other from far away until they reach the cubane structure (see Fig. 1). Our study based on the calculations of the magnetically induced current density^8,41,42 and the induced magnetic field^43–45 reveals that the C₄H₄ rings change their strongly antiaromatic nature to an aromatic transition state to again reach the antiaromatic state of cubane.

Fig. 1 The picture shows different steps in the process of bringing two C₄H₄ rings together until they join forming the cubane structure. The molecular structures are optimized for fixed interring distances d in the range of 15 ≥ d ≥ 2.96a₀ (bohr).

2 Computational methods

The molecular structures were optimized at the density functional theory (DFT) level using the B3LYP functional⁴⁶ and the semi-empirical dispersion interaction (D3(BJ))⁴⁷ in combination with basis sets of the triple-ζ polarization quality (def2-TZVP).⁴⁸ The molecular structures were constrained to the D_2h point group. For given distances between the C₄H₄ rings, the rest of the structural degrees of freedom was fully optimized. The molecular structures were optimized for interring distances d in the range of d ∈ [2.96,15]a₀ (bohr) in a step of 0.1a₀. Single-point calculations at the second-order Møller–Plesset perturbation theory (MP2)⁴⁹ and the coupled-cluster single, double, and perturbative triple (CCSD(T))⁵⁰ levels were performed for each d value. The Cartesian coordinates can be found in the ESI.† Vibrational analyses were performed on the optimized structures with d = 7.522, 4.435, and 2.961a₀ (3.996, 2.347, and 1.566 Å). The optimized structures belong to the D_2h, D_4h and O_h point groups, respectively.

Re-optimizations at the spin-component-scaled MP2 (SCS-MP2) level⁵¹ using the def2-TZVP basis sets⁴⁸ were performed at these minima (saddle points). The interring distance was not optimized. Single-point MP2 and CCSD(T) energy calculations using these geometries were repeated using quadruple-ζ polarization quality basis sets (def2-QZVP).⁴⁸

The magnetic response was addressed by calculating the magnetically induced current density^8,41,42 (J^ind) and the induced magnetic field^43–45 (B^ind) using the GIMIC^8,41,42 and Aromagnetic⁵² programs, respectively. The electronic structure calculations were carried out using the Turbomole program.^53,54 The magnetic response calculations were performed at the DFT level using the BHandHLYP functional⁵⁵ and the def2-TZVP basis sets⁴⁸ because the BHandHLYP functional yielded a good agreement with reference data for magnetic properties calculated at the CCSD(T) level.⁵⁶ We assume that the strength of the induced magnetic field depends linearly on the strength of the external one. In the presentation of the induced magnetic field, we therefore formally apply an external field of 1 T parallel (|B^ext| = 1 T) to the z axis, which coincides with the highest symmetry axis of the studied molecular systems. The analysis of B^ind can then be reduced for the discussion of its scalar z component (B^ind_z), which is the dominant one.^43–45 The ring-current strengths (I^ind) of the C₄H₄ molecules were calculated by integrating the J^ind flux through a plane which intersects one of the C–C bonds.^8,41,42 Changes in the current–density flux can be obtained by calculating profiles of the current–density strength along one coordinate of the integration plane.^8,41,42 The profile curve is the derivative of I^ind (dI^ind/dz) with respect to z-coordinate. The profile curves along the z-axis show how I^ind changes on decreasing the interring distance.

3 Results and discussion

The interaction energy between the C₄H₄ rings as a function of the interring distance is shown in Fig. 2. Similar potential energy curves are obtained at different levels of theory. The potential energy curve can be divided into three regions. In the first region (denoted as R₁), there is a weak interaction between the C₄H₄ rings due to van der Waals attraction (d ≥ 7a₀). In the second region (denoted as R₂), where the C₄H₄ rings interact more strongly, the energy is ca. 30 kcal mol⁻¹ below the energy at the van der Waals minimum calculated at the CCSD(T) level. The narrow region at short distances (R₃) is where the C₄H₄ rings bind covalently forming cubane. The global minimum (cubane) is at d = 2.961a₀ (see Table 1). However, the minimum of the potential energy curve at d = 4.435a₀ in the R₂ region is actually a saddle point with two imaginary frequencies. The van der Waals minimum at d = 7.522a₀ is also a saddle point with four imaginary frequencies (see Table 1). The same energetic behavior is confirmed by MP2 and CCSD(T) calculations using the def2-QZVP basis sets and the molecular structures optimized at the SCS-MP2/def2-TZVP level (see Table 1).^48,51

Fig. 2 The interaction energy (E^int) between the C₄H₄ rings as a function of the interring distance calculated at different levels of theory using the def2-TZVP basis set. The vertical dashed lines divide the potential energy curve into the three regions.

Table 1 Relative energies (in kcal mol⁻¹) calculated at different levels of theory using the def2-TZVP basis set. The energies and magnetic properties were obtained using structures near the minima (saddle points) of each region. The vibrational frequencies (in cm⁻¹) were calculated at the B3LYP-D3(BJ)/def2-TZVP level for the optimized structures. The NICS(0) and B^ind_z(0) values (in ppm) were calculated at the BHandHLYP/def2-TZVP level in the center of one of the C₄H₄ rings. The ring-current strengths (I^ind in nA T⁻¹) were also calculated at the BHandHLYP/def2-TZVP level

d (a0)	B3LYP-D3(BJ)	MP2	CCSD(T)	MP2a	CCSD(T)^a	Imaginary frequencies	NICS(0)	B ^ind z (0)	I ^ind
a Calculated using the def2-QZVP basis sets and the molecular structure optimized at the SCS-MP2/def2-TZVP level.
7.0	61.1	75.5	65.5	73.9	64.4	58.9i, 44.2i, 34.5i, 33.6i	28.2	113.6	−19.9
4.4	28.2	16.3	35.6	14.4	34.3	447.8i, 447.8i	−32.0	17.4	4.7
2.96	0.0	0.0	0.0	0.0	0.0	—	15.3	59.1	−4.6

---

The calculated magnetic response elucidates that the three minima correspond to the transitions from two antiaromatic rings in the R₁ region, to an aromatic transition state in R₂, and cubane in R₃, which is dominated by paratropic ring currents corresponding to antiaromaticity. The change in the tropicity along the face-to-face reaction coordinate is identified by computing the ring-current strengths for each d value as shown in Fig. 3. Along this reaction coordinate, the ring-current strength of each C₄H₄ ring goes from being strongly paratropic of ca. −20 nA T⁻¹ to diatropic of ca. 5 nA T⁻¹, and revert to a paratropic ring current of ca. −5 nA T⁻¹ when forming cubane.

Fig. 3 The ring-current strength (I^ind) as a function of the interring distance (d) calculated at the BHandHLYP/def2-TZVP level. The vertical dashed lines divide the d range into three regions.

At large distances (d > 7a₀), the interaction energy between the rings is small and dominated by the van der Waals interaction. In the R₁ region, the C₄H₄ rings are rectangular belonging to the D_2h point group. We study the magnetic response for the structure at d = 7a₀, which is near the van der Waals minimum representing the molecular structure in the R₁ region. The optimized structure at the van der Waals minimum is a saddle point with four imaginary frequencies (see Table 1).

From the magnetic point of view, the C₄H₄ rings show independent paratropic ring currents and large deshielded B^ind_z cones that overlap between the rings. Animations of the magnetically induced current density are shown in the ESI.†

The NICS(0) and B^ind_z (0) values are strongly positive (Table 1), which is practically the magnetic response of a single C₄H₄ molecule.³⁷ The antiaromatic character also explains why the R₁ structures have a rather small gap of 3.6 eV between the highest-occupied molecular orbital (HOMO) and the lowest-unoccupied molecular orbital (LUMO). The HOMO–LUMO gap for the dimer in R₁ is very similar to the one for cyclobutadiene. The aromatic transition state in R₂ has a significantly larger HOMO–LUMO gap of 4.96 eV than the one for cyclobutadiene. Cubane has by far the largest HOMO–LUMO gap of 8.23 eV. The HOMO–LUMO gap as a function of the interring distance d is shown in Fig. 4.

Fig. 4 The HOMO–LUMO gap as a function of the interring distance calculated at the B3LYP-D3(BJ)/def2-TZVP level.

The C–C bonds of the C₄H₄ rings of the optimized molecular structure at d = 4.435a₀ are equally long. Thus, the structure in R₂ belongs to the D_4h point group. The potential energy curve has sharp peaks at the boundaries between the three regions because there are different occupied frontier orbitals in the adjacent regions (see Fig. 2). For a given d value, the occupation of the frontier orbitals suddenly changes in the self-consistent-field optimization of the orbitals leading to a lower energy.

The highest occupied frontier orbitals of the molecular structure in R₂ have ungerade parity and the lowest unoccupied frontier orbitals have even parity. Since translation has ungerade parity and rotation has even parity, the formal excitation from the occupied orbitals to the unoccupied ones is translationally allowed but rotationally forbidden, which leads to the aromatic nature of the transition state.¹⁶

The HOMO of the molecular structure in R₁ belongs to the B_3g of the D_2h point group and LUMO+1 has also gerade parity implying that the formal excitation from the HOMO to LUMO+1 is rotationally allowed leading to the antiaromatic cyclobutadiene dimer at long interring distances.¹⁶ Thus, at the borderline between R₁ and R₂, the frontier B_3u and B_3g orbitals flip from occupied to unoccupied and vice versa.

The HOMO, HOMO−1, LUMO and LUMO+1 of cubane belong to the T_2u, T_2g, T_1u and A_1g irreducible representations of the O_h point group, respectively. The HOMO−1 to LUMO transition is rotationally allowed leading to antiaromaticity. The HOMO to LUMO+1 transition is translationally allowed and would contribute to the aromatic nature of cubane. Since the HOMO and HOMO−1 as well as the LUMO and LUMO+1 are almost degenerate, the contributions are expected to be of the same size with the opposite sign leading to a rather weak ring current. The maximum in the potential energy curve at the borderline between R₂ and R₃ is also due to the flipping of the occupied and virtual frontier orbitals.

The diatropic ring-current is strongest for the saddle point at d = 4.435a₀ (see Fig. 3 and 6). Following the imaginary frequencies of the saddle point at d = 4.435a₀ and relaxing the symmetry constraints lead to a syn-type structure where two C–C bonds are formed between the layers, which Li and Houk also reported.³² They pointed out that the saddle point is stabilized due to a reduction in the antiaromaticity. At the CCSD(T) level, the transition state is energetically ca. 36 kcal mol⁻¹ above cubane, which is the global minimum.

Integration of the magnetically induced current density (J^ind) passing through a plane that cuts the C–C bond of one of the C₄H₄ rings confirms that there is a diatropic ring current (I^ind) of 4.7 nA T⁻¹ that flows around each ring (see Fig. 5 and animations in the ESI†). The profiles of the ring-current strength in Fig. 6 show that the ring current at an interring distance of 7a₀ consists of two almost independent paratropic ring currents in the C₄H₄ rings. The double peak shows that the ring current is sustained in the π orbitals of the C₄H₄ rings. Cubane with an interring distance of 2.961a₀ sustains a paratropic ring current in the σ orbitals at the C₄H₄ plane. The transition state at d = 4.435a₀ sustains a diatropic ring current in the σ orbitals of the two C₄H₄ rings. However, it also sustains a strong diatropic ring current between the C₄H₄ rings. Despite this, the B^ind_z plots exhibit deshielding cones that are smaller than those in the R₁ region suggesting a lower degree of antiaromaticity. However, the calculation of the induced magnetic field does not directly reveal that the transition state is aromatic. Thus, interpretations of the aromatic/antiaromatic character based on NICS(0) and B^ind_z (0) calculations are not completely unproblematic.

Fig. 5 The pictures in left panel show the J^ind vector maps when (a) d = 7.0, (b) d = 4.4, and (c) d = 2.96a₀. The diatropic and paratropic contributions to the current density in the C₄H₄ plane are shown in blue and red, respectively. The pictures in the right panel show the B^ind_z isolines calculated in the vertical symmetry plane and in the horizontal symmetry plane of the stacked C₄H₄ rings. The calculations were performed at the BHandHLYP/def2-TZVP level.

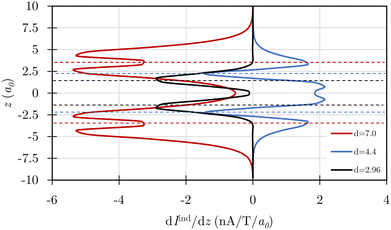Fig. 6 The ring-current strength profiles (dI^ind/dz) along the z-axis are calculated for the two C₄H₄ rings with distances of d = 7.0, 4.4, and 2.96a₀ using an integration plane that intersects both rings. The horizontal dashed lines denote the positions of the C₄H₄ rings. Integration of the dI^ind/dz curves yields twice the ring-current strengths in Table 1.

In the R₃ region, the energy decreases significantly due to the formation of interring carbon bonds between the C₄H₄ rings. Finally, the cubane structure is obtained at d = 2.961a₀ (see Fig. 2), where the aromatic nature obtained in R₂ switches to antiaromaticity. The paratropic ring current flows mainly in the planes of the four-membered rings that are perpendicular to the direction of the external magnetic field (see Fig. 5 and 6). The diatropic ring-current is the strongest for the saddle point at d = 4.435a₀ (see Fig. 3 and 6).

Integration of J^ind for cubane yields a ring-current strength of −4.62 nA T⁻¹ in each ring. The B^ind_z calculations confirm that cubane is deshielded suggesting antiaromaticity. Havenith et al. explained that the paratropicity of cubane is due to collective contributions from the four-membered rings.³¹ Although cubane has been considered to be super-antiaromatic due to the large positive NICS(0) value of 15.3 ppm,³⁰ we show here that this is not the case. When the two C₄H₄ rings approach each other, the C₄H₄ dimer reaches an aromatic transition state with different occupied frontier orbitals than at long distances between the rings. Cubane is antiaromatic sustaining paratropic ring currents in the σ orbitals of the strained sp³ bonds. The large B^ind_z value of −58.9 ppm in the middle of a C₄H₄ ring of cubane is due to the paratropic ring current in the ring plane.

4 Conclusions

We have studied how the aromatic character changes when two cyclobutadiene rings approach each other in the face-to-face orientation from far away as separate molecules to the cubane structure. The magnetically induced current density and the ring-current strength have been calculated at different distances between the C₄H₄ rings. The induced magnetic field in the vicinity of the molecule has also been calculated in each step along the reaction coordinate. The calculations show that the C₄H₄ rings are antiaromatic at long distances and that cubane is also dominated by paratropic ring currents, whereas the transition state at intermediate interring distances is aromatic sustaining diatropic ring currents in the two rings and between them. Calculations at the B3LYP-D3(BJ), MP2, and CCSD(T) levels show that the interaction energy between the C₄H₄ rings increases as they get closer. The face-to-face reaction coordinate can be divided into three regions with significantly different tropicities of the magnetically induced current density leading to significant differences in the induced magnetic field in the vicinity of the molecule. The first region of the reaction coordinate represents the regime where the C₄H₄ rings interact weakly. Their magnetic response is similar to two non-interacting antiaromatic cyclobutadiene molecules. The van der Waals minimum (saddle point) is obtained at an interring distance of 7.522a₀. The second region in the range of d = [3.4,4.7]a₀ corresponds to a transition state with strongly interacting aromatic π-stacked C₄H₄ rings belonging to the D_4h point group. The interring distance of the aromatic transition state is 4.435a₀. Finally, for short interring distances that are less than 3.4a₀, interring carbon bonds with a length of 2.961a₀ are formed yielding the cubane structure belonging to the O_h point group. The strongly strained cubane structure is known to be antiaromatic even though it has sp³ hybridized molecular orbitals forming single C–C bonds.

Author contributions

D. S. conceived the idea of the project. M. O.-I. and D. S. performed the calculations. The authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Academy of Finland through the project number 340583, the Magnus Ehrnrooth Foundation, the Waldemar von Frenckell's foundation, and the Swedish Cultural Foundation in Finland. We acknowledge computational resources from the CSC – IT Center for Science, Finland.

Notes and references

1. M. L. Waters, Curr. Opin. Chem. Biol., 2002, 6, 736–741.
2. T. Chen, M. Li and J. Liu, Cryst. Growth Des., 2018, 18, 2765–2783.
3. C. R. Martineza and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201.
4. C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2012, 651–669.
5. J. W. G. Bloom and S. E. Wheeler, Angew. Chem., Int. Ed., 2011, 50, 7847–7849.
6. G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023 10.1039/D2SC04998H.
7. M. Solà, A. I. Boldyrev, M. K. Cyrañski, T. M. Krygowski and G. Merino, Aromaticity and Antiaromaticity: Concepts and Applications, John Wiley & Sons, Ltd, 2022.
8. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
9. J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384.
10. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
11. A. Balaban, P. von Ragué Schleyer and H. S. Rzepa, Chem. Rev., 2005, 105, 3436–3447.
12. N. F. Ramsey, Phys. Rev., 1950, 78, 699–703.
13. J. A. Pople, Mol. Phys., 1958, 1, 175–180.
14. R. McWeeny, Mol. Phys., 1958, 1, 311–321.
15. C. Corminboeuf, P. von, R. Schleyer and P. Warner, Org. Lett., 2007, 9, 3263–3266.
16. D. E. Bean and P. W. Fowler, Org. Lett., 2008, 10, 5573–5576.
17. D. Sundholm, M. Rauhalahti, N. Özcan, R. Mera-Adasme, A. L. J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 1952–1962.
18. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Chem. – Eur. J., 2019, 26, 326–330.
19. D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378.
20. E. Paenurk and R. Gershoni-Poranne, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644.
21. Y.-C. Lin and D. Sundholm, J. Chem. Theory Comput., 2006, 2, 761–764.
22. L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632.
23. V. Vijay, M. Madhu, R. Ramakrishnan, A. Benny and M. Hariharan, Chem. Commun., 2020, 56, 225–228.
24. M. Orozco-Ic, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409.
25. K. Wypych, M. Dimitrova, D. Sundholm and M. Pawlicki, Org. Lett., 2022, 24, 4876–4880.
26. L.-X. Bai, M. Orozco-Ic, X. Zarate, D. Sundholm, S. Pan, J.-C. Guo and G. Merino, Molecules, 2022, 27, 7407.
27. M. Orozco-Ic, A. Restrepo, A. Muñoz-Castro and G. Merino, J. Chem. Phys., 2019, 151, 014102.
28. R. Nozawa, J. Kim, J. Oh, A. Lamping, Y. Wang, S. Shimizu, I. Hisaki, T. Kowalczyk, H. Fliegl, D. Kim and H. Shinokubo, Nat. Commun., 2019, 10, 3576.
29. P. E. Eaton and T. W. Cole, J. Am. Chem. Soc., 1964, 86, 3157–3158.
30. D. Moran, M. Manoharan, T. Heine and P. von R. Schleyer, Org. Lett., 2003, 5, 23–26.
31. R. W. A. Havenith, P. W. Fowler and E. Steiner, Chem. Phys. Lett., 2003, 371, 276–283.
32. Y. Li and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 880–885.
33. M. Alonso, J. Poater and M. Solà, Struct. Chem., 2007, 18, 773–783.
34. J. Kruszewski and T. Krygowski, Struct. Chem., 1972, 13, 3839–3842.
35. E. Matito, M. Solà, P. Salvadora and M. Duran, Faraday Discuss., 2007, 135, 325–345.
36. P. von, R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
37. G. Monaco and R. Zanasi, J. Phys. Chem. Lett., 2017, 8, 4673–4678.
38. M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764.
39. J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2006, 71, 1700–1702.
40. G. Merino, A. Vela and T. Heine, Chem. Rev., 2005, 105, 3812–3841.
41. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
42. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
43. G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371.
44. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
45. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
46. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
47. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
48. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
49. C. Hättig, A. Hellweg and A. Köhn, Phys. Chem. Chem. Phys., 2006, 8, 1159–1169.
50. D. P. Tew, W. Klopper, C. Neiss and C. Hättig, Phys. Chem. Chem. Phys., 2007, 9, 1921–1930.
51. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
52. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, 2016, Cinvestav–Mexico.
53. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
54. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
56. S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized molecular structures and animations of the current densities. See DOI: https://doi.org/10.1039/d3cp01350b

---