Sulfur–arene interactions: the S⋯π and S–H⋯π interactions in the dimers of benzofuran⋯sulfur dioxide and benzofuran⋯hydrogen sulfide

Abstract

Non-covalent interactions between sulfur centers and aromatic rings play important roles in biological chemistry. We examined here the sulfur–arene interactions between the fused aromatic heterocycle benzofuran and two prototype sulfur divalent triatomics (sulfur dioxide and hydrogen sulfide). The weakly-bound adducts were generated in a supersonic jet expansion and characterized with broadband (chirped-pulsed) time-domain microwave spectroscopy. The rotational spectrum confirmed the detection of a single isomer for both heterodimers, consistent with the computational predictions for the global minima. The benzofuran⋯sulfur dioxide dimer exhibits a stacked structure with sulfur closer to benzofuran, while in benzofuran⋯hydrogen sulfide the two S–H bonds are oriented towards the bicycle. These binding topologies are similar to the corresponding benzene adducts, but offer increased interaction energies. The stabilizing interactions are described as S⋯π or S–H⋯π, respectively, using a combination of density-functional theory calculations (dispersion corrected B3LYP and B2PLYP), natural bond orbital theory, energy decomposition and electronic density analysis methods. The two heterodimers present a larger dispersion component, but nearly balanced by electrostatic contributions.

---

Introduction

Sulfur-containing compounds are key components of living organisms, playing important biochemical and metabolical roles. As an example, the sulfur amino acids methionine and cysteine are incorporated into proteins, with the first one initiating the synthesis of virtually all eukaryotic proteins and the latter critically influencing protein folding by formation of disulfide bonds.¹ For this reason, the analysis of sulfur-centered non-covalent interactions² is of fundamental interest to understand the biological functions and reactivity of these compounds. Among the multiple non-covalent interactions observed in protein tertiary structures, the presence of sulfur–arene contacts was recognized early as a significant contributor,^3,4 as later confirmed from crystal data mining from the Brookhaven Protein Data Bank (PDB) and the Cambridge Crystallographic Database (CCD).⁵ However, it may be difficult to extract accurate information from individual intermolecular interactions using large macromolecular structures with conventional (ca. 2.5 Å) crystallographic resolution. In these cases, both computational modelling and gas-phase experimental studies can provide complementary chemically specific structural information and a physical description of the molecular forces at play. Previous computational studies concerning the interaction between aromatic rings and sulfur compounds have focused on small prototype heterodimers like methanethiol⋯benzene⁶ or hydrogen sulfide⋯benzene,^7,8 characterized by a S–H⋯π weak hydrogen bond. The use of sulfur non-covalent interactions in drug design and larger examples of arene complexation have also been reviewed elsewhere.^9,10 However, the number of high-resolution gas-phase spectroscopic studies of aggregation between sulfur compounds and π-systems is small. Examples include the dimers of hydrogen sulfide with benzene,^11,12 phenylacetylene,¹³ phenol,^14,15p-cresol¹⁶ or indole,¹⁷ or the sulfur dioxide dimers with benzene,^18–20 toluene²¹ or furan,²² loosely classified as van der Waals adducts. Here, we will explore the interactions between divalent sulfur and aromatic rings using broadband (chirped-pulse) microwave spectroscopy and jet expansions, extending previous rotationally resolved investigations on sulfur dioxide aggregation²³ and thiol microsolvation^24,25 and dimerization.^26,27 We chose heterodimers of sulfur dioxide (SO₂) and hydrogen sulfide (H₂S) to simultaneously explore both the S⋯π and the hydrogen bonded S–H⋯π interactions. In the present work the fused heterocycle benzofuran was selected as aggregation partner because of the presence of three plausible binding sites at the two six- and five-membered rings and the oxygen heteroatom. The observation of sulfur clusters is expected to offer comparison with the equivalent oxygen partners, gauging the influence of the lower electronegativity, larger polarizability and reduced hydrogen bond capacity of sulfur. This information will contribute to the description of weak non-covalent interactions involving chalcogens, which has expanded considerably in the last decade.^28,29

Methods

Experiment

The dimers of benzofuran with sulfur dioxide (BF⋯SO₂) and hydrogen sulfide (BF⋯H₂S) were prepared by supersonic expansion of the two precursors, highly diluted with neon as carrier gas. For this purpose, benzofuran was heated to ca. 310 K inside a solenoid-driven pulsed-nozzle (Parker Series 9) and pressurized with a gas line containing each of the sulfur compounds at typical concentrations of 0.5%. The expansion from stagnation pressures of ca. 2-3 bar to the vacuum chamber ultimate pressure of ca. 10⁻⁶–10⁻⁷ mbar created a vertically moving molecular jet. The nozzle orifice was 1 mm. All chemical samples were obtained commercially.

The microwave spectrum was recorded in the 2–8 GHz region with a direct-digital broadband (chirped-pulse) Fourier transform microwave spectrometer.³⁰ This spectrometer uses a fast (20 GS/s) digital arbitrary waveform generator to create a series of short (4 μs) microwave chirped-pulses, which are amplified to 20 W. The exciting pulse propagates perpendicularly to the jet molecular expansion, inducing a broadband fast-passage³¹ electric-dipole excitation. The resulting transient emission or free-induced decay is amplified, collected in the time-domain with a digital oscilloscope for ca. 40 μs per pulse, and Fourier-transformed to yield the frequency spectrum. The resonance frequencies have typical linewidths (FWHM) below 100 kHz after apodization with a Kaiser–Bessel window. The spectra were averaged for about 1 M cycles. The final frequency measurements have estimated accuracies of 10 kHz or better.

Computations

Initial guess structures were generated with a simple molecular mechanics force field (MMFF).³² These structures were then optimized with quantum mechanical density functional theory (DFT) methods. In this work, the adduct structures were first obtained using the B3LYP hybrid method and D3 two-body empirical dispersion corrections³³ (Becke-Johnson damping function³⁴). The most stable structures were later reoptimized with the B2PLYP double-hybrid method.³⁵ The Ahlrich's triple-ζ polarized basis set (def2-TZVP),³⁶ which performs reasonably well in similar clusters,²⁷ was used initially in combination with an ultrafine integration grid and normal convergence criteria. For comparison, the calculations were repeated using Dunning's correlation-consistent cc-pVTZ basis set³⁷ and the jun-cc-pVTZ variation,³⁸ removing the highest angular momentum diffuse functions. The vibrational frequencies were evaluated within the harmonic approximation. For the calculation of complexation energies the basis-sets superposition errors were accounted for within the Boys–Bernardi approximation.³⁹ The natural-bond-orbital analysis⁴⁰ used NBO version 3. All calculations were implemented in Gaussian 16.⁴¹ For the non-covalent interactions, the Johnson-Contreras analysis⁴² of the reduced electronic density function used NCIPlot.⁴³ An energy decomposition analysis was conducted with symmetry-adapted perturbation theory⁴⁴ (SAPT) at the SAPT 2 + 3(CCD)/aug-cc-pVDZ level, implemented in PSI4.⁴⁵

Results and discussion

Conformational landscape

The predictions for BF⋯SO₂ confirmed the preference for stacked structures, similar to the heterodimers with benzene¹⁸ or furan.²² However, the larger number of non-equivalent binding sites on benzofuran results in four different isomers below 5 kJ mol⁻¹ (B3LYP-D3(BJ)), shown in Fig. 1. For the B2PLYP method the last isomer converged to the global minimum. In these structures the sulfur atom of SO₂ sits on top of the benzene unit, with the oxygen atoms pointing outwards the ring (rotatable 3D Fig. S1, ESI†). The SO₂ moeity is not coplanar with the heterocyle, instead displaying a tilted orientation with sulfur closer to the ring and the two oxygens pointing outwards the ring. The predicted rotational and energetic parameters are presented in Table 1 and Tables S1, S2 (ESI†). In the case of the BF⋯H₂S dimer the situation is different, as the predictions in Table 2 and Tables S3, S4 (ESI†) suggest a tendence to form S–H⋯π hydrogen bonds. In the most stable isomer of Fig. 2 the sulfur atom is located in between the two rings, with the two S–H bonds pointing down, respectively, to the six- and the five-membered ring (rotatable 3D Fig. S2, ESI†). A second isomer ca. 2 kJ mol⁻¹ less stable has only one hydrogen atom oriented to the ring.

Fig. 1 The predicted most stable isomers of the dimer benzofuran⋯sulfur dioxide (B3LYP-D3(BJ)/def2-TZVP electronic energies in parentheses, see Table 1 and Tables S1, S2, ESI†).

Table 1 Rotational parameters of the benzofuran⋯sulfur dioxide dimer

	Theory^d			Experiment^e
	Isomer I	Isomer II	Isomer III	^32S species	^34Species
a Rotational constants (A, B, C), Watson's A-reduction centrifugal distortion constants (ΔJ, ΔJK, ΔK, δJ, δK) and electric dipole moments (μα, α = a, b, c). b Number of measured transitions (N) and standard deviation of the fit (σ). c Relative energies uncorrected (ΔE) and corrected with the zero-point energy (ΔE0), Gibbs energy (ΔG, 298K, 1 atm) and complexation energy (ΔEc, including BSSE corrections). d Calculations using B2PLYP-D3(BJ) and the def2-TZVP basis set, see also Tables S1 and S2 (ESI). e Standard errors in parentheses in units of the last digit. f Values fixed in the fit.
A/MHz^a	1070.1	1066.0	1244.1	1056.036(3)	1054.90(1)
B/MHz	830.5	830.1	666.0	811.9523(8)	802.077(1)
C/MHz	658.9	629.4	559.1	642.2063(9)	635.9851(9)
ΔJ/kHz	0.53	0.62	0.53	0.26(2)	[0.26]
ΔJK/kHz	−0.16	2.0	−1.9	2.7(1)	[2.7]
ΔK/kHz	−0.19	−2.3	2.9	−2.7(3)	[−2.7]
δ J/kHz	0.003	−0.04	0.18	[0.0]^f	[0.0]
δ K/kHz	0.54	3.7	0.90	1.1(1)	[1.1]
|μa|/D	1.5	1.8	2.2	+	+
|μb|/D	0.8	0.7	0.2	+	+
|μc|/D	0.1	1.5	0.1	−	−
N				53	17
σ/kHz				8.0	8.2
ΔE/kJ mol^−1^c	0.0	1.9	0.2
ΔE0/kJ mol^−1	0.0	1.7	2.1
ΔG/kJ mol^−1	1.5	0.3	0.0
ΔEC/kJ mol^−1	−21.30	−19.25	−19.41

---

Table 2 Rotational parameters of the benzofuran⋯hydrogen sulfide dimer

	Theory		Experiment
			^32S species		^34S species
	Isomer I	Isomer II	v = 0^+	v = 0^−	v = 0^+	v = 0^−
a Parameter definition as in Table 1. The theoretical predictions used the B2PLYP-D3(BJ) method and the def2-TZVP basis set, see also Tables S3 and S4 (ESI).
A/MHz^a	1167.9	1197.7	1174.3380(9)	1173.5247(9)	1172.814(4)	1172.033(4)
B/MHz	1087.7	1112.7	1037.3505(7)	1037.7417(6)	1004.705(1)	1005.059(1)
C/MHz	788.6	812.4	763.8964(5)	764.0018(4)	745.390(1)	745.495(2)
ΔJ/kHz	0.64	2.5	1.17(2)		1.10(4)
ΔJK/kHz	4.1	−6.9	2.47(8)		3.6(2)
ΔK/kHz	−4.5	4.8	−2.6(1)		−3.8(4)
δ J/kHz	−0.20	−0.28	0.449(9)		[0.449]
δ K/kHz	18.2	−13.0	1.81(4)		[1.81]
|μa|/D	1.4	0.1	+		+
|μb|/D	0.2	0.5	−		−
|μc|/D	0.9	0.2	+		+
N			30	30	15	19
σ/kHz			3.9		1.3
ΔE/kJ mol^−1	0.0	1.3
ΔE0/kJ mol^−1	0.0	1.5
ΔG/kJ mol^−1	0.0	1.0
ΔEC/kJ mol^−1	−14.02	−13.10

---

Fig. 2 The predicted most stable isomers of the dimer benzofuran⋯hydrogen sulfide (B3LYP-D3(BJ)/def2-TZVP electronic energies in parentheses, see Table 2 and Tables S3 and S4, ESI†).

Rotational spectra

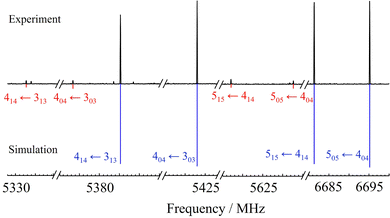
The experimental microwave spectra of the two benzofuran heterodimers are shown in Fig. S3 and S4 (ESI†), with the most prominent transitions being easily attributable to the benzofuran monomer.^46–48 The transitions of the two adducts, generally of 1/20–1/30 intensity with respect to the monomer, had appreciable signal-to-noise ratios (SNR < 150 : 1) and revealed a single isomer for both aggregates. The spectrum of BF⋯SO₂, was made of R- (J + 1 ← J) and Q-branch (J ← J) μ_a- and μ_b-type transitions (J = 1–5, K₋₁ = 0–4). As shown in Fig. 3, the spectral intensity permitted the additional assignment of the ³⁴S isotopologue in natural abundance (ca. 4%). In both cases, the Watson A-reduced Hamiltonian reproduced the experiment to experimental accuracy (Table 1). Conversely, the spectrum of BF⋯H₂S showed evidence of a large-amplitude motion within the cluster, as the rotational transitions were split into two asymmetric hyperfine components, illustrated in Fig. 4. The exchange of two half-spin fermions would result in a 1 : 3 statistical weight for the 0⁺ and 0⁻ torsional states, respectively, which is close to the observations. For this reason, the tunnelling splitting is ascribed to the exchange of the two hydrogen atoms by internal rotation of H₂S around its symmetry axis. This effect has been observed in microsolvation clusters where water behaves as weak proton donor,⁴⁹ as in benzene⋯water.⁵⁰ In our case the two torsional components were fitted independently to semirigid models, floating the rotational constants of each state, but sharing the centrifugal distortion parameters. The observations included R-branch μ_a- and μ_c-transitions (J = 0–4, K₋₁ = 0–3) for the parent and the ³⁴S isotopologue in natural abundance. The results of the fit are collected in Table 2. The observed transitions are listed in Tables S5–S8 (ESI†). No other dimer species were detected in the spectra.

Fig. 3 A section of the microwave spectrum of the dimer benzofuran⋯sulfur dioxide with transitions from the isotopologues with ³²S (blue) and ³⁴S (red). See full spectrum in Fig. S3 (ESI†).

Fig. 4 A section of the microwave spectrum of the dimer benzofuran⋯hydrogen sulfide, showing the tunnelling splittings for the isotopologues with ³²S (red/blue) and ³⁴S (black/orange). See full spectrum in Fig. S4 (ESI†).

The observed selection rules, rotational constants (Tables 1 and 2) and sulfur substitution coordinates⁵¹ (Tables S9 and S10, ESI†) were consistent with the observation of the global minimum species for the two dimers (predicted coordinates in Tables S11–S14, ESI†). Relative differences between the observed and calculated rotational constants are shown in Tables S1–S4 (ESI†). Discrimination of the different isomers is quite unambiguous. However, for the SO₂ heterodimer the rotational constants of isomers I and II are relatively close. In this case, the absence of μ_c spectrum confirmed the observation of isomer I. Fig. S5 (ESI†) illustrates the increase of μ_c in isomer II of BF⋯SO₂. A comparison of the centrifugal distortion constants is not significant in this case because not all parameters could be determined experimentally and because of the limitations of the harmonic approximation. The experiment also permitted the determination of a partial effective structure⁵² for both dimers, presented in Table 3. Assuming that the two moieties of the dimer^47,53 remain unperturbed, six structural parameters are required to locate the triatomics over the benzofuran ring.²² However, since only two isotopic species are available, we fitted only the distance between the two centers of mass (r_CM = r(X_S–X_BZ)) and the elevation (∠ (X_S–X_BZ–X)) and dihedral (τ (X_S–X_BZ–X–C₅)) of each triatomic with respect to benzofuran. Other parameters relating to the orientation of the triatomics were kept fixed to the B2PLYP structure. The resulting structures reproduce the observed rotational constants within 0.5 MHz for BF⋯SO₂ and 0.4 MHz for BF⋯H₂S (Tables S15 and S16, ESI†). The effective structures are compared with theory in Table 3 and Tables S11, S13 (ESI†). The fitted center of mass distance in BF⋯SO₂ (3.307(2) Å) is slightly shorter that those observed in the SO₂ dimers with benzene (3.485(1) Ź⁸) or furan (3.432(1) Ų²), but they share a general stacked pattern characteristic of the S⋯π interaction, with the sulfur end of the triatomic closer to the ring. For the BF⋯H₂S dimer the center of mass distance (3.660(3) Å) is also shorter than in benzene⋯H₂S (3.771 Ź¹), where the S–H⋯π interaction produces a symmetric top. The shorter distances are indicative of stronger interaction energies in the dimers with benzofuran, as suggested by the computational binding energies below.

Table 3 Effective molecular structures of the dimers of benzofuran with sulfur dioxide and hydrogen sulfide and B2PLYP-D3(BJ) predictions

	BF⋯SO2		BF⋯H2S
	r 0	r e	r 0	r e
a XS, XBZ and X denote, respectively, the center of mass of the sulfur triatomic, the center of mass of the benzofuran monomer and the middle point between atoms C5 and C6 of benzofuran. b Monomer structures in ref. 47 and 53. c Equilibrium structures according to B2PLYP-D3(BJ)/cc-pVTZ. d Standard errors in parentheses in units of the last digit. e Derived parameters in square brackets.
r CM = r(XS–XBZ)/Å ^a	3.307(2)^d	3.237	3.660(3)	3.567
∠ (XS–XBZ–X)/deg	90.7(8)	95.1	87.7(2)	88.9
τ (XS–XBZ–X–C5)/deg	−78.7(2)	−80.8	−85.7(4)	−88.2
r(H/O–XS)/Å	[1.286]^e	1.304	[1.303]	1.304
∠ (H/O–XS–XBZ)/deg	[108.7]	108.6	[45.9]	45.8
τ (H/O–XS–XBZ–X)/deg	[80.3]	79.6	[−0.6]	−0.6
r(S–H/O)/Å	[1.431]	1.458	[1.336]	1.341
∠ (S–H/O–XS)/deg	[14.0]	14.3	[1.7]	1.7
τ (S–H/O–XS–XBZ)/deg	[−66.9]	−66.4	[−164.4]	−164.5

---

The presence of a single isomer for the two dimers contrasts with the prediction of low energy isomers below 2 kJ mol⁻¹. This fact may be attributed to the presence of conformational relaxation pathways in the jet expansion,⁵⁴ associated to small interconversion barriers. Considering the weak intermolecular forces (discussed below), and that the conversion between the stable isomers involves only small structural adjustments of the triatomics, the potential barriers are expected a priori to be small. We confirmed this fact with the calculation of interconversion barriers between the two most stable isomers using DFT (B3LYP-D3(BJ)/cc-pVTZ). The predicted direct/(reverse) barriers of 2.6/(0.5) and 2.4/(0.9) kJ mol⁻¹ for BF⋯SO₂ and BF⋯H₂S, respectively, are much smaller than the empirical conversion thresholds of 5–7 kJ mol⁻¹ for collisional relaxation,⁵⁴ offering quantitative support for this hypothesis.

The non-covalent interactions in the observed dimers were analysed using several computational methods. The natural-bond-orbital (NBO) calculations in Tables S17 and S18 (ESI†) use atomic orbital overlap and density matrices to form a basis of orthonormal bond orbitals ordered by a maximum occupancy criterion. The charge transfer interactions are associated with occupancy changes from the filled to the unfilled orbitals. The most important donor–acceptor orbital associations in the BF⋯SO₂ dimer correspond to π → σ*(S) interactions, involving the donor bonding orbital BD(C_3a–C₄) of benzofuran and three antibonding orbitals of SO₂ (perturbative interaction energies E⁽²⁾ = 1.0–2.7 kJ mol⁻¹). This interaction is complemented by π(S) → σ*(C_3a) and n(S) → σ*(C_3a) back donation from SO₂ (E⁽²⁾ = 1.0 kJ mol⁻¹), so they can be properly categorized as S⋯π bonding. For BF⋯H₂S the main interactions are π → σ*(SH), involving three π donor orbitals in the ring and non-bonding orbitals of H₂S (E⁽²⁾ = 0.6–1.7 kJ mol⁻¹). Weaker π⋯π* (in BF⋯SO₂) and n⋯π* interactions originated by sulfur additionally contribute to dimer formation. As expected, the total interaction energies are much larger (ca. × 1.5) for the sulfur dioxide dimer (B2PLYP-D3(BJ): −20.5 to −22.2 kJ mol⁻¹; B3LYP-D3(BJ): −25.4 to −25.7 kJ mol⁻¹, see Table 1 and Tables S1, S2, ESI†) than for hydrogen sulfide (B2PLYP-D3(BJ): −14.0 to −14.8 kJ mol⁻¹; B3LYP-D3(BJ): −16.0 to −16.3 kJ mol⁻¹, see Table 2 and Tables S3, S4, ESI†). A similar trend is observed for a calculation of complexation energies for the benzene dimers with SO₂ (B2PLYP-D3(BJ)/def2-TZVP: −17.9 kJ mol⁻¹) and H₂S (−11.6 kJ mol⁻¹). Experimental complexation energies are available for the dimer of benzene⋯SO₂,²⁰ permitting an estimation of uncertainties for the computational values. The dissociation energy of −18.4(12) kJ mol⁻¹ obtained from photoionization techniques suggests that the B2PLYP values are slightly underestimated (ca. 3%) respect to the experiment. To the best of our knowledge, no experimental dissociation energies for H₂S dimers with benzene or furan have been determined.

A spatial distribution of the non-bonding interactions in the dimer was obtained from a Johnson–Contreras⁴² electronic density analysis, based on a density (ρ) over gradient power (∇ρ) ratio. The reduced density gradient s isosurfaces in Fig. 5 permit distinguishing attractive or repulsive regions by the sign of the second Hessian eigenvalue of the electronic density (sign(λ₂ρ)), mapping the surfaces associated to attractive (coloured in blue) or weakly attractive (coloured in green) non-covalent interactions. Fig. 5 shows large delocalized regions between the two rings for both BF⋯SO₂ and BF⋯H₂S, compatible with the interactions noticed in the NBO analysis. For BF⋯SO₂ the main interaction region is located above the C_3a–C₄ and C_7a–C_3a bonds, associated to the S⋯π interactions, while both the C_3a–C_7a bonds and the ring centers present more intense interactions in BF⋯H₂S, corresponding to the SH⋯π interactions.

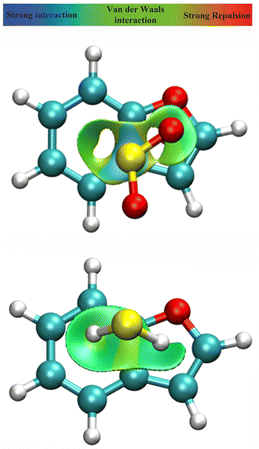Fig. 5 NCI plot^39,40 for the dimers of benzofuran with sulfur dioxide (upper panel) and hydrogen sulfide (lower panel), producing a spatial description of attractive interactions in the dimer (isosurface s = 0.5 a.u.).

The results of the SAPT energy decomposition analysis are presented in Table 4, giving insight into the components of the interaction energy. The two dimers similarly present a larger dispersion component (41% and 55%, respectively, of the total attractive energy) but nearly balanced by electrostatic contributions (34% and 35%, respectively). This energetic distribution is probably associated to the prevailing role in these complexes of the π ring electronic density and the large and polarizable molecular orbital distribution in the sulfur triatomics. In this sense both the S⋯π and S–H⋯π interactions occupy an intermediate position between the dominant dispersive character observed in π-stacking^26,27,55 and dimers involving a primary hydrogen bond, particularly alcohols,^56–58 but also some thiols like the prototypic hydrogen sulfide dimer.⁵⁹ On the other hand, the dimer of benzyl mercaptan,⁶⁰ which combines S–H⋯S and S–H⋯π interactions, presents an energy distribution close to the benzofuran dimers.

Table 4 The SAPT energy decomposition analysis of the non−covalent interactions in the benzofuran⋯sulfur dioxide and benzofuran⋯hydrogen sulfide dimers (all values in kJ mol⁻¹) using SAPT2 + 3(CCD)/aug-cc-pVDZ method

	BF⋯SO2	BF⋯H2S
a Relative percentages with respect to the total attractive energy in square brackets.
Electrostatics	−24.6 [33.6%]^a	−12.7 [35.4%]
Induction	−18.8 [25.6%]	−3.4 [9.4%]
Dispersion	−29.9 [40.8%]	−19.8 [55.2%]
Exchange	47.1	21.1
Total	−26.2	−14.8

---

Conclusions

Sulfur dioxide and hydrogen sulfide form weak dimers with benzofuran, as observed in a jet-cooled expansion by broadband rotational spectroscopy. In both aggregates a single most stable species is observed experimentally, despite DFT quantum mechanical predictions anticipating alternative low energy isomers below 2 kJ mol⁻¹. Because the conversion between stable isomers was shown to proceed through small potential barriers (<5–7 kJ mol⁻¹), the collisional relaxation mechanisms can explain the presence of a single isomer.⁵⁴ The carriers of the spectrum are reproduced to experimental uncertainty with semirigid rotor Hamiltonian models. Unlike similar SO₂ dimers of higher symmetry, like those with benzene or furan,^18,22 no tunnelling motions associated to internal large-amplitude motions were observed in benzofuran⋯sulfur dioxide. Conversely, a tunnelling motion was detected for the H₂S heterodimer, associated to the internal rotation in the triatomic. The experimental moments of inertia provided ground-state effective structures, consistent with the predicted global minima for the two dimers. In particular, SO₂ adopts a stacked position with the sulfur atom closer to the ring, while H₂S is depicted as hydrogen bonded to benzofuran. DFT D3-dispersion-corrected calculations at B3LYP and B2PLYP levels satisfactorily reproduced the observed molecular structures. The relative deviations for the rotational constants in the SO₂ dimer are kept under 2.6% for both B3LYP and B2PLYP (Tables S1–S4, ESI†), despite the larger computational cost of the later method. Small structural variations are also observed for the three used basis sets. However, the stabilization energies are predicted differently, with B3LYP giving complexation energies ca. 14–18% larger than B2PLYP for BF⋯SO₂. The structural predictions are worse for the H₂S dimer, but kept under 4.8% for all six calculations methods. In the H₂S dimer the B3LYP complexation energies are ca. 8–13% larger than for B2PLYP. Computational predictions using natural bond orbitals explain the dimer interactions as primarily originated from S⋯π and S–H⋯π interactions. This description, despite an increase in the binding energy, shows large similarities with the prototypic benzene dimers.^11,12,18 New experiments are in progress to explore the intermolecular interactions between larger sulfur compounds and aromatic systems.

Author contributions

Conceptualization, G. F. and A. L.; methodology, G. F. and A. L.; software, Y. J., W. L., R. T. S., M. J. and C. P.; validation, Y. J., W. L., R. T. S., M. J. and C. P.; formal analysis, Y. J., W. L., R. T. S., M. J., C. P., A. L., G. F.; investigation, Y. J., W. L., R. T. S., M. J.; resources, A. L. and G. F.; data curation, A. L. and G. F.; writing—original draft preparation, A. L. and G. F.; writing—review and editing, A. L., and G. F.; visualization, Y. J., W. L.; supervision, A. L. and G. F.; project administration, A. L. and G. F.; funding acquisition, A. L. and G. F.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding from the National Natural Science Foundation of China (No. 22273009), the Spanish Ministerio de Ciencia e Innovación (MCIN-AEI) and “ERDF A way of making Europe” (grant PID2021-125015NB-I00) and ERDF - Junta de Castilla y León (grants INFRARED IR2021-UVa13 and IR2020-1-UVa02) is gratefully acknowledged. J.Y. and W.L. thank the China Scholarship Council (CSC) for scholarships. M.J. thanks the Ministerio de Universidades and the Universidad de Valladolid for a “Margarita Salas” postdoctoral contract (CONREC-2021-265).

Notes and references

1. D. Voet and J. G. Voet, Biochemistry, Wiley and Sons, 4th edn, 2010.
2. A. Chand, D. K. Sahoo, A. Rana, S. Jena and H. S. Biswal, The prodigious hydrogen bonds with sulfur and selenium in molecular assemblies, structural biology, and functional materials, Acc. Chem. Res., 2020, 53, 1580–1592.
3. R. S. Morgan, C. E. Tatsch, R. H. Gushard, J. M. Mcadon and P. K. Warme, Chains of alternating sulfur and π-bonded atoms in eight small proteins, Int. J. Pept. Protein Res., 2009, 11, 209–217.
4. K. S. C. Reid, P. F. Lindley and J. M. Thornton, Sulphur-aromatic interactions in proteins, FEBS Lett., 1985, 190, 209–213.
5. R. J. Zauhar, C. L. Colbert, R. S. Morgan and W. J. Welsh, Evidence for a strong sulfur-aromatic interaction derived from crystallographic data, Biopolymers, 2000, 53, 233–248.
6. G. Duan, V. H. Smith and D. F. Weaver, Characterization of aromatic-thiol π-type hydrogen bonding and phenylalanine-cysteine side chain interactions through ab initio calculations and protein database analyses, Mol. Phys., 2001, 99, 1689–1699.
7. T. P. Tauer, M. E. Derrick and C. D. Sherrill, Estimates of the ab initio limit for sulfur–π interactions: the H₂S–benzene dimer, J. Phys. Chem. A, 2005, 109, 191–196.
8. A. L. Ringer, A. Senenko and C. D. Sherrill, Models of S/π interactions in protein structures: Comparison of the H₂S-benzene complex with PDB data, Protein Sci., 2007, 16, 2216–2223.
9. B. R. Beno, K. S. Yeung, M. D. Bartberger, L. D. Pennington and N. A. Meanwell, A survey of the role of noncovalent sulfur interactions in drug design, J. Med. Chem., 2015, 58, 4383–4438.
10. E. A. Meyer, R. K. Castellano and F. Diederich, Interactions with aromatic rings in chemical and biological recognition, 2003, vol. 42.
11. E. Arunan, T. Emilsson, H. S. Gutowsky, G. T. Fraser, G. de Oliveira and C. E. Dykstra, Rotational spectrum of the weakly bonded C₆H₆–H₂S dimer and comparisons to C₆H₆–H₂O dimer, J. Chem. Phys., 2002, 117, 9766–9776.
12. D. Wang, P. Chopra, S. Wategaonkar and A. Fujii, Electronic and infrared spectroscopy of benzene-(H₂S) n (n = 1 and 2): the prototype of the SH-π interaction, J. Phys. Chem. A, 2019, 123, 7255–7260.
13. M. Goswami and E. Arunan, Microwave spectrum and structure of C₆H₅CCH⋯H₂S complex, J. Mol. Spectrosc., 2011, 268, 147–156.
14. S. Ghosh, S. Bhattacharyya and S. Wategaonkar, Dissociation energies of sulfur-centered hydrogen-bonded complexes, J. Phys. Chem. A, 2015, 119, 10863–10870.
15. S. Bhattacharyya and S. Wategaonkar, ZEKE photoelectron spectroscopy of p-fluorophenol⋯H₂S/H₂O complexes and dissociation energy measurement using the Birge-Sponer extrapolation method, J. Phys. Chem. A, 2014, 118, 9386–9396.
16. H. S. Biswal, P. R. Shirhatti and S. Wategaonkar, O–H···O versus O–H···S hydrogen bonding I: experimental and computational studies on the p-Cresol·H₂O and p-Cresol·H₂S complexes, J. Phys. Chem. A, 2009, 113, 5633–5643.
17. H. S. Biswal and S. Wategaonkar, Sulfur, not too far behind O, N, and C: SH···π hydrogen bond, J. Phys. Chem. A, 2009, 113, 12774–12782.
18. A. Taleb-Bendiab, K. W. Hillig and R. L. Kuczkowski, Microwave spectrum of benzene SO₂: Barrier to internal rotation, structure, and dipole moment, J. Chem. Phys., 1992, 97, 2996–3006.
19. R. J. Wilson and R. L. Kuczkowski, The microwave spectrum and structure of fluorobenzene sulphur dioxide, J. Mol. Struct., 1996, 376, 1–10.
20. J. R. Grover, E. A. Walters, J. K. Newman, M. G. White, E. A. Walters and J. K. Newman, Measurement of the dissociation energies of gas-phase neutral dimers by a photoionization technique: values for trans-2-butene/sulfur dioxide, (trans-2-butene)₂, and benzene/sulfur dioxide, J. Am. Chem. Soc., 1985, 107, 7329–7339.
21. A. Taleb-Bendiab, K. W. Hillig and R. L. Kuczkowski, Microwave spectrum of toluene SO₂: Structure, barrier to internal rotation, and dipole moment, J. Chem. Phys., 1993, 98, 3627–3636.
22. J. J. Oh, L.-W. Xu, A. Taleb-Bendiab, K. W. Hillig and R. L. Kuczkowski, The microwave spectrum and structure of the furan · sulfur dioxide complex, J. Mol. Spectrosc., 1992, 153, 497–510.
23. Y. Jin, R. T. Saragi, M. Juanes, G. Feng and A. Lesarri, Interaction topologies of the S⋯O chalcogen bond: The conformational equilibrium of the cyclohexanol⋯SO₂ cluster, Phys. Chem. Chem. Phys., 2021, 23, 10799–10806.
24. M. Juanes, A. Lesarri, R. Pinacho, E. Charro, J. E. Rubio, L. Enríquez and M. Jaraíz, Sulfur hydrogen bonding in isolated monohydrates: furfuryl mercaptan versus furfuryl alcohol, Chem. – Eur. J., 2018, 24, 6564–6571.
25. M. Juanes, R. T. Saragi, R. Pinacho, J. E. Rubio and A. Lesarri, Sulfur hydrogen bonding and internal dynamics in the monohydrates of thenyl mercaptan and thenyl alcohol, Phys. Chem. Chem. Phys., 2020, 22, 12412–12421.
26. R. T. Saragi, M. Juanes, C. Pérez, P. Pinacho, D. S. Tikhonov, W. Caminati, M. Schnell and A. Lesarri, Switching hydrogen bonding to π-stacking: the thiophenol dimer and trimer, J. Phys. Chem. Lett., 2021, 12, 1367–1373.
27. R. T. Saragi, C. Calabrese, M. Juanes, R. Pinacho, J. E. Rubio, C. Pérez and A. Lesarri, π-Stacking isomerism in polycyclic aromatic hydrocarbons: the 2-naphthalenethiol dimer, J. Phys. Chem. Lett., 2023, 14, 207–213.
28. I. Alkorta, J. Elguero and A. Frontera, Not only hydrogen bonds: other noncovalent interactions, Crystals, 2020, 10, 180.
29. M. Juanes, R. T. Saragi, W. Caminati and A. Lesarri, The hydrogen bond and beyond: perspectives for rotational investigations of non-covalent interactions, Chem. – Eur. J., 2019, 25, 11402–11411.
30. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Broadband Fourier transform rotational spectroscopy for structure determination: The water heptamer, Chem. Phys. Lett., 2013, 571, 1–15.
31. J. C. McGurk, T. G. Schmalz and W. H. Flygare, Fast passage in rotational spectroscopy: Theory and experiment, J. Chem. Phys., 1974, 60, 4181–4188.
32. T. A. Halgren, MMFF VI. MMFF94s option for energy minimization studies, J. Comput. Chem., 1999, 20, 720–729.
33. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
34. A. D. Becke and E. R. Johnson, A density-functional model of the dispersion interaction, J. Chem. Phys., 2005, 123, 154101.
35. S. Grimme and F. Neese, Double-hybrid density functional theory for excited electronic states of molecules, J. Chem. Phys., 2007, 127, 1–18.
36. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
37. R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806.
38. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, Perspectives on basis sets beautiful: Seasonal plantings of diffuse basis functions, J. Chem. Theory Comput., 2011, 7, 3027–3034.
39. S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566.
40. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, 2016.
42. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing noncovalent interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506.
43. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: A program for plotting noncovalent interaction regions, J. Chem. Theory Comput., 2011, 7, 625–632.
44. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes, Chem. Rev., 1994, 94, 1887–1930.
45. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability, J. Chem. Theory Comput., 2017, 13, 3185–3197.
46. B. M. Giuliano and W. Caminati, Rotational spectrum of 2,3-benzofuran, Collect. Czech. Chem. Commun., 2003, 68, 1572–1578.
47. A. Maris, B. Michela Giuliano, S. Melandri, P. Ottaviani, W. Caminati, L. B. Favero and B. Velino, Structure, dipole moment and large amplitude motions of 1-benzofuran, Phys. Chem. Chem. Phys., 2005, 7, 3317.
48. F. J. Lovas, Microwave Spectra of Molecules of Astrophysical Interest. XXII. Sulfur Dioxide (SO₂), J. Phys. Chem. Ref. Data, 1985, 14, 395–488.
49. L. Evangelisti and W. Caminati, Internal dynamics in complexes of water with organic molecules. Details of the internal motions in tert-butylalcohol-water, Phys. Chem. Chem. Phys., 2010, 12, 14433–14441.
50. S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard and G. A. Blake, Benzene forms hydrogen bonds with water, Science, 1992, 257, 942–945.
51. J. Kraitchman, Determination of Molecular Structure from Microwave Spectroscopic Data, Am. J. Phys., 1953, 21, 17–24.
52. H. D. Rudolph and J. Demaison, in Equlibrium Molecular Structures, ed. A. Demaison, J. Boggs, J. Csaszar, CRC Press, Boca Raton, Fl, 2011, pp. 125–158.
53. M. Nakata and K. Kuchitsu, Estimation of the equilibrium structures of polyatomic molecules using isotopic differences in vibrationally averaged structures, J. Mol. Struct., 1994, 320, 179–192.
54. P. D. Godfrey, F. M. Rodgers and R. D. Brown, Theory versus experiment in jet spectroscopy: Glycolic acid, J. Am. Chem. Soc., 1997, 119, 2232–2239.
55. M. Saeki, H. Akagi and M. Fujii, Theoretical study on the structure and the frequency of isomers of the naphthalene dimer, J. Chem. Theory Comput., 2006, 2, 1176–1183.
56. R. Medel, A. Camiruaga, R. T. Saragi, P. Pinacho, C. Pérez, M. Schnell, A. Lesarri, M. A. Suhm and J. A. Fernández, Rovibronic signatures of molecular aggregation in the gas phase: subtle homochirality trends in the dimer, trimer and tetramer of benzyl alcohol, Phys. Chem. Chem. Phys., 2021, 23, 23610–23624.
57. A. Camiruaga, R. T. Saragi, F. Torres-Hernández, M. Juanes, I. Usabiaga, A. Lesarri and J. A. Fernández, The evolution towards cyclic structures in the aggregation of aromatic alcohols: the dimer, trimer and tetramer of 2-phenylethanol, Phys. Chem. Chem. Phys., 2022, 24, 24800–24809.
58. M. Juanes, R. T. Saragi, C. Pérez, L. Enríquez, M. Jaraíz and A. Lesarri, Torsional chirality and molecular recognition: the homo and heterochiral dimers of thenyl and furfuryl alcohol, Phys. Chem. Chem. Phys., 2022, 24, 8999–9006.
59. A. Das, P. K. Mandal, F. J. Lovas, C. Medcraft, N. R. Walker and E. Arunan, The H₂S dimer is hydrogen-bonded: direct confirmation from microwave spectroscopy, Angew. Chem., Int. Ed., 2018, 57, 15199–15203.
60. R. T. Saragi, M. Juanes, R. Pinacho, J. E. Rubio, J. A. Fernández and A. Lesarri, Molecular recognition, transient chirality and sulfur hydrogen bonding in the benzyl mercaptan dimer, Symmetry, 2021, 13, 2022.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional Figures and Tables with experimental results and computations. See DOI: https://doi.org/10.1039/d3cp01146a

‡ Present address: Institut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstr. 25/4.OG, 6020 Innsbruck, Austria.

---