The E₃ state of FeMoco: one hydride, two hydrides or dihydrogen?

Abstract

Hydrides are present in the reduced states of the iron-molybdenum cofactor (FeMoco) of Mo nitrogenase and are believed to play a key mechanistic role in the dinitrogen reduction reaction catalyzed by the enzyme. Two hydrides are present in the E₄ state according to ¹H ENDOR and there is likely a single hydride in the E₂ redox state. The 2-hydride E₄ state has been experimentally observed to bind N₂ and it has been speculated that E₃ may bind N₂ as well. However, the E₃ state has not been directly observed and very little is known about its molecular and electronic structure or reactivity. In recent computational studies, we have explored the energy surfaces of the E₂ and E₄ by QM/MM modelling, and found that the most stable hydride isomers contain bridging or partially bridging hydrides with an open protonated belt sulfide-bridge. In this work we systematically explore the energy surface of the E₃ redox state, comparing single hydride and two-hydride isomers with varying coordination and bridging vs. terminal sulfhydryl groups. We also include a model featuring a triply protonated carbide. The results are only mildly dependent on the QM-region size. The three most stable E₃ isomers at the r²SCAN level of theory have in common: an open belt sulfide-bridge (terminal sulfhydryl group on Fe6) and either 2 bridging hydrides (between Fe2 and Fe6), 1 bridging-1-terminal hydride (around Fe2 and Fe6) or a dihydrogen ligand bound at the Fe2 site. Analyzing the functional dependency of the results, we find that functionals previously found to predict accurate structures of spin-coupled Fe/Mo dimers and FeMoco (TPSSh, B97-D3, r²SCAN, and B3LYP*) are in generally good agreement about the stability of these 3 E₃ isomers. However, B3LYP*, similar to its parent B3LYP method, predicts a triply protonated carbide isomer as the most stable isomer, an unlikely scenario in view of the lack of experimental evidence for carbide protonation occurring in reduced FeMoco states. Distinguishing further between the 3 hydride isomers is difficult and this flexible coordination nature of hydrides suggests that multiple hydride isomers could be present during experimental conditions. N₂ binding was explored and resulted in geometries with 2 bridging hydrides and N₂ bound to either Fe₂ or Fe₆ with a local low-spin state on the Fe. N₂ binding is predicted to be mildly endothermic, similar to the E₂ state, and it seems unlikely that the E₃ state is capable of binding N₂.

---

Introduction

The nitrogenase enzymes are responsible for the reduction of dinitrogen to ammonia in a complex 2-protein system that consists of the Fe protein and the MoFe protein (in the more active and better understood Mo nitrogenase).^1–6 These proteins contain multiple iron–sulfur clusters that are responsible for electron-transfer that end up in the active-site iron-molybdenum cluster, FeMoco (a [MoFe₇S₉C] cluster), where dinitrogen binding and reduction occurs. Despite decades of detailed kinetic and spectroscopic studies, crystallography and theoretical studies, there is no consensus on a detailed reaction mechanism. Part of the complexity comes from the nature of multi-electron reduction of N₂ substrate to the product NH₃, which the enzyme accomplishes by an 8-electron mechanism:^1–6

N₂ + 8e⁻ + 8H⁺ + 16MgATP → 2NH₃ + H₂ + 16MgADP (1)

where 1 molecule of H₂ is an obligatory product for every 2 NH₃ formed. The H₂ formation is nowadays known to be a critical mechanistic step, involving hydrides, as N₂ binds to a reduced state of the MoFe protein.^7–9 Electrons and protons are shuttled via the Fe protein to the MoFe protein (accumulating at the FeMoco cluster), converting the resting S = 3/2 E₀ form^10–13 of the cofactor to alternative redox states with integer-spin states (E₁, E₃) or non-integer spin-states (E₂, E₄). Much of our current knowledge of the cofactor comes from studies of the resting-state E₀ form due to high-quality crystallographic studies^10–15 and EPR spectroscopic studies^10–13 and the fact that pure E₀ samples can be prepared. Less is known about the EPR-silent E₁ state although recent X-ray absorption and Mössbauer studies have considerably added to our knowledge.^16–18 The EPR-active E₂ state can be studied (though low populations in samples is a problem) due to unique S = 3/2 signals that can be distinguished from E₀ and it is known to relax back to E₀ by H₂ evolution under low electron-flux conditions.^1,13,19–22 Detailed kinetic and EPR/ENDOR spectroscopic studies of the E₄ state have revealed the occurrence of 2 hydrides.^8,9,23 N₂ binding has been shown to occur in this state, accompanied by obligatory H₂ formation which has been proposed to occur by a reductive elimination mechanism.^1,7–9

Since the original seminal work by Thorneley and Lowe, the E₃ state has been part of the kinetic schemes of nitrogenase such as the one shown in Fig. 1, yet very little is actually known about this state.^1,7–9,24 The original Thorneley-Lowe model suggested N₂ could bind to either E₃ or E₄ but that E₄ was the state for which N₂ reduction could occur from.^1,24 Since then, regrettably, very little additional knowledge has emerged on the identity or reactivity of this state. Direct spectroscopic or kinetic determinations of E₃ are mostly absent as mentioned in recent reviews on the spectroscopy and substrate reductions of nitrogenase.^5,6 This is due to its lack of a Kramers EPR signal from an integer-spin cluster. E₃ was once attributed to a spectroscopic signal,^5,13 however, that is now known to be an EPR signal from E₂. Kinetic studies on acetylene reduction in native MoFe protein and variants have suggested inhibition by N₂ at the E₃ redox level, however, the evidence for E₃ involvement in these reactions is indirect.^25,26

Fig. 1 The Thorneley-Lowe kinetic scheme relating E₀, E₁, E₂, E₃ and E₄ redox states.²⁴ N₂ binding to E₃ was originally suggested in the work by Thorneley and Lowe but the claim has not been substantiated. Also shown are recent suggested computational models for the E₂ and E₄ redox states.^9,34–37

Computational studies of FeMoco offer the opportunity to fill in these types of gaps in the experimental literature. Unfortunately, FeMoco is arguably the most challenging enzyme cofactor known in biology featuring 8 open-shell metal ions spin-coupled to an S = 3/2 spin state. Considerable effort has been spent on detailed electronic structure investigations into the resting E₀ state. There is some consensus on the overall redox state as well as individual oxidation states although the electronic structure is still deeply complicated and a detailed understanding and connection to the magnetic spectroscopy literature remains elusive. The determination of the interstitial atom of FeMoco (as carbide),^15,27 the high-resolution X-ray crystal structure¹⁵ as well as new determinations of metal oxidation states of the cofactor^27–30 have inspired multiple computational studies (or joint experimental-computational) into reduced states of FeMoco^9,18,31–37 and attempts to understand the mechanism of nitrogen binding and reduction at FeMoco.^{32,34,38–50} Special efforts have been devoted to studies of the E₄ state, known to contain 2 bridging hydrides.^9,32–35

Considerably fewer studies have considered the structural possibilities in the E₃ redox state, due no doubt to the lack of experimental data to compare to. In a systematic computational study by Cao and Ryde multiple structural possibilities were considered at the QM/MM level for various reduced states (E₁–E₄) of FeMoco, including E₃.³¹ The most favorable E₃ isomers found in that study consisted of both bridging and terminal hydrides as predicted by the TPSS functional or a triply carbide ion as predicted by B3LYP. A very recent study, also by Ryde and coworkers, suggests a model containing two bridging hydrides between Fe2 and Fe6 as the most favourable when using TPSS, r²SCAN, and TPSSh functionals, while B3LYP predicts a model containing a triply protonated carbide as the lowest-energy model.⁵¹ Additionally, Dance has studied the E₃ redox state with large QM-cluster calculations and found the most favorable isomer to contain dihydrogen bound to the Fe6 site with a closed protonated belt sulfide-bridge and a model consisting of two terminal/bridging hydrides and an open belt sulfide-bridge.³³

Overall, previous experimental and computational work strongly implies the existence of 1 hydride in the E₂ state^{13,19–21,31,33,36,37} and direct ENDOR-observation has convincingly demonstrated the existence of 2 hydrides (and 2 sulfur-bound protons) in the E₄ state.^8,9,23 It seems likely to assume that the E₃ redox state bears a structural similarity to either E₂ or E₄, however, it is not obvious whether the state should contain 1 or 2 hydrides. A single hydride E₃ isomer would suggest a highly simplified electron-counting scheme of 2 electrons present in the hydride and 1 electron in the Fe part, while a 2-hydride isomer implies 4 electrons associated with the hydrides and an oxidized Fe part.

We have previously shown that the binding affinity of N₂ at an Fe site in FeMoco depends strongly on the number of hydrides bound to the Fe (which appears to be connected to the ability of the Fe site to acquire a low spin-state).⁵⁰ The question of whether the E₃ state is capable of N₂ binding or not may be related to the number and coordination of hydrides present in the structure.

In this study we systematically study the energy landscape of the E₃ state by a previously established computational approach that combines QM/MM methodology to reliably treat the protein environment and previously benchmarked DFT methods together with large triple-zeta basis sets and inclusion of scalar relativistic effects and dispersion corrections. We compare 3 categories of E₃ isomers: 1-hydride isomers, 2-hydride isomers with an open belt sulfide-bridge and 2-hydride isomers with a closed belt sulfide-bridge, and a model featuring a triply protonated carbide is also included. We test 35 broken-symmetry states for 3 different spin multiplicities for each isomer with a small QM-region and the r²SCAN density functional. We assess the reliability of the resulting energy ranking of isomers by comparing results using small and large QM-regions, and discuss the functional dependency of the results. Finally, we discuss the electronic structure of the most stable isomers as well as the possibility of N₂ binding to E₃.

Computational details

Our QM/MM model is partially based on the model we previously used to study E₀, E₁, E₂, and E₄ states of FeMoco.^{18,34,36,52–56} However, in this work, as in a recent study on N₂ binding to these redox states,⁵⁰ we utilize a model of the full solvated protein consisting of 320817 atoms in total. An active region of 993 atoms, centered on one of the FeMoco active sites, is used. There are 59 atoms (link-atoms included) in the small QM-A region that consists of FeMoco, sidechains of α-Cys275, α-His442, the singly protonated homocitrate ligand^52,57,58 attached to Mo, three additional hydrogens compared to the E₀ state, and two added link-atom hydrogens. The QM-region is visualized in Fig. S1 in the ESI.† The QM-B region (145 atoms in total; link-atoms included) contains eight more residues than the QM-A region: α-Val70, α-Arg96, α-Gln191, α-His195, α-Ser278, α-Glu380, α-Phe381, and α-Arg359. In the QM-C region, there are 191 atoms (link-atoms included) and 12 more residues (10 H₂O molecules, α-Gly356, and α-Gly357) than the QM-B region (see Fig. S1 in Section 1 of the ESI†). The 10 water molecules included are present in the X-ray structure,¹⁵ as shown in Fig. S2 of the ESI.† The α-His195 residue is described as singly protonated on N_ε (see Fig. S1 in the ESI†).

As discussed in our recent study,⁵⁰ the use of these QM-A, QM-B, and QM-C regions (same as the QM-I, QM-V, and QM-VI regions, respectively, in that article) converge quite well for reaction energies with even the small and cheap QM-A region being capable of fairly accurate results compared to the larger and more expensive QM-C region (see Table S2 of the ESI† in that article⁵⁰).

In this work we used the QM-A region to systematically explore all considered E₃ models (Fig. 2) in three spin states (M_S = 0, 1 and 2) and 35 BS solutions per spin state. Different orientations of protons on bridging or terminal sulfhydryl groups S2B and S5A were investigated using the lowest-energy state of each model with the QM-A region (see Section 7 in the ESI†). The QM-B region was then used to optimize the lowest-energy state for each model based on the QM-A data (the lowest-energy orientation for protons on sulfides). Finally, single-point calculations using the QM-C region were performed on top of QM-B region optimized geometries in order to evaluate the most accurate relative energies of E₃ isomers. Broken-symmetry states of FeMoco were systematically investigated by considering all possible 35 BS solutions that can be obtained by flipping 3 of 7 open-shell Fe ions, following the original work by Noodleman and coworkers.^59,60 We note that the open-shell Mo(III) ion (present in an unusual non-Hund configuration²⁸) is part of the spin-coupling problem but the configuration arises naturally during the SCF procedure. The BS states were obtained by converging first the high spin state (M_S = 34/2) of FeMoco and then flipping the spin-density of three selected Fe ions (using a procedure present in ORCA), and finally converging the SCF to the desired state. For example, BS147 (M_S = 2) is found by flipping the Fe1, Fe4, and Fe7 to be down spin and converging to M_S = 2. Additional information on BS states is included in Section 8 of the ESI.†

Fig. 2 The eighteen structural models for the E₃ state that were systematically explored in this work, divided into categories of 2-hyd-CBS (2 hydrides with a closed belt sulfide bridge), 2-hyd-OBS (2 hydrides with an open belt sulfide bridge), 1-hyd (single hydride) and finally the sole protonated carbide model (r). Also shown are relative QM/MM energies (lowest-energy BS state and spin state) in blue, calculated using the r²SCAN functional and the small QM-A region. All the models are isomers of the common E₃ redox state surface. The lowest-energy spin state and BS state of a–r isomers are BS245 (M_S = 1), BS137 (M_S = 1), BS345 (M_S = 1), BS345 (M_S = 1), BS236 (M_S = 2), BS345 (M_S = 2), BS347 (M_S = 1), BS2356 (M_S = 0), BS235 (M_S = 2), BS147 (M_S = 1), BS147 (M_S = 1), BS346 (M_S = 2), BS147 (M_S = 1), BS247 (M_S = 2), BS14 (M_S = 2), BS14 (M_S = 2), BS346 (M_S = 2), and BS125 (M_S = 1), respectively.

The QM/MM program ASH,⁶¹ developed in our group, was used. It has a flexible interface to the OpenMM molecular mechanics library⁶² and the ORCA quantum chemistry code.⁶³ The CHARMM36 force field⁶⁴ and standard electrostatic embedding QM/MM with link atoms as well as a charge-shifting scheme⁶⁵ were utilized as in our previous papers.^{18,34,36,52–56} Geometry optimizations were performed using an interface to the geomeTRIC optimization library⁶⁶ using HDLC internal coordinates.⁶⁷

Four density functionals: r²SCAN,⁶⁸ TPSSh,^69,70 B97-D3,^71–73 and B3LYP*^74,75 were primarily used in this work to evaluate the functional dependency of the isomer energies (Results and Discussion section C). This choice is based on a recent benchmarking study on the geometries of spin-coupled iron–sulfur dimers and FeMoco compared to high-resolution X-ray crystallographic data.⁵⁶ These 4 functionals emerged as the most reliable for Fe–Fe and Mo–Fe distances and as discussed, this was found to be primarily related to the covalency of the bridging M–S bonds between metal ions. The r²SCAN functional was the most reliable functional in that study⁵⁶ (though only marginally) and it was subsequently used in our recent study on N₂ binding to multiple redox states of FeMoco.⁵⁰ In this work we used r²SCAN for all QM-A region geometry optimizations when evaluating models for E₃ in all three spin states and 35 BS solutions (Results and Discussion section B). The five lowest-energy states were then selected for each model and were QM/MM optimized using the same QM-A region with the other functionals (Results and Discussion section C). To further analyze the functional dependency we have also included results using B3LYP^76–78 and TPSS⁶⁹ and this is discussed in Section 9 of the ESI.†

An all-electron scalar relativistic treatment (ZORA⁷⁹) with recontracted segmented triple-zeta basis sets was used in this study, which has been shown to be close to the all-electron scalar relativistic basis set limit of structures of iron–sulfur compounds.⁵⁶ The D4 dispersion correction^80,81 was used in all calculations involving r²SCAN, TPSS and TPSSh while the B97-D3 and B3LYP* used the D3BJ dispersion correction (dispersion parameters for B3LYP were used). The Split-RI-J⁸² approximation for Coulomb integrals was used for all functionals and additionally the semi-numerical COSX approximation for Exchange integrals (for TPSSh and B3LYP*). A decontracted auxiliary basis set by Weigend et al.^83,84 (named SARC/J in ORCA) was used with the RI approximation. The relativistically recontracted ZORA-def2-TZVP^83,85 basis set was used on FeMoco and additional H-atoms (compared to the E₀ state) on FeMoco as well as the N₂ ligand in N₂-bound states while Mo used the SARC-ZORA-TZVP⁸⁶ basis set. The ZORA-def2-SVP basis set was used for other atoms in the QM region.

Relative energies were calculated from total electronic energies at 0 K. The effect of zero-point vibrational contributions on the relative energies of the lowest energy isomers was briefly investigated and the results are shown in Section 10 of the ESI;† the ZPVE effect is generally sufficiently small that it can be neglected, at least for E₃ isomer energies. The effects of entropy were not considered in this work. For N₂ binding energies one would expect a sizeable entropy penalty associated with the free energy of binding (∼10 kcal mol⁻¹ based on a gas phase estimate or ∼ 4 kcal mol⁻¹ if estimated from a diffusible position within the protein as suggested by Dance⁴⁹) but in this work our aim is not to derive realistic estimates of the free energy of binding. N₂ and H₂ were optimized in vacuum when calculating binding energies and dissociation energies.

Hirshfeld⁸⁷ and Mulliken⁸⁸ population analysis methods were used to derive atomic charges and spin populations. A numerical partial Hessian approach⁸⁹ was used to calculate harmonic N–N vibrational frequencies with N₂ and the binding Fe as the partial Hessian. The calculated vibrational frequencies of N₂ are shown as relative to the stretching vibration of free N₂ in the vacuum using r²SCAN/ZORA-def2-TZVP (2432 cm⁻¹).

Localized orbital analysis was performed using the Pipek–Mezey method,⁹⁰ which was used to derive FeMoco electronic configurations for the lowest-energy isomers. Approximate ligand-field diagrams of Fe-bound N₂ were obtained as described in a recent study, by the combination of diamagnetic substitution, localized orbital analysis and quasi-restricted orbital (QRO) transformation.⁵⁰

Results and discussion

We start by introducing all models considered for the E₃ state in section A. In section B we present the results of QM/MM-calculated energies using the r²SCAN density functional and a small QM-region (QM-A). In section C we explore the functional dependency of the results using 3 other density functionals (B97-D3, TPSSh and B3LYP*) while Section D compares the previous QM-A results to results calculated with the larger QM-C region. In section E we discuss the molecular and electronic structure with the help of localized orbital analysis of the 3 lowest-energy models. Finally, section F discusses N₂ binding to the E₃ redox state and comparison is made to N₂ binding in the other E_n states.

A. The E₃ models investigated

The models for E₃ discussed primarily in this work can be grouped into 3 categories as shown in Fig. 2: models with 2 hydrides with a closed belt sulfide-bridge (2-hyd-CBS, Fig. 2a–f), 2-hydride/H₂ models with an open belt sulfide-bridge (2-hyd-OBS, Fig. 2g–l) and single-hydride models (1-hyd, Fig. 2m–q). We also discuss a model containing a triple protonated carbide (C3H, Fig. 2r) for comparison as previous studies have indicated some QM protocols favouring carbide protonation in reduced FeMoco states. All 18 models contain the same number of electrons and are on the same energy surface.

Some of the 2-hydride models can be thought of as derived from E₄ models discussed in the literature (shown in Fig. 1) but lacking an S-bound H-atom. For example, models shown in Fig. 2a–d in the 2-hyd-CBS category are derived from E₄ models discussed by e.g. Ryde, Raugei and Hoffman;^9,32,35 while models in Fig. 2g and h in the 2-hyd-OBS category are more related to E₄ models from our own work.³⁴ Ryde and coworkers also calculated models CBS₂₆-2BH_26(5),37 (a), OBS₆-2BH₂₆ (g) and OBS₂-2BH₂₆ (h) in a recent study.⁵¹ The 1-hyd models (m–q) are more similar to E₂ models discussed in the literature^36,37 but feature an extra S-bound proton (and electron). We note that models CBS₃₇-OBS₂-BH₂₆ (m), 2CBS_26,37-BH₂₆₍₅₎ (o), and 2CBS_26,37-BH₂₆₍₃₎ (p) were included in a recent study.⁵¹

Additionally, we include models for E₃ suggested in the QM/MM investigations by Ryde and coworkers:^31,51CBS₂₆-BH₂₆-TH₅ (e), CBS₂₆-2TH_4,5 (f), and C3H (r), shown in Fig. 2e, f and r. The CBS₂₆-BH₂₆-TH₅ model contains a protonated closed belt sulfide-bridge between Fe2 and Fe6, a bridging hydride between Fe2 and Fe6, and a terminal hydride at Fe5. The CBS₂₆-2TH_4,5 also has a protonated closed sulfide-bridge but two terminal hydrides on both Fe4 and Fe5. Three hydrogens were added directly to the carbide in the C3H model (Fig. 2r).

We note that Dance has previously suggested OBS₆-BH₂₆-TH₂ as a model for the E₃ state (named 3H.2x.26.2b in the original work).³³ For comparison we also include OBS₂-BH₂₆-TH₆ by exchanging the sulfhydryl and hydrides positions (compare Fig. 2i and j). Dance also reported on a model with a similar hydride geometry as OBS₂-BH₂₆-TH₆ but with a CBS configuration.³³ Such a geometry could not be stabilized by us but is discussed in the ESI† (see Fig. S4).

Models featuring a dihydrogen group in the E₃ state have previously been speculated on^91,92 and suggested by calculations.^33,91 Inspired by OBS₆-BH₂₆-TH₂ and OBS₂-BH₂₆-TH₆ (Fig. 2i and j) we constructed the OBS₆-DH₂ and OBS₂-DH₆ models (shown in Fig. 2k and l). Dance previously suggested a model with a protonated closed sulfide-bridge (S2B) and H₂ at Fe6 as a candidate for E₃,³³ discussed in the ESI† and shown in Fig. S5, but such a model could either not be stabilized or found to be very high in energy.

B. Energy ranking of E₃ isomers using r²SCAN and the 59-atom QM-A region

The 18 E₃ models (a–r in Fig. 2) were optimized by QM/MM calculations using the small QM-A region, and the r²SCAN functional. For each structural isomer we explored three spin states (M_S = 0, 1, 2) and 35 possible broken-symmetry state alignments for each spin state, giving a total of 105 electronic states calculated for each structural isomer. A comparison of spin-state energies can be found in Fig. S18 for each isomer in section 8 of the ESI† and we additionally show the type of BS class that tends to be the most favorable in Table S10 (ESI†). While here we opted to systematically study the BS-state problem rigorously, it appears that for the hydride-based isomers in this work it may be sufficient for future studies to primarily focus on the BS7, BS8 and BS10 classes of broken-symmetry solutions (and to a lesser extent BS6 and BS9). Furthermore Section 12 of the ESI† shows the energies and spin populations of every BS-state calculated for each isomer.

Fig. 2 shows the relative QM/MM energy of the lowest state calculated for each isomer. The C3H model (Fig. 2r) containing a triply protonated carbide, previously discussed by Ryde and coworkers,³¹ is predicted to be much higher than other isomers and would seemingly be ruled out at the r²SCAN level of theory (note that Section C discusses the functional sensitivity of this model). Comparing the 3 different categories of hydride-based E₃ models, it is clear that 2-hyd-CBS models are predicted to be in general higher in energy than models from the other categories, featuring both the highest-energy structural isomers in the comparison (e.g. structures in Fig. 2a–d, >30 kcal mol⁻¹) and the lowest-energy structures (shown in Fig. 2e and f) are 15–16 kcal mol⁻¹ higher in energy than the lowest-energy isomer (Fig. 2k). The lowest-energy isomers in the 2-hyd-CBS category, featuring either terminal or bridging hydrides: CBS₂₆-BH₂₆-TH₅ and CBS₂₆-2TH_4,5 were previously suggested by Ryde and coworkers.³¹ Interestingly, the E₃ models (a–d) inspired by some previous E₄ models^9,32,35 are here predicted to be very high in energy (31–39 kcal mol⁻¹).

The single-hydride 1-hyd isomers are on average lower in energy than the 2-hyd-CBS isomers but are still at least 10 kcal mol⁻¹ above the lowest energy isomer (Fig. 2k) in the 2-hyd-OBS category. The most favorable 1-hyd isomer features a bridging hydride between Fe3 and Fe7 and with 2 protons on S2B and S5A.

The overall stability of the isomers in the 2-hyd-OBS category suggests an overall improved thermodynamic preference associated with an isomer having 2 hydrides instead of just 1, but only if those hydrides are allowed more flexible coordination, here by having an open belt sulfide-bridge (i.e. protonated S2B converting to a terminal sulfhydryl group on Fe2 or Fe6). This improved stability of hydride-based isomers upon allowing a protonated belt sulfide to become a terminal sulfhydryl group, is consistent with our previous work on the E₂ and E₄ states.^34,36

Three 2-hyd-OBS models emerge overall as the lowest in energy: OBS₆-DH₂ (lowest), OBS₆-BH₂₆-TH₂ (+0.2 kcal mol⁻¹) and OBS₆-2BH₂₆ (+1.3 kcal mol⁻¹). These 3 models have a terminal sulfhydryl group on Fe6 in common but differ in terms of the precise H-atom coordination. OBS₆-DH₂ furthermore differs where the H-atoms have merged to form an H₂ ligand bound side-on to Fe2.

Symmetrically related versions of these 3 models are: OBS₂-DH₆, OBS₂-BH₂₆-TH₆ and OBS₂-2BH₂₆; they are, however, not as stable, due to the position of the sulfhydryl group on Fe2 instead of Fe6. This causes a steric clash with the His195 residue as confirmed by comparison with simple cluster-continuum calculations (Fig. S3 in the ESI†). We note that this preference may also be affected by the protonation state of His195 as e.g. discussed in recent work⁵⁰ but here we chose to model His195 as singly protonated on the N_ε atom (as in the E₀ state).

The results in this section differs from previous computational work on the E₃ state by including more diverse isomers than were previously studied or by employing considerably different computational protocols. In previous QM/MM work by Ryde and coworkers,³¹2-hyd-OBS type models for E₃ were simply not included (as the hemilability of protonated sulfide bridges was not known at the time). In very recent work by Jiang and Ryde,⁵¹ the OBS₆-2BH₂₆ model was found to be the lowest-energy model (using TPSSh, r²SCAN, and TPSS) which is consistent with our results. Dance has also previously studied various E₃ isomers,³³ and an OBS₆-BH₂₆-TH₂ model was found by him to be the most stable, which is also consistent with our results. The OBS₆-2BH₂₆ and OBS₂-DH₂ isomers were not explored in Dance's work; he did, however, find a CBS₂₆-DH₆ model to be very stable. Dance also reported that CBS₂₆-BH₂₆-TH₆ is about 5 kcal mol⁻¹ higher than OBS₆-BH₂₆-TH₂. Attempts at reproducing calculations on CBS₂₆-DH₆ and CBS₂₆-BH₂₆-TH₆ models (see Fig. S4 and S5 in the ESI†), however, were unsuccessful and we attribute these differences to the different computational protocols employed (QM-cluster vs. QM/MM and BLYP vs. r²SCAN).

The energy of evolving H₂ from the E₃-OBS₆-DH₂ model, i.e. the reaction E₃-OBS₆-DH₂ → E₁-S2B + H₂ has an energy of −15.2 kcal mol⁻¹ using the QM-A region (−9.9 kcal mol⁻¹ using the QM-C region), meaning there is a reasonable driving force for E₃ → E₁ relaxation (this can be compared to a calculated E₂ → E₀ relaxation energy of −19.4 kcal mol⁻¹ using a QM-C region reported in ref. 36). The enzyme would have to prevent this favorable H₂ relaxation process by utilizing a high electron flux rate in order to reach the E₄ state (or alternatively N₂ binding) faster than the rate for H₂ evolution. Barriers for H₂ evolution were not calculated in this work but may be lower than that previously calculated for E₂ → E₀ (∼21 kcal mol⁻¹³⁶). It is also possible that the initial E₃ state formed, right after e⁻/H⁺ transfer (the details of which are unknown), is not one of the favorable 2-hyd-OBS isomers but perhaps a state closer in nature to an E₂-like isomer, perhaps one of the 1-hyd isomers shown e.g. in Fig. 2n or q. The relevant rate for H₂ evolution may then involve complex proton and/or hydride reorganization (with unknown barriers), perhaps going from 1-hyd → 2-hyd-OBS or some other pathway that leads to H₂ evolution.

C. The functional dependency of the energy ranking

A critical part of an electronic structure study of FeMoco is the choice of methodology to describe the electronic structure. In this work we utilize a scalar relativistic (using the ZORA Hamiltonian) all-electron approach with polarized triple-zeta basis sets on all FeMoco atoms, that should result in very small basis-set incompleteness errors and no errors due to effective core potential approximations (that can be large for FeS systems as discussed in our previous benchmarking study⁵⁶). This means that the primary error in the electronic structure comes from the use of broken-symmetry density functional theory and in particular the choice of functional. The choice of functional is critical for FeMoco chemistry as is well demonstrated for FeMoco E₄ isomer energies in the work by Ryde and coworkers³⁵ where different non-hybrid and hybrid functionals gave completely different results for E₄ isomer energies, in particular regarding the stability of hydride vs. protonated carbide formation.

In recent work from our group⁵⁶ we benchmarked different functionals on their ability to describe the geometries of spin-coupled Fe–Fe and Mo–Fe dimers (mostly with bridging sulfides) as well as FeMoco itself. Four functionals emerged as the most accurate: r²SCAN, B97-D3, TPSSh, B3LYP*, having considerably lower errors than other non-hybrid functionals (that have a tendency to underestimate metal–metal distances) and other hybrid functionals (that have a tendency to overestimate metal–metal distances).⁵⁶ The trends in metal–metal distances were found to correlate with covalency parameters of the Fe–S bridging bonds, suggesting that the geometric errors are reflecting directly errors made in the covalency of the metal–ligand bonds that are responsible for spin-coupling interactions in this complex spin-coupled cofactor. r²SCAN was found to have a slight edge in the study and being a non-hybrid functional (lower computational cost) we used it to generate the results in section B. We note that other FeMoco studies from our group previously used TPSSh^{18,28,30,34,36,52,55} while other researchers have utilized functionals such as TPSS, BP86, BLYP, PBE, B3LYP, B3LYP* and M06-2X.^{9,31–33,35,37–49,58,93–99}

Here, we test whether density functionals that predict similar geometric structures of spin-coupled FeS systems (including E₀ FeMoco), predict similar energies of FeMoco E₃ isomers or not. We use the same QM/MM setup and same QM-region as in section B and every isomer was optimized with each functional to allow a fair comparison and to prevent bias. The five lowest-energy BS-states for each structural isomer (from the r²SCAN comparison in Section B) were used in this comparison (see Section 9 in the ESI† for more information).

The results in Fig. 3 reveal overall a highly similar trend for 3 of the functionals: r²SCAN, B97-D3 and TPSSh. The 3 functionals are in good agreement about the 2-hyd-OBS isomers being more favorable than 2-hyd-CBS as well as 1-hyd isomers. Furthermore, these 3 functionals agree on the 3 most stable isomers: OBS₆-DH₂, OBS₆-BH₂₆-TH₂ and OBS₆-2BH₂₆.

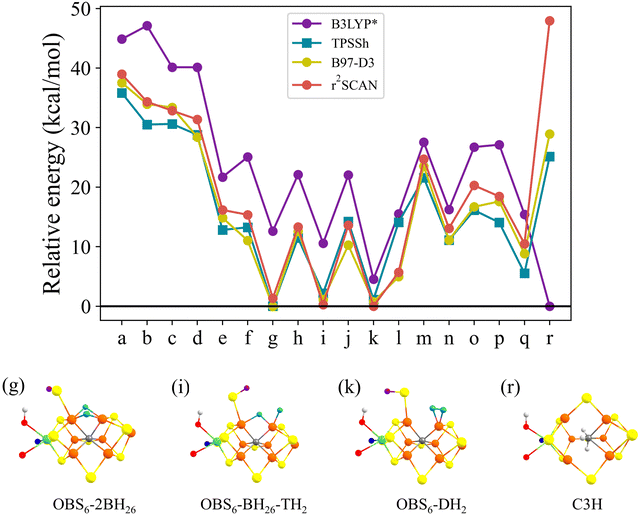Fig. 3 A comparison of the relative energies of E₃ isomers with different density functionals using QM-A region. The x-axis indicates the structural isomer from Fig. 2. r²SCAN, B97-D3, TPSSh consistently predict that the 3 most stable isomers are OBS₆-2BH₂₆,OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ while B3LYP* favours the r isomer. Note that all functionals include either D3 or D4 dispersion correction (see Computational details). Information about spin states and BS solutions of each model are available in Tables S12–S29 of the ESI.†

While the results for B3LYP* are somewhat similar, they differ in an important way: the carbide-protonated model C3H is found to be the lowest energy isomer (4.5 kcal mol⁻¹ lower than OBS₆-DH₂), in sharp contrast to r²SCAN (where C3H is the least favorable model) and TPSSh and B97-D3 (unfavorable by 25.1 and 29.8 kcal mol⁻¹). This mild preference for carbide-protonation with B3LYP* follows the well-established preference of carbide-protonation in the E₄ state by the regular 20% B3LYP hybrid. As shown in the ESI,† B3LYP favors the carbide-protonation in E₃ by ∼20 kcal mol⁻¹. The B3LYP* result is hence not entirely unexpected (differing by 15% instead of 20% HF exchange). The B3LYP*/B3LYP results are also consistent with the recent study by Jiang and Ryde⁵¹ where B3LYP predicts C3H to be the lowest energy model. Their work, however, also show TPSSh predicting the C3H model to be almost isoenergetic with OBS₆-2BH₂₆ (0.9 kcal mol⁻¹). Our TPSSh results in contrast show C3H to be unfavorable by 25.1 kcal mol⁻¹. The reason for the difference is likely rooted in the larger basis sets (ZORA-def2-TZVP) together with a ZORA relativistic treatment used in our work, while a small def2-SV(P) basis set was used by Ryde and coworkers.⁵¹

In the ESI† we have included data with the non-hybrid functional TPSS for comparison (see Fig. S19 in section 9 of the ESI†). TPSS gives a slightly different picture from r²SCAN, B97-D3, and TPSSh. The functional is overall in agreement about isomers OBS₆-2BH₂₆ and OBS₆-BH₂₆-TH₂ being low-energy but predicts isomer OBS₆-DH₂ as being considerably less stable. TPSS (like most other non-hybrid functionals) has a tendency to systematically underestimate Fe–Fe distances in spin-coupled Fe–S dimers and to give worse structures for FeMoco overall, apparently due to overestimating Fe–S bond covalency.

Overall, the results of this functional comparison show that r²SCAN, B97-D3 and TPSSh functionals predict very similar energetics for E₃ isomers. These 3 functionals have previously been found to describe well the metal–metal distances of spin-coupled iron–sulfur dimers as well as E₀ FeMoco itself. This is despite the fairly large variability in hydride isomers (1 vs. 2 hydrides or Fe-bound H₂), terminal vs. bridging hydrides and open vs. closed terminal sulfide bridges. In contrast, the B3LYP* functional, which was previously⁵⁶ found to behave similarly to r²SCAN, B97-D3 and TPSSh, favours the triply protonated carbide model (similar to its parent B3LYP functional).

There is no experimental evidence to suggest that the interstitial carbide ion of FeMoco can be protonated. In fact, a recent ¹³C ENDOR study on several reduced E_n and ligand-bound FeMoco states shows that the carbide hyperfine coupling remains unchanged, suggesting that the carbide coordination environment remains intact, consistent with a stabilizing role of the carbide. In view of this, the prediction of protonated carbide isomers by B3LYP* (and B3LYP) likely represent artifacts from these functionals. We suggest OBS₆-2BH₂₆ and OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ models as the most likely models for the E₃ state.

D. The QM-region size dependency of the energy ranking

Another critical aspect of modelling metalloenzymes is the treatment of the protein environment. In the QM/MM model used, the whole solvated protein is included in the calculation, however, only a small part is described by quantum mechanics (DFT) and the rest of the system is described by an MM forcefield (CHARMM36). The QM and MM subsystems interact via electrostatic embedding and Lennard-Jones potentials (and bonded interactions at the interface). There are always potential errors made by the definition of the QM-region, in particular residues strongly interacting with the cofactor should ideally be present in the QM-region (to avoid imperfect quantum-classical interactions). By increasing the size of the QM-region one can reduce the magnitude of such effects.

In Fig. 4 we compare the effect of using a small 59-atom QM-A region (used in Sections B and C) and using the larger 191-atom QM-C region (single-point calculations performed on the 145-atom QM-B optimized geometries). This comparison was only performed using the r²SCAN functional and only for isomers e to q (see Fig. 2) as multiple functionals consistently found isomers a–d and r to be much higher in energy than other isomers in energy. The results in Fig. 4 reassuringly reveal that the energy landscape does not change very much overall and the stability of 2-hyd-OBS isomers holds and both QM-regions predict the same 3 isomers (models OBS₆-2BH₂₆ (g), OBS₆-BH₂₆-TH₂ (i) and OBS₆-DH₂ (k)) as the most favourable. However, the larger QM-C region slightly increases the energy gap between these 3 isomers, further stabilizing OBS₆-DH₂ (3.1 and 3.3 kcal mol⁻¹ more stable than OBS₆-2BH₂₆ and OBS₆-BH₂₆-TH₂ at the r²SCAN level).

Fig. 4 The comparison of relative QM/MM energies using r²SCAN for models (e–q) between using the QM-A and QM-C regions. The labels of the x-axis indicate the models defined in Fig. 2. QM-A region contains 59 atoms while QM-C contains 191 atoms. The spin states and BS solutions are the same as Fig. 2.

Considering both the functional and the QM-region dependency we conclude that the OBS₆-DH₂, OBS₆-BH₂₆-TH₂ and OBS₆-2BH₂₆ are consistently predicted to be the most stable E₃ isomers. The dihydrogen isomer (OBS₆-DH₂) is predicted to be the most stable, with the energy gap differing depending on precisely which functional and QM-region are used. However, there is certainly uncertainty associated with these energies and we suggest any of these 3 isomers is likely to be encountered experimentally. In order to check whether these 3 isomers might be distinguished by other factors we performed additional calculations for these 3 isomers (see Section 10 in the ESI†) where we checked how much the D4 dispersion correction plays a role (a very small effect of 0.1–0.3 kcal mol⁻¹) and whether inclusion of a zero-point vibrational energy (ZPVE) correction would affect the energy ordering. The ZPVE correction was also found to be relatively small in magnitude, ∼0.7 kcal mol⁻¹ (see Section 10 in the ESI†).

E. The electronic structure of the 3 lowest energy isomers

Comparing the geometric features of the common [Fe₂H₂C] core of these isomers reveals interesting differences (see Fig. 5) when evaluated using the r²SCAN functional and QM-region C. The Fe2–Fe6 distance is considerably shorter in the OBS₆-2BH₂₆ isomers (2.41 Å) than in the OBS₆-BH₂₆-TH₂ (2.68 Å) and OBS₆-DH₂ (2.63 Å), a geometric feature likely a result of the 2 bridging hydrides. There are also considerable changes in Fe–C bond lengths in these 3 isomers, suggesting that the carbide might be pushing electron density to different degrees depending on the hydride/H₂ coordination. The Fe–H distances of the bridging hydrides are generally shorter for Fe2 than for Fe6 in OBS₆-BH₂₆-TH₂ and OBS₆-2BH₂₆, that suggest that these hydrides are not equally shared between Fe ions. The Fe2–H distances in OBS₆-DH₂ are considerably longer (1.71 Å) than the Fe–hydride distances, and with a relatively short H–H distance of 0.84 Å, a dihydrogen ligand description seems appropriate.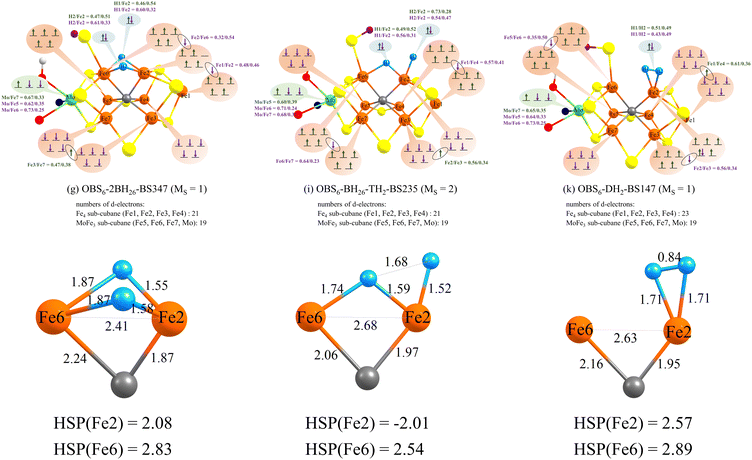

Fig. 5 Top: Electronic configurations of OBS₆-2BH₂₆, OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ derived from localized orbital analysis of the QM/MM calculation using r²SCAN and the QM-C region. The spin states and BS solutions of these three isomers are the same as Fig. 4. The localized orbitals of these three models are shown in Fig. S12–S14 in the ESI.† The green and purple numbers indicate localized orbital populations of Mo, Fe and H-atoms. Bottom: Close-up of the geometries associated with the Fe–H interactions at Fe2 and Fe6. HSP(atom) indicates the Hirshfeld spin populations of Fe2 and Fe6.

The electronic structure of these 3 isomers is also compared in Fig. 5 by electronic configuration diagrams derived from localized orbital analysis of the broken-symmetry determinants. The E₃ state has three more e⁻/H⁺ pairs than the E₀ state, having 22 d-electrons and 19 d-electrons in the Fe₄ sub-cubane and MoFe₃ sub-cubane, respectively. Analogous electron configuration diagrams for E₀ are found in Fig. S11 in the ESI† for comparison. In OBS₆-DH₂, we find that two additional electrons are present in the form of the H₂ ligand while an additional localized electron is present on Fe2 (suggesting a high-spin ferrous ion). OBS₆-BH₂₆-TH₂ and OBS₆-2BH₂₆ models have interestingly very similar electronic structures which offers a possible explanation for the very similar energies for these isomers. This is despite the different hydride coordination and the different Fe2–Fe6 distance. Unlike the dihydrogen isomer, 4 electrons are associated with the H-atoms, with localized orbitals indicating considerable Fe-character. Interestingly, there is an unusual electronic configuration for Fe2: most of the Fe-character in the hydride orbitals is associated with Fe2 rather than Fe6, which together with the asymmetric Fe–H distances previously discussed, suggests that these hydrides are not completely bridging (see localized orbital visualizations in Fig. S14 of the ESI†). The use of 4 electrons to stabilize the Fe–H bonds at first glance suggests that the cofactor has been effectively oxidized but the strong covalency of the Fe–H bonds in these states makes it difficult to make a clear assignment of oxidation states.

The comparison of electronic configurations and geometries for different functionals (B3LYP*, TPSSh, B97-D3, r²SCAN, and TPSS) is shown in Fig. S20 to S25 in the ESI.† The five functionals give similar electronic configurations and geometries for OBS₆-DH₂. For OBS₆-BH₂₆-TH₂, B3LYP*, TPSSh, B97-D3 give a similar description as r²SCAN, with an electron-deficient Fe₄ subcubane, but TPSS in contrast predicts an electron-deficient MoFe₃ sub-cubane. The electronic structure of the OBS₆-2BH₂₆ isomer is more complex; B3LYP* predicts similar electronic and geometric structures to r²SCAN, and two bridging hydrides share four electrons with Fe2, correlating with shorter Fe2-hydride distances than Fe6-hydride (see Fig. S21, ESI†), and one electron has moved from the Fe₄ sub-cubane to the hydrides (compared to the E₀ state, see Fig. S11, ESI†). In contrast, TPSSh predicts four electrons associated with Fe6–H bonds which correlates with shorter Fe6–H distances than Fe2–H distances, and an electron-deficient MoFe₃-cubane. TPSS and B97-D3 behave intermediate to the other functionals, predicting four almost equally shared electrons between Fe2 and Fe6, resulting in similar Fe2–H and Fe6–H distances and unusually Fe2 and Fe6 share an electron.

These geometric differences and electronic structure analysis clearly reveal a complex electronic structure which is not easily understood at present, requiring further studies. Also, despite similar energetics predicted by the different functionals (see Fig. 3), the electronic structure from different functionals is not always similar.

F. N₂ binding to the E₃ state

The original kinetic model by Thorneley and Lowe^1,24 suggested N₂ binding to the E₃ state, although little additional data has since appeared to support or refute that hypothesis. The Fe2–Fe3–Fe6–Fe7 face has long been suggested as a site for N₂ binding, primarily based on mutation studies.^100,101 Additionally, crystallographic studies^102–104 have shown displacement of the bridging sulfide (S2B) between Fe2 and Fe6 under certain conditions, which further implicates Fe2 or Fe6 as a likely site of ligand binding.^105,106 A recent X-ray structure study¹⁰⁴ appeared to show N₂ replacing three possible sulfur sites (S2B, S3A and S5A) but this claim is controversial.^107–109 Regardless of the precise interpretations of recent crystal structures, Fe2 and Fe6 are likely binding sites for N₂.

In previous work from our group^34,50 we showed how calculations of N₂ binding to Fe sites (specifically Fe2 and Fe6) at FeMoco is almost always connected with the formation of local low-spin states of Fe and furthermore hydrides appear to aid in the formation of such states, offering a possible explanation for why the E₄ state has an improved affinity for N₂.

As the results in this work suggest OBS₆-DH₂, OBS₆-BH₂₆-TH₂ and OBS₆-2BH₂₆ as plausible models for the E₃ state, and with all 3 models featuring either 2 hydrides or an Fe-bound H₂ it is interesting to consider whether N₂ binding might be favored to these E₃ isomers or not. As OBS₆-2BH₂₆ has a more obvious accessible binding site, we focused primarily on this isomer.

We systematically investigated N₂ binding to Fe2 of OBS₆-2BH₂₆ or Fe6 of OBS₂-2BH₂₆ in three spin states (M_S = 0, 1, 2) and 35 BS solutions using the QM-A region, and the binding energies are shown in Fig. S15 in the ESI.† The QM-A region was then expanded to the QM-C region, and the binding energies of N₂ to Fe2 or Fe6 were found to be +1.5 and +1.9 kcal mol⁻¹ (relative to OBS₆-DH₂), respectively, shown in Fig. 6, which is similar to the r²SCAN results reported by Ryde and coworkers.⁵¹

Fig. 6 N₂ binding energies using the QM-C region and r²SCAN. Also shown are relative N–N frequencies for N₂ (relative to free N₂: 2432 cm⁻¹), Hirshfeld spin populations and quasi-restricted orbital (QRO)-based ligand field diagrams of binding site Fe. The N₂@Fe2 and N₂@Fe6 have a spin state of M_S = 0 and BS states of BS147 and BS234, respectively. The spin states and BS solutions of (a) and (b) are BS347 (M_S = 1) and BS2356 (M_S = 0), respectively.

We note that Dance previously found the OBS₆-2BH₂₆-N₂@Fe2 isomer by binding N₂ to CBS₂₆-BH₂₆-TH₆ (unstable in the present study; see Fig. S4 in the ESI†), and reported that there is a barrier of 9 kcal mol⁻¹ to making the terminal hydride become bridging.^38,42

The direct binding of N₂viaOBS₂-2BH₂₆ → OBS₂-2BH₂₆-N₂@Fe6 is much stronger (−13.9 kcal mol⁻¹) but the OBS₂-2BH₂₆ isomer is higher in energy due to clashes of the terminal sulfhydryl group with the His195 residue. The addition of a translational entropy penalty would make this binding even more unfavourable and hence unlikely to occur.

Dance suggested that an H₂ ligand can enhance N₂ binding to Fe.^43,44 Therefore, we additionally explored N₂ binding to OBS₆-DH₂, and N₂ binding to OBS₆-BH₂₆-TH₂ was also attempted for completeness. N₂ binding scenarios where N₂ binds directly to Fe2 in the OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ isomers were studied in either a cis or trans orientation relative to the Fe2–carbide bond. These calculations were performed using the QM-A region and we investigated only the low spin state (M_S = 0) and we restricted the broken-symmetry state comparison to the BS6 class of solutions (BS156, BS157 and BS167) and the BS10 class of solutions (BS125, BS127, BS135, BS136, BS146 and BS147) as these were the lowest-energy BS states for the N₂-bound isomers of OBS₆-2BH₂₆-N₂@Fe2 and OBS₂-2BH₂₆-N₂@Fe6 (see Fig. S15 and Table S10, ESI†). The results in Fig. 7b reveal that N₂ binding to Fe2 in OBS₆-BH₂₆-TH₂ in a cis orientation relative to the Fe2–C bond results in a stable N₂-bound minimum but with an unfavourable binding energy (22.6 kcal mol⁻¹). Starting an optimization with N₂ instead trans to the Fe2–C bond (Fig. 7c), however, leads to the spontaneous formation of the OBS₆-2BH₂₆-N₂@Fe2 isomer (see Fig. 7d and Fig. 6). Comparing the OBS₆-DH₂ isomer instead we find that N₂ binding cis to the Fe2–C bond (Fig. 7f) is even more unfavourable (25.6 kcal mol⁻¹) and binding trans (Fig. 7g) is still fairly unfavourable compared to the OBS₆-2BH₂₆ and OBS₂-2BH₂₆ structures. These results suggest that it is rather bridging hydrides between Fe₂ and Fe₆ that enhance N₂ binding than a H₂ ligand.

Fig. 7 The binding energies (B. E.) of N₂ binding to OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ (using the QM-A region and r²SCAN), which are relative to the lowest-energy isomer OBS₆-DH₂ (Fig. 2k). The BS states of (b), (d), (f), and (g) are BS156, BS147, BS156, and BS157, respectively, and all these states are in low spin (M_S = 0). Note the energy shown in (d) differs from Fig. 6, due to different QM regions.

Comparing N₂ binding energies across the FeMoco redox series: E₀, E₁, E₂, and E₄ states (using the models discussed in our recent work⁵⁰), the binding energy of N₂ to the E₃ state is found to be marginally more favorable than E₂ and not as favorable as binding to the E₄ state (see Fig. 8), which is similar to trends reported by Ryde and Jiang.⁵¹ The ligand-field diagrams of Fe2 and Fe6 with bound N₂ in Fig. 6 (obtained from diamagnetic substitution and QROs) show that both Fe ions are low-spin Fe³⁺ in an approximate octahedral ligand-field and two d_xz and d_yz orbitals overlap with π* orbitals of N₂ (see Fig. S15, ESI†), which is very similar to that found for the E₄ state in our previous study.⁵⁰ We previously suggested that a low-spin electronic structure on the Fe site is generally encountered in almost all N₂-bound FeMoco structures, and that such spin-paired electronic structure is likely assisted by the strong sigma-donor hydrides, especially when more favorable hydride ligation is made possible by an open belt sulfide bridge.⁵⁰ While the E₃ models OBS₂-2BH₂₆ and OBS₆-2BH₂₆ models have the same di-hydride geometric and electronic structure features, the binding energy is predicted to be less than the E₄ state, probably related to an overall less-reduced Fe environment in E₃ that decreases backbonding to the N₂ ligand.

Fig. 8 The trend of N₂ binding energies in going from models of E₀ to E₄ states according to calculations from previous work⁵⁰ and this work (using r²SCAN). Also shown are approximate ligand-field diagrams, derived from a combination of localized-orbital analysis and QRO MO energies from a diamagnetically substituted model (see ref. 50). The results for the E₃ state were calculated using the QM-C region that is the same as the QM-VI region in ref. 50. The N₂ binding energy of the E₃ state is relative to the lowest-energy model OBS₆-DH₂ (Fig. 2k). The spin states and BS solutions of these five models from E₀ to E₄ states are BS147 (M_S = 1/2), BS346 (M_S = 2), BS235 (M_S = 1/2), BS147 (M_S = 0), and BS234 (M_S = 1/2), respectively.

Conclusions

In this study we have discussed the energy surface of the E₃ redox state of FeMoco and attempted to shed light on the possible forms that this complicated cofactor can take upon addition of 3 electrons and 3 protons (relative to the E₀ state). This fills an important gap in the literature in our opinion as so little is known experimentally about this state, being EPR-silent by traditional EPR spectroscopy and hard to isolate. In fact, no spectroscopic data is available on this state and only indirect kinetic data is available.^1,24 Furthermore, only a few computational studies^31,33,51 have been devoted to the state.

Our results suggest that the most likely structure of the E₃-state cofactor involves structures with a protonated S2B sulfide bridge in an open form, i.e. a terminal sulfhydryl group on Fe6, which allows a few different Fe–H structures to form (all of them involving 2 hydrides or at least 2 Fe–H interactions). One of these models includes 2 bridging hydrides between Fe2 and Fe6 (Fig. 2g), a structure similar to an E₄ model previously discussed by us and others,^9,32,34 while another model (Fig. 2i) features 1 bridging, 1 terminal hydride instead (similar to the lowest energy E₄ structure in a recent study by us⁵⁰). The third structure is a bit different, instead of featuring individual Fe–hydrides, it takes a form best described as a side-on Fe–(H₂) ligand at the Fe2 site. Energetically, these 3 structures are essentially equivalent when calculated using our QM/MM model with a small QM-region and using the r²SCAN density functional, being ∼1 kcal mol⁻¹ of each other, with the Fe–H₂ structure marginally favoured. Upon increasing the QM-region we find a slight shift in relative energies for these 3 isomers, favouring the Fe–H₂ structure, OBS₆-DH₂ (being ∼3 kcal mol⁻¹ lower in energy than the other two).

The electronic structures of these 3 states, analyzed via localized orbital analysis, show considerable differences as shown in Fig. 5. Structure OBS₆-DH₂ (k) in particular, with an Fe–H₂ interaction, features 2 localized electrons associated with the H₂, while structures OBS₆-2BH₂₆ (g) and OBS₆-BH₂₆-TH₂ (i) are more similar and feature 4 electrons associated with the bridging/terminal hydride atoms. Such a distinct difference in electronic structure might be expected to give rise to considerable functional dependency.

The functional dependency on isomer energies is predicted to be fairly mild when evaluated using 3 different functionals that we have previously found to describe the molecular and electronic structures of spin-coupled iron–sulfur clusters well: r²SCAN, B97-D3, TPSSh. The results of these three functionals show that OBS₆-2BH₂₆ (g), OBS₆-BH₂₆-TH₂ (i), and OBS₆-DH₂ (k) are the 3 most favourable models. However, the B3LYP* functional (previously found to behave similarly to the other 3 functionals for geometries)⁵⁶ interestingly favours a triply protonated carbide.

The functional dependency of FeMoco isomers is actually known to be extremely sensitive in general, especially with respect to Hartree–Fock exchange, as discussed by Ryde and coworkers for energies¹¹⁰ and Harvey and coworkers for electron density changes.¹¹¹ Functionals such as B3LYP and other hybrids with at least 20% HF exchange are e.g. known to predict interstitial carbide protonation in both E₃ and E₄ redox states^31,110 and it seems that this also applies to the 15% B3LYP* functional.

However, there is no experimental evidence for carbide protonation occurring in any FeMoco state. In fact, according to recent ¹³C ENDOR studies of multiple trapped FeMoco states with labelled interstitial carbide,¹¹² the carbide hyperfine coupling is practically unchanged. A likely interpretation is that the carbide appears more likely to have a general stabilizing role¹¹² during catalysis. Together with the observation that most hybrid functionals also predict worse FeMoco structures (overestimating Fe–Fe, Fe–S and Fe–C distances) our interpretation is that only non-hybrid functionals and functionals with 0–10% HF exchange describe FeMoco qualitatively correctly.

Uncertainty about the functional dependency nonetheless remains that needs to be evaluated on a case-by-case basis. In recent previous work we compared the energies of E₂-hyd and E₂-nonhyd isomers that were found to be highly sensitive to the use of r²SCAN vs TPSSh.⁵⁰ That sensitivity could be explained as the two isomers differing in the nature of the localization of added electrons (Fe-reduction vs. forming H⁻). Jiang and Ryde have also reported different trends for the E₂ state comparing TPSS, r²SCAN and TPSSh.³⁷ The nature of the electronic structure of reduced FeMoco isomers hence continues to present challenges to density functional treatments, both in terms of accuracy and interpretation of the complex electronic structure. The electronic structure interpretation of the E₃ isomers discussed in Section E is far from straightforward and as shown in the ESI,† different functionals also give slightly different electronic structures (different BS solutions, different Fe–H covalency and different degrees of localization/delocalization). A systematic assessment of density functionals for the description of Fe–hydride bonds in open-shell Fe compounds is likely to be useful to shed further light on these matters. Overall, our understanding of the electronic structure of hydride-based FeMoco structures remains very much incomplete and continues to surprise us. The flexibility of hydride conformers found in this study is possibly part of a general phenomenon of dynamical flexibility of Fe-bound hydrides as e.g. discussed in recent temperature-dependent studies of an [Fe₂H₂] dimer studied by Holland and coworkers.¹¹³

N₂ binding was explored to OBS₆-2BH₂₆ isomers and resulted in end-on N₂-bound isomers similar to those studied in recent work.^34,50 Conversely, N₂ binding to OBS₆-DH₂ and OBS₆-BH₂₆-TH₂ isomers was found to be unfavourable. Analysis of the electronic structure of the most favourable N₂-bound state reveals that a low-spin Fe(III) state is found at the N₂-binding Fe ion. However, the binding energy of N₂ relative to the most stable E₃ isomer (OBS₆-DH₂), is found to be slightly uphill, suggesting that the E₃ redox isomer may not be reduced enough to favourable bind N₂. Considering the overall uncertainty from factors such as QM model size, the lack of thermal contributions, as well as the functional dependency, the calculations suggest isomers OBS₆-2BH₂₆, OBS₆-BH₂₆-TH₂ and OBS₆-DH₂ as the most favourable and we do not attempt to distinguish between them at this stage. Any of these 3 states may represent species formed under experimental conditions, however, E₃ has never been isolated, so very little is actually known experimentally. Both E₂ and E₄ are known to evolve H₂ if the electron-flux rate is slower than the rate for the H₂ formation, and E₃ is likely to be similar in this respect. This means that the E₃ state would be meta-stable with respect to H₂ formation. The stable OBS₆-DH₂ isomer found in this study, containing an H₂ ligand, could actually represent a state on the path towards evolving H₂ and falling back to E₁. An isolable E₃ state may then instead be better represented by either OBS₆-2BH₂₆ or OBS₆-BH₂₆-TH₂, depending on the barriers present. Future work will have to consider the calculation of reaction pathways and barriers relating all E₃ species from the initial formation of the state until the H₂ formation.

Author contributions

The manuscript was written through contributions of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. B. acknowledges support from the Max Planck society. Y. P. acknowledges a scholarship from the China Scholarship Council and a grant from the National Natural Science Foundation of China (no. 22073010). Open Access funding provided by the Max Planck Society.

References

1. B. K. Burgess and D. J. Lowe, Mechanism of Molybdenum Nitrogenase, Chem. Rev., 1996, 96, 2983–3012.
2. O. Einsle and D. C. Rees, Structural Enzymology of Nitrogenase Enzymes, Chem. Rev., 2020, 120, 4969–5004.
3. A. J. Jasniewski, C. C. Lee, M. W. Ribbe and Y. Hu, Reactivity, Mechanism, and Assembly of the Alternative Nitrogenases, Chem. Rev., 2020, 120, 5107–5157.
4. H. L. Rutledge and F. A. Tezcan, Electron Transfer in Nitrogenase, Chem. Rev., 2020, 120, 5158–5193.
5. L. C. Seefeldt, Z. Y. Yang, D. A. Lukoyanov, D. F. Harris, D. R. Dean, S. Raugei and B. M. Hoffman, Reduction of Substrates by Nitrogenases, Chem. Rev., 2020, 120, 5082–5106.
6. C. Van Stappen, L. Decamps, G. E. Cutsail, R. Bjornsson, J. T. Henthorn, J. A. Birrell and S. DeBeer, The Spectroscopy of Nitrogenases, Chem. Rev., 2020, 120, 5005–5081.
7. Z. Y. Yang, N. Khadka, D. Lukoyanov, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, On reversible H2 loss upon N2 binding to FeMo-cofactor of nitrogenase, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16327–16332.
8. D. Lukoyanov, N. Khadka, Z. Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Reductive Elimination of H2 Activates Nitrogenase to Reduce the N identical withN Triple Bond: Characterization of the E4(4H) Janus Intermediate in Wild-Type Enzyme, J. Am. Chem. Soc., 2016, 138, 10674–10683.
9. V. Hoeke, L. Tociu, D. A. Case, L. C. Seefeldt, S. Raugei and B. M. Hoffman, High-Resolution ENDOR Spectroscopy Combined with Quantum Chemical Calculations Reveals the Structure of Nitrogenase Janus Intermediate E4(4H), J. Am. Chem. Soc., 2019, 141, 11984–11996.
10. E. Münck, H. Rhodes, W. H. Orme-Johnson, L. C. Davis, W. J. Brill and V. K. Shah, Nitrogenase. VIII. Mössbauer and EPR spectroscopy. The MoFe protein component from Azotobacter vinelandii OP, Biochim. Biophys. Acta, Protein Struct., 1975, 400, 32–53.
11. J. Rawlings, V. K. Shah, J. R. Chisnell, W. J. Brill, R. Zimmermann, E. Münck and W. H. Orme-Johnson, Novel metal cluster in the iron-molybdenum cofactor of nitrogenase. Spectroscopic evidence, J. Biol. Chem., 1978, 253, 1001–1004.
12. T. V. Morgan, L. E. Mortenson, J. W. McDonald and G. D. Watt, Comparison of redox and EPR properties of the molybdenum iron proteins of Clostridium pasteurianum and Azotobacter vinelandii nitrogenases, J. Inorg. Biochem., 1988, 33, 111–120.
13. K. Fisher, W. E. Newton and D. J. Lowe, Electron Paramagnetic Resonance Analysis of Different Azotobacter vinelandii Nitrogenase MoFe-Protein Conformations Generated during Enzyme Turnover:  Evidence for S = 3/2 Spin States from Reduced MoFe-Protein Intermediates, Biochemistry, 2001, 40, 3333–3339.
14. O. Einsle, F. A. Tezcan, S. L. A. Andrade, B. Schmid, M. Yoshida, J. B. Howard and D. C. Rees, Nitrogenase MoFe-Protein at 1.16 Å Resolution: A Central Ligand in the FeMo-Cofactor, Science, 2002, 297, 1696–1700.
15. T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Evidence for interstitial carbon in nitrogenase FeMo cofactor, Science, 2011, 334, 940.
16. S. J. Yoo, H. C. Angove, V. Papaefthymiou, B. K. Burgess and E. Münck, Mössbauer Study of the MoFe Protein of Nitrogenase from Azotobacter vinelandii Using Selective 57Fe Enrichment of the M-Centers, J. Am. Chem. Soc., 2000, 122, 4926–4936.
17. C. Van Stappen, R. Davydov, Z. Y. Yang, R. Fan, Y. Guo, E. Bill, L. C. Seefeldt, B. M. Hoffman and S. DeBeer, Spectroscopic Description of the E1 State of Mo Nitrogenase Based on Mo and Fe X-ray Absorption and Mössbauer Studies, Inorg. Chem., 2019, 58, 12365–12376.
18. C. Van Stappen, A. T. Thorhallsson, L. Decamps, R. Bjornsson and S. DeBeer, Resolving the structure of the E1 state of Mo nitrogenase through Mo and Fe K-edge EXAFS and QM/MM calculations, Chem. Sci., 2019, 10, 9807–9821.
19. D. Lukoyanov, B. M. Barney, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Connecting nitrogenase intermediates with the kinetic scheme for N2 reduction by a relaxation protocol and identification of the N2 binding state, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1451–1455.
20. D. Lukoyanov, Z. Y. Yang, S. Duval, K. Danyal, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, A confirmation of the quench-cryoannealing relaxation protocol for identifying reduction states of freeze-trapped nitrogenase intermediates, Inorg. Chem., 2014, 53, 3688–3693.
21. D. A. Lukoyanov, N. Khadka, Z. Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Hydride Conformers of the Nitrogenase FeMo-cofactor Two-Electron Reduced State E2(2H), Assigned Using Cryogenic Intra Electron Paramagnetic Resonance Cavity Photolysis, Inorg. Chem., 2018, 57, 6847–6852.
22. D. F. Harris, A. Badalyan and L. C. Seefeldt, Mechanistic Insights into Nitrogenase FeMo-Cofactor Catalysis through a Steady-State Kinetic Model, Biochemistry, 2022, 61, 2131–2137.
23. R. Y. Igarashi, M. Laryukhin, P. C. Dos Santos, H.-I. Lee, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, Trapping H- Bound to the Nitrogenase FeMo-Cofactor Active Site during H2 Evolution:  Characterization by ENDOR Spectroscopy, J. Am. Chem. Soc., 2005, 127, 6231–6241.
24. R. N. F. Thorneley and D. J. Lowe, in Molybdenum Enzymes, ed. T. G. Spiro, Wiley, New York, 1985, pp. 221–284.
25. D. J. Lowe, K. Fisher and R. N. F. Thorneley, Klebsiella pneumoniae nitrogenase. Mechanism of acetylene reduction and its inhibition by carbon monoxide, Biochem. J., 1990, 272, 621–625.
26. K. Fisher, M. J. Dilworth and W. E. Newton, Differential Effects on N2 Binding and Reduction, HD Formation, and Azide Reduction with α-195His- and α-191Gln-Substituted MoFe Proteins of Azotobacter vinelandii Nitrogenase, Biochemistry, 2000, 39, 15570–15577.
27. K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, X-ray Emission Spectroscopy Evidences a Central Carbon in the Nitrogenase Iron-Molybdenum Cofactor, Science, 2011, 334, 974–977.
28. R. Bjornsson, F. A. Lima, T. Spatzal, T. Weyhermüller, P. Glatzel, E. Bill, O. Einsle, F. Neese and S. DeBeer, Identification of a spin-coupled Mo(iii) in the nitrogenase iron–molybdenum cofactor, Chem. Sci., 2014, 5, 3096–3103.
29. T. Spatzal, J. Schlesier, E. M. Burger, D. Sippel, L. Zhang, S. L. Andrade, D. C. Rees and O. Einsle, Nitrogenase FeMoco investigated by spatially resolved anomalous dispersion refinement, Nat. Commun., 2016, 7, 10902.
30. R. Bjornsson, F. Neese and S. DeBeer, Revisiting the Mössbauer Isomer Shifts of the FeMoco Cluster of Nitrogenase and the Cofactor Charge, Inorg. Chem., 2017, 56, 1470–1477.
31. L. Cao, O. Caldararu and U. Ryde, Protonation and Reduction of the FeMo Cluster in Nitrogenase Studied by Quantum Mechanics/Molecular Mechanics(QM/MM) Calculations, J. Chem. Theory Comput., 2018, 14, 6653–6678.
32. S. Raugei, L. C. Seefeldt and B. M. Hoffman, Critical computational analysis illuminates the reductive-elimination mechanism that activates nitrogenase for N2 reduction, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10521–E10530.
33. I. Dance, Survey of the Geometric and Electronic Structures of the Key Hydrogenated Forms of FeMo-co, the Active Site of the Enzyme Nitrogenase: Principles of the Mechanistically Significant Coordination Chemistry, Inorganics, 2019, 7, 8.
34. A. T. Thorhallsson, B. Benediktsson and R. Bjornsson, A model for dinitrogen binding in the E4 state of nitrogenase, Chem. Sci., 2019, 10, 11110–11124.
35. L. Cao and U. Ryde, What Is the Structure of the E4 Intermediate in Nitrogenase?, J. Chem. Theory Comput., 2020, 16, 1936–1952.
36. A. T. Thorhallsson and R. Bjornsson, The E2 state of FeMoco: Hydride Formation versus Fe Reduction and a Mechanism for H2 Evolution, Chem. – Eur. J., 2021, 27, 16788–16800.
37. H. Jiang, O. K. G. Svensson and U. Ryde, QM/MM Study of Partial Dissociation of S2B for the E(2) Intermediate of Nitrogenase, Inorg. Chem., 2022, 61, 18067–18076.
38. I. Dance, How feasible is the reversible S-dissociation mechanism for the activation of FeMo-co, the catalytic site of nitrogenase?, Dalton Trans., 2019, 48, 1251–1262.
39. P. E. M. Siegbahn, The mechanism for nitrogenase including all steps, Phys. Chem. Chem. Phys., 2019, 21, 15747–15759.
40. L. Cao and U. Ryde, N2H2 binding to the nitrogenase FeMo cluster studied by QM/MM methods, J. Biol. Inorg. Chem., 2020, 25, 521–540.
41. L. Cao and U. Ryde, Putative reaction mechanism of nitrogenase after dissociation of a sulfide ligand, J. Catal., 2020, 391, 247–259.
42. I. Dance, Computational Investigations of the Chemical Mechanism of the Enzyme Nitrogenase, ChemBioChem, 2020, 21, 1671–1709.
43. I. Dance, Structures and reaction dynamics of N2 and H2 binding at FeMo-co, the active site of nitrogenase, Dalton Trans., 2021, 50, 18212–18237.
44. I. Dance, Calculating the chemical mechanism of nitrogenase: new working hypotheses, Dalton Trans., 2022, 51, 12717–12728.
45. I. Dance, Understanding the tethered unhooking and rehooking of S2B in the reaction domain of FeMo-co, the active site of nitrogenase, Dalton Trans., 2022, 51, 15538–15554.
46. H. Jiang and U. Ryde, Thermodynamically Favourable States in the Reaction of Nitrogenase without Dissociation of any Sulfide Ligand, Chemistry, 2022, e202103933.
47. H. Jiang, O. K. G. Svensson, L. Cao and U. Ryde, Proton Transfer Pathways in Nitrogenase with and without Dissociated S2B, Angew. Chem., Int. Ed., 2022, 61, e202208544.
48. W. J. Wei and P. E. M. Siegbahn, A Mechanism for Nitrogenase Including Loss of a Sulfide, Chemistry, 2022, 28, e202103745.
49. I. Dance, The binding of reducible N(2) in the reaction domain of nitrogenase, Dalton Trans., 2023, 52, 2013–2026.
50. Y. Pang and R. Bjornsson, Understanding the Electronic Structure Basis for N2 Binding to FeMoco: A Systematic Quantum Mechanics/Molecular Mechanics Investigation, Inorg. Chem., 2023, 62, 5357–5375.
51. H. Jiang and U. Ryde, N(2) binding to the E(0)-E(4) states of nitrogenase, Dalton Trans., 2023, 52, 9104–9120.
52. B. Benediktsson and R. Bjornsson, QM/MM Study of the Nitrogenase MoFe Protein Resting State: Broken-Symmetry States, Protonation States, and QM Region Convergence in the FeMoco Active Site, Inorg. Chem., 2017, 56, 13417–13429.
53. B. Benediktsson, A. T. Thorhallsson and R. Bjornsson, QM/MM calculations reveal a bridging hydroxo group in a vanadium nitrogenase crystal structure, Chem. Commun., 2018, 54, 7310–7313.
54. B. Benediktsson and R. Bjornsson, Quantum Mechanics/Molecular Mechanics Study of Resting-State Vanadium Nitrogenase: Molecular and Electronic Structure of the Iron-Vanadium Cofactor, Inorg. Chem., 2020, 59, 11514–11527.
55. N. Spiller, R. Bjornsson, S. DeBeer and F. Neese, Carbon Monoxide Binding to the Iron-Molybdenum Cofactor of Nitrogenase: a Detailed Quantum Mechanics/Molecular Mechanics Investigation, Inorg. Chem., 2021, 60, 18031–18047.
56. B. Benediktsson and R. Bjornsson, Analysis of the Geometric and Electronic Structure of Spin-Coupled Iron-Sulfur Dimers with Broken-Symmetry DFT: Implications for FeMoco, J. Chem. Theory Comput., 2022, 18, 1437–1457.
57. T. V. Harris and R. K. Szilagyi, Comparative Assessment of the Composition and Charge State of Nitrogenase FeMo-Cofactor, Inorg. Chem., 2011, 50, 4811–4824.
58. L. Cao, O. Caldararu and U. Ryde, Protonation States of Homocitrate and Nearby Residues in Nitrogenase Studied by Computational Methods and Quantum Refinement, J. Phys. Chem. B, 2017, 121, 8242–8262.
59. T. Lovell, J. Li, T. Liu, D. A. Case and L. Noodleman, FeMo Cofactor of Nitrogenase:  A Density Functional Study of States MN, MOX, MR, and MI, J. Am. Chem. Soc., 2001, 123, 12392–12410.
60. T. Lovell, R. A. Torres, W.-G. Han, T. Liu, D. A. Case and L. Noodleman, Metal Substitution in the Active Site of Nitrogenase MFe7S9 (M = Mo⁴⁺, V³⁺, Fe³⁺), Inorg. Chem., 2002, 41, 5744–5753.
61. ASH - a multiscale modelling program, Version 0.9; Ragnar Bjornsson, 2022.
62. P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L. P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, OpenMM 7: Rapid development of high performance algorithms for molecular dynamics, PLoS Comput. Biol., 2017, 13, e1005659.
63. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
64. R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. Mackerell, Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone phi, psi and side-chain chi(1) and chi(2) dihedral angles, J. Chem. Theory Comput., 2012, 8, 3257–3273.
65. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, QUASI: A general purpose implementation of the QM/MM approach and its application to problems in catalysis, J. Mol. Struct. THEOCHEM, 2003, 632, 1–28.
66. L.-P. Wang and C. Song, Geometry optimization made simple with translation and rotation coordinates, J. Chem. Phys., 2016, 144, 214108.
67. S. R. Billeter, A. J. Turner and W. Thiel, Linear scaling geometry optimisation and transition state search in hybrid delocalised internal coordinates, Phys. Chem. Chem. Phys., 2000, 2, 2177–2186.
68. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and Numerically Efficient r(2)SCAN Meta-Generalized Gradient Approximation, J. Phys. Chem. Lett., 2020, 11, 8208–8215.
69. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta--Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401.
70. Y. Zhao and D. G. Truhlar, A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions, J. Chem. Phys., 2006, 125, 194101.
71. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
72. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
73. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
74. M. Reiher, O. Salomon and B. Artur Hess, Reparameterization of hybrid functionals based on energy differences of states of different multiplicity, Theor. Chem. Acc., 2001, 107, 48–55.
75. O. Salomon, M. Reiher and B. A. Hess, Assertion and validation of the performance of the B3LYP functional for the first transition metal row and the G2 test set, J. Chem. Phys., 2002, 117, 4729–4737.
76. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
77. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
78. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
79. C. van Wüllen, Molecular density functional calculations in the regular relativistic approximation: Method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations, J. Chem. Phys., 1998, 109, 392–399.
80. E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112.
81. S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, r(2)SCAN-D4: Dispersion corrected meta-generalized gradient approximation for general chemical applications, J. Chem. Phys., 2021, 154, 061101.
82. F. Neese, An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix, J. Comput. Chem., 2003, 24, 1740–1747.
83. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
84. D. A. Pantazis and F. Neese, All-electron scalar relativistic basis sets for the 6p elements, Theor. Chem. Acc., 2012, 131.
85. D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4, 908–919.
86. J. D. Rolfes, F. Neese and D. A. Pantazis, All-electron scalar relativistic basis sets for the elements Rb-Xe, J. Comput. Chem., 2020, 41, 1842–1849.
87. F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chem. Acc., 1977, 44, 129–138.
88. R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833–1840.
89. H. Li and J. H. Jensen, Partial Hessian vibrational analysis: the localization of the molecular vibrational energy and entropy, Theor. Chem. Acc., 2002, 107, 211–219.
90. J. Pipek and P. G. Mezey, A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions, J. Chem. Phys., 1989, 90, 4916–4926.
91. L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Electron transfer in nitrogenase catalysis, Curr. Opin. Chem. Biol., 2012, 16, 19–25.
92. B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, Nitrogenase: A Draft Mechanism, Acc. Chem. Res., 2013, 46, 587–595.
93. I. Dance, Misconception of reductive elimination of H2, in the context of the mechanism of nitrogenase, Dalton Trans., 2015, 44, 9027–9037.
94. P. E. Siegbahn, Model Calculations Suggest that the Central Carbon in the FeMo-Cofactor of Nitrogenase Becomes Protonated in the Process of Nitrogen Fixation, J. Am. Chem. Soc., 2016, 138, 10485–10495.
95. I. Dance, New insights into the reaction capabilities of His(195) adjacent to the active site of nitrogenase, J. Inorg. Biochem., 2017, 169, 32–43.
96. L. Cao and U. Ryde, Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase, Int. J. Quantum Chem., 2018, 118, e25627.
97. I. Dance, What is the role of the isolated small water pool near FeMo-co, the active site of nitrogenase?, FEBS J., 2018, 285, 2972–2986.
98. P. E. M. Siegbahn, Is there computational support for an unprotonated carbon in the E(4) state of nitrogenase?, J. Comput. Chem., 2018, 39, 743–747.
99. W. J. Wei and P. E. M. Siegbahn, The active E4 structure of nitrogenase studied with different DFT functionals, J. Comput. Chem., 2021, 42, 81–85.
100. B. M. Barney, R. Y. Igarashi, P. C. Dos Santos, D. R. Dean and L. C. Seefeldt, Substrate interaction at an iron-sulfur face of the FeMo-cofactor during nitrogenase catalysis, J. Biol. Chem., 2004, 279, 53621–53624.
101. R. Sarma, B. M. Barney, S. Keable, D. R. Dean, L. C. Seefeldt and J. W. Peters, Insights into substrate binding at FeMo-cofactor in nitrogenase from the structure of an alpha-70(Ile) MoFe protein variant, J. Inorg. Biochem., 2010, 104, 385–389.
102. T. Spatzal, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Ligand binding to the FeMo-cofactor: Structures of CO-bound and reactivated nitrogenase, Science, 2014, 345, 1620.
103. D. Sippel, M. Rohde, J. Netzer, C. Trncik, J. Gies, K. Grunau, I. Djurdjevic, L. Decamps, S. L. A. Andrade and O. Einsle, A bound reaction intermediate sheds light on the mechanism of nitrogenase, Science, 2018, 359, 1484.
104. W. Kang, C. Lee Chi, J. Jasniewski Andrew, W. Ribbe Markus and Y. Hu, Structural evidence for a dynamic metallocofactor during N2 reduction by Mo-nitrogenase, Science, 2020, 368, 1381–1385.
105. K. L. Skubi and P. L. Holland, So Close, yet Sulfur Away: Opening the Nitrogenase Cofactor Structure Creates a Binding Site, Biochemistry, 2018, 57, 3540–3541.
106. T. M. Buscagan and D. C. Rees, Rethinking the Nitrogenase Mechanism: Activating the Active Site, Joule, 2019, 3, 2662–2678.
107. J. W. Peters, O. Einsle, D. R. Dean, S. DeBeer, B. M. Hoffman, P. L. Holland and L. C. Seefeldt, Comment on Structural evidence for a dynamic metallocofactor during N2 reduction by Mo-nitrogenase, Science, 2021, 371, eabe5481.
108. W. Kang, C. C. Lee, A. J. Jasniewski, M. W. Ribbe and Y. Hu, Response to Comment on Structural evidence for a dynamic metallocofactor during N2 reduction by Mo-nitrogenase, Science, 2021, 371, eabe5856.
109. J. Bergmann, E. Oksanen and U. Ryde, Critical evaluation of a crystal structure of nitrogenase with bound N2 ligands, J. Biol. Inorg. Chem., 2021, 26, 341–353.
110. L. Cao and U. Ryde, Extremely large differences in DFT energies for nitrogenase models, Phys. Chem. Chem. Phys., 2019, 21, 2480–2488.
111. C. Martin-Fernandez and J. N. Harvey, On the Use of Normalized Metrics for Density Sensitivity Analysis in DFT, J. Phys. Chem. A, 2021, 125, 4639–4652.
112. D. A. Lukoyanov, Z. Y. Yang, A. Perez-Gonzalez, S. Raugei, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, 13)C ENDOR Characterization of the Central Carbon within the Nitrogenase Catalytic Cofactor Indicates That the CFe6 Core Is a Stabilizing “Heart of Steel”, J. Am. Chem. Soc., 2022, 144, 18315–18328.
113. S. F. McWilliams, B. Q. Mercado, K. C. MacLeod, M. S. Fataftah, M. Tarrago, X. Wang, E. Bill, S. Ye and P. L. Holland, Dynamic effects on ligand field from rapid hydride motion in an iron(ii) dimer with an S = 3 ground state, Chem. Sci., 2023, 14, 2303–2312.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information on QM-regions, electronic structure analysis, orbitals, geometries, broken-symmetry states, relative energies. Coordinates of QM-regions included as a ZIP-archive of XYZ-files. See DOI: https://doi.org/10.1039/d3cp01106b

---