Anomalous π-backbonding in complexes between B(SiR₃)₃ and N₂: catalytic activation and breaking of scaling relations

Abstract

Chemical transformations of molecular nitrogen (N₂), including the nitrogen reduction reaction (NRR), are difficult to catalyze because of the weak Lewis basicity of N₂. In this study, it is shown that Lewis acids of the types B(SiR₃)₃ and B(GeR₃)₃ bind N₂ and CO with anomalously short and strong B–N or B–C bonds. B(SiH₃)₃·N₂ has a B–N bond length of 1.48 Å and a complexation enthalpy of −15.9 kcal mol⁻¹ at the M06-2X/jun-cc-pVTZ level. The selective binding enhancement of N₂ and CO is due to π-backbonding from Lewis acid to Lewis base, as demonstrated by orbital analysis and density difference plots. The π-backbonding is found to be a consequence of constructive orbital interactions between the diffuse and highly polarizable B–Si and B–Ge bond regions and the π and π* orbitals of N₂. This interaction is strengthened by electron donating substituents on Si or Ge. The π-backbonding interaction is predicted to activate N₂ for chemical transformation and reduction, as it decreases the electron density and increases the length of the N–N bond. The binding of N₂ and CO by the B(SiR₃)₃ and B(GeR₃)₃ types of Lewis acids also has a strong σ-bonding contribution. The relatively high σ-bond strength is connected to the highly positive surface electrostatic potential [V_S(r)] above the B atom in the tetragonal binding conformation, but the σ-bonding also has a significant coordinate covalent (dative) contribution. Electron withdrawing substituents increase the potential and the σ-bond strength, but favor the binding of regular Lewis acids, such as NH₃ and F⁻, more strongly than binding of N₂ and CO. Molecules of the types B(SiR₃)₃ and B(GeR₃)₃ are chemically labile and difficult to synthesize. Heterogenous catalysts with the wanted B(Si–)₃ or B(Ge–)₃ bonding motif may be prepared by boron doping of nanostructured silicon or germanium compounds. B-doped and hydrogenated silicene is found to have promising properties as catalyst for the electrochemical NRR.

---

Introduction

Nitrogen in its elemental formal is highly inert due to the very strong chemical bond of the nitrogen molecule. The high bond energy of the nitrogen triple bond in connection with the relatively modest bond energies of single and double bonds involving nitrogen transforms to high kinetic barriers for utilizing molecular nitrogen in chemical transformations. An important example is the Haber–Bosch process for converting nitrogen and hydrogen gas to ammonia, which relies on high temperature and pressure in combination with transition-metal catalysis. Nature also depend on transition-metal catalysis for nitrogen reduction, but the nitrogenase enzymes manage the task at ambient conditions due to a more advanced catalytic machinery.^1,2

The development of efficient catalysts for nitrogen reduction has been hampered by the weak Lewis basicity of N₂. Traditional Lewis acids, such as the boron trihalides, do not form donor–acceptor complexes with N₂. Very strong Lewis acids, such as B(CF₃)₃, bind N₂ but are too reactive to be useful in catalysis. To avoid catalyst inhibition, chemical activation of N₂ requires Lewis acids that preferentially binds N₂ with binding energies that are stronger or at least on par with the binding energies for other Lewis bases that may be present. In the terminology of theoretical catalysis, N₂ binding needs to break scaling relations for binding energies. In particular for electrochemical nitrogen reduction, the binding of N₂ has to be competitive with the binding and reduction of protons to avoid inhibition of the catalyst by hydrogen atoms.³

A number of transition metal compounds have been developed that can bind and catalytically activate N₂.^4–10 Their function has largely been attributed to the presence of low lying d-orbitals that allow for the concurrent acceptance of electron density from the N₂ σ orbital and π-backdonation towards the N₂ π* orbital. The CO molecule is isoelectronic to N₂ but a stronger Lewis acid and its catalytical activation follows a similar protocol.

Main group chemistry has been less successful in nitrogen activation, but recent studies have demonstrated fixation and reduction of N₂ by some novel hypovalent borylene compounds.^11,12 These are argued to work by a similar mechanism as the transition metal catalysts, with N₂ σ-donation into an empty sp²-hybrid orbital and π-backdonation from a fully occupied p-orbital on boron. However, it should be noted that N₂ is bound to one borylene unit B at each end and thereby a delocalized π-system similar to that of a conjugated hydrocarbon is formed.

In an attempt to characterize the N₂ binding properties of trivalent boron Lewis acids, we observed an unexpected behavior upon replacing carbon for silicon as the atom bonded to boron. Whereas B(CH₃)₃ does not bind N₂, B(SiH₃)₃ forms a complex with a very short and strong B–N bond. In Fig. 1, we show the geometries and complexation enthalpies of the complexes of B(SiH₃)₃ with N₂, NH₃ and CO, together with the same properties for the corresponding complexes of B(CF₃)₃. All values have been obtained at the DFT M06-2X/jun-cc-pVTZ level of theory, and for the B(SiH₃)₃ complexes we also compare with coupled cluster calculations with values in italics, i.e. CCSD/6-31G+(d,p) for geometries and CCSD(T)/jun-cc-pVTZ for energies.

Fig. 1 Structures optimized at the M06-2x/jun-cc-pVTZ level of theory of complexes between the Lewis acids B(SiH₃) and B(CF₃)₃ and the Lewis bases NH₃, N₂ and CO. Note the very short B–N bond length in the B(SiH₃)·N₂ complex and the strong binding, i.e. low complexation enthalpy (ΔH_Cmpl).

Beginning with the B(SiH₃)·N₂ complex, we find a very short B–N bond of 1.48 Å (1.53 Å). This is even shorter than the sum of the covalent single bond radii, which amounts to 1.56 Å.¹³ The formation of the complex results in slight increases in the B–Si and N–N bond lengths by 0.014 (0.003) and 0.012 (0.015) Å, respectively. The complexation enthalpy is −15.9 (−12.4) kcal mol⁻¹; it is congruent with a strong B–N bond but not as strong as could have been anticipated based upon the bond length.

Comparing the B(SiH₃)₃·N₂ complex to the B(SiH₃)₃·NH₃ complex, we find a considerably longer B–N bond of 1.64 Å (1.65 Å) but a stronger interaction with a complexation enthalpy of −35.2 (−34.1) kcal mol⁻¹ in the latter complex. Considering that NH₃ is a much stronger Lewis base than N₂, a much larger difference in the complexation enthalpy could have been expected. The formation of the B(SiH₃)·CO complex results in similar changes to the geometry as the formation of the B(SiH₃)₃·N₂ complex, but the B–N bond of the former is slightly longer than the B–C bond of 1.46 Å in the latter. The complexation enthalpy of −45.4 kcal mol⁻¹ is much more negative (i.e. lower) than for the N₂ complex, and despite CO being a significantly weaker Lewis base than NH₃, the CO-complex is stronger than the B(SiH₃)₃·NH₃ complex.

We continue with comparing the binding geometries and complexation enthalpies of the B(SiH₃)₃ complexes with those of the B(CF₃)₃ complexes. It should first be noted that B(CF₃)₃ is a very strong and chemically labile Lewis acid that only has been detected as a transient intermediate from thermal dissociation of B(CF₃)₃·CO.¹⁴ The complexation enthalpy of the B(CF₃)₃·N₂ complex is only slightly higher compared to the B(SiH₃)·N₂ complex, i.e. −14.7 vs. −15.9 kcal mol⁻¹, but the B–N bond is much longer in the former, i.e. 1.62 vs. 1.48 Å. On the other hand, B(CF₃)₃ forms a very strong complex with NH₃ with a complexation enthalpy of −61.2 kcal mol⁻¹, which is almost twice the strength of the interaction in the B(SiH₃)·NH₃ complex. However, the difference in B–N bond length compared to B(SiH₃)₃·NH₃ is relatively small with a bond length of 1.60 Å in B(CF₃)₃·NH₃. In contrast to B(SiH₃)₃, B(CF₃)₃ also forms a much stronger complex with NH₃ than with CO, and the bonding in B(CF₃)₃·CO is significantly weaker than in the B(SiH₃)·CO complex; although the B(CF₃)₃·CO bond is strong with a complexation enthalpy of −30.1 kcal mol⁻¹.

Summarizing the geometrical and energetics data of Fig. 1, it is indicated that B(CF₃)₃ binds all three Lewis bases with a similar mechanism and the variation in complexation enthalpy agrees with their relative Lewis basicities. B(SiH₃)₃ seems to bind NH₃ following a related mechanism, whereas the binding of N₂ and CO invokes an additional component to the binding that results in much shorter intramolecular bond lengths (B–N or B–C) and enhanced binding strengths.

The physical origin of the enhanced binding of N₂ and CO is nontrivial to deduce, but it is reasonable to anticipate a connection to the π-backbonding mechanism prevalent in transition metal compounds that activates N₂ and CO, and which has been indicated in the N₂ activating hypo-valent borylene compounds. In this study we attempt to investigate this hypothesis in greater detail but we also take a comprehensive perspective in analyzing the Lewis acid–base interactions for this type of compounds. Furthermore, we investigate the potential for optimizing the selectivity for N₂ binding and activation by means of chemical derivatization. Finally, we seek to identify nanostructured materials that are synthetically accessible and invoke the necessary chemical functionalities for use as electrocatalysts.

Methods and theoretical procedures

Structures of molecules and molecular complexes have been optimized at the M06-2X/jun-cc-pVTZ level of Kohn–Sham density functional theory. The M06-2X density functional is highly accurate for main-group chemistry, including non-covalent interactions, and it is parameterized to include short and mid-range London dispersion interactions.¹⁵ This functional has been shown produce highly accurate energetics for classical Lewis adducts, as well as frustrated Lewis pairs, with an average deviation of 0.6 kcal mol⁻¹ relative complete basis set extrapolated DLPNO-CCSD(T) energies.¹⁶ The jun-cc-pVTZ basis set is the cc-pVTZ basis set augmented with diffuse s, p, d functions on non-hydrogen atoms.¹⁷ The geometries and energies obtained with M06-2X have been compared with coupled cluster calculations at the CCSD(T)/jun-cc-pVTZ//CCSD/6-31G+(d,p) level of theory for selected systems. For comparison with periodic plane wave computations (vide infra), some computations have also been performed at the PBE/6-311+(2d,p) level of theory.

The Kohn–Sham DFT wavefunctions and electron densities obtained at the M06-2X/jun-cc-pVTZ level have been used to analyze the bonding and properties of the complexes and the interacting molecules. In particular, the canonical molecular orbitals and their energies have been used for the analysis of π-backdonation. The canonical molecular orbitals are generally very similar to the Dyson orbitals and can therefore in principle be considered physical observables.^18,19 Barends and coworkers have also argued that DFT orbitals are well suited for analyzing chemical bonding.¹⁸ Natural bond orbital analysis (NBO) have been performed for selected systems (as suggested by a referee).²⁰ NBOs are orbitals localized to bonds, lone pairs or Rydberg orbitals, and are obtained by a transformation of the the first-order reduced density matrix of the wavefunction. The NBOs are not physical observables, but the highly occupied NBOs can be considered a representation of the systems Lewis structure. The energy gain from backbonding, i.e. the transfer from highly occupied NBOs to low occupation NBOs corresponding to the π* orbitals on N₂, has been estimated using NBO second order perturbation theory. This procedure can be used to estimate intra-molecular charge transfer energies in molecular complexes, but generally produce charge transfer energies of much larger magnitude than other methods for energy decomposition analysis.^21,22

To characterize the capacity of the Lewis acids to supply electrons for π-backdonation, the average local ionization energy [Ī(r)] was computed on molecular surfaces defined by the 0.001 au electron density contour. The Ī(r) is rigorously defined by eqn (1) within generalized Kohn–Sham density functional theory.^23,24

where ε_i is the energy of orbital i, ρ_i(r) is the density of the orbital, and ρ(r) is the total electron density. According to Janak's theorem,²⁵ the negative values of the orbital energies can be considered approximations to the ionization energies, and Ī(r) can be interpreted as the average energy needed to ionize an electron at a point r in the space of a molecule or atom. Ī(r) is invariant to orbital rotation and is rigorously defined by the electron density (without orbitals) in terms of density functionals. Ī(r) can therefore be considered a physical observable.²⁶Ī(r) can also be calculated from correlated wavefunctions using energy orbitals or Dyson orbitals.²⁷ Surface Ī(r) [Ī_S(r)] has been demonstrated to be an effective tool for predicting local reactivity for electrophilic processes, such as electrophilic aromatic substitution reactions.²⁴ Minima in Ī_S(r) [Ī_S,min] reflect the positions most likely to donate electrons and thus most susceptible for electrophilic attack.

To characterize the π–holes of the Lewis acids and their capacities to participate in electrostatic interactions with Lewis bases, the surface electrostatic potential was computed at the same isodensity contour as in the Ī_S(r) computations. The V(r) is defined by,

where Z_A is the charge on nucleus A located at R_A, and ρ(r) is the electron density function. V(r) is a physical observable, and qV(r) corresponds to the electrostatic interaction energy for a positive or negative point charge (q) at different positions (r) in space. Surface maxima in V(r) [V_S,max] have been demonstrated to be efficient indicators of the most active positions for nucleophilic noncovalent interactions, such as halogen and hydrogen bond donating sites,²⁴ but also for characterizing interaction sites at Lewis acids, such as BCl₃ and BH₃.²⁸

All molecular DFT and ab initio computations have been performed using the Gaussian16 suite of programs.²⁹ The computations of Ī_S(r) and V_S(r) have been performed using the Hs95 program²⁴ of Tore Brinck and the ELF computations using the Topchem2 program.³⁰

Periodic DFT calculations using a plane-wave basis set and the PBE exchange–correlation functional have been used to analyze the binding of N₂ to boron-doped and hydrogen terminated silicene, as well as the electrocatalytic reaction nitrogen reduction reaction at the same surface. Structural optimizations, phonon frequency calculations and electronic property calculations were performed using the DFT implementation in VASP.³¹ PAW pseudopotential was applied to describe the ion–electron interaction. An energy cutoff of 400 eV was used for the plane-wave basis set. The dispersive interaction between the adsorbates and the substrate was included via the DFT-D3 scheme. All the structures were relaxed until the maximal force on the atoms was smaller than 0.02 eV Å⁻¹. Gaussian smearing with a width of 0.1 eV was used for all calculations. For boron doping we considered the silicene system. It is made from the polysilane, which is a layered structures of corrugated Si (111) planes having H-termination. The simulation cell had 17 Si, 17 H and 1 B. The Brillouin zone was sampled by 5 × 5 × 1 Monkhorst grid of k-points. A vacuum gap of 12 Å was used in the silicene simulations, as tests using longer vacuum gaps showed structures and energies to be close to converged at this size. This was further verified by applying a dipole correction to forces and energy, which gave a correction to the total energy of less than 10⁻⁶ eV for the silicene system with N₂ as adsorbate.

VASPsol was used to obtain energies in aqueous solution for vacuum optimized structures except for the gas phase molecules.³² The reaction free energies ΔG of NRR reaction steps were calculated at zero potential with respect to the standard hydrogen electrode (SHE) and at pH = 0 as ΔG = ΔE + ΔZPE − TΔS, where ΔE, ΔZPE, and ΔS are, respectively, the differences of the DFT-calculated total energy, ZPE, and entropy between reactants and products.

Projected density of states (PDOS) with resolution of atomic angular moment components were computed using VASP. A 9 × 9 × 1 Monkhorst grid of k-points and tighter cut-offs were used for the PDOS calulations of B-doped silicene. Vaspkit was used for post-processing of the data from the VASP PDOS-calculations.³³ The bands of B(SiH₃)₃·N₂ were identified with the corresponding orbitals as calculated at the PBE/6-311+G(2d,p) level. The basis set is nearly complete in the spd components for B, N and Si and should produce a charge density comparable to that obtained with the plane wave basis used in VASP.

Bader charges was computed from the VASP charge density with core charge correction using the Bader Charge Analysis code.³⁴ The size of the charge density grid used in VASP was increased until the charges converged. For comparison, charges using a number of schemes, i.e. Bader,³⁵ APT,³⁶ MK,³⁷ MBS,³⁸ NBO²⁰ and Hirshfeld³⁹ were computed at the PBE/6-311+G(2d,p) level using Gaussian16.

Results and discussion

Lewis acidities

It can first be noted that the interaction between a boron Lewis acid and a Lewis base is commonly labeled a π–hole interaction.^28,40,41 The term π–hole refers to the region of positive surface electrostatic above the interaction site on the B-atom due to an electron deficiency at that position. In contrast to a σ–hole, where the positive surface electrostatic potential can be traced to the shape of a bonding orbital, the label π–hole refers to the planar binding configuration of the interacting atom at the Lewis acid rather than the type of orbital that generate the electrostatic potential maximum. In the following discussion we will refrain from using the term π–hole bonding. One reason is that we find the term ambiguous, but more importantly because π–hole interactions have been described as dominantly electrostatic in nature.^28,41 As we will discuss later, there is an electrostatic contribution to the binding in all of the studied complexes; this contribution is more important in the binding of polar Lewis bases, such as NH₃, than for N₂ and CO, which are of low polarity and have a more unform electrostatic potential. Consequently, the anomalous bonding that we observe in the B(SiR₃)₃·N₂ and B(SiR₃)₃·CO complexes cannot be rationalized from electrostatic considerations.

To improve the understanding of the chemical mechanism and chemical requirements for selective binding of N₂ and CO, we have listed computed properties for a series of boron-based Lewis acids and their complexes with N₂, CO, NH₃ and F⁻ in Table 1. The complexation enthalpy of F⁻ is included because fluoride ion affinity has been used a general descriptor for assessing Lewis acidity.⁴² For comparison, we have also included some related Lewis acids with Al or Ga instead of B as the coordinating atom.

Table 1 Computed surface properties (V_S,max, Ī_S,min) of some selected boron and aluminum Lewis acids; NBO properties, B–N and Al–N bond lengths and complexation enthalpies (ΔH_Cmpl) for the Lewis acid complexes with N₂, NH₃, CO and F⁻

Lewis acid	V S,max (kcal mol^−1)
a Surface electrostatic potential maximum (VS,max) above the B or A atom. b V S,max of the Lewis acid in the geometry of the complex with N2. c Surface minimum of the average local ionization energy (ĪS,min) in the region above the Y–X (Y = B, Ge, Al, Ga; X = Si, Ge, C, Cl) bond, e.g. B–Si bond. Geometry of Lewis acid from its complex with N2. d NBO second order perturbation energy for the back-bonding interaction between the Y–X σ-orbitals and the N–N π* orbitals in NBO basis. e Occupation of the NBO N–N π* orbitals in the Lewis acid-N2 complex. f Intermolecular B–N (or Al–N, Ga–N) bond distance for the complex with N2. g Forms no stable complex with N2. h V S,max or ĪS,min for the geometry of the Lewis acid in its complex with NH3. i No ĪS,min above the B–H bond. ĪS(r) value above the B–H bond.
B(SiH3)3	32.9	54.3	11.47	48.0	0.31	1.477	−15.9	−35.2	−45.4	−98.5
B(Si(CH3)3)3	26.5	38.9	11.01	59.7	0.38	1.465	−19.5	−32.8	−50.6	−90.5
B(Si(SiH3)3)3	22.6	39.3	11.47	42.4	0.30	1.493	−10.1	−36.1	−38.3	−111.6
B(Si(OH)3)3	41.3	60.2	11.34	50.3	0.28	1.479	−24.9	−54.4	−54.7	−107.8
B(SiF3)3	74.0	100.7	13.92	43.0	0.22	1.505	−23.9	−56.6	−52.0	−137.5
B(GeH3)3	33.3	51.8	11.29	47.3	0.34	1.474	−16.4	−35.8	−46.5	−102.7
B(Ge(CH3)3)3	27.0	38.7	10.68	57.5	0.40	1.460	−21.0	−34.4	−52.4	−96.4
B(CH3)3	18.4	(46.0)^g^h	(12.84)^g^h	—^g	—^g	—^g	—^g	−13.9	−1.9	−61.1
B(CF3)3	76.6	111.7	17.43	10.9	0.06	1.622	−14.7	−61.2	−30.1	−139.2
B(CN)3	64.0	88.4	13.70	5.8	0.03	1.779	0.2	−45.9	−13.6	−134.0
BCl3	27.1	(56.6)^g^h	—^g	—^g	—^g	—^g	—^g	−25.5	4.0	−100.1
BH3	40.7	64.2	(13.0)^i	28.4	0.14	1.594	−5.0	−27.5	−25.3	−68.5
Al(SiH3)3	58.0	66.2	10.67	6.0	0.04	2.252	−5.2	−28.9	−13.0	−110.0
Al(CF3)3	108.4	122.1	14.95	2.4	0.02	2.157	−13.0	−50.3	−19.0	−144.3
AlCl3	71.0	90.4	12.08	0.0	0.02	2.223	−5.8	−38.3	−11.1	−121.6
GaCl3	64.0	72.9	12.16	0.6	0.01	2.488	−3.9	−33.1	−8.2	−107.8

---

First of all, we note that the suspected π-backbonding behavior that we found in complexes of B(SiH₃)₃ with N₂ and CO seems to be confined to compounds where a central boron atom is bonded to Si or Ge. Only for the B(SiR₃)₃ and the B(GeR₃)₃ compounds do we observe the very short intramolecular B–N or B–C bonds, and the enhanced binding strengths for N₂ and CO in comparison with binding strengths for NH₃ and F⁻. Substituting B for Al, or Si for C, H or Cl increase the bond length and the complexation enthalpy. In particular, B(CH₃)₃ or BCl₃ does not form a stable complex with N.

Orbital analysis of π-backbonding

It is not obvious why a compound of the type B(SiR₃)₃ or B(GeR₃)₃ should participate in π-backbonding as there are no occupied lone-pair p-orbitals on B in these compounds that can interact with the π*-orbitals of N₂ or CO. However, an analysis of the occupied orbitals of B(SiH₃) in a distorted pyramidal geometry corresponding to that in B(SiH₃)₃·N₂ shows that the two degenerate orbitals 18 and 19 as well as the degenerate HOMOs have the proper symmetry to interact with the π and π* orbitals of N₂ or CO. The first orbitals (18,19) have very little density on the B and thus would overlap only weakly with the π-type orbitals. On the other hand the orbital energy of 18 and 19 (−16.5 eV) is similar to the π orbitals (−14.8 eV) and that should favor a constructive interaction.

The HOMOs (27, 28) have a shape and extension that should enable a good overlap with the π and π* orbitals of N₂. On the other hand, the HOMO energy (−8.8 eV) is intermediate between the π energy (−14.8 eV) and the π* energy (0.8 eV), and thus we do not expect a strong interaction with either of these. Overall, the interaction of the two sets of degenerate orbitals of B(SiH₃)₃ with the π and π* orbitals of N₂ will generate four set of degenerate orbitals, eight orbitals in total, where the six orbitals of lowest energy are likely to be occupied.

Investigating the occupied orbitals of B(SiH₃)₃·N₂, we indeed find three sets of degenerate orbitals that are occupied and consistent with such an interaction, as shown in Fig. 2. The first two of these orbitals, i.e. number 22 and 23 with an energy of −16.9 eV, are strongly π bonding between B and N. These orbitals have large contributions from 18 or 19 on B(SiH₃)₃ and the π orbitals on N₂, but also a smaller contribution from one of the HOMOs that enhances the B–N π-bonding. The orbital energy (−16.9 eV) is slightly lower than orbital energy (−16.5 eV) of 18 and 19 in B(SiH₃)₃. The second type of orbital (25, 26) have contributions from the same orbitals as in 22 and 23, but is clearly non-bonding between B and N and the orbital energy (−15.9 eV) is slightly higher. Thus, the bonding 22, 23 together with the non-bonding 25, 26 will result in a significant π-bonding contribution to the B–N interaction.

Fig. 2 The top row to the left shows the molecular orbitals of B(SiH₃)₃ that have the correct symmetry for interaction with the π and π* orbitals of N₂. The bottom row shows the molecular orbitals of B(SiH₃)₃·N₂ that are formed due to these interactions. Note that orbitals 22, 23 contribute strongly and 34, 35 weakly to the π-bonding of the complex. Orbitals 25, 26 are non-bonding in this respect.

The third set of orbitals is the HOMOs, i.e. number 34 and 35 with an energy of −8.8 eV. These orbitals have a very similar shape and energy as the HOMOs of bare B(SiH₃)₃, but the orbitals of the complex have an additional contribution that can be expressed as a linear combination of the N₂ π and π* orbitals, or more exactly as a very small in phase contribution from p(π) on N₍₁₎ in the B–N₍₁₎–N₍₂₎ sequence and a somewhat larger out of phase contribution of p(π) on N₍₂₎. At first glance, it may seem the HOMOs of B(SiH₃)₃·N₂ are nonbonding with respect to B–N but a closer inspection shows that they have a slight bonding character due to the shape of the contributing HOMO of B(SiH₃)₃, which extends over the B–N bond region, and the sign (in phase) of the p(π) on N₍₁₎. The change in sign of the wavefunction between the N also means that the orbital weakens the N–N π-bond and the larger contribution from p(π) on N₍₂₎ shifts electron density towards N₍₂₎.

The fourth set of degenerate orbitals is the LUMOs of B(SiH₃)·N₂, they are essentially identical in shape and energy to the π* orbitals of N₂ and only have a minor contribution from the B(SiH₃) orbitals. These orbitals may be important for photochemical activation of B(SiH₃)·N₂ or could become partly occupied upon reduction of the complex.

Summarizing our findings we note that the B–N π-bonding characters of orbitals 22,23,34 and 35 are strengthened by reduction of the B–N distance thereby explaining the very short B–N distance in B(SiH₃)·N₂. For comparison, we have analyzed the occupied orbitals of the B(CF₃)₃·N₂ complex, and in this complex there is no orbital that has a significant π-bonding character between the B and N. The much higher importance of π-backbonding in B(SiH₃)·N₂ compared to B(CF₃)₃·N₂ is in agreement with the results of the NBO analysis. The sum of charge transfer energies from the B–Si σ bond-orbitals to the N–N π* orbitals (ΔE_σπ*) in B(SiH₃)·N₂ is 48 kcal mol⁻¹, whereas the corresponding charge transfer from the B–C sigma bond-orbitals results in a stabilization by 11 kcal mol⁻¹ (positive energy means stabilization). The second order perturbation theory procedure of NBO is known to overestimate charge-transfer energies,^21,22 but it is expected to give approximately the right trend between different molecular complexes. The occupancy of the N–N π* orbitals (occ_N2π*) is also in agreement with a much higher degree of π-backbonding in B(SiH₃)·N₂ compared to B(CF₃)₃·N₂, 0.31 versus 0.06 electrons in total over the two π* orbitals.

As indicated by the canonical molecular orbitals of Fig. 2 the π-bonding interaction in B(SiH₃)₃·N₂ is different from the classical picture of π-backbonding as a donation of electrons from occupied d-orbitals or p-orbitals into the antibonding π* orbitals of N₂. However, as discussed by Pettersson and Nilsson, the classical picture is simplified and it is not representative for the π-backbonding of transition metal surfaces with N₂ or CO.⁴³ Instead the orbitals responsible for the π bonding to the ligand on those surfaces resemble the orbitals of Fig. 2 that provides the π bonding in B(SiH₃)₃·N₂, i.e. orbitals similar to 22 and 23 of B(SiH₃)₃·N₂. It is important to remember that all orbitals have to be orthogonal; this restricts their potential shapes and symmetries, and the classical picture of π-backbonding as a simple electron donation of into π* orbitals is not consistent with the orthogonality requirement.

Assessing π-backdonation

Caution should be taken when interpreting the bonding between certain atoms in a molecule based on a few orbitals, as the canonical orbitals typically are complex and delocalized; it is the combination of all occupied orbitals that gives the total electron density and determines the bonding in the molecule. Accordingly, we find that the surface average local ionization energy [Ī_S(r)] is a better descriptor than the density or energy of any individual orbital, e.g. the HOMO, of the Lewis acid to estimate the capacity for π-bonding interaction with the π and orbitals of N₂. Ī_S(r) can be defined as a functional of the total electron density and is invariant to orbital rotation.²⁴ The positions with the lowest Ī_S(r), the Ī_S,min, are the positions from which electrons are most easily removed or donated, and the values of the Ī_S,min are indicative of the average electron binding energy at those positions.

As shown in Fig. 3, B(Si(CH₃)₃)₃ has a ring shaped area of low Ī_S(r) above the B–Si bond region (with Ī_S,_min directly above the bonds) where there is a π-bonding interaction with N₂ in B(Si(CH₃)₃)₃·N₂. Similar Ī_S,min are found in all the compounds of the types B(SiR₃)₃ and B(GeR₃)₃ that form short and strong π-type bonds with N₂ and CO, as well as in B(CH₃)₃, which forms a π-type bond with CO but not N₂. The Ī_S,min value increases with the substituent on B in the order, Ge(CH₃)₃ > Si(CH₃)₃ > GeH₃ > Si(OH)₃ > SiH₃ ≈ Si(SiH₃)₃ ≫ SiF₃ which seems to reflect the decreasing π-bond donating capacity, as the B–N bond length increases in approximately the same order, with B(Ge(CH₃)₃)₃·N₂ having the shortest bond (1.46 Å) and the B(SiF₃)₃·N₂ the longest bond (1.51 Å). Inductive donors, such as CH₃, are expected to donate electrons into the B–Si (or B–Ge) bond and strengthen the π-bond with N₂, whereas inductive acceptors, particularly F, withdraw electron from the B–Si or B–Ge bond and weaken the B–N π-bond.

Fig. 3 The left part of the figure shows the average local ionization energy [Ī_S(r)] depicted on the 0.001 au isodensity surface of B(Si(CH₃)₃)₃. Note that the regions with the lowest Ī_S(r) (dark blue) are located along B–Si bond where the π-backdonation takes place. The value of the Ī_S,min is found to reflect the π-backbonding strength in complexes between B(SiR₃)₃ or B(GeR₃)₃ and N₂. The right part of the figure shows the electrostatic potential [V_S(r)] on the same surface. Note the highly positive maximum (V_S,max) in V_S(r) over the central B atom. The magnitude of the V_S,max reflects the strength of the σ-bonding in interactions with Lewis bases, and it significantly increases in the pyramidal (tetragonal) binding conformation. The geometry of B(Si(CH₃)₃)₃ corresponds to its geometry in the complex with N₂.

It is important to remember that there is both a σ and π contribution to the bonding of N₂ and CO, and that inductive acceptors strengthen the σ-bond. Thus, there is no simple correlation between the strength of the π-bond, as indicated by the B–N bond length or Ī_S,min, and the complexation enthalpy. When it comes to B(CH₃)₃, it does not bind N₂ and binds CO only weakly; this is partly a consequence of a weaker σ-bond than in B(SiH₃)₃, but primarily due to a weaker π-bond, as indicated by a higher Ī_S,min, 12.89 eV as compared to 11.53 eV for B(SiH₃)₃. In contrast to B(CH₃)₃, BH₃ binds N₂, but weakly, due to a much stronger σ-bond interaction, as indicated by a highly positive V_S,max (vide infra), together with a significant π-bond interaction as shown by the relatively low Ī_S(r) (13.0 eV) in the π-bonding region of the Lewis acid.

Interestingly, we find that the NBO analysis, in terms of the second order charge transfer energy (ΔE_σπ*) between the B–Si σ-orbitals and the N–N π*-orbitals as well as the occupation of the latter (occ_N2π*), shows a very similar trend as the Ī_S,min value on the varying importance of π-backbonding among the boron Lewis acids (see Table 1). In particular, the strength of the π-backbonding as indicated by the Ī_S,min value follows exactly the same ordering as occ_N2π* among all of the B(SiR₃)₃ and B(GeR₃)₃ Lewis acids taken together. In contrast to occ_N2π* and particularly compared to Ī_S,min, ΔE_σπ* indicates a much higher relative importance of π-backbonding for the fluorinated boron acids, i.e. B(SiF₃)₃ and B(CF₃)₃. First, as has been found in earlier studies, the second order perturbation theory expression in NBO overestimates the charge transfer energy in molecular complexes.^21,22 In fact, we find that ΔE_σπ* for many complexes is much larger in magnitude than the total complexation enthalpy despite that the latter also has a significant σ-bonding contribution. Analyzing the contributions to ΔE_σπ* in more detail, we note that it is the numerator term, i.e. the Fock matrix elements, that varies the most and largely determines the variation in ΔE_σπ*. This term is highly dependent on the overlap of the interacting σ and π* orbitals, and consequently its magnitude depends on the B–N distance. Thus, it can be expected that the magnitude of ΔE_σπ* at least partly depends on the strength of σ-bonding.

Density difference maps

To better understand the bonding interactions of B(SiH₃)₃, we have computed the density difference (DD) maps for the complexes with N₂, NH₃ and F⁻, see Fig. 4. For comparison, we have also included the DD for the B(CF₃)₃·N₂ complex. The overall shapes of the DD are all rather similar, with a buildup of electron density above and below the B nucleus with a shape that is intermediate between a p and a sp3 orbital. Thus, in all the complexes there is an accumulation of electron density in the B–N bond region; for the DD of B(SiH₃)₃·N₂, the upper part is wider than in the other complexes consistent with a partial B–N π-bond.

Fig. 4 Density difference (DD) plots computed for Lewis complexes of B(SiH₃)₃ and B(CF₃)₃. Each DD map is computed in a plane defined by N, B and the right Si (or C). Regions with a positive deformation density upon complexation are colored green-yellow-red with increasing density in that order. Regions of negative DD are correspondingly colored green-cyan-blue. Each solid contour line corresponds to an increase or decrease in the value of the DD with 0.01 au. Note the buildup of electron density in the B–N bond region for all complexes.

On the other hand, the donut shaped depletion of electron density above the B–Si bond region should not be seen as the result of donation of electron density into the π-bond, as the corresponding depletion is slightly bigger for B(SiH₃)₃·NH₃ and much bigger for B(SiH₃)₃·F⁻. Instead we interpret this depletion as the results of a polarization of electron density from the B–Si bond region towards the region below the B resulting from the interaction with the lone pair of N₂. The depletion in B(SiH₃)₃·F⁻ is bigger and more diffuse, as F⁻ carries a full negative charge and the distribution of negative charge is not as localized as in the lone pairs of N₂ and NH₃.

An important observation from the DD of B(SiH₃)₃·N₂ is that there is a density depletion in the N–N bond region; this indicates that the B(SiR₃)₃ compounds not only binds N₂ strongly, but also weakens the N–N bond. The weakening of the N–N bond together with the buildup of π density at the outer nitrogen (N₍₂₎) activates the molecule for chemical transformation.

Comparing the DDs of the B(SiH₃)₃·N₂ and B(CF₃)₃·N₂ and reveals interesting information about the difference in bonding and reductive activation between these complexes. The overall pictures are rather similar, but there is much smaller depletion above the B–C bond region in B(CF₃)₃·N₂ compared to the B–Si region of B(SiH₃)₃·N₂; this difference is consistent with the B–Si bond density being more diffuse and polarizable and with the electron withdrawing effect of the CF₃ group. There is also a considerable difference between the N₂ π-regions of the two complexes. In both complexes there is a buildup of π-density at N₍₁₎, the N closest to the B, which can be viewed as the result of a polarization of N₂ π-density due to the high positive electrostatic potential on B. In B(SiH₃)₃·N₂, there is additionally a small buildup of electron density at the N₍₂₎, and we interpret it as the result of the π-bonding character of the interaction and the contribution to the density from the HOMOs, which have a significant p(π) contribution at N₍₂₎ (see Fig. 2). As already indicated, this build up may be important for the catalytic activation of N₂.

Electrostatic contribution to σ-bonding

Recent studies have shown that even strong donor–acceptor interactions, such as halogen and hydrogen bonds involving anionic soft Lewis bases (e.g. Br⁻), that traditionally are considered to have a significant charge transfer contribution often can be characterized and quantified by only considering electrostatics and polarization.^44,45 Here we will analyze the variation in σ-bond strength among the different complexes of Lewis acids and bases and argue that an electrostatic model can provide at least a semi-quantitative characterization of the σ-bonding.

Beginning with the B–Si compounds, their high Lewis acidities can partly be traced to a high surface electrostatic potential [V_S(r)] at the B, i.e. a high V_S,max value, see Fig. 3. The high V_S,max is not surprising considering that the B–Si Lewis bases are electron deficient at the B with an empty p-orbital as the LUMO. The value of the V_S,max increases further when the Lewis acid is distorted to the pyramidal geometry present in the complexes. In fact, the pyramidal V_S,max value (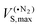 in Table 1) in many cases exceed 50 kcal mol⁻¹, which is much higher than the V_S,max of most neutral molecules except for the acidic hydrogens of strong hydrogen bond donors.

The Lewis acidity does not follow the V_S,max value strictly, e.g. N₂ binds stronger to B(Si(CH₃)₃)₃ than to B(SiH₃)₃ despite B(Si(CH₃)₃)₃ having a lower V_S,max. This behavior can be traced to the combination of a stronger π-bond and a stronger contribution from polarization in the N₂ interaction with B(Si(CH₃)₃)₃, i.e. the importance of polarization in B(Si(CH₃)₃)₃·N₂ is enhanced because of the very short B–N distance due to the π-bond interaction and the higher polarizability of CH₃ compared to H. The introduction of strongly electron-withdrawing substituents, such as CF₃, SiF₃ and CN, substantially increases the V_S,max value, and thus enhances the Lewis acidity. However, this effect is more important for the interactions with NH₃ and F⁻ than for interactions with N₂ and CO, as the electron-withdrawing substituents weaken the π-bond interaction. This is particularly evident for B(CN)₃, which is one of the strongest binders of NH₃ and F⁻, but it does not form stable complexes with N₂ and CO. The effect may be enhanced by the resonance withdrawing capacity of CN as CF₃ and SiF₃ are inductive electron acceptors.

To obtain a Lewis acid that preferentially binds N₂ and CO, substituents that donates electron density into the B–Si or B–Ge bond are preferred as these promote the formation of a π-bond with N₂ and CO. Somewhat surprisingly, we find that the detrimental effect of electron withdrawing substituents is bigger for CO binding compared to N₂ binding. Intuitively, this is not expected considering that CO by all measures have a stronger lone pair and thus should have a stronger electrostatic interaction with B. However, the π-bonding interaction seems to be more important for CO compared to N₂ and since the electron withdrawing substituents reduce the π-bonding, this effect takes precedence in the complexes with CO.

It is also interesting to note that there is stronger bonding of NH₃ to B(SiR₃)₃ and B(GeR₃)₃ compared to traditional boron based Lewis acids, e.g. B(CH₃)₃, BCl₃ and BH₃. Another anomaly is the similar complexation enthalpies of B(Si(OH)₃)₃ and B(SiF₃)₃ despite the much more positive V_S,max of the latter due to the electron withdrawing SiF₃ groups. These observations are consistent with previous reports that also NH₃ can participate in π-backbonding interactions.⁴⁶ In comparison, the fluoride affinity follows the V_S,max of the Lewis acid more closely indicating that the F⁻ interaction is dominated by electrostatics. However, due to the small size and negative charge of F⁻, also polarization plays an integral role and explains why B(CH₃)₃ and BH₃ binds F⁻ more weakly compared to the other Lewis acids. Because of the anomalously large importance of polarization and the generally very high binding strength, it can be argued that fluoride affinity is not a representative scale of general Lewis acidity. It should also be noted that boron Lewis acids generally form strong covalent bonds with F⁻.

We have also compared the boron based Lewis acids to some aluminum and gallium based Lewis acids with similar structures. Despite featuring very high V_S,max at Al or Ga, these Lewis acids bind N₂ and CO only weakly while being intermediate binders of NH₃ and strong binders of F⁻. The strongest Lewis acid of the Al-compounds is Al(CF₃)₃, and it has the highest V_S,max of all the non-charged Lewis acids that are investigated in this study. Accordingly it has the most negative F⁻ complexation enthalpy of the neutral Lewis acids, whereas the N₂ complexation enthalpy is relatively modest at −13.0 kcal mol⁻¹. We note that AlCl₃, in contrast to BCl₃, binds N₂ with a negative complexation enthalpy, but that the binding strength is reduced going to GaCl₃. In this context, it should be noted that all the Al and Ga based Lewis acids remain nearly planar around the central coordinating Al or Ga atom after coordination to N₂ and that the bonding distance is larger than the sum of the covalent radii.

Covalent character of σ-bonding

In contrast to the π-interactions, which have been analyzed in terms of orbital interactions, the σ-bonding contribution to the interactions of the boron based Lewis acids bases has so far been rationalized only in terms of electrostatics and polarization. This analysis has provided a mean for explaining the variations in the complexation enthalpy with respect to Lewis bases and the substituents on the Lewis acid. In this context, it is interesting to note that ELF-analysis, which has been shown to be a stringent tool for distinguishing between physical and covalent bonding,⁴⁷ does not provide a clear answer to whether the B–N bond is covalent or non-covalent (see Fig. S1, ESI†).

However, as pointed out by several researchers, it is more appropriate to consider a continous scale between covalent and non-covalent bonding.^28,48–51 Politzer et al. argue that the bonding in BCl₃·NH₃ is of significant coordinate covalent character based on the strength of the interaction, the relatively short B–N bond length, and the pyramidal structure of the BCl₃ in the complex.²⁸ Following the same type of reasoning, Grabowski found the B/Al–N bond length as well as the α-angle, i.e. the N-B–Cl angle in BCl₃·NH₃, to be good indicators of the covalent character of complexes of B and Al Lewis acids with nitrogen Lewis bases, i.e. NCH, NH₃, and N₂.⁵² The α-angle is expected to be close 110 degrees in a covalent complex, due to the transformation of the B- from a tetragonal (sp²) to a tetrahedral (sp³) conformation upon forming a covalent bond with the Lewis base. We have already noted that the B–N bond length is in the range of a single covalent bond, or shorter, in the complexes of B(SiR₃)₃ and B(GeR₃)₃ with N₂. The α-angle in the same complexes is in the range of 105.6–110.3 degrees (Table S1, ESI†) and thus indicates a significant covalent contribution to the bonding. However, it is difficult to estimate the covalent contribution to the σ-bonding as the both the B–N bond length and the α-angle are found to correlate with the strength of the B–N π-bond. Following similar arguments for the complexes with CO, we suggest that all the stable BR₃·N₂ and BR₃·CO complexes have some covalent character to the intermolecular interaction, but that the covalent σ-bonding character in many cases is relatively weak considering the significant π-contribution to the binding and the relatively low binding strength. The molecular orbitals that contribute most strongly to the covalent σ-bonding in B(SiH₃)₃·N₂ are depicted in Fig. 6.

In contrast, the Al and Ga based Lewis acids form complexes with N₂ (and CO) that have a relatively long Al–N or Ga–N bond and tetragonal structure, i.e. α-angle is in between 94.0 and 96.3 degrees. This indicates non-significant π-bonding and a reduced covalent character of the σ-bonding compared to the B compounds.

Realizing the B(Si–)₃ and B(Ge–)₃ bonding motifs

The B(SiR₃)₃ and B(GeR₃)₃ compounds are promising candidates for N₂ and CO activation because of their strong and selective binding of these Lewis bases. In addition, the π-bonding mechanism is likely to provide catalytic activation for chemical transformation, including nitrogen reduction. However, none of the Lewis acids of this category in Table 1 has yet been synthesized. To our knowledge, B(SiPh₃)₃ is the only molecule of this type that has been prepared.⁵³ We have made some preliminary calculations on B(SiPh₃)₃ and found it to bind N₂ relatively weakly with a complexation enthalpy of around −9 kcal mol⁻¹. The poor binding seems to be the consequence of a combination of electronic and steric crowding, and additionally there may be a kinetic barrier for binding due to steric shielding of the B atom by the phenyl groups in the free Lewis acid.

We hypothesize that it may be easier to prepare heterogenous catalysts with the favorable B(Si–)₃ or B(Ge–)₃ bonding motifs. Solid silicon and germanium have been prepared in the forms of crystals, 2-D materials and nanoparticles. This type of materials is commonly doped with boron to obtain semi-conductors. In particular for nanoparticles, it has been shown that the boron atoms accumulate at the surface, and a similar behavior is expected for larger particles and materials.^54,55 B-doped silicon nanoparticles have also been shown to be resistant against oxidation in air, which is an import property if they are to be used as electrocatalyst.⁵⁴

In Fig. 5 we show the DFT-PBE optimized structure of boron substituted and hydrogenated silicene, which is the silicon analog of graphene. As seen from the figure, this material has the advantage that the B(Si–)₃ unit has a pyramidal geometry already before binding N₂, and thus is preorganized to bind N₂. The B-doped H-silicene is a relatively strong N₂ binder and has a similar B–N bond length and N₂ binding energy as B(SiH₃)₃ when computed using the PBE functional. Assuming that the error due to the functional is similar for both compounds, we estimate a N₂ binding enthalpy close to −16 kcal mol⁻¹ for the B-doped and hydrogen terminated silicene.

Fig. 5 Periodic DFT calculations at the PBE level of boron-doped and hydrogen passivated silicene. The left part of the figure shows the simulation cell of the silicene from above the molecular plane, and the middle shows a side view. Note that the green B has a slightly pyramidal binding conformation. The right part shows the density difference (DD) map for the binding of N₂. Depleted density is in cyan whereas enhanced density in in yellow. Note the similar DD compared to B(SiH₃)₃·N₂ in Fig. 4.

We have also analyzed the projected density of states (PDOS) of B(SiH₃)₃·N₂ and compared with the PDOS of B-doped H-silicene with adsorbed N₂ [H-Silicene(B)·N₂]. In the PDOS plots (Fig. 6) of B(SiH₃)₃·N₂, the bands with large contributions from B and N are identified and the corresponding molecular orbitals are visualized. It is easily recognized that PDOS contributions are in agreement with the shape and extent of the orbitals, e.g. the backbonding π-orbitals 22, 23 have significant contributions not only from N and Si but also from B. On the other hand, orbitals 24, 25, which are non-bonding with respect to B–N have a negligible contribution from B. The HOMOs (34, 35), which we already have discussed as contributing to the π-backbonding, have almost equal contribution of B and Si, in agreement with the earlier observation that the π-backbonding is an interaction between the B–Si bond region and the N–N π-region. The LUMOs (37, 38) are nearly pure N₂ π* orbitals, which is supported by the very small PDOS contributions of B and Si. Similarly we see that the main B–N bonding σ-orbital (20) is an almost pure B–N orbital with a minor Si component in PDOS. Orbital 26 is also B–N σ-bonding but has a very limited contribution from B (and Si), and this is in agreement with a coordinate covalent character where the lone pair of N is shared with B. σ-orbital 27 is also B–N bonding with a negligible PDOS contribution from B, but this orbital is more delocalized with significant B–Si and Si–H bonding character. The major bands of σ and π-symmetry with respect to the N–N bond are found at similar relative energies and have similar contributions from N, B and Si in B(SiH₃)₃·N₂ and in H-Silicene(B)·N₂, and this indicates their electronic structures and bonding to be similar. However, the π-type orbitals (24, 25) and (34, 35), which have significant contributions from Si, have no highly similar counterparts in the silicene system and the B and N contributions are instead spread out over several bands in the corresponding energy regions. This is a consequence of H-Silicene(B) having a more delocalized electronic structure than B(SiH₃)₃.

Fig. 6 Projected density of states (PDOS) at the periodic PBE level for B(SiH₃)₃·N₂ (top) and N₂ adsorbed on B-doped and hydrogen terminated silicene (bottom). The PDOS analysis is divided into bands/orbitals of σ-symmetry (left) and π-symmetry (right) with respect to the N–N bond, i.e. B(s,p_z) and N(s,p_z) components for σ-symmetry and B(p_x,p_y) and N(p_x,p_y) components for π-symmetry. For Si all components (s,p,d) are included in both plots. In the plots for B(SiH₃)₃·N₂ the different bands with large B and N contributions are identified with the corresponding orbitals as obtained at the PBE/6-311+G(2d,p) level. The energies (in eV) are shifted so that the LUMO band is at 0 (zero) energy. In both systems the LUMO band is close to a pure N₂ π* orbital. In the top left plot, the band labeled 27 has almost equal size contributions from B and Si, but the latter is masked by the former. The same type effect is present for band 34, 35 in the top right plot.

In order to further elucidate the similarities and differences in the bonding of N₂ to B(SiH₃)₃ and to B doped H-silicene, we have also computed the Bader charges of the two systems. The computed charges of B(SiH₃)₃·N₂ are 2.3 (Si), −0.87 (B), −0.80 (N₍₁₎) 0.32 (N₍₂₎). The corresponding charges for H-Silicene(B)·N₂ are 0.92 (Si), −0.38 (B), −0.74 (N₍₁₎), 0.26 (N₍₂₎). Thus, the charge distributions are similar and both systems exhibit a large net electron transfer towards N₂ of 0.48 electrons. This indicates the σ-electron transfer from N₂ to B due to sharing of the N₍₁₎-lone pair (coordinate covalent bond) to be significantly smaller than the electron transfer due to π-backdonation. However, this result is contrasted by the small dipole moment of both systems, i.e. 0.25 D (0.05 e Å) and 0.01 D (0.002 e Å) for the molecular and silicene system, respectively. Atomic partial charges are not physical observables, and different partition schemes often give significantly different results. As the Bader method have been criticized for unphysical partioning between certain elements, e.g. hydrogen charges in hydrocarbons are often negative,⁵⁶ we decided to compare a variety of methods for calculating the charges of B(SiH₃)₃·N₂, see Table S2 (ESI†). In these calculations we used a large Gaussian basis set [6-311+G(2d,p)] together with the PBE functional to obtain a charge density for the charge calculation that is of comparable quality to that of the plane wave calculation. In addition, none of the charge derivation methods are directly dependent on the basis set. In contrast to the Bader charges, the other methods indicate a net electron transfer from N₂, and the total charge of N₂ varies in the range 0.03–0.21, e.g. 0.07 for NBO and 0.21 for the Merz–Kollman³⁷ electrostatic potential derived charge. A result common to all methods, including Bader, is that the charge on B is negative; it varies between −0.18 and −0.91. Thus, although the individual charges vary considerably, all methods support the interpretation that the bonding in these systems involves a σ-electron donation from N₂ towards the B that to some degree is balanced by π-backdonation from the B–Si bond region to N₂.

Preliminary calculations of the distal pathway for electroreduction to ammonia using the computational hydrogen electrode⁵⁷ indicate that the first reductive step (*N₂ → *N₂H) is rate-determining with a limiting potential close to 1.5 V, see Fig. 7. Moreover, the binding of N₂ is slightly favored over the binding of H, i.e. the first step of the competing hydrogen evolution reaction. This reduces the risk of the catalytic sites being inhibited by H-atoms, which is a common problem for transition metal catalysts. The computational results show that boron-doped silicon compounds have potential as catalysts for the NRR reaction but that further structural and chemical optimization will be necessary to afford a selective and highly efficient catalyst.

Fig. 7 Gibbs free energy diagram of nitrogen reduction reaction (distal mechanism, see Fig. S2, ESI†) catalyzed by boron-doped H-silicene and computed using the computational hydrogen electrode and periodic DFT at the PBE level with solvation correction.

Conclusions

Lewis acids of the types B(SiR₃)₃ and B(GeR₃)₃ are found to bind N₂ and CO with anomalously short and strong B–N or B–C bonds. The very short B–N bond in the complexes with N₂ is particularly remarkable considering that N₂ is a very weak Lewis acid. This selective binding enhancement is attributed to π-backbonding according to an analysis of the occupied orbitals in the complexes with N₂, and an analysis of the density differences associated with the formation of the complexes. However, the classical picture of π-backbonding as a donation into the unoccupied π* orbitals of N₂ is indicated to be a simplification. The π-bonding is a consequence of constructive orbital interactions between the diffuse and highly polarizable B–Si and B–Ge bond regions and the π and π* orbitals of N₂. The B–Si and B–Ge bond regions are characterized by a ring shaped area of low Ī_S(r) that has the Ī_S,_min directly above the bonds. The value of the Ī_S,_min reflects the π-bond strength in the complexes as Ī_S,_min follows the order of the B–N bond length, i.e. the shorter the bond, the lower the Ī_S,_min. The π-backbonding interaction is expected to activate the N₂ unit for chemical transformation and reduction since it decreases the electron density and increases the length of the N–N bond.

The binding of N₂ and CO by the B(SiR₃)₃ and B(GeR₃)₃ Lewis acids also has a strong σ-bond contribution. The relatively high σ-bond strength is largely connected to the high positive surface electrostatic potential [V_S(r)] above the B atom, the boron V_S,max. The magnitude of the V_S,max is further increased when the B–Si coordination becomes pyramidal upon interaction. Introduction of electron withdrawing R-substituents increases the V_S,max value and thereby the σ-bond strength, but also leads to a higher Ī_S,_min and reduced π-backbonding. Thus, such substituents increase the general Lewis basicity, but will favor the binding of regular Lewis acid such as NH₃ and F⁻ more strongly than the binding of N₂ and O₂. Another observation is that the boron based Lewis acids in contrast to Al-based Lewis acids generally have a significant coordinate covalent (dative) contribution to the σ-bonding, which is indicated by intermolecular B–X bonds that are significantly shorter than the sum of the van der Waals radii and pyramidal geometries around the central B atom in the complexes.

Our computational results for the B(SiR₃)₃ and B(GeR₃)₃ Lewis acids indicate that these types of molecules have the potential to catalyze the nitrogen reduction reaction. Unfortunately, they are highly reactive and difficult to synthesize. It may be easier to prepare heterogenous catalysts with the wanted B(Si–)₃ or B(Ge–)₃ bonding motif. Boron doped crystals, 2-D materials and nanoparticles may be prepared by regular synthesis techniques used for preparation of semiconductor materials. We have shown that such materials will have the B(Si–)₃ unit in a favorable bonding geometry for N₂ ligation. Preliminary calculations of electrochemical reduction of N₂ at boron-doped and hydrogenated silicene indicate potential for efficient catalysis but shows that further studies and optimization of chemical composition and nanostructure are needed.

Author contributions

Tore Brinck: conceptualization, data curation, formal analysis, methodology, investigation, and writing. Suman Kalyan Sahoo: data curation, formal analysis, methodology and investigation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Swedish Research Council (VR), grant number 2021-05881. Suman Kalyan Sahoo received a postdoctoral fellowship from Carl Tryggers Foundation. Computations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre in Linköping University (NSC) and the PDC Centre for High Performance Computing (PDC-HPC).

References

1. B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041–4062.
2. D. Sippel, M. Rohde, J. Netzer, C. Trncik, J. Gies, K. Grunau, I. Djurdjevic, L. Decamps, S. L. A. Andrade and O. Einsle, Science, 2018, 359, 1484–1489.
3. A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, ACS Catal., 2017, 7, 706–709.
4. B. A. MacKay and M. D. Fryzuk, Chem. Rev., 2004, 104, 385–401.
5. E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245.
6. M. D. Fryzuk, Chem. Commun., 2013, 49, 4866–4868.
7. H. Tanaka, Y. Nishibayashi and K. Yoshizawa, Acc. Chem. Res., 2016, 49, 987–995.
8. R. J. Burford, A. Yeo and M. D. Fryzuk, Coord. Chem. Rev., 2017, 334, 84–99.
9. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500.
10. Y. X. Lin, S. N. Zhang, Z. H. Xue, J. J. Zhang, H. Su, T. J. Zhao, G. Y. Zhai, X. H. Li, M. Antonietti and J. S. Chen, Nat. Commun., 2019, 10, 4380.
11. M. A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900.
12. M. A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329–1332.
13. P. Pyykkö, J. Phys. Chem. A, 2015, 119(11), 2326–2337.
14. I. B. Sivaev and V. I. Bregadze, Coord. Chem. Rev., 2014, 270, 75–88.
15. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
16. G. Bistoni, A. A. Auer and F. Neese, Chem. – Eur. J., 2017, 23, 865–873.
17. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034.
18. D. P. Chong, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2002, 116, 1760–1772.
19. M. Diaz-Tinoco, H. H. Corzo, F. Pawlowski and J. V. Ortiz, Mol. Phys., 2019, 117, 2275–2283.
20. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
21. A. J. Stone, J. Phys. Chem. A, 2017, 121, 1531–1534.
22. Y. Mao, Q. Ge, P. R. Horn and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 2401–2417.
23. P. Sjoberg, J. S. Murray, T. Brinck and P. Politzer, Can. J. Chem., 1990, 68, 1440–1443.
24. T. Brinck and J. H. Stenlid, Adv. Theory Simul., 2019, 2, 1800149.
25. J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165.
26. F. A. Bulat, M. Levy and P. Politzer, J. Phys. Chem. A, 2009, 113, 1384–1389.
27. S. V. Kohut, R. Cuevas-Saavedra and V. N. Staroverov, J. Chem. Phys., 2016, 145, 074113.
28. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2021, 23, 16458–16468.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Gaussian, Inc., Wallingford, CT, 2016.
30. D. Kozlowski and J. Pilme, J. Comp. Chem., 2011, 32, 3207–3217.
31. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
32. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
33. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
34. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
35. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
36. J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333–8336.
37. B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comp. Chem., 1990, 11, 431–439.
38. J. A. Montgomery, Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542.
39. F. L. Hirshfeld, Theoret. Chim. Acta, 1977, 44, 129–138.
40. S. J. Grabowski, Chem. Phys. Chem., 2015, 16, 1470–1479.
41. J. S. Murray and P. Politzer, Crystals, 2020, 10, 76.
42. P. Erdmann, J. Leitner, J. Schwarz and L. Greb, Chem. Phys. Chem., 2020, 21, 987–994.
43. L. G. M. Pettersson and A. Nilsson, Top. Catal., 2014, 57, 2–13.
44. T. Brinck and A. N. Borrfors, J. Mol. Model., 2019, 25, 125.
45. T. Brinck and A. N. Borrfors, J. Mol. Model., 2022, 28, 275.
46. G. M. Su, H. Wang, B. R. Barnett, J. R. Long, D. Prendergast and W. S. Drisdell, Chem. Sci., 2020, 12, 2156–2164.
47. K. Koumpouras and J. A. Larsson, J. Phys.: Condens. Matter, 2020, 32, 315502.
48. J. C. Slater, J. Chem. Phys., 1972, 57, 2389–2396.
49. M. García-Revilla, E. Francisco, P. L. Popelier and A. Martín Pendás, Chem. Phys. Chem., 2013, 14, 1211–1218.
50. M. Rahm and R. Hoffmann, J. Am. Chem. Soc., 2016, 138, 3731–3744.
51. L. J. Duarte, W. E. Richter, R. E. Bruns and P. L. A. Popelier, J. Phys. Chem. A, 2021, 125, 8615–8625.
52. S. J. Grabowski, Crystals, 2017, 7, 43.
53. B. Pachaly and R. West, Angew. Chem., Int. Ed. Engl., 1984, 23, 454–455.
54. S. Zhou, Z. Ni, Y. Ding, M. Sugaya, X. Pi and T. Nozaki, ACS Photonics, 2016, 3, 415–422.
55. T. H. Yuan, X. D. Pi and D. Yang, IEEE J. Sel. Top. Quant. Elect., 2017, 23, 1–5.
56. R. F. W. Bader and C. F. Matta, J. Phys. Chem. A, 2004, 108, 8385–8394.
57. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00248a

‡ Current address: Centre for Nano & Material Sciences, Jain University, Bangalore 562112, Karnataka, India.

---