Electronic structure of rhombus-shaped nanographenes: system size evolution from closed- to open-shell ground states†
Received
10th March 2023
, Accepted 4th April 2023
First published on 6th April 2023
Abstract
We theoretically study and characterize a set of rhombus-shaped nanographenes of increasing size, or n-rhombenes, where n = 2–6, displaying zigzag edges leading to an enhancement of the (poly)radicaloid nature and the appearance of intrinsic magnetism as a function of n. Due to that system-dependent radicaloid nature, we employ spin-flip methods able to capture the challenging physics of the problem, thus providing accurate energy differences between high- and low-spin solutions. The theoretical predictions agree with the experimentally available magnetic exchange coupling for the recently synthesized 5-rhombene, as well as with the size at which the transition from a closed-shell to an open-shell ground-state solution occurs. We also investigate if standard DFT methods are able to reproduce the trend disclosed by spin-flip methods and if the results are highly dependent on the functional choice and/or the intrinsic spin contamination.
1. Introduction
There is an increasing interest1–7 on open-shell graphene structures (i.e., nanometer-sized flat graphene nanoforms such as nanoflakes, nanoislands, etc.) with tailored edges and sizes, due to several factors, namely: (i) the dependence of total and local magnetism on the particular topology (e.g. shape and/or sublattice imbalance) of the systems, theoretically predicted time ago;8–10 and (ii) the recent advances in atomically-induced open-shell nanographene synthesis of a variety of these challenging nanoforms.11–15 As part of these research interests, we will consider in this study a family of graphene nanoforms displaying a rhombus shape arising from fusing two triangular fragments, with the chemical formula C2n2+4nH4n+2 and dubbed as n-rhombenes, with n indicating the system size (Fig. 1). More specifically, n is the number of benzenoid rings along any of both edges. These systems are predicted to have a singlet (S = 0) ground state following the Ovchinnikovs rule16 and its latter generalization known as Lieb's theorem,17 given that for these molecules an equal number of C atoms holds in the two interprenetating sublattices in which the topological structure can be decomposed. However, the closed- or open-shell nature of that singlet state might be highly dependent on the size, as well as the energy position of other high-lying states, which also prompted previous theoretical investigations.18–20
 |
| | Fig. 1 Chemical structures of the n-rhombenes studied (H atoms are not shown). | |
Going into more details, the smallest member of the family (i.e., 2-rhombene or benzo[def]phenanthrene, simply known as pyrene) has been synthesized time ago,21 and it is also found on interstellar searches,22 used as template for metal–organic frameworks,23 or for fusing other acenes and azaacenes,24 to name just a few examples of its chemical versatility and functionality. Note also that the synthesis of other members of the family had not been reported, possibly due to the increase of their polyradicaloid (or open-shell) character mentioned above, until the emergence of new atomic-scale techniques allowing their experimental realization. Actually, the surface-assisted synthesis of 4-rhombene and 5-rhombene on Au(111) was very recently reported in ref. 25, further characterized by Scanning Tunneling Microscopy (STM) and probed by inelastic electron tunnelling spectroscopy (IETS) and differential conductance spectroscopy measurements. Those experiments revealed a closed-shell singlet (S = 0) ground-state for 4-rhombene but an open-shell singlet for 5-rhombene, separated by 102 meV from a low-lying triplet (S = 1) state, in agreement with various calculations carried out concomitantly to that experimental investigation.26
However, there are still a few questions that can be treated from a computational point of view regarding these systems, as well as the evolution of electronic properties as a function of the system size, namely: the degree of (poly)radicaloid character and its characterization in terms of the number and distribution of unpaired electrons, the impact of spin contamination on the computational results, the evolution of the magnetic exchange coupling, the energy location of other viable high-spin states such as the quintet, the energy needed to oxidize and reduce the molecules, etc. Additionally, the use of standard Density Functional Theory (DFT) on these systems is not exempted from difficulties,27,28 due to the increasing open-shell character with n, unless using some non-standard extensions to deal with fractional occupation of molecular orbitals.29 The main goal of the present study is to address these open questions by means of electronic structure calculations. Nevertheless, to circumvent these difficulties and obtain highly accurate results to be taken as reference, we will also apply here more time-intensive and sophisticated methods such as the Restricted Active Space Spin-Flip (RAS-SF) method,30–32 which has been previously demonstrated to be a reliable tool to obtain very accurate results for (poly)radicaloid compounds.33 The RAS-SF will also be coupled34 with a short-range exchange–correlation energy functional (RAS-srDFT) to incorporate in a balanced way dynamical (or short-range) and non-dynamical (or long-range) correlation effects.35,36 Therefore, we will study the set of n-rhombenes, with n = 2–6, to address not only the evolution of electronic properties with the system size but also to simultaneously assess the accuracy of the methods chosen.
2. Theoretical framework
The characterization of the (poly)radicaloid nature of these compounds will be first estimated by the fractional occupation of molecular orbitals induced by (near-)degeneracy effects, which in open-shell systems can be simulated by minimizing the Gibbs electronic free energy (Gel = Eel − TelSel) of the system, at a fictitious pseudo-temperature (i.e., electronic) called Tel and imposing a Fermi–Dirac distribution around the Fermi level EF:| |  | (1) |
with fi being the fractional occupation numbers, and θ = kBTel. This kind of methods are collectively denoted as Finite–Temperature DFT (FT-DFT).37–39
Reference values for energy differences between singlet (S), triplet (T), and quintet (Q) spin states (vide infra) will be obtained by the Restricted Active Space Spin-Flip (RAS-SF) method, allowing multiple spin-flip excitations40 within the active space chosen of doubly occupied (RAS1), singly occupied (RAS2), and virtual (RAS3) subspaces. The RAS-SF Hamiltonian is defined as that of n-spin-flip excitations expanded in terms of the number of holes (particles) in the doubly occupied (virtual) space:
| | ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) nSF = nSF = ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF0 + nSF0 + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFh + nSFh + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFp + nSFp + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFhp + nSFhp + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF2h + nSF2h + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF2p+ …, nSF2p+ …, | (2) |
where
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF0
nSF0 performs all possible spin-flip excitations within RAS2 and
h and
p subindices indicate the number of holes and particles in RAS1 and RAS3, respectively. In the approximation used here
p =
h = 1;
i.e., the right side of
eqn (2) is truncated at the third term. The eigenvalues are obtained from a wavefunction expanded over a high-spin single reference restricted set of Slater determinants,

, where |
ΦR〉 are the allowed electronic configurations. These calculations will be also coupled with the PBE
41 short-range exchange–correlation energy functional, to introduce both types (long- and short-range) of electron correlation effects, briefly denoted as RAS-srPBE in the following, since this functional is chosen for this RAS-srDFT extension.
The relative energies between those low-lying and different spin states will also be obtained by Density Functional Theory (DFT), employing semi-local and both Global–Hybrid (GH) and Double–Hybrid (DH) density functionals, to bracket if the accuracy of the calculations depends on the choice of the exchange–correlation functional. The general expression for a GH functional is given by:
| | | EGHxc[ρ] = cxEEXXx + (1 − cx)Ex[ρ] + Ec[ρ], | (3) |
with the exchange contribution being a linear function of the EXact-eXchange (EXX) energy,
EEXXx, and the exchange functional,
Ex[
ρ], weighted by a coefficient
cx (note that for a semi-local functional
cx = 0). This expression can be extended to a DH form as:
| | | EDHxc[ρ] = cxEEXXx + (1 − cx)Ex[ρ] + ccEPT2c + (1 − cc)Ec[ρ], | (4) |
that is, adding the 2nd-order Perturbation Theory energy,
EPT2c, to the correlation functional,
Ec[
ρ], weighted now by the coefficient
cc. The expressions for:
| | 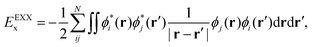 | (5) |
| |  | (6) |
with 〈
ab||
ij〉 = 〈
ab|
ij〉 − 〈
ab|
ji〉, rely both on the set of occupied ({
ϕi}) and virtual ({
ϕa}) orbitals self-consistently generated by
eqn (3) and used hereinafter. We will select for these calculations the semi-local PBE
41 (
cx = 0), the hybrid PBE0
42 (
cx = 1/4) and PBEHH (
cx = 1/2), and the double-hybrid PBE0-DH
43 (
cx = 1/2 and
cc = 1/8) exchange–correlation functionals, all of them belonging to the same non-empirical family of expressions but differing in their hybridization.
44,45 Furthermore, a Broken–Symmetry (BS) solution will also be carefully obtained at all those levels for the corresponding open-shell singlet states.
The spin-contamination associated to DFT calculations can be reduced to better estimate the singlet–triplet and singlet–quintet energy differences, or ΔEST and ΔESQ, respectively. Denoting the low-spin (Ms = 0) and high-spin (e.g. Ms = 1 for a triplet) solutions as LS and HS, respectively, one of the simplest forms has been proposed by Yamaguchi et al.46–48 exploiting the difference between the calculated mean values of the Ŝ2 spin operator for the two solutions involved, such as:
| | | ΔE(HS − LS) = δ·[E(HS) − E(LS)], | (7) |
with:
| |  | (8) |
where
nS corresponds to the 〈
Ŝ2〉 difference between the ideal spin eigenvalues,
e.g.,
nS = 2 for a singlet–triplet. In the case of
n-rhombenes, we will calculate Δ
EST and Δ
ESQ values, with S, T, and Q corresponding to the lowest-energy solutions fixing
Ms = 0 (singlet),
Ms = 1 (triplet), and
Ms = 2 (quintet) or, in other words, the S
0 − T
1 and S
0 − Q
1 energy difference. In the case of the singlet states, an open-shell solution will also be imposed which will be used to calculate those Δ
EST and Δ
ESQ values and thus infer for which value of
n the closed- and open-shell solutions might differ.
2.1 Computational details
The geometries of the compounds are initially optimized by the B97-3c method49 leading to planar structures identified by all-real 3N − 6 vibrational frequencies. The FT-DFT calculations are done with the recommended TPSS50 functional and the default temperature of 5000 K, together with the def2-TZVP basis set,51 employing the ORCA 5.0 package.52 The spatial plots of ρU(r) are done with the AVOGADRO 1.97 visualizer.53 The same ORCA 5.0 package is also used for the DFT calculations with different exchange–correlation functionals and the def2-SVP and def2-TZVP basis sets. The RIJCOSX technique,54 together with the auxiliary def2/JK and def2-nVP/C basis sets,55 is fixed for the latter calculations to alleviate the computational cost. The cc-pVTZ basis set is also used for some test calculations, employing again the corresponding auxiliary basis sets. For the RAS-SF calculations, done here with the Q-CHEM 6.0 package,56 we also assess the dependence of the results with respect to different basis sets (6-31G*, 6-311G*, def2-SVP, and def2-TZVP). For the RAS-based calculations, the number of electrons (Ne) in the number of active orbitals (No), or briefly (Ne,No), is chosen consistently with the fractional occupation disclosed at the FT-DFT level, that is, (4,4) for 2-rhombene, (6,6) for 3-rhombene, and (10,10) for the rest of n-rhombenes (4- to 6-rhombene). A triplet state was used as the high-spin reference for RAS-SF, except for n = 5–6 for which a quintet state was instead used.
3. Results and discussion
3.1 Geometrical features
The B97-3c optimized geometry for the 2-rhombene molecule, the only system for which X-ray data exists,57 are in close agreement with the experimental results (averaged error of 0.0080 Å) and very close to those calculated for consistency at the PBE0/def2-TZVP and PBE0-DH/def2-TZPV levels (averaged errors of 0.0065 and 0.0062 Å, respectively) which are known to be very accurate methods for geometry optimizations.58 The Bond Length Alternation (BLA) can be calculated by B97-3c to estimate the average difference in lengths between single and double bonds along the zigzag edges:59| |  | (9) |
where di,j is the distance between atoms i and j out of the N total C atoms. BLA values (in Å, as calculated at the B97-3c level) of 0.029, 0.033, 0.031, 0.027, and 0.023, are found from 2-rhombene to 6-rhombene, respectively, indicating only slight variations of aromaticity as a function of the system size n. Note also that these values are lower than those found before60 for oligoacetylenes of similar length, as it is also expected from the extended conjugation of the (fully planar) n-rhombenes. The same trend for BLA values is reproduced by PBE0/def2-SVP or PBE0/def2-TZVP methods, with the latter giving slightly higher values (in Å) of 0.034, 0.041, 0.040, and 0.036 for 2- to 5-rhombene, respectively. The InfraRed (IR) spectra of the set of n-rhombenes, at the B97-3c level, shows (see the ESI†) pronounced peaks at ≈850 and ≈3130 cm−1 for the CH out-of-plane bending and CH stretching, respectively, whose intensity progressively increases with the system size and thus with the number of CH bonds, in agreement with the expected results for polycyclic aromatic hydrocarbons.61
3.2 The (poly)radicaloid character of the systems
A simple yet effective estimate of the radicaloid character is obtained by the FT-DFT method, providing the energy distribution of electrons around the Fermi level, which can also be represented as a spatial density:| | 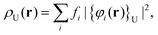 | (10) |
with fi being the fractional occupation number (0 < fi < 2) corresponding to that subset of orbitals ({φi}U) holding a fractional occupation. The integration of ρU(r) directly leads to NU, a global measure of the number of strongly correlated electrons. The NU values for the (singlet) ground-state of n-rhombenes are 0.19, 0.81, 1.85, 3.14, and 4.60 for 2-rhombene, 3-rhombene, 4-rhombene, 5-rhombene, and 6-rhombene, respectively, increasing significantly with the system size as it does also the length of the zigzag edges (see Fig. 2). This relationship can be easily understood by the real-space distribution of ρU(r), see the ESI,† which is strongly localized at those C atoms belonging to the zigzag edges, taking also into account that ρU(r) (and thus NU) is a size-extensive magnitude. This topology of ρU(r) agrees with the distribution found before for other graphene nanoribbons62 or linear and cyclic oligoacenes.63
 |
| | Fig. 2 Evolution of the NU values of n-rhombenes, as calculated by the FT-TPSS/def2-TZVP method, as a function of the zigzag length (in Å) measured as the sum of the (2n) CC bond lengths along one of the four (symmetrical) edges of the systems. | |
The evolution of the ground-state fractional occupation numbers through the n-rhombenes family is presented in Fig. 3, which includes now a large manifold of orbitals to better appreciate how the (poly)radicaloid nature evolves with the system size. It is immediately apparent that the number of orbitals with fractional occupation increases with the system size, with the ground-state of smaller n-rhombenes (n ≤ 3) displaying a vanishing or small diradicaloid character, consistent with the information available in the literature for e.g. pyrene.64 On the other hand, the larger n-rhombenes tackled here (i.e., 4-rhombene, 5-rhombene, and 6-rhombene) exhibited a more marked diradicaloid character, with a larger number of orbitals with occupation fi ≈ 1, which is also in agreement with the larger NU values found from ρU(r). Overall, the largest n-rhombenes should be considered as of a significantly (poly)radicaloid nature.
 |
| | Fig. 3 Orbital occupation numbers (fi) of n-rhombenes, as calculated by the FT-TPSS/def2-TZVP method. | |
Additionally, the degree of the (poly)radicaloid character of the compounds can also be estimated by the radical indexes Yi number65 (i = 0, 1, 2) generally obtained as Yi = fLUNO+i, with fLUNO being the fractional occupation number of the Lowest Unoccupied Natural Orbital. For a N-electron system, the Highest Occupied Natural Orbital (HONO) is defined as the (N/2)th orbital while the Lowest Unoccupied Natural Orbital (LUNO) is defined as the (N/2 + 1)th orbital, with the rest of orbitals defined correspondingly. At the RAS-SF/6-31G* level, we obtain values for each of the Y0, Y1, and Y2 index, which are respectively related to the di-, tetra-, and hexa-radicaloid character. Note that Yi ≈ 1 suggests a high radical character (e.g. Y0 = 0 for a closed-shell system and Y0 = 1 for a diradical). Fig. 4 shows the Yi values for the set of n-rhombenes, indicating a low radicaloid character for 2- and 3-rhombene, a moderate diradicaloid character for 4-rhombene, and a low to moderate tetraradicaloid character for the largest 5- and 6-rhombene. This conclusion is in qualitative agreement with previous and simplified topological approaches for the treatment of conjugated hydrocarbons.66
 |
| | Fig. 4 Radical index (Yi) of n-rhombenes, as calculated by the RAS-SF/6-31G* method. | |
3.3 Singlet–triplet and singlet–quintet energy gap
3.3.1 Results from wavefunction methods.
First of all, we will assess for 2- and 3-rhombene RAS-based methodological aspects to better bracket the accuracy of the RAS-SF results for the rest of the largest systems. The use of a large (def2-TZVP) or a cost-effective (6-31G*) basis set brings only a small difference for the target ΔE(HS − LS) values, that is ΔEST and ΔESQ energy differences: Going from def2-TZVP to 6-31G* modifies for 2-rhombene (3-rhombene) the ΔEST value by 0.05 (0.08) eV, while ΔESQ was affected by 0.14 (−0.01) eV. In this comparison, we will also include next the RAS-srPBE/6-31G* results for which, similarly, the ΔEST and ΔESQ values are only slightly affected, as can be seen in Fig. 5 summarizing the impact of these technical aspects on the results. Therefore, we will rely in the following on the cost-effective RAS-SF/6-31G* results for the largest (and more challenging) n-rhombenes as a good compromise between accuracy and computational cost.
 |
| | Fig. 5 Energy difference (in eV) between the low- and high-spin states of 2- and 3-rhombene, and NU, as calculated at various RAS-based theoretical levels. | |
The evolution of ΔEST and ΔESQ values with the system size is presented in Fig. 6, with both energy differences smoothly decreasing as a function of n (for completeness, the figure also includes the S1 state). The smaller systems, 2- to 4-rhombene, keep a substantial energy difference between low-spin and high-spin (be T1 or Q1) states, which is fully consistent with their low radicaloid character. For the longest rhombenes, the ΔEST and ΔESQ values are considerably lower, with the T1 state being always the lowest one. Actually, for the case of 5-rhombene, the T1 state is energetically predicted (RAS-SF/6-31G* level) at 139 meV above the (open-shell) S0 state, in close agreement with the experimentally determined energy difference between those states of 102 meV25 (note that the surface is known to play a negligible influence to adequatly compare experimental and calculated values according to recent studies67). For 6-rhombene, that ΔEST values slightly decreases to 56 meV, a value still few times larger than the Landauer limit68 [i.e., kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(2) ≈ 18 meV, with kB the Boltzmann constant and T the temperature] for energy dissipation at room temperature, a key magnitude for having stable spintronics devices. Note that for 6-rhombene, the ΔEST and the ΔESQ values are energetically close just separated by less than 0.2 eV.
ln(2) ≈ 18 meV, with kB the Boltzmann constant and T the temperature] for energy dissipation at room temperature, a key magnitude for having stable spintronics devices. Note that for 6-rhombene, the ΔEST and the ΔESQ values are energetically close just separated by less than 0.2 eV.
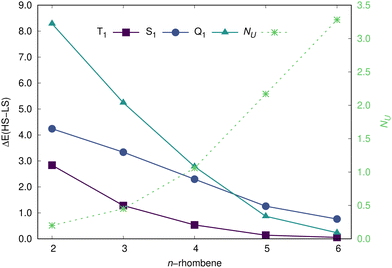 |
| | Fig. 6 Energy difference (in eV) between the low- and high-spin states of n-rhombenes, and NU, as calculated by the RAS-SF/6-31G* method. | |
The results by RAS-SF/6-31G* will also be compared for 4- to 6-rhombenes with those obtained using (Strongly-Contracted) N-electron Valence second-order Perturbation Theory or (SC-)NEVPT2,69–71 as a sanity check given the high accuracy of the latter method for related systems,72 employing the same active space (10,10) and basis set than for RAS-SF. Interestingly, the T1 state for 5-rhombene (6-rhombene) is also found lying 139 (75) meV above the S0 state, in perfect agreement with the RAS-SF results. Finally, other results from literature are compared here for the sake of completeness: (i) NEVPT2/STO-3G calculations73,74 led to negligible ΔEST values of 16 and 3 meV for 5- and 6-rhombene, respectively, and too low ΔESQ values too, thus indicating the need of more realistic basis sets; and (ii) TAO-LDA calculations64 reported ΔEST values for 4- to 6-rhombene of 440, 204, and 116 meV, closely following the trend of the values calculated here although slightly overestimating the experimental result for 5-rhombene.
3.3.2 Assessment of DFT methods.
A simple yet useful estimate of the performance of the PBE-based functionals (all calculations are done with the def2-TZVP basis set unless otherwise noticed) will be the comparison of the results with the experimentally available HOMO–LUMO gap (0.73 eV) of 4-rhombene. Due to the fact that the ground-state of 4-rhombene is experimentally predicted to be a closed-shell system, the closest estimate is provided by PBE (0.66 eV) followed by PBE0 (1.36 eV) and PBEHH (2.13 eV), thus indicating that a relatively low cx weight [see eqn (3)] is favoured in this case. Actually, a calculation with an ad hoc PBEh hybrid functional75 (for which cx = 1/10) leads to an intermediate value of 0.93 eV between those calculated by PBE and PBE0, showing how (linearly) dependent the HOMO–LUMO gap with respect to cx is. This finding prompts us to discard PBEHH (the functional with the highest cx weight) for the rest of the calculations shown here.
The FT-DFT method will be first applied for a fast estimate of the ΔEST (ΔESQ) energy differences, with calculated values (all in eV) of 1.864, 0.869, 0.430, 0.255, and 0.174 (5.239, 3.115, 1.792, 1.095, 0.741) and thus decreasing with the system size, in agreement with marked radicaloid character of the largest systems and with the T1 state lower in energy with respect to the Q1 state, as also obtained by the RAS-SF calculations. Since the relative stabilization of the HS with respect to the LS state is known to be strongly affected by the functional choice,76–78 or more specifically by the fraction of exact-exchange,79 we will next assess the performance of the PBE and PBE0 models, with the results shown in Fig. 7. When PBE is applied, the ground-state open-shell (singlet) solution collapsed to the closed-shell form for compounds 2- to 4-rhombene, but not for 5- and 6-rhombene. Thus, for 5- and 6-rhombene, the closed-shell singlet lies at 40 and 176 meV above in energy, respectively, with respect to the open-shell singlet state. This functional also provides for 5-rhombene the T1 state separated by 174 meV from the open-shell state, an energy gap slightly overestimated with respect to both experimental (102 meV) and RAS-SF (139 meV) values. The Q1 state is found much higher at 846 meV, close to the value obtained at the RAS-SF level (868 meV). In the case of 6-rhombene, the triplet lies above the singlet by 235 meV, which roughly represents a 3-fold overestimation of the RAS-SF result and evolves contrarily to the trend provided by RAS-SF and NEVPT2 results since ΔEST is found lower for 6-rhombene than for 5-rhombene. Note also that the ΔEST and ΔESQ energy differences are known to decrease for increasing radicaloid nature, as it has been previously shown for e.g. linear and cyclic acenes.63
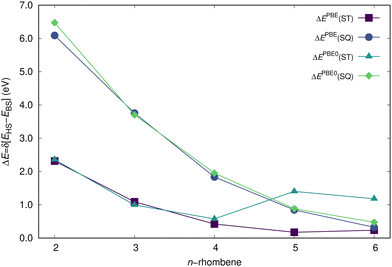 |
| | Fig. 7 Energy difference (in eV) between the low- and high-spin states of n-rhombenes, as calculated by DFT/def2-TZVP methods and spin-decontaminated as commented in the text. | |
On the other hand, the PBE0 model predicted an open-shell ground-state for 4-rhombene, contrarily to experimental results, with the corresponding closed-shell state at 170 meV higher in energy. For the case of 5- and 6-rhombene, the closed-shell singlet lies as high as 630 and 1214 meV above in energy, respectively, with respect to the open-shell singlet. Additionally, the large spin contamination (see Table 1) is identified as the responsible factor for predicting the Q1 state significantly more stable than the T1 for 5-rhombene, as already anticipated by the RAS-SF results since the manifold of states was found very close in energy for the largest systems: ΔEST and ΔESQ are predicted to be 255 and 654 meV before applying the spin correction given by eqn (8), which modifies the values to 1403 and 882 meV, respectively. A similar situation is found for 6-rhombene, with values for ΔEST and ΔESQ of 1181 and 474 meV, respectively, once the spin correction is applied, see eqn (7) and (8). Finally, the evolution with the system size of the ΔEST and ΔESQ calculated values is presented in Fig. 7 taking into account the spin correction, with all the individual values for n-rhombenes at both PBE and PBE0 methods given as part of the ESI.†
Table 1 〈Ŝ2〉 calculated values for S1, T1, and Q1 states of n-rhombenes, as calculated by DFT/def2-TZVP methods
| [n] |
PBE |
PBE0 |
| S1 |
T1 |
Q1 |
S1 |
T1 |
Q1 |
| 2 |
0.000 |
2.014 |
6.005 |
0.000 |
2.045 |
6.009 |
| 3 |
0.000 |
2.017 |
6.030 |
0.000 |
2.072 |
6.111 |
| 4 |
0.000 |
2.022 |
6.037 |
0.970 |
2.102 |
6.162 |
| 5 |
0.709 |
2.026 |
6.046 |
1.767 |
2.130 |
6.217 |
| 6 |
1.368 |
2.029 |
6.055 |
2.540 |
3.213 |
6.271 |
3.4 Charged systems
We also investigated the energy associated to charge the systems, known as adiabatic ionization potential (AIP) or electron affinity (AEA) and calculated as energy differences between charged and neutral systems all at their respective optimized geometries: AIP = EM˙+ − EM and AEA = EM − EM˙−, with EM being the energy of the neutral molecule and EM˙+ (EM˙−) the energy of the positively (negatively) charged molecule. The quasiparticle energy gap (QEG) is readily obtained as QEG = AIP − AEA. The corresponding vertical magnitudes are VIP (vertical ionization potential), VEA (vertical electron affinity), and VQEG (vertical quasiparticle energy gap) and are obtained at the ground-state geometries. We will employ the PBE0 and the PBE0-DH models to bracket the dependence of the values with the functional choice. Experimentally available AIP80 and AEA81 values for 2-rhombene (7.426 and 0.406 eV, respectively) will be used as test case to assess the accuracy of the DFT results. Whereas PBE0/def2-SVP gives values of 7.175 and 0.368 eV, respectively, the use of the larger def2-TZVP basis set produced values of 7.148 and 0.394 eV, showing a not very marked dependence of the results on the basis set size (furthermore PBE0/cc-pVTZ led to values of 7.135 and 0.356 eV, respectively). The use of PBE0-DH instead leads to values of 7.271 and 0.284 eV (def2-SVP) and 7.256 and 0.334 eV (def2-TZVP) for AIP and AEA, respectively, slightly more influenced by basis sets effects due to the inclusion of the PT2 term in eqn (4). Choosing the PBE0 functional for its good trade-off between accuracy and computational cost, and looking at the evolution of these values with the system size, see Table 2, we observe a initial decreasing values as a function of n for all the energy magnitudes collected, up to some saturation for the 4- to 6-rhombene. Additionally, the difference between adiabatic and vertical values is reduced with the system size, which is rationalized by an enhanced rigidity of the molecular backbone for the largest systems studied. For the sake of completeness, we also used the FT-DFT method to observe a qualitatively similar evolution of the values with the system size.
Table 2 Energy differences (in eV) between positively or negatively charged and neutral n-rhombenes, as calculated by PBE0/def2-TZVP
| [n] |
PBE0 |
FT-DFT |
| AIP |
VIP |
AEA |
VEA |
AQEG |
VQEG |
AIP |
VIP |
AEA |
VEA |
AQEG |
VQEG |
| 2 |
7.148 |
7.231 |
0.394 |
0.280 |
6.754 |
6.950 |
6.749 |
6.768 |
0.652 |
0.613 |
6.097 |
6.156 |
| 3 |
6.076 |
6.127 |
1.559 |
1.502 |
4.517 |
4.625 |
5.834 |
5.842 |
1.638 |
1.621 |
4.197 |
4.221 |
| 4 |
5.604 |
5.615 |
2.137 |
2.125 |
3.467 |
3.491 |
5.371 |
5.374 |
2.177 |
2.170 |
3.194 |
3.205 |
| 5 |
5.679 |
5.726 |
2.166 |
2.101 |
3.513 |
3.625 |
5.113 |
5.115 |
2.497 |
2.493 |
2.616 |
2.622 |
| 6 |
5.568 |
5.585 |
2.276 |
2.237 |
3.292 |
3.349 |
4.945 |
4.947 |
2.711 |
2.709 |
2.233 |
2.238 |
The inner reorganization energy (Λ) for holes (Λh˙+) or electrons (Λe˙−), related to charge migration and transfer between neighbouring molecules82,83 can also be obtained (in the hopping regime) from the following set of calculations:
| | | Λh(e)˙± = [EM˙±//M − EM˙±] + [EM//M˙± − EM], | (11) |
where
EM˙
±//M and
EM//M˙
± are now the energies of the charged molecule at the neutral geometry and that of the neutral at the charged geometry, respectively, with
EM˙
± being the energy of the charged structures.
84,85 We will employ the PBE0 functional also here due to its accurate results for other conjugated (semiconducting) systems.
86–88 At the PBE0/def2-TZVP level,
Λh˙
+ values of 157 and 103 meV are obtained for the smallest 2- and 3-rhombene members of the set of molecules, respectively, showing the typical evolution of these values with the system size (inversely proportional to the number of C atoms
89) and favourably comparing with for instance circum(oligo)acenes of increasing size, such as circumbenzene or coronene (C
24H
12) and circumtetracene (C
48H
18) with values of 127 and 57 meV, respectively, calculated before at the B3LYP/cc-pCVDZ level.
90 For the case of
Λe˙
−, values of 225 and 147 meV are again calculated at the PBE0/def2-TZVP level, larger than those found before for
Λh˙
+. The application of the PBE0-DH model led to
Λh˙
+ (
Λe˙
−) values of 182 and 114 meV (250 and 153 meV), thus confirming the trend found before with PBE0. Note that the reorganization energies of larger systems, following the expected evolution with the system size, would preclude the use of
eqn (11) due to the gradual transition between the incoherent (hopping) and coherent (ballistic) transport regimes.
91 As a matter of illustration, for 6-rhombene values of
Λh+ and
Λe− as low as 36 and 58 meV, respectively, are found.
4. Conclusions
We have systematically studied the electronic structure of increasingly larger rhombus-shaped molecules, or n-rhombenes, ranging from 2-rhombene (C16H10) to 6-rhombene (C96H26), due to the markedly increasing (poly)radicaloid character with the system size. The rationalization of that character is extensively done through the number and spatial extension of unpaired electrons, the fractional occupation of molecular orbitals, the frontier molecular orbital energy gap, and the total energy difference between singlet–triplet and singlet–quintet electronic states. The challenging electronic structure of these systems has prompted the use of multiconfigurational methods, such as RAS-srDFT, RAS-SF, or NEVPT2, leading to: (i) a qualitative agreement between available experimental and theoretical results for the system size at which the transition from a closed-shell to an open-shell ground-state happens, and (ii) a quantitative and close agreement between theoretical and experimental results for the singlet–triplet energy difference for 5-rhombene. This agreement facilitates us to rely on the calculated singlet–triplet energy difference for 6-rhombene (not yet synthesized) which is lower than for 5-rhombene but still larger than the Landauer limit.
The quality of those wavefunction based results also served us to assess different DFT flavors (semi-local, hybrid, and double-hybrid functionals) for estimating the energy difference between different spin states (profoundly influenced by the spin contamination). For that situation, the spin contamination is alleviated by the use of the Yamaguchi's correction, which led to qualitatively correct results for 5-rhombene but not for 6-rhombene, disagreeing thus with results from wavefunction methods. The study of charged (monocationic and monoanionic) systems showed a decreasing (increasing) evolution of ionization potentials (electron affinity) with the system size, closing thus the quasiparticle energy gap as it was also expected due to their increasing (poly)radicaloid nature. The reorganization energy for hole or electron charge carrier transport in the hopping regime, for the smallest members of the family, show reasonably low values for those molecules to act as organic molecular semiconductors. On the other hand, the low-cost FT-DFT method can be considered as an alternative for dealing with (poly)radicaloids systems, providing fast and qualitatively correct results.
Data availability
The data that supports the findings of this study are available within the article [and its ESI†] or are available from the corresponding authors upon reasonable request.
Author contributions
M. E. S.-S. and R. B.-C. contributed equally to this work.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by projects PID2019-106114GB-I00 (“Ministerio de Ciencia e Innovación”), AICO/2021/093 and PROMETEO/2021/017 (“Generalitat Valenciana”).
References
- W. Zeng and J. Wu, Open-shell graphene fragments, Chem, 2021, 7(2), 358–386 CAS.
- S. Moles Quintero, M. M. Haley, M. Kertesz and J. Casado, Polycyclic Hydrocarbons from [4n]Annulenes: Correlation versus Hybridization Forces in the Formation of Diradicaloids, Angew. Chem., Int. Ed., 2022, 61(44), e202209138 CrossRef CAS PubMed.
- Y. Gu, Z. Qiu and K. Müllen, Nanographenes and Graphene Nanoribbons as Multitalents of Present and Future Materials Science, J. Am. Chem. Soc., 2022, 144(26), 11499–11524 CrossRef CAS PubMed.
- F. de Souza, F. Pansini, A. R. Ambrozio, J. Freitas and W. L. Scopel, NMR spectral parameters of open-and closed-shell graphene nanoflakes: Orbital and hyperfine contributions, Carbon, 2022, 191, 374–383 CrossRef CAS.
- I. Badía-Domínguez, S. Canola, V. Hernandez Jolin, J. T. Lopez Navarrete, J. C. Sancho-García and F. Negri,
et al., Tuning the Diradical Character of Indolocarbazoles: Impact of Structural Isomerism and Substitution Position. The, J. Phys. Chem. Lett., 2022, 13(26), 6003–6010 CrossRef PubMed.
- D. G. de Oteyza and T. Frederiksen, Carbon-based nanostructures as a versatile platform for tunable π-magnetism, J. Phys.: Condens. Matter, 2022, 34(44), 443001 CrossRef PubMed.
- Z. Liu, S. Fu, X. Liu, A. Narita, P. Samorì and M. Bonn,
et al., Small Size, Big Impact: Recent Progress in Bottom-Up Synthesized Nanographenes for Optoelectronic and Energy Applications, Adv. Sci., 2022, 2106055 CrossRef PubMed.
- J. Fernández-Rossier and J. J. Palacios, Magnetism in graphene nanoislands, Phys. Rev. Lett., 2007, 99(17), 177204 CrossRef PubMed.
- R. Ortiz, R. A. Boto, N. García-Martínez, J. C. Sancho-García, M. Melle-Franco and J. Fernández-Rossier, Exchange rules for diradical π-conjugated hydrocarbons, Nano Lett., 2019, 19(9), 5991–5997 CrossRef CAS PubMed.
- D. Jacob and J. Fernández-Rossier, Theory of intermolecular exchange in coupled spin-1 2 nanographenes, Phys. Rev. B, 2022, 106(20), 205405 CrossRef CAS.
- A. Narita, X. Y. Wang, X. Feng and K. Müllen, New advances in nanographene chemistry, Chem. Soc. Rev., 2015, 44(18), 6616–6643 RSC.
- S. Mishra, D. Beyer, K. Eimre, J. Liu, R. Berger and O. Groning,
et al., Synthesis and characterization of π-extended triangulene, J. Am. Chem. Soc., 2019, 141(27), 10621–10625 CrossRef CAS PubMed.
- S. Mishra, D. Beyer, K. Eimre, R. Ortiz, J. Fernández-Rossier and R. Berger,
et al., Collective all-carbon magnetism in triangulene dimers, Angew. Chem., 2020, 132(29), 12139–12145 CrossRef.
- S. Mishra, J. Melidonie, K. Eimre, S. Obermann, O. Gröning and C. A. Pignedoli,
et al., On-surface synthesis of super-heptazethrene, Chem. Commun., 2020, 56(54), 7467–7470 RSC.
- S. Song, J. Su, M. Telychko, J. Li, G. Li and Y. Li,
et al., On-surface synthesis of graphene nanostructures with π-magnetism, Chem. Soc. Rev., 2021, 50(5), 3238–3262 RSC.
- A. A. Ovchinnikov, Multiplicity of the ground state of large alternant organic molecules with conjugated bonds, Theor. Chim. Acta, 1978, 47(4), 297–304 CrossRef CAS.
- E. H. Lieb, Two theorems on the Hubbard model, Phys. Rev. Lett., 1989, 62(10), 1201 CrossRef PubMed.
- L. A. Agapito, N. Kioussis and E. Kaxiras, Electric-field control of magnetism in graphene quantum dots: Ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(20), 201411 CrossRef PubMed.
- C. N. Yeh and J. D. Chai, Role of Kekulé and non-Kekulé structures in the radical character
of alternant polycyclic aromatic hydrocarbons: a TAODFT study, Sci. Rep., 2016, 6(1), 1–14 CrossRef PubMed.
- S. Ganguly, M. Kabir and T. Saha-Dasgupta, Magnetic and electronic crossovers in graphene nanoflakes, Phy. Rev. B, 2017, 95(17), 174419 CrossRef.
- T. Förster and K. Kasper, Ein konzentrationsumschlag der fluoreszenz, Z. Phys. Chem., 1954, 1(5–6), 275–277 CrossRef.
- L. Zhao, R. I. Kaiser, B. Xu, U. Ablikim, M. Ahmed and D. Joshi,
et al., Pyrene synthesis in circumstellar envelopes and its role in the formation of 2D nanostructures, Nat. Astron, 2018, 2(5), 413–419 CrossRef.
- F. P. Kinik, A. Ortega-Guerrero, D. Ongari, C. P. Ireland and B. Smit, Pyrenebased metal organic frameworks: from synthesis to applications, Chem. Soc. Rev., 2021, 50(5), 3143–3177 RSC.
- J. Li, S. Chen, Z. Wang and Q. Zhang, Pyrene-fused Acenes and Azaacenes: Synthesis and Applications, Chem. Rec., 2016, 16(3), 1518–1530 CrossRef CAS PubMed.
- S. Mishra, X. Yao, Q. Chen, K. Eimre, O. Gröning and R. Ortiz,
et al., Large magnetic exchange coupling in rhombus-shaped nanographenes with zigzag periphery, Nat. Chem., 2021, 13(6), 581–586 CrossRef CAS PubMed.
- R. Ortiz and J. Fernández-Rossier, Probing local moments in nanographenes with electron tunneling spectroscopy, Prog. Surf. Sci., 2020, 95(4), 100595 CrossRef CAS.
- G. Salvitti, F. Negri, A. J. Pérez-Jiménez, E. San-Fabián, D. Casanova and J. C. Sancho-García, Investigating the (Poly) Radicaloid Nature of Real- World Organic Compounds with DFT-Based Methods, J. Phys. Chem. A, 2020, 124(18), 3590–3600 CrossRef CAS PubMed.
- A. Omist, G. Ricci, A. Derradji, A. J. Pérez-Jiménez, E. San-Fabián and Y. Olivier,
et al., peri-Acenoacene molecules: tuning of the singlet and triplet excitation energies by modifying their radical character, Phys. Chem. Chem. Phys., 2021, 23(41), 24016–24028 RSC.
- J. D. Chai, Density Functional Theory with Fractional Orbital Occupations, J. Chem. Phys., 2012, 136(15), 154104 CrossRef PubMed.
- A. I. Krylov, Spin-flip configuration interaction: an electronic structure model that is both variational and size-consistent, Chem. Phys. Lett., 2001, 350(5), 522–530 CrossRef CAS.
- Y. Shao, M. Head-Gordon and A. I. Krylov, The spin–flip approach within time-dependent density functional theory: Theory and applications to diradicals. The, J. Chem. Phys., 2003, 118(11), 4807–4818 CrossRef CAS.
- A. I. Krylov, Spin-flip equation-of-motion coupled-cluster electronic structure method for a description of excited states, bond breaking, diradicals, and triradicals, Acc. Chem. Res., 2006, 39(2), 83–91 CrossRef CAS PubMed.
- D. Casanova, Restricted active space configuration interaction methods for strong correlation: Recent developments, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(1), e1561 CAS.
- D. Casanova, Short-range density functional correlation within the restricted active space CI method, J. Chem. Phys., 2018, 148(12), 124118 CrossRef PubMed.
- N. Orms and A. I. Krylov, Singlet–triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory, Phys. Chem. Chem. Phys., 2018, 20(19), 13127–13144 RSC.
- M. E. Sandoval-Salinas, A. Carreras, J. Casado and D. Casanova, Singlet fission in spiroconjugated dimers, J. Chem. Phys., 2019, 150(20), 204306 CrossRef PubMed.
- J. D. Chai, Thermally-assisted-occupation density functional theory with generalized-gradient approximations, J. Chem. Phys., 2014, 140(18), 18A521 CrossRef PubMed.
- S. Grimme and A. Hansen, A practicable real-space measure and visualization of static electron-correlation effects, Angew. Chem., Int. Ed., 2015, 54(42), 12308–12313 CrossRef CAS PubMed.
- C. A. Bauer, A. Hansen and S. Grimme, The fractional occupation
number weighted density as a versatile analysis tool for molecules with a complicated electronic structure, Chem. – Eur. J., 2017, 23(25), 6150–6164 CrossRef CAS PubMed.
- D. Casanova and A. I. Krylov, Spin-flip methods in quantum chemistry, Phys. Chem. Chem. Phys., 2020, 22(8), 4326–4342 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model. The, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- E. Brémond and C. Adamo, Seeking for parameter-free double-hybrid functionals: the PBE0-DH model, J. Chem. Phys., 2011, 135(2), 024106 CrossRef PubMed.
- E. Brémond, I. Ciofini, J. C. Sancho-García and C. Adamo, Nonempirical double-hybrid functionals: An effective tool for chemists, Acc. Chem. Res., 2016, 49(8), 1503–1513 CrossRef PubMed.
- J. C. Sancho-Garcia, E. Brémond, A. Pérez-Jiménez, I. Ciofini and C. Adamo, Non-empirical double-hybrid density functionals as reliable tools for electronic structure calculations, Electron. Struct., 2022, 4(4), 043001 CrossRef.
- K. Yamaguchi, H. Fukui and T. Fueno, Molecular orbital (MO) theory for magnetically interacting organic compounds. Ab-initio MO calculations of the effective exchange integrals for cyclophane-type carbene dimers, Chem. Lett., 1986,(4), 625–628 CrossRef CAS.
- K. Yamaguchi, Y. Takahara, T. Fueno and K. N. Houk, Extended Hartree- Fock (EHF) theory of chemical reactions, Theor. Chim. Acta, 1988, 73(5), 337–364 CrossRef CAS.
- S. Yamanaka, M. Okumura, M. Nakano and K. Yamaguchi, EHF theory of chemical reactions Part 4. UNO CASSCF, UNO CASPT2 and R(U)HF coupled-cluster (CC) wavefunctions, J. Mol. Struct.: THEOCHEM, 1994, 310, 205–218 Search PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 143(5), 054107 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91(14), 146401 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4(1), 1–17 Search PubMed.
- S. Kossmann and F. Neese, Comparison of two efficient approximate Hartee– Fock approaches, Chem. Phys. Lett., 2009, 481(4–6), 240–243 CrossRef CAS.
- F. Weigend, Hartree–Fock exchange fitting basis sets for H to Rn, J. Comput. Chem., 2008, 29(2), 167–175 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao and N. Mardirossian,
et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155(8), 084801 CrossRef CAS PubMed.
- R. W. Havenith, J. H. Van Lenthe, F. Dijkstra and L. W. Jenneskens, Aromaticity of Pyrene and Its Cyclopentafused Congeners Resonance and NICS Criteria. An Ab Initio Valence Bond Analysis in Terms of Kekulé Resonance Structures, J. Phys. Chem. A, 2001, 105(15), 3838–3845 CrossRef CAS.
- É. Brémond, M. Savarese, N. Q. Su, A. J. Pérez-Jiménez, X. Xu and J. C. Sancho- García,
et al., Benchmarking density functionals on structural parameters of small-/medium-sized organic molecules, J. Chem. Theory Comput., 2016, 12(2), 459–465 CrossRef PubMed.
- M. Kertesz, C. H. Choi and S. Yang, Conjugated polymers and aromaticity, Chem. Rev., 2005, 105(10), 3448–3481 CrossRef CAS PubMed.
- J. C. Sancho-García and A. J. Pérez-Jiménez, Improved accuracy with medium cost computational methods for the evaluation of bond length alternation of increasingly long oligoacetylenes, Phys. Chem. Chem. Phys., 2007, 9(44), 5874–5879 RSC.
- S. R. Langhoff, Theoretical infrared spectra for polycyclic aromatic hydrocarbon neutrals, cations, and anions, J. Phys. Chem., 1996, 100(8), 2819–2841 CrossRef CAS.
- C. S. Wu and J. D. Chai, Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT, J. Chem. Theory Comput., 2015, 11(5), 2003–2011 CrossRef CAS PubMed.
- A. Pérez-Guardiola, M. E. Sandoval-Salinas, D. Casanova, E. San-Fabián, A. J. Pérez-Jiménez and J. C. Sancho-Garcia, The role of topology in organic molecules: origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers, Phys. Chem. Chem. Phys., 2018, 20(10), 7112–7124 RSC.
- H. J. Huang, S. Seenithurai and J. D. Chai, TAO-DFT study on the electronic properties of diamond-shaped graphene nanoflakes, Nanomaterials, 2020, 10(6), 1236 CrossRef CAS PubMed.
- D. Doehnert and J. Koutecky, Occupation numbers of natural orbitals as a criterion for biradical character. Different kinds of biradicals, J. Am. Chem. Soc., 1980, 102(6), 1789–1796 CrossRef CAS.
- J. P. Malrieu and G. Trinquier, Can a topological approach predict spinsymmetry breaking in conjugated hydrocarbons?, J. Phys. Chem. A, 2016, 120(48), 9564–9578 CrossRef CAS PubMed.
- D. Jacob, R. Ortiz and J. Fernández-Rossier, Renormalization of spin excitations and Kondo effect in open-shell nanographenes, Phys. Rev. B, 2021, 104(7), 075404 CrossRef CAS.
- R. Landauer, Irreversibility and heat generation in the computing process, IBM J. Res. Dev., 1961, 5(3), 183–191 Search PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, Introduction of N-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114(23), 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350(3–4), 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, N-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117(20), 9138–9153 CrossRef CAS.
- B. Shi, D. Nachtigallova, A. J. Aquino, F. B. Machado and H. Lischka, Highlevel theoretical benchmark investigations of the UV-vis absorption spectra of paradigmatic polycyclic aromatic hydrocarbons as models for graphene quantum dots, J. Chem. Phys., 2019, 150(12), 124302 CrossRef PubMed.
- M. El Khatib, S. Evangelisti, T. Leininger and G. L. Bendazzoli, A theoretical study of closed polyacene structures, Phys. Chem. Chem. Phys., 2012, 14(45), 15666–15676 RSC.
- L. Cusinato, S. Evangelisti, T. Leininger and A. Monari, The Electronic Structure of Graphene Nanoislands: A CAS-SCF and NEVPT2 Study, Adv. Condens. Matter Phys., 2018, 2018, 9097045 Search PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119(23), 12129–12137 CrossRef CAS.
- M. Swart and M. Gruden, Spinning around in transition-metal chemistry, Acc. Chem. Res., 2016, 49(12), 2690–2697 CrossRef CAS PubMed.
- S. Song, M. C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, Benchmarks and
reliable DFT results for spin gaps of small ligand Fe (II) complexes, J. Chem. Theory Comput., 2018, 14(5), 2304–2311 CrossRef CAS PubMed.
- L. Rousseau, E. Brémond and G. Lefèvre, Assessment of the ground spin state of iron (I) complexes: insights from DFT predictive models, New J. Chem., 2018, 42(10), 7612–7616 RSC.
- M. Reiher, O. Salomon and B. Artur Hess, Reparameterization of hybrid functionals based on energy differences of states of different multiplicity, Theor. Chem. Acc., 2001, 107(1), 48–55 Search PubMed.
- J. W. Hager and S. C. Wallace, Two-laser photoionization supersonic jet mass spectrometry of aromatic molecules, Anal. Chem., 1988, 60(1), 5–10 CrossRef CAS.
- N. Ando, S. Kokubo, M. Mitsui and A. Nakajima, Photoelectron spectroscopy of pyrene cluster anions,(pyrene) n-(n= 1–20), Chem. Phys. Lett., 2004, 389(4–6), 279–283 CrossRef CAS.
- V. Coropceanu, J. André, M. Malagoli and J. Brédas, The Role of Vibronic Interactions on Intramolecular and Intermolecular Electron Transfer in π-Conjugated Oligomers, Theor. Chem. Acc., 2003, 110(2), 59–69 Search PubMed.
- F. C. Grozema and L. D. Siebbeles, Mechanism of Charge Transport in Self- Organizing Organic Materials, Int. Rev. Phys. Chem., 2008, 27(1), 87–138 Search PubMed.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, Estimation of Inner Shell Marcus Terms for Amino Nitrogen Compounds by Molecular Orbital Calculations, J. Am. Chem. Soc., 1987, 109(3), 677–682 CrossRef CAS.
- J. L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Charge-Transfer and Energy-Transfer Processes in π-Conjugated Oligomers and Polymers: A Molecular Picture, Chem. Rev., 2004, 104(11), 4971–5004 CrossRef PubMed.
- R. S. Sánchez-Carrera, V. Coropceanu, D. A. da Silva Filho, R. Friedlein, W. Osikowicz and R. Murdey,
et al., Vibronic Coupling in the Ground and Excited States of Oligoacene Cations, J. Phys. Chem. B, 2006, 110(38), 18904–18911 CrossRef PubMed.
- J. C. Sancho-García, Assessment of Density-Functional Models for Organic Molecular Semiconductors: The Role of Hartree–Fock Exchange in Charge-Transfer Processes, Chem. Phys., 2007, 331(2), 321–331 CrossRef.
- C. Sutton, J. S. Sears, V. Coropceanu and J. L. Brédas, Understanding the Density Functional Dependence of DFT-Calculated Electronic Couplings in Organic Semiconductors, J. Phys. Chem. Lett., 2013, 4(6), 919–924 CrossRef CAS PubMed.
- A. Devos and M. Lannoo, Electron-phonon coupling for aromatic molecular crystals: Possible consequences for their superconductivity, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(13), 8236 CrossRef CAS.
- J. C. Sancho-García and A. J. Pérez-Jiménez, Charge-transport properties of prototype molecular materials for organic electronics based on graphene nanoribbons, Phys. Chem. Chem. Phys., 2009, 11(15), 2741–2746 RSC.
- A. J. Perez-Jimenez and J. C. Sancho-García, Using circumacenes to improve organic electronics and molecular electronics: design clues, Nanotechnology, 2009, 20(47), 475201 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (i) IR spectra of n-rhombenes; (ii) plots of the ρU(r) spatial distribution of n-rhombenes; (iii) NU and Yi values calculated at the RAS-SF/6-31G* level for n-rhombenes; (iv) HOMO and LUMO orbital energies as calculated at various DFT/def2-TZVP levels; (v) vertical singlet–triplet and singlet–quintet energies calculated at the RAS-SF/6-31G* and DFT/def2-TZVP levels for n-rhombenes; (vi) 〈Ŝ2〉 values for singlet, triplet, and quintet states at the DFT level; (vii) plots of the (triplet and open-shell singlet) spin density spatial distribution of n-rhombenes; (viii) cartesian coordinates of n-rhombenes optimized at the B97-3c level. See DOI: https://doi.org/10.1039/d3cp01103h |
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
R.
Bernabeu-Cabañero
,
R.
Bernabeu-Cabañero
 ,
A. J.
Pérez-Jiménez
,
A. J.
Pérez-Jiménez
 ,
E.
San-Fabián
,
E.
San-Fabián
 and
J. C.
Sancho-García
and
J. C.
Sancho-García
 *
*

![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) nSF =
nSF = ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF0 +
nSF0 + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFh +
nSFh + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFp +
nSFp + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSFhp +
nSFhp + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF2h +
nSF2h + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF2p+ …,
nSF2p+ …,![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) nSF0 performs all possible spin-flip excitations within RAS2 and h and p subindices indicate the number of holes and particles in RAS1 and RAS3, respectively. In the approximation used here p = h = 1; i.e., the right side of eqn (2) is truncated at the third term. The eigenvalues are obtained from a wavefunction expanded over a high-spin single reference restricted set of Slater determinants,
nSF0 performs all possible spin-flip excitations within RAS2 and h and p subindices indicate the number of holes and particles in RAS1 and RAS3, respectively. In the approximation used here p = h = 1; i.e., the right side of eqn (2) is truncated at the third term. The eigenvalues are obtained from a wavefunction expanded over a high-spin single reference restricted set of Slater determinants,  , where |ΦR〉 are the allowed electronic configurations. These calculations will be also coupled with the PBE41 short-range exchange–correlation energy functional, to introduce both types (long- and short-range) of electron correlation effects, briefly denoted as RAS-srPBE in the following, since this functional is chosen for this RAS-srDFT extension.
, where |ΦR〉 are the allowed electronic configurations. These calculations will be also coupled with the PBE41 short-range exchange–correlation energy functional, to introduce both types (long- and short-range) of electron correlation effects, briefly denoted as RAS-srPBE in the following, since this functional is chosen for this RAS-srDFT extension.
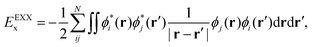



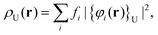


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(2) ≈ 18 meV, with kB the Boltzmann constant and T the temperature] for energy dissipation at room temperature, a key magnitude for having stable spintronics devices. Note that for 6-rhombene, the ΔEST and the ΔESQ values are energetically close just separated by less than 0.2 eV.
ln(2) ≈ 18 meV, with kB the Boltzmann constant and T the temperature] for energy dissipation at room temperature, a key magnitude for having stable spintronics devices. Note that for 6-rhombene, the ΔEST and the ΔESQ values are energetically close just separated by less than 0.2 eV.




