Fast and precise chiroptical spectroscopy by photoelectron elliptical dichroism

Abstract

The photoionization of chiral molecules by elliptically polarized femtosecond laser pulses produces photoelectron angular distributions which show a strong and enantio-sensitive forward/backward asymmetry along the light propagation direction. We report on high precision measurements of this photoelectron elliptical dichroism (PEELD). Using an optical cavity to recycle the laser pulses and increase the signal-to-noise ratio, we determine enantiomeric excesses with a 0.04% precision with a low-power femtosecond laser (4 W) in a compact scheme. We perform momentum-resolved PEELD measurements in 16 molecules, from volatile terpenes to non-volatile amino acids and large iodoarenes. The results demonstrate the high structural sensitivity of PEELD, confirming the spectroscopic interest of this technique. Last, we show how a convolutional neural network can be used to retrieve the chemical and enantiomeric composition of a sample from the momentum-resolved PEELD maps.

---

1. Introduction

The sensitivity of biological processes to molecular chirality makes chiral analysis crucially important in many scientific and industrial domains, from fundamental physics to pharmacology, food or fragrance industry. The enantiomeric purity of chiral compounds is particularly important in pharmaceutical products, since the mirror image of a therapeutic drug can be toxic.¹ Quality control thus requires to determine the enantiomeric excess of these compounds with a 0.05% error bar.² Such measurements are routinely performed by chiral chromatography, relying on the different migration times of the two enantiomers through a chiral column.² However, the speed of chromatographic measurements is intrinsically limited by the migration time needed for baseline resolving a pair of enantiomers. Moreover, the precision of the measurements strongly depends on the column and measured compounds. Chromatography is thus not suitable for continuous monitoring of the enantiomeric composition of a product, which is required with regard to the next generation of pharmaceutical manufacturing using integrated online measurement devices and real-time data analysis, in so-called Industry 4.0.³ The measurement duration issue can be solved by using non-chromatography processes that provide an instantaneous response. This is naturally the case in light-matter interaction, which has always been an important element of chiral analysis. Innovative chiroptical spectroscopies are continuously being developed,^4–8 enabling advances both in fundamental science and industry. Unfortunately, chiroptical spectroscopies are generally based on weak electric quadrupole or magnetic dipole interactions, leading to weak signals and limiting the precision of the measurements. This issue can be circumvented by using advanced experimental configurations, such as cavity-enhanced polarimetry.⁸ Alternatively, new light-matter interaction schemes, relying on physical processes providing strong chirosensitive signals within the electric-dipole approximation, have recently emerged,^9–11 offering new perspectives for precise enantiomeric excess measurements.^12–14 Here we rely on one of them: photoelectron elliptical dichroism (PEELD).¹⁵

The manuscript is organized as follows. In Section 2, we introduce the basic principle of PEELD measurements, describe the experimental setup and data analysis procedure. We measure the enantiomeric excess of a series of fenchone samples, and compare the measurements to standard GC × GC-TOF-MS measurements. In Section 3, we show that the signal-to-noise ratio of photoelectron dichroism measurements can be increased by using a new optical configuration based on a multi-pass cavity. Section 4 reports PEELD measurements in 16 molecules, demonstrating the generality and spectroscopic sensitivity of the technique. In Section 5, we show how neural networks can be used to improve the data analysis and measure the chemical and enantiomeric composition of samples. Perspectives of future applications are discussed in the concluding Section 6.

2 Photoelectron elliptical dichroism (PEELD) measurement

2.1 Photoelectron elliptical dichroism

Photoelectron circular dichroism (PECD) is a remarkably strong chiroptical process occurring when chiral molecules are photoionized by circularly polarized light.^9,10,16 The angular distribution of the ejected photoelectrons shows an asymmetry along the light propagation axis, which reverses when switching the helicity of light or the molecular handedness of the sample. For an enantiomerically pure sample, such photoelectron asymmetry is typically two orders of magnitude higher than most chiroptical effects, reaching several percents. This is due to the fact that PECD does not require magnetic dipole or electric quadrupole effects, but purely relies on electric dipole transitions. PECD was initially studied using single photon ionization by XUV pulses at synchrotrons,^10,16 before being extended to table-top schemes using multiphoton ionization by femtosecond laser pulses,^17,18 single-photon ionization by high-order harmonics,¹⁹ and strong-field ionization.²⁰

The PECD effect is proportional to the enantiomeric excess of the ionized compound. PECD was thus proposed as a new tool to determine the composition of chiral samples,^13,14,21,22 providing accuracy in the 1% range. The advent of high average power, high-repetition rate femtosecond lasers has enabled considerably speeding up multiphoton PECD measurements,²² up to a point where the time taken to switch from one laser helicity to the opposite became a bottleneck. It turned out that continuously recording the photoelectron angular distribution while scanning the ellipticity of the ionizing laser field provides richer information than simply using circularly polarized light.¹⁵ To highlight the importance of the ellipticity, this effect was called photoelectron elliptical dichroism (PEELD). The enhanced structural sensitivity of PEELD results from the influence of resonances in the multiphoton ionization process, which break the isotropy of the sample.^15,23–26

Measuring multiphoton PEELD requires a photoelectron detector, a sample introduction system, an optical system based on a femtosecond laser and a data analysis procedure. The following sections describe each of these items.

2.2 VMI detection

In order to accurately measure PEELD, a detector able to distinguish photoelectrons ejected in the forward and backward direction with respect to the light propagation axis z is needed. A broad range of instruments can be used for this purpose. The most sophisticated schemes detect the 3D momentum distribution (p_x, p_y, p_z) of the photoelectrons in coincidence with the associated ions (reaction microscope/cold target recoil imaging spectrometer COLTRIMS).^13,27,28 They enable accurate measurements but suffer from long acquisition times inherent to coincidence detection. Giving up the ion detection and reducing the dimensionality of the measurement to 2D enables using a phosphor screen and camera to image the photoelectron detector, in velocity map imaging (VMI) spectrometers,²⁹ which measure (p_x, p_z) projections of the 3D photoelectron angular distributions while integrating along p_y as shown in Fig. 1. Last, simpler detectors, integrating the electron signal ejected in the forward and backward hemispheres, can be used,^10,22,30 but they miss energy and full angular resolutions which enable distinguishing different molecular species in a mixture.¹⁵

Fig. 1 Scheme of the velocity map imaging spectrometer.

The spectrometer used in the work reported in this paper is presented in Fig. 1. It is made of a compact and low voltage VMI inspired by ref. 31, in which the design consisted of a repeller electrode and a glass resistive tube to set a smooth electric field gradient. In our case, we avoided the glass tube in order to improve the pumping efficiency, and replaced it by a stack of electrodes spaced by 5 mm and connected to each other by 100 kΩ resistors. The length of the flight-tube is 70 mm, the electrodes' diameter is 40 mm, and the voltage of the repeller is set at 125 V by a continuous power supply (1/8 A12-N4-F-M 125 V, Advanced Energy). The electrons are focused onto a double stack of microchannel plates with a 40 mm diameter (MCP) coupled to a P46 fast decay phosphor screen (F2225-21PGF assembly, Hamamatsu) which is imaged on a 16-bit sCMOS camera (CS2100M-USB, Thorlabs) with a FL = 12.5, F1.4 lens (HF12.5SA-1, Fujinon). The camera records the electron distributions at 20 frames per second (50 ms exposure time with no dead-time). The typical MCP voltage is in the range of 900 V to 1200 V depending on the amount of incoming signal, and the phosphor screen voltage is set at 3000 V.

The MCPs require working at a pressure below a few 10⁻⁵ mbar. This is achieved by a 28 m³ h⁻¹ primary pump (ACP28 G, Pfeiffer) and a 500 L s⁻¹ magnetic turbomolecular pump (ATH 500 MT, Pfeiffer) which are heated and corrosion-proof in order to ensure a long survivability against various chemical compounds. A double Helmotz coil configuration (not drawn in Fig. 1) is added to compensate for the external magnetic fields.

2.3 Sample introduction

Two setups can be used to introduce the sample into the VMI, depending on the volatility of the molecules.

If the studied molecule has a high vapor pressure (typically above 0.1 mbar at 20 °C), we simply introduce it in a quartz vial which is connected via a 4 mm inner diameter and 400 mm long stainless steel tube (100 mm in vacuum) to a 0.5 mm diameter nozzle. The pipes are heated to 70 °C to avoid condensation, and the vial is typically heated at 40 °C to increase the vapor pressure. A needle valve is used to adjust the pressure below 5 × 10⁻⁵ mbar in the VMI. The consumption rate lies in the range of 1 mg h⁻¹. The nozzle is located 20 mm away from the edge of the electrodes to avoid disturbing the electrostatic imaging lens in the VMI. The spatial extent of the gas jet is consequently very large when it reaches the region of interaction with the laser beam.

If the molecule is not volatile, a different technique must be used. Electrosprays coupled to ion optics are routinely used to put large non-volatile molecules in the gas phase in ionic forms.³² This technology was recently shown to be compatible with photoelectron circular dichroism measurements,^30,33,34 but the low density of the target requires long acquisition times. Using evaporated neutral molecules enables producing much higher densities, resulting in faster measurements, and is less expensive. In order to evaporate the solid in vacuum, we use a small stainless steel oven which can contain a few mg of sample and is set on a translation stage with a primary pumping chamber. This enables us to quickly and easily change the sample while letting the secondary pumping on. The oven is heated by a 9 W continuous multimode laser diode at 976 nm (Aerodiode). It absorbs about 30% of the incoming light, and has low degree of mechanical and thermal contact with other parts. The oven can reach easily a few hundreds of °C in a few minutes, efficiently evaporating the samples. The wireless heating is very practical to set in and remove from the vacuum.

2.4 Laser, optics

The ionization potential (I_p) of organic compounds typically lies in the range of 6–10 eV, which can be reached by non-linear absorption of a few visible photons. The first PECD measurements performed in this regime employed Ti:Sa femtosecond laser sources,^17,18 whose large footprint and cost were incompatible with industrial applications. The development of compact, high power, high repetition rate, stable and reliable Yb-doped femtosecond lasers for industrial applications such as micromachining and ocular surgery has opened new perspectives. Here we use a 4 W Yb fiber laser at 1030 nm, delivering 350 fs pulses at 100 kHz repetition rate (Satsuma, Amplitude). The laser amplifier is compact (30 × 20 × 50 cm³ coupled to 3U 19′′ rack) and can be easily integrated. The chirosensitive asymmetry in the multiphoton ionization process is stronger in the visible range than in the infrared range.²⁰ We thus frequency double the laser pulses in a 3 mm thick type-I Beta-Barium Borate (BBO) crystal producing a 515 nm beam with 2 W average power (20 μJ energy per pulse). The optical setup is presented in Fig. 2 and described below.

Fig. 2 Scheme of the optical setup.

The power of the 515 nm beam is controlled by an attenuator made of a motorized zero-order half waveplate (10RP02-14 on PR50CC, Newport) and a fixed polarizer (420-1244i45HE, Eksma) transmitting the s-polarization. After the BBO, the beam has a radius at 1/e² of 2.2 mm and is expended by a lens-based telescope with magnification of 2. The polarization state of the beam is finally controlled after the last 45° mirror by a zero-order quarter waveplate (10RP04-14, Newport) mounted on a fast and stable direct drive rotation stage (RGV 100BL-S, Newport). The beam is then focused with a f = 200 mm lens to reach a radius at 1/e² of 9 μm at focus with M² = 1.2. The maximum intensity at focus is thus 4.0 × 10¹³ W cm⁻². After the VMI, we measure the power of the laser beam with a USB powermeter (PM16-405, Thorlabs). We can correct the slow drifts that may occur with a simple feedback loop on the motorized half waveplate of the attenuator.

2.5 Polarization modulation and PEELD measurement

The PEELD measurement is performed by continuously acquiring the 2D-projection of the 3D-photoelectron angular momentum distribution PAD^raw(p_x, p_z, t), where x is the vertical axis in the laboratory frame and z is the laser propagation axis, while rotating the quarter waveplate at the constant speed of 45° s⁻¹. The helicity of the laser beam reverses every 90°, such that the fundamental frequency of the photoelectron signal modulation ω₀ corresponds to a quarter waveplate rotation of 180°.

From PAD^raw(p_x, p_z, t) we extract F(t) and B(t), the number of electrons ejected respectively in the forward and backward hemispheres of the 3D-photoelectron distribution:

We calculate the asymmetry g that is the chirosensitive signal:This asymmetry must reverse when the helicity of the ionizing radiation changes sign, i.e. every 90° as shown in Fig. 3(c). To remove artifacts due to the inhomogeneities of the detector, we thus calculate g(t) by subtracting the signals measured at opposite helicities: . The resulting signal obtained in (+)-fenchone is displayed in Fig. 3(c). It shows a non-sinusoidal behavior, which reflects the influence of resonances in the multiphoton ionization process.¹⁵ The chirosensitive signal is expected to be zero in linear polarization and switches sign with the helicity of the ionizing radiation. Consequently, the signal is odd, and its Fourier transform, displayed in Fig. 3(d) is purely imaginary. This Fourier transform is made of a series of sharp peaks at odd multiple frequencies of ω₀, that are defined as:

Ω_j = j × ω₀

where j ∈ N. The amplitude of the peaks is proportional to the amplitude of the chirosensitive signal. Measuring the amplitude of the strongest peak (at frequency Ω₃ in the present case) enables optimizing the signal-to-noise ratio and getting rid of the background noise, as in a lock-in detection scheme.

Fig. 3 Principle of photoelectron elliptical dichroism (PEELD) measurements. (a) The gaseous compound (here fenchone) is sent in the Velocity Map Imaging spectrometer (VMI), where it is ionized by the elliptically polarized laser pulses. The created photoelectrons are projected by high voltage electrodes on a detector. The measured 2D projection of the 3D photoelectron distribution is asymmetric along the laser propagation axis, showing an excess in the forward (F) or backward (B) half. (b) This photoelectron asymmetry changes sign with light or molecular handedness. (c) The asymmetry is measured continuously as the quarter waveplate rotates at 45° s⁻¹. (d) Fourier transforming these oscillations provides characteristic peaks at well-defined frequencies. The magnitude of the peaks is proportional to the enantiomeric excess of the compound. (e) Statistical analysis of the amplitude of the g(Ω₃) peak from pure (+)-fenchone, in a series of 250 measurements of 8 s duration each, showing a 0.1% relative error bar on the measured asymmetry.

In order to obtain statistical information about the precision of the measurement, we measure the oscillations of the signal for 2000 s, and subdivide the scans into subscans of 8 s, which corresponds to one full rotation of the quarter waveplate. This provides us with 250 consecutive measurements of the amplitude of the Fourier peak g(Ω₃). The histogram of these measurements is shown in Fig. 3(e). It follows a normal distribution law, centered at 〈g(Ω₃)〉 = 2.161 × 10⁻². The 68% confidence interval of a single 8 s measurement is given by ±σ, the standard deviation of the Gaussian fit. For our dataset, σ = 3.24 × 10⁻⁴. The confidence interval of a series of N measurements is given by the standard error SE defined as:

From our complete set of 250 measurements, we obtain SE = 2 × 10⁻⁵. In other words, the forward backward asymmetry in the photoelectron ejection from (+)-fenchone molecules is 〈g(Ω₃)〉 = (2.161 ± 0.002) × 10⁻² for a 33 min 20 s measurement duration. This asymmetry is determined with a relative error RSE defined as:
The error in our measurement is thus RSE = ±0.1% (or said alternatively the precision of our measurement is 99.9%). In the following section, we describe how this asymmetry can be used to determine the enantiomeric excess of a chemical sample.

2.6 PEELD with calibrated mixtures and comparison with GC × GC-TOF-MS measurement

As any chiroptical measurement, the asymmetry g measured in PEELD scales linearly with the enantiomeric excess ee of the ionized compound:

g(Ω₃) = a × ee

where a is a conversion factor that can be calibrated using an enantiopure sample (ee = 1, g_pure = a), and ee is defined as the relative excess of the (+) enantiomer with respect to the (−) one:
In order to confirm this and prove that PEELD can be used to determine accurately the ee, we performed measurements in various samples of fenchone. We started from two samples, a pure (+)-fenchone and a (−)-fenchone sample with an enantiomeric excess ee = −84 ± 4%, determined by optical rotation (OR) by the company (Sigma Aldrich). We made a few mixtures from these samples, by weighing them in different proportions with a scale with 4 mg precision to obtain 4 mixtures of 5 g each. The proportions were chosen to obtain quasi-enantiopure mixtures as well as quasi-racemic mixtures.

The asymmetry g(t) from each sample was measured in a 2000 s acquisition, and the resulting histograms are plotted in Fig. 4. The different samples produce clearly distinguishable histograms. We calibrate the enantiomeric excess by assigning the pure (+)-fenchone sample at 100% to obtain the conversion factor a from g to ee. The results of the statistical analysis of each histogram are summarized in Table 1.

Fig. 4 Distributions of the Ω₃ Fourier component of the forward backward asymmetry g, in series of 250 measurements performed in fenchone samples with various enantiomeric excesses. The average asymmetries and error bars are in the legend. The top axis shows the retrieved ee, assuming ee = 100% for the first sample (black curve).

Table 1 Enantiomeric excess measurement comparison between weighing, PEELD, and GC × GC-TOF-MS methods

Mixture	OR and weighing (%)	PEELD (%)	GC × GC-TOF-MS (%)
100/0	+100	+100	+100
99.5/0.5	+99 ± 4	+99.1 ± 0.1	+99.3 ± 0.02
50/50	+8 ± 4	+9.6 ± 0.1	+10.1 ± 0.4
30/70	−29 ± 4	−26.6 ± 0.1	−25.3 ± 0.3
1/99	−82 ± 4	−79.0 ± 0.1	−76.8 ± 0.1
0/100	−84 ± 4	−80.7 ± 0.1	−78.4 ± 0.4

---

The optical rotation measurements, on which the determination of the expected ee relies, are rather inaccurate. To circumvent this issue, we performed additional characterization of the samples by using comprehensive two-dimensional gas-chromatography coupled to reflectron time-of-flight mass spectrometry (GC × GC-TOF-MS). GC × GC is a powerful technique for the analytical separation of complex mixtures utilizing two orthogonal columns with different phase selectivities coupled by a modulation device. This configuration allows enhanced resolution power, detectability, and increased signal-to-noise ratio compared to conventional one-dimensional gas-chromatography.

The GC × GC column set consisted of a Lipodex E [octakis(3-O-butanoyl-2,6-di-O-n-pentyl)-γ-cyclodextrin] primary capillary column (24.96 m × 0.25 mm, Macherey-Nagel, Düren Germany) coupled by a dual-stage thermal jet modulator to a DB Wax (polyethylene glycol, 1.47 m × 0.1 mm, 0.1 μm, Agilent, CA, USA) secondary column. Helium was used as a carrier gas at a flow rate of 1 mL min⁻¹. The inlet was held at 230 °C, and the transfer line and the ion source at 240 °C and 230 °C, respectively. The temperature of the primary oven was held at 40 °C for 1 min, followed by an increase of 10 °C min⁻¹ to 75 °C held for 10 min, then 1 °C min⁻¹ increase to 105 °C, immediately followed by an increase of 20 °C min⁻¹ to 180 °C and held for 2 min. The secondary oven operated with a constant 30 °C offset and the modulation period was 5 s. The TOF-MS operated at 150 Hz storage rate with a 50–500 a.m.u. mass range and 35 min solvent delay. The microchannel plate detector voltage was kept at 2034.4 V. Aliquots of 1 μL of the mixtures of (+)- and (−)-fenchone in hexane at a concentration of 10⁻⁴ M were injected 15-times in the split mode with a split ratio of 1 : 200.

The GC × GC-TOF-MS analysis confirmed the enantiopurity of the (+)-fenchone sample within the detection capabilities of the instrument (Table 1). Despite carefully optimizing the GC × GC resolution, the accuracy of the ee determination of the other five scalemic samples was hampered by first-dimension peak tailing of the first eluting (−)-fenchone enantiomer overlapping with the second eluting (+)-fenchone signal. This can well explain the higher values of the absolute ee-s compared to those determined by PEELD. This is supported by the increase of this bias with increasing relative proportion of (--)-fenchone in the mixtures, and consequently higher relative contribution of the (−)-fenchone tailing to the (+)-fenchone signals. In terms of precision, GC × GC-TOF-MS outperforms PEELD only in the case of the 99.5/0.5 mixture (Table 1). This is a result of the high (+)-fenchone signal-to-noise ratio in combination with a rather negligible contribution of the tailing of the minor (−)-fenchone signal.

2.7 Improving precision by increasing measurement duration

The precision of the enantiomeric excess measurements by PEELD is determined by the error bars on the evaluation of the asymmetry g. Since the method is based on a continuous acquisition, this error bar can in principle be decreased by increasing the measurement duration, i.e. the number N of rotations of the half waveplate. The error bar should decrease as as long as the limiting factor is the signal to noise ratio on the photoelectron signal. However, other parameters could come into play and prevent the error bars to decrease. First, let us mention that the asymmetry g is intrinsically robust against variations of the pressure because it is a normalized quantity as shown in eqn (1). We thus do not need to worry about the stability of the gas source. On the other hand, PEELD relies on a non-linear process (multiphoton absorption), and is sensitive to the variations of laser intensity (see Fig. 3(d) in ref. 15). The laser source we use is quite stable, with a power stability of <1% RMS, but thermal drifts in the experimental room can affect the power of the frequency doubled laser beam. This issue is circumvented by the active stabilization of the 515 nm power in the experiment.

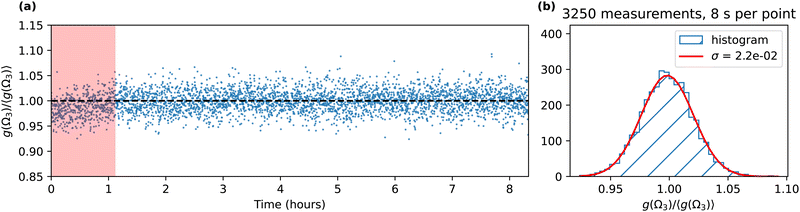
In order to estimate the stability of our measurement, we present in Fig. 5(a) the deviation of the asymmetry g(Ω₃) from its mean 〈g(Ω₃)〉 during an 8 h acquisition with active stabilization of the 515 nm laser power. The asymmetry is not stable during the first hour where we observe a slow increase, which is likely due to a thermalization of the focusing optics. After this, we observe very good stability of the asymmetry. Fig. 5(b) shows the statistical analysis of the 3250 measurements of g(Ω₃) performed after the first 500 measurements (66 min 40 s). It follows a Gaussian distribution centered at 1 with a standard deviation σ equal to 2.2 × 10⁻². Thanks to the stability of the signal, increasing the measurement duration to a few hours clearly improves the precision of the asymmetry measurement. The relative standard error is equal to 4 × 10⁻⁴, i.e., the precision of our measurement reaches 99.96%. This scheme thus enables to determine enantiomeric excess with precision above 99.95%, beyond the analytical standards required in pharmaceutical industry. Note that the continuous acquisition mode can also be used to perform live/in-line measurements where subtle changes of the ee composition of a sample can be tracked.

Fig. 5 (a) Long-term temporal evolution of the third Fourier component of the asymmetry parameter in (+)-fenchone g(Ω₃), measured every 8 s, normalized by its average value 〈g(Ω₃)〉. (b) Histogram of the 3250 measurements excluding the beginning of the experiment during which the optics were heating up (red area in (a)). The histogram follows a Gaussian law with a standard deviation σ = 2.2 × 10⁻². The relative standard error of the whole measurement is thus , meaning that we reach a precision of 99.96%.

In the following we show that high precision measurements can be performed in shorter acquisition times by implementing an optical cavity.

3. PEELD with an optical cavity

The precision of the enantiomeric excess measurement is limited by the statistical noise of the signal inherent to the MCP, such that increasing the level of the signal improves the precision. Increasing the density of the gas jet does increase the signal, but is limited by the necessity to keep the pressure below a few 10⁻⁵ mbar to operate the MCPs. Once this limit is reached, it is possible to increase the volume of ionization, for instance by using a larger focal length and increasing the energy of the laser pulses. However, this requires increasing the power of the laser source, which is costly. We present here an alternative manner to increase the signal while keeping the laser power fixed, by recycling the laser pulses in an optical cavity using the characteristic geometrical properties of the PEELD effect.

Velocity map imaging spectroscopy in an optical cavity was recently demonstrated,^35,36 using a sophisticated optical scheme relying on frequency combs. In this setup, the laser pulses coherently add up in the resonant cavity, producing an enhancement of the laser intensity enabling multiphoton ionization studies to be conducted at very high repetition rates (100 MHz). Here our approach is very different. We aim at developing a simple and robust optical scheme to recycle the intense femtosecond laser pulses after they have ionized the molecules.

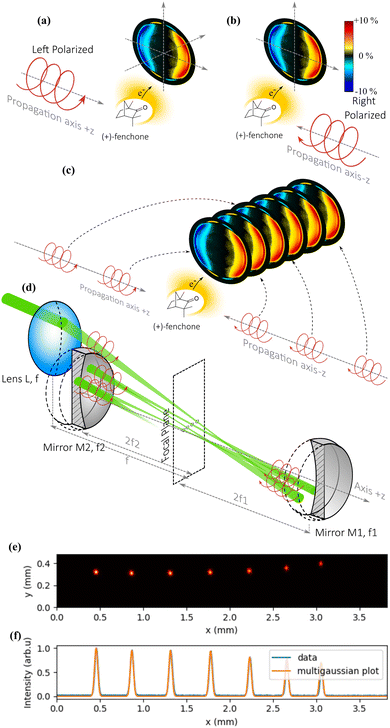
The cavity is made of two spherical mirrors at near normal incidence. Each reflection sends the focused laser pulse back into the gas mixture, allowing it to ionize new molecules. The critical point of the method is that the reflection allows to reverse not only the direction of propagation of the light, but also the helicity of the laser pulses (for example from left circular to right circular). As explained in Fig. 6(a) and (b), the photoelectron signal induced by a right circularly polarized light propagating along the +z direction is identical to that of a left circularly polarized light propagating along −z. Thus, the multiple reflections from the cavity mirrors provide PEELD signals that add up, improving the precision of the measurement as explained in Fig. 6(c).

Fig. 6 Principle of PEELD measurements using an optical cavity. The PEELD remains identical if both the helicity and the propagation direction of the ionizing light are reversed ((a) and (b)). In (c), a sequence of pulses with opposite helicities and propagation directions gives the same PEELD, but with a better signal-to-noise ratio. (d) Cavity made of spherical mirrors imaging the first focus of a lens several times. After each reflection, the direction of propagation and the helicity are switched, giving the same PEELD. (e) Measurement of the spatial profile of the laser foci with a sampling plate placed in the cavity. (f) Measurement of their horizontal profiles (blue) plotted under a sequence of equal width Gaussian functions (yellow).

For this solution to work, two conditions must be fulfilled: (i) the laser pulse must be refocused in the gas jet after each reflection to ionize the chiral molecules; (ii) the different foci must produce similar photoelectron distributions, which imposes a condition on their positions as well as on the photoelectron imaging in the spectrometer.

The optical scheme is described in Fig. 6(d). The beam arrives with an elliptical polarization and is first focused into the VMI by a plano-convex lens L of focal length f. After the focus, the beam diverges, up to a concave spherical mirror M1 of focal length f₁ positioned exactly at a distance 2 × f₁, which refocuses it in the same plane as the first focus. After this second focus, the beam diverges again and reaches a second concave spherical mirror M2 of focal length f₂ positioned exactly at a distance 2 × f₂, which refocuses it next to the first and second foci. By fine-tuning the alignment of M1 and M2, it is possible to keep the beam in the cavity for numerous reflections if the size of the initial beam is small compared to the diameter of the optics.

The cavity we used consisted of 25.4 mm diameter mirrors, M1 with f₁ = 75 mm and M2 with f₂ = 87.5 mm, allowing up to 19 passes through the gas jet. Fig. 6(e) shows half of the focal spots of the 14 passes in the cavity, corresponding to the foci of the M1 mirror, imaged by inserting a slightly reflecting plate in the middle of the cavity to extract a part of the beam. We observe in Fig. 6(f) that the full width at half maximum of the spot remains the same after 7 round trips within the resolution of our camera. We also observe that the focus moves laterally by about 0.4 mm after each round-trip (0.2 mm between each focal spot), such that the focal spots are spread over a few mm. This could lead to blurring of the photoelectron images once the ionization volume is significantly larger than 3 mm³.

In order to evaluate the performance of multipass PEELD, we performed consecutive measurements in fenchone using different numbers of reflections in the cavity. Contrary to Section 2.1, in which we focused on the spatially integrated asymmetry g(t), we analyze here the temporal oscillations of the full 2D photoelectron angular distribution PAD^raw(p_x, p_z, t), while we rotate the quarter waveplate. This will enable us to determine if the imaging conditions of the photoelectrons produced by the consecutive foci are good enough to resolve spectroscopic structures in the angular distributions.

We start by imposing an up-down symmetry on the photoelectron angular distribution:

where PAD^raw is the raw image on the camera. We then separate the angular distribution in two components, one symmetric along z and one antisymmetric:In achiral targets or when the polarization state of the ionizing light is linear, the antisymmetric part Anti(p_x, p_z, t) vanishes. We Fourier-transform each pixel of these two distributions along the time axis. Similarly to the evolution of the asymmetry g presented in Section 2.1, the temporal Fourier transform of Anti(p_x, p_z, t) is expected to be constituted of odd multiples of the fundamental modulation frequency ω₀ (i.e. Ω₁, Ω₃ …). This reflects the fact that the asymmetry changes sign with the laser helicity. On the contrary, the Fourier transform of Sym(p_x, p_z, t) should contain only even multiples of ω₀ (i.e. Ω₀, Ω₂ …), since the symmetric part of the electron distribution produced by left- or right-handed polarization is the same.¹⁵

We present in Fig. 7 the 2D-resolved Fourier components Sym(p_x, p_z, Ω₀), Anti(p_x, p_z, Ω₁), Sym(p_x, p_z, Ω₂), Anti(p_x, p_z, Ω₃), resulting from 3 min 20 s measurements (25 quarter waveplate rotations) performed with 1, 3, 5, 7 and 19 passes in the cavity. In each case the components are normalized by the maximum of Sym(p_x, p_z, Ω₀). These 2D Fourier components of the signal encode the evolution of the photoelectron angular distribution with laser ellipticity. We chose to represent only the first four Fourier components, which are the strongest ones.

Fig. 7 Symmetric, and antisymmetric Fourier components of the 2D projected photoelectron distribution in (+)-fenchone, at different frequencies Ω₀, Ω₁, Ω₂ and Ω₃ as a function of number of passes in the cavity.

When a single pass in the VMI is used, the antisymmetric images of fenchone show a granular aspect, especially visible at low (p_x, p_z), which reflects the limited signal-to-noise ratio. The symmetric components consist of a central spot surrounded by a weak ring of 0.15 atomic units (a.u.) radius and a stronger ring of 0.25 a.u. radius. These two rings correspond to electron kinetic energies of respectively 0.3 and 0.88 eV. The peak at 0.88 eV is assigned to the 4-photon ionization (4 photons of energy of 2.4 eV at 515 nm) of the highest occupied molecular orbital (HOMO) of fenchone that has an ionization potential of 8.72 eV.¹⁵ This ring shows also a slight energy splitting, which appears more clearly in the antisymmetric part of the signal, and which we attribute to two close vibrational states of the ion. The ring at 0.15 a.u. momentum (0.3 eV energy) is assigned to resonant multiphoton ionization taking place through the 7d Rydberg states, which relax onto the 3p Rydberg states over the 350 fs pulse duration.²⁶

The chirosensitive part of the signal is dominated by the contribution of the external ring. The Ω₁ component shows a rather complex structure with thinner patterns, with for instance a dip with sign reversal around (p_x, p_z) = (0.2,0.1) a.u. This reflects the high structural sensitivity of multiphoton PECD/PEELD signals. The Ω₃ component shows a much less structured angular distribution, but is strong especially around 0.25 a.u. radius.

Increasing the number of passes produces clearly smoother images. The grain of the pictures originates from the Poisson distribution law of incoming event per pixel. As the total number of electrons per pixel increases, the relative error diminishes, leading to smoother images. Remarkably, the main characteristic features of all Fourier components remain unchanged. This confirms that the PEELD signals from the multiple passes add up, thanks to the combined inversion of the light propagation direction and helicity, and that the imaging conditions of the VMI are tolerant enough to cope with the presence of multiple shifted electron sources produced by the different foci.

The benefit from using the cavity can be quantified by measuring the level of the total signal as well as evaluating the precision of the determination of the asymmetry g(Ω₃). Fig. 8(a) shows that using 19 passes enables increasing the photoelectron signal by a factor 12. This is lower than the theoretical gain (19), because of the optical losses introduced at each pass by the residual reflection of the windows of the vacuum chamber.

Fig. 8 (a) Improvement of the total photoelectron signal with the number of foci. (b) Reduction of the relative standard error with the increasing signal. These data were acquired over 25 consecutive 8 s measurements, meaning a 3 min 20 s duration for each configuration.

This signal increase clearly enables improving the precision on the determination of the chirosensitive asymmetry g(Ω₃), as shown in Fig. 8(b). The cavity thus enables us to diminish the standard error by a factor >3, from 3.8 × 10⁻³ to 1.2 × 10⁻³ reaching in 3 min 20 s a similar precision as the 33 min 20 s measurement presented in Section 2.1.

To further increase the precision of the setup, we performed a 1 h 40 min (750 points of 8 s) acquisition using the 19-pass cavity, and obtained a RSE = 4 × 10⁻⁴, similar to that obtained in an 8 h (3250 points) measurement without the cavity. This constitutes a very good precision, but is not as good as one would expect from a pure statistical point of view, taking into account the 12× increase of the signal from the 8 h scan while the acquisition time difference is 4.3×. This means that we start to be stuck to the few 0.01% level noise, that could originate from other sources of noise in the measurement.

The limit of the setup can be estimated by investigating the evolution of the standard error SE of the measurement as a function of the total signal S. The error is expected to decrease as the inverse square root of the total signal S. A fitting of the measurements, presented in Fig. 8, shows that:

The constant term represents the ultimate error that can be achieved with this setup, SE^ult = 1.6 × 10⁻⁴. The accuracy of the laser power stabilization scheme may become a limitation. Furthermore, the multipass configuration increases the thermal load on the optics, and could lead to small drifts in the beam focus position, which could degrade the stability of the setup. This could be solved by setting up an active beam-pointing stabilization device. Ultimately, it seems reasonable to expect cavity-PEELD to be able to reach RSE in the 0.01% range, way beyond the standard requirements of pharmaceutical industry, while using cost-effective low average power laser sources.

Beyond any instrumental source of error, the ultimate precision of PEELD measurement is defined by the Poisson statistic of the detection of the electrons. If N_e is the mean number of collected electrons, the standard deviation σ_e of the electron signal is , and the forward/backward asymmetric signal is 〈g〉 × N_e. The relative standard error of the asymmetry measurement is thus . For a typical PECD or PEELD signal with 〈g〉 ∼1%, it is thus necessary to detect at least N_e = 6 × 10¹⁰ electrons to reach the RSE = 4 × 10⁻⁴ that we have obtained in our measurements. This is not a limitation in our setup, in which the number of events that can be detected per laser shot is only limited by space-charge effects, which are minimized by the use of multiple distinct foci in the cavity configuration. By contrast, this is an issue in electron–ion coincidence-based detection systems,^16,18,37,38 which require recording at most one event every 10 laser shots. Using a 100 kHz laser system, and thus a counting rate of 10 kHz, leads to a measurement time of about two months to reach a RSE = 4 × 10⁻⁴.

4. PEELD measurement on a large set of molecules

We have shown that cavity-enhanced PEELD could be used to perform high precision measurements of enantiomeric excesses in fenchone. The interest of such a technique is however highly dependent on its ability to characterize a broad variety of chemicals. In this section we present the results of PEELD measurements on different sets of molecules that are used in various fields, from small and volatile terpenes to non-volatile molecules such as amino acids, and even to larger iodoarenes with masses above 500 a.m.u. These molecules are listed in Fig. 9.

Fig. 9 Representative structures of all the molecules whose PEELD is reported in this article.

For each molecule, we will first investigate the evolution of the forward/backward asymmetry g as a function of the third Stokes parameter of the ionizing radiation S₃ = sin(2α). In any standard CD, the asymmetry is purely proportional to S₃. This is not the case in PEELD, where g depends non-linearly on S₃. The evolution of g with α is related to the presence of multiple components Ω_j in the Fourier analysis of the signal, as presented in Fig. 3(b) and (c). For these 1D plots, the thickness of the line will be defined as the standard deviation of 10 subsets of a Fourier-filtered 3 min 20 s measurement. Second, in order to further illustrate the spectroscopic sensitivity of PEELD, we will present the 2D momentum-resolved Fourier components Sym(p_x, p_z, Ω_0,2) and Anti(p_x, p_z, Ω_1,3) obtained in these molecules.

4.1 Terpenes

Terpenes are volatile molecules synthesized by plants, and are important constituents of essential oils. Due to their rigid structure and lack of conformers, fenchone and camphor are considered as benchmark molecules in many PECD experiments – single photon ionization PECD,^14,39 multiphoton ionization PECD,^17,18,20,22 multiphoton PEELD,¹⁵ strong field photoionization by shaped electric fields,^40,41 as well as pump–probe spectroscopy on the femtosecond^42,43 and attosecond⁴⁴ timescales. PECD from limonene has been investigated in the multiphoton regime.^24,37,45 Single photoionization PECD has also been recently measured in limonene, as well as in α and β-pinene, with a record chiroptical asymmetry of 37% in α-pinene.⁴⁶

As all the considered terpenes have an ionization potential lying in the range of 8 to 9 eV, they are ionized in a 3 + 1 resonance-enhanced multiphoton ionization (REMPI) scheme, in which 3 photons at 515 nm (2.4 eV) populate excited (Rydberg) states from which an additional photon is absorbed to reach the continuum.

The resonant character of the multiphoton ionization process is reflected in the evolution of the chirosensitive asymmetry g with the third Stokes parameter S₃, plotted in Fig. 10. Note that the line thickness used in this figure is larger than the dispersion of the data, for the sake of visibility. In all species, g is found to evolve non-linearly with S₃, indicating an important influence of a resonance in the photoionization process.¹⁵ The asymmetry evolves quasi linearly with S₃ around 0, i.e. when the ionizing radiation is close to linearly polarized. As the ellipticity of the radiation further increases, the magnitude of the asymmetry is found to saturate around S₃ ≈ 0.6–0.7, before showing an abrupt change beyond S₃ ≈ 0.7. In most compounds, the asymmetry measured in circular polarization (S₃ = 1) is opposite to the one measured in elliptical polarization around S₃ ≈ 0.6–0.7. In limonene, the asymmetry vanishes in circular polarization. The typical magnitude of the asymmetry lies in the 2% range, except for limonene and α-pinene where g remains below 0.5%. Fenchone and camphor, two isomers whose structures differ solely in the position of their geminal methyl groups, show very opposite asymmetries. α- and β-pinene, two isomers which differ in the position of a double bond, also show very different g asymmetries. On the other hand, camphor and β-pinene present very similar evolutions. The integrated forward/backward g asymmetry thus possesses a spectroscopic sensitivity, but is not the best probe of molecular structure. More information can be obtained by plotting the momentum-resolved photoelectron distributions as already shown in Fig. 7.

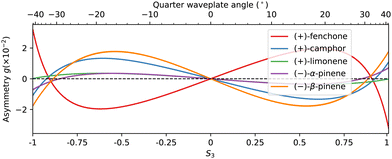Fig. 10 Forward/backward asymmetry in the photoionization of terpenes (fenchone, camphor, limonene, α-pinene and β-pinene) as a function of the third Stokes parameter S₃ of the ionizing radiation.

Fig. 11 shows the symmetric and antisymmetric parts of the photoelectron angular distribution, decomposed along the Fourier components characterizing their evolution with ellipticity. The forward/backward symmetric components obtained in all these molecules generally look similar, while the antisymmetric components present much more distinguishable patterns. This highlights the fact that PEELD is extremely sensitive to the molecular potential, as it directly arises from the interference between partial waves associated with the electronic wavepacket scattering on this chiral potential.⁴⁷ This is particularly striking in the comparison between camphor and fenchone. The Ω₁ component of camphor presents a multi-ring pattern between 0.1 and 0.2 a.u. with nodes around 45°. Its Ω₃ component shows four poles with high asymmetry. These features can be rationalized by decomposing the distributions as a sum of projections of Legendre polynomials.¹⁷

Fig. 11 Momentum-resolved PEELD measurements in terpenes (fenchone, camphor, limonene, α -pinene and β-pinene). The columns represent the Ω₀, Ω₁, Ω₂ and Ω₃ components of the photoelectron angular distribution, where the even and odd frequencies are respectively symmetric and antisymmetric along the light propagation direction z.

As already seen in Fig. 10, limonene presents an overall weaker PEELD. Its Ω₃ component shows a similar structure to that of fenchone, but its Ω₁ component is very different.

The structural sensitivity of PEELD is further illustrated by comparing α- and β-pinene. Their symmetric components are very similar. On the other hand, their Ω₁ and Ω₃ components depict very different patterns. Last, we can compare the 2D distributions of β-pinene and camphor, in which the evolution of g as a function of S₃ was found to be very close (Fig. 10). The momentum-resolved asymmetry components Anti(p_x, p_z) are clearly different.

The high structural sensitivity of the momentum-resolved Fourier components depicted in Fig. 11 enables using them as fingerprints of the molecules. We have shown in a previous publication how the chemical and enantiomeric composition of a mixture of fenchone and camphor could be extracted by using a fitting procedure based on these Fourier components.¹⁵ We will see at the end of the article how neural networks can be used to improve such analysis of chemical mixtures.

4.2 Diastereomers

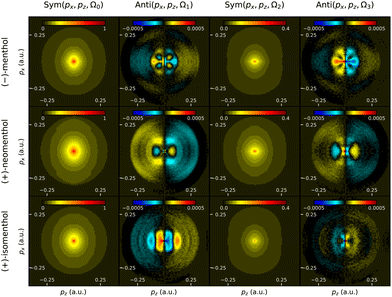
Chiral molecular structures that have more than one asymmetric center can give rise to different enantiomeric forms but also to diastereomers, which are not mirror images of one another. While enantiomers share the same physical properties against achiral measurements, diastereomers have generally different boiling points, absorption spectra, etc. However, they cannot be distinguished by mass-spectrometry, and it can be challenging to separate them using standard analysis apparatus such as chromatography. In this section we evaluate the ability of PEELD measurements to distinguish diastereomers.

Menthol possesses 3 asymmetric carbon atoms located on a cyclohexane ring. Each carbon can exist as two absolute configurations, leading to a total of 8 configurations for the menthol molecules, with 4 pairs of enantiomers. In this study we focused on three of them: menthol, isomenthol and neomenthol, which are represented in Fig. 9. To our knowledge, no investigation of PECD or PEELD measurements to distinguish diastereomers has yet been conducted.

Fig. 12 depicts the evolution of the forward/backward asymmetry in electron emission with respect to S₃. The asymmetry is quite low, hardly reaching the 1% level. In neomenthol, the asymmetry evolves quasi-linearly with S₃, indicating a weak anisotropy of the 3-photon resonant excitation process in the 3 + 1 REMPI scheme. By contrast, the signals from isomenthol and menthol are very non-linear. In menthol, the asymmetry is quasi-null as long as the Stokes parameter remains below 0.6, and increases to −1% in circular polarization. In isomenthol, the asymmetry remains lower, around 0.5%.

Fig. 12 Forward/backward asymmetry in the photoionization of diastereomers (menthol, neomenthol and isomenthol) as a function of the third Stokes parameter S₃ of the ionizing radiation.

As we have seen above, more spectroscopic information can be obtained by extracting the 2D momentum-resolved Fourier components Sym(p_x, p_z, Ω_[0,2]) and Anti(p_x, p_z, Ω_[1,3]) (Fig. 13). All symmetric components look similar with a strong component at low energy. By contrast, the chirosensitive antisymmetric components are much more structured, especially at low momentum values, and are very different from one diasteromer to another. This shows that the orientation of one methyl group in the molecule induces a drastic change on the outgoing electron wavepacket dynamics in the chiral photoionization process. Time-resolved PEELD measurements in a pump–probe scheme⁴² should thus be extremely sensitive to vibrational dynamics.

Fig. 13 Momentum-resolved PEELD measurements in diastereomers (menthol, isomenthol and neomenthol). The columns represent the Ω₀, Ω₁, Ω₂ and Ω₃ components of the photoelectron angular distribution, where the even and odd frequencies are respectively symmetric and antisymmetric along the light propagation direction z.

4.3 Amine and lactates

We now turn our attention to molecules which are often used as chiral precursors in chemical reactions: α-methylbenzylamine (1-phenylethan-1-amine), methyl lactate, and ethyl lactate. The two latter have ionization potential above 10 eV and are thus ionized through 5-photon absorption.

Fig. 14 shows the evolution of the asymmetry vs. S₃ for these three compounds. The asymmetry from α-methylbenzylamine is very low. By contrast, methyl and ethyl lactates produce chiroptical signals reaching the 2% range. The asymmetry evolves almost perfectly linearly with S₃ in ethyl lactate, indicating that the multiphoton ionization process is not significantly influenced by an anisotropy of excitation. By contrast, the signal from methyl lactate shows a maximum around S₃ = 0.8, followed by a slight decrease.

Fig. 14 Forward/backward asymmetry in the photoionization of methyl lactate, ethyl lactate and α-methylbenzylamine as a function of the third Stokes parameter S₃ of the ionizing radiation.

The lack of excitation anisotropy in methyl lactate is confirmed by the momentum-resolved Fourier decomposition displayed in Fig. 15. In the absence of anisotropy, the linear scaling of the antisymmetric signal with S₃ results in a purely sinusoidal evolution as a function of the quarter waveplate rotation, leading to a single Fourier component Ω₁. By contrast, the measurements in ethyl lactate show a strong component at Ω₃.

Fig. 15 Momentum-resolved PEELD measurements in methyl lactate, ethyl lactate and α-methylbenzylamine. The columns represent the Ω₀, Ω₁, Ω₂ and Ω₃ components of the photoelectron angular distribution, where the even and odd frequencies are respectively symmetric and antisymmetric along the light propagation direction z.

Interestingly, the momentum-resolved distributions from α-methylbenzylamine depicts a clear antisymmetric signal. The very low value of the g asymmetry observed in Fig. 14 is due to the presence of lobes of opposite sides in the forward half plane, which cancel out each other in the integrated g signal.

4.4 PEELD on non-volatile molecules: amino acids

Amino acids are of crucial importance in biology, as they constitute the building blocks of all living organisms on Earth. From a chiral point of view, the fact that all proteinogenic amino acids exhibit the same absolute configuration is one of the most exciting scientific open questions. The mechanisms leading to the emergence of homochiral proteins, from the initial symmetry breaking step towards chiral amplification, are intensively investigated.⁴⁸ In this context, designing techniques capable of detecting very small enantiomeric excesses, as well as to track the chiral composition of a mixture in real-time, will open new perspectives. Several photoelectron circular dichroism measurements of amino acids have recently been reported.^{30,33,49–53} Here we investigate the interest of PEELD measurements in small amino acids.

As described in Section 2.3 and displayed in Fig. 1, the compounds are evaporated in an oven heated by a laser diode. The level of signal obtained in these measurements is typically 4 times lower than that obtained in volatile terpene molecules.

In Fig. 16, we plot the asymmetry vs. S₃ for the three investigated amino acids: L-alanine, L-tyrosine, and l-tryptophan. The data are a bit noisy due to the low density of the gas target. The asymmetry is weak for tryptophan and the measurements in opposite enantiomers showed an imperfect mirroring. This indicate that experimental artifacts in the photoelectron imaging degrade the quality of the measurements when the chiroptical signal is low. To circumvent this issue, we extract the PEELD by differentiating the signals obtained in L- and D-tryptophans. The asymmetry reaches 1% in alanine, 0.5% in tyrosine, and remaining below 0.1% in tryptophan. The alanine curve is mainly linear, while the tyrosine is strongly non-linear and is maximized for S₃ = ±1.

Fig. 16 Forward/backward asymmetry in the photoionization of L-alanine, L-tyrosine and differential measurement between L- and D-tryptophans as a function of the third Stokes parameter S₃ of the ionizing radiation.

The 2D momentum-resolved Fourier components from these amino acids are presented in Fig. 17. As observed in the previous sections, the symmetric components do not present any spectacular features, while the antisymmetric ones are much richer. We observe clearly two rings in the Ω_1,3 components in alanine, which are probably due to two distinct ionization channels. In tyrosine, there is mainly a central feature spread at low p_x value at Ω₁ and for tryptophan, we observe a clear outer ring with a constant sign.

Fig. 17 Momentum-resolved PEELD measurements in L-alanine, L-tyrosine and differential measurement between L and D-tryptophans. The columns represent the Ω₀, Ω₁, Ω₂ and Ω₃ components of the photoelectron angular distribution, where the even and odd frequencies are respectively symmetric and antisymmetric along the light propagation direction z.

These results demonstrate the possibility to clearly measure a PEELD signal from non-volatile amino acids. This opens interesting perspectives to track ultrafast chiral electronic dynamics in these bio-relevant molecules.^54,55 The precision of the measurements could be improved by producing a denser jet of molecules, for instance using laser-based desorption.^53,56

4.5 Iodoarenes

The last molecules we analyzed are two iodoarenes which are used for the preparation of hypervalent iodine compounds. The C₂-symmetrical bis(amidoiodoarenes) 1 and 2 have been synthesized in both their (R,R)-(−)- and (S,S)-(+)-enantiomeric pure forms according to methods used for the preparation of their corresponding chiral bis(λ⁵-iodanes), which served as oxygen-atom transfer reagents in the stereoselective synthesis of natural products and analogues thereof.^57,58 These iodoarenes 1 and 2, with masses of 574 and 696 a.m.u., also constitute a good way to test the sensitivity of PEELD in large neutral systems.

For these measurements, the samples were evaporated in the oven but the level of signal remained low, typically 4 times lower than in volatile terpenes. Furthermore, the detected forward/backward asymmetries were small, such that we conducted measurements in opposite enantiomers and differentiated them to remove any imaging artifacts, as we previously done in tryptophans.

The results depicted in Fig. 18 show that a non-zero asymmetry is observed in both compounds. The values are small, maximizing around 0.05%, i.e. half the value obtained in tryptophan. In iodoarene 1, the asymmetry evolves linearly with S₃ within the error bar. By contrast, iodoarene 2 shows a clearly non-linear evolution, with a sign change of the asymmetry around S₃ ≈ 0.75. This indicates that the photoionization process of this compound is a REMPI scheme in which the photoexcitation step selects a subset of molecular orientations. This is quite remarkable given the large size of the molecule (Fig. 9).

Fig. 18 Forward/backward asymmetry in the photoionization of iodoarene 1 and iodoarene 2, obtained by differential measurement in (+) and (−) enantiomers, as a function of the third Stokes parameter S₃ of the ionizing radiation.

Plotting the 2D-momentum resolved components of the photoelectron distribution (Fig. 19) provides an additional insight into the influence of the photoexcitation step. The symmetric components show that most of the electrons are produced at very low kinetic energy in both compounds. In the antisymmetric component, we observe clearly different patterns. For the first compound, the Ω₁ component is dominated by a ring around 0.2 a.u. radius, and a more localized peak around 0.15 a.u. The Ω₃ component is very small, reflecting the quasi-linear evolution of the asymmetry with S₃. For the second compound, we observe a clear 6-fold pattern in the Ω₁ component, characteristic of higher Legendre polynomials in the angular decomposition of the photoelectron angular distribution. The Ω₃ component is clearly non-zero, and shows a similar pattern with opposite sign.

Fig. 19 Differential momentum-resolved PEELD measurements between (+) and (−) enantiomers of iodoarene 1 and iodoarene 2. The columns represent the Ω₀, Ω₁, Ω₂ and Ω₃ components of the photoelectron angular distribution, where the even and odd frequencies are respectively symmetric and antisymmetric along the light propagation direction z.

These results demonstrate the possibility to measure photoelectron elliptical dichroism in large neutral compounds. They show that PEELD maintains a structural sensitivity through the anisotropy induced by photoexcitation in the REMPI process.

5. Analyzing chemical mixtures with neural networks

The compounds we have characterized up to now were chemically pure. We have previously shown that PEELD could be used to extract the chemical and enantiomeric information from mixtures using the 2D components of the Fourier-decomposed PEELD signal as fingerprints of the molecules.¹⁵ Our previous study was restricted to a two-compound mixture, and relied on a least-square minimization procedure. In the following we demonstrate the benefits of using deep learning techniques, specifically convolutional neural networks (CNN), for a faster and more accurate analysis of multi-compound PEELD measurements encoded in a set of images. As a proof of principle, we analyze an artificial mixture of fenchone, camphor and limonene, showing a direct correspondence between angularly-resolved 2D photoelectron distribution (symmetric and antisymmetric parts integrated on a half turn of the waveplate) and chemical composition (relative amplitudes and enantiomeric excess).

The learning, testing, and validation sets were created from experimental sets of PEELD images from enantiopure samples of the two enantiomers of fenchone, camphor and limonene. Each set corresponds to ≈2500 turns of the waveplate, one turn corresponding to 160 images. Each of these enantiopure measurements was then divided into 62 subsets containing 80 images, which corresponds to half a turn of the waveplate. Each subset was further divided into two groups of 40 images, which were summed to obtain two integrated images corresponding respectively to positive and negative helicity of the ionizing field. The data obtained with opposite helicities for each pair of enantiomers were then concatenated to obtain a set of 124 images uniquely linked to the sign of the helicity, denoted as PAD_i^±(p_x, p_z), where i is either fenchone, camphor or limonene and ± represents the sign of the helicity. The symmetric part of the signal for a given species i, associated with the 2D integrated photoelectron spectrum (ISym_i(p_x, p_z)), was obtained by averaging the two ellipticity-dependent images, while the antisymmetric part (IAnti_i(p_x, p_z)) was calculated as (PAD_i⁺(p_x,p_z) − PAD_i⁻(p_x, p_z))/2, similarly to eqn (3). To eliminate experimental artefacts, both ISym and IAnti images were digitally up-down symmetrized, and respectively left-right symmetrized and antisymmetrized. They were finally normalized to the total signal, i.e. to the 2D-sum of the ISym image. For a given simulated chemical mix, these two images, constituting a single element of the basis, were generated using the following combinations:

with i = {fenchone, camphor, limonene} and where a_i and ee_i are the relative amplitude and enantiomeric excess randomly chosen from a uniform distribution with a_i ∈ [0,1] and ee_i ∈ [−1,1]. These two images were finally Gaussian smoothed with a kernel of size (9 × 9) (using the GaussianBlur function from the OpenCv python library where σ_x and σ_z, the Gaussian standard deviations along x and z are automatically computed from kernel size), before being combined into a single two-channel image (249 × 249 × 2). The first channel thus corresponds to the ISym_mix(p_x, p_z) signal and the second one to the IAnti_mix(p_x, p_z) one. The associated amplitude and enantiomeric excess values (a_i and ee_i) were stored in a vector of dimension 6 to be used as a reference during the learning step. This procedure was repeated 122 880 times in order to construct the total basis which was further divided into three sub-bases: the training, the validation and the testing one. Examples of ISym_mix(p_x, p_z) and IAnti_mix(p_x, p_z) basis images are given in Fig. 20. 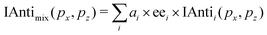The training and validation basis, which contain respectively 110 592 and 6144 elements, are both used during the network fitting step, the first one for the adjustment of the parameters, and the second one to check at the end of each epoch that there is no overfitting. The testing basis, which contains 6144 elements never seen before by the network, is used at the end of the learning procedure to check the degree of generalization of the network.

Fig. 20 Some examples of learning basis images. Top two rows: symmetric part ISym_mix(p_x,p_z); Bottom two rows: antisymmetric part IAnti_mix(p_x, p_z).

The architecture of the CNN consists of two parallel inception branches,⁵⁹ one dedicated to the prediction of the relative amplitude of each enantiomer and the other to the determination of the associated enantiomeric excess. In accordance with the original structure of the inception network, each branch has two auxiliary outputs and one main output, the dimensions of these output layers being given by the number of species present in the chemical mixture (i.e. 3 in the present case). The output layers of the amplitude branch are preceded by a sigmoid activation layer for which the values are between 0 and 1. For the enantiomeric excess branch, this activation function is replaced by an hyperbolic tangent since its natural range is [−1,1]. For each output layer (auxiliaries and main) the regression loss corresponds to the mean squared error (mse) between the network predicted values (amplitude and enantiomeric excess) and the reference values associated to the input image. The amplitude and enantiomeric excess losses are then respectively composed from the weighted mean between the losses associated with each ouptut layer, where the weights are 1 for the main and 0.3 for the auxiliary ones. Finally, the total loss is the average of the amplitude and enantiomeric excess losses. As described previously, the input data is common to both branches and consists of a set of images of dimensions 249 × 249 with two channels.

Training is performed on 2 Nvidia Quadro M5000 graphics cards with 8GB of GDDR5 memory each. The CNN is fed with 64-image batches and the total number of epochs set to 100, one epoch taking 15 minutes of computation time. The best network parameters, corresponding to the minimum value of the total training loss, are saved to be used for further predictions. At the end of each epoch, the training and validation losses are compared to prevent possible overfitting of the network.

The prediction capabilities of the best network are tested on a dataset simulating a 20 × 10³ s PEELD measurement in a mixture of the two enantiomers of fenchone, camphor and limonene. In order to test a broad variety of configurations, we impose oscillations of the chemical composition as well as on the enantiomeric composition of the different compounds. A comparison between reference and predicted values for amplitude and enantiomeric excess is presented in Fig. 21, where predicted values are Gaussian-smoothed over 10 consecutive points. The quantitative agreement is satisfactory throughout the measurement, with an error in the relative amplitudes of the compounds remaining below 0.005 for the CNN except when the amplitude is very close to zero. This demonstrates the ability of the CNN to retrieve the chemical and enantiomeric composition of the 3-compounds mixture with good accuracy. The enantiomeric excess is also retrieved with typical errors in the 1–3% range, which is satisfying since each measurement point corresponds to a 4 s duration measurement (i.e. half a turn of the waveplate). We note however that the network fails to give correct values of enantiomeric excess when the relative amplitude of the considered species is less than 3%. On the other hand, as soon as the amplitude of the species is above this limit, enantiomeric excesses are properly retrieved even when the mixture is close to racemic.

Fig. 21 Measurement of the chemical and enantiomeric composition of a simulated time-varying mixture of fenchone (blue), camphor (green) and limonene (red), by PEELD and CNN. (a) Top: Theoretical (dashed) relative amplitude of the different species, and values retrieved by the CNN (continuous). Bottom: Error in the relative amplitude determination. (b) Top: Theoretical and retrieved enantiomeric excesses. Bottom: Error on the retrieved enantiomeric excesses.

To further assess the potential of this CNN approach, we compare in Fig. 22 the simulated mixture composition with the data extracted from a conventional 2D least square fitting procedure in which the PEELD reference images (symmetric and antisymmetric respectively) are compared to a linear combination of the (symmetric and antisymmetric) enantiopure compounds images as defined in eqn (4) and (5). The relative amplitudes given by the fit, although very close to the reference data, present a systematic error (see solid lines in Fig. 22). More critically, the 2D fitting method completely fails to retrieve the enantiomeric excess values, showing errors of several 10%.

Fig. 22 Measurement of the chemical and enantiomeric composition of a simulated time-varying mixture of fenchone (blue), camphor (green) and limonene (red), by PEELD and fits. (a) Top: Theoretical (dashed) relative amplitude of the different species, and values retrieved by the 2D fits (continuous). Bottom: Error in the relative amplitude determination. (b) Top: Theoretical and retrieved enantiomeric excesses. Bottom: Error on the retrieved enantiomeric excesses.

This demonstrates the relevance of using CNN and shows the interest of this approach in the arsenal of chiral analysis, in particular for real-time monitoring of the composition and enantiomeric excess of chemical mixtures. An additional benefit of CNN is that they can be implemented using a dedicated graphics card directly interfaced to the experiment to perform real-time analysis.

6. Conclusion

We have shown that enantiomeric excesses could be determined with high precision by PEELD measurements using a simple and robust experimental scheme. Recycling the laser pulses in an optical cavity has enabled us to decrease the necessary laser power by one order of magnitude while reaching higher precision compared with our previous measurements.¹⁵ We have measured enantiomeric excesses with relative standard errors as low as 0.04% in 1 h 40 min measurements. This technique could thus be used to detect the emergence of very low enantiomeric excesses in quasi-racemic compounds, or to verify the purity of enantiopure compounds.

Next, we have extended PEELD measurements to a broad range of molecules, demonstrating the high spectroscopic sensitivity of the technique to subtle structural features, its ability to distinguish diastereomers, as well as its sensitivity to photoexcitation anisotropy even in large compounds. This confirms the interest of PEELD to track the ultrafast vibrational, vibronic and electronic dynamics of chiral molecules in time-resolved pump–probe measurements.⁴² Extending the measurements in iodoarenes to localized core photoionization by circularly polarized XUV or X-ray pulses would enable investigating the influence of their particular symmetry in the electron scattering process. The coherent superposition of the photoemission from the two iodines of an iodoarene should lead to characteristic quantum interference patterns,^60,61 which should be highly sensitive to the chirality of the target.

Last, PEELD measurements are intrinsically very fast and thus compatible with dynamic acquisition and real-time analysis. We have shown than neural networks could be used to analyze chemical mixtures with high precision and high speed. Interfacing directly the network to the experimental setup will enable live analysis of the compounds, an important requirement of Industry 4.0.³

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank R. Bouillaud, F. Blais, R. Delos, N. Fedorov, L. Merzeau for technical assistance. This project has received funding from the Agence Nationale de la Recherche (ANR-18-CE07-0027, IODOCHEM), Ministère de lEnseignement Supérieur et de la Recherche (MESR), the Centre National de la Recherche Scientifique (CNRS), the Région Nouvelle Aquitaine (RECHIRAM) and from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program no. 682978 – EXCITERS, no. 963967 – FASTEE and no. 804144 – ALIFE.

Notes and references

1. S. W. Smith, Toxicol. Sci, 2009, 110, 4–30.
2. S. Orlandini, G. Hancu, Z.-I. Szabó, A. Modroiu, L.-A. Papp, R. Gotti and S. Furlanetto, Molecules, 2022, 27, 7058.
3. N. S. Arden, A. C. Fisher, K. Tyner, L. X. Yu, S. L. Lee and M. Kopcha, Int. J. Pharm., 2021, 602, 120554.
4. L. A. Nafie, Annu. Rev. Phys. Chem., 1997, 48, 357–386.
5. N. Berova and R. Nakanishi, Circular Dichroism Principles and Applications, Wiley-VCH, New York, 2000.
6. P. Fischer and F. Hache, Chirality, 2005, 17, 421.
7. M. Oppermann, B. Bauer, T. Rossi, F. Zinna, J. Helbing, J. Lacour and M. Chergui, Optica, 2019, 6, 56–60.
8. L. Bougas, J. Byron, D. Budker and J. Williams, Sci. Adv., 2022, 8, eabm3749.
9. B. Ritchie, Phys. Rev. A, 1975, 12, 567–574.
10. N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190.
11. D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475–477.
12. D. Patterson and M. Schnell, Phys. Chem. Chem. Phys., 2014, 16, 11114–11123.
13. M. M. R. Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Nat. Commun., 2015, 6, 7511.
14. L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Géneaux and I. Powis, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706.
15. A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212.
16. L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204(Part B), 322–334.
17. C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005.
18. C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307.
19. A. Ferré, C. Handschin, M. Dumergue, F. Burgy, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, L. Merceron, E. Mével, L. Nahon, S. Petit, B. Pons, D. Staedter, S. Weber, T. Ruchon, V. Blanchet and Y. Mairesse, Nat. Photonics, 2015, 9, 93–98.
20. S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002.
21. A. Kastner, C. Lux, T. Ring, S. Züllighoven, C. Sarpe, A. Senftleben and T. Baumert, Chem. Phys. Chem., 2016, 17, 1081.
22. J. Miles, D. Fernandes, A. Young, C. M. M. Bond, S. W. Crane, O. Ghafur, D. Townsend, J. Sá and J. B. Greenwood, Anal. Chim. Acta, 2017, 984, 134–139.
23. R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306.
24. S. Beaulieu, A. Comby, D. Descamps, S. Petit, F. Légaré, B. Fabre, V. Blanchet and Y. Mairesse, J. Chem. Phys., 2018, 149, 134301.
25. A. Kastner, G. Koumarianou, P. Glodic, P. C. Samartzis, N. Ladda, S. T. Ranecky, T. Ring, S. Vasudevan, C. Witte, H. Braun, H.-G. Lee, A. Senftleben, R. Berger, G. Barratt Park, T. Schäfer and T. Baumert, Phys. Chem. Chem. Phys., 2020, 22, 7404–7411.
26. S. Beauvarlet, E. Bloch, D. Rajak, D. Descamps, B. Fabre, S. Petit, B. Pons, Y. Mairesse and V. Blanchet, Phys. Chem. Chem. Phys., 2022, 24, 6415–6427.
27. J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. Schmidt and H. Schmidt-Böcking, Rep. Prog. Phys., 2003, 66, 1463.
28. K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. Schöffler, J. Phys. Chem. A, 2019, 123, 6491–6495.
29. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477.
30. P. Krüger and K.-M. Weitzel, Angew. Chem., Int. Ed., 2021, 60, 17861–17865.
31. D. A. Horke, G. M. Roberts, J. Lecointre and J. R. R. Verlet, Rev. Sci. Instrum., 2012, 83, 063101.
32. S. Banerjee and S. Mazumdar, Int. J. Anal. Chem., 2012, 2012, e282574.
33. P. Krüger, J. H. Both, U. Linne, F. Chirot and K.-M. Weitzel, J. Phys. Chem. Lett., 2022, 6110–6116.
34. J. Triptow, A. Fielicke, G. Meijer and M. Green, Angew. Chem., Int. Ed., 2023, 62, e202212020.
35. J. Nauta, J.-H. Oelmann, A. Ackermann, P. Knauer, R. Pappenberger, A. Borodin, I. S. Muhammad, H. Ledwa, T. Pfeifer and J. R. C. López-Urrutia, Opt. Lett., 2020, 45, 2156–2159.
36. J.-H. Oelmann, T. Heldt, L. Guth, J. Nauta, N. Lackmann, V. Wössner, S. Kokh, T. Pfeifer and J. R. C. López-Urrutia, Rev. Sci. Instrum., 2022, 93, 123303.
37. M. M. R. Fanood, M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2015, 17, 8614–8617.
38. C. S. Lehmann, D. Botros and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2022, 24, 15904–15911.
39. I. Powis, C. J. Harding, G. A. Garcia and L. Nahon, Chem. Phys. Chem., 2008, 9, 475–483.
40. S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004.
41. E. Bloch, S. Larroque, S. Rozen, S. Beaulieu, A. Comby, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, R. Taïeb, A. J. Uzan, V. Blanchet, N. Dudovich, B. Pons and Y. Mairesse, Phys. Rev. X, 2021, 11, 041056.
42. A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519.
43. S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489.
44. S. Beaulieu, A. Comby, A. Clergerie, J. Caillat, D. Descamps, N. Dudovich, B. Fabre, R. Géneaux, F. Légaré, S. Petit, B. Pons, G. Porat, T. Ruchon, R. Taïeb, V. Blanchet and Y. Mairesse, Science, 2017, 358, 1288–1294.
45. M. M. R. Fanood, M. H. M. Janssen and I. Powis, J. Chem. Phys., 2016, 145, 124320.
46. H. Ganjitabar, R. Hadidi, G. A. Garcia, L. Nahon and I. Powis, J. Mol. Spectrosc., 2018, 353, 11–19.
47. I. Powis, J. Chem. Phys., 2000, 112, 301–310.
48. A. D. Garcia, C. Meinert, H. Sugahara, N. C. Jones, S. V. Hoffmann and U. J. Meierhenrich, Life, 2019, 9, 29.
49. M. Tia, B. Cunha de Miranda, S. Daly, F. Gaie-Levrel, G. A. Garcia, L. Nahon and I. Powis, J. Phys. Chem. A, 2014, 118, 2765–2779.
50. R. Hadidi, D. K. Bozanic, G. A. Garcia and L. Nahon, Adv. Phys. X, 2018, 3, 1477530.
51. S. Hartweg, G. A. Garcia, D. K. Božanić and L. Nahon, J. Phys. Chem. Lett., 2021, 12, 2385–2393.
52. R. Hadidi, D. K. Božanić, H. Ganjitabar, G. A. Garcia, I. Powis and L. Nahon, Commun. Chem., 2021, 4, 1–14.
53. C. Sparling, S. W. Crane, L. Ireland, R. Anderson, O. Ghafur, J. B. Greenwood and D. Townsend, Phys. Chem. Chem. Phys., 2023, 25, 6009–6015.
54. F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. D. Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Science, 2014, 346, 336–339.
55. M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760–10825.
56. C. R. Calvert, L. Belshaw, M. J. Duffy, O. Kelly, R. B. King, A. G. Smyth, T. J. Kelly, J. T. Costello, D. J. Timson, W. A. Bryan, T. Kierspel, P. Rice, I. C. E. Turcu, C. M. Cacho, E. Springate, I. D. Williams and J. B. Greenwood, Phys. Chem. Chem. Phys., 2012, 14, 6289–6297.
57. R. Coffinier, M. E. Assal, P. A. Peixoto, C. Bosset, K. Miqueu, J.-M. Sotiropoulos, L. Pouységu and S. Quideau, Org. Lett., 2016, 18, 1120–1123.
58. M. El Assal, P. A. Peixoto, R. Coffinier, T. Garnier, D. Deffieux, K. Miqueu, J.-M. Sotiropoulos, L. Pouységu and S. Quideau, J. Org. Chem., 2017, 82, 11816–11828.
59. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke and A. Rabinovich, Going Deeper with Convolutions, 2014.
60. H. D. Cohen and U. Fano, Phys. Rev., 1966, 150, 30–33.
61. S. E. Canton, E. Plésiat, J. D. Bozek, B. S. Rude, P. Decleva and F. Martín, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7302–7306.

---