Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Like aggregation from unlike attraction: stripes in symmetric mixtures of cross-attracting hard spheres
Gianmarco
Munaò
 *a,
Dino
Costa
*a,
Dino
Costa
 a,
Gianpietro
Malescio
a,
Jean-Marc
Bomont
a,
Gianpietro
Malescio
a,
Jean-Marc
Bomont
 b and
Santi
Prestipino
b and
Santi
Prestipino
 a
a
aDipartimento di Scienze Matematiche e Informatiche, Scienze Fisiche e Scienze della Terra, Università degli Studi di Messina, Viale F. Stagno d'Alcontres 31, 98166 Messina, Italy. E-mail: gmunao@unime.it
bUniversité de Lorraine, LCP-A2MC, UR 3469, Metz F-57078, France
First published on 10th May 2023
Abstract
Self-assembly of colloidal particles into striped phases is at once a process of relevant technological interest—just think about the possibility to realise photonic crystals with a dielectric structure modulated along a specific direction—and a challenging task, since striped patterns emerge in a variety of conditions, suggesting that the connection between the onset of stripes and the shape of the intermolecular potential is yet to be fully unravelled. Hereby, we devise an elementary mechanism for the formation of stripes in a basic model consisting of a symmetric binary mixture of hard spheres that interact via a square-well cross attraction. Such a model would mimic a colloid in which the interspecies affinity is of longer range and significantly stronger than the intraspecies interaction. For attraction ranges shorter enough than the particle size the mixture behaves like a compositionally-disordered simple fluid. Instead, for wider square-wells, we document by numerical simulations the existence of striped patterns in the solid phase, where layers of particles of one species are interspersed with layers of the other species; increasing the attraction range stabilises the stripes further, in that they also appear in the bulk liquid and become thicker in the crystal. Our results lead to the counterintuitive conclusion that a flat and sufficiently long-ranged unlike attraction promotes the aggregation of like particles into stripes. This finding opens a novel way for the synthesis of colloidal particles with interactions tailored at the development of stripe-modulated structures.
1 Introduction
The occurrence of stripes in condensed matter is an intriguing phenomenon whose origin is the subject of widespread interest.1–3 Self-assembly into striped structures is observed in a variety of systems, many of which belonging to the realm of soft matter, including, among others, colloidal dispersions,4–6 active materials,7 liquid crystals,8 amphiphilic mixtures,9 core-corona systems,10 and magnetic particles.11In the celebrated ANNNI model,12 which is the simplest (spin) model where stripes are present, spatially modulated phases are induced by superimposing to a short-range ferromagnetic interaction a directional antiferromagnetic interaction of longer range. The onset of striped phases in soft matter is somewhat similar, since being related to the competition between two antagonistic forces: an isotropic short-range attraction, originated from the van der Waals and/or depletion interactions, and a long-range (but still isotropic) repulsion, arising from electrostatic forces.13–21 On the other hand, it has been shown22–25 that “lanes” or lamellae may even appear in one-component fluids interacting via purely repulsive potentials, typically modeled by a combination of hard-sphere (HS) and square-shoulder interactions. At variance with the ANNNI model, the other examples of stripes imply a genuine spontaneous symmetry breaking: the number density acquires a modulation along a definite direction which is not apparent in the system Hamiltonian.
The formation of striped structures has been investigated, though less extensively, also in mixtures, where they have been described both in experiments4,26 and in numerical investigations.27–31 In principle, mixtures of colloidal particles with different optical characteristics can find application in photonic devices, sensors, and even microchips.32,33 In particular, a binary mixture self-assembling in a striped crystal can be assimilated to a photonic crystal with dielectric properties modulated along a specific direction. In a completely different context, striped patterns have been observed in two-component assemblies of living cells, both in vitro34,35 and in silico.36,37 For example, in ref. 36 tegumentary cells of zebrafish are modeled as hard disks of two different types, interacting through Hookean forces; upon tuning the sign and strength of the couplings, a wealth of two-dimensional patterns are obtained, including stripes.
When modeling binary mixtures, one has to fix like interactions (between particles of the same species) and the unlike, or cross interaction (between particles of different species). In ref. 27 and 29 the like interactions are HS plus square-shoulder potentials, whereas the cross interaction is a square-well (SW) potential. In ref. 31 the like interaction is a HS potential for one species and HS plus a SALR (i.e., short-range attractive and long-range repulsive) potential for the other species, while the cross interaction is modeled by a SW potential. Finally, in ref. 30 the like interactions are of SALR type, while the cross interaction has an attractive tail.
The occurrence of stripes in mixtures where particles of the same species interact through a HS plus square-shoulder potential as in ref. 27 and 29 is not surprising, considering that stripes already form in one-component systems characterised by the same interaction.22–25 On the other hand, competing interactions, as the SALR potential considered in ref. 30 and 31, are often responsible in one-component systems for self-assembling behaviours of various types, including stripes.38–41 However, ref. 31 suggests that the cross interaction too plays a role in the stabilization of stripes, as the latter are only present when the SW range is long enough.
From the above considerations, it follows that in order to better understand the formation of stripes in mixtures it is crucial to disentangle the effects of like and unlike contributions, and thoroughly investigate the impact of the cross interaction. To this aim, we examine a binary mixture of colloidal-like particles where the like interactions are simply HS, while the cross interaction features, in addition to a hard core, also a SW of variable width. A SW interaction makes it possible to precisely define and tune the range of the interspecies attraction. To exclude the possible role of size and/or composition asymmetry in the formation of stripes, as in ref. 29, we consider an equimolar mixture of HS particles with equal diameters. This model is meant to represent a mixture of two colloidal particles of similar sizes, having some degree of interspecies affinity. When modeling the cross interaction by a SW potential, the range of the attraction considered is usually very small,42–46 due to the short-range nature of colloidal interactions.47 On the other hand, there exist conditions where the mutual forces can be long-range even in colloidal solutions, for instance when screened Coulomb interactions act. Therefore, in investigating the role of the SW range in the behaviour of the model mixture, we allow for an attraction range comparable to the sphere diameter, or even larger.
We perform our investigation by means of numerical simulations; specifically, we use Monte Carlo (MC) simulations in the canonical ensemble to investigate structural properties, while employing the Gibbs Ensemble MC (GEMC) method to study liquid–vapour coexistence. Crystalline order is probed by means of orientational order parameters, whereas the relevant solid structures are identified by zero-temperature total-energy calculations. For a fast, preliminary analysis of the homogeneous mixture, we resort to the hypernetted chain (HNC) theory,48 which is extensively adopted in the literature to study the behaviour of SW fluids.49–52
We find that for small values of the attraction range the mixture behaves like a simple fluid, with the two species mixed together for every density and temperature. On the other hand, as the SW range increases, compositional order eventually sets in: both the liquid and the solid acquire a patterned structure, where stripes (i.e., bands or layers) of type-1 spheres systematically alternate with stripes of type-2 spheres. Therefore, aggregation of particles of the same species may occur as the sole result of an attraction between particles of different species.
The remainder of the paper goes as follows: in Section 2 we provide details on the mixture, the simulation and theoretical methods adopted. In Section 3 we present and discuss our results. Conclusions and perspectives follow in Section 4.
2 Models and methods
Our system is an equimolar mixture of identical hard spheres (1 and 2) with diameter σ, mutually interacting through a SW potential of range γσ: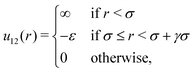 | (1) |
We carry out Monte Carlo simulations in the canonical ensemble using samples of N = 2048 particles, enclosed in a cubic simulation box with periodic boundary conditions. We typically perform up to 5 × 106 MC cycles at equilibrium, one cycle corresponding to N elementary MC moves. To speed up relaxation to equilibrium, we also implement swap moves, where the positions of two randomly chosen unlike particles are interchanged. This is necessary in order to achieve genuine equilibrium for moderate to high densities. The acceptance of all moves is ruled by detailed balance.
Liquid–vapour equilibria are obtained by GEMC simulations,53 using N = 1728 particles that initially are evenly distributed between two boxes with density ρ in the range 0.20–0.30. We typically carry out 106 GEMC cycles, one cycle corresponding to N displacement moves plus one volume exchange plus a few hundred particle exchanges plus a few tens swap moves (these numbers are just mean relative proportions of different kinds of trial moves, since at every step of the run the choice between the moves is made at random). Critical temperatures and densities are estimated by fitting the GEMC liquid–vapour coexistence points by means of the scaling law for the density difference and the law of rectilinear diameters.53
To obtain fast estimates of structural and thermodynamic properties of the fluid mixture, we solve the Ornstein–Zernike (OZ) equation combined with the hypernetted chain (HNC) closure.48 For a binary mixture, the HNC approximation for the direct correlation functions reads:
| cij(r) = exp[−βuij(r) + θij(r)] − θij(r) − 1, | (2) |
The OZ-HNC set of equations is solved using an iterative Picard algorithm on a grid of 8192 points and a mesh of 0.005σ. In the solution scheme, the HNC closure and the OZ equation are applied in real and reciprocal space respectively, with the switch between the two implemented by Fast Fourier Transforms. Calculations are done in terms of the indirect correlation function θij(r), so that the k → r Fourier inversion is performed on such a continuous function. A standard mix of two consecutive iterations has been adopted to ensure the convergence of the algorithm. We assume that convergence is reached when the difference between old and new values of θij(r) is less than 10−4 between two successive iterations.
Within the HNC theory we have determined the pseudo-spinodal line:54,55 for each fixed ρ, we reduce T gradually until the HNC iteration fails to converge. This occurs at a temperature TPS where the isothermal compressibility is usually very large and rapidly increasing on cooling. The locus TPS(ρ), i.e., the pseudo-spinodal line, can be taken as an approximation to the true spinodal line, which is where the isothermal compressibility diverges. In turn, the maximum of TPS(ρ) provides a reasonable estimate of the critical temperature Tcr.
The structure of striped patterns has been characterised through a cluster analysis, performed by using the Hoshen–Kopelman algorithm.56 In our study, two like particles are considered to be bonded together, and thus belonging to the same cluster, if their mutual separation is smaller than dbond = 1.25σ. The cluster size distribution (CSD) is defined as:
 | (3) |
 .
.
Finally, to assess the structure of the mixture in its evolution from solid to liquid, we monitor some orientational order parameters and the pair entropy per particle s2. For a binary fluid mixture, the latter is defined as:57
 | (4) |
3 Results and discussion
3.1 Emergence of stripes at low-to-moderate density
We preliminarily assess the performance of HNC in reproducing the fluid structure of the mixture as a function of T. For this purpose, in Fig. 1 we compare HNC and MC results for gij(r) (A) and Sij(k) (B) for γ = 1, ρ = 0.2, and two different temperatures. For T = 2 the distribution functions show little structure (A), as can be expected for a homogeneous fluid at high temperature. Moving to T = 1.5, the contact value of both g11(r) and g12(r) increases, as does the height of the second peak of g12(r), due to the attraction between unlike species. The behavior of structure factors for low wavevectors is more interesting (B): looking at the picture, we realize that T = 1.5 is not far away from liquid–vapor coexistence. As is clear, the HNC predictions for the fluid structure match quite well with simulation data.We anticipate that stripes occur spontaneously in the mixture, even at low density, provided that the temperature is sufficiently low. To illustrate this point, we first compute the liquid–vapour coexistence envelopes for a few values of γ using the GEMC method, while employing the HNC pseudo-spinodal line as a guide to drive GEMC simulations to the relevant region of thermodynamic parameters. We emphasize that the HNC estimate of the liquid–vapor spinodal is usually expected to be good,59–61 at least insofar as one-component fluids are considered.
GEMC liquid–vapour envelopes and HNC pseudo-spinodal lines are plotted in Fig. 2 for γ = 1, 1.5, and 2, in all cases, the shape of the coexistence curve is flat on top (the more so the smaller γ, consistently with the expected disappearance of the liquid for small enough γ) and asymmetric around the critical point. Numerical values of critical temperatures and densities are reported in Table 1. As can be expected, the critical temperature increases with γ, since a longer cross-attraction implies that critical density fluctuations are developed at higher temperatures. Noticeably, in all cases examined, the GEMC coexistence line lies above the HNC pseudo-spinodal line and the maxima along the two curves are nearly equal. Critical densities are less accurate, but this problem should be ascribed to the flatness of coexistence curves, which makes the determination of this property more uncertain. For comparison, HNC critical parameters are also reported in Table 1.
| γ | GEMC | HNC | ||
|---|---|---|---|---|
| T cr | ρ cr | T cr | ρ cr | |
| 1.0 | 1.41 | 0.22 | 1.38 | 0.20 |
| 1.5 | 2.86 | 0.28 | 2.80 | 0.25 |
| 2.0 | 4.89 | 0.26 | 4.90 | 0.25 |
Once that the liquid–vapour equilibrium is worked out, we are in the position to investigate the behaviour of the mixture within the coexistence region by means of canonical MC simulations. In Fig. 3 we show a sequence of typical equilibrium configurations drawn for different values of γ and T at increasing densities. For γ = 1 and T = 1 (top panels), the shape of the liquid–vapour interface evolves with ρ similarly as in simple fluids.62–64 Indeed, for ρ = 0.10 (A) the liquid forms a spherical droplet in equilibrium with vapour. For ρ = 0.20 (B) the shape of the droplet is cylindrical, whereas for ρ = 0.40 (C) the droplet shows a slab-like geometry. Finally, for ρ = 0.50 (D) a cylindrical hole appears in an otherwise liquid system. At each change of shape, the average energy per particle has a jump downward, a behaviour reflecting the increase in the ratio of bulk-to-surface particles. As well known, these geometric transitions are finite-size effects induced by periodic boundary conditions;65,66 they are observed in equilibrium in every system undergoing a phase separation.
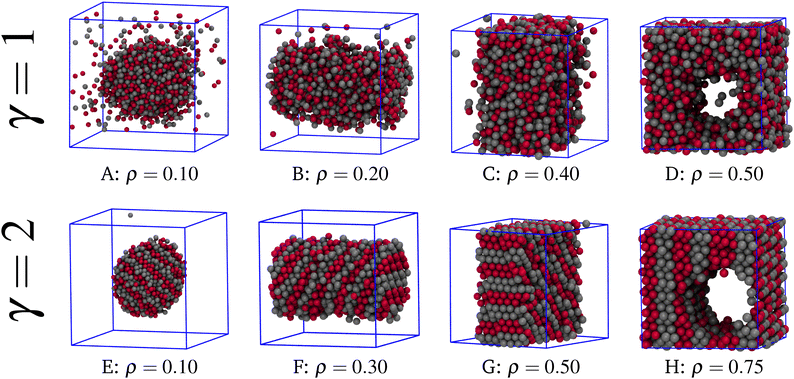 | ||
| Fig. 3 Typical equilibrium configurations for γ = 1, T = 1 (top) and γ = 2, T = 2 (bottom), for a number of densities. | ||
As is clear from Fig. 3, for γ = 1 and T = 1 the two species are randomly mixed. The same is found for γ = 2 at T = 4, a slightly subcritical temperature. On the other hand, moving to γ = 2 and T = 2 the scenario changes drastically: as can be appreciated from the bottom panels of Fig. 3, the distribution of the two species within the droplet is no longer random and patterned structures emerge spontaneously in the full range of densities. A comparison with the structures reported in panels A–D reveals that the sequence of shapes in panels E–H is identical, but type-1 and type-2 spheres are now distributed in alternating parallel stripes, a pattern that pictorially reminds us of the pigmentation of the tail of Gila monster, the largest native lizard in the US.67
The evidence of a modulated composition for γ = 2 leads us to the conclusion that aggregation of like particles into separate layers is promoted by a sufficiently long-range unlike attraction. The formation of stripes is driven by energy: planar stripes maximise the number of attracting unlike spheres, making the striped configuration more stable than its compositionally disordered counterpart. Strange as it may seem, stripes can be energetically preferred even when γ is close to zero, at least at very low temperature and very high density. Indeed, for γ = 1 stripes are not present in the liquid–vapour region but they are stable in the solid phase, as we shall show in the next section. The argument goes as follows: take, for simplicity, the two-dimensional case. If γ is small, the SW attraction only reaches the first neighbors. In a triangular crystal with single-layer stripes, the central particle has four unlike neighbors (over a total of six), while in the substitutionally disordered crystal the average number of unlike neighbors is three. Therefore, the energy (and also the enthalpy) of the striped crystal is more negative.
To further characterise the stripes observed in our system, we inquire into the distribution of particles inside the droplets, to ascertain whether it reveals some kind of spatial order. To this aim, we compute the orientational (Steinhardt) order parameters q4 and q6, which efficiently discriminate between a crystal and a dense liquid:68,69 while q4 and q6 vanish altogether in a bulk liquid, they are non-zero for crystalline environments. In panels A1 and A2 of Fig. 4 we show the statistical distribution of q4 and q6 for γ = 2, various densities, and two temperatures. Data points refer to 1000 uncorrelated configurations taken from the last part of the simulation run. For T = 4 (A1), there is no significant density dependence and q4 and q6 are close to zero. Conversely, for T = 2 (A2) the values of q4 and q6 are clearly non-zero, suggesting a local crystalline structure, and therefore that a solid–vapour separation is taking place in the mixture. In this regard, we conclude that the triple temperature for γ = 2 lies between 2 and 4.
The local coordination of spheres within a droplet can be examined through the probability distribution of the number of bonds, P(Nb), which is again computed for γ = 2 and the temperatures 2 and 4. Similarly to what we did in ref. 31, two particles are said to be bonded together when, irrespective of the types, their separation is smaller than dbond = 1.25 (we have checked that results are insensitive to the specific dbond in the range from 1.15 to 1.4). In panels B1–B4 of Fig. 4 we show results at two different densities and temperatures, distinguishing between like and unlike pairs of particles. For T = 4 and ρ = 0.10 (B1) P(Nb) is monotonically decreasing, indicating that the vapour density is relatively high and most particles are isolated. For ρ = 0.30 (B2) the maximum of the distribution moves to Nb = 1, just because of the higher density, and again no long-range order occurs. Conversely, for T = 2 (B3, B4) a sharp peak appears in all distributions, which is suggestive of crystalline order. In particular, 1–1 and 2–2 distributions show a peak at Nb = 8, whereas the 1–2 peak falls at Nb = 4—hence, on average each sphere has 12 nearest neighbors, as expected for a close-packed configuration—meaning that the majority of neighbors are of the same type as the central sphere, which in turn signals a tendency towards the local segregation of the two species. At variance with T = 4, at T = 2 the density plays no significant role.
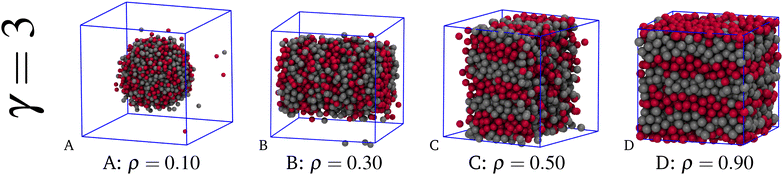
Having ascertained that for γ = 2 stripes form in a crystalline environment, an increase in the range of the SW attraction enhances the stability of stripes in two respects: (1) they become robust to the configurational disorder of a liquid environment, at least provided that ρ is not too small, and (2) they get thicker in a solid-like droplet. The first statement is illustrated in Fig. 5, where a sequence of typical equilibrium configurations is shown for γ = 3 and four increasing densities at T = 5, i.e., well below the HNC pseudo-spinodal prediction for Tcr (≈12). In the figure, the sequence of shapes in A–C is akin to panels E–G of Fig. 3, except for the major difference that the droplet in equilibrium with vapour is now liquid, as we draw from the values of the orientational order parameters. As seen in the figure, stripes are evident in the slab-like droplet (C), whereas their presence is less clear in the cylindrical droplet (B). Admittedly, in the spherical droplet (A) the surface-to-volume ratio is still too high for the mixture to sustain stripes in the liquid phase. Stripes also form at ρ = 0.9 (see panel D), a state point in which the mixture is a bulk liquid, as witnessed for example by the small values of the orientational order parameters and isothermal compressibility.
As for the thickness of solid stripes, we report in Fig. 6 two typical equilibrium configurations for γ = 2 and T = 2 (A) and for γ = 3 and T = 4 (B), at fixed ρ = 0.5—for clarity, only stripes of one type of spheres are shown. In both conditions, the mixture exhibits solid–vapour separation with a slab-like droplet. Seven stripes are counted for the state with γ = 2, whereas only five thicker stripes are seen for γ = 3. This finding will be further corroborated in the next Section. For completeness, we mention that the case γ = 1.5 and T = 0.5 is the only one in which we have found undulating, rather than planar stripes (see panel C). We can rule out an entropic effect: even though curved, stripes keep perfectly parallel to each other. Probably, stripes are undulating just to fit the slab-like droplet at this particular density.
 | ||
| Fig. 6 Slab-like solid droplets for different γ and T. In all cases ρ = 0.5. For clarity, only one species is shown. | ||
To summarize, the very existence and structure of stripes depend on the balance between energetic and entropic effects: in this regard, the former are marginally relevant for γ = 1, where indeed the mixture is compositionally disordered (at least for moderate densities and not too low temperatures); as γ increases, stripes are first formed in the solid phase and then also in the liquid phase (Fig. 5C), even in bulk (Fig. 5D), and become progressively thicker. The existence of well-definite stripes in the liquid indicates that the configurational disorder (entropy) is insufficient to suppress the compositional order promoted by energy. Entropic effects are nevertheless important, to the extent that the surface separating two adjacent stripes in the liquid is corrugated rather than flat.
We close this Section by looking at the existence of stripes from the complementary perspective of a cluster-size distribution (CSD) analysis, where by “cluster” we mean a connected assembly of like spheres. To avoid the possibility that, owing to periodic boundary conditions, the observed stripes are actually part of a unique cluster, we perform the cluster analysis by just ignoring the connection between spheres across the box edge. With this agreement, a striped phase (either solid or liquid) will be ideally characterised by a CSD with as many peaks as the apparent stripes, unless the latter are parallel to a box face, in which case the CSD has only one peak. On the contrary, a compositionally disordered phase will be described by a CSD with a prominent peak at a size of order N/2 (if the “particle color” percolates throughout the box) or with a broader peak at small size (if no such percolation occurs). Results for fixed ρ = 0.50 and different γ and T are reported in Fig. 7: for symmetry reasons, only the CSD of type-1 spheres is considered. For γ = 1 and T = 1 (liquid with a cylindrical hole, as in Fig. 3D) there is only one peak for a size comparable to the total number of type-1 spheres, meaning that they form a single aggregate, which is consistent with the absence of stripes. For γ = 1.5 and T = 0.5 and for γ = 2 and T = 2 (solid slab in vapour) the existence of multiple CSD peaks indicates that the HS are now arranged in many disconnected clusters (the stripes). For γ = 3 and T = 4 we still find a solid slab in vapour, but the behaviour of the CSD now points toward a lower number of aggregates of larger size, a clear signal that the thickness of stripes grows with γ.
 | ||
| Fig. 7 Cluster-size distribution for ρ = 0.50 and a few values of γ and T (in the legend), computed by averaging over 1000 different configurations. | ||
3.2 Stability of stripes in the solid phase
In this Section we elucidate why the stripes spontaneously emerging in our simulations actually reflect a tendency peculiar to the solid phase. To uncover the relevant crystalline phases of the mixture, we estimate the chemical potentials of a number of striped crystals and compare them with the chemical potential of a substitutionally disordered mixture (sdm), so as to confirm the preference of the system for stripe order. In order to settle the question in simple terms, we perform total-energy calculations at zero temperature, a condition for which the chemical potential is equal to the total enthalpy per particle (see, e.g., ref. 70), only considering the densest packings (fcc and hcp) and a few possible orientations of the stripes (alternating layers of type-1 and type-2 spheres). Thus, In fcc crystals, layers will be oriented perpendicularly to [001], [011], or [111] (these structures are denoted fcc001, fcc011, and fcc111, respectively). In the hcp case, layers will consist of (0001) lattice planes. For each lattice and high-symmetry direction (normal to the layers) we minimise the enthalpy of the mixture over the full range of densities, for each given pressure P. Using as many particles as needed to make the calculation exact (up to ≈30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the larger γ values), we find that the minimum enthalpy occurs at the highest density
000 for the larger γ values), we find that the minimum enthalpy occurs at the highest density  for every P, as the number of pairs of unlike spheres is always maximised at closest packing—hence, we take P = 0 in the following. The zero-temperature energy of a striped crystal is then plotted as a function of the number np of planes per stripe/layer. As far as the sdm is concerned, the total potential energy at T = 0 is averaged over ten different random equimolar compositions: it turns out that the enthalpy of the sdm as a function of pressure is again minimum for P = 0 (but the optimal density is no longer
for every P, as the number of pairs of unlike spheres is always maximised at closest packing—hence, we take P = 0 in the following. The zero-temperature energy of a striped crystal is then plotted as a function of the number np of planes per stripe/layer. As far as the sdm is concerned, the total potential energy at T = 0 is averaged over ten different random equimolar compositions: it turns out that the enthalpy of the sdm as a function of pressure is again minimum for P = 0 (but the optimal density is no longer  ).
).
Results for striped crystals are reported in Fig. 8 for a few integer and half-integer values of γ; to remove any ambiguities related to the definition of u(r) at r = 1 + γ, we have chosen ρ = 1.41 ≲ ρmax. We see that the optimal number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) p of planes per layer is an increasing function of γ, corroborating the findings of the previous section. However, due to the intrinsic discreteness of the problem, the increase of
p of planes per layer is an increasing function of γ, corroborating the findings of the previous section. However, due to the intrinsic discreteness of the problem, the increase of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) p with γ should actually be regarded as an average trend: for instance, when moving along the hcp branch
p with γ should actually be regarded as an average trend: for instance, when moving along the hcp branch ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) p decreases in the step from γ = 1.5 to γ = 2, see triangles in panels C and D. It is instructive to compare the T = 0 results for γ = 2 and 3 with the structures reported in Fig. 6. Therein, the stripes are fcc layers oriented perpendicularly to [111]. We see from Fig. 8D and E that the minimum energy for fcc111 is close to the deepest minimum which instead occurs for hcp; therefore, it cannot be excluded that entropy considerations (and a lower density) will favor fcc111 for high enough T. Gratifyingly, the energy minima corresponding to fcc111 for γ = 2 and 3 are found for a number of planes equal to 2 and 3, respectively, i.e., exactly the same numbers observed in Fig. 6.
p decreases in the step from γ = 1.5 to γ = 2, see triangles in panels C and D. It is instructive to compare the T = 0 results for γ = 2 and 3 with the structures reported in Fig. 6. Therein, the stripes are fcc layers oriented perpendicularly to [111]. We see from Fig. 8D and E that the minimum energy for fcc111 is close to the deepest minimum which instead occurs for hcp; therefore, it cannot be excluded that entropy considerations (and a lower density) will favor fcc111 for high enough T. Gratifyingly, the energy minima corresponding to fcc111 for γ = 2 and 3 are found for a number of planes equal to 2 and 3, respectively, i.e., exactly the same numbers observed in Fig. 6.
 | ||
| Fig. 8 For a number of γ values, we plot in separate panels the zero-temperature energy in units of the SW depth ε, see eqn (1), as a function of np for various striped crystals (in the legend of panel A). Notice that γ = 2 is a degenerate case, since exactly the same minimum enthalpy belongs to hcp (np = 1) and fcc001 (np = 2). | ||
In Fig. 9 we compare the enthalpies, for P = 0 and ρ = 1.41, of the most stable striped solids with the sdm (of fcc or hcp structure). Observe that this comparison is sufficient for our purposes, since for P > 0 the enthalpy gap can only be larger. We see from the picture that the best striped solid is systematically more stable than the substitutionally disordered mixtures, even for γ as small as 0.5, and its relative stability moreover grows with γ. This may seem in contrast with the outcome of our simulations for γ = 0.5, where for T = 0.5 and ρ = 1.1 we have found that stripes are rapidly wiped out by swap moves, whereas stripes made of single planes are found in simulation to be stable in hcp for γ = 1. The way out of this apparent contradiction is to recognize that the analysis made at T = 0 is only partially indicative of the behaviour of the mixture at non-zero temperature and not too high density. After all, the only kind of compositional disorder tested at T = 0 is the maximal disorder possible. The disorder observed for γ = 0.5 is indeed different: for example, in the hcp solid for T = 0.5 and ρ = 1.1, we see a predominance of like neighbors over unlike ones. In conclusion, stripes are absent for sufficiently small γ, and the minimum γ needed to observe stable stripes in the solid is probably between 0.5 and 1.
Once we have identified the most relevant solid phases of the mixture, we go on to determine the phase boundaries of the solid phase: indeed, the characterization of stripes would not be complete without identifying the thermodynamic conditions for which the compositional order of the mixture is stable or otherwise it is washed away upon e.g. isothermal expansion. Our procedure to identify the phase boundaries of the solid is based on the numerical analysis of a few structural indicators, once that a reasonable assumption about the structure of the stable solid has been done. This will allow us to obtain the approximate freezing and melting lines of the mixture. We illustrate our scheme for the representative case γ = 2: for a few temperatures in the range from 2 to 5, we expand the mixture gradually, starting from ρ = 1.1 and reducing the density in steps of 0.01 (for each density, averages are made over 2 × 105 cycles). Clearly, we do not know which striped crystal is stable at the various temperatures and densities: to keep it simple, for all temperatures we assume at ρ = 1.1 the same solid structure that is most stable at T = 0, namely, for γ = 2 (see panel D of Fig. 8), a striped fcc crystal with layers oriented perpendicularly to [001] and consisting of two planes each; we take for granted that for T ≥ 2 this solid is entropically favored over hcp with np = 1. We emphasize that the compositional order set in the initial configuration is preserved during the simulation, i.e., it resists thermal disorder and swap moves, at least insofar as the system is a bulk solid. Stripes in the solid phase should eventually fade away, as the temperature becomes sufficiently high. We have however not ascertained whether the disappearance of stripes corresponds to a true solid–solid phase transition or rather to a progressive rearrangement of particles inside the solid. Finally, it is also worth noting that swap moves are very efficient in probing the alleged stability of a striped solid: for example, for γ = 1, ρ = 1.1, and T = 0.5, if we start the simulation from a striped hcp crystal with np = 2, after about 104 cycles the mixture has spontaneously rearranged its composition to that typical of hcp with np = 1.
In order to assess the structure of the mixture during its evolution from solid to liquid and from solid to vapour, we monitor the values of q4 and q6, as well as the pair entropy per particle, s2.71 The latter is a sensitive probe of the overall translational order, as much as the Steinhardt parameters are for orientational order. The onset of coexistence will be signaled by a net decrease of the orientational order parameters and a substantial decrease of the absolute pair entropy. We plot our data in panels A and B of Fig. 10. For T ≥ 3, as ρ is progressively reduced q4 and q6 keep roughly constant down to ρ = ρ1(T); then, they start decreasing until reaching a density ρ = ρ2(T) where they vanish abruptly (A). The same densities ρ1 and ρ2 mark significant changes also in the behaviour of s2 (B), while inspection of the system configuration confirms that between ρ1 and ρ2 solid and liquid coexist. We assume that the loci ρ1(T) and ρ2(T) reasonably approximate the true melting and freezing lines, ρm(T) and ρf(T). The steady decrease of q4 and q6 between ρ1(T) and ρ2(T) is the result of the gradual increase of the liquid fraction in the mixture. A prominent exception is T = 3, where a hump is seen between ρ = 0.92 and 0.95: in this interval, the liquid droplet has the shape of a cylinder, while being spherical for higher densities. Below ρ = 0.92 the liquid is confined in a slab sandwiched by the solid. When the slab is sufficiently thin and the temperature is not too high, the liquid is striped like the solid, meaning that the compositional order of the solid propagates across the liquid. But when the slab becomes thicker, liquid stripes disappear altogether; indeed, no stripes are seen in the bulk liquid for ρ = 0.8 and T = 4. We should make γ larger to see stripes also in the liquid phase (see Fig. 5D). As established in the previous section, for T = 2 the mixture falls below the triple temperature. In this condition, the expanding solid enters, for ρ ≈ 1.02, the region of coexistence with a vapour of almost vanishing density. In this region, the values of q4 and q6 keep only a little smaller than in the bulk solid, since most of the particles are bulk-solid particles, irrespective of the shape of the solid–vapour interface. However, a series of humps occurs in all order parameters as a function of ρ: each hump corresponds to a well-definite shape and size of the vapour inclusion, which is heralded, for densities near the surrounding minima, by the formation of a thin liquid film at the interface between solid and vapour. As ρ is reduced, a spherical vapour bubble first appears, followed by cylindrical and bicylindrical64 bubbles. For still lower ρ, the solid droplet finally acquires a slab-like shape. An analogous fine structure is present in s2, see Fig. 10B, where s2 valleys correspond to maxima of q4 and q6, and vice versa.
Combining all results together, we draw in Fig. 10C the phase diagram of the equimolar mixture for γ = 2. Notice, in particular, that the triple temperature is only slightly less than 3.
4 Conclusions and perspectives
The origin of striped phases in colloids is currently the object of debate, since the connection between their onset and the intermolecular potential has not yet been elucidated in detail. Herein, we have addressed this issue by demonstrating that a system as simple as a binary mixture of identical hard spheres can have a striped structure, provided that a flat and sufficiently long-ranged cross attraction is set between the two species. In addition, stripes are the more pronounced the longer the attraction range, leading to the conclusion that like aggregation is promoted by unlike attraction. More precisely, we have used numerical and theoretical methods to study the phase behaviour of a symmetric binary mixture of hard spheres, interacting via a square-well (SW) attraction of variable range γ between unlike spheres only. Despite the extreme simplicity of the model, we identify a variety of remarkable behaviours. For γ = 1 or larger the solid phase exhibits a patterned structure, where planar stripes of particles of one species alternate with stripes of the other species. Starting from γ≈3, stripes also emerge in the bulk liquid. Occasionally, stripes are also present in the liquid coexisting with vapour or solid, even when they are absent in bulk.Stripe order, i.e., a modulation of composition along a definite direction, comes totally unexpected in a mixture of hard spheres with isotropic cross attraction. It can be explained by energy considerations: planar stripes ensure the largest possible number of attractive unlike spheres (see our zero-temperature calculations in Section 1B).
Compared with other works,27,29–31 our study clarifies that the presence of stripes essentially depends on the range of cross attraction rather than on the specific interaction between particles of the same species. We emphasize that stripes in our model arise spontaneously. This is to be contrasted with previous studies of HS mixtures, where stripes are forced to occur by a suitable confinement72 or a striped substrate.73 Another form of compositional order under equimolarity, namely the checkerboard order, which too has a low energy, could be safely excluded in the present case, since it would only be relevant for a crystal with two-sublattice structure (which is not the case of fcc and hcp).
We guess that, aside from the range, also a nearly flat profile of the cross attraction could be important in the stabilization of stripes: indeed, the freedom of particles to adjust their relative positions inside the well without affecting the energy gain is probably crucial in view of maximizing the number of contacts between unlike spheres. We postpone to a future study a thorough investigation of the role played by the shape of cross attraction and/or a departure from equimolarity in making the mixture striped.
Our findings suggest new directions for the engineerization of colloidal particles tailored at the appearance of stripe-modulated structures. According to our predictions, the emergence of stripes in the solid phase is expected for values of γ between 0.5 and 1. Since this interaction range is close to real colloidal regimes, our model is open to an experimental implementation, so as to verify whether our results are predictive of real-life behavior.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been done using the computer facilities made available by the PO-FESR 2007–2013 Project MedNETNA (Mediterranean Network for Emerging Nanomaterials).Notes and references
- T. Shinbrot and F. J. Muzzio, Nature, 2001, 410, 251–258 CrossRef CAS PubMed.
- A. J. Millis, Nature, 1998, 392, 438–439 CrossRef CAS.
- H. Meinhardt, Nature, 1995, 376, 722–723 CrossRef CAS.
- S. Das, E.-S. M. Duraia, O. D. Velev, M. D. Amiri and G. W. Beall, Appl. Surf. Sci., 2018, 435, 512–520 CrossRef CAS.
- Y. Mino, S. Watanabe and M. T. Miyahara, ACS Appl. Mater. Interfaces, 2012, 4, 3184–3190 CrossRef CAS PubMed.
- H. Löwen and J. Dzubiella, Faraday Discuss., 2003, 123, 99–105 RSC.
- Y. Mu, L. Lei, J. Zheng, W. Duan, Z. Wang, J. Tang, Y. Gao and Y. Wang, ACS Nano, 2022, 16, 6801–6812 CrossRef CAS PubMed.
- Y. Guo, S. Afghah, J. Xiang, O. D. Lavrentovich, R. L. B. Selinger and Q.-H. Wei, Soft Matter, 2016, 12, 6312–6320 RSC.
- S. Watanabe, K. Inukai, S. Mizuta and M. T. Miyahara, Langmuir, 2009, 25, 7287–7295 CrossRef CAS PubMed.
- H. Pattabhiraman and M. Dijkstra, Soft Matter, 2017, 13, 4418–4432 RSC.
- P. Tierno, T. M. Fischer, T. H. Johansen and F. Sagùes, Phys. Rev. Lett., 2008, 100, 148304 CrossRef PubMed.
- W. Selke, Phys. Rep., 1988, 170, 213–264 CrossRef.
- M. Seul and D. Andelman, Science, 1995, 267, 476 CrossRef CAS PubMed.
- A. D. Stoycheva and S. J. Singer, Phys. Rev. Lett., 2000, 84, 4657–4660 CrossRef CAS PubMed.
- K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2010, 104, 195703 CrossRef PubMed.
- J. Pekalski, A. Ciach and N. G. Almarza, J. Chem. Phys., 2014, 140, 114701 CrossRef PubMed.
- N. G. Almarza, J. Pekalski and A. Ciach, J. Chem. Phys., 2014, 140, 164708 CrossRef CAS PubMed.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef PubMed.
- H. J. Zhao, V. R. Misko and F. M. Peeters, New J. Phys., 2012, 14, 063032 CrossRef.
- J. Pekalski and A. Ciach, J. Chem. Phys., 2018, 148, 174902 CrossRef PubMed.
- N. Dlamini, S. Prestipino and G. Pellicane, Entropy, 2021, 23, 585 CrossRef PubMed.
- G. Malescio and G. Pellicane, Nat. Mater., 2003, 2, 97 CrossRef CAS PubMed.
- M. A. Glaser, G. M. Grason, R. D. Kamien, A. Kosmrlj, C. D. Santangelo and P. Ziherl, EPL, 2007, 78, 46004 CrossRef.
- G. J. Pauschenwein and G. Kahl, J. Chem. Phys., 2008, 129, 174107 CrossRef PubMed.
- J. Fornleitner and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 104118 CrossRef PubMed.
- K. Khalil, A. Sagastegui, Y. Li, M. A. Tahir, J. E. S. Socolar, B. J. Wiley and B. B. Yellen, Nat. Commun., 2012, 3, 794 CrossRef PubMed.
- C. I. Mendoza and E. Batta, EPL, 2009, 85, 56004 CrossRef.
- S. Prestipino, G. Munaò, D. Costa, G. Pellicane and C. Caccamo, J. Chem. Phys., 2017, 147, 144902 CrossRef PubMed.
- L. A. Padilla, A. A. León-Islas, J. Funkhouser, J. C. Armas-Pèrez and A. Ramìrez-Hernández, J. Chem. Phys., 2021, 155, 214901 CrossRef CAS PubMed.
- A. Ciach, A. De Virgiliis, A. Meyra and M. Litniewski, Molecules, 2023, 28, 1366 CrossRef CAS PubMed.
- G. Munaò, D. Costa, G. Malescio, J. M. Bomont and S. Prestipino, Soft Matter, 2022, 18, 6453 RSC.
- M. Maldovan and E. Thomas, Nat. Mater., 2004, 3, 593–600 CrossRef CAS PubMed.
- Y. Wang, I. C. Jenkins, T. Sinno and J. C. Crocker, Nat. Commun., 2017, 8, 14173 CrossRef CAS PubMed.
- R. Foty, C. M. Pfleger, G. Forgacs and M. S. Steinberg, Development, 1996, 122, 1611–1620 CrossRef CAS PubMed.
- D. Duguay, R. Foty and M. S. Steinberg, Dev. Biol., 2003, 253, 309–323 CrossRef CAS PubMed.
- C. E. Caicedo-Carvajal and T. Shinbrot, Dev. Biol., 2018, 315, 397–403 CrossRef PubMed.
- T. Shinbrot, Y. Chun, C. E. Caicedo-Carvajal and R. Foty, Biophys. J., 2009, 97, 958–967 CrossRef CAS PubMed.
- D. Pini and A. Parola, Soft Matter, 2017, 13, 9259–9272 RSC.
- D. Pini, Soft Matter, 2018, 14, 6595–6612 RSC.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 7775 CrossRef CAS PubMed.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 6178 CrossRef CAS PubMed.
- J. M. Harder and M. Silbert, Chem. Phys. Lett., 1980, 75, 571 CrossRef CAS.
- S. Babu, J. C. Gimel, T. Nicolai and C. De Michele, J. Chem. Phys., 2008, 128, 204504 CrossRef PubMed.
- S. Babu, J. C. Gimel and T. Nicolai, J. Chem. Phys., 2009, 130, 064504 CrossRef PubMed.
- E. Zaccarelli, F. Sciortino and P. Tartaglia, J. Chem. Phys., 2007, 127, 174501 CrossRef PubMed.
- C. Mayer, F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Phys.: Condens. Matter, 2010, 22, 104110 CrossRef PubMed.
- R. A. L. Jones, Soft Condensed Matter, Oxford University Press, 2002 Search PubMed.
- J. P. Hansen and I. R. McDonald, Theory of simple liquids, 3rd Ed., Academic Press, New York, 2006 Search PubMed.
- D. Fiocco, G. Pastore and G. Foffi, J. Phys. Chem. B, 2010, 114, 12085 CrossRef CAS PubMed.
- F. Delrio, O. Guzman and A. Malijevsky, J. Phys. Chem., 1995, 99, 187 CrossRef.
- W. R. Smith and D. Henderson, J. Chem. Phys., 1978, 69, 319 CrossRef CAS.
- D. Henderson, W. G. Madden and D. D. Fitts, J. Chem. Phys., 1976, 64, 5026 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulations, Academic Press, New York, 2nd edn, 2002 Search PubMed.
- L. Belloni, J. Chem. Phys., 1993, 98, 8080 CrossRef CAS.
- G. Malescio and S. Prestipino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 050301(R) CrossRef PubMed.
- J. Hoshen and R. Kopelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 14, 3438 CrossRef CAS.
- S. Prestipino and P. V. Giaquinta, J. Stat. Mech.: Theory Exp., 2004, 09, P09008 Search PubMed.
- S. Prestipino and P. V. Giaquinta, Entropy, 2022, 22, 1024 CrossRef PubMed.
- Y. Rosenfeld, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 6526 CrossRef CAS PubMed.
- G. Malescio, P. V. Giaquinta and Y. Rosenfeld, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, R3723 CrossRef CAS.
- G. Malescio, P. V. Giaquinta and Y. Rosenfeld, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4090 CrossRef CAS PubMed.
- K. Binder, P. Virnau, B. J. Block, P. Virnau and A. Tröster, Am. J. Phys., 2012, 80, 1099 CrossRef CAS.
- M. C. Abramo, C. Caccamo, D. Costa, P. V. Giaquinta, G. Malescio, G. Munaò and S. Prestipino, J. Chem. Phys., 2015, 142, 214502 CrossRef PubMed.
- S. Prestipino, C. Caccamo, D. Costa, G. Malescio and G. Munaò, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022141 CrossRef PubMed.
- J. Mayer and W. W. Wood, J. Chem. Phys., 1965, 42, 4268 CrossRef CAS.
- K. Binder, Phys. A, 2003, 319, 99 CrossRef.
- https://en.wikipedia.org/wiki/Gila_monster .
- J. Van Duijneveldt and D. Frenkel, J. Chem. Phys., 1992, 96, 4655–4668 CrossRef CAS.
- P. R. ten Wolde, M. J. Ruiz-Montero and D. Frenkel, J. Chem. Phys., 1996, 104, 9932 CrossRef CAS.
- S. Prestipino, F. Saija and G. Malescio, Soft Matter, 2009, 5, 2795 RSC.
- R. E. Nettleton and M. S. Green, J. Chem. Phys., 1958, 29, 1365 CrossRef CAS.
- Y. Shokef and T. C. Lubensky, Phys. Rev. Lett., 2009, 102, 048303 CrossRef PubMed.
- H. M. Harreis, M. Schmidt and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041602 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |