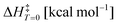A simple topology-based model for predicting the activation barriers of reactive processes at 0 K

Abstract

This work reveals an underlying correlation between the topology and energetic features of matter configurations/rearrangements by exploiting two topological concepts, namely, structural stability and persistency, leading thus to a model capable of predicting activation energies at 0 K. This finding provides some answers to the difficulties of applying Thom's functions for extracting energetic information of rate processes, which has been a limitation for exact, biological, and technological sciences. A linear relationship between the experimental barriers of 17 chemical reactions and both concepts was found by studying these systems’ topography along the intrinsic reaction coordinate. Such a procedure led to the model , which accurately predicts the activation energy in reacting systems involving organic and organometallic compounds under different conditions, e.g., the gas-phase, solvent media, and temperature. This function was further recalibrated to enhance its predicting capabilities, generating the equation 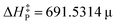for this procedure, characterized by a squared Pearson correlation coefficient (r² = 0.9774) 1.1 times higher. Surprisingly, no improvement was observed.

---

Introduction

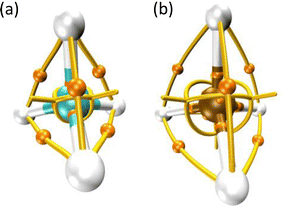
Thom's catastrophe theory (CT)¹ has tremendously impacted several branches of scientific research. Such relevant work has been applied to biological,¹ social,^2,3 technological,^4–7 and exact^8–12 sciences. Despite the popularity of CT, the connection between objects derived from it and the energy associated with a particular configuration of matter or the amount of heat needed for a process to occur is far from clear. This fact is readily evidenced in both stationary and reacting systems.^9,13–15Scheme 1 shows the molecular graph, i.e., the collection of nuclear attractors and (bond) paths connecting them,¹⁶ for the CH₄ and H₄Si molecules, panels (a) and (b), respectively. These ‘‘networks’’ are a graphical representation of the vector field created by the gradient of the electron localization function (ELF). The ELF¹⁷ is a quantum chemical tool for probing Pauli's exclusion principle; therefore, this function enables recovering Lewis objects such as bonds and valence. This means that ELF attractors (or maxima) are crucial topographical objects which shape the molecular graphs and allow us to distinguish them. Although in the majority of cases, it is determined via quantum calculations,¹⁰ it has been shown that the ELF can be obtained from experiments.^18,19 It is worth noting that any conclusive evidence concerning the distinguishability between methane and silane can be extracted by examining their topography since these molecules exhibit the same (equivalent) molecular graph. However, it is well known that such systems have different physical and chemical properties. For instance, the molar enthalpy of formation (in the gas phase at 298.15 K) is +34.3 and −74.6 kJ mol⁻¹ for H₄Si and CH₄, respectively.²⁰

Scheme 1 ELF molecular graphs of methane and silane, panels (a) and (b), respectively, showing that although these compounds have different physical–chemical properties, their molecular graphs are topographical equivalents. These textbook systems evidence the limitations of using topology to gain insights into the energetic features of matter. Yellow lines represent ELF gradient paths. Orange spheres indicate saddle points of index one.

Furthermore, over the last 25 years, the computational evidence, gained by associating topographical changes in the phase-space of the ELF¹⁷ with meaningful chemical events (e.g., formation and cleavage of bonds) along a reaction pathway through seven parametric functions,⁹ has led our community to agree on the impossibility of extracting energetic information via these polynomials (unfoldings) derived from Thom's works.¹ For instance, the energy needed for a covalent bond scission cannot be correlated with any unfolding since, in some cases, this chemical event is described via a fold-type polynomial,^13,14,21 whereas in others, through a cusp function.^9,13,14 Thus, insofar applications of CT in our field have been focused on providing information on the molecular mechanism or the relative reactivity of chemical species, leaving aside the energetic aspect of the discussion. Although our group has recently made some progress by revealing the intimate relationship between the unfoldings¹ and the pair-electron density symmetry in chemical reactions occurring in both grounds^15,22 and electronically excited states,^23–25 none of these works give any clue on how to correlate the unfoldings with, for instance, the activation barrier. To the best of our knowledge, the only effort in this direction was made more than two decades ago by Margalef-Roig, Miret-Artés, and Toro-Labbé.²⁶ They showed that if a property such as the chemical hardness, energy, or chemical potential is described through a Gibbs-like potential along a reaction coordinate, then this potential is (locally) isomorphous to a fold polynomial. This result constitutes a breakthrough, at least from a theoretical standpoint. However, the cardinality of the unfolding set is seven, and, on the other hand, applying such a result to a concrete situation, such as predicting the height of a barrier, completely fails. This scenario depicts the poor progress that has been made in unifying Thom's work with crucial chemical quantities (e.g., enthalpy of formation) and justifies the lack of studies devoted to revealing underlying relationships (if any) between energetic descriptors and the foundations of CT, despite its astonishing popularity. In fact, the impossibility of an energetic discussion concerning electron rearrangements by means of Thom's polynomials is indeed the main drawback of all methodologies based on CT. Our findings suggest that such discouraging state-of-the-art results from the absence of a measurable relationship between the qualitative description of electron rearrangements given by unfoldings and the energy demanded by the former, because this correlation is deeply rooted in the very basis of topology and not in Thom's unfoldings. This means that such a relationship is a more fundamental one.

This paper presents a promising achievement regarding the above discussion. Herein, we first show the existence of a strong correlation between crucial topological concepts, namely, persistency and structural stability, and the activation barrier of reactive processes. Quite surprisingly, such a relationship can be written in terms of a model capable of predicting energy threshold in reactions encompassing organic and organometallic compounds.

Results and discussion

Table 1 lists 17 reactions used to deduce the model (see the ESI† for further details). Activation energies (ΔH) computed via DFT functionals deviate, at most, 2.88 kcal mol⁻¹ from the corresponding experimental value after correcting the latter to 0 K (). The value of is obtained by means of the molecularity of each reacting system and the absolute temperature of the experiment.^10,29 Experimental conditions were incorporated into the proposed model by considering the solvent media, pressure, and temperature for each case. Moreover, the selected system of chemical reactions comprises a wide temperature range, i.e., from 293 to 748 K, covering an interval of experimental activation barrier of 7.7–54.0 kcal mol⁻¹.

Table 1 Computed(ΔH) corrected and experimental (E_a) activation barriers in kcal mol⁻¹

No.	Reaction	ΔH [kcal mol^−1 ]	[kcal mol^−1]	E a [kcal mol^−1]
1		5.05	5.82	7.7^27,28
2		33.70	32.49	33.5^29
3		19.64	19.34	20.5^30
4		10.43	12.44	13.6^30
5		11.85	14.41	15.6^30
6		14.94	17.82	19.0^30
7		28.69	28.34	29.3^29
8		35.98	35.37	36.3^29
9		21.12	22.62	23.7^29
10		22.90	24.01	24.6^29
11		51.79	52.50	54.0^29
12		30.58	32.30	33.2^31
13		29.59	30.24	31.9^31
14		31.78	32.00	32.9^31
15		29.94	30.57	31.4^31
16		29.40	31.45	32.3^31
17		30.70	32.74	33.6^31

---

We then follow all topographic changes associated with relevant electron reorganizations leading to the breaking of single bonds and reduction of double to single bonds along the intrinsic reaction coordinate (IRC) before the reaction system reaches the transition state configuration. These events constitute the so-called electronic preparation stages of the reaction, which are indeed the driving forces underpinning compound activation. It should be stressed that the subsequent development we present allows these chemical changes to be described by any of the seven unfoldings, enabling the generalization of Toro–Labbé and collaborators’ work.²⁶ The next step is critical since we need to measure the total energy the system needs to move throughout the preparation rearrangements; in other words, it is crucial to estimate how much energy must be added to the reacting system. From the Eyring–Polanyi³² theory, it is well-known that this amount of energy comes from external sources, namely, intermolecular collisions. Conveniently, this energy can be associated with the negative reaction force integral.³³ Thus, the integration limits correspond to the energy of reactant(s) and the structure exhibiting the last topographical change, E_r and E_* respectively:

In eqn (1), F represents the force of the reaction, R stands for the IRC, and μ is the amount of external energy needed to prepare the reacting system to undergo a chemical reaction. The reaction will not occur for values of μ lower than the one computed through eqn (1), whereas the reaction has a significant probability of proceeding for values equal or higher. Consequently, it is reasonable to take μ as the (external) control parameter.^1,4Fig. 1 presents a fragment of the IRC regarding the archetypal Diels–Alder (DA) reaction between 1,3-butadiene and ethylene for further clarifying how we exploited eqn (1). The reduction of the dienophile double bond is the last topographical change before the system reaches the transition state configuration. Thus, the energy associated with this key geometry is equal to E_* by definition.

Fig. 1 IRC fragment for the Diels–Alder reaction between 1,3-butadiene and ethylene. The reduction of the dienophile double bond constitutes the last topographic change before the reaction system reaches the transition state configuration. This means that the energy of such an ‘‘activated’’ structure is E_* blue spheres, indicating ELF maxima, which provide a natural and straightforward representation of Lewis objects (e.g., core, bond, and valence).

Not surprisingly, reaction systems with high activation barriers demand more external energy in order to surmount that threshold; therefore, the exposure of ELF maxima (i.e., the number of frames in which a critical point appears along the path) will also be long. From this, it is reasonable to conclude that this exposure factor should be correlated with the height of the activation barrier. Recall that a reaction system lying in a deep energetic well (relative to the transition state energy) will exhibit a low reactivity. The higher the local curvature of the potential energy surface (PES), where reactants and the transition state configuration are placed, the more the energy needed for the reaction to occur. Thus, PES features are the key elements underpinning both kinetic and thermodynamic aspects of reactive processes. Luckily, ELF topography accurately captures the complexities of this surface. For example, an exposure factor constitutes a suitable visual measure of the persistency^6,34–37 of a critical point (CP). Furthermore, this topological concept is an adequate metric for exploring the structural stability of CP^4,6,38–42 and, in general, the system molecular graph. A CP that remains in the molecular graph (topographic map) upon an external perturbation (μ) is frequently referred to as a persistent point. Our working hypothesis is that the concept of persistency, estimated via the external parameter μ and the activation barrier are correlated. To prove that, we compute μ using eqn (1) for each reaction listed in Table 1, and the results are shown in Table 2.

Table 2 External parameter μ in E_h

No.	μ[Eh]
1	0.006550678
2	0.052624565
3	0.028535045
4	0.007001504
5	0.015171086
6	0.021119109
7	0.023956267
8	0.036021286
9	0.032307993
10	0.034610163
11	0.075898734
12	0.045908015
13	0.045773725
14	0.048255020
15	0.043459820
16	0.043328948
17	0.044536073

---

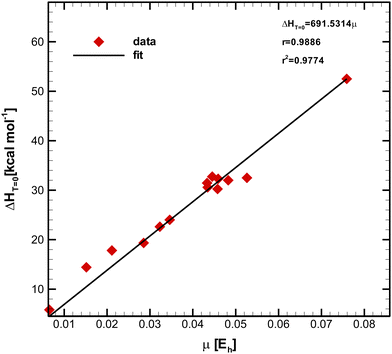
The unit of μ was kept in Hartree to minimize the statistical propagation effects of errors. Fig. 2 depicts the plot of (see Table 1) versus μ (see Table 2) obtained through the least-square method. The Pearson (product-moment) correlation coefficient (PCC), r, is a widely used statistical metric to quantify the strength of the linear relationship between a pair of variables.^43–46 For convenience, the PCC takes values between −1 and +1, where −1 corresponds to a perfect negative linear relationship, whereas the +1 value characterizes a perfect positive one. Two random variables are called linearly uncorrelated if r = 0.⁴⁷ Typically, the degree of linearity is established by partitioning the interval, and although different research fields have adopted distinct criteria,⁴⁷ most agree in describing the relationship as strong if r ≥ 0.7.^48–50 Moreover, the predicting capability of a model is a paramount practical feature. In order to measure how well the simple regression line fits the experimental data, we can simply square r,^43–45 which is called the squared Pearson correlation coefficient (SPCC), r².^43–45 The SPCC range is [0, 1]^43–45 and measures the amount of variation around the mean of the independent variable predictable from linear regression.⁴⁴ Concretely, the closer the values of r² to unity, the better the fit, and the closer the experimental points are from the line. In contrast, if r² is equal to zero, it is impossible to write a linear function containing both variables, i.e., a horizontal line is generated, meaning the predicting capability of the model is null.⁴⁴

Fig. 2 Simple linear regression plot of as a function of μ for 17 reactions, showing a very strong linear correlation between variables.

Using the slope, g, of the linear fit, we propose the following simple model for predicting the activation barrier (at 0 K) of chemical reactions in both solution and gas phase within the interval of 293–748 K:

In eqn (2), is the predicted activation energy, and g′ represents the quotient between ΔH and μ. Two details should be recalled when applying the model; first, these two latter parameters are to be determined via direct calculation; and second, the correlation information is embodied within the slope g. On the other hand, note that the unit of is kcal mol⁻¹, as desired. Different setups were considered for testing the predicted performance of the proposed tool (eqn 2): (i) organometallic compounds, (ii) reactions with activation barrier out of the fitting energy interval, and (iii) cases in which the direct calculation of the barrier is somewhat accurate, as displayed in Table 3. The experimental activation energy of reactions 1–12 is computed from the provided³⁰ rate constant using the Eyring–Polanyi theory.³² Detailed information concerning optimized geometries, values of μ and levels of theory are provided in the ESI.†

Table 3 Performance of the topology-based model

No.	Reaction	ΔH [kcal mol^−1]			Abs. error [kcal mol^−1]	Model abs. error [kcal mol^−1]
1		13.77	22.53	25.32^30	11.55	2.79
2		14.19	29.05	23.52^30	9.33	5.53
3		13.03	15.41	22.12^30	9.09	6.71
4		13.02	16.15	21.22^30	8.20	5.07
5		18.28	25.25	22.94^30	4.66	2.31
6		9.09	12.08	16.54^30	7.45	4.46
7		16.48	17.54	22.64^30	6.16	5.09
8		17.62	22.14	27.50^30	9.88	5.36
9		9.72	19.61	16.84^30	7.12	2.77
10		9.02	10.86	17.32^30	8.30	6.46
11		11.58	16.93	15.77^30	4.19	1.16
12		13.19	19.70	20.24^30	7.05	0.54
13		16.20	16.21	8.22^51,52	7.98	7.99
14		17.79	18.58	9.04^51,52	8.75	9.54
15		21.03	27.01	29.08^29	8.05	2.07
16		19.96	26.50	23.52^53	3.56	2.99
17		0.68	0.93	1.21^54,55	0.53	0.28
18		40.22	36.82	32.09^29	8.13	4.73
19		15.62	14.50	12.02^56	3.60	2.48
20		27.67	25.72	31.00^31	3.33	5.28
21		42.47	38.09	37.14^57,58	5.33	0.95
22		19.11	32.84	31.60^30	12.48	1.21

---

The cleavage/reduction of bonds criteria characterizing the electronic preparation stages and associated with the structural stability concept has to be, to some extent, generalized to study reactions where neither single bond breaks nor higher-order bond reduces (e.g., reactions 16 and 21, Table 3). In such cases, E_* corresponds to the energy associated with the first topographic change, i.e., the apparition of a new ELF maximum near the reaction center. Thus, this critical point is always involved in the electron rearrangements leading to a new Sigma bond between moieties since the reacting system is now ‘‘activated’’. It is not hard to realize that this line of thinking indeed constitutes a natural way to extend the previous criteria, as depicted in Fig. 3. This generalization seems to be reasonable considering the significant amount of computational evidence¹⁰ pointing out that the rising of an ELF maximum near a reaction center constitutes a topographical signature preluding a bond formation.

Fig. 3 IRC fragment for the textbook reaction between acetyl chloride and OH⁻. In this case, neither reduction nor scission of bonds occurs. Therefore, we select the geometry showing the first topographical change (i.e., the apparition of an ELF maximum near the hydroxyl oxygen due to the splitting of its valence shell), which marks the onset of the system activation. Blue spheres indicate ELF maxima, which provide a natural and straightforward representation of Lewis objects (e.g., core, bond, and valence).

Reactions presented in Table 3 were obtained through modern DFT functionals; nonetheless, some of them were computed by means of the smallest possible basis set, guaranteeing an adequate description of physical (e.g., electron fluxes) and chemical (e.g., predicted VSEPR⁵⁹ structure) properties of the system. Such a procedure aims to obtain a somewhat accurate characterization of the reacting system, on the one hand, while a poor estimation of the barrier, on the other, for further testing the predictive capabilities of the model. For instance, reactions [1–5, 7–9] follow this idea since they were studied using the 6-31G (reactions 1, 2, 5, 7, and 8) and 6-31G(d) (reactions 3, 4, and 9) basis sets. The case of reactions 1, 9, and 12 is quite remarkable because the estimated barrier (from direct calculations) were 11.6, 7.1, and 7.1 kcal mol⁻¹ lower than the experimental value, respectively, whereas the model prediction deviates −2.8, +2.8, and −0.5 kcal mol⁻¹, respectively. Moreover, the reaction (19) between diazomethane and norbornene, as well as the S_N2 between bromomethane and Cl⁻, show that the proposed model is capable of suggesting a more accurate barrier than the direct computed one, even in cases where the estimated activation energy using potent quantum chemical machinery deviates only 3.6 kcal mol⁻¹ from the experimental value. This fact is also evidenced in the DA reaction between 1,3-cyclopentadiene and furan-2,5-dione. However, although the estimated activation barrier for the aliphatic-Claisen rearrangement (20) of 2-(allyloxy)prop-1-ene deviates 3.3 kcal mol⁻¹ from the experimental energy, the model fails to provide a more accurate value. Furthermore, its performance for the epoxidation of isobutene (13) and α-methylstyrene (14) by dimethyldioxirane is surprisingly poor, predicting energy values slightly worse than the directly calculated ones. This might be explained by assuming that the basis set used is less flexible than required to provide an appropriate description of the physics underpinning both reaction systems. On the other hand, the oxidation reaction encompassing a transition metal (17) is crucial in the validation process because of the complexity typically associated with describing almost barrierless systems. Even current refined quantum calculation methods estimate an activation barrier of about half the experimental value. Nevertheless, the model succeeded in predicting a barrier lying 0.3 kcal mol⁻¹ below the experimental measurement, thus constituting a remarkable achievement because of the critical dropping in the relative error from 147 to 23%, corresponding to the direct and predicted calculations, respectively.

It is essential to emphasize the relevance of the application limits of the proposed topology-based model. The activation energy of the prototypical hydrogen-substituted DA between 1,3-butadiene and ethylene was experimentally determined at 800 K (about 50 K higher than the upper limit of the fitting interval). Therefore, a significant inaccuracy should be expected if eqn (2) is applied to this case. For instance, direct calculation via the ωB97X-D/6-31G(d) level estimates a barrier of 18.1 kcal mol⁻¹; in contrast, the model predicts a value 2.2 kcal mol⁻¹ lower. However, is as high as 24.3 kcal mol⁻¹.

Recalibration of the model

A straightforward mechanism for enhancing the value of r², and hence the linear correlation between and μ is filtering out the three points exhibiting the highest distance from the fit line. Such points correspond to reactions 4, 7, and 8 (see Table 1). This procedure significantly improves both coefficients, which means the corrected model should provide more accurate predictions than the uncalibrated one, as presented in Fig. 4.

Fig. 4 Recalibrated model, showing a significant improvement in its prediction capabilities.

Table 4 compares the prediction performance of both models. Note that the expected enhancement in the predictability of the corrected one is not observed, even though the correction procedure leads to a relevant improvement of r². Not surprisingly, certain flexibility of the first equation capabilities was lost by removing some statistical variability sources, leading to a null improvement of the recalibrated model since exactly half of the testing set shows more accurate barriers. It is worth noting these reactions are quite randomized, which hinders the identification of a pattern. This is evident in reactions 1, 2, and 17. However, this intriguing finding might suggest that the linear correlation is independent of the reaction set used to deduce the model, a plausible explanation that should be further investigated.

Table 4 Prediction accuracy of both models

No.	Model abs. error [kcal mol^−1]	Recalibrated model abs. error [kcal mol^−1]
1	2.79	1.91
2	5.53	6.66
3	6.71	6.11
4	5.07	4.44
5	2.31	3.29
6	4.46	3.99
7	5.09	4.41
8	5.36	4.50
9	2.77	3.53
10	6.46	6.04
11	1.16	1.82
12	0.54	0.22
13	7.99	8.62
14	9.54	10.26
15	2.07	1.02
16	2.99	4.01
17	0.28	0.25
18	4.73	6.17
19	2.48	3.04
20	5.28	4.28
21	0.95	2.43
22	1.21	2.48

---

Theory and computational details

Considering the excellent bibliographical sources available in the literature on dynamical systems (DS), structural stability of vector fields, and catastrophe theory (CT), here we will just focus on stating the main ideas. Let us first recall that the bonding evolution theory (BET)⁹ models the reaction system as a gradient DS (GDS).^35–37,39 The potential function of this GDS is the so-called electron localization function (ELF≡η)¹⁷ which is a scalar function depending on the three spatial variables of [Doublestruck R]³. Roughly speaking, the gradient of ELF, ∇η generates a vector field which can be uniquely defined by its equilibria, i.e., ∇η = 0, which yields only four types of singular (critical) points: attractors (maxima), saddle points of index one, saddle points of index two, and repellors (minima). Each of these CPs can be characterized by a pair of non-negative integers known as the rank, ω, and signature, σ. The first one indicates the number of directions (eigenvectors) or dimensions of the space, whereas the latter results from algebraically summing the sign of eigenvalues.⁵ The stability of an ELF CP requires that all its eigenvalues are real; in other words, the real part of any eigenvalue is non-zero.^6,39,60 A critical point exhibiting this characteristic is called hyperbolic or Morse-type; otherwise, they are referred to as degenerate or non-hyperbolic.³⁹ Intuitively, one can associate the stability of a CP with the persistency of its characteristics (e.g., none of its associated eigenvalues has a purely imaginary part) after the GDS is submitted to a small perturbation.^6,35–38 More precisely, it is said that there exists a homeomorphism between vector fields mapping every orbit of the unperturbed system to an orbit of the perturbed one, preserving the direction of the flow,^{6,38,39,60,61} as depicted in Scheme 2.

Scheme 2 Unperturbed and perturbed phase-space portraits, panels (a) and (b), respectively, showing that the vector field created by the gradient of ELF is structurally stable since there exists a homeomorphism that preserves the number and orientation of trajectories. Colored balls represent critical points of ELF. Oriented lines indicate ELF gradient paths.

The topographic map or phase-space portrait (i.e., the collection of all CPs and the set of trajectories connecting them^39,62) is said to be structurally stable if all CPs of the potential function (e.g., ELF) preserve their type (σ) and hyperbolic characteristic (ω) after an external perturbation is applied to the GDS, meaning that the unperturbed map (Scheme 2, panel a) and the perturbed one (Scheme 2, panel b) are orbitally equivalent. Thus, the number and orientation of trajectories remain unchanged.^38,39 The notion of structural stability was first introduced by Andronov and Pontryagin under the name of ‘‘grossier’’ (roughness).^6,42 Peixoto⁶³ extended their work by ‘‘embedding’’ a DS on a 2-dimensional smooth manifold, postulating the necessary and sufficient conditions that a DS must fulfill to be classified as a structurally stable system:

(i) there is only a finite number of CPs, all generic (hyperbolic);

(ii) the α-(starting point of the trajectory) and β-limit (converging point of the trajectory) sets of every trajectory can only be CPs or closed orbits (collection of trajectories);

(iii) no trajectory connects saddle points (the possibility of self-connection is also excluded);

(iv) there is only a finite number of close orbits, all simple (hyperbolic).

Peixoto's landmark paper reveals the deep connection between DSs and the underlying topological structure that supports it since conditions (i), (ii), and (iii) coincide with the ones stated by Andronov and Pontryagin.^6,42,43 The third condition is crucial for further understanding Thom's catastrophe theory^4,64 and provides a straightforward way to explore the coalesces mechanism of CPs in the ∇η phase portrait.⁶ Nevertheless, the topographic map contains not only CPs but also a large number of the so-called wandering points. A wandering point always describes an unbound trajectory in the sense that such a trajectory will not return to the starting point.^6,39,60 Therefore, these types of points behave radically differently from critical ones. Because of an external deformation (perturbation), two critical points can merge, and consequently, a wandering point is generated. Such an abrupt change in the number of CPs is typically referred to as a (local) bifurcation.^38,65 In (generic) function families with more than one parameter, more than two CPs merge, and the outcome (i.e., a wandering point or a new CP) can be readily predicted by following the Poincaré–Hopf theorem.⁶⁶ Not surprisingly, these events can occur in the opposite direction, in other words, the splitting of a non-hyperbolic CP into two new Morse-type critical points, for instance. Catastrophe theory¹ is a robust mathematical program that succeeded in describing all possible (abrupt) discontinuous changes in functions defined on a 2-dimensional real space through a set of seven parametric polynomials called universal unfoldings. Nonetheless, the unfoldings can be rewritten in a convenient way, making them suitable for probing the phase portrait of generic families on [Doublestruck R]³, albeit the structural stability conditions (i–vi) must be satisfied.^4,64 Within CT¹ applications, the term bifurcation is usually replaced by the catastrophe one (or by an elaborated combination of both words, e.g., catastrophe bifurcation). Thom realized that in the vicinity of a local bifurcation, the geometric shape of the potential function could be replicated by adjusting the value of the polynomial parameter(s). Because of this, the parameter is frequently called a control parameter. Thus, by changing its value, one can remove the degeneracy exhibited by the topographic map upon the action of external forces, leading to a new denomination for the control parameter, namely, external control parameter, μ,⁵ as shown in Scheme 3.

Scheme 3 The ∇η phase portrait exhibits a catastrophic bifurcation at μ = μ_* since two CPs appear/disappear. Colored balls represent critical points of ELF.

Silvi, Krokidis, and Noury⁹ proposed a methodology they coined bonding evolution theory that allows following the changes in the phase portrait of the ELF (along a reaction coordinate) resulting from external forces acting on the reacting system and formally classifying them via the universal unfoldings. It should be stressed that these changes are typically associated with relevant chemical events such as the bond-breaking and bond-forming processes. Moreover, there is a general agreement in interpreting the ELF as a local measure of the excess in the kinetic energy density of electrons due to Pauli's exclusion principle.^67,68 Thus, ELF allows the recovery of key chemical notions introduced by Lewis on the basis of empirical evidence, such as, the concepts of valence, core, and electron sharing.^69,70 Not surprisingly, BET has been used to gain deeper insights into different bonding situations, encompassing gas-phase and solid-state systems.¹⁰

Reactant, product, and transition state (TS) geometries were optimized with the Gaussian 16 suite of programs.⁷¹ For each of the studied reactions, an IRC was performed in order to confirm that the optimized TS structure indeed connected the reactant(s) with the expected product(s). The wave function of each point on the IRC was obtained by means of a single-point calculation at the same level of theory used for optimizing the corresponding structure. The analysis of the ELF phase-space portrait was conducted using the Multiwfn package of programs.⁷² Because of the astonishing advances in terms of computational processing power, the simple regression equation can be straightforwardly obtained through commercial packages, for instance, the Excel spreadsheet. However, we used Python 3.7.7 for such a purpose.

Conclusions

Some progress has been made concerning the limitation of topology in providing meaningful information on the energetic features of reacting systems. Here, it is first shown that there exists a strong linear correlation between topological concepts, such as persistency and structural stability, and the activation energy of reactive processes. Then, this statistical relationship is used as a topology-based model for predicting barriers at 0 K for both organic and organometallic reaction systems. It should be stressed that, within the framework of bonding evolution theory, this model naturally comprises the set of parametric polynomials resulting from Thom's works, which constitutes an additional achievement due to the significant generalization. The first fit was performed over the experimental data of 17 reactions via a simple linear regression, leading to the predicted equation , characterized by the Pearson correlation coefficient and its squared value r = 0.9402 and r² = 0.8839, respectively. Such numbers indicate a high linear correlation between variables, on the one hand, and the reliability of the model in terms of its predictability capability, on the other. Not surprisingly, this equation succeeded in predicting barriers as high as 15.8 and 20.2 kcal mol⁻¹ with deviations of 1.2 and 0.5 kcal mol⁻¹, respectively. Even in the case of a remarkably complex reacting system like the oxidation reaction involving a transition metal (Ti), the accuracy of the model was significant considering that the experimental activation energy is only 1.2 kcal mol⁻¹ and the fit equation predicted 0.9 kcal mol⁻¹. Moreover, the model provided reasonable barrier values that ranged from 2.1 to 6.7 kcal mol⁻¹ for most of the other reactions. However, it failed to give an enhanced barrier for the epoxidation of isobutene and α-methylstyrene by dimethyldioxirane, predicting slightly less accurate values than the direct computed ones. We believe that this fact might be related to the suitability of the level of theory employed for describing both the physical and chemical properties of the reaction systems. The experimental data were ‘‘cleaned up’’ by filtering out the three most distant points from the regression line to improve the predicting capabilities of the linear equation. Thus, the new model 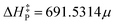was obtained altogether with its associated metrics r = 0.9886 and r² = 0.9774. Based on these fitting parameters, one would expect a significant improvement in its predicting capabilities; nonetheless, no improvement in the model performance was observed. The recalibration process indeed led to eliminating some sources of statistical variabilities; however, it seems that certain flexibility of the model was also lost such that both factors compensated. Alternatively, the model independence on the reaction set might be the underlying cause underpinning this curious result, which is a plausible explanation that needs to be carefully assessed since it would evidence the general character of our findings.

It is mandatory to take all possible care when applying any proposed models since the barriers of reactions used for the fitting were experimentally determined within the [293, 748] K range. Therefore, a high degree of inaccuracy should be expected when applying either linear fit equation beyond both limits. For instance, the model underestimates the barrier of the archetypal Diels–Alder reaction by ∼8 kcal mol⁻¹, which is not surprising considering that the activation energy was experimentally determined at 800 K. This work opens several research directions concerning the widening of the temperature interval through incorporating other reactions and the recalibration of the model such that its predicting capabilities improve. Moreover, both topographical concepts exploited here, structural stability and persistency, could be used for probing the statistical width of activated complexes. On the other hand, it should be further investigated whether the correlation between topology and energetic descriptors of reactive processes can be strengthened by including other concepts from this powerful and elegant branch of mathematics. These findings can be transferred to other research fields to explore rate processes of different natures.

Data availability

(ESI†) available: optimized cartesian coordinates for reactants, products, first-order saddle points, and values of μ See DOI: …

Author contributions

L. A.-H., E. C.: project supervision, conceptualization, data analysis, and manuscript writing; L. A.-H., C. G., M. D.-N.: calculations, reaction paths, and characterization; C. G., M. D.-N.: data analysis and calculations. All authors reviewed and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are deeply grateful to Prof. John M. Guckenheimer for his precise observations and comments, which have helped us improve this work. Moreover, the authors thank UNAB and the ANID/CONICYT PhD scholarships awarded to C. Guerra and L. Ayarde-Henríquez, respectively. Also, we are indebted to the Fondo Nacional de Ciencia y Tecnología (FONDECYT-ANID, Chile) for the continuous financial and academic support provided through Projects No. 1181582, 1221383, and 1231018.

References

1. R. Thom, Structural Stability and Morphogenesis, CRC Press, New York, 1972.
2. E. C. Zeeman, Sci. Am., 1976, 234, 65–83.
3. S. J. Guastello, J. Appl. Psychol., 1987, 72, 165–182.
4. R. Gilmore, Catastrophe Theory for Scientists and Engineers, Dover Publications, Pennsylvania, 1993.
5. T. Poston and I. Stewart, Catastrophe Theory and Its Applications, Pitman Publishing Limited, London, 1979.
6. J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, New York, 1983.
7. J. G. Vickroy and J. A. Dutton, J. Atmos. Sci., 1979, 36, 42–52.
8. B. Kliem, J. Lin, T. G. Forbes, E. R. Priest and T. Török, Astrophys. J., 2014, 789, 1–13.
9. X. Krokidis, S. Noury and B. Silvi, J. Phys. Chem. A, 1997, 101, 7277–7282.
10. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña, E. Rincón, P. Pérez and E. Chamorro, J. Phys. Chem. A, 2021, 125, 5152–5165.
11. F. Parisi, L. Sciascia, F. Princivalle and M. Merli, Ceram. Int., 2019, 45, 2820–2827.
12. C. Guerra, L. Ayarde-Henríquez, E. Chamorro and A. Ensuncho, ChemPhotoChem, 2023, e202200263.
13. J. Andrés, P. Gonz and V. S. Safont, Int. J. Quantum Chem., 2014, 114, 1239–1252.
14. J. Andrés, S. Berski and B. Silvi, Chem. Commun., 2016, 52, 8183–8195.
15. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña, E. Rincón, P. Pérez and E. Chamorro, Chem. Phys. Chem., 2022, 23, e202200343.
16. R. Bader, Atoms in Molecules A Quantum Theory, Clarendon Press, Oxford, 1994.
17. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
18. V. Tsirelson and A. Stash, Chem. Phys. Lett., 2002, 351, 142–148.
19. D. J. Grimwood, I. A. N. Bytheway and D. Jayatilaka, J. Comput. Chem., 2003, 24, 470–483.
20. D. R. Lide, G. Baysinger, L. I. Berger, R. N. Goldberg, H. V. Kehiaian, K. Kuchitsu, D. L. Roth and D. Zwillinger, CRC Handbook of Chemistry and Physics, (Ed.:D. R. Lide), CRC Press, Florida, 2005, pp. 519–518.
21. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña, C. Cárdenas, P. Pérez and E. Chamorro, Phys. Chem. Chem. Phys., 2021, 23, 20598–20606.
22. L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, New J. Chem., 2022, 46, 12002–12009.
23. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña and E. Chamorro, Chem. Phys. Chem., 2021, 22, 2342–2351.
24. C. Guerra, L. Ayarde, M. Duque and E. Chamorro, Chem. Phys. Chem., 2022, 23, e202200217.
25. C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña and E. Chamorro, J. Phys. Chem. A, 2022, 126, 395–405.
26. J. Margalef-Roig, S. Miret-Artés and A. Toro-Labbé, J. Phys. Chem. A, 2000, 104, 11589–11592.
27. J. M. Tedder and J. C. Walton, Adv. Phys. Org. Chem., 1978, 16, 51–86.
28. J. Korchowiec and T. Uchimaru, J. Phys. Chem. A, 1999, 11, 93–102.
29. V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger and K. N. Houk, J. Phys. Chem. A, 2003, 107, 11445–11459.
30. S. Y. Tang, J. Shi and Q. X. Guo, Org. Biomol. Chem., 2012, 10, 2673–2682.
31. T. R. Ramadhar and R. A. Batey, Comput. Theor. Chem., 2011, 976, 167–182.
32. S. Glasstone, K. Laidler and H. Eyring, The Theory of Rate Processes:The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena, McGraw-Hill Book Company, New York, 1941.
33. A. Toro-Labbé, S. Gutiérrez-Oliva, J. S. Murray and P. Politzer, Mol. Phys., 2007, 105, 2619–2625.
34. D. Castrigiano and S. Hayes, Catastrophe Theory, CRC Press, New York, 2018.
35. J. Jurgen, Dynamical Systems, Springer-Verlag Berlin Heidelberg, Berlin, 2005.
36. A. Katok and B. Hasselblatt, Introduction to the Modern Theory of Dynamical Systems, Cambridge University Press, New York, 1996.
37. M. Brin and G. Stuck, Introduction to Dynamical Systems, Cambridge University Press, New York, 2003.
38. D. Miche, Bifurcations and Catastrophes, Springer-Verlag Berlin Heidelberg, Berlin, 2000.
39. C. Robinson, Dynamical Systems, CRC Press, New York, 1999.
40. J. Sotomayor, Dynamical Systems, ed. M. Peixoto, 1973, pp. 561–582.
41. P. Holmes, Phys. Rep., 1990, 193, 137–163.
42. E. V. Zhuzhoma and V. S. Medvedev, Proc. Steklov Inst. Math., 2008, 261, 112–135.
43. J. Benesty, J. Chen, I. Huang and Y. Cohen, Noise Reduction in Speech Processing, Springer-Verlag Berlin Heidelberg, New York, 2009.
44. A. G. Asuero, A. Sayago and A. G. González, Crit. Rev. Anal. Chem., 2006, 36, 41–59.
45. J. Benesty, J. Chen and Y. Huang, IEEE Trans. Audio Speech Lang. Process., 2008, 16, 757–765.
46. M. Baak, R. Koopman, H. Snoek and S. Klous, Comput. Stat. Data Anal., 2020, 152, 107043.
47. S. Boslaugh, Statistics in a Nutshell: A Desktop Quick Reference, O’Reilly, California, 2013.
48. R. Ceravolo, E. Matta, A. Quattrone and L. Z. Fragonara, Earthquake Eng. Struct. Dyn., 2017, 46, 2399–2417.
49. H. Akoglu, Turk. J. Emerg. Med., 2018, 18, 91–93.
50. U. Atique, S. Iqbal, N. Khan, B. Qazi, A. Javeed, K. M. Anjum, M. S. Haider, T. A. Khan, S. Mahmood and S. Sherzada, Fresenius Environ. Bull., 2020, 29, 3013–3025.
51. J. Liu and K. N. Houk, J. Org. Chem., 1998, 63, 8565–8569.
52. P. Gisdakis and N. Rösch, Eur. J. Org. Chem., 2001, 719–723.
53. K. Tanaka, G. Mackay, J. Payzant and D. Bohme, Can. J. Chem., 1976, 54, 1643–1659.
54. A. Delabie, C. Vinckier, M. Flock and K. Pierloot, J. Phys. Chem. A, 2001, 105, 5479–5485.
55. P. M. Futerko and A. Fontijn, J. Chem. Phys., 1991, 95, 8065–8072.
56. D. H. Ess and K. N. Houk, J. Phys. Chem. A, 2005, 109, 9542–9553.
57. D. H. Powers and S. D. Tarbel, J. Am. Chem. Soc., 1956, 78, 70–71.
58. G. C. Lloyd-Jones, J. D. Moseley and J. S. Renny, Synthesis, 2008, 661–689.
59. R. Gillespie and R. Nyholm, Q. Rev., Chem. Soc., 1957, 11, 339–380.
60. N. Pierre, Dynamical Systems, Springer-Verlag, Berlin, 1994.
61. V. Z. Grines, T. V. Medvedev and O. V. Pochinka, Developments in Mathematics Dynamical Systems on 2- and 3-Manifolds, Springer International Publishing, Switzerland, 2016.
62. R. Gilmore, Encyclopedia of Applied Physics, VCH Publisher, New York, 1992.
63. M. Peixoto, Topology, 1962, 1, 101–120.
64. V. Arnold’d, V. Afrajmovich, Y. Il’yashenko and L. Shil’nikovn, Dynamical Systems V, Springer-Verlag Berlin Heidelberg, Berlin, 1994.
65. T. Bedford and J. Swift, London Mathematical Society Lecture Note Series, Cambridge University Press, London, 2008.
66. R. G. Bums, H. Capel, P. Cartier, C. Cercignani, J. M. C. Clark, P. Clement, A. M. Cohen, J. W. Cohen, P. Conrad, H. S. M. Coxeter, R. F. Curtain, M. H. A. Davis, M. V. Dekster, C. Dellacherie, G. van Dijk, H. C. Doets, I. Dolgachev, A. Dress, J. J. Duistermaat, D. van Dulst, H. van Duyn, H. Dym, A. Dynin, M. L. Eaton, W. Eckhaus, P. van Emde Boas, H. Engl, G. Ewald, V. I. Fabrikant, A. Fasano, M. Fliess, R. M. Fossum, B. Fuchssteiner, G. B. M. van der Geer, R. D. Gill, V. V. Goldberg, J. de Graaf, J. Grasman, P. A. Griffith, A. W. Grootendorst, L. Gross, P. Gruber, K. P. Hart, G. Heckman, A. J. Hermans, W. H. Hesselink, C. C. Heyde, M. W. Hirsch, K. H. Hofmann, A. T. de Hoop, P. J. van der Houwen, N. M. Hugenholtz, J. R. Isbell, A. Isidori, E. M. de Jager, D. Johnson, P. T. Johnstone, D. Jungnickel, M. A. Kaashoek, V. Kac, W. L. J. van der Kallen, D. Kanevsky, Y. Kannai, H. Kaul, E. A. de Kerf, W. Klingenberg, T. Kloek, J. A. C. Kolk, G. Komen, T. H. Koomwinder, L. Krop, B. Kuperschmidt, H. A. Lauwerier, J. van Leeuwen, H. W. Lenstra Jr., J. K. Lenstra, H. Lenz, M. Levi, J. Lindenstrauss, J. H. van Lint, F. Linton, A. Liulevicius, M. Livshits, W. A. J. Luxemburg, R. M. M. Mattheij, L. G. T. Meertens, I. Moerdijk, J. P. Murre, H. Neunzert, G. Y. Nieuwland, G. J. Olsder, B. ørsted, F. van Oystaeyen, B. Pareigis, K. R. Parthasarathy, K. R. Parthasarathy, I. I. Piatetskii-Shapiro, H. G. J. Pijls, N. U. Prabhu, E. Primrose, A. Ramm, C. M. Ringel, J. B. T. M. Roerdink, K. W. Roggenkamp, G. Rozenberg, W. Rudin, S. N. M. Ruysenaars, A. Salam, A. Salomaa, P. Saunders, J. P. M. Schalkwijk, C. L. Scheffer, R. Schneider, J. A. Schouten, F. Schurer, J. J. Seidel, A. Shenitzer, V. Snaith, T. A. Springer, J. H. M. Steenbrink, J. D. Stegeman, F. W. Steutel, P. Stevenhagen, I. Stewart, R. Stong, L. Streit, K. Stromberg, L. G. Suttorp, D. Tabak, F. Takens, R. J. Takens, N. M. Temme, S. H. Tijs, B. Trakhtenbrot, N. S. Tmdinger, L. N. Vaserstein, M. L. J. van de Vel, F. D. Veldkamp, W. Vervaat, P. M. B. Vitanyi, N. J. Vlaar, H. A. van der Vorst, J. de Vries, F. Waldhausen, B. Wegner, J. J. O. O. Wiegerinck, J. C. Willems, J. M. Wills, B. de Wit, S. A. Wouthuysen, S. Yuzvinskii and L. Zalcman, Encyclopaedia of Mathematics, Kluwer Academic Publishers, Dordrecht, 1991.
67. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
68. A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412.
69. B. Silvi, J. Mol. Struct., 2002, 614, 3–10.
70. A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088–1096.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016.
72. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01008b

---