 Open Access Article
Open Access ArticleForce field refinement for reproducing experimental infrared spectra of ionic liquids†
András
Szabadi
 ab,
Aleksandar
Doknic
ab,
Aleksandar
Doknic
 c,
Jonathan
Netsch
c,
Jonathan
Netsch
 a,
Ádám Márk
Pálvögyi
a,
Ádám Márk
Pálvögyi
 d,
Othmar
Steinhauser
d,
Othmar
Steinhauser
 a and
Christian
Schröder
a and
Christian
Schröder
 *a
*a
aDepartment of Computational Biological Chemistry, Faculty of Chemistry, University of Vienna, Währingerstr. 17, A-1090 Vienna, Austria. E-mail: christian.schroeder@univie.ac.at
bUniversity of Vienna, Doctoral School in Chemistry (DoSChem), Währingerstr. 42, 1090 Vienna, Austria
cResearch Network Data Science, University of Vienna, Kolingasse 14-16, Vienna, Austria
dInstitute of Applied Synthetic Chemistry, Vienna Technical University, Vienna, Austria
First published on 11th July 2023
Abstract
We employ polarizable molecular dynamics simulations with the newly developed FFGenOpt parametrization tool to reproduce IR spectra of several ionic liquid cations and anions in the gas phase. Our results show that polarizable force fields in the bulk phase provide a reasonable compromise between computational effort and accuracy for investigating IR spectra when treating the transition from gas to liquid phase carefully. Although collectivity seems to play only a minor role, the liquid phase not only changes the electrostatic environment of the molecules but also introduces friction and intermolecular interactions altering the IR spectrum significantly. In addition to the classical force field approach, we also tested if the additional computational effort of machine learning potentials justifies their application in reproducing IR spectra. However, the main purpose of this work is to improve the quality of polarizable force fields concerning vibrations and not the prediction of IR spectra which can be better done with quantum-mechanical cluster approaches.
1 Introduction
Ionic liquids have garnered substantial attention in the past two decades due to their outstanding properties, such as high thermal and chemical stability, negligible vapor pressure, and large electrochemical windows, making them ideal candidates for applications such as electrolytes in batteries,1–4 benign solvents,5 and extraction media.6 Understanding the structural composition of ionic liquids, their ion interactions, and their dynamics is crucial to predict and optimize their potential for various applications. Infrared spectroscopy has proven to be an effective method7–10 to investigate these phenomena on a single-particle and collective basis, with the mid-IR regime (approximately 4000 to 400 cm−1) providing information on the presence or absence of different conformers, and the far-IR region (ca. 400 to 40 cm−1) offering insight into the intermolecular dynamics of the liquid system, allowing the analysis of hydrogen-bond networks for instance.8,9,11Due to its simplicity, quantum-mechanical (QM) calculations remain a popular method for interpreting features of experimental IR spectra.7,12–15 However, as ionic liquids consist of cations and anions in a heterogeneous network, gas phase QM calculations are usually not capable of reproducing an IR spectrum from 40 cm−1 to 4000 cm−1, even more, if several conformers of the cations and anions exist. Quantum-cluster calculations starting from ion pairs to medium-sized clusters9,16–19 may help to capture essential features of intermolecular interactions only visible in the liquid phase. The parallel existence of several cationic and anionic conformers can be modeled by ab initio molecular dynamics (AIMD)17,20,21 propagating the nuclei on a classical energy surface but calculating the electronic structure at each step. While this limits system size considerably (to about a hundred atoms and a few dozen picoseconds), anharmonicity, reactivity, and electron orbitals become accessible. An emerging new field bridging the gap between the computational cost of AIMD and classical molecular dynamics is using machine learning (ML) potentials, utilizing machine learning to predict the resulting potential at each geometry. The advantage of such networks is that they can yield results with comparable accuracy to the data set they were trained on (usually AIMD data) at a fraction of the cost, as the propagation of the system is done using classical mechanics. The drawback lies in the nontrivial training process, requiring large data sets and extensive validation to ensure transferability. Additionally, only processes visible in AIMD trajectories (<200 ps) are covered by these ML potentials.
However, for the evaluation of the frequency-dependent complex refractive index n(ω) = n′(ω) + i·n′′(ω) one needs the high-frequency imaginary part of the dielectric spectrum Σ(ω) close to the IR region
| Σ′′(ω) = 2n′(ω)·n′′(ω) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms are available, making conformational sampling for relatively small organic molecules a non-issue. In order to recover some of the electronic interactions, different approaches have been established.23 One of these is the Drude-oscillator model, where each non-hydrogen atom receives a virtual particle with a small mass tethered to it by a harmonic bond. These virtual particles represent the polarization of the surrounding electrons, allowing the molecule's dipole moment to adjust to the local electric field quickly and without rearranging the nuclear coordinates. Although the number of interacting particles is increased this way, no fundamentally new interactions are introduced, i.e., existing force fields can be utilized by only adding a polarizability parameter for the required atoms.
000 atoms are available, making conformational sampling for relatively small organic molecules a non-issue. In order to recover some of the electronic interactions, different approaches have been established.23 One of these is the Drude-oscillator model, where each non-hydrogen atom receives a virtual particle with a small mass tethered to it by a harmonic bond. These virtual particles represent the polarization of the surrounding electrons, allowing the molecule's dipole moment to adjust to the local electric field quickly and without rearranging the nuclear coordinates. Although the number of interacting particles is increased this way, no fundamentally new interactions are introduced, i.e., existing force fields can be utilized by only adding a polarizability parameter for the required atoms.
Alternative approaches to address the challenge of targeting vibrational frequencies have been explored in the literature, including AFMM,24 ForceBalance,25 and the Open Force Field Initiative,26 among others. AFMM employs a slow converging Monte Carlo algorithm to optimize bond and angle force field parameters. The alignment of QM and FF normal modes in the gas phase is based on frequencies and eigenvectors. However, it should be noted that AFMM may encounter issues such as the possibility of multiple assignments of FF modes to specific QM modes and difficulties in finding optimized parameters when far from the initial guesses. ForceBalance, on the other hand, utilizes systematic and reproducible procedures for FF optimizations intending to match experimental and/or QM data. While ForceBalance offers flexibility in matching various target data, it is important to note that the vibrational mode matching is just one component of the overall optimization merit function and may be overruled by structural and energetic considerations. The Open Force Field Initiative builds upon the parametrization methodology of ForceBalance.27 In our current work, we introduce FFGenOpt, our in-house Python program that employs a genetic algorithm to optimize force field parameters to accurately reproduce QM normal modes.
Our investigation centers around four model systems encompassing commonly utilized imidazolium cations and various anions found in ionic liquids. We direct our attention towards comparing polarizable FF and ML-based trajectories, with a specific focus on their ability to faithfully reproduce experimental IR spectra in the liquid phase. However, it is important to highlight that our primary interest lies in the polarizable FF approach, as it enables the simulation of various dynamical properties, including the heterogeneous dynamics exhibited by ionic liquids. For example, extending the applicability of the polarizable FF to the IR region allows for the computation of the frequency-dependent refractive index n(ω) as well as various solvation dynamics phenomena in the THz regime.
2 Theory
2.1 IR spectra
Infrared spectra capture the fluctuations of molecular dipoles upon excitation via electromagnetic waves. These fluctuations comprise both single-particle and collective modes of motion. Molecular dipoles can be evaluated by | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) iβ are the coordinates of atom β of molecule i. As ions have a net charge qi, the molecular dipole moment has to be defined with respect to a reference point. We use the center-of-mass of the molecule i as it is also the center for translation and rotation of that molecule, consequently facilitating the interpretation.28,29 The collective rotational dipole moment
iβ are the coordinates of atom β of molecule i. As ions have a net charge qi, the molecular dipole moment has to be defined with respect to a reference point. We use the center-of-mass of the molecule i as it is also the center for translation and rotation of that molecule, consequently facilitating the interpretation.28,29 The collective rotational dipole moment ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) D(t) is the sum of all molecular dipole moments:
D(t) is the sum of all molecular dipole moments: 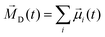 .28 The auto-correlation function of the collective rotational dipole moment consists of the auto-correlation functions of the individual molecular dipoles plus their cross-correlation functions:30
.28 The auto-correlation function of the collective rotational dipole moment consists of the auto-correlation functions of the individual molecular dipoles plus their cross-correlation functions:30 | (3) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (0)·
(0)·![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (t)〉.17,20,31
(t)〉.17,20,31
In principle, the IR absorption coefficient α(ω) can be obtained from the imaginary part of the dielectric constant Σ′′(ω):32–35
 | (4) |
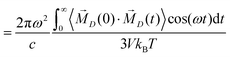 | (5) |
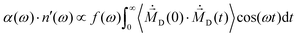 | (6) |
 | (7) |
 can be computed via numerical differentiation or using the velocities instead of the coordinates from the trajectory:16
can be computed via numerical differentiation or using the velocities instead of the coordinates from the trajectory:16 | (8) |
 | (9) |
Several quantum correction factors f(ω) exist in literature31,37 affecting the peak heights as a function of frequency ω. The one closest to experiment37 is
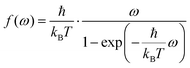 | (10) |
The noise of the correlation functions in eqn (6) and (7) can be damped at longer times by multiplying with an apodization function38 exp(−a t2) using a = 0.5 ps−2 which is half of the value used in ref. 31. This smooths the peak shape and makes Savitzky-Golay noise filtering obsolete.
Classical FF-based simulations cannot model nuclear quantum effects, which play a role in vibrations of hydrogens participating in hydrogen bonds.39–41 However, including explicitly nuclear quantum effects in ab initio MD simulations39,41 changes the IR spectrum of water only above 2700 cm−1, which is usually out of reach for classical MD simulations as bonds involving hydrogens are kept fixed by the SHAKE algorithm. Nevertheless, nuclear quantum effects may be present in our ML-based trajectories to some extent.
2.2 FFGenOpt
The FF parameters for most ionic species (either fixed-charge42–44 or polarizable45) are usually derived from quantum mechanics (QM) energy calculations and validated using thermodynamic parameters (e.g. heat capacity, compressibility, density) and radial distribution functions. Being able to automatically convert the parameters of such studies to IR spectroscopy-based terms would provide new insight into the intermolecular dynamics of ionic liquids and the ability of different force fields to reproduce IR spectra. While automated force field-generating tools exist, these either rely on chemical similarity to an existing database (such as the paramchem webserver46) or require lengthy trajectories and expensive QM calculations (e.g. force matching47,48).We present FFGenOpt, an automated Python-based tool for generating FF parameters targeting vibrational spectra. It first calculates the FF normal modes and vibrational frequencies of a single molecule in the gas phase. Subsequently, the dot products of the target QM and FF normal mode eigenvectors are computed, which are used in a linear assignment problem to map the two sets of vectors onto each other in a one-to-one fashion applying the Hungarian method.49 Before the mapping, the ratio of the corresponding eigenvalues (i.e. the frequencies) can be used as a weight to discourage matching closely aligned normal modes with large frequency differences.
Fig. 1 depicts the general procedure of the force field refinement. A fitness score is evaluated based on the matching, and an initial population is generated consisting of various sets of FF parameters. The members (=sets) are sorted by fitness, with some discarded (elitism). If the population reaches a critical minimum diversity D, it is purged, with only the member with the highest fitness score surviving, and a new initial population is generated. If the diversity is high enough, the genetic algorithm is called. The genetic algorithm of FFGenOpt uses crossover operations designed for a continuous search space, such as simulated binary crossover50 and blend crossover.51 Mutations of population members are simulated by adding Gaussian random vectors. After improvement, the population is sorted by fitness, and the loop is executed again. Otherwise, a random search algorithm is called first before sorting the population. Exhaustive descriptions, along with the source code, use-case examples and a tutorial are available on github (https://github.com/cbc-univie/FFGenOpt).
3 Methods
3.1 FFGenOpt targets
We focus in this work on the ionic liquids 1-ethyl-3-methyl-imidazolium acetate [C2mim]OAc, 1-ethyl-3-methyl-imidazolium triflate [C2mim]OTf, 1-ethyl-3-methyl-imidazolium dicyanamide [C2mim]N(CN)2, and 1-butyl-3-methyl-imidazolium tetrafluoroborate [C4mim]BF4. Initial FF parameters for C2mim+, N(CN)2−, and OTf− were taken from ref. 52, for C4mim+ and BF4− from ref. 16, and for OAc− from ref. 53. FFGenOpt was used to generate new parameters for each ion separately, with at least 100 generations of optimization per species.QM geometries and vibrational frequencies were computed using Psi454 at the MP2/cc-PVDZ level of theory. Although conventional wisdom holds that augmented basis sets should be used for anion QM calculations, the computed normal modes did not show a significant deviation between the cc-PVDz, cc-PVTZ, and the aug-cc-PVTZ basis sets (see ESI†). The same was also observed when comparing against DFT methods such as B3LYP, with or without Grimme dispersion correction D3. The only noticeable change occurred between the HF and MP2 methods. For this reason, the computationally less demanding MP2/cc-PVDZ level of theory was chosen as the target for the QM frequency calculations. Please note that gas phase QM calculations usually apply frequency scaling factors,55,56 which are user-defined in FFGenOpt. These scaling factors are a function of the functional and basis set and, thus, the major reason for the insensitivity of QM frequencies afterward.
3.2 Polarizable molecular dynamics
The resulting new parameters were then evaluated by calculating the IR spectra from trajectories produced identically: initial configurations consisting of 500 ion pairs were generated by packmol,57 followed by a steepest descent/adopted base Newton-Raphson minimization in charmm.58 Subsequently, 10 ns of equilibration runs with an integration time step of 0.5 fs were produced in OpenMM59 in the NPT ensemble at a pressure of 1 atm at 300 K under periodic boundary conditions. Non-bonded interactions were cut off at 12 Å, and electrostatic (Coulomb) terms were handled using the particle mesh Ewald method. Polarizability was modeled by using mobile Drude particles of 0.4 atomic mass units attached to non-hydrogen atoms with a force constant of 1000 kcal mol−1 Å−2. The velocity-Verlet integrator was set up with a friction coefficient of 1 ps−1 and a collision frequency of 10 ps−1 for non-Drudes (T = 300 K), and 200 ps−1 for Drudes (T = 1 K). The production runs consisted of 100 ps−1 in the NVT ensemble using identical settings to the equilibration, with every 10th frame written to disk, resulting in a net time step of 5 fs on disk. Usually, the SHAKE algorithm keeps the hydrogen-heavy atom bond length constant in FF-based MD simulations. However, this way, vibrational frequencies above 2500 cm−1 cannot be detected. Turning off SHAKE still produces stable trajectories with frequencies above 2500 cm−1, but lower frequencies are fortunately unaffected (see ESI†). The trajectories were analyzed via python scripts using the utilities provided in MDAnalysis.60,613.3 Machine learning based potentials
Machine learning can be used to predict IR spectra.10 However, we use ML potentials to generate trajectories with 12 ion pairs whose random starting configuration was also generated by packmol. ANI-2x62 was chosen as the molecular potential, using a pure machine learning-based system for [C2mim]N(CN)2, [C2mim]OTf and [C2mim]OAc. As boron atoms were not present in the training data set of this potential, [C4mim]BF4 was simulated using a mixed setup, with the cation described by ANI-2x and the anion by the FF of ref. 16. In this case, only the bonded interactions between the atoms of the cation are calculated via the ML potential. Cation–anion and anion–anion interactions are modeled using the force field. Due to the nature of the ML potential, no virtual particles (Drude oscillators, lone pairs, etc.) were included in the topology of the ions. The ANI-2x systems were equilibrated for 1 ns in the NPT ensemble at the same pressure and temperature as the polarizable FF trajectories using the Langevin integrator with a step size of 1 fs. Due to the size of the system, non-bonded interactions were cut off at 6.5 Å, which should not interfere with periodic boundary conditions. The production run consisted of 100 ps in the NVT ensemble, with every fifth step written to disk, resulting in a net time step of 5 fs as well. For calculating the IR spectra of the ML system, the same partial charges were used as defined in the force fields of the polarizable FF systems.3.4 Experiment
Experimental infrared spectra were recorded on a PerkinElmer Spectrum 65 FT IR spectrometer equipped with a specac MK II Golden Gate Single Reflection ATR unit. The samples were dried for four days at 40 °C and 0.5 mbar and used without further purification.4 Results and discussion
4.1 Force field parameters
Transferability and accuracy are two opposing concepts in the design of force fields. Transferability ensures that the FF can be used for similar compounds. For example, in ionic liquids, the parametrization of the imidazolium rings should be kept fixed, although various alkyl chains may be attached to the aromatic nitrogens. This way, the properties of similar compounds can be compared more easily as differences are more likely based on various functional groups and not a completely different FF. However, using general energy potentials for families of molecules reduces the accuracy of the FF for a particular molecule, which is true for reproducing experimental infrared spectra. As a compromise between transferability and accuracy, usually no new FF potentials and atom types are introduced, adopting instead the existing potentials for each molecule. Consequently, the bond, angle, and dihedral potentials of C2mim+ and C4mim+ may have slightly different force constants but still share corresponding equilibrium distances and angles as well as the multiplicities of the dihedral potentials. Also, Lennard-Jones parameters, partial charges, and polarizabilities are not changed to preserve the collective structure and dynamics of the ionic liquids. The resulting force constants for each ion, as output by FFGenOpt, along with the original values taken from the appropriate references, are collected in the tables of the ESI.†4.2 Normal modes in the gas phase
FFGenOpt is capable of reproducing the vibrational frequencies with correct normal mode vectors of QM gas phase calculations with qualitative accuracy as shown in Fig. 2. The dashed line represents 100% agreement between the force field and the QM frequencies. The gray area indicates a discrepancy of 100 cm−1. These FF vs. QM normal modes not only coincide in frequency but also have similar eigenvectors, which were also checked by visual inspection. The most problems concern acetate (gray up triangles), where the agreement can only be improved by adding additional dihedral potentials with different multiplicities and anharmonic potentials. Despite that, the original FF potentials were kept for transferability, and only the force constants were varied. Minor problems also exist for a C–H stretching mode of C2mim (off-diagonal blue pentagons) as the automated alignment in FFGenOpt has problems with normal modes having very similar eigenvectors. However, a frequency penalty exists in FFGenOpt for large frequency discrepancies, which solves most but not all of these problems. The penalty should not be too large as otherwise the alignment of the normal mode vectors becomes obsolete.Even so, a reasonable agreement between FF (blue) and QM normal modes (yellow) does not automatically result in a good reproduction of experimental IR spectra of the liquid ionic liquid, as shown in Fig. 3 for [C4mim]BF4. Although the B–F stretching modes near 1132 cm−1 of the FFGenOpt FF (blue line) matches the QM frequencies of 1126 cm−1 quite well (yellow line), this peak is red-shifted by 80 cm−1 in the experimental spectrum (green line) of liquid [C4mim]BF4. Also, the second peak of the FFGenOpt FF (blue) at 1230 cm−1 is roughly 70 cm−1 higher than the corresponding experimental peak. Nevertheless, the better agreement between the FFGenOpt optimized FF (blue line) than the original polarizable FF (red line) from ref. 16 is apparent. This applies not only to the overall shape of the spectra but also to the positions of the peaks.
 | ||
| Fig. 3 Juxtaposition of experimental (green) and FF infrared spectra of [C4mim]BF4 in the liquid phase. The red line corresponds to the original polarizable FF,16 whereas the blue line stems from the FFGenOpt-optimized FF. The yellow curve was obtained by Gaussian broadening of the cation and anion's gas phase line spectra. | ||
4.3 Infrared spectra in the liquid phase
The critical distinguishing factor between QM calculations in the gas and the liquid phase is the intermolecular interactions between the molecular ions. In principle, QM calculations of small clusters can also capture these intermolecular interactions.11,17,19 This way, the computation of normal modes and their eigenvectors is still possible. However, using the QM-optimized structure of the cluster for the normal mode computation of an FF may yield imaginary frequencies as this structure might not be the energetic minimum of the FF. Consequently, mapping QM and FF normal modes becomes more complicated but might still be an option for future versions of FFGenOpt. As the number of cations and anions needed to produce good results is not known a priori, AIMD might be a viable alternative for the calculation of normal modes and, subsequently, the IR spectrum of that ionic liquid,11,17,20 especially if the number of ions pairs is eight or higher.9,63,64 Even so, ab initio MD does not always perform better in reproducing experimental IR spectra than polarizable FF simulations.16 Possible drawbacks of this approach include high computational costs and a discrepancy in the signal intensities despite good frequency matching.11The effect of intermolecular interactions in FF-based simulations may be exemplified by the substitution of the molecular dipole moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) in eqn (7) with the collective dipole moment
in eqn (7) with the collective dipole moment ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) D in eqn (6). The former equation omits all collective rotations as evidenced in eqn (3). Both IR absorptions can be calculated from MD simulations and are depicted for [C2mim]OTf in Fig. 4. Interestingly, the collective approach in eqn (6) (green line) does not change the peak positions at all, and only the amplitudes are slightly affected. This outcome contradicts the conventional dielectric behavior observed at lower frequencies in the THz and GHz regimes, where cross-correlations primarily define the peak structures. Collective rotational motions of the dipoles may be too slow to be detected at IR frequencies. However, the local environment may still influence the molecular dipoles
D in eqn (6). The former equation omits all collective rotations as evidenced in eqn (3). Both IR absorptions can be calculated from MD simulations and are depicted for [C2mim]OTf in Fig. 4. Interestingly, the collective approach in eqn (6) (green line) does not change the peak positions at all, and only the amplitudes are slightly affected. This outcome contradicts the conventional dielectric behavior observed at lower frequencies in the THz and GHz regimes, where cross-correlations primarily define the peak structures. Collective rotational motions of the dipoles may be too slow to be detected at IR frequencies. However, the local environment may still influence the molecular dipoles ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i. For example, the induced dipoles contributing to the molecular dipole respond to the electrostatic field exerted by the other molecules. This might be rather strong in ionic liquids as cage structures are formed.52,65 The ion cages may also influence the permanent molecular dipoles and their fluctuations. Furthermore, hydrogen bonds to the carboxylic group of acetate, for example, significantly change the C–O stretching modes. The multitude of these various interactions has severe consequences for the IR spectra of the ions in the liquid phase. The overall rattling of the molecular ions in their cages can be characterized by the auto-correlation function of the current 〈J(0)·J(t)〉, i.e. the vibrations of the ionic center-of-masses. It is of minor importance for the IR absorption and restricted to the frequency region below 200 cm−1.
i. For example, the induced dipoles contributing to the molecular dipole respond to the electrostatic field exerted by the other molecules. This might be rather strong in ionic liquids as cage structures are formed.52,65 The ion cages may also influence the permanent molecular dipoles and their fluctuations. Furthermore, hydrogen bonds to the carboxylic group of acetate, for example, significantly change the C–O stretching modes. The multitude of these various interactions has severe consequences for the IR spectra of the ions in the liquid phase. The overall rattling of the molecular ions in their cages can be characterized by the auto-correlation function of the current 〈J(0)·J(t)〉, i.e. the vibrations of the ionic center-of-masses. It is of minor importance for the IR absorption and restricted to the frequency region below 200 cm−1.
 | ||
| Fig. 4 Computational infrared absorption of [C2mim]OTf in the liquid phase using the FFGenOpt FF. The absorption can be obtained from one trajectory using eqn (6) (green) or eqn (7) (cations blue, anions orange). The auto-correlation of the current 〈J(0)·J(t)〉 (gray) describes the rattling of the ions in their cages. | ||
Fig. 5 shows the comparison between the experimental (green lines) and the computational IR spectra. As already noticed in Fig. 3 for [C4mim]BF4, all FFGenOpt optimized spectra (blue lines) have a significantly improved agreement with the experimental spectrum compared to the original force field in red. This applies to the peak positions and their shape. Only the IR spectrum of [C2mim]OTf in Fig. 5a misses some important peaks around 1200 cm−1. An MD simulation based on ML potentials (orange line) is more capable of capturing the main features of the experimental spectrum between 1300 cm−1 and 1000 cm−1 in case of [C2mim]OTf and thus may be a promising alternative to polarizable FF simulations.
Despite being smaller by a factor of 50 in size, the computational cost of the ML-based potentials is more than one order of magnitude higher, limiting its general applicability. Additionally, some chemical elements like boron are not available in ANI-2x.62 Consequently, polarizable FF simulations and ML potentials have to be mixed. In the case of [C4mim]BF4, the forces on the imidazolium are computed via the ML potentials, and the FF propagates the BF4− anions. Interestingly, this combination shifts the BF4−-peak very close to the experimental IR frequency of 1050 cm−1 although the anions were described by the polarizable FF and not the ML-based potential (see ESI†).
Although still faster than ab initio MD simulations, the huge increase in computational time by ML-based potentials is not always justified, as the corresponding IR spectra (yellow lines) do not automatically agree better with the experiment than polarizable FF simulations (blue lines). In the case of [C2mim] OAc, polarizable FF simulations perform as good as the ML-based potentials (see Fig. 5b) and even outperform ML-based potentials in the case of [C2mim]N(CN)2 in Fig. 5c. The experimental peak structure between 2050 and 2250 cm−1 is blue-shifted by 200 cm−1 and broadened significantly for the ML-based potentials. Also, the experimental double peak structure at 1220 cm−1 is reduced to one peak. In contrast, the experimental peak structure between 2050 and 2250 cm−1 (green) is red-shifted by 100 cm−1 in the FFGenOpt based trajectories (blue). Also, the double structure at 1220 cm−1 is red-shifted by roughly 250 cm−1.
Based on the unsatisfactory agreement of ML-based potentials and polarizable FF simulations, we also tried to mix both force fields for the very same molecule in a dual topology approach by calculating the resulting forces for both potentials and interpolating between the two (λ-state of 0.5). This leads to the orange spectrum in Fig. 5c, which improves the description of the peak region between 2050 and 2250 cm−1. Unfortunately, the double peak at 1220 cm−1 is now slightly blue-shifted.
In analogy to QM scaling factors in the gas phase,55,56 one might similarly contemplate scaling factors for force constants in the liquid phase.66 Given that the viscosity in the liquid phase significantly exceeds that of the gas phase, it is reasonable to infer that all vibrations should exhibit oscillations at lower frequencies. This phenomenon can be replicated by applying a scaling factor to the force constants of bonds and angles. The resulting red-shifts of particular IR peaks of our ionic liquids are shown in Fig. 6. Interestingly, all red-shifts are a linear function of the scaling factor with different slopes for the various peaks. For a particular ionic liquid, the slopes may be very similar if the frequency difference is not too much as visible for [C2mim]OAc and [C4mim]BF4. Usually, a scaling factor of roughly 0.98 counteracts the red-shifts of the FF peaks mentioned before. As demonstrated in the ESI,† scaling factors below 0.80 induce significant spectrum alterations and are consequently unsuitable for our purposes.
 | ||
| Fig. 6 Red-shift of particular IR peaks when applying a uniform scaling factor to all bond and angle force constants of the polarizable FF. | ||
5 Conclusion and outlook
Our parametrization tool FFGenOpt improves bonded force field parameters to reproduce infrared spectra. Thereby, polarizable force field simulations may be an option for investigating IR spectra as a reasonable compromise between computational effort and accuracy. As indicated in Fig. 5, essential features can be reproduced, including peak positions and relative intensities. The increased viscosity of the liquid phase compared to the gas phase can be accounted for by using scaling factors for the force constants, further improving the agreement between simulations and experiments. In future versions, FFGenOpt may be expanded to include the analysis of the normal modes of clusters ranging up to a few ion pairs to reduce the resulting red-shift of the IR peaks.The computational cost is at least one order of magnitude lower than simulations based on machine learning (yellow curves), while the agreement with the experiment is comparable between FF and ML approaches. The combination of the polarizable force field and machine learning potentials produces good agreement with the experiment, although at the cost of poor statistics. Concerning consistency, polarizable FF trajectories are preferred as they can also be used to compute other structural and dynamics properties, which are neither accessible by ab initio nor ML-based MD simulations. This way, all computational data are at the same level of theory, which facilitates the interpretation as discrepancies cannot arise from various computational approaches with different approximations.
Our simulations also showed that collective effects captured by eqn (6) play a minor role as the computation of IR spectra based on the molecular dipole moments leads to very similar results. Nevertheless, the auto-correlations 〈![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e153.gif) (0)·
(0)·![[small mu, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e153.gif) (t)〉 of the molecular dipoles are completely different in gas and liquid phase which emphasizes that the local environment of the molecules is of uttermost importance for the IR spectra.
(t)〉 of the molecular dipoles are completely different in gas and liquid phase which emphasizes that the local environment of the molecules is of uttermost importance for the IR spectra.
Data availability
The manual, source code and examples for FFGenOpt are available on github (https://github.com/cbc-univie/FFGenOpt), along with the force fields and input scripts used for trajectory production and analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Anne Strate from the University of Rostock for providing experimental infrared spectra of [C2mim]OTf.References
- I. Osada, H. de Vries, B. Scrosati and S. Passerini, Angew. Chem., Int. Ed., 2016, 55, 500–513 CrossRef CAS PubMed.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- A. Lewandowski and A. Świderska-Mocek, J. Power Sources, 2009, 194, 601 CrossRef CAS.
- M. Ishikawa, T. Sugimoto, M. Kikuta, E. Ishiko and M. Kono, J. Power Sources, 2006, 162, 658–662 CrossRef CAS.
- Y. H. Choi and R. Verpoorte, Curr. Opin. Food Sci., 2019, 26, 87–93 CrossRef.
- G.-T. Wei, Z. Yang and C.-J. Chen, Anal. Chim. Acta, 2003, 488, 183–192 CrossRef CAS.
- J. Clarke-Hannaford, M. Breedon, T. Rüther, P. Johansson and M. J. Spencer, Chem. – Eur. J., 2021, 27, 12826–12834 CrossRef CAS PubMed.
- T. Buffeteau, J. Grondin and J.-C. Lassègues, Appl. Spectrosc., 2010, 64, 112–119 CrossRef CAS PubMed.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903 RSC.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- K. Wendler, M. Brehm, F. Malberg, B. Kirchner and L. Delle Site, J. Chem. Theory Comput., 2012, 8, 1570–1579 CrossRef CAS PubMed.
- S. A. Katsyuba, E. E. Zvereva, A. Vidiš and P. J. Dyson, J. Phys. Chem. A, 2007, 111, 352–370 CrossRef CAS PubMed.
- F. M. Vitucci, F. Trequattrini, O. Palumbo, J.-B. Brubach, P. Roy and A. Paolone, Vib. Spec., 2014, 74, 81–87 CrossRef CAS.
- B. Cao, J. Du, S. Liu, X. Zhu, X. Sun, H. Sun and H. Fu, RSC Adv., 2016, 6, 10462–10470 RSC.
- O. Palumbo, A. Cimini, F. Trequattrini, J.-B. Brubach, P. Roy and A. Paolone, Phys. Chem. Chem. Phys., 2020, 22, 7497–7506 RSC.
- A. Szabadi, R. Elfgen, R. Macchieraldo, F. L. Kearns, H. Lee Woodcock, B. Kirchner and C. Schröder, J. Mol. Liq., 2021, 337, 116521 CrossRef CAS.
- B. Kirchner, J. Blasius, L. Esser and W. Reckien, Adv. Theory Simul., 2021, 4, 2000223 CrossRef CAS.
- S. Taherivardanjani, R. Elfgen, W. Reckien, E. Suarez, E. Perlt and B. Kirchner, Adv. Theory Simul., 2022, 5, 2100293 CrossRef CAS.
- S. A. Ktsyuba, T. P. Gerasimova, S. Spicher, F. Bohle and S. Grimme, J. Comput. Chem., 2022, 43, 279–288 CrossRef PubMed.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622 RSC.
- J. Kiefer, K. Noack, T. C. Pennad, M. C. Ribeirod, H. Webere and B. Kirchner, Vib. Spectrosc., 2017, 91, 141–146 CrossRef CAS.
- N. R. Dhumal, J. Kiefer, D. Turton, K. Wynne and H. J. Kim, J. Phys. Chem. B, 2017, 121, 4845–4852 CrossRef CAS PubMed.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed.
- A. C. Vaiana, Z. Cournia, I. B. Costecsu and J. C. Smith, Comput. Phys. Commun., 2005, 167, 34–42 CrossRef CAS.
- L.-P. Wang, J. Chen and T. van Voorhis, J. Chem. Theory Comput., 2013, 9, 452–460 CrossRef CAS PubMed.
- D. L. Mobley, C. C. Bannan, A. Rizzi, C. I. Bayly, J. D. Chodera, V. T. Lim, N. M. Lim, K. A. Beauchamp, D. R. Slochower and M. R. Shirts, et al. , J. Chem. Theory Comput., 2018, 14, 6076–6092 CrossRef CAS PubMed.
- Y. Qiu, D. G. A. Smith, S. Boothroyd, H. Jang, D. F. Hahbn, J. Wagner, C. C. Bannan, T. Gokey, V. T. Lim, C. D. Stern, A. Rizzi, B. Tjanaka, G. Tresadern, X. Lucas, M. R. Shirts, M. K. gilson, J. D. Chodera, C. I. Bayly, D. L. Mobley and L.-P. Wang, J. Chem. Theory Comput., 2021, 17, 6262–6280 CrossRef CAS PubMed.
- C. Schröder and O. Steinhauser, J. Chem. Phys., 2010, 132, 244109 CrossRef PubMed.
- C. Schröder and O. Steinhauser, J. Phys.: Condens. Matter, 2016, 28, 344008 CrossRef PubMed.
- M. Śmiechowski, Spectrochim. Acta, Part A, 2021, 260, 119869 CrossRef PubMed.
- S. Ueno, Y. Tanimura and S. Ten-no, Int. J. Quantum Chem., 2013, 113, 330–335 CrossRef CAS.
- R. Zwanzig, Nonequilibrium statistical mechanics, Oxford University Press, 2001 Search PubMed.
- D. A. McQuarrie, Statistical Mechanics, University Science Books, 2000 Search PubMed.
- W. Chen, M. Sharma, R. Resta, G. Galli and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245114 CrossRef.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed.
- D. C. Marinica, G. Grégoire, C. Desfrançois, J. P. Schermann, D. Borgis and M. P. Gaigeot, J. Phys. Chem. A, 2006, 110, 8802–8810 CrossRef CAS PubMed.
- M.-P. Gaigeot and M. Sprik, J. Phys. Chem. B, 2003, 107, 10344–10358 CrossRef CAS.
- B. Boulard, J. Kieffer, C. C. Phifer and C. A. Angell, J. Non-Cryst. Solids, 1992, 140, 350–358 CrossRef CAS.
- O. Marsalek and T. E. Markland, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- D. Berta, D. Ferenc, I. Bakó and A. Madarász, J. Chem. Theory Comput., 2020, 16, 3316–3334 CrossRef CAS PubMed.
- X. Xu, Z. Chen and Y. Yang, J. Am. Chem. Soc., 2022, 144, 4039–4046 CrossRef CAS PubMed.
- C. Hanke, S. Price and R. Lynden-Bell, Mol. Phys., 2001, 99, 801–809 CrossRef CAS.
- J. K. Shah, J. F. Brennecke and E. J. Maginn, Green Chem., 2002, 4, 112–118 RSC.
- J. N. Canongia Lopes, J. Deschamps and A. A. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- K. Goloviznina, Z. Gong and A. A. Padua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1572 CAS.
- https://cgenff.umaryland.edu/ .
- P. S. Hudson, S. Boresch, D. M. Rogers and H. L. Woodcock, J. Chem. Theory Comput., 2018, 14, 6327–6335 CrossRef CAS PubMed.
- P. Hudson, K. Han, H. Woodcock and B. Brooks, J. Comput.-Aided Mol. Des., 2018, 32, 983–999 CrossRef CAS PubMed.
- H. W. Kuhn, Naval Res. Logistics Quartely, 1955, 2, 83–97 CrossRef.
- K. D. abd R. B. Agrawal, Complex Systems, 1994, 9, 115–148 Search PubMed.
- L. J. Eshelman and J. D. Schaffer, Foundations of genetic algorithms, Elsevier, 1993, pp. 187–202 Search PubMed.
- A. Szabadi, P. Honegger, F. Schöfbeck, M. Sappl, E. Heid, O. Steinhauser and C. Schröder, Phys. Chem. Chem. Phys., 2022, 24, 15776–15790 RSC.
- P. Chatterjee, E. Heid, C. Schröder and A. D. MacKerell, Biophys. J., 2019, 116, 142a CrossRef.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. OBrien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- https://cccbdb.nist.gov/vsfx.asp .
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30(13), 2157–2164 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. MacKerell Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545 CrossRef CAS PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, 1–17 CrossRef PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, D. L. Dotson, J. Domanski, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, 102–109 Search PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 3830–3834 CrossRef CAS PubMed.
- C. J. Johnson, J. A. Fournier, C. T. Wolke and M. A. Johnson, J. Chem. Phys., 2013, 139, 224305 CrossRef PubMed.
- C. Schröder, J. Chem. Phys., 2011, 135, 024502 CrossRef PubMed.
- J. Baker, A. A. Jarzecki and P. Pulay, J. Phys. Chem. A, 1998, 102, 1412–1424 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00932g |
| This journal is © the Owner Societies 2023 |



