The effect of hetero-atoms on spin exchange coupling pathways (ECPs): a computational investigation

Abstract

The effect of heteroatoms on exchange coupling pathways and the presence of more than one coupling paths are investigated. The lone pairs of sp²-hybridized heteroatoms contribute to aromaticity but do not play any pivotal role in the spin coupling between two spin centers. A conceptual model to describe this behavior of heteroatoms has been introduced, and we name it as the hetero-atom blocking effect. With the occurrence of two π-orbital exchange coupling pathways (ECPs) via bridgehead heteroatoms (B-, N-, O-, or S-), the magnetic exchange coupling constants (J) can be viewed as a signed sum of different individual pathways. The effect of σ-electron coupling is also investigated in this work.

---

Introduction

Organic materials with desirable properties can be synthesized by first preparing organic magnetic molecules with high-spin ground states, which requires local spin densities on the spin-bearing sites and high-spin alignment between them.^1,2 A series of theoretical approaches, including the Hückel analysis of Longuet-Higgins,³ VB-theoretical treatment of Ovchinnikov,⁴ and the modified Hückel analysis of Simpson and Davidson,^5,6 have provided guidance for the prediction of ground states of simple planar π-conjugated systems, although there is a possibility of extending the analysis to planar σ, π carbenoid sites.^7–11

It is presumed that high-spin molecules can be designed with desired resultant spin with large organic couplers with properly incorporated two or more suitable local spin bearing sites. m-Phenylene coupled organic diradicals are one of the most reliable and robust high-spin couplers, whereas the corresponding p-phenylene one usually produces low-spin species.³ The first organic spin quintet was produced using two methylene (or carbene) groups with a m-phenylene coupler.¹² Nonetheless, the same coupler was later used to produce a quintet spin state with bisnitrene.^13,14 Onwards, different types of organic entities have been used as couplers to obtain high-spin and low-spin interactions.^15–21

Generally, high-spin interaction occurs when the exchange coupling pathway (ECP) of the coupler consists of an even number of bonds. In contrast, a low-spin interaction is observed for the spin circulation via an odd number of bonds in the coupler.^22,23 However, the presence of more than one spin polarization path, the existence of heteroatoms in the spin propagation path, and non-planarity of the molecule make it tricky to predict the state of magnetism.²⁴ At first glance, one would presume a competition between the two spin propagation paths (hetero- and homo-atomic paths). However, for a high-spin species, the even route (homo-atomic) is complemented by the odd atomic (hetero-atomic) path via a coupler as the heteroatomic pathway contributes two π electrons (if the hetero-atom is not involved in resonance). Several works have been carried out on the effect of a coupler between the spins.^25,26 The role of linear and bent polyacene couplers was studied by Shil et al.²⁷ Most studies on the effect of couplers assumed that the spin coupling occurs through a conjugated carbon chain. There are some studies on aromatic couplers having hetero-atoms but the authors did not emphasize the effect of spin propagation via the hetero atoms. In previous studies,^16,28 it is common to observe at least one conjugated carbon-based coupling pathway between the radical sites. For aromatic systems, there are two coupling pathways, either carbon-based or one carbon and another hetero-atom based pathway. Since there is always a carbon-based coupling pathway, we get a reasonable spin coupling constant, and one usually overlooks the hetero-atoms.^16,28

Now, logically, one question arises that what will happen if there are two coupling pathways through hetero-atoms? Shil²⁹ categorically showed in his work that if there are two coupling pathways instead of one, the spin coupling constant increases. Rajca and co-workers³⁰ synthesized and characterized homocyclic diradicals having one and two parallel ECPs. As a logical consequence, here we plan to measure the exchange couplings in organic heterocyclic diradicals and their corresponding homocyclic counterpart having one and two similar parallel ECPs whose two ends are attached to two nitroxyl radicals. Hence, we have designed diradicals with one ECP having a 3,3′ biphenyl unit connected through boron, carbon, nitrogen, oxygen, and sulphur atoms as a bridgehead spacer between bis-nitroxyl moieties. On the other hand, the diradicals having two parallel ECPs contain two such spacer units. This shows a different approach to regulate the exchange coupling between the two diradical analogues with two spin propagation paths with hetero-atomic pathways.

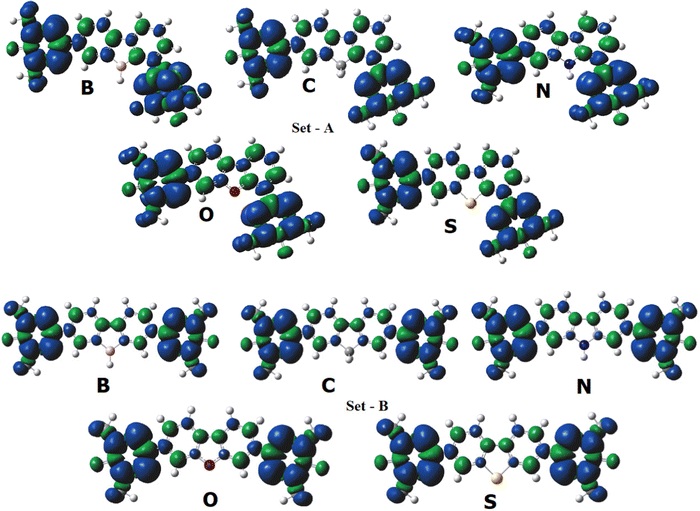
We divide this work into two parts. In the first part (part-I), we focus on the contribution of hetero-atoms in the spin propagation path to regulate the magnetic interaction in organic diradicals. We have chosen heteroatom (B-, N-, O-, and S-atoms) substituted diphenylene methane as a coupler fragment with bis-oxo-verdazyl (bis-OV) as radical moieties. In part-I, we made two sets: in set-A, two of the bis-OV radicals are ferromagnetically coupled, whereas in set-B, two of the bis-OV radicals are antiferromagnetically coupled (Fig. 1). In part-I diradicals, there are two pathways for spin coupling: through conjugated carbon atoms and via heteroatoms.

Fig. 1 Schematic diagram of set A and set B bis-oxo verdazyl diradicals (part-I diradicals).

In the second part (part-II), we see the effect of the presence of more than one heteroatomic parallel coupling pathways along with the changes in coupling constant values irrespective of the heteroatomic paths. The part-II diradicals (Fig. 2) have spin coupling pathways only via single homo- or hetero-atoms (when there is one ECP) or double homo- or hetero-atoms (when there are two ECPs). In this part, we put hetero-atoms in cyclic diradical systems proposed by Rajca³⁰ to observe the effect of hetero-atoms on exchange coupling as the spin propagation is forced to follow the hetero-atomic path having no p–π–p–π conjugation. The reason is that the bridging hetero-atoms are sp² and sp³ hybridized, having no p–π bonds.

Fig. 2 Schematic diagram of bis-nitroxide based diradicals having one (ECP-I) and two parallel exchange coupling (ECP-II) paths (part-II diradicals).

In part-I diradicals, we will see what happens if there are two coupling pathways, one via conjugated carbon and another via heteroatoms. In contrast, in part-II diradicals, we will observe the effect of the number of hetero-atomic pathways if there is only one heteroatom in the coupling path and/or the impact of doubling the parallel hetero-atomic exchange coupling path. Our objective is to explain the incremental increase in the exchange coupling value in the diradicals having two ECP compared with the diradicals with one ECP.

Methodology

An interested reader may find a detailed description of the computational strategy adopted here.^{15,17–21,28,29,31–37} However, a concise draft of the most relevant part of this section is given below. The Heisenberg Hamiltonian

Ĥ = −2JŜ₁·Ŝ₂ (1)

is used to describe exchange coupling in these systems having two unpaired spins on two different centers. In the above eqn (1),J is designated as the exchange coupling constant and Ŝ₁·and Ŝ₂ are the local spins on the two spin-bearing sites, respectively. In the multiconfigurational method, J is related with the following equation for a diradical,

E(S = 1) − E(S = 0) = −2J. (2)

In the density functional theoretical framework, different equations are used to evaluate the exchange coupling constants. However, in this work, we have used the well-accepted Yamaguchi formula³⁸

to evaluate the exchange-coupling constant. In eqn (3),E_BS and E_T denote the energy of the broken-symmetry singlet (BS) and triplet state and 〈S²〉_T and 〈S²〉_BS represent average spin square values in the triplet and BS state, respectively.

From eqn (1) for a diradical, one can say (Ĥ = −2JŜ₁·Ŝ₂ and S₁ = S₂ = ½), ΔE_ST = 2J. Here, J is the effective exchange interaction, which may be expressed in terms of the spin densities, ρ_i and ρ_j, and the effective exchange integral, J^eff_ij, between the connecting sites i and j, giving^39,40

J = J^eff_ijρ_iρ_j, for ECP-I systems (4)

J = 2J^eff_ijρ_iρ_j, for ECP-II systems (5)

Therefore, |ΔE_ST| should be exactly doubled when the introduction of the second alike parallel ECP does not affect the J^eff_ijρ_iρ_j terms. The disjoint character of singly occupied molecular orbitals (SOMOs) of ECP-I and ECP-II diradicals is an important factor in dropping the change of ρ_i and ρ_j. However, conformations of ECP-I and ECP-II diradicals affect both ρ_iρ_j and J^eff_ij.

The geometry optimizations of part-I diradicals have been carried out using B3LYP, M06, and PBE0 with the 6-311++G(d,p) basis set.^41,42 Part-II diradicals were optimized also with the same three functionals, combined with the 6-311+G(d,p) basis set. We used Gaussian16 software for all the calculations.⁴³

Results and discussion

This work presents the results of the first principles study on the role of hetero-atoms as a coupler between two spin centres. In this study a state-of-the-art DFT method was employed to perform all the calculations.

Magnetic exchange coupling constant

The magnetic exchange coupling constants of part-I diradicals are presented in Table 1 and those of part-II diradicals are shown in Table 2. For part-I diradicals, there are two coupling pathways: through conjugated carbon and via hetero-atoms. The more the number of coupling pathways, the stronger the coupling strength, as we see from the earlier work.²⁹ Part-I diradicals have different hetero-atoms in the hetero-atomic exchange pathway. The coupling constant should vary with other heteroatoms. If we look at Table 1, we can see that the coupling constants remain approximately unaltered, which suggests that the hetero-atoms do not participate properly in the spin exchange through them.

Table 1 Magnetic exchange coupling constant values of the part-I (set A and set B) diradicals with different levels of theory with the 6-311++G(d,p) basis set

Heteroatoms	Exchange-coupling constants, J (cm^−1)
	B3LYP		M06		PBE0
	Set-A	Set-B	Set-A	Set-B	Set-A	Set-B
B	5.41	−20.66	6.50	−20.18	9.50	−30.20
C	6.75	−18.12	7.07	−17.88	10.24	−25.89
N	4.82	−17.67	5.37	−17.54	8.01	−24.72
O	7.19	−17.58	7.82	−17.21	10.87	−24.79
S	4.75	−17.25	5.04	−17.08	8.01	−24.51

---

Table 2 Intramolecular exchange-coupling constants (J, cm⁻¹) of the Part-II diradicals using different level of theory

Diradicals	Exchange-coupling constants, J (cm^−1)
	B3LYP/6-311+G(d,p)	M06/6-311+G(d,p)	PBE0/6-311+G(d,p)
B-ECP-I	−3.95	−12.53	−6.81
B-ECP-II	−8.13	−15.91	−11.03
C-ECP-I	−0.89	−2.19	−1.97
C-ECP-II	−1.76	−1.97	−0.88
N-ECP-I	−1.77	−1.97	−3.30
N-ECP-II	−7.02	−7.91	−9.23
O-ECP-I	−1.09	−2.20	−1.98
O-ECP-II	−7.24	−8.12	−6.80
S-ECP-I	−0.88	−1.98	−1.76
S-ECP-II	−1.10	−3.51	−1.10

---

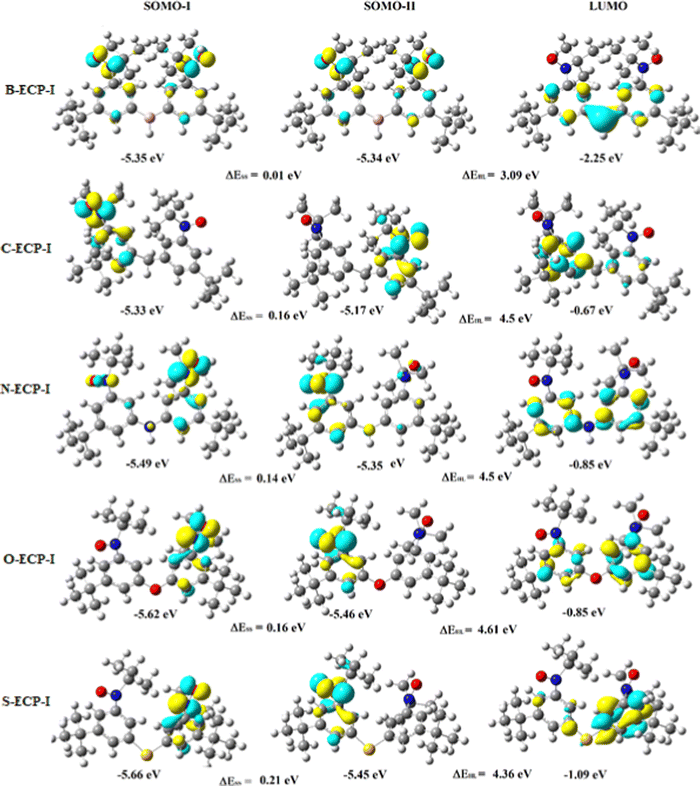
The exchange coupling constants of the part-II diradicals are listed in Table 2. Here, we are planning to discuss the general trend of the results of J values obtained with the B3LYP functional. The reason for doing so is discussed in the later part of this sub-section. From Table 2, it is clear that the coupling constants of the diradicals are very low. Here, the lone pairs are involved in sp³ hybridization for N-, O-, and S-bridgehead atoms in their respective diradicals, except B-conjugated diradicals. The B-atom is sp² hybridized as it has vacant pure p–π orbitals. Here, the low value of J depicts that the involvement of lone pairs in conjugation with the two adjacent phenyl groups is much less (for N-, O- and S-atom) compared to the condition when the electrons are present in the non-hybrid pure p-orbitals (for B-atom). The above statement is true even if the π-bonds of the phenyl groups are already present at the allylic position with the lone pairs of the hetero-atoms (N-, O- and S-atoms). Moreover, the electron-deficient B-atom is present at the allylic position from both of the two adjacent phenyl rings. This makes them in conjugation (by back donation) with each other. The back donation from both the ends of phenyl p–π-electrons makes the B-atom much less electron-deficient than what is expected if no back donation happens. Nonetheless, as B-atom is sp² hybridized, its planarity and low electronegativity (among the heteroatoms taken here) make everything possible for σ conjugation and σ–π resonance. As a result, we get a higher value of J for B-containing diradicals among all the diradicals.

In C-bridged diradicals, the bridging C-atom is sp³ hybridized; hence it is out of the plane with no lone pairs on it with moderate electronegativity among all the bridging atoms taken here, and hence, the J value is essentially low. In the case of N-bridged diradicals, the N-atom is sp³ hybridized, so the N-atom is out of the plane with a bit higher electronegativity than C. However, sp³ hybridized N has one lone pair on it; hence, lone pairs are involved in conjugation with the allylic π-electrons of two adjacent phenyl rings. Hence, generally the J value should remain slightly higher than that of C-based species despite higher electronegativity of the N-atom. A notable point is that this general trend does not hold good for all functionals. B3LYP and PBE0 functionals follow this trend whereas the M06 functional fails to follow this trend in the ECP-I case. In the case of O-bridgehead diradicals, the O-atom is sp³ hybridized and hence out of the plane. The electronegativity of the O-atom is highest among all the bridging atoms taken herein in this work. So, in general for ECP-I cases, one could say that due to less conjugation, J values are lowest among all the heteroatomic (in the 2nd period of periodic table) bridgehead diradicals, although it has two lone pairs. This means that generally the effect of electronegativity is more significant that the effect of the lone pair. However, an exception is found in the ECP-I case with the M06 functional when compared with the N-atom values. The same types of deviations are found in ECP-II cases with B3LYP and M06 functionals. On the other hand, in S-bridging diradicals, the S-atom is sp³ hybridized and being in the 3rd period of the periodic table, it is the largest in size among all the bridging atoms taken here. Hence, S-bridgehead diradicals show the lowest J values among all the heteroatom bridged systems, although the electronegativity of the S-atom is lower than that of the O-atom. However, from Table 2, an exception to the above stated general trend (as predicted using the B3LYP functional) is observed using the M06 functional in the ECP-I case when comparing with S- and N-bridgehead moieties. Nonetheless, if one considers the C-bridgehead species with M06 and PBE0 functionals, one should observe smaller values for the ECP-I case as compared with the ECP-II case. Hence, one can conclude that hindrance of spin propagation due to out of planarity has a more pivotal role in predicting the J value than the electronegativity as far as the bridging heteroatom based spin propagation path is concerned. In general, when the number of coupling paths increases from one to two, the coupling constant increases. This in turn confirms previous observation²⁰ and the fact that the addition of ECP will increase the J value.²⁹ Interestingly, when the conjugation path breaks with the sp³ hybridized –CH₂– group, we still get a coupling constant. This observation suggests that if there is no π conjugation between the spin centres, there is still a coupling via σ-electrons (although very small). When the coupling occurs through sp³ hybridized hetero-atoms, they behave almost similarly as there is no π-electron conjugation, which is evident from the coupling constant values (Table 2, bridging by –CH₂– and other hetero-atoms). Suppose the hetero-atom is sp² hybridized and has a π-bond, for example, pyridine, then spin coupling occurs easily as the lone pair is not involved in resonance and hence participate in exchange coupling.¹⁶ The most important observation (with the B3LYP results) from the coupling constants of part-II diradicals is that the coupling constant gets doubled, and more if we double the parallel exchange coupling path. However, there are some exceptions to it with the other functionals. With the PBE0 functional, the ECP-II values are smaller than the ECP-I values for C- and S-bridgehead diradicals. The same observation is also made with the M06 functional on C-bridgehead diradicals, as well. As already mentioned in the Methodology part that |ΔE_ST| should be accurately doubled when the introduction of the second alike parallel ECP does not affect the J^eff_ijρ_iρ_j terms. The disjoint character of singly occupied molecular orbitals of ECP-I and ECP-II diradicals is an important factor in minimizing the perturbation of ρ_i and ρ_j. Nonetheless, conformations of ECP-I and ECP-II diradicals will also affect both ρ_iρ_j and J^eff_ij.³⁰ From molecular orbital plots (Fig. 3 and 4), we find that the singly occupied molecular orbitals (SOMOs) are non-disjoint¹⁶ in nature; hence J values of ECP-II should not be exactly twice the respective ECP-I's J values. This observation will greatly impact the design of magnetic materials with a high value of magnetic exchange coupling constant, which is a need for future technology. This has also been observed experimentally by the Rajca group³⁰ with no hetero-atom in the coupling pathways.

Fig. 3 The molecular orbital of the part-II (ECP-I) diradicals (B3LYP/6-311 + G(d,p) level calculations). Here, the iso-value for molecular orbital plots is set as 0.05. Pink, red, grey, yellow, blue, white atoms represent the boron, oxygen, sulphur, nitrogen and hydrogen elements, respectively.

Fig. 4 The molecular orbital of the part-II (ECP-II) diradicals (B3LYP/6-311+G(d,p) level calculations). Here, the iso-value for molecular orbital plots is set as 0.05. Pink, red, grey, yellow, blue, white atoms represent the elemental boron, oxygen, sulphur, nitrogen and hydrogen respectively.

One general point to be discussed here from the consequences of the above trend of the magnetic exchange coupling constant values is that there are some cases (already mentioned above) where one cannot observe identical behaviour to get expected relations among the J values in ECP-I and ECP-II cases (for all three exchange correlation functionals that we have used here) based on the electronegativity, lone pair, dihedral angle consideration or by the combinations of all of them. As far as the functionals are concerned, it is very tricky to tell the better one among the functionals. The difference in results arises among the functionals due to the difference in percentage of the non-local and local part of the exchange and correlation. In a study, Ali and Oppeneer⁴⁴ found that the M06-2X functional is a good choice for their studies compared to M06 and PBE0 functionals. In another work, Bhattacharya et al.³⁷ found that B3LYP is better for investigating exchange correlation values than the M06-2X functional. In another work, Bhattacharya et al.³⁴ found that the choice of functionals depends on the systems to be investigated. Here, in this work, we have found that B3LYP results matched profoundly with each other after a series of test runs than the other functionals, although M06 and PBE0 functional results were the next most accurate after B3LYP results. From Table 2, one can easily say that B3LYP is the best chosen functional in this work. However, the other functionals do not change the sign of the magnetic exchange coupling constant (the magnetic nature of the diradicals), although the magnitude of the same does not always follow the same expected trend. Nonetheless, it is obvious from Fig. 5 (tells the graphical representation of J with different ECPs) that, in all functionals, the ECP-II values for C- and S-bridged species are very close to ECP-I values. In the case of the PBE0 functional, the decreasing trend of the J values for C- and S-bridged diradicals are observed in ECP-II cases as compared to the corresponding ECP-I values. In contrast, if we consider the S-bridged diradicals with the B3LYP functional, the J value of ECP-II is not doubled as compared to the ECP-I case. It can be said that among fifteen sets of ECP-I and respective ECP-II cases (every five pairs of each ECP-I and ECP-II diradicals are calculated with three different functionals) of results, enhancement in J values from ECP-I to ECP-II does not happen only in three non-B3LYP cases. Nonetheless, J values of ECP-II were not doubled as compared to the corresponding ECP-I values in some cases, we found that they triplicated or quadruplicated, or sextuplicated. The reason behind this very fact lies in the values of ρ_i,ρ_j of the spin bearing sites (as shown in Tables S13 and S14, ESI†), planarity, electronegativity of the bridgehead atoms, etc. It is also known³⁰ that if the SOMOs of ECP-I and its respective ECP-II diradicals are disjoint in nature, then an exact doubling of J values occurs. However, from a closer inspection of Fig. 3 and 4, it is obvious that the SOMOs are non-disjoint in nature and consequently one does not find an exact doubling of J values from ECP-I to ECP-II diradicals. It may also be noted that similar observations were made by Rajca et al.³⁰ There they found more than doubled J values for the ECP-II case compared to the ECP-I case (with homoatomic bridgehead path) by SQUID magnetometry and EPR spectrometry which is well supported by theoretical calculations.

Fig. 5 Plots of J (in cm⁻¹) vs. ECP-I and ECP-II of part-II diradicals. The panels from left to right show the plots with B3LYP, M06 and PBE0 functionals with the 6-311+G(d,p) basis set.

In part-II diradicals, the exchange coupling constant is lowest for the S-containing diradicals and highest for B-containing diradicals as shown using B3LYP and PBE0 functionals in the ECP-I case (see Table 2). From N- to S-bridgehead species, the exchange coupling constant decreases gradually in the ECP-I case as evident from B3LYP and PBE0 functionals. In the ECP-II case, the abovementioned trend is followed by the same species with the PBE0 functional only. This trend of the spin coupling constant (Table 2) can also be elucidated with the support of planarity of the heteroatoms with the coupling path in terms of dihedral angles (Table 3). The dihedral angles also increase from N- to O- to S-bridgehead diradicals clearly depicting the enhancement of non-planarity, lowering of spin delocalization and consequently decreasing trend of J values are observed. The B-containing diradical gives the highest value of the magnetic exchange coupling constant with all the functionals because of the near planar structure of the B-atom at the bridgehead with the adjacent atoms in the coupling path. Also, due to its electron-deficient properties, it can host electrons in its vacant pure p-orbital (back donation) to enable coupling. The lowest coupling constant value is observed for S-connected diradicals, if one considers the J values among heteroatom bridgehead diradicals, as obvious from B3LYP and PBE0 functionals, because of their larger size and non-planar structure with the adjacent atoms of the coupling path (having larger dihedral angles with the specified functionals). It is very clear from the bar graph (Fig. 6) that all the dihedral angles with one coupling path are smaller than the dihedral angles having two coupling paths. The C-(sp³ hybridized) and S-bridgehead (larger in size because of the 3rd period element) diradicals have the larger values of dihedral angles in both ECP-I and ECP-II cases. Among the hetero-atomic bridged diradicals, S-bridgehead diradicals show the highest value of dihedral angles.

Table 3 Dihedral angles (ϕ₁ and ϕ₂) between bridgehead-heteroatoms and the adjacent phenyl rings of the part-II diradicals using all functionals having the 6-311+G(d,p) basis set

Diradicals	Dihedral angle (ϕ in degree)
	B3LYP		M06		PBE0
	ϕ 1	ϕ 2	ϕ 1	ϕ 2	ϕ 1	ϕ 2
B-ECP-I	27	—	27	—	27	—
B-ECP-II	32	32	34	34	34	34
C-ECP-I	73	—	67	—	71	—
C-ECP-II	82	82	80	80	81	81
N-ECP-I	30	—	30	—	28	—
N-ECP-II	65	65	63	63	64	64
O-ECP-I	48	—	40	—	39	—
O-ECP-II	72	70	70	70	71	71
S-ECP-I	53	—	43	—	43	—
S-ECP-II	87	87	78	78	84	84

---

Fig. 6 The bar graph depicting dihedral angles (degree) of the part-II diradicals with B3LYP, M06 and PBE0 functionals with 6-311+G(d,p) level calculations.

Spin density analysis

Whenever we discuss spin exchange coupling, it is obvious that spin density is discussed. The spin coupling between two spin centers occurs via conjugated systems and we always get spin density on the coupler. More the spin density delocalizes from spin center to the coupler, the stronger is the coupling constant. If there is no spin density on the coupler, we can assume that the coupling pathway is less favorable. Now, let us look at Fig. 7 which shows the spin density plot of the part-I diradicals (both set A and set B). We can see that all the hetero-atoms have nearly zero spin density, suggesting that the hetero-atomic pathway for spin coupling is not favorable. Spin density (for the B3LYP functional) on the heteroatoms of set A diradicals are B – 0.003, C – 0.005, N – 0.001, O – 0.055 and S – 0.000, respectively. The spin density on heteroatoms in set B diradicals is B – 0.002, C – 0.003, N – 0.001, O – 0.010, and S – 0.000, respectively. The spin coupling constant for the set A diradicals with hetero-atoms (N-, O-, and S-atom) on the coupling path remains the same. This signifies that the presence of heteroatoms does not affect the coupling constant. However, for B-containing diradicals, the coupling constant is highest among the series because B has a vacant orbital and accepts the electrons from the nearby radical centers via back donation. For set B diradicals, the distance of heteroatoms from the radical centers reduces by one atom count compared to the set A diradicals; this increases the probability of participation of heteroatoms in the spin coupling path. This is observable in the coupling constant values (From Table 1). The S-containing diradicals have the lowest value of J (with B3LYP and PBE0 functionals) in ECP-I cases as far as the heteroatomic bridged diradical systems are concerned. The reason behind it is that as the sulphur atom is a 3rd period element in the periodic table, and hence bigger in size than the other bridging elements which remain in the 2nd period of the periodic table. This will make it out of the plane and hinder the itinerant exchange resulting in zero spin density on it.

Fig. 7 The spin density plot of the part-I (set A and set B) diradicals (B3LYP/6-311++G(d,p) level calculations). Here, the iso-value for spin density is taken as 0.0005. The blue sign represents the up-spin whereas green sign represents the down-spin. Pink, red, grey, yellow, blue, white atoms represent the elemental boron, oxygen, sulphur, nitrogen and hydrogen, respectively.

Fig. 8 suggests that the spin coupling in one or both ways are partially blocked due to hetero-atoms (ECP-II) which results in a small coupling constant. However, if the hetero-atom is sp² hybridized (in the case of B-bridged diradicals) with non-hybrid pure p-orbitals we can have spin density on hetero atoms,¹⁶ which suggests that π-electron-lone pair conjugation is needed for favorable spin propagation in hetero-atomic pathways.

Fig. 8 The spin density of the part-II diradicals (B3LYP/6-311+G(d,p) level calculations). Here, the iso-value for spin density is taken as 0.001. The blue sign represents the up-spin whereas the yellow sign represents the down-spin. Pink, red, grey, yellow, blue, white atoms represent the elemental boron, oxygen, sulphur, nitrogen and hydrogen, respectively.

Molecular orbitals

The magnetic exchange coupling constant results from the interaction between two magnetic orbitals. The energy gap between magnetic orbitals controls the magnitude of magnetic interaction. However, it depends on the system under study. Apart from the magnetic orbitals, the vacant orbital, especially the lowest unoccupied molecular orbital (LUMO), plays a crucial role in the magnetic interaction of diradicals. The energy distance between the highest occupied molecular orbital (HOMO) and the LUMO significantly impacts the magnetic exchange coupling constant. If we look at the HOMO–LUMO gap in Fig. 3, 4, 9 and 10 we can see that the HOMO–LUMO gap is lowest for all the B-containing diradicals compared to the other hetero-atom containing diradicals. The exchange coupling constant values are higher for B containing diradicals. The energy and spatial position of the magnetic orbitals and LUMO plays a vital role in the magnetic exchange coupling constant. It has been found that if LUMO resides between the magnetic orbital, the exchange coupling between the spins favored.²⁷ If we see the molecular orbital picture of the diradicals in Fig. 3, 4, 9 and 10, we can observe that all the LUMOs are in between the magnetic orbitals, i.e., singly occupied molecular orbitals (SOMOs). We have seen in the previous section that the B-containing diradicals give the highest magnetic exchange coupling constant. The spatial distribution of the molecular orbitals can explain this phenomenon. If we closely look at the LUMOs of all the diradicals, we can see that the orbital coefficient on the heteroatoms is negligible except B-containing species. This fact implies that the exchange interaction occurs via LUMO. If there is no LUMO coefficient on an atom in the exchange pathways, it gives a low magnetic exchange coupling constant value.

Fig. 9 The molecular orbital of the part-I (set A) diradicals (B3LYP/6-311++G(d,p) level calculations). Here, the iso-value for molecular orbital is taken as 0.02. Pink, red, grey, yellow, blue, white atoms represent the elemental boron, oxygen, sulphur, nitrogen and hydrogen, respectively.

Fig. 10 The molecular orbital of the part-I (set B) diradicals (B3LYP/6-311++G(d,p) level calculations). Here, the iso-value for the molecular orbitals is set as 0.05. Pink, red, grey, yellow, blue, white atoms represent the elemental boron, oxygen, sulphur, nitrogen and hydrogen, respectively.

The orbital concept

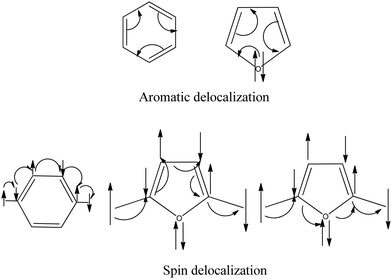
From the above discussion, it is clear that the sp² hybridized hetero-atoms without a π-bond are not suitable for spin coupling. In the valence bond model, the π-orbitals on every atom of the π-network are considered singly occupied.⁷ Now, we make a conceptual model to explain the reason based on the valence bond theory. We know that the lone pairs of heteroatoms in heterocyclic complexes participate in aromaticity. In the aromatic delocalization of π-electrons, the pair of electrons (bond or lone pair) move around the ring. If we consider the delocalization of radical electrons, the single electron moves from one site to another to make the magnetic interaction (Fig. 11). All the atoms have one electron in the path of spin movement through the carbon atoms.

Fig. 11 Schematic diagram for the aromatic and spin delocalization.

On the other hand, if there is a heteroatom in the path, the heteroatoms have two electrons on them as lone pairs. When spin propagates through homo-atomic pathways, it makes bonding situations with the nearest atoms. When the heteroatoms come into the coupling path with lone pairs, this bonding situation breaks. In this case, to make the bonding situation, the lone pairs should break, which is not favorable. This discussion signifies that the lone pairs restrict the spin propagation pathway through the heteroatoms.

We draw the π-orbitals and lone pairs of the molecules in Fig. 12. Fig. 12(a) and (b) represent the ferromagnetic interaction. Fig. 12(c) and (d) represent the antiferromagnetic situation. We see that all the π-electrons, including the radicals, are in a bonding situation (Fig. 12(a) and (c)) when the propagation occurs through carbon pathways. Now, if we look at Fig. 12(b) and (d), the spin propagates through heteroatoms; now the question is, what will happen when the spin passes through hetero-atoms? The spin propagation stops at the heteroatoms, which causes the low value of the spin coupling constant between the spin centers. We may call this effect a heteroatom blocking effect.

Fig. 12 Orbital picture with lone pairs of the some specified diradicals taken from our work.

Conclusions

Here, in this work, we have reported the computational investigation of the effect of heteroatoms in the spin coupling pathways between two spin centres in organic diradicals. We clarified that heteroatoms restrict the spin coupling through them by the participation of the lone pairs in hybridized heteroatoms in the spin propagation path. The lone pairs of sp² hybridized heteroatoms in cyclic molecules participate in aromatic conjugation; hence they do not participate in spin propagation. The VB orbital concept shows that the lone pair has to break to participate in spin propagation, and this phenomenon is not favourable energetically. Hence, the heteroatoms stay inactive in spin propagation between the two spin centres. However, unlike other heteroatoms, B-atoms favour exchange coupling between radical centres through spin propagation due to its vacant non-hybrid pure p-orbitals. In both ECP-I, and ECP-II cases for part-II diradicals, the highest values of J are observed by the B-bridged systems in all functionals. And the lowest J value is observed for the S-bridged systems with the B3LYP functional, whereas in other functionals the values are different for the lowest J. For the N-bridged system, J is a bit lower than the B-bridged species as observed using all functionals and a bit higher than the O-bridged system as viewed using B3LYP and PBE0 functionals. The reason for such a trend of J values is explained in the Results and discussion section, which tells that the spin propagation is determined in the decreasing order of the presence of non-hybrid pure vacant p-orbitals (B-atom), lone pairs (N-atom), electronegativity (O-atom) and size (S-atom) of the heteroatoms with the p–π bonded electrons of the adjacent phenyl rings. The spin density values (see Table S13 for ECP-I and Table S14 for ECP-II in ESI†) at the respective radical sites indicate the above fact. The average spin densities on the radical sites are 0.4609, 0.4551, 0.4709 and 0.4688 for B-, N-, O-, and S-bridgehead diradicals, respectively. As oxygen is the most electronegative element among all the bridgehead elements in the respective diradicals, less spin propagation happens through the O-bridgehead atom and hence the spin density value is highest at the radical sites. In N-bridgehead diradicals, due to the presence of lone pairs little more spin propagation happens between the radical sites from one end to the other and hence the spin density values on the radical sites are a bit less than the previous (O-) case. In S-bridgehead diradicals, the spin density values at the radical sites are in between those of the previous two cases (N- and O-). The reason is that S- is large (3rd-period element) and so it remains out of the plane than the other bridging elements; hence, spins are restricted in S-bridgehead during the flow of spin from one radical site to another, but as it is less electronegative than O-, it has less tendency to retain the spin with it. In the case of B-bridgehead diradicals the back donation leads to more possibility of spin flow from one spinning site to the other, meaning that with the enhancement of spin flow from one end to the other the spin density on the radical sites remains moderate indeed. Another point to be noted here is that in every case of heteroatomic bridgehead species, the spin densities on the radical sites are lower in ECP-II than in their respective ECP-I cases, which means, the spins are more delocalised and the J values are higher. We also found that to favour magnetic exchange, it is necessary to have a non-zero LUMO coefficient on the atoms of the exchange pathways. The B3LYP results have shown that magnetic exchange coupling constant can be made a bit more (S-bridged), almost a bit less or more than doubled (C-bridgehead and B-bridgehead diradical),²⁰ quadruplicated (N-bridgehead diradicals) and almost septuplicated (O-bridgehead diradicals) by doubling the parallel exchange pathways. Hence, proper stacking of these types of diradicals and appropriate designing with more than one parallel ECP will provide us with new opportunities to obtain magnetic materials with high exchange coupling constants.

Author contributions

S. Shil has planned, designed and executed relevant calculations of the part-I diradical systems. D. Bhattacharya has planned, designed and implemented relevant calculations of the part-II diradical systems. S. Shil and D. Bhattacharya have written this paper. Y. P. Ortiz made some of the Gaussian runs for part-II systems. A. Misra and D. J. Klein both have given their scientific suggestions and read the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

S. Shil is thankful to SERB, India, for funding via grant no. SRG/2022/000822. D. Bhattacharya, Y. Ortiz and Douglas J. Klein acknowledge the support (via grant BD-0894) from the Welch Foundation of Houston, Texas. A. Misra is thankful to SERB-India (CRG/2019/000262) for funding. Y. P. Ortiz acknowledges the use of the MIZTLI super-computing facility of DGTIC-UNAM. E. Ali is acknowledged for his valuable suggestions.

References

1. H. Iwamura and N. Koga, Acc. Chem. Res., 1993, 26, 346–351.
2. H. Iwamura, Adv. Phys. Org. Chem., 1990, 179–253.
3. H. C. Longuet-Higgins, J. Chem. Phys., 1950, 18, 265–274.
4. A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297–304.
5. W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587–4594.
6. W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1981, 14, 69–76.
7. D. J. Klein, C. J. Nelin, S. Alexander and F. A. Matsen, J. Chem. Phys., 1982, 77, 3101–3108.
8. S. A. Alexander and D. J. Klein, J. Am. Chem. Soc., 1988, 110, 3401–3405.
9. Y. Teki, T. Takui, M. Kitano and K. Itoh, Chem. Phys. Lett., 1987, 142, 181–186.
10. N. N. Tyutyulkov, S. H. Karabunarliev and S. I. Tsonchev, Synth. Met., 1989, 32, 51–61.
11. N. Tyutyulkov, P. Schuster and O. Polansky, Theor. Chim. Acta, 1983, 63, 291–304.
12. K. Itoh, Chem. Phys. Lett., 1967, 1, 235–238.
13. H. Tukada, K. Mutai and H. Iwamura, J. Chem. Soc., Chem. Commun., 1987, 1159.
14. T. Ishida and H. Iwamura, J. Am. Chem. Soc., 1991, 113, 4238–4241.
15. V. Polo, A. Alberola, J. Andres, J. Anthony and M. Pilkington, Phys. Chem. Chem. Phys., 2008, 10, 857–864.
16. D. Bhattacharya and A. Misra, J. Phys. Chem. A, 2009, 113, 5470–5475.
17. D. Bhattacharya, S. Shil, A. Misra and D. J. Klein, Theor. Chem. Acc., 2010, 127, 57–67.
18. D. Bhattacharya, S. Shil, A. Panda and A. Misra, J. Phys. Chem. A, 2010, 114, 11833–11841.
19. D. Bhattacharya, S. Shil and A. Misra, J. Photochem. Photobiol., A, 2011, 217, 402–410.
20. D. Bhattacharya, A. Panda, S. Shil, T. Goswami and A. Misra, Phys. Chem. Chem. Phys., 2012, 14, 6905–6913.
21. D. Bhattacharya, S. Shil, A. Misra, L. Bytautas and D. J. Klein, Phys. Chem. Chem. Phys., 2015, 17, 14223–14237.
22. C. Trindle and S. N. Datta, Int. J. Quantum Chem., 1996, 57, 781–799.
23. C. Trindle, S. Nath Datta and B. Mallik, J. Am. Chem. Soc., 1997, 119, 12947–12951.
24. V. Polo, A. Alberola, J. Andres, J. Anthony and M. Pilkington, Phys. Chem. Chem. Phys., 2008, 10, 857–864.
25. D. Cho, K. C. Ko and J. Y. Lee, Int. J. Quantum Chem., 2016, 116, 578–597.
26. D. Cho, K. C. Ko and J. Y. Lee, J. Phys. Chem. A, 2014, 118, 5112–5121.
27. S. Shil, M. Roy and A. Misra, RSC Adv., 2015, 5, 105574–105582.
28. E. Ali and S. N. Datta, J. Phys. Chem. A, 2006, 110, 2776–2784.
29. S. Shil, Int. J. Quantum Chem., 2018, 118, e25543.
30. A. Rajca, S. Rajca and J. Wongsriratanakul, Chem. Commun., 2000, 1021–1022.
31. S. Shil, S. Paul and A. Misra, J. Phys. Chem. C, 2013, 117, 2016–2023.
32. D. Bhattacharya, S. Shil, T. Goswami, A. Misra, A. Panda and D. J. Klein, Comput. Theor. Chem., 2013, 1024, 15–23.
33. D. Bhattacharya, S. Shil, T. Goswami, A. Misra and D. J. Klein, Comput. Theor. Chem., 2014, 1039, 11–14.
34. D. Bhattacharya, S. Shil, A. Misra, L. Bytautas and D. J. Klein, Int. J. Quantum Chem., 2015, 115, 1561–1572.
35. S. Shil and C. Herrmann, Inorg. Chem., 2015, 54, 11733–11740.
36. P. Sarbadhikary, S. Shil, A. Panda and A. Misra, J. Org. Chem., 2016, 81, 5623–5630.
37. D. Bhattacharya, S. Shil, A. Misra, L. Bytautas and D. J. Klein, J. Phys. Chem. A, 2016, 120, 9117–9130.
38. K. Yamaguchi, Y. Takahara, T. Fueno and K. Nasu, Jpn. J. Appl. Phys., 1987, 26, L1362–L1364.
39. Y. Teki and K. Itoh, in Magnetic Properties of Organic Materials, ed. P. M. Lathi, Marcel Dekker, New York, 1999.
40. H. M. McConnell, J. Chem. Phys., 1963, 39, 1910.
41. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
42. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, 2016.
44. M. E. Ali and P. M. Oppeneer, J. Phys. Chem. Lett., 2011, 2, 939–943.

---

Footnote

† Electronic supplementary information (ESI) available: The optimized coordinates of the molecules. See DOI: https://doi.org/10.1039/d3cp00394a

---