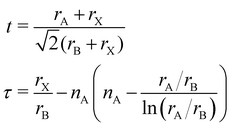Computational workflows for perovskites: case study for lanthanide manganites

Abstract

Robust computational workflows are important for explorative computational studies, especially for cases where detailed knowledge of the system structure or other properties is not available. In this work, we propose a computational protocol for appropriate method selection for the study of lattice constants of perovskites using density functional theory, based strictly on open source software. The protocol does not require a starting crystal structure. We validate this protocol using a set of crystal structures of lanthanide manganites, surprisingly finding N12+U to be the best performing method for this class of materials out of the 15 density functional approximations studied. We also highlight that +U values derived from linear response theory are robust and their use leads to improved results. We investigate whether the performance of methods for predicting the bond length of related gas phase diatomics correlates with their performance for bulk structures, showing that care is required when interpreting benchmark results. Finally, using defective LaMnO₃ as a case study, we investigate whether the four shortlisted methods (HCTH120, OLYP, N12+U, PBE+U) can computationally reproduce the experimentally determined fraction of Mn^IV+ at which the orthorhombic to rhombohedral phase transition occurs. The results are mixed, with HCTH120 providing good quantitative agreement with experiment, but failing to capture the spatial distribution of defects linked to the electronic structure of the system.

---

1 Introduction

One of the prerequisites for predicting any material properties using computational methods is to have a good starting point for the structure of the material. As shown by the series of blind crystal structure prediction benchmarks, predicting experimentally-observed crystal structures reliably and without prior information about the lattice is still a difficult and open question.¹ However, suppose one wants to determine a property of several materials from a single material class with a reasonably well-defined structural motif; for instance the phonon modes of perovskites. In this case, it may be more beneficial to determine an energy minimum that sacrifices agreement with the experimental structure, but allows us to calculate the phonon spectrum using a trusted method. This is especially important in density functional theory (DFT) when applied to solid state systems, as it has been repeatedly shown that the use of a combination of density functional approximations (DFAs) may be required to obtain the best possible description of the material.^2,3

In this work, we discuss a computational workflow for modelling structures of perovskites using DFT. Several stipulations are specified for the workflow:

(1) The structures obtained have to be energy minima. This ensures that they can be subsequently used to calculate the second derivatives at the same level of theory, which is important for determining most thermochemical properties, a range of mechanical properties, and the dielectric behaviour of the system.

(2) Only the crystal system and atomic composition of the unit cell are known a priori. This ensures the workflow can be applied to study novel materials for which an experimental crystal structure is not yet determined.

(3) Only open source tools may be included in the workflow. This ensures the workflow can be applied by anyone, regardless of their academic affiliation or if it is for commercial purposes.

The workflow is shown schematically in Fig. 1. Specifically, we aim to find an affordable DFA capable of predicting the structures of orthorhombic LnMnO₃ perovskites (where Ln = {La, Pr, Sm, Eu, Yb}). We choose to use DFT, as the ligand field effects present in several of the selected materials make the use of classical potentials more complex.⁴ While the workflow may be used with any DFA, for the systems studied here, the computation of Hartree–Fock exchange would be prohibitively expensive. Therefore, our choice of methods is effectively restricted to the generalised gradient approximation (GGA) family. We focus on lanthanide manganite perovskites, as they show interesting catalytic properties⁵ and the behaviour of their dielectric properties in operando is known.⁶ The structures reported here can therefore be re-used in a further study of the electronic conductivity of these perovskites. Additionally, structures of their orthorhombic forms have been accurately determined using neutron powder diffraction,^7–11 or low-temperature X-ray diffraction,¹² allowing for a comparison with high-quality experimental data. This results in a case study that is of a manageable size, yet challenging for electronic structure calculations due to the presence of lanthanides (relativistic effects) as well as manganese (multiple spin states). Finally, we verify that DFAs that are able to predict the crystal structures of stoichiometric perovskites with a reasonable accuracy continue to do so for defect structures, as well as rhombohedral analogues. To address this last point, we focus on the defect-induced orthorhombic to rhombohedral phase transition in LaMnO₃, which has been studied experimentally in detail.^7,13

Fig. 1 Proposed computational workflow for geometries of perovskites. An initial list of DFAs is ranked and sorted using a benchmark of bond lengths of lanthanide diatomics (1). At the same time, mash (2) is used to produce initial trial structures of perovskites. These structures are used to determine +U corrections (3) for the top ranked methods from the initial benchmark. A reduced set of DFAs, including methods with +U corrections, is then benchmarked using perovskite structures (4). Having obtained a final ranking, the performance of the best-performing DFAs is evaluated on a LaMnO₃ case study (5).

2 State of the art

Of the five perovskites investigated here, the LaMnO₃ is certainly the most computationally studied material. The series of publications by Gavin and Watson is perhaps the most relevant here: the first publication focuses on determining the best DFA for determining lattice parameters and electronic structure of the stoichiometric perovskite,¹⁴ before applying their methodology (PBEsol+U) to study surfaces and oxygen defects.^15,16 Our work differs from theirs in two key points: (i) we do not use the experimental crystal structure as a starting point, and (ii) we investigate the bulk effects caused by La-vacancies, as opposed to surface effects caused by oxygen defects. In fact, several other computational studies (using PW91) focus on the surface of the perovskite^17,18 rather than its bulk behaviour, which is not surprising given its catalytic activity.⁵

The computational studies of PrMnO₃ include a study of the electronic structures, surface relaxation, and oxygen defect formation energies of its cubic and orthorhombic structures (using PW91+U),¹⁹ as well as a particularly interesting comparative study of CaMnO₃ and PrMnO₃ using inelastic neutron scattering and DFT (with PBE).²⁰ The experimental phonon spectrum of PrMnO₃, as well as the IR and Raman spectra, are fairly well reproduced by these calculations.²⁰ Both studies use the experimental structure as a starting point in their calculations.

For SmMnO₃, several studies have focused on the effect of dopants in the structure. Dopant segregation on the surfaces of SmMnO₃ and LaMnO₃ has been investigated (using PW91+U) and explained as a function of cation size mismatch.²¹ The metal-to-insulator transition induced by H-doping has been investigated in several perovskites (using PBEsol+U), including SmMnO₃.²² Most other computational research focuses on the surface behaviour of, and kinetics over, the mullite phase of SmMn₂O₅, which seems to be a more active catalyst than the perovskite SmMnO₃.^23,24

The remaining two perovskites considered here, EuMnO₃ and YbMnO₃, are relatively poorly studied. Perhaps the most relevant work concerning either of the two is the recent study of charge transfer between Eu and Mn.²⁵ The study (carried out using PBEsol+U) focuses on the changes in structure of EuMnO₃ driven by different magnetic moments of the two elements. The experimental structure is again used as a starting point for the calculations.

A look at the methods employed in the computational studies of the five perovskites listed above reveals that PBEsol+U is the most widely applied one, followed by the related PW91+U. In both cases, a DFA of the GGA family (PBEsol²⁶ and PW91²⁷) is combined with a so-called Hubbard term (+U),²⁸ an energy “penalty” for electronic states, tailored to reproduce the metallic as well as insulating behaviour of materials.²⁹ The approaches for choosing appropriate values of the +U correction are described in detail elsewhere.³⁰ Given the frequent use of GGA+U in the literature, it is somewhat surprising that a benchmark study of DFAs focused on predicting octahedral tilting in perovskites³¹ omitted +U variants of the studied GGAs completely. Instead, “hybrid” DFAs that include a fraction of Hartree–Fock exchange (HFx) were included, and they were found to outperform the (uncorrected) GGAs across the board.³¹ GGA+U is generally considered to be sufficient for determining ground-state properties (structure, band gap) of perovskites, but the determination of more complex quantities, such as the pressure-induced insulator to metal transition in LaMnO₃, would require the use of hybrid DFAs.³² In such cases, a hybrid functional with a screened HFx should be applied,³ with the range-separation (screening) constant tuned accordingly for each studied system.³² However, for the prediction of lattice constants, even the (uncorrected) GGAs were shown to perform comparably to hybrid DFAs.³¹

3 Computational methods

3.1 DFT calculations

All DFT calculations were carried out using the pw.x code from the Quantum ESPRESSO package (versions 6.6 and 7.0).^33,34 The DFAs were computed using the built-in interface with the exchange–correlation functional library libxc (compiled against libxc version 4.3.4)³⁵ throughout this work. Basis sets and pseudopotentials from the SSSP Efficiency pseudopotential library (version 1.1, PBE parametrisation)^36,37 were used whenever possible. For calculations involving the exchange-hole dipole moment dispersion correction (XDM),^38,39 the projector-augmented wave pseudopotentials from the PSlibrary (version 0.3.1) were used.⁴⁰ The computational details for the diatomic, single unit cell, and supercell calculations of the studied systems are included in the respective Results sections for clarity.

3.2 Starting structures

A key step in the proposed computational workflow is to be able to determine reasonable starting structures of orthorhombic perovskites using only their atomic composition. For this purpose, we have developed mash.⁴¹ Our tool is heavily inspired by the excellent program SPuDS by Lufaso and Woodward,⁴² and for most applications we would recommend SPuDS (or the recently developed python interface, PySPuDS) over mash. However, while SPuDS is available for download free of cost, it is not open source, so we chose to develop and use mash (version 1.0) for this work.

Given the formula of the perovskite (ABX₃), the requested Glazer tilt system, and output file format (xyz file, cif file, or pw.x-compatible input template), mash generates multiple trial unit cells according to the following protocol:

1. The elements in the formula supplied (ABX₃) are parsed, and based on the anion (X), combinations of possible integer charges of the cations are deduced.

2. The mendeleev library⁴³ is used to obtain the ionic radii of A, B, and X (denoted r_A, r_B, r_X) for all possible spin and charge combinations, and the perovskite tolerance factors t⁴⁴ and τ⁴⁵ are calculated from these radii and the number of A-site atoms in the unit cell (n_A):

3. For each of these candidate structures, if τ < 4.18, the candidate is likely to be a perovskite, otherwise the candidate structure is discarded. The tolerance factor τ is used instead of Goldschmidt's factor t as τ has been shown to outperform t in predicting perovskite stability.⁴⁵

4. The Glazer tilt angle ϕ is calculated from t, using a polynomial fit to the data of Lufaso and Woodward.⁴² This tilt was shown to be approximately correct for orthorhombic perovskites (tilt system a⁻b⁺a⁻).⁴² The tilt angle is currently applied indiscriminately for all implemented tilt systems in mash (cubic a⁺a⁺a⁺, orthorhombic a⁻b⁺a⁻, rhombohedral a⁻a⁻a⁻).

5. The appropriate supercell is generated using Wyckoff positions, as described in ref. 46. All candidate structures are saved in separate output files.

Using mash for the set of five perovskites, we obtain a set of 13 starting structures: 2 each for LaMnO₃ and PrMnO₃ (Ln^IIIMn^III with high and low Mn spin states); 3 each for SmMnO₃, EuMnO₃ and YbMnO₃ (also including Ln^IIMn^IV).

3.3 Linear-response +U values

As discussed previously, GGA+U is a popular level of theory applied to study solid state systems, including perovskites. However, the +U values for a given element are not universal, and would ideally be fitted for each compound, each DFA, and each property of interest.³⁰ As such, many parametrisations of GGA+U may exist for a given system, requiring benchmarking.¹⁴

To address this issue, while obtaining reasonable +U values without further a priori information, we have decided to use +U values obtained using linear-response theory, as described by Cococcioni and Kulik.^47,48 In this approach, +U is obtained from the difference of the inverted self-consistent response function χ from the non-interacting response χ₀ on each site, where the response functions χ are calculated as the partial derivatives of the total energy E with respect to localised potential shifts of strength α:

The linear response functions χ are obtained here by a linear regression to Es calculated using α values in the range of ±0.08 eV. The atomic orbitals are orthogonalised using the ortho-atomic keyword in Quantum ESPRESSO. Previous works have shown that the choice of appropriate orbital projections is crucial, as the calculated +U values might differ by up to an order of magnitude when using ortho-atomic or atomic Hubbard projectors.⁴⁹ For a multiple-site system, the χ, χ₀, and by extension U, become matrices, where the off-diagonal elements U_IJ correspond to the response at site I due to perturbations on site J. The +U s for sites in a multiple-site system are therefore the diagonal elements of the matrix, U_II. Note that strictly speaking, such +U corrections, as implemented in Quantum ESPRESSO, correspond to U_eff = U − J, where U would be the on-site Coulomb and J would be the on-site exchange interactions. However, in the current work, the +U values correspond to the diagonal elements of the U_eff matrix.

The +U values in this work are calculated using the linear-response approach for each of the three elements (except La) in each of the five perovskites for four of the DFAs studied (PBE, PBEsol, WC, and N12), using the unit cells obtained with mash. The calculated values are shown in Table 1. For comparison, literature GGA+U values include the PBE+U values of 4.5 eV for Mn 3d and 5.5 eV for O 2p to model LaMnO₃,¹⁴ a PW91+U value of 3.1 eV for Mn 3d to model PrMnO₃,¹⁹ a PW91+U and PBEsol+U value of 4.0 eV for Mn 3d in SmMnO₃,^21,22 and the AFLOW standard values of 4.0 eV for Mn 3d, 5.5 eV for Pr 4f, 6.4 eV for Sm 4f, 5.4 eV for Eu 4f, and 6.3 eV for Yb 4f.⁵⁰ While there is some consistency between functionals for a given element in the dataset shown in Table 1 (the few exceptions are the N12+U values for Mn and O in LaMnO₃ and Mn in PrMnO₃), the values obtained from the linear-response approach are generally quite different from the literature values, including the AFLOW standard.⁵⁰

Table 1 GGA+U values, in eV, as calculated using linear-response theory

Perovskite	Element	PBE+U	PBEsol+U	WC+U	N12+U
LaMnO3	La 4f	—	—	—	—
	Mn 3d	5.689	5.701	5.702	6.877
	O 2p	8.002	7.977	8.019	9.215
PrMnO3	Pr 4f	3.802	3.848	3.845	3.875
	Mn 3d	3.008	3.810	3.504	6.172
	O 2p	6.237	6.320	6.332	6.079
SmMnO3	Sm 4f	3.826	3.891	3.973	3.999
	Mn 3d	6.940	6.806	6.910	6.345
	O 2p	6.599	6.909	5.994	6.334
EuMnO3	Eu 4f	2.883	2.919	2.912	2.811
	Mn 3d	6.618	6.648	6.646	6.581
	O 2p	5.446	5.478	5.499	5.300
YbMnO3	Yb 4f	4.733	4.781	4.766	4.710
	Mn 3d	6.795	6.817	6.825	6.763
	O 2p	5.757	5.793	5.813	5.611

---

3.4 Defective LaMnO₃ supercell lattices

The defective supercells used to investigate the phase transition between orthorhombic and rhombohedral LaMnO₃ can be created by removing La atoms from the systems being modelled. Each La atom removed from the system has to be compensated by an increase in the oxidation state of 3 Mn atoms from III+ to IV+, in order to maintain charge neutrality. In other words, upon removal of a single La atom from the unit cell of orthorhombic LaMnO₃, the fraction of Mn^IV+ is 75%. In order to obtain smaller fractions of Mn^IV+, a supercell has to be used. For instance, with a 2 × 3 × 2 orthorhombic supercell (La₄₈Mn₄₈O₁₄₄), each La defect would correspond to a 6.25% increase in the fraction of Mn^IV+. However, choosing just four La atoms to remove out of the 48 La atoms in the 2 × 3 × 2 supercell (i.e. in combinatorial notation ) results in 194 580 possible combinations; with one more La defect (i.e.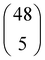) the number of combinations increases to 1 712 304. To constrain the number of supercells to a manageable number, we use defective orthorhombic and rhombohedral supercells, derived from the respective 2 × 3 × 2 and 2 × 4 × 1 stoichiometric supercells (both La₄₈Mn₄₈O₁₄₄), with 1 to 4 La defects spanning the range from 6.25% to 25% Mn^IV+.

As our calculations use periodic boundary conditions, many of the above defective supercells are related to each other by symmetry. Rather than explicitly considering the symmetry relations in the supercell, we instead calculate the potential energy of a set of equivalent ABO₃ defective supercells, using the effective medium theory calculator from the ase.calculators.emt module of the package ase (version 3.21).⁵¹ For convenience, the parameters for Al, Ni and O have been used as A, B, and O, respectively. Defective supercells with the same potential energies (to within 6 decimal places) are considered symmetry-equivalent, therefore, all but one of each set is removed from further consideration. The resulting number of unique defective orthorhombic (Pnma) and rhombohedral (R3c) supercell lattices, generated by ase, is shown in Table 2. These supercell lattices provide the sets of A-site positions which are to be removed from the LaMnO₃ supercells prior to their evaluation by DFT.

Table 2 Number of unique defective lattices generated using ase from the Pnma and R3c stoichiometric supercells. The sum of weights of each defective lattice as well as the total number of combinations ( where n = 48 and k ∈ {1, 2, 3, 4}) included for comparison

Supercell	Pnma	R3c			% Mn^IV+
La48Mn48O144	1	1	—	—	0.00%
La47Mn48O144	1	1	1	48	6.25%
La46Mn48O144	21	18	47	1128	12.50%
La45Mn48O144	213	138	1081	17 296	18.75%
La44Mn48O144	2479	1448	16 215	194 580	25.00%

---

4 Results and discussion

4.1 Equilibrium bond lengths in lanthanide diatomics

The usual way of selecting an appropriate DFA in computational chemistry in general is by benchmarking several candidate methods using a related, but simpler system.⁵² This approach is also often applied in the solid state.⁵³ Instead, we first focus on calculating the equilibrium bond lengths (r_e) in diatomic lanthanide oxides and halides, in analogy with ref. 54.

The reference r_e values for 17 lanthanide diatomics are available, including other spectroscopic constants, from calculations using a composite method exceeding the CCSD(T) level of theory.⁵⁵ Our calculations are performed by placing the two atoms 1 Å apart in a 10 × 10 × 10 Å box, and then relaxing the structure with the BFGS algorithm using the default convergence criteria (change in energy between steps dE < 10 mRy, maximum force F < 1 mRy a₀⁻¹) and a range of DFAs. The calculations are spin-unrestricted, with a Γ-centered 3 × 4 × 3 Monkhorst-Pack k-point grid, and energy cut-offs of 65 Ry and 780 Ry for the wavefunction and density, respectively. While this computational approach may be unusual for isolated gas-phase systems, it was used to maintain consistency with the method used for extended systems, below. For completeness, comparison with results performed with Γ-point only and the Makov–Payne correction for isolated systems⁵⁶ are shown in Fig. S1 (ESI†).

The results, obtained with the SSSP Efficiency pseudopotential library (version 1.1, PBE parametrisation) are shown in Fig. 2. The distribution of the absolute deviations from the reference r_e is shown using box plots. The set of 17 diatomics is shown in blue; a subset of the 5 La-containing diatomics is shown in orange. We note that the RMSD of the reference data from the best known experimental values of r_e is below 10 mÅ for the whole dataset, and below 3 mÅ for the La-subset.⁵⁵ Therefore, the significantly larger deviations in the bond lengths that we obtain across the board in our calculations would be spectroscopically significant. The best overall performers are the PBE, N12, B86BPBE, and OLYP DFAs. We note that in general, the La-containing subset is more challenging than the overall set, as in most cases the median of the deviations in the larger set (navy) is well below the first quartile of the La-containing subset. The exceptions to this behaviour are the two DFAs developed especially for solids: PBEsol and WC, which are the best performers for the La-containing subset. The N12 and PBE DFAs also show good performance for the La-containing subset, coming in 3rd and 4th place, while also yielding consistent results for the full dataset. Therefore, the methods chosen for determination of +U corrections (see Fig. 1) are WC, PBEsol, N12 and PBE. On the other hand, the worst performer is BLYP – in fact, only 13 out of the 17 diatomics could be optimised with this DFA.

Fig. 2 Absolute deviations of r_e calculated with DFAs w.r.t. CCSD(T) reference values⁵⁵ plotted as a box plot (whiskers span 0th to 100th percentile, box spans 1st to 3rd quartile) for a set of 17 lanthanide diatomics (blue). Results for the La-subset containing 5 diatomics are shown in orange. The medians are denoted by vertical lines in navy and red, respectively.

While DFAs and their implementations in computational codes are often benchmarked extensively,³⁶ this is not often the case for the basis sets and core electron representations used in solid-state calculations (pseudopotentials, projector-augmented waves, etc.).³⁷ For completeness, the effect of pseudopotentials and their (lack of) parametrisation for the corresponding DFAs on the above results is evaluated by comparing the results of five of the well-performing DFAs (PBE, N12, OLYP, WC, and PBEsol), with results from calculations using the PBEsol parametrisation, both using the SSSP Efficiency library (version 1.1), as well as to the set of optimised norm-conserving Vanderbilt pseudopotentials from the SG15 ONCV library (version 1.2, archive dated Feb. 2020).⁵⁷ While norm-conserving pseudopotentials generally require higher cutoff values than their ultrasoft counterparts, the benchmarks performed as part of the SSSP project³⁶ show the properties of Mn, which is the hardest of the studied elements, are well-converged with the SG15 ONCV pseudopotential above 60 eV for the wavefunction cutoff. Note that this is below the 65 eV cutoff suggested by the SSSP Efficiency library for the ultrasoft GBRV pseudopotential for Mn.⁵⁸ The difference in results (see Table S1, ESI†) between the two parametrisations of SSSP Efficiency (PBE vs. PBEsol) is negligible, below 1 mÅ in the RMSD of r_e in all five cases. We can therefore conclude that the effect of any DFA-related “mis-parametrisation” of the pseudopotentials on their performance in bond lengths is marginal. However, comparison between the SSSP Efficiency and the SG15 ONCV libraries shows the choice of an appropriate pseudopotential library is crucial, as the RMSDs of r_e for the La-containing diatomics obtained with the SG15 ONCV library are at least double that of the SSSP Efficiency library, if not higher.

Finally, we discuss the effect of dispersion corrections. The results, obtained with the projector-augmented wave pseudopotentials from the PSlibrary (version 0.3.1) are shown in Fig. 3. Neither XDM (α₁ = 0.3275, α₂ = 2.7673)^38,39 nor the D3(BJ) dispersion correction (a₁ = 0.4289, s₈ = 0.7875, a₂ = 4.4407)^38,59,60 can systematically improve on the results of the PBE DFA for this dataset.

Fig. 3 Effect of dispersion correction on the distribution of absolute deviations from reference r_e. Colours are as in Fig. 2.

4.2 Lattice constants of lanthanide manganites

In the second step of our computational workflow, we compare the computed crystal structures of the five lanthanide perovskites against experimental crystal structures obtained from room temperature diffraction studies of LaMnO₃ from ref. 7, PrMnO₃ from ref. 8, SmMnO₃ from ref. 12, EuMnO₃ from ref. 9, and YbMnO₃ from ref. 10. Note that the use of low-temperature data, where available,^10,12,61 does not significantly affect the results below. The combined cell and geometry relaxations are started from the orthorhombic unit cells as calculated by mash, using the BFGS algorithm with 1 atm cell pressure as the convergence threshold, while restricting the cell to maintain an orthorhombic shape. All calculations are performed using spin-unrestricted DFT with the wavefunction and density cut-offs of 65 Ry and 780 Ry, respectively. A Γ-centered, 3 × 4 × 3 Monkhorst-Pack k-point grid was used. As the effects of DFA-related parametrisation of the pseudopotentials on the bond lengths were shown above to be negligible, the PBE parametrisation of the SSSP Efficiency pseudopotential library (version 1.1) has been used with each DFA in this work. If multiple candidate structures are generated by mash for a single perovskite, the successfully optimised supercell with the lowest deviation in the figure of merit is used for comparison.

There are several ways of comparing crystal structures quantitatively. Three methods are implemented in the program critic2,^62,63 including approaches based on the radial distribution functions (RDF), and powder diffraction patterns (POWDER). With both of these methods, a dissimilarity score of 0 corresponds to an identical structure. The results obtained when using the POWDER method are shown in Fig. 4. When considering the overall dataset (blue), three DFAs (WC, PBEsol, N12) of the best-performing set in the diatomics benchmark perform rather poorly, barely improving on the mash-generated starting structures. For these three DFAs, the most challenging structure is the SmMnO₃ perovskite (POWDER score >0.72), which is predicted by mash rather well (POWDER score ∼0.15). For LaMnO₃ (orange), only the PW86PBE DFA shows an improvement over mash – it is also the best-performing DFA for the whole set. On the other hand, when we use the RDF method in critic2 (see Fig. S2, ESI†), the DFAs are grouped much closer together with no clear best performer. With the exception of BLYP, all other DFAs significantly improve over the starting structures generated with mash, approximately halving the dissimilarity score. This qualitative disagreement between the two methods for comparison of crystal structures in critic2 is puzzling, as both metrics should include the effects of lattice constants as well as the atomic positions within the lattice.

Fig. 4 Dissimilarity scores calculated with the POWDER method in critic2 using computed and experimental crystal structures of lanthanide perovskites. Values obtained for the initial structures generated by mash included for comparison. Average score for a set of five perovskites shown in blue, standard deviation of the set indicated using error bars, and the score for the LaMnO₃ perovskite shown in orange.

Given the issues identified with the above approach, we resorted to a simpler figure of merit, i.e. the relative RMSD of the computed lattice constants from the experimental reference values. The resulting relative signed deviations of computed lattice constants are shown as violin plots in Fig. 5. The relative RMSDs are shown as blue dots for the whole dataset and orange dots for LaMnO₃, respectively. The relative RMSDs for the five perovskites are significant, and even in the best cases are still above 3% of the lattice constant. From the change in the shape and narrower width of the violin plots, we can see that the structures generated by mash are generally improved by optimisation using a DFA. However, in the particular case of LaMnO₃, this optimisation may actually lead to a higher RMSD than that obtained with the guess generated by mash. Critically, three of the DFAs that performed well for La-containing diatomics (WC, PBEsol, and N12, cf.Fig. 2) perform rather poorly here, both for the whole dataset and for LaMnO₃. This is particularly surprising for the WC and PBEsol DFAs, which were designed for use in solid state applications. The performance of a DFA in predicting the gas-phase bond lengths of lanthanide diatomics is therefore a rather poor predictor of performance in determining the lattice constants of lanthanide perovskites. For the overall dataset, there is no clear best performer, with several DFAs yielding a relative RMSD of ∼3%. For LaMnO₃, the only DFAs able to outperform mash with a relative RMSD below 1.9%, are OLYP and HCTH120.

Fig. 5 Violin plot of relative signed deviations of computed lattice constants of lanthanide perovskites from experimental reference values. The deviations of lattice constants obtained with mash are included for comparison. Relative RMSDs for the set of five perovskites shown as blue dots, and the relative RMSDs for the LaMnO₃ perovskite shown as orange dots.

The effect of +U correction on the performance of selected DFAs is shown in Fig. 6. The four DFAs for which the +U correction has been determined have been chosen based on their performance for diatomics, which, as we now know, may not have been the best criterion. Based on the results in Fig. 6, the +U correction determined using linear response theory can systematically reduce the overprediction in lattice constants of lanthanide perovskites, with the violin plots becoming much more symmetric around zero. In fact, for the whole dataset, N12+U and WC+U are the two best performing methods from those studied, with relative RMSD of 2.4% and 2.7%, respectively. Finally, as shown in Fig. S3 (ESI†) neither the XDM dispersion correction (evaluated with several of the studied DFAs) nor the D3(BJ) dispersion correction (evaluated with PBE DFA) provides a systematic improvement in the performance of the uncorrected functionals. In most cases, the dispersion corrections shift the violin plots of the signed deviations to higher values.

Fig. 6 Violin plot comparing the performance of DFAs with +U corrections in predicting lattice constants of lanthanide perovskites. Colours are as in Fig. 5. The results for DFAs with +U shown in cyan for clarity.

4.3 Defect-induced phase transition in LaMnO₃

Finally, we use the above lattice constant benchmarks to select methods for prediction of the defect-induced phase transition between orthorhombic (Pnma) and rhombohedral (R3c) LaMnO₃. This case study requires a reasonable performance in predicting geometries. However, a good prediction of relative energies of the Pnma and R3c supercells is required for quantitative agreement with experimental data. Note that unlike in some theoretical studies of perovskite phase transitions, where the effects of bulk pressure are investigated,^64,65 here we focus on predicting the phase transition caused by defects in the structure of the perovskite. For this case study, we shortlisted the DFAs OLYP and HCTH120, as they were the best performers for LaMnO₃ lattice constants, as well as N12+U, which was the best performer in the overall lattice parameter benchmarks. Finally, we have also included PBE+U, to allow comparison between a “non-empirical” DFA (PBE) and a systematically optimised DFA (N12).

To compare our results with experimental data, we turn to the investigation of Wold and Arnott, who prepared a series of lanthanum manganites with Mn^IV+ fractions between 0.02 and 30%, and determined their phase transition temperatures.¹³ We note that a non-zero fraction of Mn^IV+ in a pure La–Mn–O system can be caused by both A-site defects (La_1−xMn^III_1−3xMn^IV_3xO₃) as well as B-site defects in isolation (LaMn^III_1−4xMn^IV_3xO₃), or a combination of the two, leading to excess O in the structure (e.g. LaMn^III_1−2xMn^IV_2xO_3+x). The experimental trend (black, Fig. 7), obtained for defective perovskites of the latter (LaMnO_3+x) type, shows two regimes: a non-linear section below 21% Mn^IV+, and a linear trend above this percentage.¹³ The non-linear section is attributed to the destruction of the long-range bond-ordering effect in orthorombic manganites⁶⁶ caused by an unequal occupation of the e_g orbitals in Mn^III+ (d_z² occupied, d_x²−y² empty). The bond-ordering effect is increasingly disrupted as a function of increasing Mn^IV+, causing the non-linearity and an abrupt change in the overall behaviour. The linear section above 21% Mn^IV+ is caused by the decreased size of Mn^IV+ compared to Mn^III+, allowing an easier reorganisation into the denser R3c structure. A linear regression of the transition temperatures in highly-defective structures¹³ predicts the R3c to be more stable than Pnma at T = 0 K when the fraction of Mn^IV+ sites reaches 43.7(7)%.

Fig. 7 Difference in the energies of the defective rhombohedral (R3c) and orthogonal (Pnma) supercells, per mole of Mn, as a function of Mn^IV+ sites. Results calculated using single-point energies, with OLYP (orange), HCTH120 (green), N12+U (red), and PBE+U (blue). Experimental data, adapted from ref. 13, shown in black.

The first analysis of the performance of the DFAs is undertaken using defective supercells derived from the geometry of the relaxed stoichiometric LaMnO₃ supercell. The appropriate Pnma and R3c supercells are optimised (cell and geometry) with each DFA, with convergence criteria of dE < 1 μRy, F < 10 μRy a₀⁻¹ and cell pressure <1 bar. The orthorhombic unit cells were constrained to Pnma symmetry with the lattice parameters a, b, c relaxed. The rhombohedral unit cells were constrained to monoclinic symmetry (a 2 × 4 × 1 supercell generated from the La₆Mn₆O₁₈ rhombohedral unit cell is not rhombohedral anymore, as b = 2 × a) with the lattice parameters a, b, c as well as the angle γ = ∠ab relaxed. Then, the defective supercells are created by removing the A-site positions using the supercell lattices generated using ase (shown in Table 2). Finally, single-point energy calculations of each of the defective supercells is performed with the corresponding DFAs. All of these calculations were spin-unrestricted, with a single k-point at the Γ point, and with a 65 Ry and 780 Ry cutoff for the wavefunction and density, respectively.

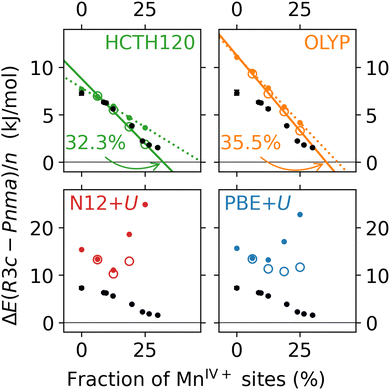
The results obtained from single point calculations are shown in Fig. 7, with the difference in the single point energies of the structures ΔE(R3c−Pnma) normalised by the number of Mn atoms in the supercell (n = 48). As expected, all four DFAs predict the correct stability ordering in the stoichiometric case, where the Pnma phase is the energetically favoured one. For the OLYP (orange) and HCTH120 (green) methods, the Pnma → R3c transition point can be determined by linear regression of the data followed by extrapolation. The linear regressions are reasonable with R² > 0.99 in both cases, and the transition points obtained (39.9% and 47.5%, respectively) are in a good agreement with the result obtained by extrapolating the experimental data (43.7(7)%). However, the qualitative behaviour of the two DFAs is a little different, as OLYP overstabilises the Pnma phase compared to HCTH120 and experiment.

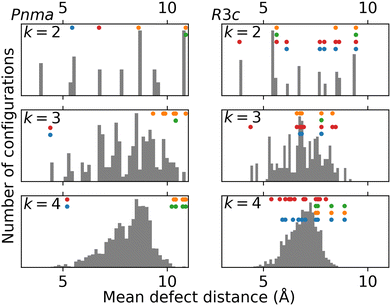
The situation is very different with both GGA+U methods. First, the convergence of the self-consistent cycle with both GGA+U methods is very slow for some of the defective structures, in several cases requiring more than 100 iterations and often requiring adjustment of the mixing parameters. Second, the stability trend obtained is clearly non-linear, with the highly defective Pnma structures calculated to be significantly more stable than their R3c counterparts. This can be partially explained by looking at the mean defect distances in the lowest-energy Pnma structures, shown in the left panel of Fig. 8. Both OLYP and HCTH120 clearly prefer to maximise the separation between La defects. With PBE+U and N12+U, an in-plane arrangement of defects is preferred, leading to a smaller, but not necessarily minimal mean defect distance in the lowest energy structures. The structures preferred by the +U methods therefore offer further qualitative support for the presence of the long-range bond-ordering effect below 21% Mn^IV+.⁶⁶ The differences between the +U results and the other two DFAs are likely a consequence of the self-interaction error in OLYP and HCTH120, leading to an overly delocalised electronic structure. The +U correction reduces the self-interaction error, and localises the defective state. For the R3c structures (see right panel of Fig. 8), no such trend is observed, and the mean defect distance does not seem to be a good predictor of stability. In fact, several defective supercell lattices are consistently predicted to be among the minimum structures, regardless of the DFA used. In conclusion, none of the four DFAs fully capture the phase transition behaviour. While reasonable agreement with the experimental Pnma → R3c transition point is obtained using OLYP and HCTH120, the experimentally observed non-linearity is not reproduced. By contrast, the long-range bond-ordering effect can be observed with GGA+U methods, which, however, do not seem to predict a phase transition at all.

Fig. 8 Comparison of the mean defect distances in the orthorhombic (Pnma) and rhombohedral (R3c) defective supercell lattices with the number of A-site defects, k ∈ {2,3,4}. The lowest energy structures (up to 5 kJ mol⁻¹ above the minimum energy structure) obtained with PBE+U (blue), N12+U (red), OLYP (orange), and HCTH120 (green) are indicated by dots.

One reason for the poor agreement of our calculations with experimental data may be due to our comparison of total energies obtained from calculations (E ∼ U(0 K)) with free energies obtained from the experimental data. A computational determination of Gibbs free energies (G = H − TS), which ought to be directly comparable to the experimental data, would require the calculation of the cell pressure and volume (pV) for each defective lattice, obtaining the enthalpy (H = U + pV); and, more importantly, the calculation of thermochemical corrections for each defective lattice, which would then allow us to calculate the canonical partition function (Q) and therefore the entropy (S) for both the R3c and Pnma structures. Both steps would require a significant further computational expense. However, if we assume the pV term is approximately constant between a R3c structure and a Pnma structure with the same number of defects, it will cancel out, and we can use the Helmholtz free energy (A = U − TS). We cannot account for vibrational effects without further calculations, involving cell relaxation and determination of the phonons, which would be expensive for such large supercells. However, we can account for the energy lowering effect that any other structures, with total energy E_i = E₀ + ΔE_i, lying near the structure with the lowest total energy E₀, have on the internal energy U at a finite temperature T. We can also determine the entropy term S arising due to the degeneracy w_i of each of these structures (see Table 2). For this, we use the following equations,

where β is the Boltzmann factor 1/k_BT and k_B is the Boltzmann constant. Note that E₀ is determined for each cell symmetry and number of defects separately. We can then evaluate the difference in the Helmholtz free energies of the two cell symmetries, ΔA(R3c − Pnma)/n, at a finite temperature, with results at 1000 K shown in Fig. S4 (ESI†) (circles). By comparing to the total energies (ΔE(R3c − Pnma)/n, shown as dots), we can see the magnitude of the effect is rather small, but increases as a function of the number of defects, and may become appreciable at >30% Mn^IV+. However, the sign of the correction is different for PBE+U (blue) when compared to HCTH120 (green), which we again attribute to the preference of PBE+U for an ordered in-plane arrangement of defects, which leads to a smaller entropy in the orthorhombic case, and therefore S(R3c − Pnma) > 0.

Another reason for the poor performance of the DFAs in the above analysis may be due to the use of single point calculations, with only the stoichiometric Pnma and R3c supercell relaxed. In light of the computational workflow introduced in the Introduction, we investigate the effect the relaxation of the atoms and the cell on the predicted phase transition behaviour. For this purpose, we relax a subset of the defective supercells with total energies within 5 kJ mol⁻¹ of the lowest single-point energy, for each combination of supercell geometry, DFA, and number of defects. The number of relaxed supercells is shown in Table 3. As above, the Pnma supercells were constrained to an orthorhombic geometry (a, b, c relaxed), while the R3c supercells were constrained to a monoclinic shape (a, b, c, γ relaxed). All of these relaxations were spin-unrestricted, with a single k-point at the Γ point, using convergence criteria of dE < 1 μRy, F < 10 μRy a₀⁻¹ and cell pressure <1 bar, and with a 65 Ry and 780 Ry cutoff for the wavefunction and density, respectively.

Table 3 Number of relaxed defective supercell lattices, where k is the number of A-site defects

DFA	Pnma				R3c
	k = 1	2	3	4	1	2	3	4
OLYP	1	1	6	4	1	3	1	3
HCTH120	1	3	5	9	1	2	1	4
PBE+U	1	1	2	1	1	3	4	4
N12+U	1	1	2	1	1	3	4	3

---

The results are shown in Fig. 9. In all cases, the relaxation of the structures leads to a smaller energy difference between the R3c and Pnma cells, shifting any predicted phase transition to a lower fraction of Mn^IV+ sites. This is most likely due to the additional relaxation of the R3c supercells, when compared to the Pnma supercells, as shown in Fig. S5 (ESI†). As in the single-point energy results, a linear regression of the HCTH120 and OLYP results fits all four datapoints with R² > 0.99. The relative discrepancy between the predicted transition points obtained with the two GGA methods shrinks to about 10%. Notably, the results of HCTH120 calculations (green) are in an excellent quantitative agreement with the experimental data, especially when also considering the results for the stoichiometric supercell (which is also relaxed): out of the four methods studied, it is the only method which reproduces the non-linearity in the experimental data at lower fractions of Mn^IV+ sites. However, this agreement may be coincidental, given that HCTH120 does not stabilise the in-plane ordering of vacancies in the orthorhombic structures (no long-range bond-ordering effects). The behaviour of the GGA+U methods is again different from the former two DFAs. Both methods still fail to predict the Pnma → R3c phase transition. The trends shown in Fig. S5 (ESI†) show that while the relaxation energy increases almost linearly with the number of Mn^IV+ defects in the R3c structure, it plateaus at around −0.4 Ry in the Pnma structure. While little is known about the behaviour of the N12 DFA in solids, the uncorrected PBE as well as PBE+U DFAs are known to over-bind (see also the shape of the violin plots in Fig. 6). It may well be that in this case PBE+U over-stabilises the orthorhombic cells. One remedy may be the use of a dispersion-corrected GGA+U, such as PBE+U+XDM, which has been reported to improve upon PBE+U for cell volumes and formation enthalpies of uranium compounds.⁶⁷ To conclude, in order to obtain agreement with the experimental data, it is crucial to allow the defective supercells to relax from the parent stoichiometric geometry. Quantitiative agreement with experiment is in this case obtained with HCTH120. However, it might be the case of “the right answer for the wrong reasons”, as the qualitative behaviour related to the electronic structure of the system is not captured. Conversely, with PBE+U and N12+U, the electronic structure trends are partially captured, but the results are not accurate for quantitative use.

Fig. 9 Effect of cell and geometry optimisations (circles) on the difference in rhombohedral (R3c) and orthogonal (Pnma) supercell energies as a function of Mn^IV+ sites. Single point energy results (dots) included for comparison. Colours as in Fig. 7.

We could identify several reasons for the apparent failure to predict the experimentally observed phase transition behaviour. First, it might be necessary to keep the R3c defective structures constrained to a rhombohedral shape (a = b, γ = 120°), in order to avoid over-relaxation; this can be achieved by doubling the supercell size with a nominal doubling of the computational cost. Second, method selection has been based on performance for lattice constants of orthorhombic cells, without considering the apparently more important rhombohedral case, or their relative energies; the key challenge here is gathering enough benchmark-quality lattice parameters of the relevant phases, as the increased computational cost of the benchmark itself would be marginal. Third, thermochemical corrections and zero-point energies are not considered in the current study; including the calculation of numerical second derivatives as a routine step of the workflow would, with the current supercell size (∼330 atoms), be extremely costly; the zero-point effects might, however, be approximated using a smaller supercell. Fourth, the transition point should ideally not be extrapolated, but interpolated from calculated data; as already noted above, an increase in k from 4 to 5 increases the number of combinations more than 8-fold, so adding an additional 5th or 6th defect would require strategies for identification of the lowest-energy structure candidates by methods other than direct comparison. Fifth, Mn^IV+ sites might be also created by B-site defects or O-site non-stoichiometry in the perovskite. Finally, a more robust analysis might be possible if the phase transitions of more than one system is considered, to avoid bias from experimental data.

5 Conclusions

In this work, we proposed a computational workflow compatible with the investigation of novel materials, for which crystal structures may not be available. We have introduced the program mash, capable of predicting candidate structures for cubic, orthorhombic, and rhombohedral perovskites, which can then be used as a starting point for further work. Based on both the POWDER score using critic2^62,63 and direct lattice constant comparisons with experimental data, the performance of mash is remarkable, in some cases better than that obtained with subsequent geometry optimisation using DFT.

We have also evaluated whether the standard computational approach to method selection based on benchmarking using a simple system leads to a good performance for a related, more complex system. Good performance of a method for predicting equilibrium geometries of diatomic lanthanide molecules does not correspond to a good performance in predicting lattice constants of lanthanide perovskites. It may be that the systems chosen here are simply too different (extended vs. isolated) even when the same property (geometries) is being evaluated.

The best performing DFAs in this work for predicting the lattice constants of orthorhombic lanthanum-containing perovskites are HCTH120 and OLYP. For lanthanide perovskites in general, the best performance is surprisingly obtained by N12+U. Additionally, all GGA+U results improve upon the performance of the base functional, confirming that the linear response framework^47,48 for determining +U corrections is robust, provided that an appropriate projection of the Hubbard manifold is used.⁴⁹ The use of dispersion corrections with the DFAs studied does not lead to a systematic improvement in the predicted lattice constants of the bulk systems studied; we note that dispersion effects may be crucial when comparing total energies.

We have evaluated whether the above three DFAs can be used to predict a more complex observable, such as the phase transition in defective LaMnO₃ as function of the fraction of Mn^IV+ sites. The results are encouraging, especially with HCTH120, which was predicted to perform well based on our benchmarks. We highlight the importance of cell relaxation in such studies. However, while numerical agreement with the experimental data¹³ could be obtained using HCTH120, some qualitative aspects related to the electronic structure, including the description of long-range bond-ordering effects stabilising in-plane orientation of defects,⁶⁶ was not achieved. On the other hand, GGA+U methods are able to capture at least some of these qualitative aspects.

Finally, we provide several pointers for further work in this area. More targeted and thorough benchmarking is necessary for method selection in extended systems, in analogy with the recent transformative work in molecular systems (see e.g. ref. 68 and 69). The use of screening methods faster than DFT is necessary to filter through the combinatorial space in defective supercells, thus allow focusing computational time on a smaller set of more challenging calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

PK thanks the Forrest Research Foundation for funding. JDG thanks the Australian Research Council for funding. This work was supported by resources provided by the Pawsey Supercomputing Centre (project f97) and the National Computational Infrastructure (project f97), with funding from the Australian Government and the Government of Western Australia.

Notes and references

1. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Report on the Sixth Blind Test of Organic Crystal Structure Prediction Methods, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459,  DOI:10.1107/S2052520616007447.
2. C. Cazorla and T. Gould, Polymorphism of Bulk Boron Nitride, Sci. Adv., 2019, 5, eaau5832,  DOI:10.1126/sciadv.aau5832.
3. K. T. Williams, L. K. Wagner, C. Cazorla and T. Gould, Combining Density Functional Theories to Correctly Describe the Energy, Lattice Structure and Electronic Density of Functional Oxide Perovskites, 2020.
4. S. M. Woodley, P. D. Battle, C. R. A. Catlow and J. D. Gale, Development of a New Interatomic Potential for the Modeling of Ligand Field Effects, J. Phys. Chem. B, 2001, 105, 6824–6830,  DOI:10.1021/jp010742u.
5. G. Koch, M. Hävecker, D. Teschner, S. J. Carey, Y. Wang, P. Kube, W. Hetaba, T. Lunkenbein, G. Auffermann, O. Timpe, F. Rosowski, R. Schlögl and A. Trunschke, Surface Conditions That Constrain Alkane Oxidation on Perovskites, ACS Catal., 2020, 10, 7007–7020,  DOI:10.1021/acscatal.0c01289.
6. P. Kraus, E. H. Wolf, C. Prinz, G. Bellini, A. Trunschke and R. Schlögl, Towards Automation of Operando Experiments: A Case Study in Contactless Conductivity Measurements, Digital Discovery, 2022, 1, 241–254,  10.1039/D1DD00029B.
7. J. Rodríguez-Carvajal, M. Hennion, F. Moussa, A. H. Moudden, L. Pinsard and A. Revcolevschi, Neutron-Diffraction Study of the Jahn-Teller Transition in Stoichiometric LaMnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R3189–R3192,  DOI:10.1103/PhysRevB.57.R3189.
8. D. Sánchez, J. A. Alonso and M. J. Martínez-Lope, Neutron-Diffraction Study of the Jahn–Teller Transition in PrMnO₃, J. Chem. Soc., Dalton Trans., 2002, 4422–4425,  10.1039/B208660N.
9. T. Mori, N. Kamegashira, K. Aoki, T. Shishido and T. Fukuda, Crystal Growth and Crystal Structures of the LnMnO₃ Perovskites: Ln = Nd, Sm, Eu and Gd, Mater. Lett., 2002, 54, 238–243,  DOI:10.1016/S0167-577X(01)00569-9.
10. Y. H. Huang, H. Fjellvåg, M. Karppinen, B. C. Hauback, H. Yamauchi and J. B. Goodenough, Crystal and Magnetic Structure of the Orthorhombic Perovskite YbMnO₃, Chem. Mater., 2006, 18, 2130–2134,  DOI:10.1021/cm052758t.
11. H. Okamoto, N. Imamura, B. Hauback, M. Karppinen, H. Yamauchi and H. Fjellvåg, Neutron Powder Diffraction Study of Crystal and Magnetic Structures of Orthorhombic LuMnO₃, Solid State Commun., 2008, 146, 152–156,  DOI:10.1016/j.ssc.2008.01.036.
12. H. Maeda, Y. Ishiguro, T. Honda, J.-S. Jung, S. Michimura, T. Inami, T. Kimura and Y. Wakabayashi, Structural Investigation of Magnetocapacitive SmMnO₃, J. Ceram. Soc. Jpn., 2013, 121, 265–267,  DOI:10.2109/jcersj2.121.265.
13. A. Wold and R. J. Arnott, Preparation and Crystallographic Properties of the Systems LaMn_1−xMn_xO_3+λ and LaMn_1−xNi_xO₃+λJA-1106, J. Phys. Chem. Solids, 1959, 9, 176–180,  DOI:10.1016/0022-3697(59)90207-0.
14. A. L. Gavin and G. W. Watson, Modelling the Electronic Structure of Orthorhombic LaMnO₃, Solid State Ionics, 2017, 299, 13–17,  DOI:10.1016/j.ssi.2016.10.007.
15. A. L. Gavin and G. W. Watson, Modelling Oxygen Defects in Orthorhombic LaMnO₃ and Its Low Index Surfaces, Phys. Chem. Chem. Phys., 2017, 19, 24636–24646,  10.1039/C7CP02905E.
16. A. L. Gavin and G. W. Watson, Defects in Orthorhombic LaMnO₃ – Ionic versus Electronic Compensation, Phys. Chem. Chem. Phys., 2018, 20, 19257–19267,  10.1039/C8CP02763C.
17. E. A. Kotomin, R. A. Evarestov, Yu. A. Mastrikov and J. Maier, DFT Plane Wave Calculations of the Atomic and Electronic Structure of LaMnO₃(001) Surface, Phys. Chem. Chem. Phys., 2005, 7, 2346,  10.1039/b503272e.
18. Y. A. Mantz, New LaMnO₃ Surface Energy Results Obtained from Density-Functional Theory, Surf. Sci., 2020, 695, 121500,  DOI:10.1016/j.susc.2019.121500.
19. Y. Zhou, Z. Lü, B. Wei, Z. Wang and X. Zhu, Electronic Structure and Surface Properties of PrMnO₃(001): A Density Functional Theory Study, Solid State Commun., 2015, 201, 31–35,  DOI:10.1016/j.ssc.2014.10.005.
20. S. K. Mishra, M. K. Gupta, R. Mittal, A. I. Kolesnikov and S. L. Chaplot, Spin-Phonon Coupling and High-Pressure Phase Transitions of R MnO₃ (R = Ca and Pr): An Inelastic Neutron Scattering and First-Principles Study, Phys. Rev. B, 2016, 93, 214306,  DOI:10.1103/PhysRevB.93.214306.
21. W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, Cation Size Mismatch and Charge Interactions Drive Dopant Segregation at the Surfaces of Manganite Perovskites, J. Am. Chem. Soc., 2013, 135, 7909–7925,  DOI:10.1021/ja3125349.
22. S. Yao, P. Yoo and P. Liao, A Computational Study of Hydrogen Doping Induced Metal-to-Insulator Transition in CaFeO₃, SrFeO₃, BaFeO₃ and SmMnO₃, Phys. Chem. Chem. Phys., 2019, 21, 25397–25405,  10.1039/C9CP04669K.
23. Z. Chen, X. Liu, K. Cho, R. Chen and B. Shan, Density Functional Theory Study of the Oxygen Chemistry and NO Oxidation Mechanism on Low-Index Surfaces of SmMn₂O₅ Mullite, ACS Catal., 2015, 5, 4913–4926,  DOI:10.1021/acscatal.5b00249.
24. J. Ding, G. Li, X. Wu, D. Weng, Z. Yang and R. Ran, Palladium Promoted SmMn₂O₅ Catalyst with Highly Efficient Oxygen Species for Methane Combustion, 2021 DOI:10.2139/ssrn.3962014.
25. L. Xu, Q. Liu, J. Meng, W. Liao, X. Liu and H. Zhang, Eu–Mn Charge Transfer and the Strong Charge– Spin– Electronic Coupling Behavior in EuMnO₃, Inorg. Chem., 2021, 60, 1367–1379,  DOI:10.1021/acs.inorgchem.0c02498.
26. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406,  DOI:10.1103/PhysRevLett.100.136406.
27. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687,  DOI:10.1103/PhysRevB.46.6671.
28. J. Hubbard, Electron Correlations in Narrow Energy Bands, Proc. R. Soc. A, 1963, 276, 237–257,  DOI:10.1098/rspa.1963.0204.
29. The Hubbard Model at Half a Century, Nat. Phys., 2013, 9, 523 DOI:10.1038/nphys2759.
30. S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami and N. K. Allam, in Density Functional Calculations - Recent Progresses of Theory and Application, ed. G. Yang, InTech, 2018 DOI:10.5772/intechopen.72020.
31. P. García-Fernández, S. Ghosh, N. J. English and J. A. Aramburu, Benchmark Study for the Application of Density Functional Theory to the Prediction of Octahedral Tilting in Perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 144107,  DOI:10.1103/PhysRevB.86.144107.
32. C. Franchini, Hybrid Functionals Applied to Perovskites, J. Phys.: Condens. Matter, 2014, 26, 253202,  DOI:10.1088/0953-8984/26/25/253202.
33. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502,  DOI:10.1088/0953-8984/21/39/395502.
34. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., Advanced Capabilities for Materials Modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901.
35. S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, Recent Developments in Libxc—A Comprehensive Library of Functionals for Density Functional Theory, SoftwareX, 2018, 7, 1–5,  DOI:10.1016/j.softx.2017.11.002.
36. K. Lejaeghere, G. Bihlmayer, T. Bjorkman, P. Blaha, S. Blugel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Duak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Granas, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Kucukbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordstrom, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunstrom, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Reproducibility in Density Functional Theory Calculations of Solids, Science, 2016, 351, aad3000,  DOI:10.1126/science.aad3000.
37. G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, Precision and Efficiency in Solid-State Pseudopotential Calculations, npj Comput. Mater., 2018, 4, 72,  DOI:10.1038/s41524-018-0127-2.
38. A. D. Becke and E. R. Johnson, A Unified Density-Functional Treatment of Dynamical, Nondynamical, and Dispersion Correlations, J. Chem. Phys., 2007, 127, 124108,  DOI:10.1063/1.2768530.
39. A. D. Becke and E. R. Johnson, Exchange-Hole Dipole Moment and the Dispersion Interaction Revisited, J. Chem. Phys., 2007, 127, 154108,  DOI:10.1063/1.2795701.
40. A. Dal Corso, Pseudopotentials Periodic Table: From H to Pu, Comput. Mater. Sci., 2014, 95, 337–350,  DOI:10.1016/j.commatsci.2014.07.043.
41. P. Kraus, Mash: A Program for Generating Guess Structures of ABX₃ Perovskites, 2020 DOI:10.5281/zenodo.7492808.
42. M. W. Lufaso and P. M. Woodward, Prediction of the Crystal Structures of Perovskites Using the Software Program SPuDS, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725–738,  DOI:10.1107/S0108768101015282.
43. L. Mentel, Mendeleev - A Python Package with Properties of Chemical Elements, Ions, Isotopes and Methods to Manipulate and Visualize Periodic Table, 2021,  DOI:10.5281/zenodo.5233824.
44. V. M. Goldschmidt, Die Gesetze der Krystallochemie, Die Naturwissenschaften, 1926, 14, 477–485,  DOI:10.1007/BF01507527.
45. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New Tolerance Factor to Predict the Stability of Perovskite Oxides and Halides, Sci. Adv., 2019, 5, eaav0693,  DOI:10.1126/sciadv.aav0693.
46. M. O'Keeffe and B. G. Hyde, Some Structures Topologically Related to Cubic Perovskite (E2₁), ReO₃ (D0₉) and Cu₃Au (L1₂), Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3802–3813,  DOI:10.1107/S0567740877012114.
47. M. Cococcioni and S. de Gironcoli, Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA+U Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105,  DOI:10.1103/PhysRevB.71.035105.
48. H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach, Phys. Rev. Lett., 2006, 97, 103001,  DOI:10.1103/PhysRevLett.97.103001.
49. N. E. Kirchner-Hall, W. Zhao, Y. Xiong, I. Timrov and I. Dabo, Extensive Benchmarking of DFT+U Calculations for Predicting Band Gaps, Appl. Sci., 2021, 11, 2395,  DOI:10.3390/app11052395.
50. C. E. Calderon, J. J. Plata, C. Toher, C. Oses, O. Levy, M. Fornari, A. Natan, M. J. Mehl, G. Hart, M. Buongiorno Nardelli and S. Curtarolo, The AFLOW Standard for High-Throughput Materials Science Calculations, Comput. Mater. Sci., 2015, 108, 233–238,  DOI:10.1016/j.commatsci.2015.07.019.
51. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The Atomic Simulation Environment—a Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29, 273002,  DOI:10.1088/1361-648X/aa680e.
52. P. Morgante and R. Peverati, The Devil in the Details: A Tutorial Review on Some Undervalued Aspects of Density Functional Theory Calculations, Int. J. Quantum Chem., 2020, 120, e26332,  DOI:10.1002/qua.26332.
53. D. Rappoport, N. R. M. Crawford, F. Furche and K. Burke, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, R. H. Crabtree, C. M. Lukehart, D. A. Atwood and R. A. Scott, John Wiley & Sons, Ltd, Chichester, UK, 2009, p. ia615 DOI:10.1002/0470862106.ia615.
54. G. A. McCarver, R. J. Hinde and K. D. Vogiatzis, Selecting Quantum-Chemical Methods for Lanthanide-Containing Molecules: A Balance between Accuracy and Efficiency, Inorg. Chem., 2020, 59, 10492–10500,  DOI:10.1021/acs.inorgchem.0c00808.
55. V. G. Solomonik and A. N. Smirnov, Toward Chemical Accuracy in Ab Initio Thermochemistry and Spectroscopy of Lanthanide Compounds: Assessing Core–Valence Correlation, Second-Order Spin–Orbit Coupling, and Higher Order Effects in Lanthanide Diatomics, J. Chem. Theory Comput., 2017, 13, 5240–5254,  DOI:10.1021/acs.jctc.7b00408.
56. G. Makov and M. C. Payne, Periodic Boundary Conditions in Ab Initio Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022,  DOI:10.1103/PhysRevB.51.4014.
57. D. R. Hamann, Optimized Norm-Conserving Vanderbilt Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117,  DOI:10.1103/PhysRevB.88.085117.
58. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Pseudopotentials for High-Throughput DFT Calculations, Comput. Mater. Sci., 2014, 81, 446–452,  DOI:10.1016/j.commatsci.2013.08.053.
59. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104,  DOI:10.1063/1.3382344.
60. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465,  DOI:10.1002/jcc.21759.
61. J. B. A. A. Elemans, B. van Laar, K. R. van der Veen and B. O. Loopstra, The Crystallographic and Magnetic Structures of La_1−xBa_xMn_1−xMe_xO₃ (Me = Mn or Ti), J. Solid State Chem., 1971, 3, 238–242,  DOI:10.1016/0022-4596(71)90034-X.
62. A. Otero-de-la-Roza, M. Blanco, A. M. Pendás and V. Luaña, Critic: A New Program for the Topological Analysis of Solid-State Electron Densities, Comput. Phys. Commun., 2009, 180, 157–166,  DOI:10.1016/j.cpc.2008.07.018.
63. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Critic2: A Program for Real-Space Analysis of Quantum Chemical Interactions in Solids, Comput. Phys. Commun., 2014, 185, 1007–1018,  DOI:10.1016/j.cpc.2013.10.026.
64. Q. Li, Z. He and Q. Cao, Theoretical Study of the R3c-to-Pnma Phase Transition in BiAlO₃, Comput. Mater. Sci., 2018, 152, 211–216,  DOI:10.1016/j.commatsci.2018.05.053.
65. M. Yaseen, M. K. Butt, A. Ashfaq, J. Iqbal, M. M. Almoneef, Misbah, M. Iqbal, A. Murtaza and A. Laref, Phase Transition and Thermoelectric Properties of Cubic KNbO₃ under Pressure: DFT Approach, J. Mater. Res. Technol., 2021, 11, 2106–2113,  DOI:10.1016/j.jmrt.2021.02.017.
66. J. B. Goodenough, Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO₃, Phys. Rev., 1955, 100, 564–573,  DOI:10.1103/PhysRev.100.564.
67. M. S. Christian, E. R. Johnson and T. M. Besmann, Interplay between London Dispersion, Hubbard U, and Metastable States for Uranium Compounds, J. Phys. Chem. A, 2021, 125, 2791–2799,  DOI:10.1021/acs.jpca.0c10533.
68. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215,  10.1039/C7CP04913G.
69. P. Morgante and R. Peverati, Statistically Representative Databases for Density Functional Theory via Data Science, Phys. Chem. Chem. Phys., 2019, 21, 19092–19103,  10.1039/C9CP03211H.

---

Footnote

† Electronic supplementary information (ESI) available: The mash code is available at https://github.com/PeterKraus/mash. Version 1.0 used in this work is archived under DOI: https://doi.org/10.5281/zenodo.7492808. The complete code archive including all Quantum ESPRESSO calculation input and output files, as well as postprocessing scripts used to generate the figures in this manuscript, is available on Zenodo under DOI: https://doi.org/10.5281/zenodo.7874704. See DOI: https://doi.org/10.1039/d3cp00041a

---