Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spontaneous mirror symmetry breaking and chiral segregation in the achiral ferronematic compound DIO†
Neelam
Yadav‡
a,
Yuri P.
Panarin‡
b,
Wanhe
Jiang
c,
Georg H.
Mehl
 c and
Jagdish K.
Vij
c and
Jagdish K.
Vij
 *a
*a
aDepartment of Electronic and Electrical Engineering, Trinity College Dublin, The University of Dublin, Dublin 2, Ireland. E-mail: jvij@tcd.ie
bDepartment of Electrical and Electronic Engineering, TU Dublin, Dublin 7, Ireland
cDepartment of Chemistry, University of Hull, Hull, HU6 7RX, UK
First published on 7th March 2023
Abstract
An achiral compound, DIO, known to exhibit three nematic phases namely N, NX and NF, is studied by polarizing microscopy and electro-optics for different surface conditions in confinement. The high temperature N phase assigned initially as a conventional nematic phase, shows two additional unusual features: the optical activity and the linear electro-optic response related to the polar nature of this phase. An appearance of chiral domains is explained by the spontaneous symmetry breaking arising from the saddle-splay elasticity and followed by the formation of helical domains of the opposite chirality. This is the first example of helical segregation observed in calamitic non-chiral molecules in the nematic phase. As reported previously, the ferronematic NF shows strong polar azimuthal surface interaction energy which stabilizes a homogeneous structure in planar aligned LC cells rubbed parallel and exhibits a twisted structure in cells with antiparallel buffing. The transmission spectra are simulated using Berreman's 4 × 4 matrix method. The observed agreement between the experimental and the simulated spectra quantitatively confirms the presence of twisted structures in antiparallel rubbed cells.
1. Introduction
Despite predictions made by Born for the existence of a ferroelectric nematic (NF) over a century ago,1 the NF phase has only been discovered in 2017 independently by Mandle et al.2 and Nishikawa et al.3 in two different compounds RM734 and DIO respectively, each of which has a large dipole moment of ∼10 Debye. RM734 exhibits two nematic phases, a conventional nematic (N) and the lower temperature NX phase. The NX is found to have antiparallel molecular associations and is separated from N by a weak first-order transition.2 Later, Mertelj et al.4 showed that the NX phase forms a splay modulated structure with a period varying from 5 to 10 μm. This arises presumably from the wedge-shaped molecules of RM734 and the phase is therefore denoted as the splay nematic phase (NS).5–7 Chen et al.8 gave the first major demonstration of ferroelectricity in the NX phase of RM734 and they proved it unambiguously as the ferroelectric nematic (NF).The second material, DIO exhibits three variants of nematic phases, these were originally termed as M1, M2 and MP on cooling from the isotropic phase. The high-temperature M1 phase was designated as an ordinary paraelectric nematic (N), while the low-temperature MP, identified as a polar mesophase that exhibits ferroelectric-like polarization, demonstrates electrical switching and generates a large second harmonic signal. The intermediate M2 phase shows field-induced polarization properties. This compound has recently been reexamined by X-ray diffraction9 and it was observed that M2 is a density modulated phase, with a period of 8.6 nm with a slightly splayed director distribution, designated as antiferroelectric SmZA. However, Sebastian et al.10 found the structure of SmZA is identical to the splay NS phase,4 thus belonging to the class of modulated nematic phases. This shows that the characteristic behavior, and the structure of some of these new phases continues being debated, and are not yet fully understood. It needs further detailed investigations using a range of complementary physical techniques.
The major objective of the work presented in this article is the study of the high-temperature nematic phase of ferronematic material DIO, the study of which so far has not received much attention. However, this phase, though identified as an ordinary nematic, has some unique dielectric properties such as exhibition of collective relaxation process. This was observed in the high-temperature nematic phase in both known ferronematic compounds DIO,11,12 RM7345 and its homologues.7 The collective relaxation process is directly related to the polarity and it might thus be unique for ferronematic materials. In case of RM734 built from the drop-shaped molecules, the theoretical models suggest the importance of including the flexo-dipolar terms in the Landau energy expansion. These are found to play an important role in providing stability to the ferroelectric nematic phase13–15 with different splay deformations.
Usually, the polarity in the LC is related to the chirality and the optical activity, hence the observations of optically active properties are anticipated in the high temperature N phase. To find these properties, DIO has been studied under different cell conditions and configurations. The observance of chirality in the high-temperature nematic phases of DIO is not yet reported.
2. Results and discussion
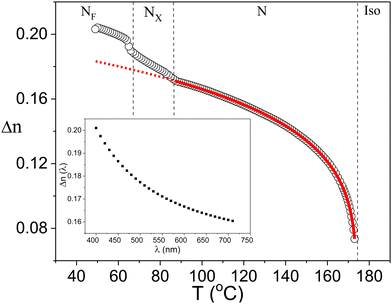
The structure of the compound DIO and its phase transition temperatures are given in Fig. 1. The phase sequence using differential scanning calorimetry (DSC) is found as Iso–N–Nx–NF; here Iso refers to the isotropic state, N to the ordinary nematic phase, NX to an unknown nematic whereas NF refers to the ferroelectric nematic phase. NX is found to have modulated structure at the nanoscale level, and it exhibits smectic-like SmZA antiferroelectric behaviour.9 The nomenclature for the phases of DIO adopted here follows from the works of Nishikawa et al.3 and of Chen et al.9 The NX phase is also termed as the splayed nematic (NS) by Sebastian et al.,4,10 and as unknown NX by Gorecka et al.11 Hereafter we refer it to NX for the reasons given above. DIO was first synthesized by Nishikawa et al.3 but for the works reported here, it is resynthesized by the group of G. H. Mehl at the University of Hull, Hull, UK. The details of the synthesis of this compound are given in the supplementary information. | ||
| Fig. 1 Molecular structure, the phase-sequence, and the transition temperatures of the DIO compound on cooling at the rate of 0.2 °C min−1. | ||
2.1. Optical textures and birefringence measurements of the three nematic phases in planar-aligned cells
The textural studies using polarized optical microscopy (POM) are extremely useful for determining the structure of the LC phases. The textures of DIO were recorded in thin planar and homeotropic aligned cells.3,16 We commenced experimental studies of this material using commercial planar cells (E.H.C. Co. Ltd, Japan) with antiparallel buffing. The cells used were of six different cell spacings: 2, 4, 15, 25 μm and a homeotropic aligned cell of the thickness of 4 μm. Fig. 2 shows textures of DIO in planar aligned cells of thickness 4 μm. The cell is mounted on the rotational hot stage of the POM, the angle between the rubbing and the crossed polarizer/analyzer directions is fixed at ψ = 45°.Homogeneous and uniform textures are observed for all temperature/phases as reported earlier in different studies3,9–11 except that the NF phase shows a sharp texture transition at a temperature of ∼3 °C below the NX–NF transition temperature. This behavior is discussed in Section 2.3. A change in the color of the texture with temperature depends on the optical retardation experienced by the beam of light (π·Δn·d)/λ and hence on the birefringence Δn(T). Δn(T) increases gradually under slow cooling which results from an increase in the order parameter with a reduction in the temperature.
The birefringence measurements are made using an optical spectral technique17 on a planar homogenous aligned 25 μm thick cell. The transmittance (T) spectra of the cell from achromatic light source were measured using an Avantes AvaSpec-2048 fiber spectrometer as a function of temperature, varying from a temperature of 173 °C (just below the isotropic to nematic transition temperature) down to the lower temperatures in the NF phase. In such a homogeneous cell, the transmittance T is given by:
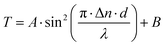 | (1) |
In eqn (1)A is the scaling factor, B accounts for the leakage of light through the cell, d is the cell thickness and Δn is the birefringence. The latter is dependent on the wavelength of light due to dispersion which is governed by an extended Cauchy equation as:
 | (2) |
The temperature dependence of the birefringence in the high-temperature nematic phase was fitted to the Haller equation:18
 | (3) |
2.2. Observation of the chiral domains in the high temperature N phase
The temperature dependence of the birefringence indicates that the high-temperature nematic phase is a conventional nematic.3,9–11 However, one observes that this phase surprisingly is also dielectrically active, i.e. the phase shows up collective relaxation processes explained by the existence of some polar groups (clusters/domains). In the LCs, the polarity and the chirality are closely related properties, hence one can expect that this phase is optically active and is chiral. However, the chirality is not reported in the high-temperature nematic phase in the studied ferronematic compound so far. They might exist in the bulk but can be suppressed by the surface interaction in thin planar cells. This raises an interesting question – as to what textures can possibly be realized in the bulk?In general, textures of the ordinary nematic planar cells with two (anti-) parallel rubbed surfaces along Z-axis is governed by the following free energy expansion:
 | (4) |
To check this assumption, we record textures of specially prepared cells with different alignment conditions. The cells were prepared by sandwiching two ITO glass substrates, coated with RN1175 (Nissan Chemicals) with only one rubbed surface while the other substrate is kept non-rubbed to ensure azimuthal degeneration of the surface anchoring energy. For brevity, hereafter we refer to such cells as “1-rubbed cells”. In such cells, the molecular director at the rubbed surface is fixed along the rubbing direction, while the director on the opposite surface is azimuthally degenerated (not fixed) and eqn (4) simplifies to
 | (5) |
 and φ1 = 0, i.e., the optical activity is not affected and the realized texture should show the natural structure of that of the bulk. Therefore, the achiral nematic (q = 0) should form a homogeneous planar texture as in the two rubbed surfaces cells. This was confirmed by the textures of the typical nematic 5CB as shown in Fig. 4.
and φ1 = 0, i.e., the optical activity is not affected and the realized texture should show the natural structure of that of the bulk. Therefore, the achiral nematic (q = 0) should form a homogeneous planar texture as in the two rubbed surfaces cells. This was confirmed by the textures of the typical nematic 5CB as shown in Fig. 4.
Surprisingly, textures of the studied achiral compound DIO in the N, NX subphases are not homogeneous but these exhibit two types of domains of the opposite optical activity as shown in Fig. 5, so that  and the molecular director on both surfaces are: φ1 = 0 and φ2 = ±q·d. Such textures do not exhibit full extinction between the crossed polarizers (Fig. 5b) and though appear uniform, however the rotation of analyzer reveals the existence of two types of distinguishable domains as shown in Fig. 5, which can darken to some order (depending on the Gooch and Tarry condition20 by rotating the analyzer by an angle φ2 = ±20°, (Fig. 5a and c). This means that the domains of opposite (optical activity) chirality do exist even in the ordinary (paraelectric) nematic phase and emerge just below the Iso-N phase transition temperature. Hence, this natural texture represents a conglomerate of stochastically distributed chiral areas/domains with the experimentally determined optical activity. The inherent optical rotation is found to be ∼4 deg per μm. As expected, similar chiral domains were observed in 8 μm cells made from both unrubbed polymer coated (Fig. 6) or pure uncoated ITO (Fig. 7) plates.
and the molecular director on both surfaces are: φ1 = 0 and φ2 = ±q·d. Such textures do not exhibit full extinction between the crossed polarizers (Fig. 5b) and though appear uniform, however the rotation of analyzer reveals the existence of two types of distinguishable domains as shown in Fig. 5, which can darken to some order (depending on the Gooch and Tarry condition20 by rotating the analyzer by an angle φ2 = ±20°, (Fig. 5a and c). This means that the domains of opposite (optical activity) chirality do exist even in the ordinary (paraelectric) nematic phase and emerge just below the Iso-N phase transition temperature. Hence, this natural texture represents a conglomerate of stochastically distributed chiral areas/domains with the experimentally determined optical activity. The inherent optical rotation is found to be ∼4 deg per μm. As expected, similar chiral domains were observed in 8 μm cells made from both unrubbed polymer coated (Fig. 6) or pure uncoated ITO (Fig. 7) plates.
 | ||
| Fig. 5 POM textures of a 7 μm thick one surface rubbed cell at 170 °C (a) the analyzer is rotated clockwise by 20° (b) crossed polarizers and the (c) analyzer rotated anticlockwise by 20°. | ||
 | ||
| Fig. 6 The textures of 8 μm, unrubbed (both surfaces) cell for different polarizer configurations at a temperature of 160 °C in the nematic phase. | ||
 | ||
| Fig. 7 Textures of 6 μm cell made from two bare ITO coated glass plates for different polarizer positions at 160 °C in the nematic phase. | ||
This confirms our assumption that the optical activity is suppressed in two rubbed surface planar cells, where optically active textures are affected by both surfaces, see eqn (4).
This raises another question as to why the optical activity is observed in an achiral nematic system? Here we deal with an interesting and important phenomenon – Spontaneous Mirror Symmetry Breaking. It should be noted that similar phenomena, polarity, and chirality were also reported in the Bent-Core (BC) LCs21 in nematic phases22,23 and the model for the chiral formation of domains was suggested in the latter reference. However, those reported systems are non-homogeneous but consist of the so-called cybotactic, smectic-like polar domains that are randomly distributed in the ordinary nematic phase in which the volume ratio is temperature dependent and it increases on cooling.24
Later, these phenomena were observed in homogeneous non-chiral nematic phases such as: the bent-core (BC) LCs;25,26 twist-bent nematics, (NTB)27,28 and even in some isotropic liquids.29 The symmetry breaking in the first two systems is caused by a strong non-calamitic shape of the bent-core molecules or the dimers, different in shape from DIO. As the shape of DIO molecules is calamitic rather than bent-core, the physical origin of chirality may be different. One of the possible mechanisms could be similar to the explanation given for molecules that exhibit chirality in isotropic liquids.29 The important features of these compounds are: (i) large net molecular dipole moment; (ii) the molecular core consisting of three or more aromatic rings.
The first property i.e., extremely large dipole moment is observed in all known ferronematics. Recently Lavrentovich30 noticed that in order to form the ferroelectric state in the nematic phase, the dipole moments in these materials, μ should be as large as ∼10 D, such that the interactions withstand the thermal fluctuations, that tentatively satisfy the equation,  , where V is the molecular volume, kBT is the thermal energy. Therefore, the pre-requisites for the formation of ferroelectric nematic phase are that the constituent molecules should have a large net dipole moment and a specific relative arrangement of the neighboring molecular dipoles. This has theoretically been confirmed by Madhusudana.31
, where V is the molecular volume, kBT is the thermal energy. Therefore, the pre-requisites for the formation of ferroelectric nematic phase are that the constituent molecules should have a large net dipole moment and a specific relative arrangement of the neighboring molecular dipoles. This has theoretically been confirmed by Madhusudana.31
The second property, i.e. the three or more aromatic rings molecular core might be responsible for the chiral formation and the segregation of molecules of opposite chirality. The aromatic rings in such molecules29 have two stable states twisted at some angle between the two neighboring rings which can be positive for clockwise (or right, R) or negative for anticlockwise (or left, L) rotations. In the case of a compound having three or more aromatic rings, the rings may twist either in the left or the right direction forming LL… and RR… respectively or rotate in the opposite direction consecutively to form non-chiral non-helical conformers LR…/RL. A left-handed helical conformer LL is shown in Fig. 8a, where three principal rings are numbered as 1–3. Fig. 8b shows the side view of the angular orientations of these three rings with angles of rotation α12 ≅ −20° and α23 ≅ −48° between them. The molecular modeling software Gaussian 09 gives global minimum energy levels at E = 192.884 kJ mol−1 for helical conformers and local minimum of E = 192.961 kJ mol−1 for non-helical conformers. This implies that helical conformers of DIO (LL/RR) thermodynamically are more stable than the non-helical conformers (LR/RL). Possible reasons may include conformers of the same chirality having denser molecular packing, leading to a lower potential energy for the homochiral domains and hence the gain achieved in the strength of chiral discrimination (−ΔHcd) exceeds entropic penalty of the de-mixing process (T·ΔS).29,32 However, the energy gap between the chiral and non-chiral conformers appears to be too small to exceed kBT Hence it cannot be the only reason for the formation of chirality and for affecting the molecular segregation. The other explanation could be that as proposed recently by Revignas et al.33 for hard rod-like molecules. They theoretically showed that the calamitic nematics have an intrinsic tendency to twist around the ordering axis due to the saddle-splay contribution to the elastic free-energy.
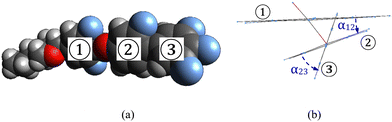 | ||
| Fig. 8 (a) van der Waals molecular shape of the left helical conformer LL of DIO and (b) the side view of the aromatic rings 1–3. Rotation angles α12 ≅ −20° and α23 ≅ −48°. | ||
Furthermore, this twisted organization is likely to contribute to the chiral segregation of helical molecular conformers as these could stabilize the conformations by a co-operative coupling occurring between the molecular and the nano structural twist sense, thus increasing the energy gain of the homochiral packing. So, we can conclude that the chirality in the ordinary nematic phase of the compound DIO, arises from the saddle-splay elasticity which might be accompanied by chiral segregation of helical molecular conformers of the opposite sense. These chiral domains may be suppressed by the surface interactions and this can be the reason as to why these were not observed previously.3,11,16
2.3. Ferroelectric nematic phase (NF): twisted structure
The interesting feature involves observing unusual textures in the NF phase in a 4 μm thick cell shown in Fig. 9a–g. The angle between the analyzer (A) and the polarizer (P) is varied in this experiment. At the temperature ∼3 °C below the NX–NF phase transition the homogeneous texture (Fig. 9a) transforms to the ‘yellow texture B’ (Fig. 9b), which does not show the extinction between the crossed polarizers and looks magenta between parallel polarizers (Fig. 9e). The rotation of the analyzer by angles of ± 10° from the crossed positions are shown (c, d) and rotations by ± 10° from the parallel positions of P and A are marked (f and g). These textures show two domains in which their colors are swapped by the opposite rotations of the analyzer from the crossed polarizers position. Similar textures were observed in the other NF compound, RM734 and their director distribution were found to be twisted.34–37 | ||
| Fig. 9 The POM textures from a 4 μm thick cell with unidirectional antiparallel rubbing of substrates at a temperature of 62 °C in the NF phase. The homogeneous texture (a). (also Fig. 2c) transforms to the twisted texture (b). (also Fig. 2d). The textures c to g are recorded for different angles between the P and A, angles are shown in the right bottom corner of Figures. | ||
This phenomenon is explained by the large polar azimuthal anchoring surface energy, as suggested by the Boulder group.34 This polar in-plane anisotropy stabilizes the homogeneous planar structure for the parallel rubbing and gives twisted structure for the antiparallel rubbing and this is due to the strong polar term in the azimuthal anchoring energy (WP) which should be added to the free-energy expansion (eqn (4)).37 This gives:
 | (6) |
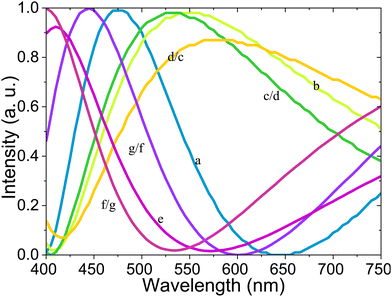 | ||
| Fig. 10 Simulated optical spectra corresponding to the textures (a–g) shown in Fig. 9 in the NF phase. The colors of the curves correspond to the RGB values of the simulated spectra. | ||
2.4 Electro-optical dynamics in the high temperature N phase
Results obtained from the POM show polarity and chirality of the domains in the high-temperature nematic phase. The domains display a strong dependence on the cell thickness, surface treatment and temperature/phase of the sample. To investigate a development of the polar order with temperature, we performed electro-optical (EO) measurements using planar-aligned cells. The electric field of varying voltages (0.1–10 V) at frequencies (6 Hz–100 kHz) with a sine-wave dependence of voltage on time was applied across the LC cell placed between the crossed polarizers such that the angle between the rubbing direction, and the polarizer/analyzer axis, is 45°.40 The output signal from the photodetector was fed to the input of a DSP lock-in amplifier (SR830) and the intensity of the transmitted light through the cell was recorded for the first and the second harmonics of the applied signal.A change in the transmittance through the cell is exclusively dependent on a change in the macroscopic refractive index Δneff. The effective birefringence is dependent on the angle θ between the LC director and the electric field as:
 | (7) |
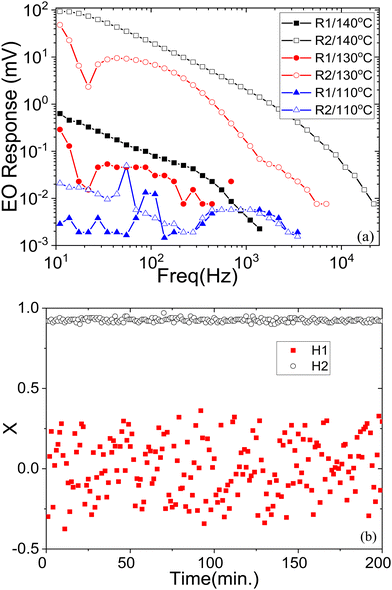
For a conventional paraelectric nematic phase, the output of electro-optical signal is only of the second harmonic and is strongly dependent on the frequency of the applied field. For frequencies much lower than the relaxation frequency of the LC structure, the electro-optic response gives a maximum signal for the second harmonic. For frequencies much higher than the LC relaxation frequency, the electrooptic response is small. For intermediate frequencies, the second-harmonic electrooptic response decreases with an increase in the frequency as the 1st order low-pass filter with a slope of −20 dB per decade. This scenario is observed in the higher temperature range of the N nematic, i.e., for T ≥ 150 °C. However, the polarity and the chirality exist even in the paraelectric N nematic phase at lower temperatures. Therefore, one may expect the first harmonic response to appear arising from the polar interactions with the electric field. Fig. 11a shows the frequency dependence of the complex valued signal of magnitude R and the phase angle θ (R·exp(jθ) = X + jY), X and Y are the real and imaginary parts of the signal in the Cartesian coordinates for both the first and the second harmonics of the applied sinusoidal signal of amplitude 5 V, for three temperatures below the benchmark temperature of 150 °C. These are set at 140 °C, 130 °C and 110 °C. These temperatures correspond to the higher temperature nematic phase of DIO. However, the characteristics of the EO response are different for these three temperatures. For 140 °C, there is a lower output of the first harmonic than of the second one. The spectra for the first and the second harmonics show two slopes: −20 dB per decade in the low frequency range and the −40 dB per decade in the high frequency range. At a mid-temperature in the nematic phase (130 °C), the response is similar, but level of the noise signal is higher, especially for the 1st harmonic. At the lowest temperature of 110 °C, the spectra are not regular but extremely noisy. To elucidate this feature, we plot the dependence of the real part X of the signal R as a function of time in Fig. 11b at a fixed frequency of 28 Hz, measured as a function of time at an interval of one minute.
Both the magnitude and the phase part of the 2nd harmonic signal is stable with time while the 1st harmonic output shows no regularity with time and the output is noisy. The observation of the first harmonic signal R1 is not as dominant as from the twist bend structure found before, in that case the signal was obtained from a single chiral domain28 unlike here. This observed phenomenon has a rather simple explanation. In such cells a homogeneously planar texture is stabilized initially in the N phase. At the Iso-N phase transition temperature, homogeneously uniform structure in these antiparallel rubbed cells is due to the quadrupolar term (WQ) in the azimuthal anchoring energy (see eqn (4) and this quasi-stable structure is retained in the entire temperature range of the N phase. However, for the electric field greater than 0.3 V μm−1 applied to the ITO electrodes across the cell in the N phase, the POM images show an emergence of the two sets of chiral polar domains (Fig. 12), which remain in the cell even after the field is removed.
The space ratio of these domain is not exactly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as seen from Fig. 12b where the total area of the right domains (appearing dark under uncrossed polarizers) is less than of the left-handed domains. Moreover, this changes after each state of ON/OFF applied signal. The right-handed domains produce positive response whereas the left-handed domains lead to the opposite response. Therefore, the real part of the magnitude and the sign of response is proportional to the enantiomer excess, defined as
1, as seen from Fig. 12b where the total area of the right domains (appearing dark under uncrossed polarizers) is less than of the left-handed domains. Moreover, this changes after each state of ON/OFF applied signal. The right-handed domains produce positive response whereas the left-handed domains lead to the opposite response. Therefore, the real part of the magnitude and the sign of response is proportional to the enantiomer excess, defined as  , changes in the signal observed are irregular with time. The 2nd harmonic response is driven by the non-polar interaction Δε·E2 and is regular and stable with time.
, changes in the signal observed are irregular with time. The 2nd harmonic response is driven by the non-polar interaction Δε·E2 and is regular and stable with time.
Once formed, these domains continue to exist even after the electric field is removed. Uncrossing the polarizers by an angle +12° in a specific direction darkens one set of domains and brightens the other, as seen in Fig. 12b. The opposite is observed for rotation in the opposite direction −12° (texture not shown in Fig. 12). The rotation of the hot stage mounted on the rotational stage however does not affect the relative brightness of these domains. This shows that the domains are chiral and are of opposite chirality with the polarization of light rotated as ∼ ±1 deg per μm, by each domain. The value is lower than of the natural optical rotation (∼4 deg per μm) achieved for one-sided rubbed cell (Fig. 5) due to the unwinding effect of the rubbed surfaces.
3. Conclusion
The studied achiral compound shows three nematic subphases: NF, NX. N, where N is an ordinary nematic phase with a conventional Δn(T) dependence on temperature in planar-aligned cells. However, this phase exhibits some unusual features: (a) optical activity and (b) linear EO response. It consists of chiral domains of the opposite chirality. The appearance of these domains is explained by Spontaneous Symmetry Breaking occurring due to the saddle-splay elasticity followed by separation of the stable helical conformers of the opposite chirality. This is the first example of helical segregation observed in calamitic achiral molecules in the nematic phase. The other unusual feature (related to the chirality) is the polarity which is responsible for the observation of the electrooptic response (EO) at the fundamental frequency (linear response) of the applied signal in addition to the second harmonic response in ordinary nematics. The ferroelectric nematic NF exhibits a strong polar azimuthal surface interaction energy which stabilizes the homogeneous structure in a planar aligned cell rubbed parallel and forms the twisted structures in the cell rubbed antiparallel.Conflicts of interest
There are no conflicts to declare.Acknowledgements
One of the authors NY thanks the Irish Research Council for awarding the Government of Ireland PDF 2021, GOIPD/2021/858; WJ thanks the CSC, China for a PhD scholarship and Station B23 at Diamond Light Source (UK), projects SM30755 and SM31552 are acknowledged. The work of the Dublin group was funded by Science Foundation Ireland 21/US/3788 under the US-Ireland program. We thank one of the referees for making many valuable suggestions.References
- M. Born, Sitzungsber. Preuss. Akad Wiss., 1916, 30, 614 Search PubMed.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2017, 23, 14554 CrossRef CAS PubMed.
- H. Nishikawa, K. Shiroshita, H. Higuchi, Y. Okumura, Y. Haseba, S.-I. Yamamoto, K. Sago and H. Kikuchi, Adv. Mater., 2017, 29, 1702354 CrossRef PubMed.
- A. Mertelj, L. Cmok, N. Sebastián, R. J. Mandle, R. R. Parker, A. C. Whitwood, J. W. Goodby and M. Čopič, Phys. Rev. X, 2018, 8, 041025 CAS.
- N. Sebastián, L. Cmok, R. J. Mandle, M. Rosario de la Fuente, I. Drevenšek Olenik, M. Čopič and A. Mertel, Phys. Rev. Lett., 2020, 124, 037801 CrossRef PubMed.
- R. J. Mandle, S. J. Cowling and J. W. Goodby, Liq. Cryst., 2021, 48, 1780 CrossRef CAS.
- R. J. Mandle, N. Sebastián, J. Martinez-Perdiguero and A. Mertelj, Nat. Commun., 2021, 12, 4962 CrossRef CAS PubMed.
- X. Chen, E. Korblova, D. Dong, X. Wei, R. Shao, L. Radzihovsky, M. A. Glaser, J. E. Maclennan, D. Bedrov, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14021–14031 CrossRef CAS PubMed.
- X. Chen, V. Martinez, E. Korblova, G. Freychet, M. Zhernenkov, M. A. Glaser, C. Wang, C. Zhu, L. Radzihovsky, J. E. Maclennan, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(8), e2217150120, DOI:10.1073/pnas.2217150120.
- N. Sebastián, M. Copic and A. Mertelj, Phys. Rev. E, 2022, 106, 021001 CrossRef PubMed.
- S. Brown, E. Cruickshank, J. M. D. Storey, C. T. Imrie, D. Pociecha, M. Majewska, A. Makal and E. Gorecka, ChemPhysChem., 2021, 22, 2506 CrossRef CAS PubMed.
- N. Yadav, Yu. P. Panarin, J. K. Vij and W. Jiang, Two mechanisms for the formation of ferronematic phase in DIO as studied by dielectric spectroscopy, J. Mol. Liq., 2023 DOI:10.1016/j.molliq.2023.121570.
- M. P. Rosseto and J. V. Selinger, Phys. Rev. E, 2020, 101, 052707 CrossRef CAS PubMed.
- E. I. Kats, Phys. Rev. E, 2021, 103, 012704 CrossRef CAS PubMed.
- A. V. Emelyanenko, V. Yu Rudyak, S. A. Shvetsov, F. Araoka, H. Nishikawa and K. Ishikawa, Phys. Rev. E, 2022, 105, 064701 CrossRef CAS PubMed.
- F. Caimi, G. Nava, R. Barboza, N. A. Clark, E. Korblova, D. M. Walba, T. Bellini and L. Lucchetti, Soft Matter, 2021, 17, 8130 RSC.
- O. E. Panarina, Yu. P. Panarin, F. Antonelli, J. K. Vij, M. Reihmann and G. Galli, J. Mater. Chem., 2006, 16, 842 RSC.
- I. Haller, Prog. Solid State Chem., 1975, 10, 103–118 CrossRef.
- N. A. Clark and S. T. Lagerwall, Appl. Phys. Lett., 1980, 36, 899 CrossRef CAS.
- C. Gooch and H. Tarry, J. Phys. D: Appl. Phys., 1975, 8, 1575–1584 CrossRef.
- T. Niori, T. Sekine, J. Watanabe, T. Furukawa and H. Takezoe, J. Mater. Chem., 1996, 6, 1231 RSC.
- G. Pelzl, A. Eremin, S. Diele, H. Kresse and W. Weissflog, J. Mater. Chem., 2002, 12, 2591–2593 RSC.
- J. A. Olivares, S. Stojadinovic, T. Dingemans, S. Sprunt and A. Jakli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041704 CrossRef CAS PubMed.
- S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, V. P. Panov, A. Lehmann, M. Poppe, M. Prehm and C. Tschierske, Nat. Commun., 2016, 7, 11369 CrossRef CAS PubMed.
- V. Gortz and J. W. Goodby, Chem. Commun., 2005, 3262–3264 RSC.
- P. S. Salter, P. W. Benzie, R. A. Reddy, C. Tschierske, S. J. Elston and E. P. Raynes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031701 CrossRef CAS PubMed.
- V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801 CrossRef CAS PubMed.
- V. P. Panov, R. Balachandran, M. Nagaraj, J. K. Vij, M. G. Tamba, A. Kohlmeier and G. H. Mehl, Appl. Phys. Lett., 2011, 99, 261903 CrossRef.
- C. Dressel, T. Reppe, M. Prehm, M. Brautzsch and C. Tschierske, Nat. Chem., 2014, 6, 971 CrossRef CAS PubMed.
- O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14629 CrossRef CAS PubMed.
- N. V. Madhusudana, Phys. Rev. E, 2021, 104, 014704 CrossRef CAS PubMed.
- S. Toxvaerd, Phys. Rev. Lett., 2000, 85, 4747 CrossRef CAS PubMed.
- D. Revignas and A. Ferrarini, Phys. Rev. Lett., 2023, 130, 028102 CrossRef CAS PubMed.
- X. Chen, E. Korblova, M. A. Glaser, J. E. Maclennan, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104092118 CrossRef CAS PubMed.
- N. Sebastián, R. J. Mandle, A. Petelin, A. Eremin and A. Mertelj, Liq. Cryst., 2021, 48, 2055 CrossRef.
- P. Rudquist, Sci. Rep., 2021, 11, 24411 CrossRef CAS.
- B. Basnet, M. Rajabi, H. Wang, P. Kumari, K. Thapa, S. Paul, M. O. Lavrentovich and O. D. Lavrentovich, Nat. Commun., 2022, 13, 3932 CrossRef CAS PubMed.
- D. W. Berreman, J. Opt. Soc. Am., 1972, 62, 502 CrossRef CAS.
- Z. Wan, J. Li, M. Huang and S. Aya, Measurement, 2022, 204, 11208 CrossRef.
- S. Sreenilayam, N. Yadav, Yu. P. Panarin, J. K. Vij and G. S. Shanker, J. Mol. Liq., 2022, 351, 118632 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00357d |
| ‡ Joint first authors. |
| This journal is © the Owner Societies 2023 |