A combined BET and IQA–REG study of the activation energy of non-polar zw-type [3+2] cycloaddition reactions

Abstract

A combined Bonding Evolution Theory (BET) and Interacting Quantum Atoms-Relative Energy Gradient (IQA–REG) study is carried out on a non-polar zw-type [3+2] cycloaddition (32CA) reaction. BET is the joint use of Catastrophe Theory and the topology of the Electron Localization Function (ELF) to characterise molecular mechanisms, while IQA is a quantum topological energy partitioning method and REG is a method to compute chemical insight at atomistic level, usually in connection with energy. This 32CA reaction involves the simplest nitrone with ethylene and has been studied here at B3LYP/6-311G(d,p) level within the context of Molecular Electron Density Theory (MEDT), which is based on the idea that changes in electron density, and not molecular orbital interactions, are responsible for chemical reactivity. We aim to determine the origin of the high activation energy of 32CA reactions involving zwitterionic three-atom-components. The BET study and IQA–REG method are applied to the overall activation energy path. While BET suggests that the barrier is mainly associated with the rupture of the nitrone C=N double bond, IQA–REG indicates that it is mainly related to the rupture of the ethylene C=C double bond. The present study shows that activation energies can be accurately and easily described by IQA–REG, and its complementary use with BET helps achieving a more detailed description of molecular mechanisms.

---

1. Introduction

In recent years there has been a growing interest to interpret chemical reactivity by means of the analysis of the electron density as the only physical observable responsible for chemical structure and properties. In this context, Domingo proposed in 2016 the molecular electron density theory (MEDT)¹ as a new theory, opposed to the widespread frontier molecular orbital (FMO) theory,² to explain organic chemical reactivity. According to MEDT it is the changes in electron density, and not molecular orbital interactions, that determine any chemical event. Therefore, any study of reactivity within the framework of MEDT demands the use of quantum chemical tools based on the analysis of density functions such as the electron localisation function (ELF)^3,4 or the electron density itself through the Quantum Theory of Atoms in Molecules (QTAIM).^5,6

MEDT has been extensively applied to the study of [3+2] cycloaddition (32CA) reactions.^7–12 The topological analysis of the ELF of the simplest three-atom-components (TACs), i.e. neutral species whose core framework consists of three contiguous heavy nuclei sharing an electron density corresponding to a total electron count of 8 electrons, allowed finding four different electronic structures, namely, pseudodiradical, pseudo(mono)radical, carbenoid and zwitterionic (see Fig. 1),^13–16 respectively abbreviated as pdr, pmr, cb and zw. When the structures of TACs and their reactivity towards ethylene were compared, a very good structure–reactivity relationship was found, which allowed classifying 32CA reactions into the four corresponding pdr-, pmr-, cb-, and zw-type reactions,⁷ respectively (Fig. 1). The reactivity of TACs decreases in the order pseudodiradical > pseudo(mono)radical ≥ carbenoid > zwitterionic, in such a way that, while pdr-type 32CA reactions take place very easily,¹³ zw-type reactions demand adequate nucleophilic/electrophilic activation of the reagents to take place.¹⁵ This classification was established depending not only on the ground state structure of the TAC but also on the reaction mechanism.

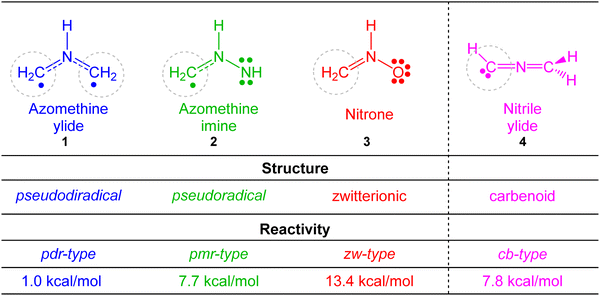Fig. 1 Electronic structure of simplest TACs and proposed reactivity types in 32CA reactions. MPWB1K/6-311G(d) gas phase activation energies of the non-polar 32CA reactions between the four simplest TACs 1–4 and ethylene 5, relative to the corresponding molecular complexes, are given in kcal mol⁻¹.⁷

The bonding evolution theory (BET),¹⁷ which consists of the joint use of the topological analysis of the ELF³ and mathematical catastrophe theory^18–20 along the intrinsic reaction coordinate (IRC) path,²¹ is one of the most powerful methods to study molecular mechanisms. BET divides the IRC in a series of structural stability domains or phases separated by catastrophes, which are characterised by a change in the number and/or type of ELF valence basins in the structures along the reaction path. In this way, a chemical reaction is viewed as a sequence of phases connected by a catastrophe that can be related to chemical events such as bond forming or bond breaking processes, the creation or annihilation of lone pairs and other types of electron pair rearrangements. Moreover, BET enables the analysis of the variation of electron populations in regions of the topological space along the reaction path, thus allowing for a detailed description of bonding changes. As electron populations can be associated with Lewis’ bonding model,²² BET constitutes an appealing way to represent molecular mechanisms with chemically meaningful drawings. BET has been applied to the study of a wide variety of organic chemical reactions,^23–25 specifically cycloaddition reactions,^26–28 providing accurate descriptions of their molecular mechanisms.

These BET mechanistic studies have allowed establishing two models for the formation of C–X (with X = C, O, N) single bonds, namely, the sharing model^29,30 and the donating model³⁰ (see Fig. 2). While the sharing model demands the homolytic rupture of multiple bonds to give rise to the creation of the pseudoradical centers³¹ that will form the new single bonds,³¹ the donation mechanism demands the initial depopulation of the β-conjugated carbon of a substituted ethylene.³⁰ This feature is only possible when strong electron-withdrawing groups, such as –CHO or –NO₂, are present at the α-position. The donating model is mainly observed in cb-type 32CA reactions involving the participation of carbenoid species^32,33 and in polar reactions involving heteroatoms such as oxygen.^15,33,34

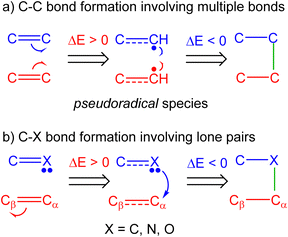Fig. 2 (a) Sharing model and (b) donation model for the formation of C–X (X = C, N, O) single bonds. The X atom being a carbon in the donation model ‘b’ implies a carbenoid or carbanionic center.

The sharing model accounts for the reactivity trend in many 32CA reactions.⁷ Considering that pseudoradical centers are required for C–C single bond formation,²⁹ pseudodiradical TACs are already prepared to react, while zwitterionic TACs need to break the corresponding C=X multiple bonds to create the necessary pseudoradical centers (see Fig. 3). These changes in zw-type 32CA reactions demand an additional energy cost,⁷ which has shown to be lowered by the polar character of the reaction associated with the favourable nucleophilic/electrophilic interactions between the reagents at the transition state structures (TSs).^35,36

Fig. 3 Bonding changes associated with the formation of the new C–C single bonds along the four types of non-polar 32CA reactions.

Nitrones are one of the most common zwitterionic TACs. Many BET studies^15,37–43 of several inter- and intramolecular experimental 32CA reactions of substituted nitrones with ethylene derivatives of different nature have shown that the chemical events taking place in these zw-type 32CA reactions follow: (a) depopulation of the C=N double bond with formation of the carbon pseudoradical center and nitrogen non-bonding electron density region, (b) depopulation of the C=C double bond with formation of the corresponding pseudoradical centers, and (c) formation of the new C–C and C–O single bonds in different asynchronicity depending on the substituents and polar character of the 32CA reaction. Among these steps, the early depopulation of the C=N bond is usually the most drastic change in terms of population and total energy variations in the corresponding phase. Thus, the activation energies of zw-type 32CA reaction of nitrones have been related to the energy cost demanded for the rupture of the nitrone C=N double bond, by selecting the greatest change in ELF valence basin population in the phase of highest energy variation on going from reagents to the TS.^15,37

However, there is no direct relation between populations and energy variations in the BET framework because while the former are related to a given molecular region, the latter are associated with the whole system. In addition, the population of a region may substantially vary but this is not necessarily correlated to a strong variation in the energy associated with it and vice versa. In other words, a huge population change might require no energy cost at all. Therefore, an energy decomposition analysis (EDA) method developed within the umbrella of quantum chemical topology^44,45 (QCT) is necessary in order to properly characterise the energies associated with the corresponding bonding changes along the reaction. Note that the literature is riddled with studies carried out using Morokuma-based EDA.^46–48 This method and, consequently, the interpretations that arise from it, have shown to be prone to flaws due to the process-dependency of their energy components, which include molecular orbital interactions.^49,50

In 2005, Blanco et al. developed a parameter-free and reference-free energy decomposition scheme based on QTAIM, called interacting quantum atoms (IQA).⁵¹ IQA divides the total energy of a system into intra- and inter-atomic contributions of different nature. Similar to the topological analysis of the ELF, IQA can be applied to every structure of an IRC. However, the amount of energy contributions that are retrieved scales quadratically with the number of atoms of a system. In order to study all possible energetic terms without any bias or arbitrary parameters, Thacker and one of us developed the relative energy gradient (REG) method.⁵² REG systematically inspects the correlation between each partitioned energy term and the total energy of the system. REG then ranks all correlations, one for each atomic energy term, in an automated fashion to determine the subset that best describes the behaviour of the total system as it goes through its change. The combination of both IQA and REG can help discerning the origin of reaction barriers.⁵² Indeed, IQA–REG has already been successfully applied to a wide variety of interactions and phenomena,^52–56 proving itself to be an indispensable, minimal but powerful and general method in the chemist's toolbox for mechanistic studies.

In the present article the combination of BET and IQA–REG quantum chemical techniques is used for the first time in order to exploit the advantages of such a combined approach. Note that BET was already applied in the past together with an IQA analysis but performed only at the stationary points.⁵⁷ Herein, the IQA–REG is applied to the simplest zw-type 32CA reaction of nitrone 3 with ethylene 5 (see Scheme 1) to investigate the origin of the activation barrier and probe the BET-based hypothesis that the higher barrier (Fig. 1) of non-polar zw-type 32CA reactions of nitrones is mainly caused by the rupture of the C=N double bond bearing the highest energy cost among all the other bonding changes towards the TS. In this study, the application of IQA–REG to (a) the whole activation IRC path from reagents to TS, and (b) four separate segments selected through BET (see Fig. 4) is compared. The present study not only reports a new valuable way to study reaction mechanisms but also provides new insights into the origin of the lower reaction rates of zwitterionic TACs such as nitrones.

Scheme 1 32CA reaction between the simplest nitrone 3 and ethylene 5, yielding isoxazolidine 6viaTS.

Fig. 4 Application of IQA–REG to (a) the whole activation IRC path from reagents to TS, and (b) four separate segments of the activation IRC path, established through BET and bounded by vertical dashed lines. Technically, BET characterises only three phases. The dashed-line on the left is in grey because of the division made in Section 3.3, but this is not a true BET division. The position of TS is marked in red.

2. Computational methods

DFT calculations were performed with the B3LYP functional^58,59 and the 6-311G(d,p) basis set,⁶⁰ using the Berny analytical gradient method for optimisations.^61,62 The stationary points were characterised by vibrational frequency computations in order to verify that TSs had indeed only one imaginary frequency. The IRC paths²¹ were traced to obtain the energy profiles connecting each TS to the two associated minima in the potential energy surface using the Hratchian–Schlegel Hessian-based Predictor–Corrector integrator.^63–65 Optimisations and IRCs were carried out with the GAUSSIAN16 suite of programs.⁶⁶

The topological analysis of the ELF³ of the B3LYP/6-311G(d,p) monodeterminantal wavefunctions was carried out using the TopMod⁶⁷ package with a cubical grid of step size of 0.1 Bohr. Currently, the use of monodeterminantal wavefunctions in mechanistic studies of thermal organic reactions that do not involve radical species, such as the one studied herein, is well accepted.⁶⁸ The BET¹⁷ study was performed over a total of 221 nuclear configurations considering both activation and reaction paths. Molecular geometries and ELF valence basin attractor positions were visualised using the GaussView program.⁶⁹

A stand-alone script based on the Ramer–Douglas–Peucker algorithm⁷⁰ was used to find a reduced but still suitable number of points, on which to run the IQA–REG analysis, out of the 136 points belonging to the activation IRC path; an RMSE value of 0.05 kcal mol⁻¹ was considered for the overall activation energy path and 0.025 kcal mol⁻¹ for the BET phases (see S8 in ESI,† for more information). The IQA analysis was performed with the AIMAll package⁷¹ using the corresponding B3LYP/6-311G(d,p) monodeterminantal wavefunctions. In order to test the effect of dispersion interactions on the IQA–REG outcomes, the wevefunctions and IQA–REG analysis were computed including Grimme's D3 dispersion corrections with Becke–Johnson damping.⁷² In a REG-IQA-D3 analysis the total energy considered is the sum of the intra- and inter-atomic IQA components plus inter-atomic dispersion obtained from the D3 program by Grimme,⁷³ given that D3 is an additive scheme. The REG analysis was carried out via the in-house program REG.py.^52,74

The IQA scheme divides the total energy into two main energy contributions: the intra-atomic energy, E^A_intra, and the interatomic energy, V^AB_inter.⁵¹ The interatomic energy is in turn divided into two additional terms: the interatomic electrostatic energy (typically referred to as “classical”), V^AB_cl, and the interatomic exchange–correlation energy, V^AB_xc, in such a way that V^AB_inter = V^AB_cl + V^AB_xc. While E_intra has been associated with steric effects,⁷⁵V_cl is related to electrostatic interactions,^76,77 and V_xc quantifies covalency.⁷⁸ Recently, it has been suggested⁷⁹ that plain V^AB_inter terms should not be used as covalent-bond strength descriptors because the electrostatic terms tend to cancel out thanks to electroneutrality and because their long-range nature makes them inadequate to define chemical bonds. Thus, chemical graphs are suggested to be primarily related to V^AB_xc.⁷⁹ Since an organic chemical reaction is mainly about the making and breaking of bonds, which is what chemists denote with dashes in the Lewis diagrams (i.e. chemical graphs), the REG analyses have been performed on a full IQA partitioning, delivering both V^AB_xc and V^AB_cl. The REG method⁵² compares the gradient of a given energy contribution E_i against the gradient of the total energy E_total, using linear regression: E_i(s) = m_REG,iE_total(s) + c_i, where s is the control coordinate (IRC in our case) governing the change in the system, m_REG,i is the REG value itself, and c_i is the y-intercept, which has currently no known chemical meaning. Thus, the REG method is only valid when the Pearson correlation coefficient R is close to 1. The REG values allow a semi-quantitative interpretation of the individual energy terms contributions to the total energy. Both the sign and the magnitude of the REG value are important. In summary, (energy) terms E_i with large positive REG_i values contribute the most to the total behaviour of the system, i.e. they increase (decrease) if the total energies increase (decrease), while terms with large negative REG_i values work against the total behaviour of the system, i.e. they decrease (increase) if the total energies increase (decrease). For instance, in the activation energy path, energy terms with positive REG values are unfavourable and contribute to the barrier, while those with negative REG values are favourable and facilitate the reaction. Ranking the energies from largest to smallest produces an ordered list of IQA energy terms that directly contribute towards (or against) a given energy segment, which in our case coincides with a barrier. This list provides a chemically intuitive interpretation for each energy segment being considered.

3. Results and discussion

This section has been divided into three subsections: (i) a BET study of the 32CA reaction of nitrone 3 with ethylene 5 in order to characterise the molecular mechanism in terms of bonding changes; (ii) an IQA–REG analysis along the activation energy path (Fig. 4a) in order to determine the main factors contributing to the energy barrier; and finally, (iii) an application of the IQA–REG method within the four segments characterised through BET along the activation path (Fig. 4b) in order to probe whether the total energy variations associated with these topological phases are indeed related to the expected population changes and to investigate any differences with respect to the energy decomposition analysis performed considering no BET partition of the reaction path. An additional section describing the potential energy surface of the 32CA reaction between nitrone 3 and ethylene 5 is provided in ESI.†

3.1. BET study of the zw-type 32CA reaction between nitrone 3 and ethylene 5

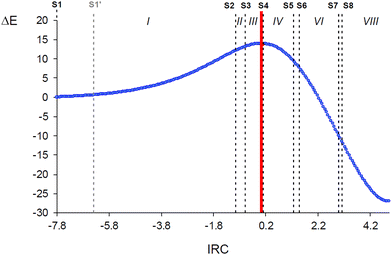
Many BET studies of 32CA reactions of substituted nitrones with different types of ethylene and acetylene derivatives have already been performed characterising their molecular mechanism^{15,34,37–40} but the simplest one involving nitrone 3 and ethylene 5 has never been explored in detail. Only BET data at the MPWB1K/6-311G(d) computational level have been reported in ref. 7 with no further discussion. In addition, the present BET study aims to serve as a representative simple example on how BET would be used to interpret the origin of a given reaction barrier, beyond the description of the bonding changes, in order to analyse then how the resulting interpretation is related to the IQA–REG results. Consequently, despite the many BET mechanistic studies of other 32CA reactions involving nitrones, this BET study of the simplest 32CA reaction between nitrone 3 and ethylene 5 is indispensable for the purposes of the present work.

BET allowed finding seven catastrophes, S2–S8, associated with a change in number and/or type of ELF valence basins in the core reacting system, which divide the reaction path into eight topological phases (marked with roman number in Fig. 5) related to different bonding changes (see Table 1). The objective of the work is focused on the activation energy path. Hence only the bonding changes taking place from reagents to the TS along Phases I–III are described, as is clear from Fig. 5. ELF valence basin populations for the catastrophes found along the zw-type 32CA reaction of nitrone 3 with ethylene 5 are gathered in Table 1, while the phases in which the IRC is divided are shown in Fig. 5. Note that structure S1′ is only included for a later analysis in Section 3.3.

Fig. 5 Phases in which the IRC associated with the zw-type 32CA reaction between nitrone 3 and ethylene 5 is topologically divided. The red line indicates the position of the TS, while black dashed lines separate the phases defined by structures S_i. Relative energies (ΔE, in kcal mol⁻¹) are given with respect to the first structure S1.

Table 1 ELF valence basin populations (in average number of electrons, e), relative energies with respect to the first structure of the IRC (ΔE, in kcal mol⁻¹), IRC values (in Å amu^1/2), and C1–C5 and O3–C4 distances (in Ångströms, Å), for the S1–S9 structures along the zw-type 32CA reaction of nitrone 3 with ethylene 5

Structures	S1	S1′	S2	S3	TS	S4	S5	S6	S7	S8	S9
Phases		I	II		III	IV		V	VI	VII	VIII
d(C1–C5)	3.413	3.197	2.332	2.272	2.163	2.153	1.957	1.919	1.697	1.683	1.542
d(O3–C4)	2.984	2.865	2.265	2.226	2.153	2.146	2.010	1.982	1.772	1.753	1.448
IRC	−7.84	−6.45	−0.99	−0.64	0.00	0.06	1.22	1.45	2.96	3.08	4.88
ΔE	0.0	0.5	12.0	13.0	13.9	13.9	9.5	7.7	−9.9	−11.4	−27.1
V(C1,N2)	3.69	3.69	2.75	2.61	2.36	2.34	2.07	2.03	1.86	1.85	1.77
V(N2)			0.86	1.04	1.35	1.38	1.78	1.85	2.17	2.19	2.35
V(N2,O3)	1.46	1.45	1.31	1.29	1.24	1.23	1.15	1.13	1.03	1.03	0.92
V(C4,C5)	1.70	1.66	1.55	3.16	3.14	2.86	2.44	2.37	2.07	2.06	1.90
V′(C4,C5)	1.66	1.69	1.66
V(O3)	3.01	3.00	2.97	2.97	2.95	2.95	2.91	2.91	2.76	2.75	2.52
V′(O3)	2.84	2.83	2.85	2.85	2.86	2.86	2.88	2.88	2.70	2.70	2.55
V′′(O3)									0.34
V(C1)			0.31	0.36	0.47	0.48	0.66
V(C5)						0.28	0.57
V(C4)							0.13	0.17	0.33
V(C1,C5)								1.29	1.64	1.66	1.85
V(O3,C4)										0.68	1.22

---

Phase I, −7.84 ≤ IRC < −0.99 Å amu^1/2, starts at the first structure of the reaction path, S1 (d(C1–C5) = 3.413 Å and d(O3–C4) = 2.984 Å), and ends at the structure right before the second catastrophe structure, S2 (see Fig. 5). The topological analysis of the ELF of S1 usually resembles that of the separated reagents. At S1, the nitrone moiety presents a V(C1,N2) disynaptic basin integrating 3.69 e, a V(N2,O3) disynaptic basin with 1.46 e, and two V(O3) and V′(O3) monosynaptic basins integrating to a total of 5.85 e. The ethylene system is characterised by two V(C4,C5) and V′(C4,C5) disynaptic basins integrating a total population of 3.36 e, which would be 4.0 e for an ideal double bond. According to Lewis’ bonding model,²² these populations can be related to a nitrone C1=N2 double bond, an N2–O3 single bond, three O3 oxygen lone pairs, and an underpopulated ethylene C4=C5 double bond (see Scheme 2). The ELF charges at the N2 and O3 atoms are +1.20 and −0.67 e, respectively. Thus, nitrone 3 is classified as a zwitterionic TAC due to the absence of any pseudoradical or carbenoid center.⁷

Scheme 2 ELF Lewis-like structures representing the bonding changes taking places along the activation IRC path of the 32CA reaction between nitrone 3 and ethylene 5. Energy costs of Phases I–III are given below the arrows, in kcal mol⁻¹.

During the long Phase I of 118 structures, the population of the nitrone C1=N2 double bond increases by 0.20 e, while the nitrone N2–O3 single bond and the ethylene C4=C5 double bond are both depopulated by approximately 0.15 e (see Table S2 in ESI,† for the ELF populations of the last structures of each BET phase). At the end of Phase I, the V(C1,N2) disynaptic basin has reached 3.89 e. This is interesting taking into account that this bond has to break in order to form the C1 pseudoradical center and N2 non-bonding electron density, and so, a depopulation should have been expected instead. A closer look suggests that this population comes from both N2–O3 and N2–H bonding regions, which depopulate by 0.14 and 0.04 e, respectively. The most relevant change along Phase I is therefore the accumulation of electron population in the C1=N2 bonding region, while the N2–O3 and C4=C5 bonding regions are depopulated to a slightly lesser extent. These changes demand the highest overall energy cost along the activation energy path, of about 12.0 kcal mol⁻¹ (see Table 1).

The short Phase II (see Fig. 5), −0.99 ≤ IRC < −0.64 Å amu^1/2, begins at S2 (d(C1–C5) = 2.332 Å and d(O3–C4) = 2.265 Å) and comprise only 6 structures. At S2, the V(C1,N2) disynaptic basin is suddenly depopulated by 1.14 e and two new V(N2) and V(C1) monosynaptic basins are created with initial populations of 0.86 and 0.31 e, respectively (see Fig. 6). These ELF topological changes are associated with the rupture of the C1=N2 double bond, which is now characterised as a partial double bond, leading to the formation of a pseudoradical center at the C1 carbon and the N2 non-bonding electron density present at the final isoxazolidine 6 (see Schemes 1 and 2). This means that instead of gathering their density at the N2 nitrogen directly, the N2–O3 and N2–H regions preferred to redistribute it first into the C1=N2. This change might look drastic in terms of population but, given the proximity between S2 and the last structure of Phase I, it only demands an energy cost of 0.2 kcal mol⁻¹.

Fig. 6 ELF basin attractor positions at TS and the structures characterising Phases I–III along the activation IRC path of the 32CA reaction between nitrone 3 and ethylene 5. ELF valence basin populations are given in brackets, in average number of electrons, e.

Along Phase II, the most relevant population changes, considered from the last structure of Phase I to the last structure of Phase II, are the strong depopulation of the C1–N2 region by 1.25 e and gathering of 1.01 e at the N2 nitrogen, which have an overall energy cost of only 1.0 kcal mol⁻¹. This emphasises that the greatest population changes do not necessarily mean a huge total energy variation, as pointed out in the Introduction.

Finally, Phase III, −0.64 ≤ IRC ≤ 0.00 Å amu^1/2, begins at S3 (d(C1–C5) = 2.272 Å and d(O3–C4) = 2.226 Å) and ends at the TS of the 32CA reaction (d(C1–C5) = 2.163 Å and d(O3–C4) = 2.153 Å) (see Fig. 5). At S3, the two V(C4,C5) and V′(C4,C5) disynaptic basins integrating a total population of 3.21 e at the end of Phase II (see Table S2 in ESI†) have merged into a new single V(C4,C5) disynaptic basin integrating 3.16 e (see Fig. 6). Although this topological change has been associated with the rupture of double bonds,⁸⁰ in terms of the Lewis’ bonding model²² this change has no chemical meaning (see the unvaried structure of S3 compared to S2 in Scheme 2).

Along Phase III, which is monitored by 12 geometries along the IRC, the most relevant variations in electron population still imply the C1–N2 bonding region and the N2 atom. While the population in the former decreases by 0.28 e, the population at the latter increases by 0.34 e. The C1 pseudoradical center gathers 0.12 e. These changes present the lowest energy cost along the activation path, about 0.9 kcal mol⁻¹. Note that Phase I-1, 0.5 kcal mol⁻¹, is only the consequence of including S1′ in Section 3.3.

3.2. IQA–REG analysis of the overall activation energy path of the zw-type 32CA reaction between nitrone 3 and ethylene 5

Given that changes in individual ELF valence basin populations are found not relate to energy variations of the total system, an IQA–REG analysis was performed over the whole activation energy path in order to rigorously quantify the weight that the bonding changes actually have on the barrier as well as determine their stabilising or destabilising role. The IQA terms with the largest REG values are given in Table 2, while Pearson correlation coefficients R are given in Table S3 in ESI.† Table S3 (ESI†) also lists the REG values as ratios, for a reason that will be given below. This ratio is defined as a given REG value divided by the largest (originally, not absolute value) positive REG value. For example, the entry of V_xc(N2,O3) in Table S3 (ESI†) is 0.50 because it is equal to 1.74/3.50. A similar Table S4 in ESI,† gathers the IQA–REG analysis performed with D3(BJ) dispersion corrections. A comparison of the data given in Table 2 and Table S4 (ESI†) shows that the effect of dispersion on the total energy does not change the outcome of the IQA–REG analysis without dispersion.

Table 2 Twelve largest REG_i values corresponding to the full IQA partitioning along the activation IRC path associated with the zw-type 32CA reaction between nitrone 3 and ethylene 5. Energies, in kcal mol⁻¹, of the two most relevant V^AB_xc terms with positive and negative REG values are represented by using coloured arrows. Labels indicate regions of the chemical graph. Label ‘Ea’ corresponds to the activation energy with respect to the first structure of the reaction path, S1, while ‘other’ refers to the sum of the energies of every other full-partitioned IQA energy terms contributing towards or against the barrier. While the relative size of the coloured arrows is accurate, arrows in grey are only an approximation, indicated by the dashed top line

Energy term	REG
V xc(C4,C5)	3.50
V xc(C1,N2)	1.79
V xc(N2,O3)	1.74
V cl(C1,N2)	1.51
E intra(O3)	1.12
E intra(C4)	1.10
V xc(N2,C4)	−0.42
V cl(N2,O3)	−0.42
V cl(C4,C5)	−0.68
E intra(N2)	−1.66
V xc(O3,C4)	−2.73
V xc(C1,C5)	−3.23

---

IQA–REG results show that the V_xc(C4,C5) energy term, which is associated with the covalent character of the C4–C5 partial double bond of ethylene 5, is the one contributing the most to the barrier, with a REG value of 3.50. The positive sign of this value indicates that the bonding changes taking place in the ethylene C4–C5 region from the first structure S1 to the TS, i.e. a depopulation of about 0.22 e (see Table 1), are energetically destabilising. The next energy terms contributing to the barrier, V_xc(C1,N2), V_xc(N2,O3) and V_cl(C1,N2), are related to the bonding changes taking place in the nitrone C1–N2–O3 core structure and present significantly lower REG values that are similar each other, ranging from 1.79 to 1.51. It is worth noting the joint presence of V_xc(C1,N2) and V_cl(C1,N2), which indicates that unfavourable electrostatics develop in the C1=N2 region as a consequence of its depopulation on going towards the TS. The behaviour of V_xc(N2,O3) is in agreement with the depopulation of the N2–O3 region by 0.22 e (see Table 1). However, note that in this case V_cl(N2,O3) has a negative REG value. Finally, the two E_intra(O3) and E_intra(C4) terms, associated with the unfavourable deformation of the O3 and C4 topological volumes, have some participation as well, with REG values of 1.12 and 1.10, respectively. This is only a consequence of the shorter O3–C4 distance⁷⁵ compared to the C1–C5 one all along the activation IRC path, although the new C1–C5 single bond forms first at S6 (see Table 1).

On the other hand, the terms most contributing against the barrier, i.e. energetically stabilising the whole system, are the V_xc(C1,C5) and V_xc(O3,C4) terms, associated with a favourable electron density gathering in these regions. This can be verified by a QTAIM analysis in the regions involved. Indeed, the electron density at the corresponding bonding critical points at the TS has increased by 0.057 (C1–C5) and 0.044 (O3–C4) e Å⁻³ compared to the values at S1. Although the C1–C5 distance is (slightly) longer than the O3–C4 distance along the activation IRC path (see Table 1), as noted above, the changes in the C1–C5 region have a slightly higher stabilising effect, REG = −3.23, than those in the O3–C4 region, REG = −2.73. These values already provide a glimpse into the bond formation asynchronicity regardless of the distances, and without the need for a BET study towards the product. Note that the V(C1,C5) disynaptic basin is created before the V(O3,C4) one (see Table 1). These findings show that the unfavourable deformation of the atoms, involved in the new single bond formation as they approach each other, is not always accompanied by a favourable gathering of electron density in that region. In other words, a closer distance between atoms might not lead to a greater favourable density accumulation and vice versa, which supports that the asynchronicity in bond formation should not be inferred¹⁵ only from the geometrical symmetry of TSs.⁸¹ The E_intra(N2), with a high REG value of −1.66, is also worth mentioning. This energy term is related to a favourable steric release of the N2 nitrogen from reagents to TS, due to an expansion of its atomic basin^75,82 (see Table 1). Finally, unlike V_cl(C1,N2), two terms associated with favourable electrostatic interactions in the C4–C5 and N2–O3 regions appear with small REG values of −0.68 and −0.42, respectively.

The REG values of V^AB_cl terms may have either the opposite or the same sign as the corresponding V^AB_xc of the same region, thus adding to or cancelling out the latter. See, for instance, the cases of the C1–N2 and C4–C5 regions in Table 2. Thus, considering the V^AB_inter terms instead of the V^AB_cl and V^AB_xc ones separately might change the interpretation of the activation barrier. In order to check this out, the REG values of the five most relevant V^AB_inter terms were gathered in Table 3 while Pearson correlation coefficients were included in Table S5 in ESI.† Now, the V_inter(C1,N2) term is the highest contributor to the barrier, followed by the V_inter(C4,C5) and V_inter(N2,O3). This would mean that despite the higher weight of exchange–correlation in the C4–C5 region, the unfavourable electrostatics developed in the C1–N2 (as a consequence of its depopulation) makes its rupture even tougher.

Table 3 REG_i values for the five most relevant V^AB_inter energy terms coming from IQA partitioning along the activation IRC path associated with the zw-type 32CA reaction between nitrone 3 and ethylene 5

Energy term	REG
V inter(C1,N2)	3.30
V inter(C4,C5)	2.82
V inter(N2,O3)	1.32
V inter(O3,C4)	−3.06
V inter(C1,C5)	−3.32

---

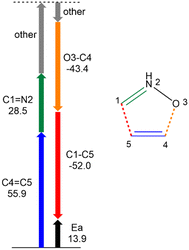
This different interpretation of the barrier depending on the analysis of V^AB_cl and V^AB_xc, or V^AB_inter terms is very important qualitatively. As has been mentioned, Martín Pendás and coworkers have recently shown that electrostatics decay too slowly, which leads to over- or underestimating the strength of interactions and, when included in the energy, yields interpretations that clearly disagree with the chemist's view of chemical bonds.⁷⁹ Thus, following their suggestion that V^AB_inter terms should not be used as covalent-bond strength descriptors,⁷⁹ the present IQA–REG analysis allows concluding that the high activation energy of the zw-type 32CA reaction between nitrone 3 and ethylene 5 is mainly due to the rupture of the ethylene C4=C5 double bond. Even though the rupture of both C1=N2 and C4=C5 bonds is relevant, the latter is more energy-demanding, i.e. 55.9 versus 28.5 kcal mol⁻¹. This finding is indeed in agreement with the harder character of ethylene 5, η = 7.76 eV, than that of nitrone 3, η = 5.55 eV, within Conceptual DFT (CDFT),^83,84 which suggests the former molecule less prone to density changes. This interpretation of the high activation barrier can be understood as a consequence of the zwitterionic structure of nitrone 3, which presents no reactive pseudoradical center able to ease the rupture of the inert unsubstituted ethylene C4=C5 double bond, unlike pseudodiradical TACs participating in pdr-type reactions (see Fig. 1).⁷

3.3. IQA–REG analysis at the BET topological phases along the activation energy path of the zw-type 32CA reaction between nitrone 3 and ethylene 5

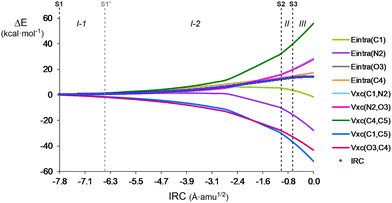
BET is able to divide the IRC path into different topological phases associated with different chemical events. Here IQA–REG is applied in the phases of the activation energy path to investigate if this method can identify whether the energy terms have a variable weight at different stages of the reaction and determine how this segmented analysis changes from the overall picture given above in Section 3.2. Note that the total behaviour of the system does not necessarily have to be maintained during the whole activation path. This type of analysis could help reveal events that might have been unidentified with BET and give a more detailed view of the energy changes and, therefore, of the mechanism.

Due to the aforementioned importance of V^AB_xc terms to characterise bond rupture and formation energetics, REG was applied to a full IQA partitioning. The intra-atomic and the interatomic electrostatic and exchange–correlation IQA terms with the largest REG values along Phases I–III are given in Table 4, while Pearson correlation coefficients are given in Table S6 in ESI.† The variation from S1 to TS of the most relevant energy terms is graphically represented in Fig. 7.

Table 4 Twelve largest REG_i values corresponding to the full IQA partitioning along Phases I–III of the activation IRC path associated with the zw-type 32CA reaction between nitrone 3 and ethylene 5

Phase I-1		Phase I-2		Phase II		Phase III
Energy term	REG	Energy term	REG	Energy term	REG	Energy term	REG
V xc(C4,C5)	2.49	V xc(C4,C5)	2.58	V xc(C4,C5)	6.98	V xc(C4,C5)	17.17
E intra(C4)	2.46	V xc(N2,O3)	1.29	V cl(C1,N2)	4.98	V cl(C1,N2)	14.24
E intra(C5)	1.90	V xc(C1,N2)	1.28	V xc(C1,N2)	3.72	V xc(C1,N2)	9.05
E intra(C1)	1.88	E intra(C4)	1.03	V xc(N2,O3)	3.45	V xc(N2,O3)	8.60
E intra(O3)	1.76	E intra(O3)	0.99	E intra(O3)	1.48	E intra(O3)	3.29
E intra(N2)	1.20	E intra(C5)	0.65	E intra(C4)	1.24	E intra(C4)	2.74
V xc(O3,C5)	−0.66	V xc(N2,C4)	−0.36	V cl(N2,O3)	−0.93	V cl(N2,O3)	−2.53
V cl(N2,C4)	−0.77	V xc(N2,C5)	−0.38	V cl(C4,C5)	−1.35	V cl(C4,C5)	−3.24
V xc(N2,C5)	−1.22	V cl(C4,C5)	−0.51	E intra(C1)	−1.67	E intra(C1)	−5.21
V cl(C1,N2)	−1.33	E intra(N2)	−0.86	V xc(O3,C4)	−4.52	V xc(O3,C4)	−11.17
V xc(C1,C5)	−2.70	V xc(O3,C4)	−2.21	E intra(N2)	−4.81	E intra(N2)	−13.10
V xc(O3,C4)	−3.40	V xc(C1,C5)	−2.39	V xc(C1,C5)	−6.32	V xc(C1,C5)	−16.12

---

Fig. 7 Variation of the most relevant IQA energy terms along Phases I–III. Relative energies, ΔE, are given with respect to the first structure of the reaction path, S1. E_intra(O3), in grey, cannot be observed because it overlaps with E_intra(C4), in orange.

First of all, the REG values obtained at different energy segments of either the same IRC path or another one cannot be quantitatively compared to each other. This is due to the different gradient of the total energy (ΔE) at each segment analysed and the ordinary least squares regression used to compute the REG values.⁵² A larger energy variation in the total system normally leads to small REG values, while the contrary holds true: small energy variations in the total system lead to larger REG values. Consequently, only ratios of terms accounting for their relative participation in each segment are meaningful and can be compared to each other. For instance, the larger negative REG value of V_xc(O3,C4) in Phase III, by 7.77 units with respect to that in Phase I-1 (see Tables 4, −11.17 versus −3.40), does not necessarily mean a greater participation of that term in Phase III; indeed, when ratios are compared, the participation of V_xc(O3,C4) with respect to the most relevant V_xc(C4,C5) term is lower in Phase III, −0.65, than in Phase I-1, −1.37 (see Table S6 in ESI†). These ratios are given in Tables S3–S6 in ESI,† with respect to the highest positive REG value in each segment.

On the other hand, as Phase I is the longest one towards the TS, it was additionally divided at S1′ into two sections, Phase I-1 and Phase I-2 (see Fig. 5), based on chemically meaningful changes in the ELF Lewis-like structures without a BET catastrophe; in this case, the turning point S1′ is associated with the depopulation of the N2–O3 bond to a permanent partial single bond (see Scheme 2).

In Phase I-1, the reagents begin to approach each other and, therefore, no bonding changes and/or interatomic interactions are expected. Accordingly, IQA–REG analysis shows that the energy profile in this early section of the IRC is mainly dominated by E_intra terms, i.e. steric effects, with only a slightly higher participation of V_xc(C4,C5), related to the covalency of the ethylene C4=C5 double bond. Besides, V_xc(O3,C4) and V_xc(C1,C5), with REG values of −3.40 and −2.70, are worth mentioning among the interatomic terms, since they present the highest absolute REG values in the segment. These results indicate that, at the earliest stage of the reaction, the favourable interactions taking place between the atoms that will lead to the new bond formation, stabilise the total system more than any other destabilising factor, which accounts for the driving force of the reaction. The latter observation is explained by looking at the relative ratios of the REG coefficients, −1.37 and −1.09 (see Table S6 in ESI†), which are even higher in absolute value than those obtained from the analysis of the overall activation path, −0.78 and −0.92 (see Table S3 in ESI†). The nitrone V_xc(C1,N2) and V_xc(N2,O3) terms present REG values of 0.91 and 0.88, respectively, showing the negligible participation of those bonds in this section of the IRC (despite the high stabilizing V_cl(C1,N2) term (see Table S6, ESI†), which is worth noting by taking into account its unfavourable nature when the whole activation path is considered, (see Table 2)). Similarly, unlike the analysis at the full activation path, it is also worth mentioning the initial unfavourable character of E_intra(N2), with a REG value of 1.20, which contrasts with its overall stabilising effect (Table 2).

In Phase I-2, both V_xc(N2,O3) and V_xc(C1,N2) start to have a relevant contribution to the barrier, with positive REG values of 1.29 and 1.28, respectively, but V_xc(C4,C5) retains its greatest role with REG = 2.58 (see Fig. 7). Thus, despite the populations of the C1–N2 and C4–C5 regions change by 0.20 and 0.14 e along Phase I-2, respectively (see Section 3.1), the latter still has a greater importance in the energy cost of this IRC segment. These results imply that the unexpected increase of the population in the nitrone C1=N2 double bond is unfavorable, which is reasonable taking into account that a rupture of a covalent double bond is usually associated with a progressive depopulation of that region and, in this case, the C1=N2 one is rather increasing its double bond character over its ground state capacity. On the other hand, E^A_intra terms lose importance, but E_intra(N2) becomes stabilising (see Fig. 7), which could be related to the initial gathering of electron density on the N2 nitrogen to form the V(N2) monosynaptic basin at S2 (see Table 1). The relative ratios of the stabilising V_xc(C1,C5) and V_xc(O3,C4) terms slightly decrease and are now below that of the most destabilising V_xc(C4,C5) term, but they start to show the bond formation asynchronicity despite the longer C1–C5 distance. Interestingly, in this segment the contribution of E_intra(O3) becomes comparable to that of E_intra(C4), with ratios of ca. 0.4 (see Table S6 in ESI,† and the overlap of both terms in Fig. 7). Note that in the previous Phase I-1, E_intra(C4) had a greater prominence, with a relative ratio of 0.99 over the 0.71 ratio of E_intra(O3).

In Phase II, the V_xc(C4,C5) term keeps having the greatest REG value, 6.98. The most noticeable change is that the V_xc(C1,N2) term with REG = 3.72 overcomes the V_xc(N2,O3) term with REG = 3.45; however, both keep presenting very similar ratios of 0.53 and 0.49, respectively (see the overlap between V_xc(N2,O3) and V_xc(C1,N2) in Fig. 7). This indicates that the negligible depopulation of the nitrone N2–O3 region by only 0.03 e contributes to the phase energy cost similarly to the depopulation of C1–N2 bond by 1.25 e. This change emphasises, once again, that ELF population changes are not necessarily directly related to their energy contribution. Note, likewise, that the population changes in C1–N2 are much higher in Phase II than in Phase I-2, but their weight to the total energy is also similar. In practice this means that the ELF population of a bond can change less than another one but have a higher or similar contribution to the barrier, and vice versa. Interestingly, no matter if the population increases (Phase I-2) or decreases (Phase II) in the C1–N2 region, V_xc(C1,N2) is always destabilising. We are also note the progressive change in the role of E_intra(C1), which goes from significantly destabilising in Phase I-1 (REG = 1.88) to negligible in Phase I-2 (REG = 0.42). This energy contribution stabilises in Phase II (REG = −1.67), a phenomenon that is related to the formation of the C1 pseudoradical center at S2 (see Table 1). Another remarkable change is the appearance of the V_cl(C1,N2) term with a high positive REG value of 4.98. However, as electrostatic interactions do not play a relevant role in the chemical transformations of covalent bonds,⁷⁹i.e. organic reactions, its impact on the reaction barrier is not discussed here.

Finally, in Phase III no significant changes with respect to the IQA–REG analysis in Phase II are observed (see the relative ratios of the energy terms in Table S7, ESI†).

4. Conclusions

A combined BET and IQA–REG study of the non-polar zw-type 32CA reaction of the simplest nitrone with ethylene has been performed at B3LYP/6-311G(d,p) level in the spirit of MEDT, in order to determine three matters: (a) the origin of the activation barrier of zw-type 32CA reactions involving zwitterionic TACs such as nitrones, (b) the usefulness of such a combined application of these two topological methodologies and what additional insights can be extracted from the application of IQA–REG to the partitioned BET phases, and (c) whether ELF valence basin population changes can be related to total energy variations.

In terms of the first matter, while BET suggests that the activation energy of this non-polar zw-type 32CA reaction is mainly associated with the rupture of the nitrone C1=N2 bond, IQA–REG indicates that the high energy cost is rather related to the rupture of the ethylene C4=C5 double bond. This apparently contradictory outcome can be rationalised as a consequence of arbitrarily considering that in BET, the higher ELF population variation of a region along the activation path, the higher the energy cost associated with that change. However, the IQA–REG interpretation actually makes sense within BET if we consider that, precisely because the nitrone C1=N2 region is more labile than the ethylene C4=C5 one, its depopulation is easier energetically. Given that IQA–REG is a more trustworthy tool to establish the origin of reaction barriers, the high activation energy of the non-polar 32CA reaction between nitrone 3 and ethylene 5 can be concluded to be a consequence of the zwitterionic structure of nitrone 3; not because it demands an extra energy cost to create the pseudoradical centers necessary for the formation of the new single bonds, as was suggested before,⁷ but because the absence of pseudoradical centers cannot facilitate the rupture of the inert unsubstituted ethylene double bond. This different interpretation between BET and IQA–REG is subtle but significant.

In terms of the second matter, the combined application of BET and IQA–REG offers a very detailed description of molecular mechanisms. While BET describes mechanisms in terms of population changes that can be related to the traditional chemical graphs used by chemists, IQA–REG determines and ranks the role of those changes energetically. In addition, IQA–REG, when applied to the BET phases, enables to characterise the variable role of the energy terms at different stages of the reaction path, i.e. the sequence of energy changes, which yields a more detailed understanding of the energetics of the reaction. In this case study, though, no significant variations throughout the activation path are observed. The different stages of the activation path are always dominated by V_xc(C4,C5), while both V_xc(C1,N2) and V_xc(N2,O3) terms associated with the nitrone covalent framework have an equitable lower participation. This is in agreement with the harder character of ethylene 5 than nitrone 3, which suggests a stronger resistance of the former to density changes.

In terms of the third matter, the lower ELF depopulation of C4=C5, 0.20 e, compared to that of C1=N2, 1.33 e, from the beginning of the reaction to the TS, emphasises how ELF-valence-basin populations and total energy changes cannot be directly related, given that V_xc(C4,C5) term has a greater positive REG value than V_xc(C1,N2). In several cases it has been observed that a greater variation in the population of a given ELF valence basin does not correspond to a greater (stabilising or destabilising) role of the interactions associated with that molecular region in the variation of the total energy of the system.

More generally, the present study has intended to emphasise how IQA–REG allows characterising the energy costs of the bonding changes in order to explain the origin of activation energies within the electron density perspective of MEDT. IQA–REG is simple and straightforward, and can offer invaluable insight to experimental and theoretical organic chemists. First, the physical meaning of the decomposed IQA energy terms can be easily related to common chemical concepts, making IQA–REG attractive and familiar to the organic chemist. Second, identifying the most relevant factors contributing to a reaction barrier, with a comprehensible chemical language, enables more efficient synthetic designs by targeting the corresponding sites with appropriate substituents. In this case, we explain why proper substitution on the ethylene or another type of TAC is needed to lower the high barrier associated with the rupture of the ethylene/acetylene multiple bond in non-polar zw-type 32CA reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 846181 (M. R.-G.), and has also received funding from Ministry of Science and Innovation (MICINN) of the Spanish Government, project PID2019-110776GB-I00 (AEI/FEDER, UE) (L. R. D). F. F. expresses gratitude to UKRI/EPSRC for PhD funding enhanced by AstraZeneca.

References

1. L. Domingo, Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry, Molecules, 2016, 21, 1319.
2. K. Fukui, Molecular orbitals in chemistry, physics, and biology. A Tribute to R. S. Mulliken, Academic Press, New York, 1964, pp. 513–537.
3. A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403.
4. B. Silvi and A. Savin, Classification of chemical bonds based on topological analysis of electron localization functions, Nature, 1994, 371, 683–686.
5. R. F. W. Bader and H. Essén, The characterization of atomic interactions, J. Chem. Phys., 1984, 80, 1943–1960.
6. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990.
7. M. Ríos-Gutiérrez and L. R. Domingo, Unravelling the Mysteries of the [3+2] Cycloaddition Reactions, Eur. J. Org. Chem., 2019, 267–282.
8. K. Kula, J. Dobosz, R. Jasiński, A. Kącka-Zych, A. Łapczuk-Krygier, B. Mirosław and O. M. Demchuk, [3+2] Cycloaddition of diaryldiazomethanes with (E)-3,3,3-trichloro-1-nitroprop-1-ene: an experimental, theoretical and structural study, J. Mol. Struct., 2020, 1203, 127473.
9. M. Soleymani and Z. Kazemi, Chegeni, A molecular electron density theory study on the [3+2] cycloaddition reaction of 5,5-dimethyl-1-pyrroline N-oxide with 2-cyclopentenone, J. Mol. Graphics, 2019, 92, 256–266.
10. P. Woliński, A. Kącka-Zych, B. Dziuk, K. Ejsmont, A. Łapczuk-Krygier and E. Dresler, The structural aspects of the transformation of 3-nitroisoxazoline-2-oxide to 1-aza-2,8-dioxabicyclo[3.3.0]octane derivatives: experimental and MEDT theoretical study, J. Mol. Struct., 2019, 1192, 27–34.
11. N. Acharjee, Understanding the geometry and [3+2] cycloadditions of nitrile imine in terms of molecular electron density theory, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2019, 58A, 645–652.
12. N. Acharjee, H. A. Mohammad-Salim and M. Chakraborty, Unveiling the synthesis of spirocyclic, tricyclic, and bicyclic triazolooxazines from intramolecular [3+2] azide-alkyne cycloadditions with a molecular electron density theory perspective, Struct. Chem., 2022, 33, 555–570.
13. L. R. Domingo, E. Chamorro and P. Pérez, Understanding the High Reactivity of the Azomethine Ylides in [3+2] Cycloaddition Reactions, Lett. Org. Chem., 2010, 7, 432–439.
14. L. R. Domingo and M. Ríos-Gutiérrez, A Molecular Electron Density Theory Study of the Reactivity of Azomethine Imine in [3+2] Cycloaddition Reactions, Molecules, 2017, 22, 750.
15. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, A Molecular Electron Density Theory Study of the Reactivity and Selectivities in [3+2] Cycloaddition Reactions of C,N-Dialkyl Nitrones with Ethylene Derivatives, J. Org. Chem., 2018, 83, 2182–2197.
16. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, An MEDT study of the carbenoid-type [3+2] cycloaddition reactions of nitrile ylides with electron-deficient chiral oxazolidinones, Org. Biomol. Chem., 2016, 14, 10427–10436.
17. X. Krokidis, S. Noury and B. Silvi, Characterization of Elementary Chemical Processes by Catastrophe Theory, J. Phys. Chem. A, 1997, 101, 7277–7282.
18. R. Gilmore, Catastrophe Theory for Scientists and Engineers, Courier Corporation, North Chelmsford, MA, USA, 1981.
19. A. E. R. Woodcock and T. Poston, A Geometrical Study of Elementary Catastrophes, Springer, Berlin, Germany, 1974.
20. R. Thom, Structural Stability and Morphogenesis: An Outline of a General Theory of Models, Westview Press, Boulder, CO, USA, 1976.
21. K. Fukui, Formulation of the reaction coordinate, J. Phys. Chem., 1970, 74, 4161–4163.
22. G. N. Lewis, THE ATOM AND THE MOLECULE, J. Am. Chem. Soc., 1916, 38, 762–785.
23. L. R. Domingo, M. Ríos-Gutiérrez, B. Silvi and P. Pérez, The Mysticism of Pericyclic Reactions: A Contemporary Rationalisation of Organic Reactivity Based on Electron Density Analysis, Eur. J. Org. Chem., 2018, 1107–1120.
24. J. Munárriz, R. Laplaza and V. Polo, A bonding evolution theory study on the catalytic Noyori hydrogenation reaction, Mol. Phys., 2019, 117, 1315–1324.
25. E. Chamorro, M. Duque-Noreña, S. Kaya, E. Rincón and P. Pérez, On the electron flow sequence driving the hydrometallation of acetylene by lithium hydride, J. Mol. Model., 2018, 24, 305.
26. V. Polo, J. Andres, S. Berski, L. R. Domingo and B. Silvi, Understanding Reaction Mechanisms in Organic Chemistry from Catastrophe Theory Applied to the Electron Localization Function Topology, J. Phys. Chem. A, 2008, 112, 7128–7136.
27. S. Berski, J. Andrés, B. Silvi and L. R. Domingo, New Findings on the Diels–Alder Reactions. An Analysis Based on the Bonding Evolution Theory, J. Phys. Chem. A, 2006, 110, 13939–13947.
28. J. Andrés, V. S. Safont, M. Oliva, K. L. Caster and F. Goulay, A bonding evolution theory study of the reaction between methylidyne radical, CH (X²Π), and cyclopentadiene, C₅H₆, Int. J. Quantum Chem., 2022, 122, e26892.
29. L. R. Domingo, A new C–C bond formation model based on the quantum chemical topology of electron density, RSC Adv., 2014, 4, 32415–32428.
30. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, A new model for C–C bond formation processes derived from the Molecular Electron Density Theory in the study of the mechanism of [3+2] cycloaddition reactions of carbenoid nitrile ylides with electron-deficient ethylenes, Tetrahedron, 2016, 72, 1524–1532.
31. L. R. Domingo and J. A. Sáez, Understanding the Electronic Reorganization along the Nonpolar [3+2] Cycloaddition Reactions of Carbonyl Ylides, J. Org. Chem., 2011, 76, 373–379.
32. M. Ríos-Gutiérrez and L. R. Domingo, The carbenoid-type reactivity of simplest nitrile imine from a molecular electron density theory perspective, Tetrahedron, 2019, 75, 1961–1967.
33. A. Kącka-Zych, Understanding the uniqueness of the stepwise [4+1] cycloaddition reaction between conjugated nitroalkenes and electrophilic carbene systems with a molecular electron density theory perspective, Int. J. Quantum Chem., 2021, 121, e26440.
34. M. Ríos-Gutiérrez, P. Pérez and L. R. Domingo, A bonding evolution theory study of the mechanism of [3+2] cycloaddition reactions of nitrones with electron-deficient ethylenes, RSC Adv., 2015, 5, 58464–58477.
35. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, How does the global electron density transfer diminish activation energies in polar cycloaddition reactions? A Molecular Electron Density Theory study, Tetrahedron, 2017, 73, 1718–1724.
36. M. J. Aurell, L. R. Domingo, P. Pérez and R. Contreras, A theoretical study on the regioselectivity of 1,3-dipolar cycloadditions using DFT-based reactivity indexes, Tetrahedron, 2004, 60, 11503–11509.
37. L. R. Domingo, M. Ríos-Gutiérrez and N. Acharjee, A Molecular Electron Density Theory Study of the Lewis Acid Catalyzed [3+2] Cycloaddition Reactions of Nitrones with Nucleophilic Ethylenes, Eur. J. Org. Chem., 2022, e202101417.
38. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, A molecular electron density theory study of the [3+2] cycloaddition reaction of nitrones with strained allenes, RSC Adv., 2017, 7, 26879–26887.
39. M. Ríos-Gutiérrez, A. Darù, T. Tejero, L. R. Domingo and P. Merino, A molecular electron density theory study of the [3+2] cycloaddition reaction of nitrones with ketenes, Org. Biomol. Chem., 2017, 15, 1618–1627.
40. A. K. Nacereddine, C. Sobhi, A. Djerourou, M. Ríos-Gutiérrez and L. R. Domingo, Non-classical CH⋯O hydrogen-bond determining the regio- and stereoselectivity in the [3+2] cycloaddition reaction of (Z)-C-phenyl-N-methylnitrone with dimethyl 2-benzylidenecyclopropane-1,1-dicarboxylate. A topological electron-density study, RSC Adv., 2015, 5, 99299–99311.
41. P. Merino, M. Chiacchio, L. Legnani and T. Tejero, BET & ELF Quantum Topological Analysis of Neutral 2-Aza-Cope Rearrangement of γ-Alkenyl Nitrones, Molecules, 2017, 22, 1371.
42. H. A. Mohammad-Salim, Understanding the Reactivity of C-Cyclopropyl-N-Methylnitrone Participating in [3+2] Cycloaddition Reactions Towards Styrene with a Molecular Electron Density Theory Perspective, J. Mex. Chem. Soc., 2021, 65, 129–140.
43. S. A. Mohammed Salih, H. A. Basheer and H. A. Mohammad-Salim, Unveiling [3+2] Cycloaddition Reactions of N-Methyl-C-3-Bromophenyl-Nitrone to Dimethyl Maleate: Molecular Electron Density Theory Perspective, J. Mex. Chem. Soc., 2022, 66, 560–574.
44. P. L. A. Popelier, in Intermolecular Forces and Clusters I, ed. D. J. Wales, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, vol. 115, pp. 1–56.
45. P. L. A. Popelier, in Drug Discovery, ed. L. Banting and T. Clark, Royal Society of Chemistry, Cambridge, 2012, pp. 120–163.
46. R. D. J. Froese, J. M. Coxon, S. C. West and K. Morokuma, Theoretical Studies of Diels–Alder Reactions of Acetylenic Compounds, J. Org. Chem., 1997, 62, 6991–6996.
47. K. Morokuma and K. Kitaura, Chemical Applications of Atomic and Molecular Electrostatic Potentials, Plenum, New York, 1981, pp. 215–242.
48. F. M. Bickelhaupt, Understanding reactivity with Kohn–Sham molecular orbital theory: E2–S_N2 mechanistic spectrum and other concepts, J. Comput. Chem., 1999, 20, 114–128.
49. D. M. Andrada and C. Foroutan-Nejad, Energy components in energy decomposition analysis (EDA) are path functions; why does it matter?, Phys. Chem. Chem. Phys., 2020, 22, 22459–22464.
50. J. Poater, D. M. Andrada, M. Solà and C. Foroutan-Nejad, Path-dependency of energy decomposition analysis & the elusive nature of bonding, Phys. Chem. Chem. Phys., 2022, 24, 2344–2348.
51. M. A. Blanco, A. Martín Pendás and E. Francisco, Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules, J. Chem. Theory Comput., 2005, 1, 1096–1109.
52. J. C. R. Thacker and P. L. A. Popelier, The ANANKE relative energy gradient (REG) method to automate IQA analysis over configurational change, Theor. Chem. Acc., 2017, 136, 86.
53. P. L. A. Popelier, P. I. Maxwell, J. C. R. Thacker and I. Alkorta, A relative energy gradient (REG) study of the planar and perpendicular torsional energy barriers in biphenyl, Theor. Chem. Acc., 2019, 138, 12.
54. I. Alkorta, J. C. R. Thacker and P. L. A. Popelier, An interacting quantum atom study of model S_N2 reactions (X⁻⋯CH₃X, X = F, Cl, Br, and I), J. Comput. Chem., 2018, 39, 546–556.
55. I. Alkorta, A. F. Silva and P. L. A. Popelier, An Interacting Quantum Atoms (IQA) and Relative Energy Gradient (REG) Study of the Halogen Bond with Explicit Analysis of Electron Correlation, Molecules, 2020, 25, 2674.
56. J. C. R. Thacker and P. L. A. Popelier, Fluorine Gauche Effect Explained by Electrostatic Polarization Instead of Hyperconjugation: An Interacting Quantum Atoms (IQA) and Relative Energy Gradient (REG) Study, J. Phys. Chem. A, 2018, 122, 1439–1450.
57. J. Munárriz, E. Velez, M. A. Casado and V. Polo, Understanding the reaction mechanism of the oxidative addition of ammonia by (PXP)Ir(I) complexes: the role of the X group, Phys. Chem. Chem. Phys., 2018, 20, 1105–1113.
58. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
59. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
60. W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
61. H. B. Schlegel, Modern Electronic Structure Theory, World Scientific Publishing, Singapore, 1994.
62. H. B. Schlegel, Optimization of equilibrium geometries and transition structures, J. Comput. Chem., 1982, 3, 214–218.
63. H. P. Hratchian and H. B. Schlegel, Theory and Applications of Computational Chemistry: The First 40 Years, Elsevier, Amsterdam, 2005, pp. 195–249.
64. H. P. Hratchian and H. B. Schlegel, Accurate reaction paths using a Hessian based predictor–corrector integrator, J. Chem. Phys., 2004, 120, 9918–9924.
65. H. P. Hratchian and H. B. Schlegel, Using Hessian Updating To Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method, J. Chem. Theory Comput., 2005, 1, 61–69.
66. M. J. Frish, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
67. S. Noury, X. Krokidis, F. Fuster and B. Silvi, Computational tools for the electron localization function topological analysis, Comput. Chem., 1999, 23, 597–604.
68. Y. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Theory and Modeling of Asymmetric Catalytic Reactions, Acc. Chem. Res., 2016, 49, 750–762.
69. R. Dennington, T. A. Keith and J. M. Millam, 2016.
70. D. H. Douglas and T. K. Peucker, Algorithms for the reduction of the number of points required to represent a digitized line or its caricature, Cartographica, 1973, 10, 112–122.
71. AIMAll (Version 19.10.12), T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019 (http://aim.tkgristmill.com).
72. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
73. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
74. F. Falcioni Available Online: Github.Com/FabioFalcioni/REG.Py (Accessed on 18 January 2023).
75. A. L. Wilson and P. L. A. Popelier, Exponential Relationships Capturing Atomistic Short-Range Repulsion from the Interacting Quantum Atoms (IQA) Method, J. Phys. Chem. A, 2016, 120, 9647–9659.
76. P. L. A. Popelier and D. S. Kosov, Atom–atom partitioning of intramolecular and intermolecular Coulomb energy, J. Chem. Phys., 2001, 114, 6539–6547.
77. P. L. A. Popelier, L. Joubert and D. S. Kosov, Convergence of the Electrostatic Interaction Based on Topological Atoms, J. Phys. Chem. A, 2001, 105, 8254–8261.
78. A. Martín Pendás, E. Francisco, M. A. Blanco and C. Gatti, Bond Paths as Privileged Exchange Channels, Chem. – Eur. J., 2007, 13, 9362–9371.
79. A. Martín Pendás, J. L. Casals-Sainz and E. Francisco, On Electrostatics, Covalency, and Chemical Dashes: physical Interactions versus Chemical Bonds, Chem. – Eur. J., 2019, 25, 309–314.
80. S. Berski, J. Andrés, B. Silvi and L. R. Domingo, The Joint Use of Catastrophe Theory and Electron Localization Function to Characterize Molecular Mechanisms. A Density Functional Study of the Diels–Alder Reaction between Ethylene and 1,3-Butadiene, J. Phys. Chem. A, 2003, 107, 6014–6024.
81. W. T. Borden, R. J. Loncharich and K. N. Houk, Synchronicity in Multibond Reactions, Annu. Rev. Phys. Chem., 1988, 39, 213–236.
82. B. C. B. Symons, D. J. Williamson, C. M. Brooks, A. L. Wilson and P. L. A. Popelier, Does the Intra-Atomic Deformation Energy of Interacting Quantum Atoms Represent Steric Energy?, ChemistryOpen, 2019, 8, 560–570.
83. R. G. Parr and W. Yang, Density-functional theory of atoms and molecules, Oxford University Press; Clarendon Press, New York: Oxford [England], 1989.
84. L. Domingo, M. Ríos-Gutiérrez and P. Pérez, Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity, Molecules, 2016, 21, 748.

---

Footnote

† Electronic supplementary information (ESI) available: Analysis of the potential energy surface associated with the 32CA reaction between nitrone 3 and ethylene 5. Table S2 with ELF data for the last structures of Phases I–III. Table S3 with relative weights and Pearson correlation coefficients R of the twelve full-partitioned IQA terms with largest REG_i values along the activation IRC path associated with the zw-type 32CA reaction between nitrone 3 and ethylene 5. Table S4 with the twelve largest REG_i values and Pearson correlation coefficients R corresponding to the full-partitioned IQA terms including D3(BJ) dispersion corrections. Table S5 with the relative weights and Pearson correlation coefficients R for the five most relevant V^AB_inter energy terms coming from IQA partitioning along the activation IRC path of the studied reaction. Table S6 with relative weights and Pearson correlation coefficients R of the twelve full-partitioned IQA terms with largest REG_i values along Phases I–III of the activation IRC path of the case study reaction. Summary description of the Ramer–Douglas–Peucker algorithm used for point selection of the IQA–REG analyses. See DOI: https://doi.org/10.1039/d3cp00329a

---