 Open Access Article
Open Access ArticleHeight-dependent oscillatory motion of a plastic cup with a camphor disk floated on water†
Risa
Fujita
,
Nami
Takayama
,
Muneyuki
Matsuo
 ,
Makoto
Iima
,
Makoto
Iima
 and
Satoshi
Nakata
and
Satoshi
Nakata
 *
*
Graduate School of Integrated Science for Life, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan. E-mail: nakatas@hiroshima-u.ac.jp; Fax: +81-824-24-7409; Tel: +81-824-24-7409
First published on 9th May 2023
Abstract
We have developed a self-propelled object, which is composed of a plastic cup and a camphor disk, on water to reflect its three-dimensional shape in the nature of motion. The self-propelled object, of which the driving force of motion is the difference in the surface tension, exhibited oscillatory motion between motion and rest. The period and the maximum speed of oscillatory motion increased and decreased depending on the height of the cup, h, respectively. Two types of diffusion coefficients were estimated based on the diffusion of camphor molecules which were indirectly visualized using 7-hydroxycoumarin. The experimental result on the period of oscillatory motion depending on h could be reproduced by the numerical calculation based on the diffusion of camphor molecules around the object and the diffusion coefficients which were experimentally estimated. The experimental results suggest that characteristic features of motion can be created based on the three-dimensional shape of the object.
Introduction
Many kinds of inanimate self-propelled objects have been developed to transport in a small space and respond to the external stimulation, e.g., chemotaxis and phototaxis.1–6 Some of objects can be driven by the difference in the surface tension around them when floating on water.7–9 The motion direction depends on the shape of the water chamber, that is, the internal or external boundaries in contact with the water surface.10–12 This dependency suggests that the spatial distribution of a surface-active substance emanating from an object on water is influenced by the boundaries of the container. However, because its motion is restricted to an air–water surface, most of the previous reports have only considered the two-dimensional spatial distribution of a surfactant.A camphor boat or a camphor disk, wherein the driving force is the difference in the surface tension around the object floated on water, has been investigated as a simple inanimate system since the camphor systems are easily manufactured.10–26 In addition, sustainable motion can be observed for 1 h, i.e., the time that the non-equilibrium camphor concentration around the object is maintained.10 Camphor systems also exhibit characteristic motion sensitive to the boundary shape.11,12
In order to consider not only the two-dimensional diffusion of camphor molecules at the air–water interface but also the three-dimensional diffusion of camphor molecules in water, we studied a self-propelled object with camphor disks glued inside a plastic cup placed on water. The period and the maximum speed of oscillatory motion depended on the cup height. These results are discussed in terms of the distance travelled by camphor molecules in the cup and the amount of molecules leaving the cup. The oscillation period was quantitatively reproduced by numerical calculations based on two modes of camphor diffusion. The characteristic features of self-propulsion can be adjusted by changing the size and shape of the three-dimensional object.
Marangoni flows due to the concentration gradient of camphor around the disk were observed in the present system. The influence of the Marangoni flow on self-propulsion has been reported.13–15,27–29 That is, the speed of the camphor disk is sensitive to the depth of the narrow water chamber, but is not sensitive to the depth of the water chamber with a large surface area such as the present system. Therefore, we discuss the period of oscillatory motion based on the diffusion of camphor molecules in the present paper.
The motion of self-propelled objects on water was generally reflected in the shapes of their two-dimensional boundaries. In comparison with these objects, we proposed a novel self-propelled object which is created three-dimensionally in this study. In addition, the experimental results on the period of oscillatory motion have not been well reproduced by numerical calculations in our previous paper.16 In the present study, the experimental results on the period of oscillatory motion depending on h have been very well reproduced by numerical calculations since we succeeded in indirectly visualizing the diffusion of camphor molecules around the camphor boat.
Experimental
(+)-Camphor was purchased from Wako Chemicals (Osaka, Japan). Water was purified by filtering through active carbon, ion-exchange resin, and Millipore Milli-Q filtering system (Merck, Germany; resistance: 18 MΩ cm). Fig. 1 shows a schematic of the self-propelled object composed of a camphor disk (diameter: 3 mm, thickness: 1 mm, mass: 5 mg) and a plastic cup. The plastic cup was made using a three-dimensional plotter (Roland, SRM-20, Japan). Water (volume: 100 mL) was poured into a glass Petri dish (inner diameter: 155 mm; depth: 15 mm) as the water phase (depth: 6 mm). The self-propelled object was carefully placed on water to prevent air from entering the cup. The cup height, h, was varied to examine the effect of camphor molecule diffusion dissolved from the disk on the oscillatory motion at h = 0, 0.5, 1.0, 1.5, and 1.8 mm. | ||
| Fig. 1 Schematic illustration of the self-propelled object composed of a plastic cup and camphor disk. The height of the cup, h, was changed as a variable parameter (h = 0, 0.5, 1.0, 1.5, or 1.8 mm). | ||
To indirectly visualize the camphor molecule distribution under the plastic cup, a solid disk (diameter: 3.0 mm; thickness: 1.0 mm; mass: 5 mg) was prepared with 1 wt% 7-hydroxycoumarin (7-HC) and 99 wt% camphor. A self-propelled object for visualization composed of a plastic cup and solid disk was placed on water (volume: 10 mL) in a glass Petri dish (diameter: 45 mm), and then observed under UV irradiation (wavelength: 365 nm, AS ONE Corporation, Handy UV Lamp UV-16, Japan) from above in a dark box. The concentration of camphor (Ccam) was estimated based on a calibration curve obtained from the intensities of the green channel (I) in an image of 7-HC solutions with several concentrations (Fig. 4). At least 4 self-propelled objects were used for each experimental condition to confirm the reproducibility of the results. The object motion was monitored using a digital video camera (SONY, HDR-CX590, Japan; minimum time resolution, 1/30 s) and the images were analysed using an image processing system (National Institute of Health, Bethesda, Image J, USA). Experiments were performed in an air-conditioned room at 293 ± 2 K. Numerical calculations were performed using the formula manipulation software, Mathematica (Wolfram).
Results
First, the self-propelled object was placed on water and observed with variable cup height, h. Fig. 2 shows the time variation of the self-propulsion speed at different values of h. An oscillatory motion between rest and rapid acceleration was observed in the examined h values (Movies S1–S3, ESI†). With increasing h, the oscillation period increased and the maximum speed decreased. Fig. 3a and b show the average values of the period and the maximum speed of the oscillatory motion, vmax, respectively. The period of oscillatory motion exhibited a linear dependence on h, whereas vmax monotonically decreased with increasing h. | ||
| Fig. 2 Time variation of the self-propelled object speed at h = (a) 0, (b) 1.0, and (c) 1.8 mm. See also Movies S1–S3 (ESI†). | ||
 | ||
| Fig. 3 (a) Period and (b) vmax of the oscillatory motion of the self-propelled objects as a function of h. | ||
The distribution of camphor molecules was measured indirectly using 7-HC to evaluate the camphor concentration variations in the plastic cup. Fig. 4a and b show snapshots of the self-propelled object from a top view at h = (a) 0 and (b) 0.5 mm. At h = 0 mm, 7-HC molecules dissolved from the solid disk isotropically diffused at t = 0 and 45 s, anisotropically at t = 95 and 110 s, and finally spilled out from the plastic disk at t = 135 and 155 s (Fig. 4a). Shortly after the spill, the object moved in the opposite direction to that of the 7-HC spill. Similar behaviour was observed at h = 0.5 mm (Fig. 4b). The diffusion length (L) under the plastic cup and diffusion time of the camphor molecules beside the plastic cup were analyzed to evaluate their diffusion coefficient under the plastic cup as the minimum diffusion length (Fig. 4c, Fig. S3 and Table S1, ESI†). The green colour intensities were analysed at points Pin and Pfirst near the inner walls of the plastic cup and around the solid disk in the diffusion region (Fig. S1a, ESI†). The average values of Iin/Ifirst before acceleration were 0.92 ± 0.01 and 1.00 ± 0.03 at h = 0 and 0.5 mm, respectively (Fig S1b, ESI†). Based on snapshots of the self-propelled objects from the top view after 1/3 s of acceleration, the camphor concentrations remaining in the cups were evaluated at h = 0 and 0.5 mm (Fig. S2, ESI†). After the acceleration of the object, the amount of camphor remaining in the cup at h = 0.5 mm was larger than that at h = 0 mm (Fig. S2c, ESI†).
 | ||
| Fig. 4 Snapshots of the self-propelled objects from a top view under UV irradiation for h = (a) 0 and (b) 0.5 mm. (c) Time variation of the diffusion length (L) under the plastic cup. After t = 155 and 220 s, the object was accelerated at h = 0 and 0.5 mm, respectively (Movies S4 and S5, ESI†). | ||
In Fig. 5, the diffusion of camphor molecules from x0 to x1 is defined as the 1st diffusion and from x1 to x2 is defined as the 2nd diffusion. Fig. 5 suggests that three diffusion modes could be considered to understand the oscillation period for a self-propelled object with a cup, as schematically shown in Fig. S2 (ESI†). Step I: homogenous diffusion of camphor molecules around the camphor disk adhered to the plastic plate bottom (Fig. 5a). Step II: heterogeneous rapid diffusion of camphor molecules around the camphor disk (Fig. 5a). Step III: diffusion of camphor molecules along the outer wall of the cup. For simplicity, the oscillation period for the self-propelled object with a cup is determined by two diffusion types, that is, the 1st and 2nd diffusion. The diffusion coefficients  and
and  for the 1st and 2nd diffusion, which were obtained from the time average value of the diffusion coefficient, were 4.14 × 10−8 and 3.38 × 10−9 m2 s−1, respectively (see the, ESI†). When h = 0, the camphor concentration was estimated based on the relationship between the green colour intensity and 7-HC concentration (Fig. S4, ESI†). The threshold camphor concentration from the resting state to acceleration, C0, was 3 mM determined by the green intensity of the water phase.
for the 1st and 2nd diffusion, which were obtained from the time average value of the diffusion coefficient, were 4.14 × 10−8 and 3.38 × 10−9 m2 s−1, respectively (see the, ESI†). When h = 0, the camphor concentration was estimated based on the relationship between the green colour intensity and 7-HC concentration (Fig. S4, ESI†). The threshold camphor concentration from the resting state to acceleration, C0, was 3 mM determined by the green intensity of the water phase.
To clarify the effect of h on motion, the friction coefficient, μ, was evaluated for 5 plastic cups with different h values based on the previously described method.17 The μ value was almost independent of h under the present conditions (Fig. S5, ESI†).
Discussion
At first, we describe the mechanism of oscillatory motion at h = 0.10,16 While camphor molecules are accumulated at the basement of the plastic plate, the camphor boat doesn’t move since the surface tension around it is balanced (state A as the resting state). When the accumulated camphor molecules are anisotropically leaked to the water surface due to the anisotropic distribution of camphor molecules around the disk enhanced by the Marangoni flow, the camphor boat is accelerated in the direction of higher surface tension, i.e., the opposite side to the leakage (state B as the moving state). As state B reverts to state A, oscillatory motion is maintained by the repetition between states A and B.Based on the experimental results and literature,15 the relationship between the oscillatory motion and height of the self-propelled object h will be discussed. The increase in oscillation period with increasing h suggests that the oscillation period depends on the diffusion length of the camphor molecules from the disk (Fig. 2 and 3a). The decreased maximum speed of oscillation with increasing h suggests that the acceleration force decreases with increasing h because the friction coefficient is almost independent of h (Fig. 2, 3b, and Fig. S5, ESI†). This indicates that the amount of camphor molecules developed from the disk to the water surface decreases with increasing h because the acceleration force depends on the amount of developed camphor molecules, and accumulated camphor molecules at h = 0 mm easily spill out to the water surface. In contrast, the diffusion is hindered at h > 0 mm owing to the existence of the cup (Fig. S1, ESI†). In fact, the amount of camphor remaining inside the cup after acceleration at h = 0.5 mm was larger than that at h = 0 mm (Fig. S2, ESI†). Fig. 4 suggests that the oscillation period is determined by the time required to accumulate camphor molecules in the cup. The diffusion of camphor molecules into the boat was visualized using 7-HC. Isotropic diffusion (step I) and anisotropic diffusion (step II), which may be strengthened by Marangoni flow, were observed during the 1st diffusion mode inside the cup.
As 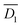 is larger than
is larger than  , the height dependency on the period of oscillation is more effective than the diameter dependency on it. Actually, the height dependency on the period of oscillation is larger than the diameter dependency on it comparing with the experimental data from the previous paper.16
, the height dependency on the period of oscillation is more effective than the diameter dependency on it. Actually, the height dependency on the period of oscillation is larger than the diameter dependency on it comparing with the experimental data from the previous paper.16
As indicated in Fig. 5b, we consider the diffusion on both the horizontal and lateral axes as the minimum diffusion length. Obvious Marangoni flows are observed when the camphor molecules are leaked at the point x2, which is the contact point between the cup and the water surface. Therefore, the period of oscillation is independent of Marangoni flows since the period of oscillation corresponds to that of state A. In addition, the existence of anisotropic diffusion suggests that the period of oscillation depends on the chemical property of the plastic plate in contact with the water phase. We previously reported that the direction of oscillatory motion is determined by the chemical property of the plastic plate.26 Furthermore, the concentration gradient is almost constant since the threshold camphor concentration to induce the acceleration is estimated at C0 = 3 mM. Therefore, the effect of Marangoni flows on the acceleration is independent of h.
According to our previous paper,17 7.7 μmol was dissolved into the water phase for 1 hour of observation. As the amount of a camphor disk at the initial condition is 33 μmol, 77 wt% mass of the camphor disk remains for one examination, i.e., the temporal decrease in the mass of camphor disk has little effect on the oscillatory motion.
The relationship between the oscillation period and diffusion of camphor molecules was also considered. Herein, the elapsed time tm is defined as that required for the camphor concentration at the triplet point on the solid, water, and air phases, C, to reach the threshold value of C0 = 3 mM. If C reaches C0, the object can move from the resting state because the driving force of motion, which depends on the water phase camphor concentration, is activated. If the camphor molecules at the base of the object completely spill out after acceleration, C is reset to zero for each oscillation. Therefore, tm corresponds to the oscillatory motion period. The value of tm was calculated to clarify the relationship between the oscillation period and h based on the 1st and 2nd diffusion modes.
According to Fick's first law, the time-averaged value of the diffusion coefficient for the n th diffusion, 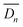 , was expressed by eqn (1).
, was expressed by eqn (1).
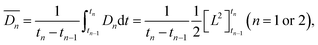 | (1) |
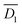 and
and  were estimated as 4.14 × 10−8 and 3.38 × 10−9 m2 s−1, respectively. The estimation of
were estimated as 4.14 × 10−8 and 3.38 × 10−9 m2 s−1, respectively. The estimation of 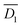 and
and  is described in ESI.†
is described in ESI.†
The diffusion process of camphor molecules supplied from the camphor disk was modeled by a one-dimensional diffusion equation, as expressed by eqn (2).
 | (2) |
For the convenience of numerical analysis, it was assumed that  continuously changes to reach
continuously changes to reach  at x = x1, as indicated using a general function in eqn (3).
at x = x1, as indicated using a general function in eqn (3).
 | (3) |
Here, x1 is described by lh (= h × 10−3 m), that is,  (m), where lh = 0, 0.5 × 10−3, 1.0 × 10−3, 1.5 × 10−3, and 1.8 × 10−3 m. lt = 1 × 10−3 m, lr = 3.5 × 10−3 m (see Fig. 5b). It was assumed that C at t = 0, C(x, 0) can be described by eqn (4).
(m), where lh = 0, 0.5 × 10−3, 1.0 × 10−3, 1.5 × 10−3, and 1.8 × 10−3 m. lt = 1 × 10−3 m, lr = 3.5 × 10−3 m (see Fig. 5b). It was assumed that C at t = 0, C(x, 0) can be described by eqn (4).
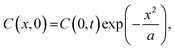 | (4) |
As the boundary conditions, C(0, t) = 7.88 mM was chosen, which is the saturated camphor concentration in water.16 In addition, C(x2 + 8 × 10−3 m, 0) = 0 mM since the camphor molecules distributed on water are sublimate,30 that is, C = 0 mM at x = x2 + 8× 10−3 (m) as the boundary condition with or without camphor. The shortest camphor diffusion distance from the edge of the camphor disk, which corresponds to x2, can be expressed in terms of h, i.e.,  (m), where ld (= 0.2 × 10−3 m) is the thicknesses of the plastic cup tops (see Fig. 1). According to the above assumptions, time tm is equal to the oscillation period when C reaches C0 (3 mM).
(m), where ld (= 0.2 × 10−3 m) is the thicknesses of the plastic cup tops (see Fig. 1). According to the above assumptions, time tm is equal to the oscillation period when C reaches C0 (3 mM).
Fig. 6 shows tm as a function of h obtained from eqn (2)–(4). The experimental results can be reproduced numerically based on the combination of the 1st and 2nd diffusions.
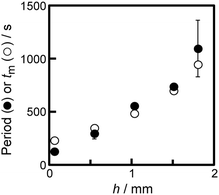 | ||
| Fig. 6 Numerical results of tm (open circles) and experimental results of the period of oscillatory motion (filled circles) as a function of h. The data of the experimental results correspond to those in Fig. 3a. | ||
Conclusions
Previous studies considered the two-dimensional diffusion of camphor molecules. Herein, we constructed a novel experimental system considering the three-dimensional diffusion of camphor molecules using a plastic cup with a camphor disk. The oscillatory motion between the motion and stop was observed and the period and maximum speed of the oscillatory motion depended on the height of the cup edge h. The friction coefficient μ was almost independent of h, indicating that the amount of camphor molecules that reached the water surface during acceleration decreased with increasing h. The maximum speed of the camphor boat depended on the amount of camphor molecules developed. This means that present self-propulsion is reflected in the three-dimensional shape since the accumulated camphor molecules into the cup are difficult to develop to the water surface during the acceleration. The diffusion of camphor molecules into the boat was visualized using 7-HC. Isotropic diffusion (step I) and anisotropic diffusion (step II), which may be strengthened by Marangoni flow, were observed during the 1st diffusion mode inside the cup. A formula that reflects the characteristic diffusion during the 1st diffusion mode inside the cup and 2nd diffusion outside the cup (step III) was proposed. Using this relation, the experimental results were quantitatively reproduced using numerical calculations. The present system is valid to design the novel self-propelled object three-dimensionally by reflecting the hydrodynamic effect as the Marangoni effect and the diffusion and accumulation of molecules that generate the driving force.Author contributions
Risa Fujita: writing – original draft, experiments. Nami Takayama: experiments. Muneyuki Matsuo: analysis, editing-original draft. Makoto Iima: analysis, editing-original draft. Satoshi Nakata: planning, editing-original draft, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by JSPS KAKENHI (No. 17K05835, 17KT0123, 20H01712, 22K14657), the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (No. 20221004) to S. N. and M. M., The Sasakawa Scientific Research Grant from The Japan Science Society to R. F., the JSPS Bilateral Joint Research Project between Japan and the Polish Academy of Sciences (JPJSBP120204602), and the JSPS-Hungary Bilateral Joint Research Project (JPJSBP120213801).Notes and references
- H. Wang and M. Pumera, Chem. Soc. Rev., 2020, 49, 3211–3230 RSC.
- P. Illien, R. Golestanian and A. Sen, Chem. Soc. Rev., 2017, 46, 5508–5518 RSC.
- Z. Huang, P. Chen, G. Zhu, Y. Yang, Z. Xu and L. T. Yan, ACS Nano, 2018, 12, 6725–6733 CrossRef CAS PubMed.
- F. Soto, E. Karshalev, F. Zhang, B. E. F. de Avila and J. Wang, Chem. Rev., 2022, 122, 5365–5403 CrossRef CAS PubMed.
- M. Zarei, Small, 2018, 14, 1800912 CrossRef PubMed.
- B. Wang, K. Kostarelos, B. J. Nelson and L. Zhang, Adv. Mater., 2021, 33, 2002047 CrossRef CAS PubMed.
- S. Yuan, X. Lin and Q. He, J. Colloid Interface Sci., 2022, 612, 43–56 CrossRef CAS PubMed.
- B. Greydanus, M. Saleheen, H. Wu, A. Heyden, J. W. Medlin and D. K. Schwartz, J. Colloid Interface Sci., 2022, 614, 425–435 CrossRef CAS PubMed.
- O. Gendelman, M. Frenkel, B. P. Binks and E. Bormashenko, J. Phys. Chem. B, 2020, 124, 695–699 CrossRef CAS PubMed.
- S. Nakata, V. Pimienta, I. Lagzi, H. Kitahata and N. J. Suematsu, Self-Organized Motion, Physicochemical Design Based on Nonlinear Dynamics, RSC-Ebook, Cambridge, 2018 Search PubMed.
- S. Nakata, H. Yamamoto, Y. Koyano, O. Yamanaka, Y. Sumino, N. J. Suematsu, H. Kitahata, P. Skrobanska and J. Gorecki, J. Phys. Chem. B, 2016, 120, 9166–9172 CrossRef CAS PubMed.
- S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 10326–10338 RSC.
- Y. Matsuda, N. J. Suematsu, H. Kitahata, Y. S. Ikura and S. Nakata, Chem. Phys. Lett., 2016, 654, 92–96 CrossRef CAS.
- Y. Xu, N. Takayama, Y. Komasu, N. Takahara, H. Kitahata, M. Iima and S. Nakata, Colloids Surf., A, 2022, 635, 128087 CrossRef CAS.
- H. Kitahata, S. Hiromatsu, Y. Doi, S. Nakata and M. R. Islam, Phys. Chem. Chem. Phys., 2004, 6, 2409–2414 RSC.
- R. Tenno, Y. Gunjima, M. Yoshii, H. Kitahata, J. Gorecki, N. J. Suematsu and S. Nakata, J. Phys. Chem. B, 2018, 122, 2610–2615 CrossRef CAS PubMed.
- N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Langmuir, 2014, 30, 8101–8108 CrossRef CAS PubMed.
- J. Sharma, I. Tiwari, D. Das, P. Parmananda and V. Pimienta, Phys. Rev. E, 2020, 101, 052202 CrossRef CAS PubMed.
- N. J. Suematsu and S. Nakata, Chem. – Eur. J., 2018, 24, 6308–6324 CrossRef CAS PubMed.
- R. J. G. Loffler, M. M. Hanczyc and J. Gorecki, Phys. Chem. Chem. Phys., 2019, 21, 24852–24856 RSC.
- H. Morohashi, M. Imai and T. Toyota, Chem. Phys. Lett., 2019, 721, 104–110 CrossRef CAS.
- R. Fujita, T. Matsufuji, M. Matsuo and S. Nakata, Langmuir, 2021, 37, 7039–7042 CrossRef CAS PubMed.
- Y. Xu, N. Takayama, H. Er and S. Nakata, J. Phys. Chem. B, 2021, 125, 1674–1679 CrossRef CAS PubMed.
- H. Kitahata, Y. Koyano, R. J. G. Löffler and J. Górecki, Phys. Chem. Chem. Phys., 2002, 24, 20326–20335 RSC.
- S. Nakata, T. Matsufuji, J. Gorecki, H. Kitahata and H. Nishimori, Phys. Chem. Chem. Phys., 2020, 22, 13123–13128 RSC.
- S. Nakata, N. Kawagishi, M. Murakami, N. J. Suematsu and M. Nakamura, Colloids Surf., A, 2009, 349, 74–77 CrossRef CAS.
- Y. S. Ryazantsev, M. G. Velarde, R. G. Rubio, E. Guzmán, F. Ortega and P. López, Adv. Colloid Interface Sci., 2017, 247, 52–80 CrossRef CAS PubMed.
- Y. S. Ryazantsev, M. G. Velarde, E. Guzman, R. G. Rubio, F. Ortega and J.-J. Montoya, J. Colloid Interface Sci., 2018, 527, 180–186 CrossRef CAS PubMed.
- V. G. Levich and D. B. Spalding, Physicochemical Hydrodynamics, Advance Publications Limited, London, 1977 Search PubMed.
- J. Kestin, M. Sokolov and W. A. Wakeham, J. Phys. Chem. Ref. Data, 1978, 7, 941–948 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00318c |
| This journal is © the Owner Societies 2023 |

