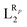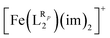Fine-tuning of the spin-crossover properties of Fe(III) complexes via ligand design

Abstract

Exploring the chemical space of a given ligand aiming to modulate its ligand field strength is a versatile strategy for the fine-tuning of physical properties such as the transition temperature (T_1/2) of spin-crossover (SCO) complexes. The computational study presented herein aims at systematically exploring the extent to which the ligand substituent effects can modulate T_1/2 in two families of Fe(III) SCO systems with a N₄O₂ coordination environment and at identifying the best descriptors for fast and accurate prediction of changes in T_1/2 upon ligand functionalization. B3LYP* calculations show that the attachment of substituents to β-ketoiminato fragments (L₁) leads to drastic changes in T_1/2, while functionalization of phenolato moieties (L₂) allows for a finer degree of control over T_1/2. Natural Bond Orbital (NBO) charges of the donor atoms, Hammett parameters for both para and meta-functionalization of L₂, and Swain–Lupton parameters for L₁ and para-functionalization of L₂ have been found to be the suitable descriptors for predicting the changes in T_1/2. Further analysis of the ligand-field splitting in such systems rationalizes the observed trends and shows that ligand substituents modify both the σ and π bonds between the Fe(III) center and the ligands. Thus, we provide simple yet reliable guidelines for the rational design of new SCO systems with specific values of T_1/2 based on their ligand design.

---

1. Introduction

Switchable materials^1–4 are key components in the design of nanodevices, because their intrinsic dual behavior or bistability allows them to achieve two different equilibrium states, thus making them perfect candidates for their use as molecular gates or their implementation in spintronic devices. Spin-crossover (SCO) molecules are a particular case of switchable systems, in which a single molecule is able to access two alternative electronic states close in energy.⁵ This change in the molecular spin-state, which can be triggered by an external stimulus, with the most common one being temperature but also pressure or electromagnetic radiation, induces significant changes in the physical properties of the system. In particular, changes in the magnetic moment, the bond lengths or the absorption spectra can be observed upon spin-transition.⁶ The phenomenon, reported for the very first time nearly a century ago,⁷ has been the subject of intense research in chemistry and physics, and a wide range of SCO molecules, involving first row transition metal ions and different degrees of nuclearity, have been reported in the literature.^8–18

A key parameter to characterize SCO systems is the transition temperature (T_1/2), which is defined as the temperature with equal populations of both spin states. The extreme sensitivity of the energy difference between the two spin states to changes in the ligand environment can be exploited to control T_1/2via ligand engineering. In fact, the strategy of attaching different substituents to a given parent ligand with the goal of modulating the ligand field strength has been long used for Fe(II) SCO complexes,^19–28 which are the most common type of SCO systems. Many of the studies on ligand substituent effects on Fe(II) complexes that have appeared in the literature over the last few years report solution measurements and/or Density Functional Theory (DFT) calculations of isolated complexes.^29–43

These techniques allow for an evaluation of the SCO properties of a given complex in the absence of crystal-packing effects and they thus allow for an unambiguous assessment of how substituents affect T_1/2 through the modulation of the electron density of the ligands and/or intramolecular steric interactions. The ability to predict in a quick and accurate way the effect of a ligand substituent on T_1/2 is key for the design of new SCO complexes with tailored switching temperatures. For this reason, significant efforts have been recently made to establish correlations between T_1/2 and electronic descriptors (e.g. Hammett parameters) as well as to achieve a detailed understanding of how substituents affect the strength of the ligand field by means of extensive studies based on solution measurements and/or DFT calculations of a large number of Fe(II) complexes with different substituents.^16,44–48 Comprehensive studies aimed at establishing correlations between SCO properties and simple structural parameters have been reported, too.⁴⁹

Even though the first SCO compound ever reported contained an Fe(III) metal center, it has not been until very recently that complexes with such metal ions are being considered an alternative to Fe(II) complexes for the development of SCO systems.^50–59 Although Fe(II) still vastly dominates the field of SCO, Fe(III) complexes offer certain advantages, such as their open air stability, which makes them quite appealing from the point of view of actual implementations. Like in the case of Fe(II) complexes, it has been shown in several investigations that the SCO properties of Fe(III) complexes can be tuned through ligand substituents.^60–67 Recent studies using solution measurements and/or DFT calculations of isolated complexes have evaluated the effect of ligand substituents on T_1/2 of different types of Fe(III) compounds, including complexes prepared with quinolylsalicylaldimine,^68–71N-ethyl-N-(2-aminoethyl)salicylaldiminate,⁷²N-methyl-N-(2-aminoethyl)salicylaldiminate⁷³ and 2-((E)-(2-(ethylamino)ethylimino)methyl)-X-methoxyphenol.⁷⁴ Despite the most valuable insights provided by these studies, a full picture on the effect of substituent groups on the SCO properties of Fe(III) complexes is still missing. In fact, to the best of our knowledge, no comprehensive studies dealing with a large dataset of substituents have been yet reported. This obviously hinders the use of ligand functionalization as a tool to fine-tune the ligand field strength and, thus, T_1/2 of Fe(III)-based SCO molecules is obtained. In seeking to tackle this problem, herein, we present the results of a computational study that has been carried out with the goal of addressing the following issues: (i) explore the extent that T_1/2 of a given parent Fe(III) SCO molecule can be modulated via ligand functionalization with substituents of different electron-withdrawing or electron-donating capabilities; (ii) establish correlations between T_1/2 and electronic-structure descriptors that serve as a guide to the design of new Fe(III) SCO molecules; (iii) analyze the modulation of T_1/2 in terms of changes in the splitting energies of the d-orbitals.

The systematic study presented in this work has been carried out using two different parent molecules with a N₄O₂ donor atom set, which gives rise to the most common coordination environment in Fe(III)–SCO complexes. The two parent systems, [Fe(L^R₁)(im)₂]⁺ and , have two imidazole (im) ligands in the axial positions and a tetradentate ligand in the equatorial positions: L₁ = N,N′-ethylene-bis(acetylacetoniminato-N,N′,O,O′) and L₂ = (2,2′-(ethane-1,2-diylbis((nitrilo)eth-1-yl-1-ylidene))diphenolato. As can be seen from Fig. 1, different R substituent groups can be attached to these two tetradentate ligands. In the case of L₁, we will consider two chelate ring substituents in each β-ketoiminato fragment. In the case of L₂, in turn, we will functionalize each phenolato moiety with a substituent that will be placed either in para (R_p) or in meta position (R_m) with respect to the O donor atom. It should be mentioned that complexes with R_p or R_m = –OMe have already been reported.⁷⁵ Using the experimentally known systems [Fe(L^R₁)(im)₂]⁺ (R = –Me)⁷⁶ (R = H) as a starting point,⁷⁷ our calculations show that it is possible to modulate T_1/2via ligand functionalization in such systems and that, in fact, linear correlations can be extracted to predict and rationalize the behavior of such quantity in the studied systems. This article is organized as follows. We will first introduce the computational methodology used in this article. In the Results and discussion section, we will first investigate the extent to which the T_1/2 of [Fe(L^R₁)(im)₂]⁺ and can be tuned through ligand functionalization. Then, we will establish which are the best descriptors for a quick and accurate prediction of the observed substituent effects. After that, we will provide a rationale for the observed trends on the basis of splitting energies of the d-orbitals. Finally, the conclusions will be presented.

Fig. 1 Schematic representation of the two systems studied in this work. Left, [Fe(L^R₁)(im)₂]⁺ (L₁ = N,N'-ethylene-bis(acetylacetoniminato-N,N′,O,O′)), and right, (L₂ = (2,2′-(ethane-1,2-diylbis((nitrilo)eth-1-yl-1-ylidene))diphenolato)), im = imidazole, and R = R_p = R_m = –NH₂, –OMe, –F, –Cl, –Br, –CH₃, –H, –CN and –CH₃.

1.1. Computational details

Over the last few years, several computational studies devoted to calculating T_1/2 in SCO systems have appeared in the literature and showed that using Density Functional Theory (DFT) calculations, it is possible to accurately compute spin-state energy gaps in SCO systems,^78–91 and their corresponding T_1/2.⁹² In some cases, such studies are able to generate models that rationalize the experimentally reported trends in families of SCO molecules by analyzing the underlying electronic structure in terms of d-based molecular orbitals.^38,93–95 Recently, we have benchmarked several DFT methods against a large data set of Fe(III) SCO systems.⁹⁶ From that study, it was clear that both TPSSh^97,98 and B3LYP*⁹⁹ are able to correctly predict the energy window for SCO to occur in such systems and, in particular, B3LYP* was able to minimize the error with respect to the calculation of the corresponding T_1/2. B3LYP* has been also benchmarked against correlated multiconfigurational wave function calculations and proven to provide accurate geometries, vibrational frequencies, spin-state energy gaps and absorption spectra for Fe(III) SCO systems.¹⁰⁰ For these reasons, we have chosen the B3LYP* exchange–correlation functional to explore ligand–substituent effects on the SCO properties of Fe(III) complexes.

The adiabatic energy gaps between the sextet spin states (S = 5/2) and the doublet spin states (S = 1/2) of the [Fe(L^R₁)(im)₂]⁺ and 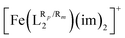systems have been evaluated by means of DFT full optimizations. These calculations have been carried out using the Gaussian 16 (revision B0.1)¹⁰¹ electronic structure package with a 10⁻⁸ convergence criterion for the density matrix elements, using the latest triple-ζ basis set with polarization functions for all elements (def2-TZVP).^102,103 The corresponding vibrational analysis was done for all optimized structures to ensure that they were minimums along the potential energy surface. The transition temperatures (T_1/2) were estimated by means of the following expression, which holds under the condition of thermodynamic equilibrium:

In this equation, ΔH_HS–LS is the enthalpy difference between the HS and LS states and ΔS_HS–LS is the entropy difference between the HS and LS states. The ΔH_HS–LS value is obtained through eqn (2):

ΔH_HS–LS = ΔE_HS–LS + ΔH_vib (2)

where ΔE_HS–LS and ΔH_vib are, respectively, the adiabatic energy difference and the vibrational enthalpy difference between the HS and LS states. The vibrational enthalpy of each state can be obtained by means of the frequencies of the vibrational normal modes (ν_i) and a standard equation in statistical thermodynamics:

The ΔS_HS–LS value, in turn, can be computed through eqn (4):

ΔS_HS–LS(T) = ΔS_elec + ΔS_vib(T) (4)

where ΔS_elec and ΔS_vib are, respectively, the electronic entropy difference and the vibrational entropy difference between the HS and LS states. The electronic entropy (S_elec) of each state can be straightforwardly obtained by means of eqn (5):

S_elec = R ln(2S + 1) (5)

Finally, the calculation of the vibrational enthalpy of each state can be done by means of another standard equation in statistical thermodynamics:⁹⁶

The analysis of the splitting of the d-orbitals has been performed by means of n-electron valence perturbation theory (NEVPT2)¹⁰⁴ calculations on the low-spin states (S = 1/2) of the systems, as implemented in the ORCA 4.0 computer code.^105,106 In these calculations, we employed the def2TZVP basis set, including the corresponding auxiliary basis set for the correlation and Coulomb fitting. The active space contains the 5 d-orbitals of the metal and 5 electrons, and the ab initio ligand-field theory (AILFT)¹⁰⁷ approach was employed to extract the related orbitals.

2. Results and discussion

2.1. Impact of ligand substituents on T_1/2 for [Fe(L^R₁)(im)₂]⁺ and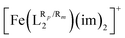

The investigation of ligand substituents’ effects on the SCO properties of [Fe(L^R₁)(im)₂]⁺ and (Fig. 1) was done through a selection of substituents that ranged from electron withdrawing groups (EWG) to electron donor groups (EDG), aiming to cover the whole range of inductive and resonance effects over the ligand field. The results collected in Table 1 show that functionalization has a very large impact on the spin-state energy and enthalpy gaps of [Fe(L^R₁)(im)₂]⁺, as well as on the corresponding T_1/2. In fact, the range of T_1/2 values afforded by the substituents is so large (∼450 K) that in some cases, the SCO behavior may be suppressed as a result of an exceedingly high value of T_1/2. The degree of change in spin-state energy gaps and T_1/2 values that can be achieved upon functionalization of the aromatic rings of the 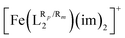system is smaller than that observed for the [Fe(L^R₁)(im)₂]⁺ system (cf.Tables 2 and 3). Remarkably, the para functionalization on the aromatic rings has a larger effect on the spin-state energy gap than the meta functionalization, which results in a different degree of tunability of T_1/2 depending on the type of isomer. Specifically, T_1/2 ranges from 243 K to 302 K (cf.Table 2) and from 174 K to 320 K (cf.Table 3) for meta and para functionalization, respectively.

Table 1 Effect of ligand substituents on the spin-state energy gap (ΔE), enthalpy change (ΔH), entropy change (ΔS) and computed T_1/2 for the [Fe(L^R₁)(im)₂]⁺ functionalized system

R	ΔE/kcal mol^−1	ΔH/kcal mol^−1	ΔS/cal K^−1 mol^−1	T 1/2/K
–NH2	1.87	2.99	15.13	187
–OMe	3.32	4.28	14.55	283
–F	3.90	4.95	15.40	308
–Br	4.45	5.48	15.43	343
–Cl	4.90	5.94	15.32	374
–CH3	7.08	8.13	15.07	521
–H	7.60	8.77	15.81	536
–CN	8.92	10.05	16.95	574
–CF3	9.61	10.69	16.18	641

---

Table 2 Effect of ligand substituents on the spin-state energy gap (ΔE), enthalpy change (ΔH), entropy change (ΔS) and computed T_1/2 for the meta-functionalized system. The σ_m Hammett constant associated with each substituent is also given

Rm	σ m	ΔE/kcal mol^−1	ΔH/kcal mol^−1	ΔS/cal K^−1 mol^−1	T 1/2/K
–NH2	−0.161	2.62	3.66	14.25	245
–CH3	−0.069	2.92	3.99	15.74	243
–H	0.000	2.92	3.95	14.74	256
–OMe	0.115	2.58	3.60	14.94	230
–F	0.337	3.36	4.37	14.42	291
–Cl	0.373	3.32	4.32	14.48	285
–Br	0.393	3.32	4.33	14.46	286
–CF3	0.430	3.52	4.54	14.76	294
–CN	0.560	3.53	4.54	14.38	302

---

Table 3 Effect of ligand substituents on the spin-state energy gap (ΔE), enthalpy change (ΔH), entropy change (ΔS) and computed T_1/2 for the para-functionalized system. The σ_p Hammett constant associated with each substituent is also given

Rp	σ p	ΔE/kcal mol^−1	ΔH/kcal mol^−1	ΔS/cal K^−1 mol^−1	T 1/2/K
–NH2	−0.660	1.66	2.74	14.85	174
–OMe	−0.268	1.58	2.63	14.68	168
–CH3	−0.170	2.73	3.81	15.52	234
–H	0.000	2.92	3.95	14.74	256
–F	0.062	2.80	3.84	14.79	247
–Cl	0.227	2.95	3.98	14.59	260
–Br	0.232	3.00	4.02	14.55	263
–CF3	0.540	3.69	4.70	15.00	301
–CN	0.660	3.68	4.68	14.04	320

---

Therefore, while L^R₁ offers a platform to control, but also to switch on or off the SCO behavior in this family of compounds, the ligand provides with a much finer degree of control over the transition temperature. This difference is due to, obviously, the ligand design itself. In L^R₁, the R groups are directly connected to the acetylacetoniminato group, thus heavily impacting the frontier molecular orbitals and the charge distribution in the ligand. In the systems, this effect is subtler due to the fact that the aromatic rings are being functionalized with EDG or EWG groups, an effect that impacts in the phenolate group, but in a smoother way. It is important to stress that regardless of the system and position of substituents, functionalization with EWG (EDG) groups leads to an increase (decrease) in T_1/2 in all systems considered herein. This is in line with the ligand substituent effects observed in Fe(II) complexes in which pyridine-based ligands are functionalized in the para position.^44,46,47 Although very scarce (see Table S10 in the ESI†), the available data in solution for the , [Fe(L^pOMe₂)(im)₂]⁺ and [Fe(L^mOMe₂)(im)₂]⁺ systems support our computed values for T_1/2.^75,108

2.2. Assessment of descriptors for predicting the effect of ligand substituents on T_1/2

After having demonstrated the strong effects of ligand substituents on T_1/2 of [Fe(L^R₁)(im)₂]⁺ and , we will now investigate the correlation between changes in T_1/2 and changes in different types of descriptors with the goal of identifying the best descriptors for a quick and accurate prediction of T_1/2 variations upon functionalization. We will first investigate the performance of descriptors associated with the substituents. Specifically, we will consider electronegativity,¹⁰⁹ Hammett parameters,^110,111 and Swain–Lupton resonance parameters.¹¹² As it may be seen in Fig. S7 and S8 (ESI†), the values of substituent electronegativity do not correlate at all with the T_1/2 values of [Fe(L^R₁)(im)₂]⁺ (S7) (ESI†) and barely correlate with the T_1/2 values of (S8) (ESI†). The correlation between electronegativity and T_1/2 substantially improves when considering functionalization in the meta position in the aromatic rings of (S8) (ESI†). Notwithstanding such an improvement, the correlation is not yet good enough to allow for an accurate prediction of T_1/2 variations. The difference in performance of the electronegativity descriptor depending on the type of functionalization of (meta vs. para) hints at a strong impact of π-bonding resonance effects induced by substituents in the para position, not captured in the electronegativity. Indeed, a good correlation exists between the σ_p Hammett parameter and the T_1/2 values of the systems (see Fig. 2). Correlations of similar quality between σ_p values and experimentally measured T_1/2 values have been reported for Fe(II) complexes.^44,46 The correlation between the σ_m Hammett parameter and T_1/2 of is slightly worse than the correlation observed for substituents in the para position (see Fig. 2). Yet, the correlation found between σ_m and T_1/2 is better than the correlation between electronegativity and T_1/2. As it may be seen in Fig. S1 (ESI†), Hammett parameters are not reliable for an accurate prediction of the impact of substituents on the β-ketoiminato fragments of the [Fe(L^R₁)(im)₂]⁺ system, especially in the case of σ_m values, which barely correlate with T_1/2 values. The better correlation of σ_p with T_1/2 for [Fe(L^R₁)(im)₂]⁺ as compared to σ_m is highly suggestive of the importance of π-bonding resonance effects. In fact, a good correlation is found between Swain–Lupton resonance parameters and T_1/2 for [Fe(L^R₁)(im)₂]⁺ (see Fig. 3). These resonance parameters also correlate well with the T_1/2 values of (see Fig. 3), which is in line with the good correlations found between Swain–Lupton parameters and the spin-state energy gaps of substituted [Fe(bpy)₃]²⁺ complexes.⁴⁷

Fig. 2 Correlation between the computed T_1/2 with the Sigma Hammett constants for the (R = –NH₂, –OMe, –F, –Cl, –Br, –CH₃, –H –CN and –CH₃) system. Left, and right ligands (R² = 0.79 and 0.88, respectively).

Fig. 3 Correlation between the computed T_1/2 with the Swain–Lupton parameters for the [Fe(L^R₁)(im)₂]⁺ (left) and (right) systems (R = –NH₂, –OMe, –F, –Cl, –Br, –CH₃, –H –CN and –CH₃). (R² = 0.89 and 0.86, respectively).

The results presented thus far in this subsection demonstrate that descriptors associated with the electronic properties of substituents provide an efficient tool for a quick and reasonably accurate prediction of ligand-substituent effects on the SCO behavior of Fe(III) complexes. In particular, Hammett parameters correlate well with T_1/2 when considering functionalization of phenolato moieties. Remarkably, our work has also shown that Swain–Lupton resonance parameters lead to an accurate prediction of changes in T_1/2 in systems where a β-ketoiminato fragment is functionalized, thus allowing for predictions that go beyond substitutions in aromatic rings.

We will now turn our attention to the performance of descriptors obtained from the DFT calculations carried out for the coordination compounds. Given that the crystal field felt by the Fe(III) ions depends on the charge of the coordinating atoms, we will focus on descriptors associated with such charge. As done in a previous study of Fe(II)–SCO complexes,⁴⁶ we have chosen the NBO charges, i.e., the charges obtained from a Natural Bond Orbital analysis. As it may be seen in Fig. 4, a clear correlation between T_1/2 (and also the spin-state energy gap) of [Fe(L^R₁)(im)₂]⁺ and the NBO charge of the N donor atoms of the L^R₁ ligand can be found. Notably, the good correlation is found for both the LS and HS states. A multiple regression using the NBO charges on the N and O donor atoms as independent variables does not result in a better tool for predicting changes in T_1/2 because the charge on the O atom barely correlates with T_1/2. In contrast, a good correlation can be obtained between the NBO charge of the O donor atom of the ligand and the T_1/2 and spin-state energy gap values of (see Fig. S3, ESI†). This is understandable due to the fact that this donor atom is going to be more affected by the aromatic ring functionalization, as it is directly bonded to the ring. Note, however, that the changes in the partial charge of the O donor atom in 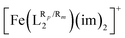are much more subtle than the changes in the partial charge of the N donor atom in [Fe(L^R₁)(im)₂]⁺. As shown in Fig. S4 (ESI†), Mulliken charges of the N-donor atom can also be used to extract some correlations with the computed spin-state energy gap for all studied systems, but their performance is poorer with respect to the NBO ones, and these correlations can only be outlined for one of the two accessible spin-states.

Fig. 4 Correlation between the spin-state energy gap (ΔE, left) and the computed T_1/2 (right) against the NBO charge on the N atom of the L^R₁ ligand of the [Fe(L^R₁)(im)₂]⁺ system. Red for high-spin and blue for low-spin state, respectively. (R² = 0.92 and 0.91 for the ΔE correlation, and 0.87 and 0.86 for the T_1/2 correlation, high-spin and low-spin, respectively).

The good correlations obtained between T_1/2 and the NBO charges of donor atoms in the Fe(III) complexes mean that the impact of a given substituent on the T_1/2 values of [Fe(L^R₁)(im)₂]⁺ and can be accurately predicted without having to perform two DFT calculations. Only one DFT calculation is required, thus halving the amount of computer time needed. Given the good correlation found for both spin states, the DFT calculation can be performed in either the LS or the HS state. In an attempt to further reduce the computational effort, we investigated whether ligand-substituent effects on the SCO temperature can be accurately predicted by means of NBO charges of the free ligand. Unfortunately, the correlation between NBO charges and T_1/2 substantially worsens when considering free ligands (see Fig. S5, ESI†), thereby preventing the use of DFT-obtained charges in free ligands as a tool for a quick and accurate prediction of changes in T_1/2 in the systems considered herein, with the only exception of the L^p₂ ligand, for which a poor correlation can be observed (S5) (ESI†). Our results on the NBO charges of free ligands contrast with the excellent correlations found for some of the Fe(II) complexes reported in ref. 46. Other attempts to find descriptors obtained from DFT calculations of the free ligands for a quick and accurate prediction of changes in T_1/2 were unsuccessful too. The energy of the HOMO for both, in the complex and as free ligand, correlates properly with the T_1/2 for systems, but such correlation disappears for [Fe(L^R₁)(im)₂]⁺, thus making also this descriptor less universal than one would like to (S6) (ESI†).

2.3. Rationalizing ligand-substituent effects based on the splitting energies of d-orbitals

We will now analyze the electronic structure of [Fe(L^R₁)(im)₂]⁺ and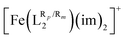 with the goal of providing more insight into the observed ligand-substituent effects. In general, the expected splitting of the Fe(III) d-orbitals in an octahedral ligand field will follow the well-known 2 (e_g) over the 3 (t_2g) pattern. The results from AILFT calculations carried out on the optimized LS (S = 1/2) geometries of [Fe(L^R₁)(im)₂]⁺ show that this is indeed the case (see Fig. 5). The degeneracy within the t_2g and e_g manifolds is also lifted with the exception of some [Fe(L^R₁)(im)₂]⁺ systems, in which the degeneracy within the t_2g manifold is only partially lifted (see Fig. 5). The energy gap between the t_2g and e_g levels (Δ_Oct, computed as the energy difference between the average energy of the e_g orbitals and the average energy of the t_2g orbitals) correlates well with ΔE (see Fig. 5) and, in consequence, with T_1/2 (see Fig. 5). The changes in the ligand field, though, cannot be traced back to the changes in energy of a single orbital, but rather to the overall electronic structure in the system. The observed changes in the energy of both e_g-type and t_2g-type orbitals upon functionalization provide evidence that substituents tune the SCO properties through modifications of both the σ and π bonds between the Fe(III) center and the ligand, in line with the findings reported for Fe(II) complexes in ref. 44. These results are in agreement with those reported in ref. 72 for a series of Fe(III) complexes.

Fig. 5 Left, correlations between the computed d-MOs splitting and the spin-state energy gap (ΔE_HS–LS) and computed transition temperature (T_1/2) of [Fe(L^R₁)(im)₂]⁺. Right, energy of the five d-MOs extracted from the ab initio ligand field theory applied to the NEVPT2 calculation on the low-spin (S = 1/2) optimized geometry. (R² values are 0.84 and 0.89, respectively).

3. Conclusions

In this work, the B3LYP* functional, which has been recently benchmarked for spin-crossover Fe(III) systems, has been used to explore how chemical modifications on the ligand design can be harnessed for the fine tuning of the T_1/2 in two families of Fe(III)–SCO compounds. In particular, our results illustrated that in the [Fe(L^R₁)(im)₂]⁺ system, a broad range of T_1/2 is accessible by changing the R group attached to the β-ketoiminato fragment, and for the system, the possibility of tuning the T_1/2 in a finer way becomes accessible, not only as a function of the R group attached to the phenolato moiety, but also depending on its position on the aromatic ring. In all cases, the observed trends in the T_1/2 can be understood by the changes in the splitting of the d-based manifold of orbitals. The different energy gaps between the t_2g and e_g orbitals as a function of the substituent, in turn, result from energy changes of both types of orbitals, thus showing that ligand substituents modify both the σ and π bonds between the Fe(III) center and the ligands.

Our results have also shown that a correlation between the NBO partial charges of the donor atoms of the ligands (N and O for L₁ and L₂, respectively) in the complex and its T_1/2 can be outlined. This is particularly relevant, because it implies that one can estimate T_1/2, just by computing only one of the two spin-states, thus reducing in more than half the computational cost of such studies. Similarly, the electron donor or electron withdrawing character of the R substituents in the system, measured with the corresponding σ_p or σ_m Hammett parameters, also shows a linear relationship with the computed T_1/2. The more the EWG of the R group is, the smaller the T_1/2. Moving beyond substituent effects on aromatic rings, a linear correlation between Swain–Lupton parameters of the substituents attached to the L₁ ligand and the T_1/2 values for the [Fe(L^R₁)(im)₂]⁺ system has been found. In all cases, such relationships allow for a rational design of new SCO systems with specific properties, a powerful tool for the design of new molecules capable of undergoing the transition at given temperatures.

Although ultimately one must synthesize such systems in order to validate our results, and crystal packing effects may play a role in the overall behavior of such species (S10), the presented data will help synthetic chemists in the design of new molecular SCO systems that can operate at specific T_1/2 for the [Fe(L^R₁)(im)₂]⁺ and families. Moreover, our results provide with a simple, yet quantitative tool that allows for the virtual screening of new Fe(III)-based spin-crossover systems with tailored properties based on the ligand design.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

J. C. thanks the Spanish MICINN for a Ramón y Cajal research contract (RYC2018-024692-I) and Spanish MICINN research grant (PID2020-115165GB-I00). J. R.-A. thanks the Spanish MICINN for the following research grants: CTQ2017- 87773-P/AEI/FEDER and PID2020-117803GB-I00. J. R.-A. also acknowledges financial support from the Generalitat de Catalunya (2021SGR00354 grant). D. V., J. C., and J. R.-A. thank the Spanish Structures of Excellence María de Maeztu program (CEX2021-001202-M). We also thank L. G.-C. for the table of contents illustration.

References

1. O. Sato, Nat. Chem., 2016, 8, 644–656.
2. G. Ke, C. Duan, F. Huang and X. Guo, InfoMat, 2020, 2, 92–112.
3. Z.-S. Yao, Z. Tang and J. Tao, Chem. Commun., 2020, 56, 2071–2086.
4. M. Deumal, S. Vela, M. Fumanal, J. Ribas-Arino and J. J. Novoa, J. Mater. Chem. C, 2021, 9, 10624–10646.
5. P. Gütlich and H. A. Goodwin, Top. Curr. Chem., 2012, 1–47.
6. P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427.
7. L. Cambi and L. Szegö, Ber. Dtsch. Chem. Ge. (A B Ser.), 1931, 64, 2591–2598.
8. F. Varret, A. Bleuzen, K. Boukheddaden, A. Bousseksou, E. Codjovi, C. Enachescu, A. Goujon, J. Linares, N. Menendez and M. Verdaguer, Pure Appl. Chem., 2002, 74, 2159–2168.
9. J. A. Real, A. B. Gaspar and M. C. Muñoz, Dalton Trans., 2005, 2062.
10. W. Huang, X. Ma, O. Sato and D. Wu, Chem. Soc. Rev., 2021, 50, 6832–6870.
11. M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119.
12. S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892.
13. K. Senthil Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205.
14. G. Molnár, M. Mikolasek, K. Ridier, A. Fahs, W. Nicolazzi and A. Bousseksou, Ann. Phys., 2019, 531, 1900076.
15. G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862.
16. M. A. Halcrow, Dalton Trans., 2020, 49, 15560–15567.
17. M. Wang, Z.-Y. Li, R. Ishikawa and M. Yamashita, Coord. Chem. Rev., 2021, 435, 213819.
18. K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521.
19. E. Konig, G. Ritter and B. Kanellakopulos, J. Phys. C: Solid State Phys., 1974, 7, 2681–2690.
20. K. Nakano, N. Suemura, K. Yoneda, S. Kawata and S. Kaizaki, Dalton Trans., 2005, 740.
21. J.-F. Létard, C. Carbonera, J. A. Real, S. Kawata and S. Kaizaki, Chem. – Eur. J., 2009, 15, 4146–4155.
22. V. Martínez, A. B. Gaspar, M. C. Muñoz, G. V. Bukin, G. Levchenko and J. A. Real, Chem. – Eur. J., 2009, 15, 10960–10971.
23. J. A. Rodríguez-Velamazán, C. Carbonera, M. Castro, E. Palacios, T. Kitazawa, J.-F. Létard and R. Burriel, Chem. – Eur. J., 2010, 16, 8785–8796.
24. J. A. Kitchen, J. Olguín, R. Kulmaczewski, N. G. White, V. A. Milway, G. N. L. Jameson, J. L. Tallon and S. Brooker, Inorg. Chem., 2013, 52, 11185–11199.
25. J. G. Park, I.-R. Jeon and T. D. Harris, Inorg. Chem., 2015, 54, 359–369.
26. M. Halcrow, Crystals, 2016, 6, 58.
27. T. Kosone, T. Kawasaki, I. Tomori, J. Okabayashi and T. Kitazawa, Inorganics, 2017, 5, 55.
28. T. Kuroda-Sowa, R. Isobe, N. Yamao, T. Fukumasu, T. Okubo and M. Maekawa, Polyhedron, 2017, 136, 74–78.
29. J. A. Kitchen, N. G. White, M. Boyd, B. Moubaraki, K. S. Murray, P. D. W. Boyd and S. Brooker, Inorg. Chem., 2009, 48, 6670–6679.
30. K. Takahashi, Y. Hasegawa, R. Sakamoto, M. Nishikawa, S. Kume, E. Nishibori and H. Nishihara, Inorg. Chem., 2012, 51, 5188–5198.
31. I. Nikovskiy, A. Polezhaev, V. Novikov, D. Aleshin, A. Pavlov, E. Saffiulina, R. Aysin, P. Dorovatovskii, L. Nodaraki, F. Tuna and Y. Nelyubina, Chem. – Eur. J., 2020, 26, 5629–5638.
32. K. Senthil Kumar, S. Vela, B. Heinrich, N. Suryadevara, L. Karmazin, C. Bailly and M. Ruben, Dalton Trans., 2020, 49, 1022–1031.
33. I. A. Nikovskiy, A. V. Polezhaev, V. V. Novikov, D. Y. Aleshin, R. R. Aysin, E. K. Melnikova, L. M. Carrella, E. Rentschler and Y. V. Nelyubina, Crystals, 2021, 11, 922.
34. D. Y. Aleshin, I. Nikovskiy, V. V. Novikov, A. V. Polezhaev, E. K. Melnikova and Y. V. Nelyubina, ACS Omega, 2021, 6, 33111–33121.
35. H.-C. Liang, Y. Pan, H.-L. Zhu, Y.-S. Meng, C.-H. Liu, T. Liu and Y.-Y. Zhu, Inorg. Chem. Front., 2022, 9, 2343–2352.
36. H.-J. Lin, D. Siretanu, D. A. Dickie, D. Subedi, J. J. Scepaniak, D. Mitcov, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2014, 136, 13326–13332.
37. I. Prat, A. Company, T. Corona, T. Parella, X. Ribas and M. Costas, Inorg. Chem., 2013, 52, 9229–9244.
38. J. Cirera and E. Ruiz, Inorg. Chem., 2016, 55, 1657–1663.
39. W. Phonsri, D. S. Macedo, K. R. Vignesh, G. Rajaraman, C. G. Davies, G. N. L. Jameson, B. Moubaraki, J. S. Ward, P. E. Kruger, G. Chastanet and K. S. Murray, Chem. – Eur. J., 2017, 23, 7052–7065.
40. A. Kimura and T. Ishida, Inorganics, 2017, 5, 52.
41. C. Bartual-Murgui, S. Vela, M. Darawsheh, R. Diego, S. J. Teat, O. Roubeau and G. Aromí, Inorg. Chem. Front., 2017, 4, 1374–1383.
42. C.-F. Wang, Z.-S. Yao, G.-Y. Yang and J. Tao, Inorg. Chem., 2019, 58, 1309–1316.
43. B. Wilson, H. Scott, R. Archer, C. Mathonière, R. Clérac and P. Kruger, Magnetochemistry, 2019, 5, 22.
44. L. J. Kershaw Cook, R. Kulmaczewski, R. Mohammed, S. Dudley, S. A. Barrett, M. A. Little, R. J. Deeth and M. A. Halcrow, Angew. Chem., Int. Ed., 2016, 55, 4327–4331.
45. S. Rodríguez-Jiménez, M. Yang, I. Stewart, A. L. Garden and S. Brooker, J. Am. Chem. Soc., 2017, 139, 18392–18396.
46. A. Kimura and T. Ishida, ACS Omega, 2018, 3, 6737–6747.
47. D. C. Ashley and E. Jakubikova, Inorg. Chem., 2018, 57, 9907–9917.
48. L. Bondì, S. Rodríguez-Jiménez, H. L. C. Feltham, A. L. Garden and S. Brooker, Inorg. Chem. Front., 2021, 8, 4846–4857.
49. H. Phan, J. J. Hrudka, D. Igimbayeva, L. M. Lawson Daku and M. Shatruk, J. Am. Chem. Soc., 2017, 139, 6437–6447.
50. T. Gebretsadik, Q. Yang, J. Wu and J. Tang, Coord. Chem. Rev., 2021, 431, 213666.
51. S. Hayami, Z. Gu, H. Yoshiki, A. Fujishima and O. Sato, J. Am. Chem. Soc., 2001, 123, 11644–11650.
52. P. J. Koningsbruggen, Y. Maeda and H. Oshio, Top. Curr. Chem., 2012, 259–324.
53. M. Nihei, T. Shiga, Y. Maeda and H. Oshio, Coord. Chem. Rev., 2007, 251, 2606–2621.
54. D. J. Harding, P. Harding and W. Phonsri, Coord. Chem. Rev., 2016, 313, 38–61.
55. A. I. Vicente, A. Joseph, L. P. Ferreira, M. de Deus Carvalho, V. H. N. Rodrigues, M. Duttine, H. P. Diogo, M. E. Minas da Piedade, M. J. Calhorda and P. N. Martinho, Chem. Sci., 2016, 7, 4251–4258.
56. S. Kang, Y. Shiota, A. Kariyazaki, S. Kanegawa, K. Yoshizawa and O. Sato, Chem. – Eur. J., 2016, 22, 532–538.
57. W. Phonsri, P. Harding, L. Liu, S. G. Telfer, K. S. Murray, B. Moubaraki, T. M. Ross, G. N. L. Jameson and D. J. Harding, Chem. Sci., 2017, 8, 3949–3959.
58. T. Boonprab, S. J. Lee, S. G. Telfer, K. S. Murray, W. Phonsri, G. Chastanet, E. Collet, E. Trzop, G. N. L. Jameson, P. Harding and D. J. Harding, Angew. Chem., Int. Ed., 2019, 58, 11811–11815.
59. M. Nakaya, R. Ohtani, L. F. Lindoy and S. Hayami, Inorg. Chem. Front., 2021, 8, 484–498.
60. E. V. Dose, K. M. M. Murphy and L. J. Wilson, Inorg. Chem., 1976, 15, 2622–2630.
61. M. F. Tweedle and L. J. Wilson, J. Am. Chem. Soc., 1976, 98, 4824–4834.
62. S. Floquet, A. J. Simaan, E. Rivière, M. Nierlich, P. Thuéry, J. Ensling, P. Gütlich, J.-J. Girerd and M.-L. Boillot, Dalton Trans., 2005, 1734–1742.
63. W. Phonsri, D. S. Macedo, C. G. Davies, G. N. L. Jameson, B. Moubaraki and K. S. Murray, Dalton Trans., 2017, 46, 7020–7029.
64. W. Phonsri, L. Darveniza, S. Batten and K. Murray, Inorganics, 2017, 5, 51.
65. T. Nakanishi, A. Okazawa and O. Sato, Inorganics, 2017, 5, 53.
66. Z.-K. Liu, Z.-S. Yao and J. Tao, Inorg. Chem., 2021, 60, 10291–10301.
67. H.-J. Sheng, C.-C. Xia, X.-Y. Zhang, C.-C. Zhang, W.-J. Ji, Y. Zhao and X.-Y. Wang, Inorg. Chem., 2022, 61, 12726–12735.
68. W. Phonsri, D. J. Harding, P. Harding, K. S. Murray, B. Moubaraki, I. A. Gass, J. D. Cashion, G. N. L. Jameson and H. Adams, Dalton Trans., 2014, 43, 17509–17518.
69. J. Sirirak, D. Sertphon, W. Phonsri, P. Harding and D. J. Harding, Int. J. Quantum Chem., 2017, 117, e25362.
70. S. Ashoka Sahadevan, E. Cadoni, N. Monni, C. Sáenz de Pipaón, J.-R. Galan Mascaros, A. Abhervé, N. Avarvari, L. Marchiò, M. Arca and M. L. Mercuri, Cryst. Growth Des., 2018, 18, 4187–4199.
71. S. E. Lazaro, A. Alkaş, S. J. Lee, S. G. Telfer, K. S. Murray, W. Phonsri, P. Harding and D. J. Harding, Dalton Trans., 2019, 48, 15515–15520.
72. B. Dey, A. Mondal and S. Konar, Chem. – Asian J., 2020, 15, 1709–1721.
73. M. A. Al-Azzani, F. Al-Mjeni, R. Mitsuhashi, M. Mikuriya, I. A. Al-Omari, C. C. Robertson, E. Bill and M. S. Shongwe, Chem. – Eur. J., 2020, 26, 4766–4779.
74. B. Dey, A. Gupta, S. Kapurwan and S. Konar, ChemistrySelect, 2020, 5, 14677–14684.
75. T. Fujinami, M. Ikeda, M. Koike, N. Matsumoto, T. Oishi and Y. Sunatsuki, Inorg. Chim. Acta, 2015, 432, 89–95.
76. Y. Nishida, K. Kino and S. Kida, J. Chem. Soc., Dalton Trans., 1987, 1157.
77. T. Fujinami, M. Koike, N. Matsumoto, Y. Sunatsuki, A. Okazawa and N. Kojima, Inorg. Chem., 2014, 53, 2254–2259.
78. M. Reiher, Inorg. Chem., 2002, 41, 6928–6935.
79. H. Paulsen and A. X. Trautwein, J. Phys. Chem. Solids, 2004, 65, 793–798.
80. O. S. Siig and K. P. Kepp, J. Phys. Chem. A, 2018, 122, 4208–4217.
81. S. Song, M.-C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theory Comput., 2018, 14, 2304–2311.
82. G. Prokopiou and L. Kronik, Chem. – Eur. J., 2018, 24, 5173–5182.
83. S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945.
84. A. Fouqueau, M. E. Casida, L. M. L. Daku, A. Hauser and F. Neese, J. Chem. Phys., 2005, 122, 044110.
85. M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066.
86. K. P. Jensen and J. Cirera, J. Phys. Chem. A, 2009, 113, 10033–10039.
87. S. R. Mortensen and K. P. Kepp, J. Phys. Chem. A, 2015, 119, 4041–4050.
88. S. Vela, M. Fumanal, J. Ribas-Arino and V. Robert, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314.
89. K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727.
90. J. P. Janet and H. J. Kulik, Chem. Sci., 2017, 8, 5137–5152.
91. D. C. Ashley and E. Jakubikova, Coord. Chem. Rev., 2017, 337, 97–111.
92. J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105.
93. J. Cirera and F. Paesani, Inorg. Chem., 2012, 51, 8194–8201.
94. J. Cirera and E. Ruiz, Inorg. Chem., 2018, 57, 702–709.
95. L. Navarro, F. Rodriguez and J. Cirera, Dalton Trans., 2021, 50, 8704–8710.
96. D. Vidal, J. Cirera and J. Ribas-Arino, Dalton Trans., 2021, 50, 17635–17642.
97. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
98. J. P. Perdew, J. Tao, V. N. Staroverov and G. E. Scuseria, J. Chem. Phys., 2004, 120, 6898–6911.
99. O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729–4737.
100. S. Saureu and C. de Graaf, Phys. Chem. Chem. Phys., 2016, 18, 1233–1244.
101. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B0.1, Gaussian, Inc., Wallingford, CT, 2016.
102. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
103. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
104. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
105. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
106. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
107. S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25.
108. Y. Nishida, S. Oshio and S. Kida, Inorg. Chim. Acta, 1977, 23, 59–61.
109. S. G. Bratsch, J. Chem. Educ., 1985, 62, 101.
110. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103.
111. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
112. C. G. Swain and E. C. Lupton, J. Am. Chem. Soc., 1968, 90, 4328–4337.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00250k

---