Aggregation patterns of curcumin and piperine mixtures in different polar media

Abstract

This work reports a thorough molecular dynamics investigation on the aggregation patterns of curcumin and piperine in water, ethanol and a mixture of both solvents. The low solubility of curcumin in water results in a rapid formation of very stable dimers for both keto and enol tautomers. In agreement with a higher solubility, piperine molecules move closer and farther apart several times during the simulation, which indicates the formation of a less stable dimer in water. In contrast, both curcumin and piperine are soluble in ethanol and, thus, dimers can hardly be formed in this media. In comparison with a pure-water solvent, a 30 : 70 mixture of ethanol and water significantly reduces the probability of formation of most dimers of curcumin and piperine molecules. The simulations show that larger clusters may be complex structures, but the formation of stacks (in the case of piperine and enol tautomer of curcumin) and cages (when the keto tautomer of curcumin is involved) are not rare. Furthermore, it is shown that each single molecule presents a certain degree of mobility in the cluster, especially on the surface, but without leading to dissociation.

---

1 Introduction

Curcumin is a natural yellow pigment, which is present in the rhizome of turmeric (Curcuma longa L.) and has been used as a spice as well as for traditional medicinal purposes.¹ Several biological and pharmacological properties have been associated to curcumin^2–5 and, since it adsorbs in the visible region of the light spectrum, this molecule may be considered a valuable candidate to be used as photosensitizer in photodynamic therapy.^2,6 However, the pharmacological properties of curcumin appear to be limited by the reduced bioavailability,^7,8 which has been attributed to the low aqueous solubility,⁹ poor membrane permeability,¹⁰ and extensive hepatic and intestinal metabolism.^11,12 Although curcumin has enolic and phenolic groups in its structure, the aliphatic conjugated bridge linking them makes the molecule very little soluble in water (i.e., 0.001 mg g⁻¹ in water at 25 °C^13,14) which have required the development of appropriate drug delivering strategies. For instance, biopolymer nanoparticles can be used to incorporate and deliver curcumin molecules,^15,16 while the release of the drug in the physiological medium may be facilitated by electrostimulation.¹⁷ Curcumin appears in both keto and enol forms in aqueous solutions, whereas the enol tautomer dominates in ethanol.^18,19 From a computational view point, only a few investigations on curcumin have been carried out.^20–22 In particular, the enol–enol, keto–keto and enol–keto dimers of curcumin were optimized at the B97-D/TZVP level of theory by Karatas et al.²⁰ These authors have concluded that the stabilization of all dimers is mainly due to π–π interactions between the benzene rings of two individual molecules, but weak electrostatic contributions involving oxygen and hydrogen atoms may also play a role in the case of keto–keto dimer.²⁰

A propose for increasing the bioavailability of curcumin is co-administration with piperine, which is a bioactive molecule of black pepper (Piper nigrum L.). In this approach, piperine appears to retard the metabolism of curcumin,^23–25 having as a consequence the enormous enhancement of its bioavailability.²⁶ By other side, it is not expected a priori an enhancement of the solubility of curcumin due to the presence of piperine, since this compound is also little soluble in water (0.164 mg g⁻¹ at 25 °C).^27,28 Nonetheless, conflicting perspectives on the solubility of curcumin–piperine mixtures have appeared in literature as a result of different experiments and calculations. Based on quantum chemical calculations and docking, Patil et al.²⁹ proposed the formation of a piperine–curcumin intercalation complex, which acts inside the organism by enhancing the curcumin transport to the target site. Indeed, the excretation of curcumin is avoided by the possibility of piperine to bind to enzymes responsible for curcumin's glucuronosylation, which enhances its bioavailability.²⁹ By employing spectroscopic and spectrometric methods, Traxler et al.³⁰ observed that the 1 : 1 complex between curcumin and piperine, predicted by the quantum calculations of Patil et al.,²⁹ is relatively weak and therefore appears to indicate that it cannot explain the bioavailability enhancement due to an increase of solubility. Since such experimental studies³⁰ were carried out in methanol and a mixture of methanol, acetonitrile and only 1% of water, it is perhaps inappropriate to extract conclusions about the strength of the curcumin–piperine complex in a pure aqueous solution. Actually, Wang et al.³¹ have used a co-amorphous curcumin–piperine formulation to create a supersaturated solution, which leads to a dissolution concentration more than three times higher than the crystalline curcumin. In addition, the same authors have estimated from spectroscopic experiments that curcumin–piperine interactions are significant in the co-amorphous formulation.³¹ In turn, Nag et al.²² identified the enol curcumin as the preferential tautomeric form that is better stabilized in the presence of piperine. Although there is an enormous amount of work, from different perspectives, on the curcumin and piperine systems, the lack of detailed knowledge at the molecular level for these compounds in solution is evident.

Molecular dynamics (MD) is a powerful computational technique that has been applied to study different types of phenomena occurring in solution. It allows for the calculation of an array of properties, such as diffusion coefficients,^32–37 viscosity,^38–40 conductivity,⁴¹ density,^42–44 heat capacity,^42,45 free energy,^46,47 and radial and spatial distribution functions.^48,49 Moreover, MD simulations allow for a detailed molecular-level perspective of the phenomena by visualizing typical trajectories, calculating microscopic properties (e.g., radius of gyration, solvent accessible surface area or SASA, hydrogen bonds) as a function of time and applying clustering techniques to envisage the most significant structural motifs.

Aside from experimental methodologies, computational techniques have also been adopted in the investigation of the aggregation phenomenon and host–guest interaction of some important biological systems. Specifically, MD simulations have been employed to characterize the aggregation patterns of bile salts in aqueous solutions,⁵⁰ show up the influence of amphiphile conformation in the aggregates morphology and solution organization,⁵¹ access the role of β-cyclodextrins aggregation in the solubilization of an antiviral medication,⁵² and explore the aggregation of a polymer–drug conjugate in the context of the anticancer-therapeutic development.^53–55

Despite the deep knowledge about curcumin and piperine aggregation coming from experimental work, as far as we know, an insightful MD investigation that leads to understanding the influence of piperine on curcumin aggregation in various media is still lacking in the literature. In this work, we aim at contributing for a better elucidation of the curcumin and piperine aggregation in several polar media by employing MD simulations. Particularly, we intend to evaluate the influence of piperine on the curcumin self-aggregation, while characterizing the main structural features of the aggregates. The article has the following structure. Section 2 describes the methodology and details the protocol adopted for the MD simulations and the trajectory analysis. In Section 3, the results are presented and discussed. Finally, major conclusions are gathered in Section 4.

2 Systems and methods

2.1 Solutions of curcumin and piperine

We have applied MD simulations to elucidate about the aggregation patterns of curcumin, piperine, and mixture of both molecules in different polar media. The study was conducted mainly for aqueous solutions, but we have also explored the effect on the aggregation by using as a solvent the ethanol and the mixture of ethanol with water in volume percentages of 30% and 70%, respectively. For simplicity, the latter is hereafter referred as “(30 : 70) solvent mixture”.

We show in Fig. 1 schematic representation of the enol–keto (hereafter simply referred as enol or CEK) and keto–keto (hereafter simply referred as keto or CKK) tautomers of curcumin, and piperine (hereafter referred as PIP). Since a chemical equilibrium can be established between the two tautomeric species, depending on the pH of the solution (which is not explicitly considered in this study), curcumin may appear in the enol form, as the keto tautomer or in a mixture of both;⁵⁶ the designation CUR is adopted for curcumin whenever referring to a non-specific tautomer. As the pH increases from low to high values, the presence of the keto form diminishes in the aqueous solution, while the enol tautomer becomes more important. It has also been shown⁵⁶ that keto tautomer are usually prevalent in aqueous solutions, whereas organic solvents favor the enolic form. We should also mention that the CEK and CKK tautomers present distinct 3D structures (see Fig. S1 of the ESI†): CKK has a V-shape structure and CEK is essentially planar. Similarly, the structure of piperine can be considered almost planar when excluding the piperidine ring at the edge of the molecule.

Fig. 1 Solute molecules employed in this work: (a) enol–keto (CEK) and (b) keto–keto (CKK) tautomeric structures of curcumin;(c) piperine molecule (PIP).

For each solvent, we have considered several solute systems to be studied by the MD simulations. These systems include sets of two and four solute molecules that were separated apart in the beginning of the simulations. The former ones correspond to all possible combinations of piperine and the two tautomers of curcumin, that is, CEK–CEK, CKK–CKK, CEK–CKK, CEK–PIP, CKK–PIP, and PIP–PIP. In turn, the simulations with four solute molecules are the following: 4CEK, 4CKK, and 2CEK + 2CKK by using water as solvent, and 2CEK + 2PIP and 2CKK+ 2PIP with either water or the (30 : 70) solvent mixture. The volume was adjusted to obtain a concentration of the solution as low as 0.0058 M in all simulations; the box side employed for each simulation as well as the corresponding number of solute and solvent molecules are presented in Tables S1 and S2 of the ESI.†

2.2 Molecular dynamics simulations

MD simulations were carried out at 298.15 K with the 2019 version of the GROMACS package^57,58 which has support for NVIDIA GPUs used for the present calculations. In the construction of the topology of the system, we have employed the usual procedure for the AMBER force field with GAFF2 parameters.⁵⁹ We note that the general AMBER force fields (GAFF) are an extension of AMBER for modeling organic molecules and, hence, they were developed to be compatible among each other. Actually, GAFF has parameters that are transferable for most organic and pharmaceutical molecules containing H, C, N, O, S, P, and halogen atoms. Moreover, the parameterization of GAFF⁵⁹ included organic molecules with aromatic, aliphatic, carbonyl, and enol groups that are also present in the systems studied in the present work. In addition, this force field has been successfully validated against experimental data for a wide range of organic molecules by different research groups,^60,61 and it has also been applied to build up the topology of curcumin and piperine.^61–64 Accordingly, the system was prepared for each MD simulation as follows:

1. The OpenBabel program⁶⁵ was used for the generation of the 3D molecular structures of the CEK and CKK tautomers of curcumin, and piperine (PIP). The structures so obtained were optimized at the DFT-B3LYP/6-31G* level of theory with the GAMESS package.⁶⁶

2. Furthermore, the corresponding partial charges ascribed to the atoms of each solute molecule (Fig. S1, ESI†) were derived by employing the RESP fitting protocol, which has been implemented in the RED program.⁶⁷ These atomic charges are given in Tables S3 and S4 of the ESI.†

3. The geometry and topology were converted to the input format of GROMACS through the acpype script.⁶⁸ The AMBER force field was used with the GAFF2 parameters.⁵⁹

4. The initially non-interacting solute molecules were separated from each other inside the simulation (cubic) box. The volume of the box was chosen so that a specific molar concentration could be obtained. Then, the simulation box was filled with solvent molecules that can be either water, ethanol or both (see Section 2.1). Water molecules were described with the TIP4P-2005 model,⁶⁹ whereas ethanol has employed the AMBER force field with the parameters proposed by Alvarez-Garcia et al.⁷⁰ The procedure for generating the pre-equilibrated mixed solvent box is described in the ESI.†

5. Once the system is assembled, the equilibration stage begins with the energy minimization in order to relax the system and, hence, diminish the repulsions among the molecules inside the simulation box.

6. The equilibration proceeds with two consecutive short simulations of 1 ns, being the first (second) within the NVT (NPT) ensemble. This procedure allows the system to reach the desired temperature of 298.15 K and pressure of 1 bar, using the velocity-rescaling thermostat^71,72 (0.1 ps of coupling time) and the Parrinello–Rahman barostat⁷³ (2 ps of coupling time), respectively.

The production stage of the MD simulation has been carried out during 500 ns within the NVT ensemble for each set of initial conditions. The integration of the classical equations of motion has employed the leapfrog method with a time step of 2 fs. During the integration of the trajectory, bond constraints were applied by using the LINCS (i.e., linear constraint solver) scheme.⁷⁴ Also, periodic boundary conditions were employed in all simulations and the long-range electrostatic energy was evaluated by using the particle mesh Ewald method,^75,76 with a cutoff of 10 Å for both Coulomb and van der Waals interactions.

We should emphasize that most of the simulations have begun with all the solute molecules quite far apart from each other. However, additional simulations beginning with preformed homodimers (i.e., CEK–CEK, CKK–CKK, and PIP–PIP) and two separated monomers have been carried out in order to assess the influence of the type of precursor on the structure of 2CEK + 2PIP and 2CKK + 2PIP aggregates in water. To illustrate how the dissociation of curcumin dimers occurs in ethanol, we have also performed two short simulations (∼5 ns) departing from preformed CEK–CEK and CKK–CKK structures. All such dimers were chosen to be the most prevalent structures formed during the simulations in water.

Finally, we have calculated several physical quantities with the software tools available in GROMACS^57,58 and VMD⁷⁷ so that the supra-molecular complex formed during the MD simulations could be characterized. Our analysis relies on the following properties: (i) radial distribution functions (RDF); (ii) distances between molecules or atoms represented as a function of the simulation time; (iii) cluster analysis; (iv) average number of solvent molecules (either water or ethanol) around the solute molecules; (v) pair–wise interaction energies and number of hydrogen bonds; (vi) visual inspection of the trajectories. In the calculation of the most probable structure resulting from aggregation during a simulation, the cluster analysis was performed over the part of the trajectory where all the solute molecules are totally aggregated (i.e., incomplete aggregation was not analyzed). For counting the occurrence of specific conformations, we have used the “single linkage”' method, which is the default in the “cluster” module of the GROMACS package. This method calculates the distances or similarities between all objects, then the closest pair of clusters are combined into a single cluster, according to the cutoff defined for the root-mean-square deviation (RMSD). In this work, the RMSD cutoff was established for each simulation by trial and error, so that only a reduced number of structures would become prevalent (i.e., avoiding a pool of structures with extremely low frequencies of appearance).

3 Results and discussion

The aggregation of various curcumin and piperine molecules in different polar solvents was investigated by employing the MD simulations described in Section 2. In this context, the solute aggregates that arise in the simulations are analysed and discussed in this section resorting to their structural and dynamical properties.

3.1 Propensity of curcumin and piperine to form dimers in polar media

As a first step to understand the aggregation of curcumin and piperine in polar media, we have performed MD simulations with two solute molecules in water, ethanol and (30 : 70) solvent mixture. In the case of curcumin, the study explores the interactions of both CKK and CEK tautomers.

3.1.1 In water. Fig. 2 displays the solute–solute RDF (top panels) and the distance between the corresponding centers of mass as a function of time (bottom panels) for six simulations, each one for a different pair of curcumin and piperine molecules in water. A very prominent peak of the RDF can be observed at approximately 0.45 nm for the simulations involving curcumin (alone or with piperine), which is compatible with the observation from the corresponding bottom panels of Fig. 2 that a dimer can be formed in the first nanoseconds of each simulation and the two molecules keep together until the end of the trajectory; nonetheless, the CEK–PIP complex is formed very rapidly, while the CKK–PIP one needs about 70 ns to stabilize. The formation of such a curcumin–piperine complex in water has been already suggested in previous investigations, which were based on electronic-structure calculations²⁹ as well as on spectroscopic and spectrometric methods.³⁰ Regarding simulations with two curcumin molecules, the plots in Fig. 2 (panels a, b, and f) constitute a clear evidence of high propensity for self-aggregation of both tautomers, which is in agreement with the expected low solubility of curcumin in water. A similar outcome has been previously noticed by Hazra et al.⁷⁸ in a MD study where the hydrogens bound to the carbons of methoxy group of curcumin were treated as united atoms.

Fig. 2 Six simulations of distinct pairs of solute molecules in water: (a) CEK–CEK; (b) CKK–CKK; (c) CEK–PIP; (d) CKK–PIP; (e) PIP–PIP; (f) CEK–CKK. Solute–solute RDFs are represented in upper panels, while the corresponding center-of-mass distances as a function of time are shown in the bottom panels.

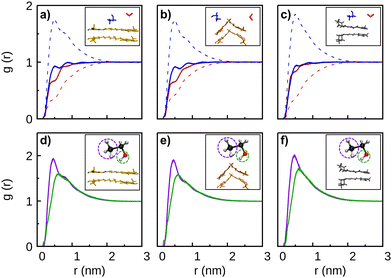
Additionally, Fig. 2 shows that the RDF peak for the simulation with two piperine molecules is relatively small and, accordingly, the corresponding distance-plot indicates that the PIP–PIP complex can be formed during the trajectory, but only lasts for a very limited time-interval. Such difficulty of piperine to form long-lasting stable-dimers is compatible with the higher solubility in water of this molecule in comparison to curcumin. A contribution for this difference in the solubility of curcumin and piperine in water appears to be the strong interaction that can be established between the O1 atom of piperine with the hydrogens of the solvent molecules. Indeed, it is clear from Fig. S2 (panels a–c) of the ESI† that the PIP(O1)–water(H) RDF curve has a maximum around 0.25 nm (which exceeds the corresponding probability at bulk), while the analogous CEK(O)–water(H) and CKK(O)–water(H) peaks do not overcome the bulk value.

Although each dimer in the present work may assume various shapes, we represent in Fig. 3 the most probable structures that were estimated through cluster analysis carried out over the corresponding trajectories. Due to the essentially planar shape of CEK, the main structure of the dimer shows the two molecules stacked in an anti-parallel motif, i.e., the H1 atom of one monomer is oriented to the H15 atom of the other and vice-versa (see Fig. S1, ESI† for the labels of atoms of the curcumin and piperine molecules). Stacked structures are also likely to occur for the PIP–PIP and CEK–PIP dimers, but now showing a parallel motif. In contrast, the CKK–CKK dimer leads preferentially to a structure where the two monomers fit in a V-shape, with paired H1–H1 and H15–H15 atoms. We should note that the CKK–CKK structure displayed in Fig. 3 accounts for 89% of the motifs of the simulation whereas CEK–CEK has a lower probability (22%), even though a lower cutoff had been imposed to the former. This might be a result of self-confinement of the two CKK molecules in such V-shape configuration while, by contrast, the two CEK molecules are more free to move away and leave the stacked configuration shown in Fig. 3. Although in a smaller extent, the self-confinement effect that, somehow, hinders the relative motion of both molecules, is also apparent in the CKK–PIP and CEK–CKK dimers by the high frequencies of appearance displayed. In particular, we note that the structures of CKK–PIP and CEK–CKK show a similar pattern (i.e., a quasi-planar molecule that fits in the concave part of the V-shaped CKK structure), which appears to be the optimal packing of the two molecules of each dimer.

Fig. 3 Main structural motifs of the six studied dimers, which were obtained by cluster analysis of the MD trajectories. Frequencies of appearance of the represented structures (in %) for a given RMSD cutoff (values in parentheses): (a) 22% CEK–CEK (0.08 nm), (b) 89% CKK–CKK (0.05 nm), (c) 89% PIP–PIP (0.20 nm), (d) 37% CEK–PIP (0.10 nm), (e) 55% CKK–PIP (0.10 nm), and (f) 93% CEK–CKK (0.20 nm). Key for colors: CEK molecules (yellow), CKK molecules (orange), PIP molecules (black). The H1 atoms in all molecules are displayed in green color, while the H15 (H18) ones in curcumin (piperine) are in magenta.

3.1.2 In ethanol. To shed light on how the formation of the above-mentioned dimers is affected by the solvent, we have performed similar simulations with the water being replaced by ethanol. The corresponding solute–solute RDFs and distance plots are displayed in Fig. 4. It is apparent from this figure that the formation of stable dimers involving curcumin and/or piperine molecules is unlikely to occur in ethanol. Furthermore, we have complemented this investigation by studying the behavior of curcumin aggregates in ethanol. For that, we have run a couple of short trajectories beginning with a CEK–CEK (or CKK–CKK) dimer in ethanol; the corresponding movies are in the ESI.† By the inspection of these movies, we conclude that the dimers promptly separate into the corresponding monomers (i.e., after a few nanoseconds of simulation). Actually, there is experimental evidence^79,80 that both curcumin and piperine are quite soluble in ethanol. Although this constitutes a polar media (like water), the ethanol molecule has a non-polar group (–CH₂–CH₃) that may contribute to the solvation of both curcumin and piperine. Besides this, it is apparent in Fig. S2 (panels d–f) of the ESI† that, in particular, the H1 atom of ethanol molecules has a great probability to be at a close distance (∼0.25 nm) from the O12, O10 and O12, and O1 atoms of CEK, CKK, and PIP molecules, respectively.

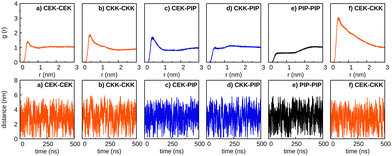Fig. 4 As in Fig. 2, but for ethanol as solvent.

3.1.3 In (30 : 70) solvent mixture. The nonpolar environment diminishes when considering for the solvent a mixture of ethanol and water. Thus, we represent in Fig. 5 the results obtained for the simulations with the “(30 : 70) solvent mixture”. We observe in this figure that the probability of forming dimers is clearly increased in comparison to the case of pure ethanol as solvent (Fig. 4). Especially, the increase of the polar environment appears to favor the formation of CEK–PIP and CEK–CEK dimers, where the planar structure of the CEK molecule may favor the interaction with the other monomer. Nonetheless, these dimers appear to be less stable than in pure water, since the two solute molecules approach each other and move apart several times during the simulations. In addition, the presence of an amount of 30% of ethanol is sufficient to significantly destabilize the CKK–CKK and CKK–PIP dimers that, as mentioned above, are very stable in pure water. In contrast, such solvent effect is less apparent in the case of the PIP–PIP dimer, though it is clearly more soluble in ethanol than in water (cf.Fig. 2 and 4).

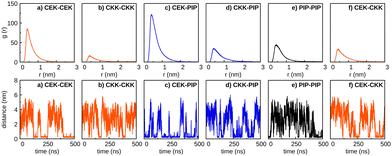Fig. 5 As in Fig. 2, but for a (30 : 70) solvent mixture. See the text.

A detailed insight on how the solvent molecules surround the CEK–CEK, CKK–CKK, and PIP–PIP dimers can be obtained from Fig. 6. In the top panels of this figure, we compare the solute–solvent RDFs in pure water and pure ethanol with the corresponding ones in a (30 : 70) solvent mixture. Whereas the RDF for ethanol shows two small peaks for short distances, the corresponding curves for water indicate a lack of solvent molecules in the surroundings of the dimer. Such effect is less apparent for the PIP–PIP dimer, which is a signature of the expected lower hydrophobicity of piperine. In the case of the (30 : 70) solvent mixture, we observe in Fig. 6 (panels a, b, and c) a high peak of the ethanol-dimer RDF and a lowering of the probability of finding water molecules next to the solute. We conclude that, for the mixture of solvents, the first solvation shell is essentially occupied by ethanol (see Fig. S4, ESI†), which thus pushes the water molecules away from the dimer; however, note in Fig. S4 (ESI†) that some water molecules are able to occupy positions in the first solvation shell by approaching the oxygen atoms of curcumin, as shown by the short-distance peak arising in the corresponding atom–atom RDFs (cf. Fig. S3, ESI†). The preference for having ethanol in the first solvation shell is similar for both tautomers of curcumin, but it is more amplified for the piperine dimer; this is also apparent from the strongest PIP(O1)–ethanol(H1) peak in panel f of Fig. S3 (ESI†) in comparison with the CEK(O12)–ethanol(H1) and CKK(O10/O12)–ethanol(H1) ones, respectively, in panels d and e of the same figure. All these results are similar to those observed for the solvation of single CEK, CKK, and PIP monomers (cf. Fig. S5, ESI†). Moreover, it is apparent from Fig. 6 (panels d, e and f) that, regardless of the solute, the ethanol molecules turn preferentially their –CH₃ groups to the dimer. Indeed, the maximum probability of finding the –CH₃ group of ethanol is closer to the dimer than the corresponding –OH group.

Fig. 6 Solute–solvent RDFs for the dimers CEK–CEK (a), (d), CKK–CKK (b), (e), and PIP–PIP (c), (f). Top panels: center-of-mass RDFs related to water (ethanol) are represented by red (blue) lines; solid lines refer to simulations in pure solvents (water or ethanol), while dashed curves are for the (30 : 70) solvent mixture. The inserts represent the corresponding dimers, as well as one molecule of water (in red) and one molecule of ethanol (in blue). Bottom panels are for simulations with the (30 : 70) solvent mixture: ethanol-dimer RDFs by taking as reference the –CH₃ (purple line) or –OH (green) groups of the ethanol. The inserts represent the corresponding dimers as well as an ethanol molecule with the reference groups marked by a dashed circle.

We have further investigated how the presence of ethanol near the CEK–CEK dimer influences its dissociation in the (30 : 70) solvent mixture. To such endeavor, we represent in Fig. 7 the number of water and ethanol molecules nearby the CEK–CEK dimer (or the separated monomers) throughout the simulation. It is apparent from Fig. 7 (panels b and c) that, in an average sense, the amount of ethanol is larger than the amount of water in the surroundings of the CEK molecules. This is compatible with a first solvation shell mostly occupied by ethanol, as already pointed out above (cf. RDFs in Fig. 6). However, we should note that, since the (30 : 70) solvent mixture has more water than ethanol, it is necessary an initial reorganization of the solvent to obtain an excess of ethanol around the CEK molecules. In fact, the migration of ethanol molecules from the bulk to the surroundings of the solute (which implies the displacement of water in the reverse direction) is observed during the first 2 ns of the simulation (see Fig. 7(e)).

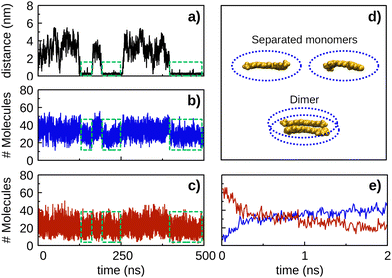Fig. 7 Number of solvent molecules within a cut-off distance of 3 Å from the solute molecules (i.e., the ellipsoids defined in panel d) as a function of time for the CEK–CEK simulation of Fig. 5(a). The corresponding CEK–CEK distance plot as a function of time (black line) is included in panel a to facilitate the analysis of the results. The number of ethanol (water) molecules is shown by the blue (red) line in panel b (panel c). Green dashed lines identify the time intervals where the CEK–CEK dimer is formed. The average number of ethanol (water) molecules around the CEK–CEK dimer (i.e., within the green dashed lines) is 28 (19), while around the separated monomers (i.e., outside the green dashed lines) the corresponding value is 34 (22). Panel e is a zoom of panels b and c over the initial 2 ns, showing the number of ethanol (blue line) and water (red line) molecules. The plots regarding the solvent distribution were obtained using the VMD software.

Moreover, it is interesting to notice in Fig. 7 that the number of solvent molecules nearby the solute tends to decrease when the dimer is formed (i.e., as highlighted by the green dashed lines in panels b and c). This is an expected behavior since some solvent molecules have to be kicked out from the surroundings of the solute as the two monomers approach to form the dimer. In the opposite direction, the dissociation of the CEK–CEK dimer leads to an average increase in the number of solvent molecules nearby the solute, but this is more significant in the case of ethanol than for water. Indeed, there is an average increase of 6 (3) ethanol (water) molecules nearby the solute when the dimer dissociates. Thus, it appears from this result that CEK–CEK dissociation is promoted by a subtle imbalance nearby the dimer, which corresponds to an increase in the amount of ethanol in comparison to water.

3.1.4 Energetic and hydrogen-bonding analysis. We turn now the analysis of the results so that one can assess the importance of the solute–solute, solute–solvent, and solvent–solvent energy components to the formation of CEK–CEK, CKK–CKK, and PIP–PIP dimers. For that, we have plotted those energy components as a function of the simulation time (see Fig. S6 and S7 in the ESI†). As a general trend, we observe in Fig. S6, ESI† that the formation of a dimer corresponds to a solute–solute energy decrease and a complementary increase in the solute–solvent energy. In water, the average values of CEK–CEK and CKK–CKK interaction energies appear to be similar, though the CKK–CKK component shows larger amplitude oscillations with time. In turn, the PIP–PIP interaction energy does not decrease as much as the CEK–CEK and CKK–CKK components when the corresponding dimer is formed. Also, the PIP–water energy component is clearly smaller than the corresponding ones for both tautomers of curcumin. In addition, the range of energy explored by PIP–water interactions is much smaller in comparison to the corresponding components for curcumin, and this seems to be independent of having a dimer or two separated monomers in the solution. Such differences may be a consequence of a distinct number of pair interactions that can be established for each system: the curcumin molecule has 47 atoms, while piperine has only 40.

In ethanol, as no dimer is stable, the solute–solute energy is essentially zero during most of the time. Nonetheless, we observe in Fig. S6 (ESI†) that the solute–solute interaction energy for curcumin (both CEK–CEK and CKK–CKK) peaks down for very short time intervals when two monomers approach each other during the simulation; this kind of event is more rare for piperine, which suggests a weaker interaction for the PIP–PIP pair. It is apparent from Fig. S6 (ESI†) that, as already noticed for the simulations in water, the solute–ethanol energy component (and the corresponding energy range explored) is larger for curcumin than in the case of piperine.

Although similar behavior regarding the solute–solvent energy components can be observed in Fig. S6 (ESI†) for the simulation with the solvent mixture, it is worth noting that the solute–solute interaction tends to explore a larger range of energies when the dimer is formed. This is particularly apparent for the CEK–CEK dimer and it may be attributed to the presence of ethanol molecules in the first solvation shell that are expected to destabilize the dimer.

Concerning the solvent–solvent interaction, the differences in the relative values of the energy observed in Fig. S7 (ESI†) result essentially from the distinct number of solvent molecules employed in the simulations (cf. Tables S1 and S2, ESI†). Besides that, there are two interesting aspects that should be emphasized in Fig. S7 (ESI†). First, the amplitude of the energy interval spawned by the ethanol–ethanol interaction in the solvent mixture is smaller than in the simulations with pure ethanol. This may be rationalized by the fact that part of the ethanol molecules are somehow confined in the first solvation shell. Second, the average energy values calculated along the solvent-mixture simulation for the water–water, ethanol–ethanol, and water–ethanol interactions present oscillations that are not observed in the simulations with the pure solvents. Clearly, this is an indication of large imbalanced fluctuations of the number of ethanol and water molecules that can be exchanged between the bulky solvent and the first solvation shell.

To complement this information, we have also calculated the number of hydrogen bonds as a function of time for all pairs of solute molecules. The main results are shown in Fig. S8 (ESI†) for the simulations in water, ethanol, and the solvent mixture; in the case of the PIP–PIP interaction, however, no hydrogen bond can be formed, because piperine has no hydrogens bonded to oxygens or nitrogen. Conversely, heterodimers involving piperine (i.e., CEK–PIP, and CKK–PIP) show occasionally one hydrogen bond, since oxygen atoms of piperine may work as hydrogen acceptors. In the case of interactions involving both tautomers of curcumin, the formation of one (and, less frequently, two) hydrogen bond(s) is observed, and this is more likely to occur in water than in ethanol or in the solvent mixture. Nonetheless, most of the time during the simulations no hydrogen bond is formed between the two solute molecules; hence, it is not expected that solute–solute hydrogen-bonding could develop a relevant role on the dimer formation. In turn, the number of solute–solvent hydrogen bonds in Fig. S9 (ESI†), despite the large oscillation, does not appear to change significantly, on average sense, during the simulation time. Moreover, it is apparent from Fig. S9 (ESI†) that water (ethanol) is the solvent displaying a greater (smaller) number of hydrogen bonds along each simulation. Since the formation (dissociation) of a solute dimer preferentially occurs in water (ethanol), such phenomena can hardly be controlled by hydrogen bonding.

3.2 Self-aggregation of curcumin in water

In previous section, we observed that the formation of curcumin dimers is likely to occur in water, regardless the tautomeric species considered. Conversely, the formation of CEK–CEK, CEK–CKK and CKK–CKK dimers, as well as the aggregation of several curcumin molecules (see Fig. S10, ESI†), can hardly occur in ethanol.

To further investigate the self-aggregation of curcumin in water, we have carried out three simulations containing four solute molecules, i.e., 4CEK, 4CKK and 2CEK + 2CKK, respectively. The six RDFs and the corresponding solute–solute distances for the three simulations are displayed in Fig. 8. It is apparent from the plots of the distances that the aggregation of the four molecules does not occur simultaneously, but it is rather stepwise. Actually, a great delay is observed between the formation of a first dimer and the complete aggregation, which is particularly significant in the case of 2CEK + 2CKK (>150 ns); in contrast, the aggregation of four CEK molecules is the most rapid one, with the process ending up in the first ∼100 ns of the simulation.

Fig. 8 Simulations involving 4CEK molecules (panels a and d), 4CKK molecules (panels b and e) and 2CEK + 2CKK molecules (panels c and f) in water: RDFs (top panels) and inter-monomer distances (bottom panels). Key for colors inserted in the top panels also applies for the corresponding bottom panels.

It is also worth noting in Fig. 8 that most of the RDFs show a prominent peak at short distances, but there are other with two distinct maxima. This indicates that the relative position of different pairs of monomers may change even after the self-aggregation process, as it is apparent from the small oscillations of the distances in the bottom plots. Furthermore, the cluster analysis of the last part of the trajectory (where the aggregation is already complete) reveals that a stacked pile (both in parallel and anti-parallel orientation of the phenyl rings) arises as the most prevalent structure (29%) in the simulation with 4CEK molecules, whereas two motifs with similar probability are observed in the case of 4CKK (see Fig. 9). Indeed, one expects that stacking four planar CEK molecules should be easier than packing four V-shape CKK structures. Besides the structures displayed in Fig. 9, several other motifs (e.g., showing different orientations of the H1 and H15 atoms) could be found in the simulations, though with a lower frequency. Indeed, such aggregates are expected to be very fluxional, i.e., they are able to change frequently from one structure to another. Note also that we had to fix at a larger value the cutoffs for the RMSD of the cluster analysis of the 4CKK simulation in order to get a relative small number of distinct structures; this is less acute for the other two simulations.

Fig. 9 Most representative structures of 4CEK (panel a), 4CKK (panels b and c) and 2CEK + 2CKK (panels d and e) obtained by cluster analysis of the MD trajectories performed in water. Frequencies of appearance of the represented structures (in %) for a given RMSD cutoff (values in parentheses): (a) 29% (0.19 nm), (b) 23% (0.35 nm), (c) 18% (0.35 nm), (d) 11% (0.15 nm), and (e) 5% (0.15 nm). The H1 atoms are displayed in green color, while H15 in curcumin are in magenta.

3.3 Heterogeneous curcumin–piperine aggregation

We have also investigated the influence of piperine on the self-aggregation of curcumin in aqueous media by running simulations for PIP and either CEK or CKK tautomers. For that, we have carried out the simulations 2CEK + 2PIP and 2CKK + 2PIP (cf. Section 2.1); similar simulations with the same solute molecules in ethanol were also performed for comparison (see Fig. S11 of the ESI†). In Fig. 10, we represent the RDFs and the inter-monomer distances as a function of time for the two simulations in water. It is apparent from this figure that the highest RDF peak corresponds to the CEK–CEK (PIP–PIP) interaction for the 2CEK + 2PIP (2CKK + 2PIP) simulation. The CEK–CEK peak was expected from the strong interaction observed for the dimer, but the PIP–PIP one is, in some way, surprising since a very stable dimer could hardly be formed (cf. Section 3.1). Such effect might be a result of the concomitant aggregation of a CKK molecule to the PIP–PIP dimer, which can be observed from the two distance-plots of the 2CKK + 2PIP simulation. Thus, the strong CKK–PIP interaction seems to work as a “glue” for the PIP–PIP aggregation. A similar behavior is also found in the 2CEK + 2PIP simulation, where the formation of the CEK–CEK dimer drags a nearby PIP molecule to the cluster.

Fig. 10 2CEK + 2PIP (top panels) and 2CKK + 2PIP (bottom panels) simulations in water: RDFs (panels a and d) and inter-monomer distances (panels b, c, e and f). The inserts in panels b and e highlight the variation of the distances between alike monomers in the last part of the trajectory.

Moreover, the complete aggregation of the four molecules occurs in less than 100 ns, but the monomers in the cluster appear to have a certain mobility during the remaining part of the trajectory, as highlighted by the non-negligible variation of the inter-monomer distances represented in the inserts of Fig. 10 (panels b and e). However, the mobility of the molecules in the cluster may be better perceived by looking at the variation of the distances between the H1 atoms (labelled with green color in Fig. 3) of different monomers, as displayed in Fig. S12 of the ESI.† A certain oscillatory behavior of those distances indicates that H1 atoms of different monomers come closer and farther away from each other from time to time, thus, pointing out to a sliding motion over the cluster, without affecting its integrity. This was confirmed by the visual inspection of the corresponding trajectory movies and it is sketched through the frames represented in Fig. 11. Indeed, the relative orientation of H1/H18 atoms of PIP change from the CEK–PIP dimer at 3 ns until the formation of the first tetramer at 76 ns; the formation of a totally stacked structure occurs slightly latter, i.e., at 77 ns. Also the result of the trajectory cluster-analysis in Fig. S13 (ESI†) indicates that a totally stacked structure with two CEK monomers in the middle is the prevalent motif (19%). A second most important structure (frequency of 10%), with a piperine molecule standing transversal to the pile, is another signature of structural arrangements occurring after the complete aggregation. In turn, the structure of the cluster formed in the 2CKK + 2PIP simulation tends to fit the planar PIP molecules in the concave part of V-shape CKK monomers, which then preferentially forms a cage containing the PIP–PIP dimer. Such structural motif takes about 100 ns or even more to arise in the simulation (cf.Fig. 11). Although the cage structure is by far the most prevalent one, a panoply of other shapes with non-negligible probability are apparent in the cluster analysis of Fig. S13 (ESI†). Because of this, we may conclude that the mobility of monomers after complete aggregation leads to more pronounced structural changes during the 2CKK + 2PIP simulation than for the case of 2CEK + 2PIP.

Fig. 11 Trajectory frames representing the main stages until the aggregation of the four monomers in the (a) 2CEK + 2PIP and (b) 2CKK + 2PIP simulations in water. For the latter, beyond 162 ns, the structure alternates between A and B. Key for colors: CEK (yellow), CKK (orange) and PIP (dark grey); H1 atoms are displayed in green, while the H15 (H18) ones of curcumin (piperine) are in magenta. The corresponding simulation time is represented for each frame.

In order to investigate whether the main structure of the cluster depends on the type of dimer that is precursor of the aggregation, we have performed four additional simulations beginning with one dimer already formed. Thus, we have carried out two 2CEK + 2PIP simulations (one beginning with CEK–CEK dimer and the other with PIP–PIP dimer) and two 2CKK + 2PIP simulations (one beginning with CKK–CKK dimer and the other with PIP–PIP dimer), whose main results are displayed in Fig. 12. From the comparison between the inter-monomer distances in this figure with the corresponding ones in Fig. 10, we conclude that the pre-formation of a dimer tends to delay the complete aggregation. Then, it appears that inducing a certain order in the nucleation process leads to additional rearrangements of the monomers already aggregated, so that the capture of the remaining solute molecules is not immediately favored. Furthermore, we observe in Fig. 12 that the main structures tend to be distinct from those obtained in the aggregation of randomly distributed monomers (Fig. S13, ESI†). The only exception is the formation of the CKK–CKK cage structure containing a stacked PIP–PIP dimer (panel b of Fig. 12), which is the prevalent motif as it was also the case for the simulation departing from randomly distributed monomers (panel c of Fig. S13, ESI†). When departing from the PIP–PIP dimer, however, each one of the CKK monomers preferentially surround one PIP rather than forming the cage with the stacked PIP molecules (see panel d of Fig. 12). Also totally stacked structures are no more prevalent in the simulations involving CEK monomers. Actually, the main structure is composed by a PIP monomer stacked over the initial CEK–CEK dimer and the remaining PIP molecule standing essentially perpendicular to the pile, which is similar to the second most prevalent motif in the aggregation from the corresponding randomly distributed monomers (panel b of Fig. S13, ESI†). In the simulation beginning with the PIP–PIP dimer, the main structure has the CEK–CEK and PIP–PIP dimers oriented in transversal positions (panel c of Fig. 12).

Fig. 12 2CEK + 2PIP (panels a, e, and panels c, g) and 2CKK + 2PIP (panels b, f, and panels d, h) simulations starting with one dimer already formed in water (i.e., at t = 0), as indicated by the initial structures on the top. Panels a–d show the most representative structures obtained by cluster analysis; the frequencies of appearance of the represented structures in the respective trajectories are: (a) 65%; (b) 16%; (c) 55%; (d) 69%. RMSD cutoffs are (in nm): 0.3 (panels a, e and d), 0.20 (panels b, e and c). Key for colors in the aggregates: CEK (yellow), CKK (orange) and PIP (dark grey); H1 atoms in each molecule are displayed in green, while H15 (H18) atoms in curcumin (piperine) are in magenta. Panels e–h display the corresponding inter-monomer distances as a function of the simulation time: CUR1–PIP1 (green), CUR1–PIP2 (purple), CUR1–CUR2 (orange), PIP1–PIP2 (black), CUR2–PIP1 (red), CUR2–PIP2 (blue).

Finally, we look at the effect of using a (30 : 70) solvent mixture on the joint aggregation of curcumin (either CEK or CKK) and piperine. For that, we have run two simulations whose results are reported in Fig. 13. Regarding the simulation of 2CEK + 2PIP in the (30 : 70) solvent mixture, we observe from Fig. 13 that CEK–CEK dimer is likely to be formed, even though it can dissociate and reform from time to time. We further note that other dimers can be also formed during the simulation, but complete aggregation is only achieved in a small time interval. Clearly, this indicates a certain degree of instability of the formed aggregate due to the presence of the ethanol molecules. Such type of behavior (and even enhanced) is also observed in Fig. 13 for the simulation of 2CKK + 2PIP in the (30 : 70) solvent mixture. In this case, however, the formation of CKK–PIP dimers are the most likely to occur during the simulation, while the CKK–CKK dimer appears to be quite unstable.

Fig. 13 Simulations of 2CEK + 2PIP (panels a–c) and 2CKK + 2PIP (panels d–f) in the (30 : 70) solvent mixture: RDFs for pairs of solute molecules (panels a and d) and the corresponding inter-monomer distances (panels a, c, e, and f). Monomers are labelled as CEK1, CEK2, CKK1, CKK2, PIP1, and PIP2. Key for colors are inserted in the panels.

4 Conclusions

We have employed MD simulations to carry out a detailed investigation of the aggregation of both curcumin and piperine in polar media. Water, ethanol and a mixture of both have been considered for the solvent. In the case of curcumin, both enol and keto tautomers have been studied. In agreement with previous experimental results, the present MD study shows that curcumin presents low solubility in water, since dimers can be formed after few nanoseconds of simulation and do not dissociate until the end of the trajectory. Conversely, piperine dimers that eventually form in aqueous solution do not last for a long time, thus confirming the experimental evidence of having greater solubility than curcumin. Actually, the atom–atom RDFs in water show that a relevant interaction can be established between the oxygen atom of the carbonyl group of piperine and the hydrogens of water, which may contribute to the larger solubility of this solute in comparison to curcumin.

Regarding the aggregation of curcumin in water, we have observed that the most frequent dimer motifs are mainly linear (for CEK–CEK) or V-shaped (for CKK–CKK) stacked structures. In the case of the CEK–CKK dimer, the most likely structure corresponds to the CEK monomer fitted in the concave part of CKK. In turn, the aggregation of a large number of CEK monomers also tends to form stacked motifs, whereas V-shaped stacks, accompanied by concave-fitted monomers, have been the structures mostly observed in the simulations with several CKK molecules. The aggregation of a mixture of CEK and CKK monomers in water leads to more complex structures where, nonetheless, stacked motifs and concave-fitted monomers are still apparent.

Due to the carbon chain of ethanol, this solvent can easily separate the two molecules forming the dimer. Actually, we have observed in the MD simulations that any dimer rapidly dissociates in a solution of ethanol. Even a small amount of ethanol (30% in a binary mixture with water) has shown to reduce significantly the stability of those dimers. In such a solvent mixture, the first solvation shell is mainly occupied by ethanol molecules that tend to turn the carbon chain to the solute dimers, while the hydroxyl group can establish hydrogen bonds with the external water molecules located in the second solvation shell. Nonetheless, a few water molecules may appear in the first solvation shell, mostly in the neighborhood of the oxygen atoms of the curcumin molecules.

The addition of piperine to curcumin in an equimolar aqueous solution does not prevent the joint aggregation. In contrast, the complete aggregation in a mixture of water and ethanol is only achieved in a small time interval. Given the ability of both CEK and CKK to capture a piperine monomer, it is even possible that the total aggregation of 2CEK + 2PIP and 2CKK + 2PIP might occur in a shorter time period than simulations of 4CEK and 4CKK. The aggregation of 2CEK + 2PIP tends to form stacked motifs, with the CEK–CEK dimer preferentially in the middle of the stack, while 2CKK + 2PIP leads to cage structures of two CKK molecules that embrace the PIP–PIP dimer. Nonetheless, the present simulations indicate that such structures may depend on which dimer is formed at first. For instance, the prior formation of the PIP–PIP dimer leads to more complex structures of the aggregate. Moreover, prior formation of specific dimers makes the total aggregation to occur during a longer time period than in the case of initial random distribution of curcumin and piperine monomers.

Despite the formation of prevalent motifs in the simulations with several monomers in water, it becomes clear from the present study that all the arising structures are quite fluxional, i.e., showing a sliding motion of the monomers over the cluster. Such motion, however, does not destroy the integrity of the aggregates that keep non-dissociated until the end of the simulation. Conversely, the interaction of the aggregates with the molecules of a solvent like ethanol (even in a small amount) can amplify the above mentioned sliding motion so that the dissociation becomes possible.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the support from the Coimbra Chemistry Centre (CQC-IMS), which is financed by the Portuguese “Fundação para a Ciência e a Tecnologia'” (FCT) through the Project UIDB/00313/2020, co-funded by COMPETE2020-UE. We are also grateful for the provision of computational time in the supercomputer resources hosted at Laboratório de Computação Avançada, Universidade de Coimbra and Minho Advanced Computing Center (projects references: CPCA_A2_7081_2020 and CPCA_A2_7083_2020). This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology).

Notes and references

1. S. S. Bharat, B. Aggarwal and Y.-J. Surh, The Molecular Targets and Therapeutic Uses of Curcumin in Health and Disease, Springer, US, 2007.
2. K. Beyer, F. Nikfarjam, M. Butting, M. Meissner, A. König, A. Ramirez Bosca, R. Kaufmann, D. Heidemann, A. Bernd, S. Kippenberger and N. Zöller, J. Cancer, 2017, 8, 1271–1283.
3. E. Schraufstätter and H. Bernt, Nature, 1949, 164, 456–457.
4. Z. Hussain, H. E. Thu, M. W. Amjad, F. Hussain, T. A. Ahmed and S. Khan, Mater. Sci. Eng., C, 2017, 77, 1316–1326.
5. A. C. da Silva, P. D. de Freitas Santos, J. T. do Prado Silva, F. V. Leimann, L. Bracht and O. H. Gonçalves, Trends Food Sci. Technol., 2018, 72, 74–82.
6. Q.-Q. Yang, A. K. Farha, G. Kim, K. Gul, R.-Y. Gan and H. Corke, Trends Food Sci. Technol., 2020, 97, 341–354.
7. P. Anand, A. B. Kunnumakkara, R. A. Newman and B. B. Aggarwal, Mol. Pharmaceutics, 2007, 4, 807–818.
8. N. Dhillon, B. B. Aggarwal, R. A. Newman, R. A. Wolff, A. B. Kunnumakkara, J. L. Abbruzzese, C. S. Ng, V. Badmaev and R. Kurzrock, Clin. Cancer Res., 2008, 14, 4491–4499.
9. C. Mohanty, M. Das and S. K. Sahoo, Expert Opin. Drug Delivery, 2012, 9, 1347–1364.
10. R. Wang, J. Han, A. Jiang, R. Huang, T. Fu, L. Wang, Q. Zheng, W. Li and J. Li, Int. J. Pharm., 2019, 561, 9–18.
11. A. Sehgal, M. Kumar, M. Jain and D. Dhawan, Food Chem. Toxicol., 2011, 49, 3002–3006.
12. I. Gülseren, A. Guri and M. Corredig, Food Funct., 2014, 5, 1218–1223.
13. Y. Shen, A. Farajtabar, J. Xu, J. Wang, Y. Xia, H. Zhao and R. Xu, J. Chem. Thermodyn., 2019, 131, 410–419.
14. R. Lv, X. Zhang, R. Xing, W. Shi, H. Zhao, W. Li, A. Jouyban and W. E. Acree, J. Chem. Thermodyn., 2022, 167, 106718.
15. K. Hu, X. Huang, Y. Gao, X. Huang, H. Xiao and D. J. McClements, Food Chem., 2015, 182, 275–281.
16. S. Chen, Q. Li, D. J. McClements, Y. Han, L. Dai, L. Mao and Y. Gao, Food Hydrocolloids, 2020, 99, 105334.
17. A. Puiggalí-Jou, P. Micheletti, F. Estrany, L. J. del Valle and C. Alemán, Adv. Healthcare Mater., 2017, 6, 1700453.
18. S. Mondal, S. Ghosh and S. P. Moulik, J. Photochem. Photobiol., B, 2016, 158, 212–218.
19. Y. Manolova, V. Deneva, L. Antonov, E. Drakalska, D. Momekova and N. Lambov, Spectrochim. Acta, Part A, 2014, 132, 815–820.
20. D. Karataş, A. Tekin, F. Bahadori and M. S. Çelik, J. Mater. Chem. B, 2017, 5, 8070–8082.
21. S. Manimaran, K. SambathKumar, R. Gayathri, K. Raja, N. Rajkamal, M. Venkatachalapathy, G. Ravichandran and C. Lourdu EdisonRaj, Nat. Prod. Bioprospect., 2018, 8, 369–390.
22. A. Nag, P. Chakraborty, G. Natarajan, A. Baksi, S. K. Mudedla, V. Subramanian and T. Pradeep, Anal. Chem., 2018, 90, 8776–8784.
23. M. Kakarala, D. E. Brenner, H. Korkaya, C. Cheng, K. Tazi, C. Ginestier, S. Liu, G. Dontu and M. S. Wicha, Breast Cancer Res. Treat., 2010, 122, 777–785.
24. V. Sharma, B. Nehru, A. Munshi and A. Jyothy, Methods Find. Exp. Clin. Pharmacol., 2010, 32, 227–232.
25. P. Rinwa and A. Kumar, Brain Res., 2012, 1488, 38–50.
26. G. Shoba, D. Joy, T. Joseph, M. Majeed, R. Rajendran and P. S. S. R. Srinivas, Planta Med., 1998, 64, 353–356.
27. B. Shao, C. Cui, H. Ji, J. Tang, Z. Wang, H. Liu, M. Qin, X. Li and L. Wu, Drug Delivery, 2015, 22, 740–747.
28. S. Alshehri, N. Haq and F. Shakeel, J. Mol. Liq., 2018, 250, 63–70.
29. V. M. Patil, S. Das and K. Balasubramanian, J. Phys. Chem. A, 2016, 120, 3643–3653.
30. F. Traxler, J. Schinnerl and L. Brecker, Monatsh. Chem., 2020, 151, 325–330.
31. R. Wang, J. Han, A. Jiang, R. Huang, T. Fu, L.-C. Wang, Q. Zheng, W. Li and J. Li, Int. J. Pharm., 2019, 561, 9–18.
32. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
33. J. Wang and T. Hou, J. Comput. Chem., 2011, 32, 3505–3519.
34. L. F. Martins, M. C. B. Parreira, J. P. P. Ramalho, P. Morgado and E. J. Filipe, Fluid Phase Equilib., 2015, 396, 9–19.
35. E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliot, Living J. Comput.l Mol. Sci., 2019, 1, 6324.
36. S. von Bülow, J. T. Bullerjahn and G. Hummer, J. Chem. Phys., 2020, 153, 021101.
37. J. R. C. Santos, P. E. Abreu and J. M. C. Marques, J. Mol. Liq., 2021, 340, 117106.
38. J. Zhou and P. Ranjith, J. Colloid Interface Sci., 2021, 585, 250–257.
39. E. Sneha, A. Revikumar, J. Y. Singh, A. D. Thampi and S. Rani, J. Mol. Graphics Modell., 2020, 101, 107764.
40. Z. Lou and M. Yang, Comput. Fluids, 2015, 117, 17–23.
41. T. C. Lourenço, L. G. Dias and J. L. F. Da Silva, ACS Appl. Energy Mater., 2021, 4, 4444–4458.
42. J. Wang and T. Hou, J. Chem. Theory Comput., 2011, 7, 2151–2165.
43. H. Wang, S. Yang and B. Wei, Chem. Phys. Lett., 2012, 539–540, 30–34.
44. L. Wu, L. Chen and H. Sun, Mol. Simul., 2017, 43, 510–518.
45. R. Bhowmik, S. Sihn, V. Varshney, A. K. Roy and J. P. Vernon, Polymer, 2019, 167, 176–181.
46. E. King, E. Aitchison, H. Li and R. Luo, Front. Mol. Biosci., 2021, 8, 712085.
47. Y. Xiang, R.-G. Xu and Y. Leng, J. Membr. Sci., 2022, 643, 120078.
48. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023.
49. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
50. F. Mustan, A. Ivanova, G. Madjarova, S. Tcholakova and N. Denkov, J. Phys. Chem. B, 2015, 119, 15631–15643.
51. M. J. Servis, B. Sadhu, L. Soderholm and A. E. Clark, J. Mol. Liq., 2022, 345, 117743.
52. Á. Piñeiro, J. Pipkin, V. Antle and R. Garcia-Fandino, J. Mol. Liq., 2021, 343, 117588.
53. L. X. Peng, L. Yu, S. B. Howell and D. A. Gough, J. Chem. Inf. Model., 2011, 51, 3030–3035.
54. S. T. Ngo, S.-T. Fang, S.-H. Huang, C.-L. Chou, P. D. Q. Huy, M. S. Li and Y.-C. Chen, J. Chem. Inf. Model., 2016, 56, 1344–1356.
55. R. M. de Souza, R. H. Ratochinski, M. Karttunen and L. G. Dias, J. Chem. Inf. Model., 2020, 60, 522–536.
56. F. Payton, P. Sandusky and W. L. Alworth, J. Nat. Prod., 2007, 70, 143–146.
57. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
58. H. Lindahl, M. J. Abraham and D. van der Spoel, GROMACS 2019 Source code, 2018.
59. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
60. J. Loschwitz, A. Jäckering, M. Keutmann, M. Olagunju, O. O. Olubiyi and B. Strodel, Data Brief, 2021, 35, 106948.
61. I. Doytchinova, M. Atanasova, E. Salamanova, S. Ivanov and I. Dimitrov, Biomolecules, 2020, 10, 1323.
62. T. D. Martin, A. J. Malagodi, E. Y. Chi and D. G. Evans, J. Phys. Chem. B, 2019, 123, 551–560.
63. P. Haris, V. Mary, M. Haridas and C. Sudarsanakumar, J. Chem. Inf. Model., 2015, 55, 2644–2656.
64. Q. Han, N. Wu, H.-L. Li, J.-Y. Zhang, X. Li, M.-F. Deng, K. Zhu, J.-E. Wang, H.-X. Duan and Q. Yang, J. Agric. Food Chem., 2021, 69, 7534–7544.
65. N. M. O’Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
66. M. W. Schmidt, K. K. Baldridge, J. A. Boats, S. T. Elbert, M. S. Gorgon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. Montgomery, Jr., J. Comput. Chem., 1993, 14, 1347.
67. F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, N. G. R. Lelong, D. Lelong, W. Rosanski and P. Cieplak, Phys. Chem. Chem. Phys., 2010, 12, 7821–7839.
68. A. W. S. Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367.
69. J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
70. D. Alvarez-Garcia and X. Barril, J. Med. Chem., 2014, 57, 8530–8539.
71. H. J. C. Berendsen, in Computer Simulations in Material Science, ed. M. Meyer and V. Pontikis, Kluwer Academic Publishers, Dordrecht, 1991, pp.139–155.
72. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
73. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
74. B. Hess, H. Bekker, H. Berendsen and J. Fraaije, J. Comput. Chem., 1998, 18, 1463–1472.
75. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
76. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
77. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
78. M. Hazra, S. Roy and B. Bagchi, J. Chem. Phys., 2014, 141, 18C501.
79. A. Araiza-Calahorra, M. Akhtar and A. Sarkar, Trends Food Sci. Technol., 2018, 71, 155–169.
80. S. Alshehri, N. Haq and F. Shakeel, J. Mol. Liq., 2018, 250, 63–70.

---

Footnote

† Electronic supplementary information (ESI) available: (i) simulation-box specifications and atomic charges; (ii) details for the mixed-solvent box construction; (iii) atom-atom RDFs; (iv) movies of CEK–CEK and CKK–CKK dimers in ethanol; (v) details about the simulations with the (30 : 70) solvent mixture; (vi) energetic analysis in simulations with homodimers; (vii) solute-solute and solute-solvent hydrogen bonds in simulations with dimers; (viii) plots of the simulation of 2CEK + 2CKK in ethanol; (ix) additional plots from curcumin–piperine simulations. All input files required to reproduce the electronic structure calculations and MD simulations. See DOI: https://doi.org/10.1039/d3cp00096f

---